Frostbiteエンジンのコースノートの中でUnreal Engine 4のコースノートの引用がいくつかあったので,Unreal Engineの方も折角なので和訳しておこうと思います。
毎度のことながら,誤字・誤訳等が多々ありますので,予めご了承ください。
また,誤訳をご指摘頂ける場合は,正しい翻訳例と共にご指摘頂けると幸いです。
ちなみにFrostbiteエンジンのコースノートの和訳は以下になります。
- 超雑訳 Moving Frostbite to Physically Based Rendering 2.0(1)
- 超雑訳 Moving Frostbite to Physically Based Rendering 2.0(2)
- 超雑訳 Moving Frostbite to Physically Based Rendering 2.0(3)
- 超雑訳 Moving Frostbite to Physically Based Rendering 2.0(4)
- 超雑訳 Moving Frostbite to Physically Based Rendering 2.0(5)
- 超雑訳 Moving Frostbite to Physically Based Rendering 2.0(6)
- 超雑訳 Moving Frostbite to Physically Based Rendering 2.0(7)
- 超雑訳 Moving Frostbite to Physically Based Rendering 2.0(8)
※図は,Brain Karis, “Real Shading in Unreal Engine 4”,
SIGGRAPH 2013 Course:Physically Based Shading in Theory and Practice, p.1 より引用
Introduction
約一年前,我々はいつかシェーディングモデルを改善するのと,より物理べースのマテリアルワークフローを利用することに投資することを決めました。これはより現実味のある画像を描画したいという部分的な衝動によるものでしたが,マテリアル作成のより物理ベースへのアプローチとマテリアルレイヤーリングの使用を通じて達成できることにもまた関心がありました。アーティストはこれは巨大なワークフローと品質の向上であるということを感じており,そして私は全てに別のスタジオで直接これらの利益を見ていました,そのスタジオではオフラインでコンポジットされたマテリアルレイヤーへと移行していました。Epic においてテクニカルアーティストの1人がシェーダ内で期待できる十分な結果をもつレイヤリングを行う実験をし,これが追加の要求となりました。
この目標をサポートするために,我々はマテリアルのレイヤリングがシンプルで効率的にするために必要ということが分かりました。ちょうどよいタイミングで物理ベースシェーディングとシュガーラッシュに対して使用されたマテリアルモデルに関係のある Disney のプレゼンテーション[2]がやってきました。Brent Burley はオフライン向け映画レンダリングについて十分洗練された非常に小さなマテリアルパラメータセットであることをデモンストレーションしました。また彼は極めて実践的なシェーディングモデルで多くのサンプルされたマテリアルにしっかりと適合することを示しました。彼らの研究は我々に対するインスピレーションと基礎になっており,彼らの”指針”のように我々自身が持つシステムについての目標を定めました:
Real-Time Performance
● まず第一に,一度に表示可能な大量のライトを使用するために効率的である必要があります。
Reduced Complexity
● 可能な限り少ないパラメーターとすべきです。大きなパラメータ配列は結果として,決定麻痺,試行錯誤,あるいは単一の意図した効果のために多くの値を変える必要がある相互連結したプロパティのいずれになります。
● イメージベースドライトと,解析的な光源は相互に使用できるようにする必要があり,そのため,パラメーターはライトタイプのすべてに渡って一貫性した反応を示さなければなりません。
Intuitive Interface
● 屈折率のような物理的なものと対比して,単純で理解しやすい値が好ましいです。
Perceptually Linear
● マスクを通じたレイヤリングをサポートすることを切望しますが,ピクセルごとに一回のみのシェードを可能にします。これが意味するのは,パラメータブレンドされたシェーディングはシェードされた結果をブレンディングすることと可能な限りきっちりと合致しなければなりません。
Easy to Master
● 透過物体と不透明物体の技術的な理解を必要とすることを回避したいです。同様に,物理的に妥当な基本マテリアルを生成するために必要とされる労力も最小限にしたいです。
Robust
● 物理的に妥当なマテリアルを誤って作成するのを困難にすべきです。
● パラメータの組み合わせすべては可能な限り頑健で妥当性があるべきです。
Expressive
● 我々が保持するのが可能なシェーディングモデルの数をディファードシェーディングは制限するので,基本シェーディングモデルは実世界に存在するマテリアルの99%をカバーために十分に分類できる必要があります。
● レイヤー可能なマテリアルのすべてはそれらをブレンドするために同じパラメータセットを共有する必要があります。
Flexible
● 他のプロジェクトとランセンシーは同じフォトリアリズムの目標を共有できない恐れがあり,そのためノンフォトリアリスティックレンダリングを十分に可能にする柔軟性が必要です。
Shading Model
Diffuse BRDF
Burleyのディフューズモデルを評価しましたが,Lambertianディフューズ(式1)と比べて小さな変化のみしか見れず,そのため我々は追加コストを正当化できませんでした。さらに,任意のより洗練されたディフューズモデルはイメージベースドライティングあるいは球面調和ライティングで効率的に使用するのが難しいです。結果として,我々はその他の選択を評価することに努力を注ぎませんでした。
\[
f({\bf l}, {\bf v}) = \frac{{\bf c_{\rm diff}}}{\pi} \tag{1}
\]
ここで,\({\bf c_{\rm diff}}\) はマテリアルのディフューズアルベドです。
Microfacet Specular BRDF
一般的な Cook-Torrance[5,6] マイクロファセットスペキュラーシェーディングモデルは次になります:
\[
f({\bf l}, {\bf v}) = \frac{D({\bf h}) \, F({\bf v}, {\bf h}) \, G({\bf l}, {\bf v}, {\bf h})}{4 \, ({\bf n} \cdot {\bf l})({\bf n} \cdot {\bf v})} \tag{2}
\]
このコースのかなり細かいことについては[9]を参照してください。
我々は Disney モデルで開始し,各項をより効率的な代替のものと比較し重要性を評価しました。これは聞くよりもかなり難しいです;各項について発表された式は正確な比較に不可欠な同じ入力パラメータを使用する必要性はありません。
Specular D
法線分布関数(NDF)について,我々は Disney の GGX/Trowbridge-Reitz の選択がコストに合うものであると分かりました。Blinn-Phong を使用する以上の追加のコストはかなり少なく,そしてはっきりと異なり,ロング”テール”によって生み出される自然な見た目はアーティストを引き付けました。また我々は \(\alpha = Roughness^2\) という Disney の再パラメータ化を適用しました。
\[
D({\bf h}) = \frac{\alpha^2}{\pi(({\bf n} \cdot {\bf h})^2 (\alpha^2 – 1) + 1)^2} \tag{3}
\]
Specular G
他のどのオプションよりもスペキュラー幾何減衰項について多くのオプションを評価しました。最終的に,Schlickモデル[19]を使用するのを決めましたが,\(k = \alpha/2\) であり,そのため GGX に対する Smith モデル[21]をより良く適合します。この修正で,Schlick モデルは \(\alpha = 1\) についての Smith に正確に一致し,範囲[0, 1]について極めて近い近似となります(図2に示します)。また我々は2乗する前に \(\frac{Roughness + 1}{2}\) を用いてラフネスを再マッピングすることによって”ギラギラさ”を減らすために Disney の修正を使用する選択をしました。この調整は解析的な光源にのみ使用されるということに注意することが重要です; イメージベースドライティングを適用する場合,視射角における結果はあまりにも暗くなりすぎます。
\begin{eqnarray}
k = \frac{(Roughness + 1)^2}{8} \\
G_1({\bf v}) = \frac{{\bf n} \cdot {\bf v}}{({\bf n} \cdot {\bf v})(1 – k) + k} \\
G({\bf l}, {\bf v}, {\bf h}) = G_1({\bf l}) \, G_1({\bf v}) \tag{4}
\end{eqnarray}
Specular F
フレネルについて,Schlick の近似[19]を使用する典型的な選択をしましたが,小さな変更を持ちます:指数を置き換えるために球面ガウシアン近似[10]を使用します。計算するがわずかに効率的で,違いは微小です。式は次になります:
\[
F({\bf v}, {\bf h}) = F_0 + (1 \, – \, F_0) 2 ^{(-5.55473({\bf v} \cdot {\bf h}) – 6.98316({\bf v} \cdot {\bf h}))} \tag{5}
\]
ここで,\(F_0\) は垂直入射におけるスペキュラーリフレクタンスです。
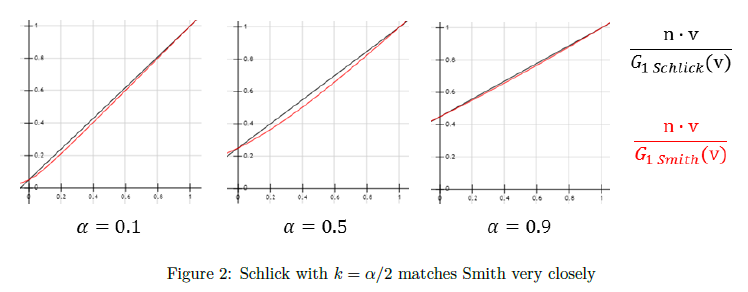
※図は,Brain Karis, “Real Shading in Unreal Engine 4”, p.4 より引用
Image-Based Lighting
イメージベースドライティングでこのシェーディングモデルを使用するために,放射輝度積分を解く必要があり,それは重点サンプリングを用いてなされます。以下の式はこの数値的な積分を説明しています:
\[
\int_H L_{i}({\bf l}) f({\bf l}, {\bf v}) \cos \theta_{\bf l} {\rm d}{\bf l} \approx \frac{1}{N} \sum^N_{k = 1} \frac{L_i({\bf l}_k) f({\bf l}_k, {\bf v}) \cos \theta_{{\bf l}_k}}{p({\bf l}_k, {\bf v})} \tag{6}
\]
以下のHLSLコードは我々のシェーディングモデルでこれを行う方法を示しています:
00001: float3 ImportanceSampleGGX( float2 Xi, float Roughness , float3 N ) 00002: { 00003: float a = Roughness * Roughness; 00004: 00005: float Phi = 2 * PI * Xi.x; 00006: float CosTheta = sqrt( (1 - Xi.y) / ( 1 + (a*a - 1) * Xi.y ) ); 00007: float SinTheta = sqrt( 1 - CosTheta * CosTheta ); 00008: 00009: float3 H; 00010: H.x = SinTheta * cos( Phi ); 00011: H.y = SinTheta * sin( Phi ); 00012: H.z = CosTheta; 00013: 00014: float3 UpVector = abs(N.z) < 0.999 ? float3(0,0,1) : float3(1,0,0); 00015: float3 TangentX = normalize( cross( UpVector , N ) ); 00016: float3 TangentY = cross( N, TangentX ); 00017: // Tangent to world space 00018: return TangentX * H.x + TangentY * H.y + N * H.z; 00019: } 00020: float3 SpecularIBL( float3 SpecularColor , float Roughness , float3 N, float3 V ) 00021: { 00022: float3 SpecularLighting = 0; 00023: 00024: const uint NumSamples = 1024; 00025: for( uint i = 0; i < NumSamples; i++ ) 00026: { 00027: float2 Xi = Hammersley( i, NumSamples ); 00028: float3 H = ImportanceSampleGGX( Xi, Roughness , N ); 00029: float3 L = 2 * dot( V, H ) * H - V; 00030: 00031: float NoV = saturate( dot( N, V ) ); 00032: float NoL = saturate( dot( N, L ) ); 00033: float NoH = saturate( dot( N, H ) ); 00034: float VoH = saturate( dot( V, H ) ); 00035: 00036: if( NoL > 0 ) 00037: { 00038: float3 SampleColor = EnvMap.SampleLevel( EnvMapSampler , L, 0 ).rgb; 00039: 00040: float G = G_Smith( Roughness , NoV, NoL ); 00041: float Fc = pow( 1 - VoH, 5 ); 00042: float3 F = (1 - Fc) * SpecularColor + Fc; 00043: 00044: // Incident light = SampleColor * NoL 00045: // Microfacet specular = D*G*F / (4*NoL*NoV) 00046: // pdf = D * NoH / (4 * VoH) 00047: SpecularLighting += SampleColor * F * G * VoH / (NoH * NoV); 00048: } 00049: } 00050: 00051: return SpecularLighting / NumSamples; 00052: }
重点サンプリングでも,実行するためにまだ多くのサンプルが必要です。サンプル数はミップマップ[3]によって著しく減少することが可能ですが,十分な品質のために16以上の数が必要になります。ローカルリフレクションのためにピクセルごとに多くの環境マップをブレンドするので,それぞれに対して実質的に単一サンプルに与えることのみができます。
Split Sum Approximation
これを達成するために,上記の2つの総和へと分解することによって(式7)総和を近似します。各分解した総和は事前計算することが可能です。この近似は定数\(L_i({\bf l})\)については正確であり,一般的な環境についてほとんど正確です。
\[
\frac{1}{N} \sum^N_{k=1} \frac{L_i({\bf l}_k) f({\bf l}_k, {\bf v}) \cos \theta_{{\bf l}_k}}{p({\bf l}_k, {\bf v})} \approx \left( \frac{1}{N} \sum^N_{k=1} L_i({\bf l}_k) \right) \left( \frac{1}{N} \sum^N_{k=1} \frac{f({\bf l}_k, {\bf v}) \cos \theta_{{\bf l}_k}}{p({\bf l}_k, {\bf v})} \right) \tag{7}
\]
Pre-Filtered Environment Map
異なるラフネス値に対する最初の総和を事前計算し,キューブマップのミップマップレベル内に結果を格納します。これはゲーム業界の多く[1,9]で使用される代表的なアプローチです。小さな違いの1つのは重点サンプリングを用いたシェーディングモデルが GGX 分布を持つ環境マップを畳み込みするということです。従ってマイクロファセットモデルなので,分布の形状はサーフェイスに対する視野角に基づいて変化します。そのため,この角度がゼロ,すなわち\({\bf n} \, = \, {\bf v} \, = \, {\bf r}\) を仮定しています。この等方性の仮定は近似の2つ目のソースになり,残念なことにグレージング角における非常に長い反射を得ることができないということを意味しています。分離した近似を比較すると,これは実際には IB Lの解法について誤差の大きな源になります。以下のコードに示すように,\(\cos \theta_{{\bf l}_k}\) によって重みづけすることによってより良い結果を達成することがわかりました。
00001: float3 PrefilterEnvMap( float Roughness , float3 R ) 00002: { 00003: float3 N = R; 00004: float3 V = R; 00005: 00006: float3 PrefilteredColor = 0; 00007: 00008: const uint NumSamples = 1024; 00009: for( uint i = 0; i < NumSamples; i++ ) 00010: { 00011: float2 Xi = Hammersley( i, NumSamples ); 00012: float3 H = ImportanceSampleGGX( Xi, Roughness , N ); 00013: float3 L = 2 * dot( V, H ) * H - V; 00014: 00015: float NoL = saturate( dot( N, L ) ); 00016: if( NoL > 0 ) 00017: { 00018: PrefilteredColor += EnvMap.SampleLevel( EnvMapSampler , L, 0 ).rgb * NoL; 00019: TotalWeight += NoL; 00020: } 00021: } 00022: 00023: return PrefilteredColor / TotalWeight; 00024: }
Environment BRDF
2つ目の総和は他のすべてを含んでいます。これはソリッドホワイトの環境,すなわち \(L_i({\bf l}_k) = 1\) を持つスペキュラー BRDF を積分することと同等です。Schlick のフレネル近似を置き換えすることにより,つまり,\(F({\bf v}, {\bf h}) = F_0 + (1 \, – \, F_0)(1 \, – \, {\bf v} \cdot {\bf h})^5\) で,\(F_0\)が積分の外に因数分解することができるということが分かりました:
\[
\int_H f({\bf l}, {\bf v}) \cos \theta_{\bf l} {\rm d}{\bf l} = F_0 \int_H \frac{f({\bf l}, {\bf v})}{F({\bf v}, {\bf v})} \left( 1 \, – (1 – {\bf v} \cdot {\bf h})^5 \right) \cos \theta_{\bf l} {\rm d}{\bf l} + \int_H \frac{f({\bf l}, {\bf v})}{F({\bf v}, {\bf h})} (1 – {\bf v} \cdot {\bf h})^5 \cos \theta_{\bf l} {\rm d}{\bf l} \tag{8}
\]
2つの入力(\(Roughness\) と\(\cos \theta_{\bf v}\))と2つの出力(スケールと\(F_0\)へのバイアス)を経て,それらのすべては都合良く範囲[0, 1]内になります。この関数の結果を事前計算し,2次元のルックアップテクスチャ(LUT)に格納します。
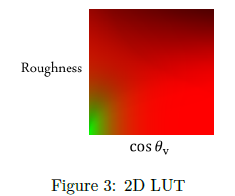
※図は,Brain Karis, “Real Shading in Unreal Engine 4”,
SIGGRAPH 2013 Course:Physically Based Shading in Theory and Practice, p.6 より引用
この作業が完了した後で,ほぼ同じ解決策につながる既存および同時研究を発見しました。五反田は3次元 LUT[8]を使用する一方で,Drobot は2次元 LUT へとこれを最適化し[7],我々が行った方法とほぼ同じです。さらに―このコースのパートとして― Lazarov は類似した積分について解析的な近似を結び付けて表すことによってさらに進んだことを行っています[11]。
00001: float2 IntegrateBRDF( float Roughness , float NoV ) 00002: { 00003: float3 V; 00004: V.x = sqrt( 1.0f - NoV * NoV ); // sin 00005: V.y = 0; 00006: V.z = NoV; // cos 00007: 00008: float A = 0; 00009: float B = 0; 00010: 00011: const uint NumSamples = 1024; 00012: for( uint i = 0; i < NumSamples; i++ ) 00013: { 00014: float2 Xi = Hammersley( i, NumSamples ); 00015: float3 H = ImportanceSampleGGX( Xi, Roughness , N ); 00016: float3 L = 2 * dot( V, H ) * H - V; 00017: 00018: float NoL = saturate( L.z ); 00019: float NoH = saturate( H.z ); 00020: float VoH = saturate( dot( V, H ) ); 00021: 00022: if( NoL > 0 ) 00023: { 00024: float G = G_Smith( Roughness , NoV, NoL ); 00025: float G_Vis = G * VoH / (NoH * NoV); 00026: float Fc = pow( 1 - VoH, 5 ); 00027: A += (1 - Fc) * G_Vis; 00028: B += Fc * G_Vis; 00029: } 00030: } 00031: 00032: return float2( A, B ) / NumSamples; 00033: }
最終的に,重点サンプリングされたリファレンスを近似するために,事前計算された総和を乗算します:
00001: float3 ApproximateSpecularIBL( float3 SpecularColor , float Roughness , float3 N, float3 V ) 00002: { 00003: float NoV = saturate( dot( N, V ) ); 00004: float3 R = 2 * dot( V, N ) * N - V; 00005: 00006: float3 PrefilteredColor = PrefilterEnvMap( Roughness , R ); 00007: float2 EnvBRDF = IntegrateBRDF( Roughness , NoV ); 00008: 00009: return PrefilteredColor * ( SpecularColor * EnvBRDF.x + EnvBRDF.y ); 00010: }
※図は,Brain Karis, “Real Shading in Unreal Engine 4”,
SIGGRAPH 2013 Course:Physically Based Shading in Theory and Practice, p.8 より引用
※図は,Brain Karis, “Real Shading in Unreal Engine 4”,
SIGGRAPH 2013 Course:Physically Based Shading in Theory and Practice, p.8 より引用
Material Model
我々のマテリアルモデルは視線をリアルタイムレンダリングのために効率性を目的とした,Disney のものを単純化したモデルです。パラメータの数を制限することは G-Buffer のスペース,テクスチャストレージの削減,そしてアクセスを最適化するのに極めて重要で,ピクセルシェーダにおいてマテリアルレイヤーのブレンディングのコストを最小化します。
以下が我々の基本マテリアルモデルです:
BaseColor
単一色。理解するのがより容易な概念です。
Metallic
透明物体のリフレクタンスと不透明のリフレクタンスを理解する必要はなく,そのため誤差の余地がより少ないです。
Roughness
その意味は非常に明確です,一方で光沢は常に説明する必要があります。
Cavity
小規模のシャドウイングに対して使用されます。
BaseColor,Metallic,そしてRoughness は Disney のモデルと同様ですが,Cavity パラメータは述べられていません,そのため説明するのがふさわしいです。Cavity はランタイムシャドウイングシステムが処理可能ものよりも小さいジオメトリ由来のシャドウイングを指定するために使用し,大抵法線マップ上に表現されるのみのジオメトリのためです。例としては床板あるいは布の縫い目の間の隙間です。
最も注目すべき切り捨ては Specular パラメータです。実際には我々は Infiltrator デモの完成までは使用していましたが,最終的には好ましくありませんでした。まず第一に,我々は”スペキュラー”がやっかいなパラメータ名で,多くの混乱を引き起こし,アーティストがスペキュラー強度を制御することからRoughness を制御することへの移行するのに若干障害となりました。アーティストとグラフィックスプログラマーは同じように一般的にその範囲を忘れ,実際のデフォルトが Burley の 0.5(反射率の4%に相当)であるときに,デフォルトが 1 であると仮定します。これは Specular が効果的に使用されるケースでほとんどもっぱら小さなスケールのシャドウイングのためです。屈折率(IOR)の値が非金属についてほとんど重要でないことがわかったので,そのため最近はスペキュラーをより理解しやすいCavityパラメータに置き返しました。非金属の \(F_0\) は現在定数0.04です。
以下のDisneyモデルからのパラメータは我々の基本マテリアルに採用する選択をせず,代わりに特別ケースとして取り扱います:
Subsurface
異なるシャドウマップをサンプルします。
Anisotropy
多くのIBLサンプルを必要とします。
Clearcoat
2倍のIBLサンプルを必要とします。
Sheen
Burleyのノートにうまく定義されていません。
Elemental デモにおける氷に対して使用された Subsurface を除いて作品上でこれらの特別ケースのモデルは使用されていません。更に,スキンについて特別なシェーディングモデルを持っています。将来,特化されたシェーディングモデルをより多くサポートするために我々はハイブリッドのディファード/フォワードシェーディングアプローチを適用することを考えています。現在純粋なディファードシェーディングアプローチで,異なるシェーディングモデルはG-Buffer上に格納されたシェーディングモデル id から動的分岐で処理されます。
Experiences
数回見てきたある状況があります。アーティストにラフネス変化を使用するのに移行を始めるを伝え,”スペキュラーカラーを使用してきたのと同じようにラフネスを使ってください”,そしてすぐ後に興奮と驚きをもって聞きました:”もうやってる!” しかし,興味深いコメントが後に続きました:”ラフネスは逆になった感じがする”。アーティストがスペキュラーハイライトを明るくするのと同等にテクセルをより明るくするものとして彼らが書くテクスチャーを見たいということが判明しました。画像にラフネスを保存する場合,明るさは粗さに同等のとき,より激しさが少ないハイライトにつながります。
数えきれない数受ける質問は”メタリックはバイナリですか?”で,もともとは混合やレイヤードマテリアルの頭にいれて説明しました。単に”はい!”というのが最も良いということを学びました。その理由はアーティストは開始時に絶対的にパラメータを設定するのが消極的ということです;非常に共通するのは 0.8 の値のメタリックを持つ金属を見つけることでしょう。次に説明されるマテリアルレイヤーは 0 または 1 のどちらかでメタリックでない場合の 99% を説明するための方法にすべきです。
もはや再現できないマテリアルの形式上で,移行の間いくつかの問題がありました。Epic において現在作成中のゲーム Fortnite 由来の最も重要な設定です。Fortnite は非写実的なアートの方向性を有しており,意図的にディフューズとスペキュラーリフレクタンスに対して補色を使用しており,物理的に妥当でなく,新しいマテリアルモデルにおいて表現できないものです。長い議論の後で,先の開発であったため Fortnaite における品質を維持するためにエンジンが切り替えられるようにディフューズカラー/スペキュラーカラーのサポートを継続を決定しました。しかしながら,シュガーラッシュ上での Disney の使用により証明されたように非写実的なレンダリングを不可能にする新しいモデルを好きだと思えません。そのため,将来のプロジェクトのすべてについて使用できるように意図しました。
Material Layering
共有ライブラリから供給されるマテリアルレイヤーをブレンディングすることは我々の前のアプローチに数多くの利益を提供し,各指定されたモデルについてオーサされたテクスチャからの値で個々のパラメータを指定します:
● 数多くのアセットの至る所で作品を再利用します。
● 単一のアセットに対する複雑性を減らします。
● ゲームの見た目を定義するマテリアルの統一化と集中化をし,より簡単にアートと技術の方向付けを可能とします。
完全にこの新しいワークフローを受け入れるために、我々のツールを再考する必要がありました。Unreal Engine は UE3 の寿命を早めるためノードグラフベースのマテリアルエディタを特色としました。このノードグラフは入力(テクスチャ,定数),操作,そして出力を指定し,シェーダコードへとコンパイルされます。
マテリアルレイヤリングの主な目的はこの作業の多くのためでしたが,驚くべきことにオーサリングとマテリアルレイヤーをブレンディングをサポートするためにツール側へ追加する必要があるものは非常に少なかったです。UE4 のマテリアルエディタにおけるノードグラフのセクションは既に関数へとグループされており,複数のマテリアルから使用されます。この機能性はマテリアルレイヤーを実装する際に違和感なく適用されます。システム上の固定化された関数としての代わりにノードベースエディタ内でマテリアルレイヤーを保持し,プログラム可能な方法でマップされることと組み合わせることのためのレイヤーを可能にします。ワークフローを効率化するために,マテリアルの出力のすべてを保持する新しいデータ型,マテリアル属性を追加しました。この新しい型は,その他の型のように,シングルピン,ワイヤーに沿ってパスされる,そして直接出力されるようなマテリアル関数の受け入れと受け渡すことができます。これらの変化で,以前のテクスチャと同じ方法で入力,組み合わせ,操作そして出力としてマテリアルレイヤーはドラッグイン可能です。実際には,マテリアルグラフの多くは特定マテリアルをカスタムするための主要なことはレイヤーがマップされるのとブレンドされる方法としてレイヤーの適用なのでより単純になる傾向があります。これは存在するために使用されるパラメータの特定操作よりもかなり単純になります。
知覚的に線形なマテリアルパラメータの小規模なセットを持つため,実際にシェーダ内で完全にレイヤーをブレンドすることは実用的です。これは純粋なオフラインコンポジットシステムを超える品質上の相当な増加を提供することを我々は感じています。テクスチャデータの明白な解像度は異なる周波数におけるデータをマップできるようにするためかなり高くなる可能性があります:頂点ごとあるいはテクスチャデータの低周波は一意になる可能性があり,ブレンドマスクのレイヤー,法線マップとしてキャビティマップはメッシュごとに指定され,そしてマテリアルレイヤーはメッシュのサーフェイスをまたいでタイル化されます。より高度な場合はさらに多くの周波数を使用可能性があります。我々はシェーダコストのため使用可能なレイヤー数を実質的に制限し,アーティストは問題のある制限をまだ見つけていません。
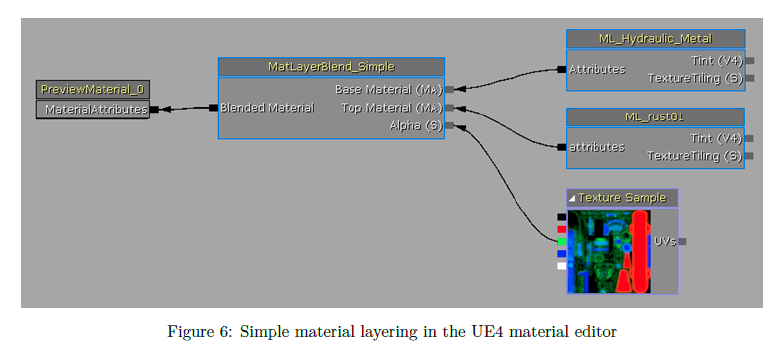
※図は,Brain Karis, “Real Shading in Unreal Engine 4”,
SIGGRAPH 2013 Course:Physically Based Shading in Theory and Practice, p.11 より引用
懸念事項を引き起こす領域は複数のセクションへとメッシュを分離することによって結果としてより多くのドローコールとなるシェーダ内のレイヤリング制限近辺で作業した場合におけるアーティストです。CPU 側のコード最適化のため UE4 におけるドローコール数はより良くなっていることを除きますが,これは将来に問題となる可能性があるように見えます。我々がまだ調査していない領域は 100% に近づくレイヤーをもつ範囲上のシェーダコストを減らすために動的ブランチを使用することです。
これまでのところ,マテリアルレイヤーで我々の経験はかなり有益になりました。生産性の向上と品質上の大きな改善の両方が見られました。我々は簡単に検索するのとレイヤーをプレビューすることによってアーティストのマテリアルのライブラリへのインタフェースを向上することを望んでいます。また,我々は,膨大な数のレイヤーとより良いスケーラビリティを提供するのをサポートするために現在のランタイムシステムに加えてオフラインのコポジット/ベイクシステムを調査する予定です。

※図は,Brain Karis, “Real Shading in Unreal Engine 4”,
SIGGRAPH 2013 Course:Physically Based Shading in Theory and Practice, p.11 より引用
※図は,Brain Karis, “Real Shading in Unreal Engine 4”,
SIGGRAPH 2013 Course:Physically Based Shading in Theory and Practice, p.12 より引用
Lighting Model
シェーディングと同じように,より物理ベースにすることによってライティングモデルを改善することを望みました。ライトのフォールオフと非パンクチュアルソースの放射に注目した2つの領域は一般的にエリアライトとして知られています。
ライトのフォールオフを改善することは比較的に単純です:物理的に正確な逆平方フォールオフを適用し,ルーメンの放射輝度単位に切り替えました。そうは言っても,この種のフォールオフ関数がゼロに到達する距離を持たないことを処理するある小さな複雑さを持ちます。しかし,リアルタイムとオフライン計算の両方についての効率性のため,我々はまだ人為的にライトの影響を制限する必要があります。これを達成するための多くの方法[4]がありますが,ライトの影響の大部分が比較的に影響を与えずに保つような方法で窓の逆平方関数を選択し,一方でまだゼロへの柔らかな転移を提供します。アート的にロックされたライティングを持つ際に重要になる可能性がある効果的な明るさを変化せずにライトの半径を調整することによって,これは良い性質を持ちますが,ライトの範囲はまだパフォーマンスの理由のために調整する必要があります。
\[
{\bf falloff} = \frac{{\rm saturate}(1 – (distance/lightRadius)^4)^2}{distance^2 + 1} \tag{9}
\]
分母の1は光源に近い距離において関数が破綻するのを妨げるためにあります。物理的な正確性が要求されない場合についてのアーティストが操作可能なパラメータを提示することが可能です。
特に,多くの局所照明を持つシーンにおけるこの単純な変化が作る品質の違いはお金を持ち去ることに対する最も大きなバンという音のようになることを意味しています。

※図は,Brain Karis, “Real Shading in Unreal Engine 4”,
SIGGRAPH 2013 Course:Physically Based Shading in Theory and Practice, p.13 より引用
Area Lights
面光源はより現実的な画像を生成だけでありません;それらは物理ベースマテリアルを使用するときにかなり重要です。不自然に見える極小のスペキュラーハイライトに結果としてなるため,面光源なしではアーティストは非常に低いラフネス値をペイントすることを直感的に避ける傾向があることがわかりました。本質的に,アーティストはパンクチュアルソースからエリアライトの効果を再現しようと試みました。
残念なことに,この反応はシェーディングとライティング間の結び付けを招き,物理ベースレンダリングの核となる原則の1つを破壊します:マテリアルは生成されたところから異なるライティング環境で使われる際に修正すべきではないです。
エリアライトは研究の活発な領域です。オフラインレンダリングにおいて,一般的な解決策は光源のサーフェイス上に多くの点からライトすることで,つまり,均一サンプリングまたは重点サンプリングのどちらかを使用することです[12][20]。これは完全にリアルタイムレンダリングについて実現困難です。以前に説明している可能な解決策は,ここでは要求となります:
● 一貫したマテリアルの見た目
- ディフューズBRDFとスペキュラーBRDFを持って評価されたエネルギー量は著しく異なることはできない。
● 立体角がゼロに近づくにつれてポイントライトモデルに近づく
- これを達成するためにシェーディングモデルのあらゆる側面を失いたくない。
● どこでも使用するのに十分高速
- 一方で,前述された”バイアスされたラフネス”問題を解くことができません。
Billboard Reflectsion
ビルボード反射[13]は離散光源について使用可能なIBLの形式です。放射された光を格納する2次元の画像は3次元空間に矩形へとマップされます。環境マップの事前フィルタリングと同じように,画像はスペキュラー分布コーンの異なるサイズについて事前フィルタされます。この画像からのスペキュラーシェーディングを計算することはコーントレーシングの形式として考えることができ,ここでは,コーンはスペキュラー NDF を近似します。コーンの中心におけるレイはビルボード平面と交差します。画像中の交差点はこのとき,テクスチャ座標として使用され,交差におけるコーンの半径は適切な事前フィルタされたミップレベルを得るために使用されます。悲しいことに,画像は容易な方法で非常に複雑なエリアライトを表現することができる一方で,ビルボード反射は複数の理由のため2番目の要件を満たすことができません:
● 画像は平面上で事前フィルタされます。そのため,制限された立体角は画像空間上で表現することができます。
● レイが平面と交差しないときはデータが存在しません。
● ライトベクトル \({\bf l}\) は未知あるいは反射ベクトルと仮定されます。
Cone Intersection
コーントレーシングは事前フィルタリングを必要としません;解析的に実行可能です。球に対してコーンをトレースした実験のバージョンは Oat のコーンとコーンの交差式[15]を用いることでしたが,実用するにはあまりにもコストが高すぎました。最近 Drobot によって提案された代替手法[7]はシェーディング点に面するディスクとコーンが交差します。NDF を近似する多項式は交差範囲についての区分積分となります。
Drobot の最近の進歩で,これは研究について興味深い領域になったように思われますが,現在の形式では,我々の要求を実現できません。コーンを使用するため,スペキュラー分布は放射上にシンメトリーでなければいけません。これは非常に重要なマクロファセットスペキュラーモデルの特徴である延ばされたハイライトを除外します。さらに,ビルボード反射のように,シェーディングモデルによって必要とされる定義されたライトベクトルが存在しません。
Specular D Modification
昨年に提案されたアプローチ[14]は光源の立体角に基づいてスペキュラー分布を調整することです。背後にある理論は一致するコーン角について\(D({\bf h})\)と同じ光源の分布を考慮することです。その他によってある分布を畳み込むことは新しいコーンを導出するためにコーン両方の角度を追加することによって近似を可能にします。これを達成するために,式3から\(\alpha\)を効果的なコーン角度へと変換し,光源の角度を追加し,逆変換します。この\(\alpha’\)は今,\(\alpha\)の代わりに使用されます。これを行うために以下の近似を使用します:
\[
\alpha’ = {\rm saturate}\left( \alpha + \frac{sourceRadius}{2 * distance} \right) \tag{10}
\]
効率的なものの,残念なことにこのテクニックは非常にグロッシーなマテリアルは大きなエリアライトでライティングするときに粗さが出現するので我々の最初の要件を実現しません。これは明らかに聞こえるかもしれませんが,スペキュラーNDFがコンパクトであるとき― Blinn-Phong が例です―にテクニックははるかに良い動作をし,したがって光源の分布により合致します。我々が選択したシェーディングモデル(GGX に基づく)について,実行可能ではありません。

※図は,Brain Karis, “Real Shading in Unreal Engine 4”,
SIGGRAPH 2013 Course:Physically Based Shading in Theory and Practice, p.15 より引用
Representative Point
特定のシェーディング点について,光源のサーフェイス上の単一の代表点としてエリアライトから来るすべての光を扱う場合に,我々のシェーディングモデルは直接使用することができます。理想的な選択は最も大きな寄与を持つ点です。Phong 分布について,これは反射レイへの最も小さな角度を持つ光源上の点となります。
このテクニックは以前に発表されました[16][22],しかしエネルギー保存に取り組むことはありませんでした。放射された光の原点を移動することによって,効果的にライトの立体角を増加しますが,追加エネルギーについて埋め合わせされません。それを補正することはエネルギーの差分がスペキュラー分布に依存するので立体角で除算するよりもわずかに複雑です。例えば,粗いマテリアルについての入射光の方向が変化することはエネルギー上で非常に小さな変化の結果となりますが,グロッシーなマテリアルについてエネルギー上の変化は極めて大きくなります。
Sphere Lights
スフィアライトについての放射照度はスフィアが水平より上である場合ポイントライトと等しくなります[18]。直感に反しているにもかかわらず,これは水平より下側にスフィアが下がる際の不正確性を受け入れる場合にスペキュラー照明を対処するためのみに必要とされるということを意味しています。我々はレイへの最短を距離を持つ点を見つけることによって反射レイへの最も小さな角度を持つ点を求めることを近似します。スフィアについてこれは分かりやすいです:
\begin{eqnarray}
{\bf centerToRay} &=& ({\bf l} \cdot {\bf r}) \, {\bf r} \, – \, {\bf L} \\
{\bf closestPoint} &=& {\bf L} + {\bf centerToRay} * {\rm saturate} \left( \frac{sourceRadius}{|{\bf centerToRay}|} \right) \tag{11} \\
{\bf l} &=& \|{\bf closestPoint}\|
\end{eqnarray}
ここで,\({\bf L}\) はシェーディング点からライト中心へのベクトルで,\(sourceRadius\) はライトスフィアの半径で,\({\bf r}\) は反射ベクトルです。レイがスフィアに交差する場合において,計算された点はスフィア中心へのレイ上の最近接点になります。一旦正規化すると,同一になります。
スフィアのサーフェイスへと放出される光の原点を移動することによって,我々はスフィアの定められた角度によって効果的にスペキュラー分布を広げます。マイクロファセット分布でないにも関わらず,これは正規化されたPhong 分布の最も良い使用方法と説明することができます:
\begin{eqnarray}
I_{point} = \frac{p + 2}{2\pi} \cos^p \phi_r \tag{12} \\
I_{sphere}
=
\begin{cases}
\frac{p+2}{2\pi} & {\rm if} \, \phi_r \lt \phi_s \\
\frac{p+2}{2\pi} \cos^p (\phi_r – \phi_s) & {\rm if} \, \phi_r \geq \phi_s
\end{cases} \tag{13}
\end{eqnarray}
ここで,\(\phi_r\) は \({\bf r}\) 間の角度で,\(\phi_s\) はスフィアの定めれた角度の半分です。\(I_{point}\) は正規化され,半球についての積分結果は 1 であることを意味しています。\(I_{sphere}\) はもはや,はっきりと正規化されず,指数 \(p\) に依存し,積分は大きくなる可能性があります。
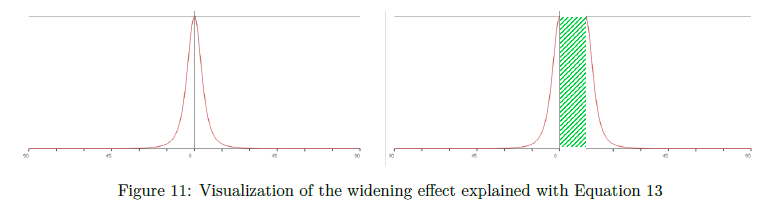
※図は,Brain Karis, “Real Shading in Unreal Engine 4”,
SIGGRAPH 2013 Course:Physically Based Shading in Theory and Practice, p.16 より引用
このエネルギー上の増加を近似するために,我々はライトの立体角に基づき分布を広げた先に説明したスペキュラー\(\rm D\) の修正によって使用されるのと同じ論法を適用します。より広い分布に対して正規化係数を使用し,元の正規化係数を置き換えます。GGX についての正規化係数は \(\frac{1}{\pi\alpha^2}\) となります。代表点操作についての正規化の近似を導出するためにオリジナルによって新しく広げられた正規化係数を除算します:
\[
{\rm SphereNormalization} = \left( \frac{\alpha}{\alpha’} \right) ^2 \tag{14}
\]
代表点手法の結果は我々の要求すべてに合致します。エネルギー保存を正確に処理することによって,マテリアルは同じ光源サイズにも関わらず振る舞います。グロッシーなマテリアルはまだシャープなエッジのスペキュラーハイライトを生み出し,BRDF への入力を修正するのみで,我々のシェーディングモデルは影響を受けません。最後に,アーティストが好むいたる場所で効率的に十分使用できます。
Tube Lights
スフィアライトは電球を表現する場所で有益で,チューブライト(カプセル)は実世界においてかなり一般的である蛍光灯を表現するに役立ちます。長さをもつチューブライトを解くことから始めますが,線形ライトしても知られるように半径ゼロです。線分について放射照度はセグメントが水平より上側にあるかぎり解析的に積分することが可能です[16,17]:
\[
\int^{{\bf L}_1}_{{\bf L}_0} \frac{{\bf n} \cdot {\bf L}}{|{\bf L}|^3} \, d{\bf L} = \frac{ \frac{{\bf n} \cdot {\bf L}_0}{|{\bf L}_0|} + \frac{{\bf n} \cdot {\bf L}_1}{|{\bf L}_1|} }{ |{\bf L}_0| |{\bf L}_1| + ({\bf L}_0 \cdot {\bf L}_1)} \tag{15}
\]
ただし,\({\bf L}_0\) と \({\bf L}_1\) はシェーディング点からセブメントの端点へのベクトルです。

※図は,Brain Karis, “Real Shading in Unreal Engine 4”,
SIGGRAPH 2013 Course:Physically Based Shading in Theory and Practice, p.17 より引用
我々は負の放射照度,ゼロ除算そして長さがゼロのときにポイントライトフォールオフに一致するを防ぐために,この式を修正します:
\[
{\rm irradiance} = \frac{2 * {\rm saturate} \left( \frac{{\bf n} \cdot {\bf L}_0}{2 |{\bf L}_0|} + \frac{{\bf n} \cdot {\bf L}_1}{2 |{\bf L}_1|} \right) }{ |{\bf L}_0| |{\bf L}_1| + (|{\bf L}_0| \cdot {|{\bf L}_1|} ) + 2} \tag{16}
\]
線形ライトスペキュラーについて以下の式において \(t\) について解く必要があります:
\begin{eqnarray}
\begin{split}
{\bf L}_d &=& {\bf L}_1 \, – \, {\bf L}_0 \\
{\bf l} &=& \|{\bf L}_0 + {\rm saturate}(t) {\bf L}_d \|
\end{split}
\tag{17}
\end{eqnarray}
Picott[16]は \({\bf r}\) への最も小さい角度に対する \(t\) が分かりました:
\[
t = \frac{ ({\bf L}_0 \cdot {\bf L}_d)({\bf r} \cdot {\bf L}_0) \, – \, ({\bf L}_0 \cdot {\bf L}_0)({\bf r} \cdot {\bf L}_d) }{({\bf L}_0 \cdot {\bf L}_d)({\bf r} \cdot {\bf L}_d) \, – \, ({\bf L}_d \cdot {\bf L}_d)({\bf r} \cdot {\bf L}_0) } \tag{18}
\]
スフィアの場合のように,もっとも小さいな角度を近似し,代わりに最短距離について解きます:
\[
t = \frac{({\bf r} \cdot {\bf L}_0)({\bf r} \cdot {\bf L}_d) – ({\bf L}_0 \cdot {\bf L}_d)}{|{\bf L}_d|^2 – ({\bf r} \cdot {\bf L}_d)^2} \tag{19}
\]
最近接点を常に見つけられないような適切に処理されていないエッジの場合が存在しますが,計算するのは多少安く,式18のような単に妥当な結果として生み出すように思われます。
式18と19の両方はレイの代わりに線として \({\bf r}\) を扱うので,線分から離れたところを指すレイを適切に処理する解決方法がないということに気づくことが重要です。これは反射レイがライトに向かって指すことから離れたところ指すことへと移行するときに発生します。計算された点と各端点との間で選択することによって対処することが可能ですが,これはコストが高いです。現時点では単にアーティファクトを受け入れます。
エネルギーを保存するために,スフィアライトに対して同じ概念を適用します。スペキュラー分布はライトの定めれた角度によって広げられますが,このとき1次元上のみで,そのために我々は GGX[2] の異方性版を使用します。異方性 GGX についての正規化係数は \(\frac{1}{\pi \alpha_x \alpha_y}\) で,ただし等方性における\(\alpha_x = \alpha_y = \alpha\) です。これは次を与えます:
\[
{\rm LineNormalization} = \frac{\alpha}{\alpha’} \tag{20}
\]
ライトの原点のみを変更し,エネルギー保存項を適用するため,これらの操作は蓄積可能です。線分とスフィアをもって行うことは,形状の畳み込みを近似し,チューブライトの振る舞いをかなりうまくモデルします。チューブライトの結果を図13に示します。

※図は,Brain Karis, “Real Shading in Unreal Engine 4”,
SIGGRAPH 2013 Course:Physically Based Shading in Theory and Practice, p.18より引用
エネルギー保存を持つ代表点手法はシンプルな形状に対して効果的であることが分かり,将来スフィアやチューブを凌駕するその他の形状に対して適用を考えています。実際には,より複雑で複数の色付けされた光源を表現するためにテクスチャ矩形へ適用を望んでいます。
Conclusion
シェーディングの領域,マテリアルとライティングにおいて,より物理ベースの実装への我々の移行は非常に成功したことが証明されました。最新の Infiltrator デモのビジュアルに非常に貢献し,将来のプロジェクトすべてについてこれらの改善を使用する予定です。実際に,この作業が開始する前に開発になったプロジェクト Fortnite へとこれらの実用的な変化は組み込まれました。我々はより大きな柔軟性の目標と様々なシーンのすべてとハードウェアのレベルすべてが物理ベースアプローチの利点を取ることが可能な目標を持つスケーラビリティを持つこれらの分野における改善を継続していきます。
Achknowledgementsの和訳は省略いたしますので,各自で原文に当たってください



