前回は,4.6 Sunまでを訳しました。
今回は,4.7 Area lightsと 4.8 Emissive surfacesを訳してみます。
毎度のことながら,誤訳等がありますので予めご了承ください。
間違いを指摘して頂ける場合は,正しい翻訳例と共にご指摘頂けると幸いです。
4.7 Area lights
実世界のライトは物理的な形状をすべて持つので,実世界のライティングに合致するために,物理ベースレンダリングにおいてエリアライトは重要となります。この形状は特に粗さにおいて,アーティストがサーフェイスのマテリアル特性を把握するのを容易にします。これまでは,パンクチュアルライトで,アーティストはサーフェイスの粗さを調整することによって極微小のスペキュラーハイライトを隠す傾向があり,これゆえライティングとマテリアルを一緒にしました。パンクチュアルソースは光源の良い近似になる可能性がありますが,状況に依存します(距離,関与媒体など)。後で見るように,エリアライトはIBLと概念的に近いので相互作用を緩和します。より重要なのは,エリアライトは柔らかなライティングを提供し,スペキュラーエイリアシングを減らすことです。
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.38 より引用
Frostbiteでは,エリアライトの異なる形状をサポートします:球,ディスク,チューブ,そして矩形です。エリアライトによって照明された点の発する輝度は次によって与えられます:
\[
L_{out} = \int_{\Omega+} f({\bf v}, {\bf l})\, V({\bf l})\, L_{in} \langle {\bf n} \cdot {\bf l} \rangle \, {\rm d}{\bf l} = \int_{\Omega_{\rm light}} f({\bf v}, {\bf l}) \, L_{in} \, \langle {\bf n} \cdot {\bf l} \rangle {\rm d}{\bf l} \tag{29}
\]
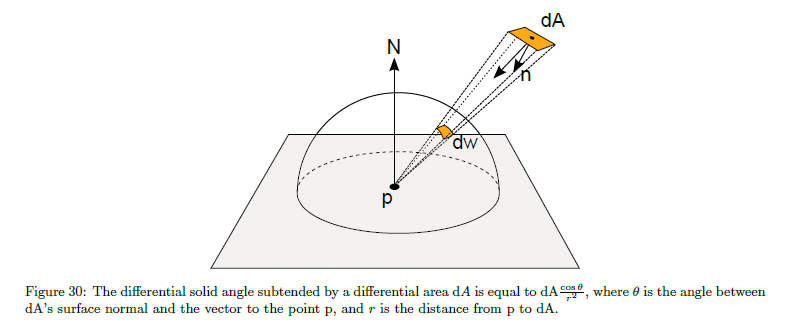
関数\(V\)はエリアライトがシェードポイントから到達可能である場合に1になり,そうでない場合は0になります。関数\(V\)はエリアライトの形状とそのシャドウの両方を考慮することができるようになります。このセクションでは,エリアシャドウは考慮しません。これはセクション4.10.4で説明します。したがって\(V\)はライトの形状の可視性のみを表現し,\(\Omega_{\rm light}\) はエリアライトに対する立体角です。この立体角についての積分は面積についての積分として再記述できます,図30を参照:
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.38 より引用
\[
L_{out} = \int_A f({\bf v}, {\bf l}) \, L_{in} \frac{\langle {\bf n} \cdot {\bf l} \rangle \langle n_a \cdot -l \rangle }{distance^2} \, {\rm d}A \tag{30}
\]
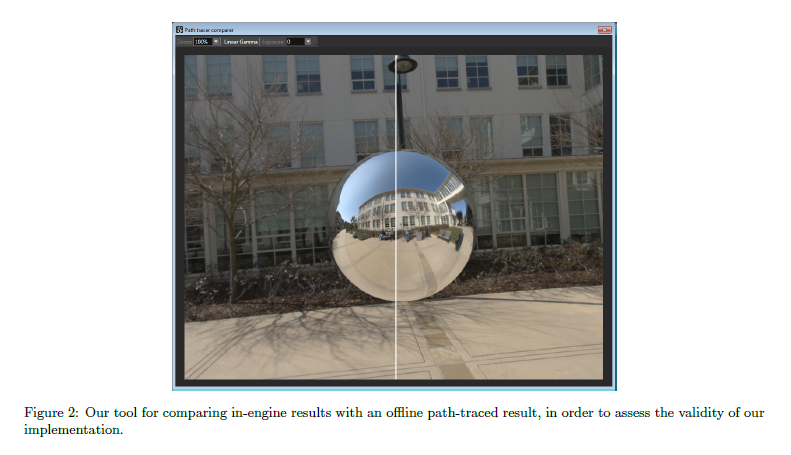
この式は解析解を常に持ちませんが,モンテカルロと重点サンプリングで数値的に積分することができます。セクション2で説明したようにエリアライトすべてを重点サンプルするエンジン内のリファレンスを実装しました。Appendix Aでコードを提示します。必然的に,この種の計算は制作物に対してあまりに高価であり,我々は近似を開発しました。エンジン内のリファレンスモードは近似の正確性をチェックするための計り知れない程貴重なツールになりました。
ディフューズライティングとスペキュラーライティングの積分は各エリアライトのタイプごとに個別に説明します:
\begin{eqnarray}
L_{out} &=& \int_{\Omega_{\rm light}} f_d({\bf v}, {\bf l}) \, L_{in} \, \langle {\bf n} \cdot {\bf l} \rangle \, {\rm d}{\bf l} &=& \int_A f_d({\bf v}, {\bf l}) \, L_{in} \frac{\langle {\bf n} \cdot {\bf l} \rangle \langle {\bf n}_a \cdot -{\bf l} \rangle}{distance^2} {\rm d}A \tag{31} \\
L_{out} &=& \int_{\Omega_{\rm light}} f_r({\bf v}, {\bf l}) \, L_{in} \, \langle {\bf n} \cdot {\bf l} \rangle \, {\rm d}{\bf l} &=& \int_A f_r({\bf v}, {\bf l}) \, L_{in} \frac{\langle {\bf n} \cdot {\bf l} \rangle \langle {\bf n}_a \cdot -{\bf l} \rangle }{distance^2} {\rm d}A \tag{32}
\end{eqnarray}
Remark:このドキュメント内で表現されたエリアライトは執筆時において製品に使われていません。30fpsのゲームを目標とするだけでなく,映画にも向けています。したがって,我々は非最適化バージョンのみを提供します。
4.7.1 Area light unit
物理的な光の単位で,エリアライトのサイズとそれらの強度は互いに結び付けられています。アーティストは2つの強度単位を選択することが可能です:
● Luminous power: 発光強度は,ルーメン(lm)で指定され,すべての方向にライトによって放射される可視光の総量を記述します。この量はライトの大きさに依存しません。ライトの大きさが増加することはシーンの照明レベルを変化させません。しかしながら,そのようなライトによって生成されるハイライトは同じ強度がより広い面積について分布するので面積が増加するにつれて薄暗くなります。図31の最初の行を参照してください。
● Luminance: 輝度は,ニト(\({\rm cd/m^2}\))で指定あるいは露出値(EV)で指定され,可視光のサーフェイス強度を記述します。この単位が使われるとき,ライトによって放射されるエネルギー総量は大きさに依存します。シーンにおける照明レベルは面積が増加するにつれて増えますが,そのようなライトによって生成されたハイライトは強度を一定に保ちます。図31の下段を参照して下さい。
実際にはエリアライトの設定としてアーティストはめったに輝度を使用しません。普通は表示としてディフューズサーフェイスについて全面にわたって放射する光であるのが適しています。
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.40 より引用
便宜上,ライティングの計算について体系的に強度を輝度へと変換します。任意の方向に放射されるLambertianの放射状の点のため照度は放射面積\(A\)によって除算された光度\(\phi\)と射影された立体角に等しくなります:
\[
L = \frac{\phi}{A \int_{\Omega+} \langle {\bf l} \cdot {\bf n} \rangle {\rm d}{\bf l} } = \frac{\phi}{A \pi} \tag{33}
\]
発光強度から輝度への変換に関する定式化は表12で示されます。EVから輝度への変換はセクション4.3で詳細に説明します。
※表は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.40 より引用
パンクチュアルライトが輝度の単位を持たない理由が今明確になりました。エリアライトについてライティングを計算するとき,効率的にライト範囲について積分を行い,輝度で取り扱いします。しかし,パンクチュアルライトは面積を持たず,ゆえに光度に依存します。しかしながら,Frostbiteでは,パンクチュアルとエリアライトは同じインターフェイスを共有します。この共通インタフェースをサポートするために,アーティストが強度を制御するために輝度単位を指定する場合,自動的にパンクチュアルライトを1cmの小さなエリアライトへと推進することにしました。この小さなハックはアーティストに対して見えないところで実行され意識する必要がなく,パンクチュアルとエリアライト間の遷移をスムーズにするために便利です。輝度単位は稀に使われ,したがって,このハックはパフォーマンスに害を与えることはありません。パンクチュアルライトとして考えられるべき線分と錘台ライトもまた複雑性のためエリアライトとして考慮されます。ですので,チューブあるいは矩形ライト各々からの違いはありません。
4.7.2 Diffuse area lights
4.7.2.1 General
最初に,Disney diffuse BRDFのケースを見る前に,Lambertian diffuse BRDF\(\frac{\rho}{\pi}\) に関するエリアライトの積分を解いてみます。エリアライトが均一で一定強度\(L_{in}\)を持つと仮定します。従って,式31からのディフューズライティングの積分は次のように再記述できます:
\[
L_{out} = \frac{\rho}{\pi} \int_{\Omega_{\rm light}} L_{in} \langle {\bf n} \cdot {\bf l} \rangle = \frac{\rho}{\pi} E(n) \tag{34}
\]
ここで照度\(E\)は次のように定義されます:
\[
E(n) = \int_{\Omega_{\rm light}} L_{in} \langle {\bf n} \cdot {\bf l} \rangle {\rm d}{\bf l} = \int_A L_{in} \frac{\langle {\bf n} \cdot {\bf l} \rangle \langle {\bf n}_a \cdot -{\bf l} \rangle}{distance^2} {\rm d}A \tag{35}
\]
セクション4.4においてみたように式13で照度を計算することに対する逆平方則はエリアライトに関して有効ではありません。ただし,このエリアライトがレシーバーのサーフェイスから十分に遠く離れている場合は除きます。セクション4.7.3を参照。ゆえに,エリアライトの照度を計算するために,式35を解く必要があります。
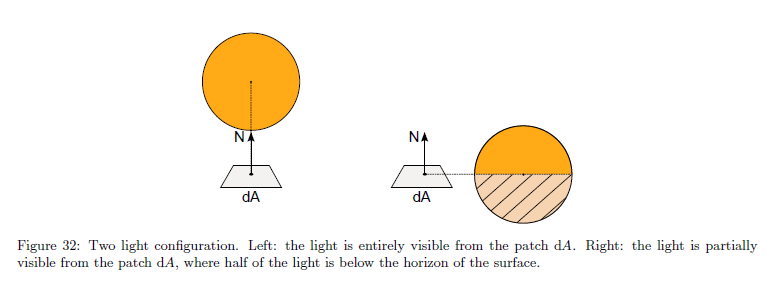
エリアライトは大きな立体角に及ぶ可能性があり,シェードされた点の下側に部分的に及ぶことさえあります。この場合において,エリアライトのライティングはオブジェクトをぐるりと包み,柔らかい見た目に結果としてなります。この”水平の場合”を正確に扱わずに,ラップされたライティング強度は不正確になり,もはやエリアライトによるライティングのように見えません。図32と33を参照してください。式35を解くために異なるいくつかの方法が存在します。それらの中には水平を横断しないシェードされた点からの小さな立体に対するエリアライトだけのものがあります。その他のものは水平な場合を処理しますが,不正確な強度を持ちます。次のセクションでは,正確な強度を持つ大きなエリアライトのケースを解くときに”正確な水平方向の取り扱い”としての方法を説明します。
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.41 より引用
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.42 より引用
Analytic integration: 積分は複雑ですが,いくつかの制約上では解析的な方法が存在します。幸いにも,種々雑多な設定についての解法と2つのその他の科学分野において利用できる光の種類があります: 光輸送と熱伝導です。光輸送において,ラジオシティシステムで使われた,良く知られている異なる面積 \(P_i\) と \(P_j\) 間のフォームファクターは次のように定義されます:
\[
{\rm FormFactor} = \int_{x \in P_i} \int_{y \in P_j} \frac{\cos \theta \cos \theta\,’}{\pi r^2}\, V(x, y) \,{\rm d}x {\rm d}y \tag{36}
\]
この方程式は式35の一般形です。別のサーフェイスによってシェードされるサーフェイスを扱う一方で,式35はサーフェイスによってシェードされる点を扱います。サーフェイスによってシェードされる点に関してラジオシティシステムによって様々な解決方法が提供されます。式内にLambert BRDF由来の\(\pi\)による除算が存在していることに注意してください。これは,我々の照度の定義は\(\frac{1}{\pi}\) の項を含まないので,キャンセルするために\(\pi\)によって定式化したフォームファクターに基づく解析解を乗算する必要があることを意味しているので重要です:
\[
E(n) = \int_{\Omega_{\rm light}}\, L_{in} \, \langle {\bf n} \cdot {\bf l} \rangle \, {\rm d}{\bf l} = L_{in}\, \pi\, {\rm FormFactor} \tag{37}
\]
放射輸送では,形態係数と呼ばれる同等の公式が存在します。形態係数は\(F_{a \rightarrow b}\)で記載され,サーフェイスAから出てサーフェイスBに衝突する放射の割合です。熱伝導の分野は様々なサーフェイスから点が受領する放射エネルギーに関する解析解の大規模な集合を提供します。簡略化のため,同じ公式を共有するので,たとえ同じセマンティックを持たないとしてもフォームファクターと形態係数の両方をフォームファクターとして呼ぶことにします。フォームファクターは正確な水平の扱いを伴う,あるいは無しで定式を持つ可能があります。球とディスクエリアライトについてフォームファクター法を採用することを選択しました。網羅性のため,Appendix Eで矩形ライトに関するものも提供されますが,我々はそれを導入しませんでした。フォームファクター表現の多くは複雑です。ここでは,式の再表現をするための選択をせず,コードリストに一致するもののみを提供しました。詳細については提示された参考資料を参照してください。
4.7.2.2 Sphere area lights
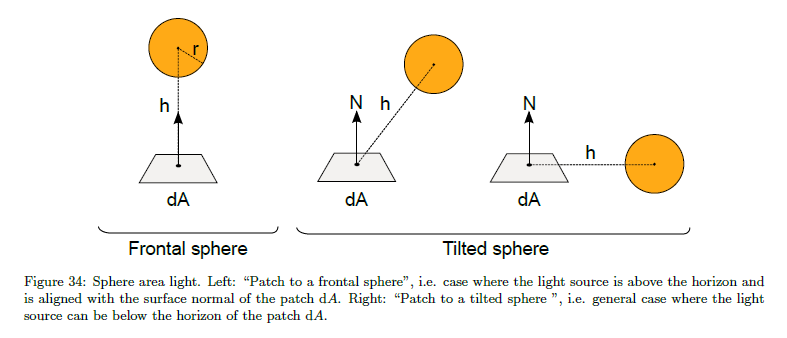
● Quilez[Quí06]は水平の場合を取り扱わない解法を提供しました。[Mar95]で提示された”正面の球への修正”に似ています。Quilezのバージョンはエリアライトの中心がサーフェイス法線に合致しない場合を取り扱うのを可能にするための\(\langle {\bf n} \cdot {\bf l} \rangle\)の追加要素を持ちます。しかしながら,水平より上側であることは不十分で,公式は水平より上側の立体角に対して小さなもののみ動作します。図36を参照。
● ”傾いた球への修正”の設定は[Mar95]で提供され,水平の場合を正しく取り扱います。別の式は[Sny96]のSnyderによって提供されています。
“正面の球への修正”と”傾いた球への修正”は図34で示されます。Quilezの式と”傾いた球への修正”はリスト7で報告され,結果は図35で示されます。
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.43 より引用
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.43 より引用
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.44 より引用
※リストは,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, pp.43-44 より引用
Remark: セクション4.7.1は光の強度単位を用いることで光の領域に非依存なレベルの照明を行うことを主張します。(一般性の損失なしで)水平方向の処理なしの定式を用いることによって,光強度\(\phi\)を持つスフィアエリアライトの照度は次で与えられます:
\[
E = L_{in}\, \pi \,\, {\rm FormFactor} = \frac{\phi}{4\pi^2r^2} \, \pi \, \frac{r^2}{d^2} \langle {\bf n} \cdot {\bf l} \rangle = \frac{\phi}{4 \pi d^2} \, \langle {\bf n} \cdot {\bf l} \rangle \tag{38}
\]
この式は式19のポイントライトの照度に合致し(\(\langle {\bf n} \cdot {\bf l} \rangle = 1\)を考慮しています),球の表面積に依存しません。またセクション4.4の実世界の計測に合致します。
4.7.2.3 Disk area lights
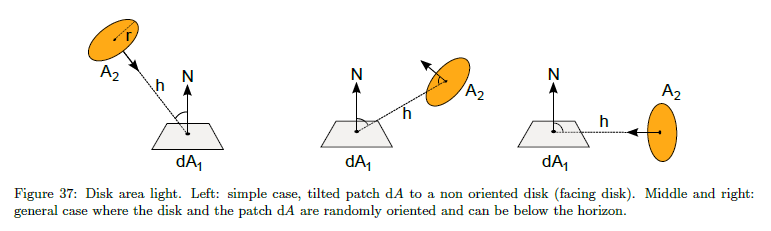
● Coombe[CH05]は指向性のディスクに対して正確な水平方向の取り扱いなしの解法を提案しました。球のように,水平より上側であることが十分でなく,水平よりも上側で制限された方向を持つ立体角に対して小さなもののみ式は動作します。
● 放射輸送カタログ[HSM10a]の設定[HSM10b]は水平の場合を正確に扱えますが,傾いた平面と無指向性ディスクに制限されます。図37を参照。ディスクの向きを考慮するために,\({\bf n}_{\rm light}\)のライト平面法線で,追加の\(\langle {\bf n}_{\rm light} \cdot -{\bf l} \rangle\)によって式を乗算します。この追加は立体角に対して小さく制限された方向内で水平より上側のリファレンスに合致するのを可能としますが,その他の場合において小さな相違を持ちます。我々の目的に対する結果は十分良いです。
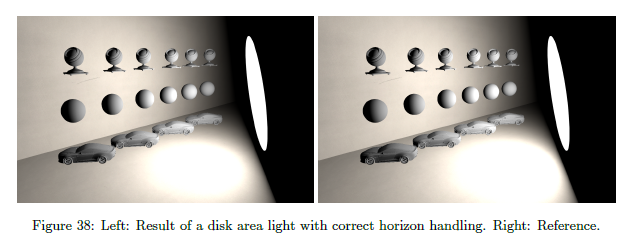
これらの2つの場合の式はリスト8で記載され,結果は図38で示されます。
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.45 より引用
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.45 より引用
※リストは,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, pp.45-46 より引用
Remark: スフィアライトとポイントライトの照度比較と同じように,ディスクとFrostbiteの一定の光の強度を持つスポットライトの照度式を比較しました。水平方向の取り扱いなしの定式を用いて(一般性の損失無しで),光の強度\(\phi\)を持つディスクエリアライトについての照度は次で与えられます
\begin{eqnarray}
E = L \, \pi \, {\rm FormFactor} &=& \frac{\phi}{\pi^2 radius^2} \, \pi \frac{radius^2}{distance^2 + radius^2} \langle {\bf n} \cdot {\bf l} \rangle \\
&=& \frac{\phi}{\pi \, distance^2 + \pi \, radius^2} \langle {\bf n} \cdot {\bf l} \rangle \tag{39}
\end{eqnarray}
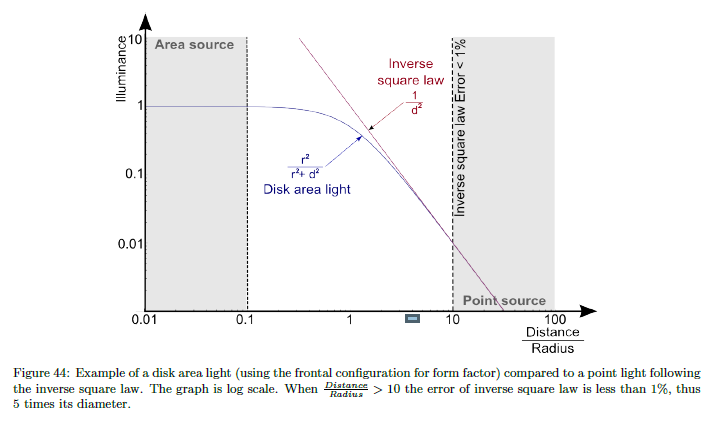
Frostbiteでは光の強度の単位の性質を再現するための目的でスポットライトに対する光の強度のための変換が選ばれました。この式と式21は密接で(\(\langle {\bf n} \cdot {\bf l} \rangle = 1\)を持つ),(半径が減り,追加の項が消えるので)あるものから別のものへとスムーズにフェードするのを可能とします,図39を参照してください。そのため,光の強度を持つ面積から独立している照明レベルの状態は我々の光強度の近似では完全に正確ではありませんが,十分にうまく動作することが分かりました。
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.46 より引用
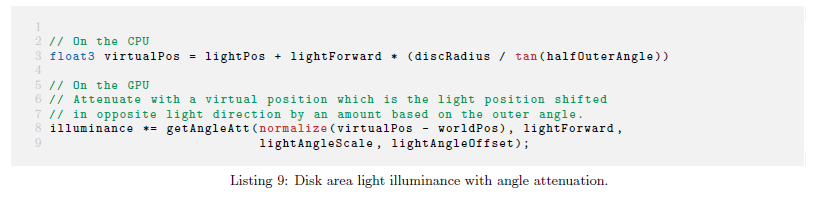
ディスクエリアライトはFrostbiteでのスポットライトに似ており,角度の減衰をサポートします。この角度の減衰は単純にスポットライトの平滑化と共に遷移を行うために任意の現実的な検討無しで照度に適用されます。角度の減衰はエリアライトに対するシャドウを計算する方法に似たライトの位置をフェイクすることによってスポットライトに関して同じ式を得ます。リスト9とセクション4.10.4を参照してください。
※リストは,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.47 より引用
4.7.2.4 Sphere and disk area lights merging
三角関数の恒等式と遊んだ後で,前のセクションと同様に正しい水平方向の取り扱いをする公式でスフィアとディスクエリアライトの両方を表現することが可能です。角度に対してのみ異なり,ゆえに評価コードを共有することが可能です。リスト10は詳細を含んでいます。高価な三角関数の逆関数はAMDのGCNアーキテクチャ上で効率的に近似することが可能です[Dro14c]。
※リストは,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, pp.47-48 より引用
4.7.2.5 Rectangular area lights
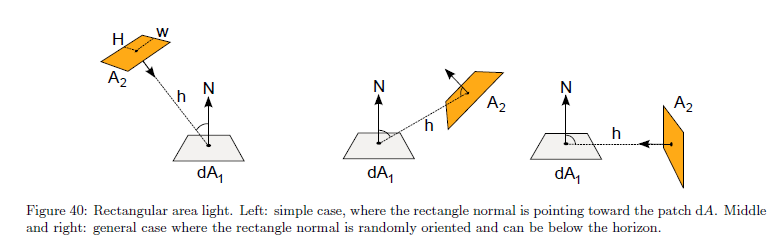
矩形ライトに関して水平方向を正しく扱った任意の手頃なフォームファクターの解法を見つけられませんでした。図40は異なる設定のハイライトです。従って,我々は代替手法を探しました。網羅性のため,Appendix Eに水平方向の処理なしでの矩形ライトに対するフォームファクターを提示しました。
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.48 より引用
Most representative point: Drobot[Dro14b]はライトの立体角によって重み付けされた単一表現可能なディフューズポイントライトで照度の積分を近似することを提案しました:
\[
E(n) = \int_{\Omega_{\rm light}} L_{in} \langle {\bf n} \cdot {\bf l} \rangle \, {\rm d}{\bf l} \, \approx \, \Omega_{\rm light} \, L_{in} \, \langle {\bf n} \cdot {\bf l} \rangle \tag{40}
\]
この近似は,小さな立体角についての有効です。\({\bf l}\) の良い選択で向上できる可能性があり,従って大きな立体角へと拡張できる可能性があります。\({\bf l}\) はシェードされた点から大多数の代表点(MRP)と呼ばれるエリアライト上の点へと向かう方向を示します。MRPはディフューズのライティング積分を行うときに最も高い値を持つ点です。ライト位置がMRPへと移動するので水平方向の場合を正確に処理する手法です。これは水平を考慮することによって立体角の計算を正確にすることを意味し,従ってこの立体角内でMRPを持ちます。残念なことに,これは負荷の高い操作です。立体角は以下の積分で計算することができます:
\[
\Omega_{\rm light} = \int_{\Omega+} V({\bf l}) \, {\rm d}{\bf l} = \int_{\Omega_{\rm light}} {\rm d}{\bf l} \tag{41}
\]
この式は\(L\)と\(\langle {\bf l} \cdot {\bf n}\rangle\)がない照度の積分に似ています。 フォームファクタよりも新しい類似手法で数値的か解析的のどちらかで解ける可能性があります。指向性の矩形の立体角に対する解析式は,水平方向の取り扱いは無いですが,[UFK13]によって提示されています。パフォーマンスの理由のため,Drobot[Dro14a]は指向性の矩形を配置する際に水平方向の取り扱いなしで正ピラミッド立体角[Pla]を使用することを提案しました。これらの立体角の式はリスト11に集約されます。Mathar[Mat14]は水平方向の処理を持つ常に面する矩形についての立体角の式を提示しましたが,あまりにも複雑であり,指向性の矩形を取り扱えません。
※リストは,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.49 より引用
MRPアプローチの品質は立体角の計算の正確さに依存します。残念なことに,水平の立体角を取り扱うことのコストは我々のリアルタイムの制限下では手頃に扱えません。したがって,代替手法を見つけました。改善したDrobotのMRPアプローチとAppendix Eで提示し,スクリーンショットの比較をAppendix Eで提示しました。
Structured sampling of the light shape:任意の関数について次のように記述できることが分かっています:
\[
\int_{\Omega} f(x) \, {\rm d}{\bf l} = \Omega \, {\rm Average} [f(x)] \tag{42}
\]
従って,定数\(L_{in}\)の仮定を持つと,次のように記述可能です:
\[
E(n) = \int_{\Omega_{\rm light}} L_{in} \langle {\bf n} \cdot {\bf l} \rangle {\rm d}{\bf l} = \Omega_{\rm light} L_{in} {\rm Average}[ \langle {\bf n} \cdot {\bf l} \rangle ] \tag{43}
\]
立体角について\(\langle {\bf n} \cdot {\bf l} \rangle\) の平均を求めることは容易ではありませんが,ライト位置の集合をうまく選択することで近似できます。リアルタイムの制約を念頭において,ライティング面の対象を最大化するライト位置集合\(N\)を選択することによって前述されているコサインの平均を選択します。矩形ライトの場合は,4角と中心を取ります:
\[
E(n) = \int_{\Omega_{\rm light}} L_{in} \langle {\bf n} \cdot {\bf l} \rangle \, \approx \, {\Omega_{\rm light}} \, L_{in} \, \frac{1}{N} \sum^{N}_{i=1} {\rm max}( \langle {\bf n} \cdot {\bf l}_i \rangle, 0 ) \tag{44}
\]
このアプローチの利点は,コサインをクランプすることで,面法線によって定義された正方向の半球上に位置する点を制限し,水平の立体角の取り扱いを暗黙的に可能とすることです。MRPのアプローチは最も重要な1つである,1つのサンプルを持つ積分を重点サンプリングすることに基づいています。この1つはライトの形状の知見に依存した積分の構造化サンプリングに基づいています。これは低い数に制限された積分であるときにより正確であることが証明されています[Dup+13]。
矩形のエリアライトに対してこの手法を適用し,水平方向での立体角の計算なしでラップされたライティングについての真の強度を持つことを可能とします。しかしながら,5サンプルのみ使用することによるアンダーサンプリングのためわずかに知覚できるバインディングアーティファクトが表に現れ,これは図41で示されます。コードはリスト12で提示されます。
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.51 より引用
※リストは,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.50 より引用
Remark: エリアライトの近似を開発するために,我々はMathematica上でフレームワークを作成しました(このドキュメントへのガイドファイルとして提供されます)。このフレームワークはここにおいてとAppendix Eで説明されるいくつかの手法についての様々な誤差推定を含んでいます。我々の経験から,正しいMRP(ブルートフォースによって決定される)と真の立体角を用いたとしても,MRPアプローチは我々のディフューズエリアライティングに対する構造化サンプリングのアプローチより正確性が低いです。
4.7.2.6 Tube area lights
Frostbiteでは,カプセル,すなわち各末端で2つの半球を持つ円柱としてチューブエリアライトは表現されます。図42を参照してください。フォームファクタあるいはカプセルに対する立体角を求めることは難しい問題で,リアルタイムの制限を持つことは適しません。我々は円柱と2つの半球へと分離することによってカプセルを近似する選択をし,前の結果を利用します:
● 円柱からの照度は円柱のサイズから生成された面する矩形ライトで近似します。
● 2つの半球からの照度はシェードされた点から円柱の軸への近接点に配置された級のフォームファクタによって近似されます。
● 両方の照度は最終的な照度を得るために加算されます。リスト13と図43を参照。
この分離と近似にも関わらず,結果は十分ground truthに近くなります。
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.52 より引用
※リストは,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.52 より引用
4.7.3 Five times rule
受信点からエリアライトが遠く離れているとき,逆平方則によって照度を近似することが可能です。照度についての一般的な経験則は5倍則です[Rye]:適用するために逆平方則について”光源までの距離が光源の最も大きな面積の5倍よりも大きくすべき”というものです。図44を参照。我々はディフューズエリアライトとレシーバーへの距離の性質に基づいた逆平方則をより単純にするため複雑な照度計算を最適化するためにこのルールを使用します。Frostbiteにおけるスフィアとディスクエリアライトについてのコード例をリスト14で提示します。このコードは実際には使用されていません。なぜかというと,これらの場合は単純で,既に角度に対する元来のコードのテストによって処理されているからです。矩形とチューブライトを取り扱うことはよりトリッキーでさらに深い研究が必要です。
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.53 より引用
※リストは,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.53 より引用
4.7.4 Diffuse area light with Disney’s diffuse
これまでの導出全てはLambertian BRDFについて行われました。しかし,マテリアルモデルのセクションで述べたように,我々の標準マテリアルはDisneyディフューズ項を使用します。解析的な手法はサポートされず,構造化サンプリングのアプローチにおいて各サンプルに対してモデルの評価を呼び出すことは負荷が高いです。それを取り扱うために,我々はLambertianエリアライトの照度に単一ライト方向に対するDisneyディフューズ評価を適用することを選択しました。
\[
L_{out} = f_d ({\bf v}, {\bf l}) \, E(n) \tag{45}
\]
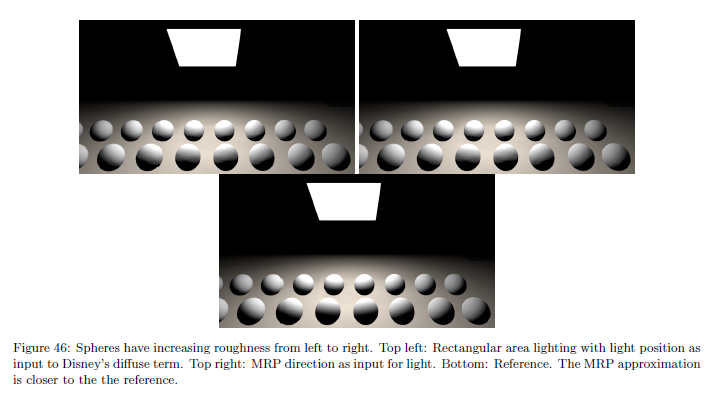
\({\bf l}\) について最も単純な選び方はライト位置を使用することです。いくつかのライトタイプについて,この近似は十分良いです。図45を参照。しかしながら,より良い選択方法はDrobotのアプローチにおいてのように大多数の代表点の方向を取ることです。図46参照。Frostbiteでは,パフォーマンスの理由によりDisneyディフューズ項に対する入力としてライト位置を使用しました。
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.54 より引用
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.54 より引用
BRDFローブの支配的な方向を考慮することによって,この近似を改善することが可能です。この支配的な方向の計算はセクション4.9.3でより詳細に説明します。我々は面法線のシフトによって,その方向を読み戻します。リスト15を参照してください。しかしながら,差分はあまりにも分からず,シェーダの負荷を減らすためにシフトを適用する選択をしませんでした。
※リストは,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, pp.54-55 より引用
4.7.5 Specular area lights
リアルタイム制限下でのスペキュラーエリアライトは本当に複雑な問題です。BRDFの入力数(視線ベクトル,f0,ラフネス)と矩形のような標準ライトの形状の1つ(幅,高さ,向き,非一定強度)は実行が難しいためライトプルーブと同様に事前計算を行います(セクション4.9を参照)。文献上で利用可能な現在の解法はGGXスペキュラーモデルについての基準との比較に耐えられません。DrobotのMRPアプローチ[Dro14b]はPhongモデルについてのみうまく動作し,Karisの反射レイ[Kar13]からの最短距離は良いエネルギー保存を欠損し,グレージング角においてうまく振る舞いません。エリアライトに対するフィルタされた重点サンプリング[CPF10]と同様の他の算術的に重い手法に触発されて別の方法を試してみましたが,シェーダコストはひどく高くなりました。我々はground truthに合わせないことを決め,単純に最高のビジュアルを持つより安価な方法を取りました。我々のライトはKarisのアプローチを使用していますが,ディスクと矩形に対して粗悪なエネルギー保存項を良くするものを見つけることができませんでした。図47を参照。
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.55 より引用
粗い面に対するスペキュラーエリアライトの積分をわずかに改善するために,BRDFローブの支配的な方向を考慮に入れました。支配的な方向の計算はセクション4.9.3でより詳細に説明します。ミラー方向のシフトによってその方向を読み戻します。リスト16を参照。エリアライトに対するバージョンはライトプローブに対して使用するものよりも単純です。我々の場合については十分であることが分かりました。図48はミラーと支配的な方向の利用の比較を示しています。これはG simthの相関がある項と相関がない項の両方でうまく動作します。
※リストは,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.55 より引用
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.56 より引用
Remark: ライトとサーフェイスのプロパティに依存することに留意することが重要であり,ディフューズエリアライトに対する照度の計算はスペキュラーエリアライトへ適用可能であるかもしれません(パンクチュアルライトとは違い,ここではLambertのコサインが常にディフューズとスペキュラーの両方に適用されます)。実際に,BRDFのコーンの重点との交差によって定められ,ライトの形状は異なり,Lambertのコサインに関して異なる積分となります。
4.8 Emissive surfaces
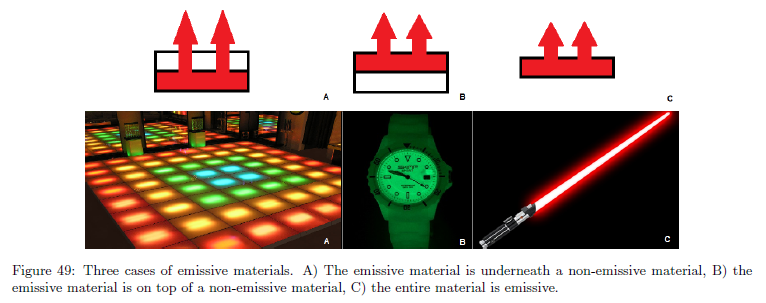
実世界では,エミッシブサーフェイスはエリアライトに似ています。それらは他の任意の光源のようにサーフェイスのすぐ近くで明るくなる光を放ちます。ゲームにおいては,パフォーマンスの制限のため伝統的なライトのようにサーフェイスのエミッシブ部分を取り扱うことは可能ではありません。Frostbite内では,区別をつけました: 1) ソースサーフェイスを表示するエミッシブライト,そして 2) 光を放つエリアライトです。エミッシブライトは他の任意のライトのようにエミッシブカラーとエミッシブ強度を提供することによってシェーダ内でピクセル精度で生成されます。輝度(\(cd.m^{-2}\))あるいは露出値(EV)のどちらか一方で強度は提供されます。これらのエミッシブライトは1つもライティングせず,視覚的な色のみです。しかしながら,強度がカメラセンサーをsaturateするときブルーミングを生み出します。セクション5.1を参照してください。エミッシブサーフェイスの3つの場合について大まかに指定することが可能です(図49参照):
A 非エミッシブマテリアルの表面下のエミッシブマテリアル。
B 非エミッシブマテリアル上部のエミッシブマテリアル。
C マテリアル全体がエミッシブ。
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.56 より引用
ケースBとCは非常に近く,Bを除いた状態で,エミッシブレイヤー下のマテリアルを潜在的に見えます。Frostbiteでは,暗黙的にケースCをサポートするケースBのみを取り扱います。エミッシブサーフェイスを効率的にレンダリングすることは容易ではありません。ディファード手法とディファードデカール(GBuffer生成パスの後で描画される)と互換性があるようにするエミッシブ不透明オブジェクトを適切に描画するために,GBufferへとエミッシブ情報を格納することが必要となります。これは追加のバッファを必要とし,コストが高くなります。Frostbiteでは,異なるパスを持ちました:
Transparent objects
エミッシブはサーフェイスの描画中適用されます。
Forward opaque objects
エミッシブはサーフェイスの描画中適用されます。
Deferred lit opaque objects with full emissive
エミッシブはサーフェイスの追加の描画パスにおいて適用されます:サーフェイスは2度描画されます。
Deferred lit opaque objects with cheap emissive
エミッシブはラジオシティバッファに格納され,間接照明と同時に適用されます。
間接ディフューズライティングはG-Buffer生成時にディフューズアルベドと一緒に構成されませんが,ディフューズアルベドを修正するため後でデカールできるようになります。アーティストが正確性のためにパフォーマンスとトレードしたい場合において,エミッシブ値はラジオシティバッファ内へと格納できるようにします。このアプローチでのトラブルは現在エミッシブカラーがディフューズアルベドと一緒にされていることです。ラジオシティバッファが適用されたときに,ディフューズアルベドによってラジオシティバッファを乗算します。したがって,エミッシブ項も乗算します。ディフューズアルベドを修正したデカールもまた,この場合においてエミッシブを修正します。このようなわけで我々はそれを”チープな”エミッシブと呼びます。リスト17。別の制約はディフューズを持たないような金属オブジェクトでこのテクニックは動作しないということです。
※リストは,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Parctice, p.57 より引用
図50はフォワードとチープディファードエミッシブの結果の例を示しています。この特有の場合では視覚的な結果が一致しています。
※リストは,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Parctice, p.57 より引用
Remark: 我々はエリアライトの配置時に正しい強度で自動的にエミッシブ形状を生成するためのツールを開発しました。図51に例を示します。これは説得力のあるビジュアルシーンを生成し,またライトをデバッグするアーティストを助けます。
※リストは,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Parctice, p.58 より引用