大変申し訳ございません。
下記の通り、誤記がありましたので謹んでお詫びして訂正いたします。
第1刷
P.245 中央部の数式
【誤】
\begin{eqnarray}
x &=& r \sin \theta \cos \theta \\
y &=& r \cos \theta \\
z &=& r \sin \theta \sin \theta
\end{eqnarray}
【正】
\begin{eqnarray}
x &=& r \sin \theta \sin \phi \\
y &=& r \cos \theta \\
z &=& r \sin \theta \cos \phi
\end{eqnarray}
P.245 6行目
【誤】
また,立体角は平面角2つを用いて表すことも可能です。球の半径を\(r\),天頂角を\(\theta\),方位角\(\phi\)とした場合,3次元空間上の任意の点は球面座標を使って次のように表せます。
円弧の長さは半径\(r\)と平面角の積で求められるので,方位角方向の弧の長さは \(r \sin \theta d\phi\)で表されます。同様にして,天頂角方向の弧の長さを求めると\(r d\theta\)となります。
方位角方向と天頂方向の円弧によって形成される面積\(dA\)を考えると,次のようになります。
【正】
また,立体角は平面角2つを用いて表すことも可能です。球の半径を\(r\),仰角を\(\theta\),方位角\(\phi\)とした場合,3次元空間上の任意の点は球面座標を使って次のように表せます。
円弧の長さは半径\(r\)と平面角の積で求められるので,方位角方向の弧の長さは \(r \sin \theta d\phi\)で表されます。同様にして,仰角方向の弧の長さを求めると\(r d\theta\)となります。
方位角方向と仰角方向の円弧によって形成される面積\(dA\)を考えると,次のようになります。
P.245 図7.2
【誤】
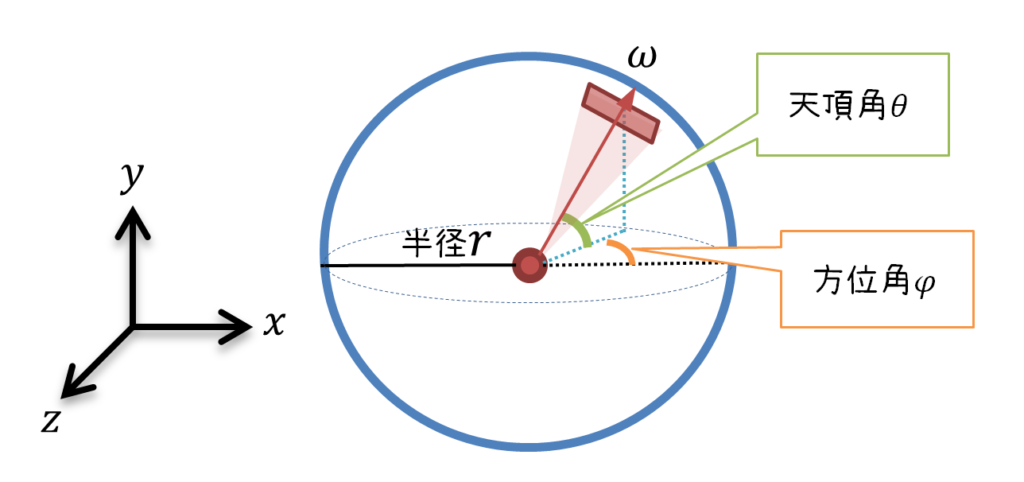
【正】
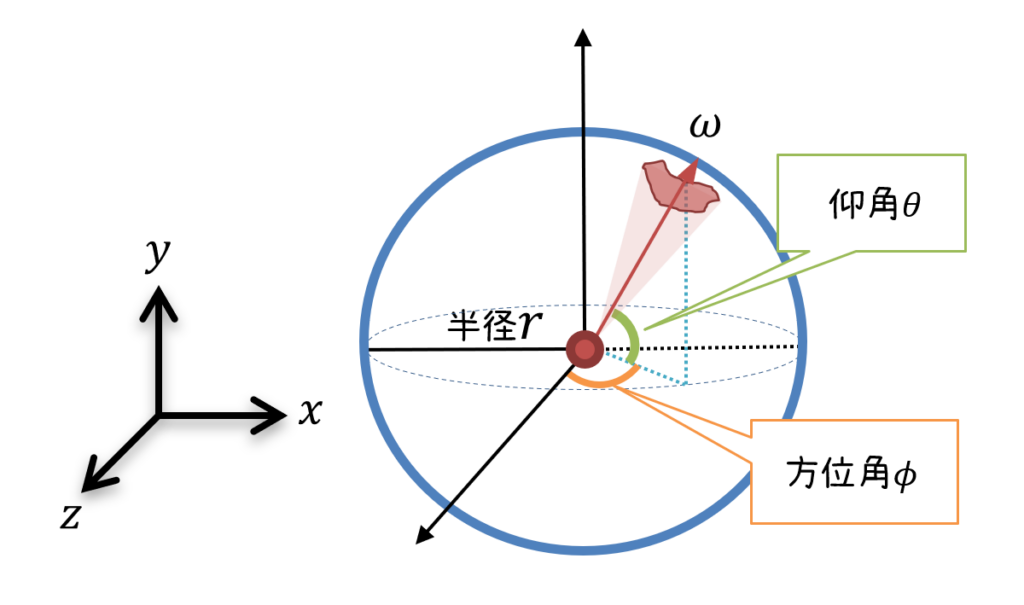
P.341 リスト10.16
【誤】
auto invW = 1.0f / float(w - 1);
auto invH = 1.0f / float(h - 1);
【正】
auto invW = 1.0f / float(w);
auto invH = 1.0f / float(h);
サンプルプログラム Chapter.10 IESProfile.cpp
【誤】
auto idx = (w - 1) * y + x;
【正】
auto idx = w * y + x;
第2刷
P.245 6行目
【誤】
また,立体角は平面角2つを用いて表すことも可能です。球の半径を\(r\),天頂角を\(\theta\),方位角\(\phi\)とした場合,3次元空間上の任意の点は球面座標を使って次のように表せます。
円弧の長さは半径\(r\)と平面角の積で求められるので,方位角方向の弧の長さは \(r \sin \theta d\phi\)で表されます。同様にして,天頂角方向の弧の長さを求めると\(r d\theta\)となります。
方位角方向と天頂方向の円弧によって形成される面積\(dA\)を考えると,次のようになります。
【正】
また,立体角は平面角2つを用いて表すことも可能です。球の半径を\(r\),仰角を\(\theta\),方位角\(\phi\)とした場合,3次元空間上の任意の点は球面座標を使って次のように表せます。
円弧の長さは半径\(r\)と平面角の積で求められるので,方位角方向の弧の長さは \(r \sin \theta d\phi\)で表されます。同様にして,仰角方向の弧の長さを求めると\(r d\theta\)となります。
方位角方向と仰角方向の円弧によって形成される面積\(dA\)を考えると,次のようになります。
P.245 図7.2
【誤】
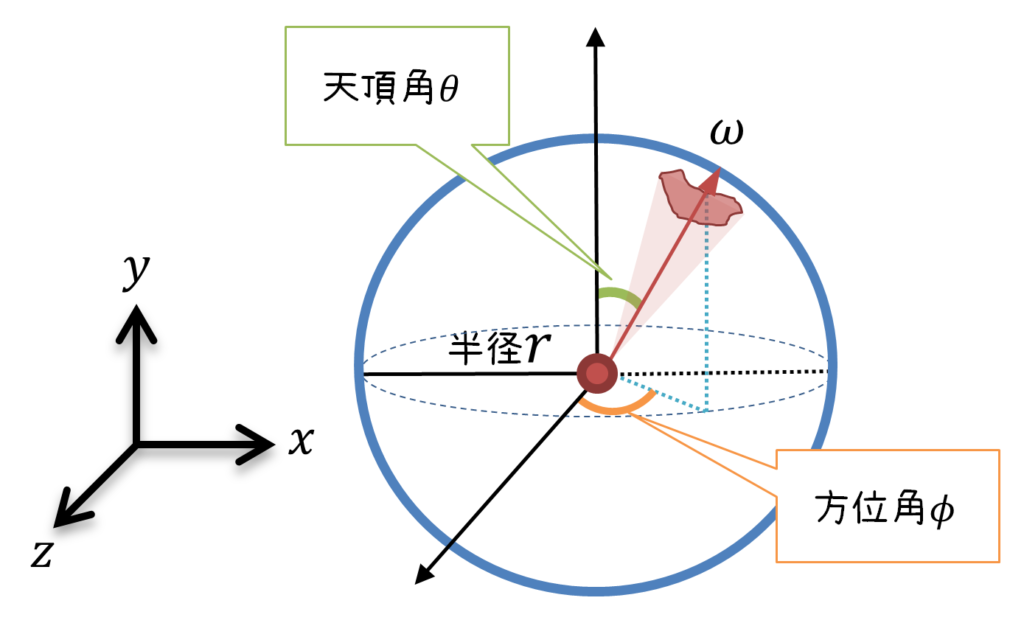
【正】



