この記事はレイトレ合宿2アドベントカレンダーの6週目の記事です。
こんにちわ、Pocolです。
ついに自分のアドベントカレンダーの順番が来てしまいました。
結局最後まで,ネタに困ったのですが前々から自分が実装したいなぁ~と思っているProgressive Photon Mapping(PPM)について紹介してみようと思います。
(※きちんと紹介できるか自信ないので,間違っていたら指摘して頂けると助かります。)
紹介は大まかに2つの部分に分け,前半が論文の超雑訳で,後半は実装についての説明になります。
さて,まずはPPMの話に入る前にフォトンマッピングについて触れなければならないのですが…
昨年の合宿で林さんが説明くださっていますので,下記の資料に目を通してください。
また,自分のようにレイトレ素人童貞の方はholeさんがまとめてくださっている「物理ベースレンダラedupt」の資料を一読することをお勧めします。
あと,Bee先生のProgressive Photon Mappingについて論文はhttp://users-cs.au.dk/toshiya/ppm.pdfからダウンロードできるようです。
Overview
フォトンマッピングは2パスアルゴリズムでした。最初のパスはフォトントレーシングで,フォトントレーシングでは光源からシーンへのフォトンが追跡され,面と交差したところでフォトンマッピングに格納します。2つ目のパスはシーンでのフォトンマップを用いて放射輝度推定を行いレンダリングします。
フォトンマップが与えられると,任意の表面位置xにおける放射輝度は次のように推定されます:
\[
L(x, \vec{\omega}) \approx \sum^{n}_{p=1} \frac{fr(x, \vec{\omega}, \vec{\omega}_{p})\phi_{p}(x_{p}, \vec{\omega}_{p})}{\pi r^{2}}
\tag{1}
\]
ここで,\(n\)は入射輝度を推定するのに用いる近傍フォトンの数です。\(\phi_{p}\) は\(p\)番目のフォトンの光束です。\(fr\)はBRDFで,\(\vec{\omega}\)は出射方向で,\(\vec{\omega_{p}}\)は入射方向です。\(r\)は\(n\)個の近傍フォトンを含む球の半径です。この推定が想定しているのは,フォトンの局所的な集合がxにおける入射輝度を表し,\(x\)周囲の表面は局所的に平らであることです。式(1)における放射輝度推定はフォトンマッピングにおいてバイアスの基となります。フォトントレーシングステップは非バイアスですが,結果としてのフォトンの値は放射輝度推定の一部としてブラーされます。フォトンの密度が増加するについて,放射輝度推定は正しい解に収束し,これがフォトンマッピングの一貫性のあるアルゴリズムにしています。正しい解に収束させるのを確実にするためには,フォトンマッピングと放射輝度推定において無限の数のフォトンを使用することが必要となります。その上で半径はゼロに収束すべきです。フォトンマップ上で\(N\)個のフォトンを用いてこの要件を満たすことができますが,放射輝度推定において\(\beta\in]0:1[\) で\(N^{\beta}\)個のフォトンを持つ場合のみです。\(N\)が無限に近づくときに\(N\)と\(N^{\beta}\)の両方は無限に近づきますが,\(N^{\beta}\)は\(N\)よりも限りなく小さくなり,それを保証するのは半径\(r\)がゼロに収束することです。これは[Jensen 2001]のように記述することができます:
\[
L(x, \vec{\omega}) = \lim_{N \to \infty}\sum^{\lfloor N^{\beta} \rfloor}_{p=1}\frac{fr(x, \vec{\omega}, \vec{\omega}_{p})\phi_{p}(x_{p}, \vec{\omega}_{p})}{\pi r^{2}}
\tag{2}
\]
すべてのフォトンはメモリに格納されるので,標準的なフォトンマッピングにおいてこの結果は理論的な関心だけです。これでは任意の精度で解を得ることができなくなります。Progressive Photon Mappingではすべてのフォトンをメモリへ格納することなく,式(2)の要件を満たす放射輝度推定値を紹介しています。
Progressive Radiance Estimate
古典的なフォトンマップの放射輝度推定は式(1)で与えられるようなフォトンの局所的密度の推定に依存しています。局所的密度\(d(x)\)の推定は次のようになります。
\[
d(x) = \frac{n}{\pi r^{2}}
\tag{3}
\]
推定は半径rの球内の\(n\)個の近傍フォトンの配置に基づきます。想定しているのは表面が局所的に平らで,ディスク内にフォトンが配置されていることです。別のフォトンマップを生成し,同じディスク内で\(n’\)個のフォトンが\(x\)において見つかる可能性がある場合は,次にように異なる密度推定\(d’\)になるかもしれないです:
\[
d'(x) = \frac{n’}{\pi r^{2}}
\tag{4}
\]
気を付けてほしいのは,式(3)と同じ半径を使用している点です。\(d(x)\)と\(d(x)’\)の平均をとることによって,半径\(r\)ディスク内のより正確な密度を得ることが可能です。
このアプローチはChristensen[Jensenら 2004]によって提案されており,よりスムーズな放射輝度推定を導きますが,最終結果はそれぞれ個別のフォトンマップよりも詳細ではありません。さらに平均化手法は一貫性がなく,この方法はxにおいて正しい値に収束しません。代わりとして一定半径内の平均値を計算します。その結果,半径内での詳細さは解決することができませんが,精度が効果的に各々個別のフォトンマップでフォトンの総数によって制限されます。
漸進的な放射輝度推定は最終推定が正しい解に収束するような方法で,複数のフォトンマップの結果を結びつけます。これは個別のフォトンマップによって捕捉されない照明の細部を解決することができます。キーとなる洞察は,蓄積されたフォトンの数が増加する間,各衝突点における放射輝度推定で半径を減少する新しいテクニックがこれを可能にします。式(2)に従ってフォトン密度が極限において無限になることを保障します。どのようにフォトン密度が漸進的に増加されるかについては後述します。レイトレーシングパスで生成された各衝突点において放射輝度推定を行います。最初に\(x\)における半径\(R(x)\)をピクセルのフットプリントとして非ゼロの値に設定します。尚,各衝突点を中心とした半径を推定するためにフォトンマップを使用して、最初のフォトントレースパスの後半径を推定することも可能です。
Radius Reduction
各衝突点は半径\(R(x)\)を持ちます。目標はこの半径内で蓄積されたフォトンの数\(N(x)\)を増加させる間,\(R(x)\)を減少させることです。衝突点\(x\)における密度は式(3)を用いて計算されます。フォトントレーシングの回数が実行され,\(x\)において\(N\)個のフォトンが蓄積されたということを想定しています。もう一回追加のフォトントレーシングステップを行い,半径\(R(x)\)内で\(M(x)\)個のフォトンが見つかったときに,それら\(M(x)\)個のフォトンを\(x\)に加算し,新しいフォトン密度\(\hat{d}(x)\)となります:
\[
\hat{d}(x) = \frac{N(x)+M(x)}{\pi R^{2}}
\tag{5}
\]
アルゴリズムの次のステップは,\(dR(x)\)によって半径\(R(x)\)を減少することです。半径\(R(x)\)内でフォトン密度が一定であると仮定した場合に,半径\(\hat{R}(x) = R(x) – dR(x)\)のディスク内の新しいフォトンの総数を計算することが可能です:
\[
\hat{N}(x) = \pi\hat{R}(x)^{2}\hat{d}(x) = \pi(R(x) – dR(x))^{2}\hat{d}(x)
\tag{6}
\]
導出は下記のようになります。
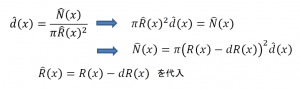
式(2)における一貫性を満たすために,各イタレーションにおいてフォトンの総数を調整する必要があります(すなわち\(\hat{N}(x) > N(x)\))。単純化のために,各イタレーションの後でフォトンの割合を保つための制御パラメータ\(\alpha = (0, 1)\)を使用します。したがって,\(\hat{N}(x)\)は次のように計算されます:
\[
\hat{N}(x) = N(x) + \alpha M(x)
\tag{7}
\]
これは各イタレーションにおいて\(\alpha M(x)\)個の新しいフォトンを加算したいと言っています。式(5), (6), (7)を結びつけることによって実際の減少半径\(dR(x)\)を計算することができます:
\begin{eqnarray}
& & \pi(R(x) – dR(x))^{2}\hat{d}(x) = \hat{N} \nonumber \\
& \Leftrightarrow & \pi(R(x) – dR(x))^{2}\frac{N(x) + M(x)}{\pi R(x)^{2}} = N(x) + \alpha M(x) \nonumber \\
& \Leftrightarrow & dR(x) = R(x) – R(x)\sqrt{\frac{N(x) + \alpha M(x)}{N(x) + M(x)}}
\tag{8}
\end{eqnarray}
最終的に,減少された半径\(\hat{R}(x)\)は次のように計算されます:
\[
\hat{R}(x) = R(x) – dR(x) = R(x)\sqrt{\frac{N(x) + \alpha M(x)}{N(x) + M(x)}}
\tag{9}
\]
注意してほしいのは,式(9)は各衝突点で個別に解くということです。
Flux Correction
衝突点が\(M(x)\)個のフォトンを受け取った時に,それらのフォトンによってキャリーされた光束を累積する必要があります。加えて,前のセクションで述べた半径の減少を考慮してこの光束を調整する必要があります。各衝突点はBRDFによって事前乗算済みで正規化されていない受け取ったすべての光束を保存しています。この量を\(\tau(x, \vec{\omega})\)と呼び,\(N(x)\)個のフォトンについては次のように計算されます:
\[
\tau_{N}(x, \vec{\omega}) = \sum^{N(x)}_{p=1}fr(x, \vec{\omega}, \vec{\omega}_{p})\phi_{p}'(x_{p}, \vec{\omega}_{p})
\tag{10}
\]
ここで,\(\vec{\omega}\)は衝突点における入射レイの方向で,\(\vec{\omega}_{p}\)は入射フォトンの方向で,\(\phi_{p}(x_{p}, \vec{\omega}_{p})\)は正規化されていないフォトン\(p\)によってキャリーされた光束です。注意してほしいのは,この段階における光束は標準のフォトンマッピングにおけるように放出されたフォトンの数で除算されていないということです。同様にして,\(M(x)\)個の新しいフォトンについては次の式で与えられます:
\[
\tau_{M}(x, \vec{\omega}) = \sum^{M(x)}_{p=1}fr(x, \vec{\omega}, \vec{\omega}_{p})\phi_{p}'(x_{p}, \vec{\omega}_{p})
\tag{11}
\]
半径が一定である場合は,単純に\(\tau_{M}(x, \vec{\omega})\)を\(\tau_{N}(x, \vec{\omega})\)に加えることができますが,半径は減少されているので,減少された半径の外側に漏れるフォトンを考慮する必要があります。
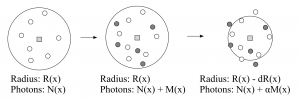
[HACHISUKA et al. 2008]より引用
これらのフォトンを見けるための一つの方法は,ディスク内のすべてのフォトンのリストを保持し,減少されたディスク半径に存在にしないものを削除することです。しかしながら,この方法はフォトンのリストに対してあまりに多くのメモリを必要とするので実用的ではありません。代わりにディスク内で照明とフォトン密度が一定であることを仮定し,以下のような適合結果になります:
\begin{eqnarray}
\tau_{\hat{N}}(x, \vec{\omega}) & = & (\tau_{N}(x, \vec{\omega}) + \tau_{M}(x, \vec{\omega}))\frac{\pi\hat{R}(x)^{2}}{\pi R(x)^{2}} \nonumber \\
& = & \tau_{N+M}(x, \vec{\omega})\frac{\pi (R(x)\sqrt{\frac{N(X) + \alpha M(x)}{N(x) + M(x)}})^{2}}{\pi R(x)^{2}} \nonumber \\
& = & \tau_{N+M}(x, \vec{\omega})\frac{N(x) + \alpha M(x)}{N(x) + M(x)}
\tag{12}
\end{eqnarray}
ここで,\(\tau _{N+M}(x, \vec{\omega}) = \tau _{N}(x, \vec{\omega}) + \tau _{M}(x, \vec{\omega})\) と\(\tau _{\hat{N}}(x, \vec{\omega})\)は\(\hat{N}(x)\)個のフォトンに一致する減少されたディスク半径に対する減少した値です。フォトン密度とフォトン密度による照明がディスク内で一定であるという仮定は初期段階では正しくないかもしれませんが,厳密には照明における不連続点を除いて,半径が小さくなるにつれて次第に正しくなります。照明の不連続が未定義であるのと厳密には不連続における衝突点を有する確率がゼロであるので,問題にはなりません。
Radiance Evaluation
各フォトントレースパスの後で,衝突点における放射輝度を評価することができます。現在の半径と現在インターセプトしたBRDFで乗算済みの光束を保存した量を思い出しましょう。評価された放射輝度はピクセルの重みが乗算されており,衝突点と関連があるピクセルに加算されています。放射輝度を評価するには,\(\tau(x, \vec{\omega})\)を正規化するために,放出されたフォトンの総数\(N_{emitted}\)を知る必要があります。放射輝度の評価は以下のようになります:
\begin{eqnarray}
L(x, \vec{\omega}) & = & \int_{2\pi}fr(x, \vec{\omega}, \vec{\omega}’)L(x, \vec{\omega}’)(\vec{n}\cdot\vec{\omega}’)d\omega’ \nonumber \\
& \approx & \frac{1}{\Delta A} \sum^{n}_{p=1}fr(x, \vec{\omega}, \vec{\omega}_{p})\Delta\phi_{p}(x_{p}, \vec{\omega}_{p}) \nonumber \\
& = & \frac{1}{\pi R(x)^{2}} \frac{\tau(x, \vec{\omega})}{N_{emitted}}
\tag{13}
\end{eqnarray}
通常のフォトンマッピングと同様に,この定式はBRDFと光束を事前乗算して,\(\tau(x, \vec{\omega})\)として保存しているのでランバートマテリアルに限定されません。気をつけてほしいのは,半径\(R(x)\)はライティングされていない領域(すなわち\(M(x) = 0\))内のR(x)によって定義されるディスクの場合には減少されないということです。この状況は一見すると一貫性の条件を壊しますが,依然として正しい解\(L(x, \vec{\omega})=0\)に収束します。従って,\(\tau(x, \vec{\omega})\)は増加せず,\(N_{emitted} \rightarrow \infty\)であると,\(L(x, \vec{\omega}) \rightarrow 0\)です。\(R(x)とN(x)\)の収束特性の形式分析がまだ行われていませんが,下図に示すように漸進的放射輝度推定は半径\(R(x)\)がゼロへと減少する間に正確な放射輝度値\(L(x)\)へと収束し,フォトンの数\(N(x)\)は無限大に増加します。
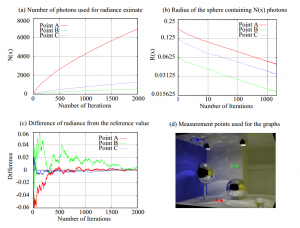
[HACHISUKA et al. 2008]より引用
漸進的放射輝度推定が確実にするのは,各イタレーションにおいて各衝突点でのフォトン密度が増加することで,それゆえ式(2)に従う一貫性があります。
Implementation
smallppmに少しだけ手を加えてレンダリングしてみました。
まず,smallppmのソースコードですが,以下のURLからダウンロードできます。
http://users-cs.au.dk/toshiya/smallppm_exp.cpp
これに少し手を加えたものをGithubにアップロードしました。
https://github.com/ProjectAsura/sample_ppm
smallppmでは,準モンテカルロ法を用いてますが,準モンテカルロ法についてよくわかっていないので説明を省きます。
説明が欲しい方はsyoyoさんが書いている「グローバルイルミネーション入門」あたりを参考にするとよいかと思います。
まず,全体の流れですが下記のような感じで論文に書いてある通りに,レイトレーシングパスを実行して,次にフォトントレーシングパスを実行して,放射輝度評価を行うといった感じです。
//-------------------------------------------------------------------------------------------
// メインエントリーポイントです.
//-------------------------------------------------------------------------------------------
int main(int argc, char **argv)
{
auto w = 1024; // 画像の横幅.
auto h = 768; // 画像の縦幅.
auto s = 10000; // s * 1000 photon paths will be traced
auto c = new Vector3[ w * h ];
trace_ray( w, h );
trace_photon( s );
density_estimation( c, s );
save_to_bmp( "image.bmp", w, h, &c[0].x, 2.2 );
delete [] c;
c = nullptr;
return 0;
}
次に個別の処理を見ていきます。まずはtrace_ray()からです。
trace_ray()ではカメラ位置からレイを飛ばす処理を行います。この辺の処理はeduptに詳しい解説があるのでそちらを参照してください。
trace()メソッドについては後述します。
//-------------------------------------------------------------------------------------------
// eye rayを追跡します.
//-------------------------------------------------------------------------------------------
void trace_ray( int w, int h )
{
auto start = std::chrono::system_clock::now();
// trace eye rays and store measurement points
Ray cam(
Vector3(50, 48, 295.6),
normalize(Vector3(0, -0.042612, -1))
);
auto cx = Vector3( w * 0.5135 / h, 0, 0 );
auto cy = normalize( cross( cx, cam.dir ) ) * 0.5135;
for (int y = 0; y < h; y++)
{
fprintf( stdout, "\rHitPointPass %5.2f%%", 100.0 * y / (h - 1) );
for (int x = 0; x < w; x++)
{
auto idx = x + y * w;
auto d = cx * ((x + 0.5) / w - 0.5) + cy * (-(y + 0.5) / h + 0.5) + cam.dir;
trace( Ray(cam.pos + d * 140, normalize(d)), 0, true, Vector3(), Vector3(1, 1, 1), idx );
}
}
fprintf( stdout, "\n" );
// build the hash table over the measurement points
build_hash_grid( w, h );
auto end = std::chrono::system_clock::now();
auto dif = end - start;
fprintf( stdout, "Ray Tracing Pass : %ld(msec)\n", std::chrono::duration_cast<std::chrono::milliseconds>(dif).count() );
}
続いて,フォトントレーシングパスの処理です。一応OpenMPを使っています。
genp()メソッドでフォトンレイを生成して,あとはtrace()メソッドで追跡する感じです。
//-------------------------------------------------------------------------------------------
// photon rayを追跡します.
//-------------------------------------------------------------------------------------------
void trace_photon( int s )
{
auto start = std::chrono::system_clock::now();
// trace photon rays with multi-threading
auto vw = Vector3(1, 1, 1);
#pragma omp parallel for schedule(dynamic, 1)
for (int i = 0; i < s; i++)
{
auto p = 100.0 * ( i + 1 ) / s;
fprintf( stdout, "\rPhotonPass %5.2f%%", p );
int m = 1000 * i;
Ray r;
Vector3 f;
for ( int j = 0; j < 1000; j++ )
{
genp( &r, &f, m + j );
trace( r, 0, false, f, vw, m + j );
}
}
fprintf( stdout, "\n" );
auto end = std::chrono::system_clock::now();
auto dif = end - start;
fprintf( stdout, "Photon Tracing Pass : %ld(sec)\n", std::chrono::duration_cast<std::chrono::seconds>(dif).count() );
}
さて肝心のtrace()メソッドですが下記のようになります。
//////////////////////////////////////////////////////////////////////////////////////////////
// HitRecord structure
//////////////////////////////////////////////////////////////////////////////////////////////
struct HitRecord
{
Vector3 pos;
Vector3 nrm;
Vector3 flux;
Vector3 f;
double r2;
unsigned int n;
int idx;
};
//-------------------------------------------------------------------------------------------
// レイを追跡します.
//-------------------------------------------------------------------------------------------
void trace( const Ray &r, int dpt, bool m, const Vector3 &fl, const Vector3 &adj, int i )
{
double t;
int id;
dpt++;
if (!intersect(r, t, id) || (dpt >= 20))
return;
auto d3 = dpt * 3;
const RenderSphere &obj = sph[ id ];
auto x = r.pos + r.dir*t, n = normalize( x - obj.pos );
auto f = obj.color;
auto nl = ( dot(n, r.dir ) < 0 ) ? n : n*-1;
auto p = ( f.x > f.y && f.x > f.z ) ? f.x : ( f.y > f.z ) ? f.y : f.z;
if ( obj.type == MaterialType::Matte )
{
if (m)
{
// eye ray
// store the measurment point
auto hp = new HitRecord;
hp->f = mul(f,adj);
hp->pos = x;
hp->nrm = n;
hp->idx = i;
hitpoints.push_back( hp );
}
else
{
// photon ray
// find neighboring measurement points and accumulate flux via progressive density estimation
auto hh = (x - hpbbox.mini) * hash_s;
auto ix = abs(int(hh.x));
auto iy = abs(int(hh.y));
auto iz = abs(int(hh.z));
// strictly speaking, we should use #pragma omp critical here.
// it usually works without an artifact due to the fact that photons are
// rarely accumulated to the same measurement points at the same time (especially with QMC).
// it is also significantly faster.
{
auto list = hash_grid[ hash( ix, iy, iz ) ];
for( auto itr = list.begin(); itr != list.end(); itr++ )
{
auto hp = (*itr);
auto v = hp->pos - x;
// check normals to be closer than 90 degree (avoids some edge brightning)
if ((dot(hp->nrm,n) > 1e-3) && (dot(v,v) <= hp->r2))
{
// unlike N in the paper, hp->n stores "N / ALPHA" to make it an integer value
auto g = (hp->n * ALPHA + ALPHA ) / ( hp->n * ALPHA + 1.0 );
hp->r2 = hp->r2 * g;
hp->n++;
hp->flux = ( hp->flux + mul( hp->f, fl ) / D_PI ) * g;
}
}
}
// use QMC to sample the next direction
auto r1 = 2.0 * D_PI * halton( d3 - 1, i );
auto r2 = halton( d3 + 0, i );
auto r2s = sqrt( r2 );
auto w = nl;
auto u = normalize(cross((fabs(w.x) > .1 ? Vector3(0, 1, 0) : Vector3(1, 0, 0)), w));
auto v = cross( w, u );
auto d = normalize( u * cos( r1 ) * r2s + v * sin( r1 ) * r2s + w * sqrt( 1 - r2 ));
if ( halton( d3 + 1, i ) < p )
trace(Ray(x, d), dpt, m, mul(f,fl)*(1. / p), mul(f, adj), i);
}
}
else if ( obj.type == MaterialType::Mirror )
{
trace(Ray(x, reflect(r.dir, n)), dpt, m, mul(f,fl), mul(f,adj), i);
}
else
{
Ray lr( x, reflect( r.dir, n ) );
auto into = dot(n, nl ) > 0.0;
auto nc = 1.0;
auto nt = 1.5;
auto nnt = (into) ? nc / nt : nt / nc;
auto ddn = dot( r.dir, nl );
auto cos2t = 1 - nnt * nnt * ( 1 - ddn * ddn );
// total internal reflection
if (cos2t < 0)
return trace(lr, dpt, m, mul(f, fl), mul(f, adj), i);
auto td = normalize(r.dir * nnt - n * ( ( into ? 1 : -1 ) * ( ddn * nnt + sqrt( cos2t ))));
auto a = nt - nc;
auto b = nt + nc;
auto R0 = a * a / ( b * b );
auto c = 1 - (into ? -ddn : dot(td, n));
auto Re = R0 + (1 - R0) * c * c * c * c * c;
auto P = Re;
Ray rr(x, td);
auto fa = mul( f, adj );
auto ffl = mul( f, fl );
if (m)
{
// eye ray (trace both rays)
trace( lr, dpt, m, ffl, fa * Re, i );
trace( rr, dpt, m, ffl, fa * (1.0 - Re), i );
}
else
{
// photon ray (pick one via Russian roulette)
( halton( d3 - 1, i ) < P )
? trace( lr, dpt, m, ffl, fa * Re, i )
: trace( rr, dpt, m, ffl, fa * (1.0 - Re), i );
}
}
}
eduptの方に一度目を通してれば,レイを飛ばす処理については説明不要かと思います。
大事なのは,通常のフォトンマッピングと同じく拡散反射面でのみ衝突点を生成するということでしょうか。あとは英文コメントにもありますが,NではなくN / αとしてフォトン数をnに入れているので,論文通りの式に戻すためには,α倍することが必要となります。なぜこんなことをしているかというとコメントにもあるように整数演算したいからというのが理由だそうです。分かりづらいので論文通りにするために,α倍してdoubleで個数を保持しようかと思ってみたのですが,浮動小数点演算による累積誤差が大きくなりそうな気がしたので辞めました。
つづいて,最近傍フォトンを見つけるためにsmallppmではハッシュグリッドを使っているようです。
オリジナルコードは自前でリストを作っていたのですが,これをstd::listとstd::vectorを使って書き直しました。
やっていることはまず大きなバウンディングボックスを作っておいて,そのバウンディングボックス内での相対座標からハッシュコードを生成しているようです。
//-------------------------------------------------------------------------------------------
// ハッシュグリッドを構築します.
//-------------------------------------------------------------------------------------------
void build_hash_grid
(
const int w,
const int h
)
{
// find the bounding box of all the measurement points
hpbbox.reset();
for( auto itr = hitpoints.begin(); itr != hitpoints.end(); ++itr )
{ hpbbox.merge( (*itr)->pos ); }
// heuristic for initial radius
auto size = hpbbox.maxi - hpbbox.mini;
auto irad = ((size.x + size.y + size.z) / 3.0) / ((w + h) / 2.0) * 2.0;
// determine hash table size
// we now find the bounding box of all the measurement points inflated by the initial radius
hpbbox.reset();
auto photon_count = 0;
for( auto itr = hitpoints.begin(); itr != hitpoints.end(); ++itr )
{
auto hp = (*itr);
hp->r2 = irad *irad;
hp->n = 0;
hp->flux = Vector3();
photon_count++;
hpbbox.merge( hp->pos - irad );
hpbbox.merge( hp->pos + irad );
}
// make each grid cell two times larger than the initial radius
hash_s = 1.0 / (irad * 2.0);
// build the hash table
hash_grid.resize( photon_count );
hash_grid.shrink_to_fit();
for( auto itr = hitpoints.begin(); itr != hitpoints.end(); ++itr )
{
auto hp = (*itr);
auto min = ((hp->pos - irad) - hpbbox.mini) * hash_s;
auto max = ((hp->pos + irad) - hpbbox.mini) * hash_s;
for (int iz = abs(int(min.z)); iz <= abs(int(max.z)); iz++)
{
for (int iy = abs(int(min.y)); iy <= abs(int(max.y)); iy++)
{
for (int ix = abs(int(min.x)); ix <= abs(int(max.x)); ix++)
{
int hv = hash( ix, iy, iz );
hash_grid[ hv ].push_back( hp );
}
}
}
}
}
つづいて,genp()メソッドですが,フォトンレイを生成だけで,下記のようになります。
明るさとか光源位置を変えたい場合は下記メソッドをいじってみてください。
//-------------------------------------------------------------------------------------------
// フォトンレイを生成します.
//-------------------------------------------------------------------------------------------
void genp( Ray* pr, Vector3* f, int i )
{
// generate a photon ray from the point light source with QMC
(*f) = Vector3( 2500, 2500, 2500 ) * ( D_PI * 4.0 ); // flux
auto p = 2.0 * D_PI * halton( 0, i );
auto t = 2.0 * acos( sqrt(1. - halton( 1, i ) ));
auto st = sin( t );
pr->dir = Vector3( cos( p ) * st, cos( t ), sin( p ) * st );
pr->pos = Vector3( 50, 60, 85 );
}
最後に放射輝度評価ですが,式(13)をそのままコードに落とした感じの以下の処理になります。
//-------------------------------------------------------------------------------------------
// 密度推定を行います.
//-------------------------------------------------------------------------------------------
void density_estimation( Vector3* color, int num_photon )
{
// density estimation
for( auto itr = hitpoints.begin(); itr != hitpoints.end(); ++itr )
{
auto hp = (*itr);
auto i = hp->idx;
color[i] = color[i] + hp->flux * ( 1.0 / ( D_PI * hp->r2 * num_photon * 1000.0 ));
}
}
あとは,この結果をBMPなりの画像ファイルに出力すればレンダリング終了となります。
PPM説明するといってもほとんど理解できていないので,中身のない説明になってしまいましたが,一応紹介したよ!ということで終わりにします。
Progressive Photon Mappingに関係する論文で,”Stochasitic Progressive Photon Mapping”や”Progressive Photon Mapping: A Probabilistic Approach”といった論文があるので,興味がある方は一読されると良いかもしれません。また前者の”Stochastic Progressive Photon Mapping”について,レイトレ合宿!!でnikqさんが実装されたコードが公開されているので,そちらを参考すると良いかと思います。
References
- ・JENSEN, H. W., 2001. Realistic Image Synthesis Using Photon Mapping. A. K. Peters, Ltd., Natick, MA.
- ・CHRISTENSEN, P.H., AND BATALI, D. 2004. An irradiance atlas for global illumination in complex production scenes. In Proceedings of Eurographics Symposium on Rendering 2004, 133-141
- ・HACHISUKA, T., OGAKI, S., AND JENSEN, H. W. 2008. Progressive photon mapping. ACM Transactions on Graphics(SIGGRAPH Asia Proceedings) 27, 5, Article 130.
- ・HACHISUKA, T., smallppm_exp.cpp, http://users-cs.au.dk/toshiya/smallppm_exp.cpp
- ・HAYASHI, S., フォトンマッピング入門, http://www.slideshare.net/ssuser2848d3/ss-25795852
- ・HOLE, 物理ベースレンダラ edupt解説, http://www.slideshare.net/h013/edupt-kaisetsu-22852235?qid=b3784530-dd5d-4d81-905a-7e5a6a8a1966&v=default&b=&from_search=1
- ・nikq, rlr, https://github.com/nikq/rlr