前回は,エリアライトとエミッシブライトに関する記述を和訳しました。
今回は,IBLについて和訳していきます。
毎度のことながら,誤訳等が多々ありますので,予めご了承ください。
また,誤訳を指摘して頂ける場合は,正しい翻訳例と共にご指摘頂けると幸いです。
4.9 Image based lights
イメージベースドライト(IBL)は点を囲む入射照明を表現するのを可能とします。この周囲照明は環境へとオブジェクトを”なじむ”のを作り出すため重要です。よくアーティストによる”反射”として持ち込まれるように,この入射照明はBRDFの式\(f\),すなわち,スペキュラー部分\(f_r\)だけなく\(f_d\)部分の両方の標準マテリアルに対しての部分すべてに一貫して適用されるために必要となります。レイヤードマテリアルのようにより高度なマテリアルのため,すべてのレイヤーはこのライティングによる影響を受ける必要があります。シェーダ内に直接反射テクスチャを追加することによってこの照明を”捏造”することはライティングとマテリアル情報間のキーの分離を壊し,異なる環境においてアセットを再利用するのを困難にします。IBL \(L\)とBRDF \(f\) 間の相互作用を計算することは,以下の積分の評価を必要とするコストが高い操作です:
\[
L({\rm v}) = \int_{\Omega} f({\bf l}, {\bf v}, {\Theta}) \, L({\bf l}) {\rm d}{\bf l} \tag{46}
\]
積分式は視線方向\({\bf v}\),マテリアルモデル \(f\),そしてパラメータ \(\Theta\)(フレネル,ラフネス,アルベド,など)を持ちます。オブジェクトを環境へと継続的に適合し,さらに良い反射近似を提供するために,すべての状況において反射を提供可能することが必要となります。このため,我々はDrobot[Dro13]によってインスピレーションされたIBLの4つのタイプを利用します。これらの各タイプはあるタイプあるいは入射照明を表現するのを可能とします:
● Distance light probe: 周囲の遠く離れた照明をキャプチャし,いかなる視差(つまり,空,遠くの建物,背景に書かれるもの,など)も含みません。これは少なくとも反射の正確なタイプですが,任意に利用できます。
● Local light probes: ビューの一点から特定の領域に含まれるすべてのオブジェクトをキャプチャーします(キューブマップ)。これらのキャプチャーは周囲のジオメトリに合わせるためにアーティストによって念入りに調整されたシンプルなプロキシジオメトリ(例,球あるいはボックス)へと再プロジェクションされます。この反射のタイプはディスタントライトプローブよりも正確ですが,オブジェクトの照明と視差は完全にキャプチャされません。
● Screen Space Reflections: 深度バッファに対してレイマーチングすることによってライトバッファに基づいた反射をキャプチャーします。これは短距離から中距離範囲の反射を捉え,接触する硬化材の良い反射を保証します。これは我々の反射の最も正確な情報源の一つとなります。
● Planar Reflections: エンジンによって自動的にセットアップされるかあるいはアーティストによる手動制御による平面によってミラーされたシーンを描画することによって反射をキャプチャーします。このリフレクションタイプは,平面上にある反射を想定しており,道や建物あるいは水面のようなほとんどフラットなサーフェイスについてうまく動作します。
Static vs. Dynamic: ディスタントライトプローブとローカルライトプローブは普通は特定の瞬間における周囲のライティングをキャプチャーしたものとして”静的な”ライティング情報を含んでいます。それらのコンテントは要求に応じて再読み込み,あるいは要件と割り当てられたパフォーマンスバジェットに応じて毎フレームリフレッシュすることのが可能です。SSRと平面反射は”動的な”ライティング情報を含んでおり,従ってビュー依存の性質のため毎フレーム更新されます。それらの計算はコストを減らすために数フレームにまたがって広げることが可能です。
SSRと平面反射を簡潔に説明する一方で,このセクションは主にローカルとディスタントライトプローブに焦点を当てます。最初に,ライトプローブの取得とそれらのライティング単位を説明します。このとき,フィルタリング,評価法,そして最後に異なるIBLの合成を説明します。
4.9.1 Light probe acuquisition and unit
Frostbiteでは,IBLは定義により画像データに関連しています。それらのすべてはライティングパイプラインの出力であるので輝度単位を使用します。
4.9.1.1 Distant light probe
ディスタントライトプローブはキャプチャーした周囲の環境をキューブマップとして表現します。アーティストはディスタントライトプローブを得るための2つの方法を持ちます:
● 随意的な背景と一緒に構成された物理ベースのスカイを通じてライティングを得ること。
● 実世界から得たハイダイナミックレンジ画像(HDRI)を使用すること。
Frostbiteはディスタントライトプローブをキャプチャーに使用可能な物理ベースのスカイを使用します。ディスタントライトプローブは状況の変化を取り扱う際に(時間サイクル,天候変化など)要求に応じて更新することが可能です。スカイライティングは他の任意のライトのように輝度へと変換されます。キャプチャー時において,ライティングパイプラインのみを考えます。任意のカラーマネージメント操作を含むすべてのポストプロセスを取り除き(トーンマッピング,カラーグレーディング…),RGBA16FのテクスチャフォーマットのHDRへと結果の輝度を格納します。
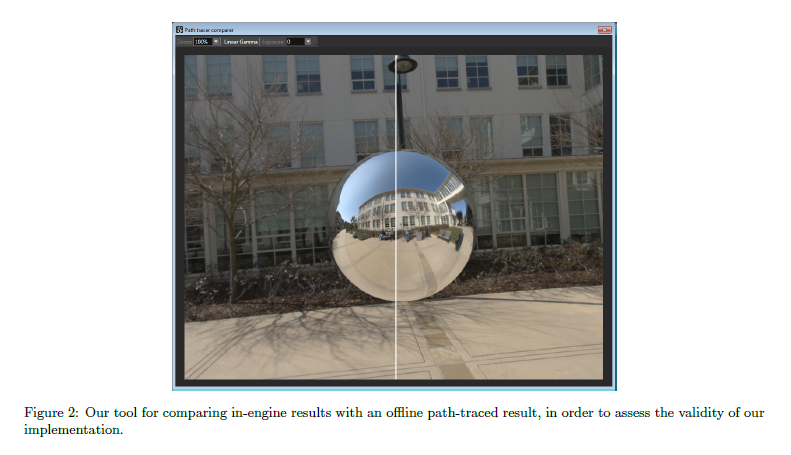
実世界のディスタントライトプローブの良い利用を行うことは既得の知識を必要とします。取得されたHDR画像は静的な性質のためにゲーム内において最終的なライティングに使用されることは稀です。それらはむしろデザインされたアセットについての入射照明とマテリアルプロパティの自然光に正確な反応の検証に使われます。しかしながら,取得されたHDRIはゲーム内のライティングと混合する必要があるときに,注意が必要となります。HDRIテクセルに格納されているものが明らかでないからです。カメラは輝度値を出力したものと考えられますが,カメラレスポンスとポストプロセスの段階は最も高い輝度値と最も低い輝度値の両方をそぎ落とします。出力されたピクセルはもはや輝度値を表現しませんが,むしろデバイス依存の値はオリジナルシーンの輝度に関係します。実際の過程の輝度からピクセル値への変換の詳細はセクション5.1で詳しく説明します。
HDRI creation: LDRカメラで,以下のキャプチャーの複雑な過程と絶対輝度範囲[DM97]において再構築はHDR画像を取得するのを可能とします。その過程は複数の露出値を持つシーンを取ることと(Luminance HDR[Ana]のような)ソフトウェアで後に合成することを意味しています。ソフトウェアはデバイス依存のレスポンスカーブを逆変換することによってオリジナルシーンの輝度値を再構築します。良好な画像を取得することとカメラレスポンスカーブを特定できるようにすることの2重の問題は,アーティストによって生成された大部分のHDR画像は相対輝度あるいは事前発光された輝度値のみを表現することを意味しています,図52を参照してください。その他のライトタイプとディスタントライトプローブを混合するために,相対輝度値を微調整するためにアーティストに乗算を提供します。Mac-Bethチャート,カメラ設定,そして,うまく分かった輝度値に基づいて手動キャリブレーションで,アーティストは絶対輝度値に正常に戻すための良い要因を求めることが可能です。正確に再構築された画像において,晴天は\(8000 \, cd.m^{-2}\)付近の輝度を持ち,曇りは\(2000 \, cd.m^{-2}\)付近になります。夜のシーンでは,\(3000\)から\(5000 \, cd.m^{-2}\)の値は道のストリートのライト照明下はめったに見れません。月の輝度は\(2500 \, cd.m^{-2}\)付近で,その他のオブジェクトは 環境ライティングのみでライティングするとき,値 \(<\, 1 \, cd.m^{-2}\) で必要以上に非常に暗いです[McN]。
Strong light sources: 得られたHDRIでは,事前積分の間のノイズを避けるためとそれらの可視性を処理するためにライトプローブから強い光源を取り除くことが必要です(次のセクション参照)。例として,ライトプローブへとベイクする代わりに太陽をディレクショナルライトとして適用することは,きちんと太陽によるシャドウイングを処理することを可能とします。HDRIから太陽を取り除くことは単純にコピーすることと,太陽に周囲空の小さな一部分をペーストすることを必要とします。
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.60 より引用
4.9.1.2 Local light probes
ローカルライトプローブはボリューム周囲の限定された範囲内における周囲のオブジェクトをキャプチャーします。ローカル環境に合致することが目的となります。この取得は常にエンジン内で実行され,次のいずれになる可能性があります:”ベイクされた”オフラインあるいはキャプチャーされたもの,要求に応じて更新されるもの,あるいはランタイムで毎フレーム更新されるもの。どれを選択するかはバジェットと要件(オブジェクトが移動する,ライティング環境が変化するなど)に依存します。ローカルライトプローブをキャプチャーすることは次のレンダリングの問題を引き起こします:
● Order-dependency: それらはまだキャプチャーされないのでローカルライトプローブでシーンをライティングすることができません。この卵と鶏の問題はローカルライトプローブが他のものの後でキャプチャーされる場合にキャプチャーする順序依存状態の問題を引き起こします。
● Metallic surfaces: キャプチャー時にディフューズ寄与あるいはスペキュラー寄与のどちらも持たないので金属表面は問題があり,結果として黒い見た目になります。ライトバウンスをシミュレートするために数回でローカルライトプローブをキャプチャーできる可能性がありますが,金属の部屋の場合は大きな数のバウンスが必要とされます。別の可能性はディスタントライトプローブを利用することですが,屋外環境に対して明らなライトリークが出現する可能性があります。
● View-dependent effects: ローカルライトプローブは単一点からキャプチャされ(つまり,キューブマップの中心),グロッシーと鏡のような面からくる入射照明はビュー依存のためキャプチャーされたものよりも視点からは悪くなります。
これらの問題を解決するために,ライトプローブを取得する間はマテリアルのスペキュラーコンポーネントを無効にします。スペキュラー項のみを持つ金属表面は,ディフューズアルベドとしてフレネル \(f_0\) を用いることによってディフューズ面のように近似されます。キャプチャーする間,アルファチャンネルへと周囲のオブジェクトの可視性を格納します。これは後で,ローカルライトプローブの寄与をフェードするためにIBL合成の間に使用されます。図53はキャプチャーされたローカルライトプローブの例を示しています。
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.61 より引用
Participating media: 例として霧がかった環境において,理想的にはローカルライトプローブの寄与を評価するときに中間透過率を考慮に入れるべきです。ローカルライトプロープへと直接フォグを取得することは3次元の関数モデル(theta, phi, depth)の代わりに2次元の関数モデル(theta, phi)であるので正確に動作しません。したがって,この単純な2次元の関数で,陰影付けされた点とローカルライトプローブのプロキシジオメトリ間の実際の透過率を計算することは不可能です。
4.9.2 Light probe filtering
積分式46は視線方向\({\bf v}\),マテリアルモデル\(f\),そして,そのパラメータ\(\Theta\) に依存しています。通常そのような積分は解析解を持たず,典型的にはモンテカルロ法のような確率論の積分技法による数値評価を必要とします。そのような積分を直接的に評価することはフレームごとの各ピクセルに対して多くのサンプルを必要とします。これは可能である一方で,ゲームのような高いパフォーマンスアプリケーションの背景においては現実的ではありません。重点サンプリングはサンプルの数を減らすのを可能としますが,たとえマルチプルインポータンスサンプリング(MIS)でも,毎フレーム各ピクセルを評価するために必要とされるサンプルの数はあまりにもコストが高すぎます。
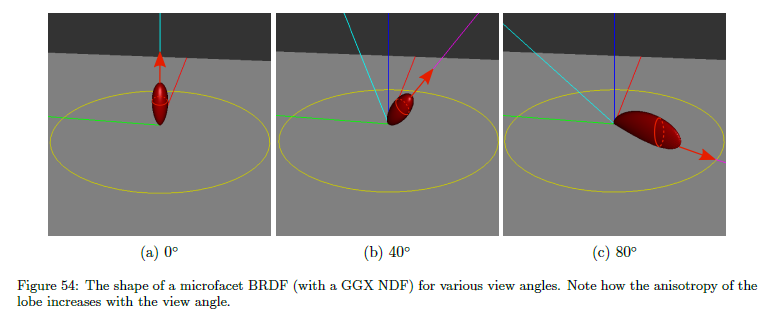
Specular pre-integration: この評価を簡略化するために,ある近似を作成することによって事前積分を可能とします。各\({\bf v}\)と \(\Theta\) に対するこの事前組み込みされた式は非常に大きなメモリフットプリントを必要とします。したがって,最初の近似はビュー依存を取り除くことです。これはBRDFの粗悪な近似を招きますが,許容できるトレードオフです: マイクロファセットフレームワークと/あるいは半角パラメータライゼーションに基づくBRDFの形状は図54に示すように視野角に強く依存します。入射方向の法線において,BRDFの形状は等方性となります。グレージング角においてBRDFの形状は異方性となります。事前組み込みされた式46に対するビュー依存を取り除くことはすべての視野角においてBRDFの形状が等方性であるという仮定を作ります。これはキービジュアルの相違を招き,悪用される反射を妨げます。この近似は図55上で示されるようにフラットサーフェイス上でかなり気付く可能性がありますが,湾曲したサーフェイス上では低減します。
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.62 より引用
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.63 より引用
事前積分の次元を更に減らすために,ラフネス\(\alpha\)と入射角\(0^{\circ}\) におけるフレネル値 \(f_0\) を持つ, \(\Theta = (f_0, \alpha)\)へのパラメータの数を減らす必要があります。先に述べたように,式46は数値的な積分を必要とします。”事前ベイクされた”ローカルライトプローブについて,この積分式はオフラインですべての計算が行われるので,任意のパフォーマンスの懸念をせずに行うことができます。しかしながら,要望に応じたライトプローブのために,ローカルライトプローブは継続的に更新あるいは,アーティストによる迅速な操作(ローカルライトプローブの配置,ディスタントライトプローブの回転)パフォーマンスが重要であり,良い品質/スピートの比率に達する必要があります。重点サンプリングは被積分関数の重要な部分の計算に着目することによって収束のスピートアップに使うことが可能です:
\[
L(v) = \frac{1}{N} \sum^{N}_{i} \frac{f_r({\bf l}_i, {\bf v}, {\Theta}) \, L({\bf l}_i)}{p_r({\bf l}_i, {\bf v}, \Theta)} \langle {\bf n} \cdot {\bf l}_i \rangle \tag{47}
\]
\(p_r\)はBRDFの確率密度関数を表しています。\({\bf l}_i\)は\(p_r\)から生成されたサンプルです。KarisはマクロファセットBRDFの場合において,積分式47が2つの項の積へと分解することによって近似可能であることを示しました:LDとDFGです。\(p_r = D({\bf h}, \alpha)\langle {\bf n} \cdot {\bf h} \rangle J({\bf h})\)と,ハーフベクトルからライティングベクトル \(J({\bf h}) = \frac{1}{4\langle {\bf v} \cdot {\bf h} \rangle}\) へのヤコビアン\(J\)の変換で,次を得ます:
\begin{eqnarray}
L(v) &=& \frac{1}{N} \sum^{N}_{i} \frac{f_r({\bf l}, {\bf v}, \Theta) \, L({\bf l})}{p_r({\bf l}, {\bf v}, \Theta)} \langle {\bf n} \cdot {\bf l} \rangle \tag{48} \\
&=& \frac{1}{N} \sum^{N}_{i} \frac{D({\bf h}, \alpha) \, F({\bf v}, {\bf h}, f_0, f_{90}) \, G({\bf l}, {\bf v}, {\bf h}, \alpha) }{4 \langle {\bf n} \cdot {\bf l} \rangle \langle {\bf n} \cdot {\bf v} \rangle} \frac{1}{p_r({\bf l}, {\bf v}, \Theta)} L({\bf l}) \langle {\bf n} \cdot {\bf l} \rangle \tag{49} \\
&=& \frac{1}{N} \sum^{N}_{i} \frac{D({\bf h}, \alpha) \, F({\bf v}, {\bf h}, f_0, f_{90}) \, G({\bf l}, {\bf v}, {\bf h}, \alpha) }{4 \langle {\bf n} \cdot {\bf v} \rangle} \frac{1}{p_r({\bf l}, {\bf v}, \Theta)} L({\bf l}) \tag{50} \\
&=& \frac{1}{N} \sum^{N}_{i} \frac{D({\bf h}, \alpha) \, F({\bf v}, {\bf h}, f_0, f_{90}) \, G({\bf l}, {\bf v}, {\bf h}, \alpha) }{4 \langle {\bf n} \cdot {\bf v} \rangle} \frac{4 \langle {\bf v} \cdot {\bf h} \rangle}{D({\bf h}, \alpha) \langle {\bf n} \cdot {\bf h} \rangle} L({\bf l}) \tag{51} \\
&=& \frac{1}{N} \sum^{N}_{i} \frac{F({\bf v}, {\bf h}, f_0, f_{90}) \, G({\bf l}, {\bf v}, {\bf h}, \alpha)}{\langle {\bf n} \cdot {\bf v} \rangle \langle {\bf n} \cdot {\bf h} \rangle} \langle {\bf v} \cdot {\bf h} \rangle \, L({\bf l}) \tag{52} \\
& \approx & \underbrace{ \frac{1}{N} \sum^{N}_{i} \frac{F({\bf v}, {\bf h}, f_0, f_{90}) \, G({\bf l}, {\bf v}, {\bf h}, \alpha)}{\langle {\bf n} \cdot {\bf v} \rangle \langle {\bf n} \cdot {\bf h} \rangle} \langle{\bf v} \cdot {\bf h} \rangle }_{\rm DFG \, term} \underbrace{\frac{1}{\sum^{N}_{i} \langle{\bf n} \cdot {\bf l} \rangle} \sum^{N}_{i} L({\bf l}) \langle {\bf n} \cdot {\bf l} \rangle}_{\rm LD \, term} \tag{53}
\end{eqnarray}
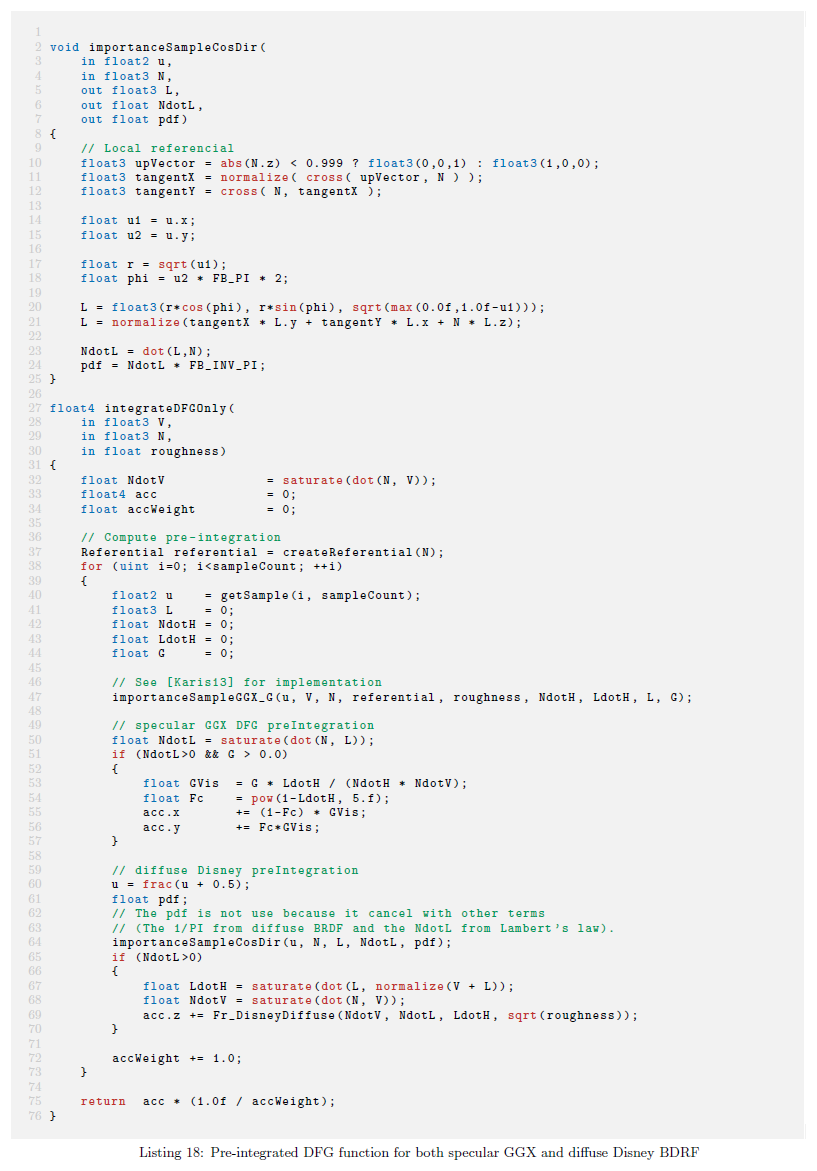
この分解は2つの独立した項 \(DFG\) と \(LD\) へと導き,個別に事前計算することが可能となります。\(LD\)項は各ライトプローブに対して計算するのに必要となりますが,一方\(DFG\)は一度のみ計算し,すべてのライトプローブに対して再利用します。リスト18はDFG項を示しています。LD項内にある余分な \(\langle {\bf n} \cdot {\bf l} \rangle\) も異なる重みづけしている \(\frac{1}{\sum^{N}_{i} \langle {\bf n} \cdot {\bf l} \rangle}\)も同じと気づくことができます。これらの経験による項はこの積分の可分性の粗い仮定から被る再構築されたライティングの積分を改善するためにKarisによって導入されました。これらの項は数学的な導出は存在せず,定数\(L({\bf l})\)と正確な合致を持つことを目的としています。[Kar13]によって示されるように,フレネル項のSchlickの公式を用います:
\[
F({\bf v}, {\bf h}, f_0, f_{90}) = f_0 + (f_{90}\, – \,f_0)(1 \,- \,\langle {\bf v} \cdot {\bf h} \rangle )^5 \tag{54}
\]
DFG項は視野角\(v\) とラフネス\(\alpha\),事前計算の外側の残った\(f_0\)と\(f_{90}\)のみに依存する2次元関数によって表現することが可能です。この2次元関数は2つの項を格納します:\({\rm DFG_1}\)と\({\rm DFG_2}\)です。
\begin{eqnarray}
DFG({\bf v}, {\bf l}, f_0, f_{90}, \alpha) &=& \frac{1}{N} \sum^{N}_{i} \frac{(f_0 + (f_{90} – f_0))(1 – \langle {\bf v} \cdot {\bf h} \rangle)^5 \, G({\bf l}, {\bf v}, {\bf h}, \alpha)}{\langle {\bf n} \cdot {\bf v} \rangle \langle {\bf n} \cdot {\bf h} \rangle} \, \langle {\bf v} \cdot {\bf h} \rangle \tag{55} \\
&=& \frac{1}{N} \sum^{N}_{i} (f_0 + (f_{90} – f_0) F \, c) \, G_{Vis} \\ &{\bf with}& \, G_{Vis} = \frac{G({\bf l}, {\bf v}, {\bf h}, \alpha)}{\langle {\bf n} \cdot {\bf v} \rangle \langle {\bf n} \cdot {\bf h} \rangle} \, \langle {\bf v} \cdot {\bf h} \rangle , \, F \, c = (1 – \langle {\bf v} \cdot {\bf h} \rangle )^5 \tag{56} \\
&=& \frac{1}{N} \sum^{N}_{i} f_0 \, G_{Vis} + f_{90} \, F \, c \, G_{Vis} – f_0 \, F \, c \, G_{Vis} \tag{57} \\
&=& f_0 \underbrace{\frac{1}{N} \sum^{N}_{i} (1 – F \, c) \, G_{Vis}}_{\rm DFG_1 \, term} + f_{90} \underbrace{\frac{1}{N} \sum^{N}_{i} F \, c \, G_{Vis}}_{\rm DFG_2 \, term} \tag{58}
\end{eqnarray}
※リストは,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, pp.64-65 より引用
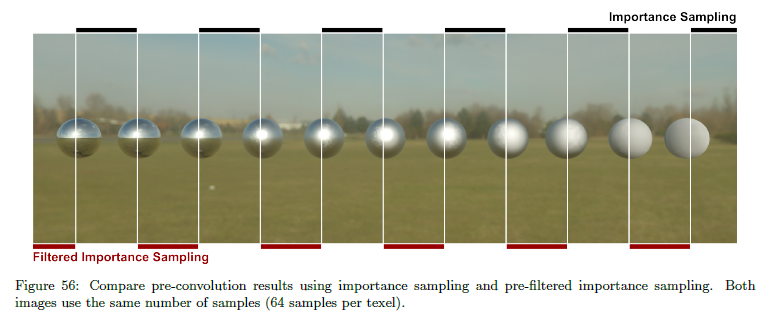
LD項は日の時間変化のような入射照明の変更があるごとに再計算する必要があります。これはLDがライタイムにおいて再計算する必要があり,従って高速で頑健である必要があるということを意味しています。重点サンプリングを使用することは収束を改善しますが,かなり小数のサンプルを必要とします。事前フィルタされた重点サンプリングはKrivánekらによって導入されました。[KC08]は低い確率のサンプルについて事前フィルタされた値を利用することによってサンプルの数を減らすことを可能にします。図56を参照してください,小さなバイアスを導入するコストでこれは著しく収束を向上します。リスト19はLD項を示しています。高いコントラストの環境において,特に中と高ラフネス\(\alpha\)値について依然としていくつかノイズが観測されます。これは主に高いコントラストのライトプローブ(本当に高い強度を持ついくつかのピクセル)半球上のBRDFのローブの大きなサポート(特にGGXのようなロングテールのNDF)によって引き起こされます。このノイズを取り除くために,サンプルの数を増やすかあるいはテクセルごとのサンプルパターンを回転/ジッタリングすることによってバイアスに相関性あるノイズをトレードすることが可能です。これはあるゴーストアーティファクトを招きますが,大抵ノイズよりも知覚しづらいです。
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.66 より引用
※リストは,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.66 より引用
Difffuse pre-integration: 現在まで,我々はスペキュラー \(f_r\) 部分を持つ入射照明の積分のみを考慮してきました。先に述べたように,マテリアル部分のすべてが同じ入射照明を受けることは極めて重要です。これゆえ,ライティングはディフューズ部分\(f_d\)に対しても積分することが必要です。\(f_d\)は視野角\({\bf v}\)とディフューズDisney BRDFを使用するのでラフネス\(\alpha\) に依存するので,我々は,DFGとLDの2つの項へと積分を分解することによってスペキュラー部分についてのように事前組み込みを利用します。LD項について,入射照明は\(\langle {\bf n} \cdot {\bf l} \rangle\) によって重みづけされた一定のLambertianローブで積分されます。これはRamamoorthiら[RH01]によって示されたように,あるいは重点サンプリングによって球面調和基底で効率的に行うことが可能です。我々はこの低角周波ローブに適合させるので,(以下のDisneyローブ分布の代わりとして)コサイン分布に従うサンプル分布を持つ重点サンプリングを使用します。\(p_r = \frac{\langle {\bf n} \cdot {\bf l} \rangle}{\pi}\) を意味し:
\begin{eqnarray}
L(v) &=& \frac{1}{N} \sum^{N}_{i} \frac{f_d({\bf l}, {\bf v}, \Theta) \, L({\bf l})}{p_r ({\bf l}, {\bf v}, \Theta)} \, \langle {\bf n} \cdot {\bf l} \rangle \tag{59} \\
&=& \frac{1}{N} \sum^{N}_{i} \frac{\pi \, f_d({\bf l}, {\bf v}, \Theta) \, L({\bf l})}{\langle {\bf n} \cdot {\bf l} \rangle} \, \langle {\bf n} \cdot {\bf l} \rangle \tag{60} \\
&=& \frac{1}{N} \sum^{N}_{i} \pi \, f_d({\bf l}, {\bf v}, \Theta) \, L({\bf l}) \tag{61} \\
& \approx & \underbrace{\frac{\pi}{N} \sum^{N}_{i} f_d({\bf l}, {\bf v}, \Theta)}_{\rm DFG \, term} \, \underbrace{\frac{1}{N} \sum^{N}_{i} L({\bf l})}_{\rm LD \, term} \tag{62}
\end{eqnarray}
LD項の計算はリスト20で見ることができます。DFG項は様々な視野角\(v\) とラフネス\(\alpha\) に対してディフューズDisney BRDFを積分することによって計算され,リスト18を参照してください。
※リストは,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.67 より引用
Storage: これらの事前積分の結果を格納することは文献ではよく無視されますが,重要な細目です。DFG項は\(128^2\)の解像度を持つ2次元テクスチャへと容易に格納することができます。LD項は3次元関数で,16ビットの浮動小数のキューブテクスチャのセットへと格納することができます(Frostbiteでは,要求された品質に応じて\(128^2\)から\(512^2\)の解像度を使用しますが,良好な品質を持つ平滑な/鏡面のような面を表現するのを可能とする最小値として\(256^2\)であることがわかりました。事前積分されたライティングの周波数は\(\alpha\) が増加するにつれて段々と低くなるので,事前フィルタされた結果をミップレベルへと格納することができます。このストレージは\(\alpha_{\rm lin}\)(知覚的に線形なラフネス) を \(mipLevel\)へとマッピングする関数によって定義されます。図57と図58に示すように,\(\alpha_{\rm lin}\) の指数-2のマッピングが良い結果を与えます。一方で,線形マッピングは全体の分布をより良く与え,中間範囲のラフネスを保ち,低いラフネスに対してほんのわずかにブラーを導入します。我々は指数-2にするのを決定しました:
\[
mipLevel = \sqrt{\alpha_{\rm lin}} \, mipCount \tag{63}
\]
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.68 より引用
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.68 より引用
4.9.3 Light probe evaluation
ランタイムにおいて,ローカルとディスタントライトプローブは環境由来の光を考慮して評価されます。一方で,ディフューズとスペキュラーの事前積分の両方はビュー依存した方法で行われ,実際のディフューズ\(f_d\)とスペキュラー\(f_r\)の項はビュー依存になります。これが意味にするのはそれらのローブの方向が視線ベクトル\({\bf v}\)に依存するということです。スペキュラー\(f_r\)項について,事前積分された値をフェッチすることについてミラー反射を用いる代わりに,主要な方向におけるBRDFを評価します(つまり,セクション3.1でみた”オフスペキュラーピーク”)。
このシフトをモデルするために,視野角に依存した最も高い値の偏差とマテリアルラフネスを観察しました。このドキュメントのMathematicaのガイドファイルとして利用できます。我々が提案したモデルは浅い視野角において絶縁体マテリアルに対する正確な振る舞いを不完全にキャプチャーします。これはなぜかというと,ある角度において実際のローブを”出現する”のみだからです。幸いなことに,フレネル値は視野角でゆっくり増加し,これはほとんど知覚できるエラーはなく,この近似は十分に良いです。リスト21を参照。また我々はオリジナルの最もフィットした近似よりも良い結果を与える支配的な方向のスペキュラーローブの近似をより単純にいくつかの実験の後で観測しました,リスト22を参照。評価と手法の比較の結果は図59で示されます。G Smithと相関がある項と相関がないものに対して支配的な方向の近似を行いました。それは双方に対して単純でうまく動作するように見えます。
※リストは,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.69 より引用
※リストは,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.69より引用
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.71より引用
純粋なLambertianサーフェイスについて,BRDFはビュー依存であるので方向のシフトは存在しません。しかしながら,再帰反射Disneyディフューズ項について,非線形の方法における支配的な方向のシフトは遠く離れます。単純な線形モデルを見せるスペキュラー項についてのように同じ解析を適用することは比較的正確にこの振る舞いをキャプチャーすることが可能です。リスト23を参照。Frostbiteにおいて,入射ディフューズライティングはGBuffer生成の間,適用します。したがって,支配的な方を正確に取り扱うことはこの段階において,適用するのが必要になります。正確な支配的な方向を取り扱うことによって得られた違いは捉えにくく,我々は採用しないことを決めしました。更に,デカールはセクション3.3でハイライトされたように正確にサポートできません。
※リストは,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.70より引用
スペキュラーとディフューズ項の両方に対してディスタントライトプローブについてのライティングを評価するためのコードはリスト24で示されます。
※リストは,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.70より引用
Energy conservation: 言及したように,ライトプローブはライティングの一貫性を得るためにマテリアルのスペキュラーとディフューズ部分の両方に対して評価されます。この場合において1つはライティングを2度適用すると考えることができ,とりわけ粗い表面の場合において両方の積分が半球上で実行されます。しかし,DisneyディフューズBRDFがマテリアルモデルのエネルギー保存を保証する修正のおかげで,入射エネルギーがスペキュラーとディフューズの項に適切な割合でエネルギーを増加させることなく影響与えます。
Re-projection: 周囲環境の視差を考慮に入れるために,ローカルライトプローブは取得されたライティング情報をリプロジェクションするためにプロキシジオメトリを使用します。Frostbiteでは,2つのタイプのリプロジェクションボリュームをサポートします:球と指向性ボックスです。これらのボリュームは手動で配置され,可能な限り周囲のジオメトリに近くなるように近似するためにアーティストによってセットアップされます。ランタイムにおいて,ローカルライトプローブ内のオブジェクトはサンプリング方向とプロキシジオメトリの間で交差し,この交差に基づいて的確な方向でローカルライトプローブを評価します[LZ12]。ライトプローブはボリュームの中心から事前畳み込みされ,交差方向を補正することは高いラフネス値に対するアーティファクトを生み出す可能性があります。アーティファクト(とげとげしい不連続性)を制限するために,補正された方向からラフネスに基づく元来の方向へ滑らかに補間します。さらに,我々はチューブマップのキャプチャーの中心へと移動するオフセットベクトルを提供しました。これはアーティストに問題である解像度を増加させること,またボリュームの中における望ましくないオブジェクト位置の周囲を得ることを可能とします。
我々のローカルライトプローブはマテリアルのスペキュラー部分についてのみ使用されます。スペキュラー項のローカルライトプローブについてライティングを評価するのためのコードはAppendix Fで提示されます。ディフューズコンポーネントについて,ライティング情報はラジオシティシステムから生じ,ライトマップあるいはプローブボリュームを通じて入射照明のクエリを可能とします。ディフューズライティングは再帰反射ローブの支配的な方向で評価されます。
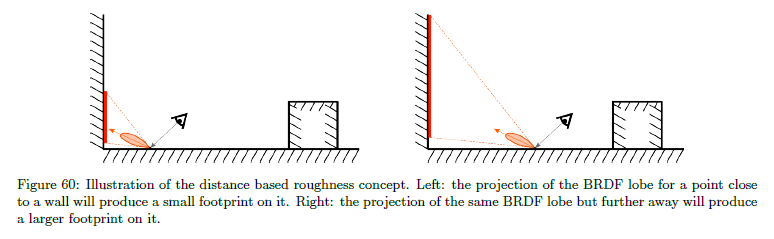
Distance based roughness: BRDFのローブは入射照明が半球上で積分される方法で記述されます。この角度の記述は距離に依存したBRDFのフットプリントを生成します。与えられた陰影付けされた点について,オブジェクトの反射はオブジェクトが陰影付けされた点に近づいたときに鋭くなり,離れ動くにつれてますますブラーがかかるようになります。図60と61を参照。ローカルライトプローブプロキシジオメトリは陰影付けされた点と入射照明の間の距離を計算することを可能とします。この情報で,おおざっぱなBRDFのフットプリントの近似を環境へとキャストすることができます。評価中に,相似なフットプリントに合わせるためにBRDFのラフネスを修正し,この”距離に基づくラフネス”を近似します。リスト25参照。
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.72より引用
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.73より引用
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.72より引用
このラフネス補正を計算するために,支配的なBRDFの方向に沿ったNDFの境界をコーンを計算します。バウンディングコーンの角度\(\theta_{lim}\)は受けたエネルギーのパーセンテージ\(E\)を持つ,すなわち\(E = 75 \%\)の場合に,NDFボリュームの\(75\%\)を覆うコーンになります(詳細なプロットはMathematicaのガイドファイルで利用できます),\(\theta_{lim} = {\rm atan}\left({\frac{E\alpha^2}{1-E}}\right)\)によるラフネス\(\alpha\)に関係します。このコーンとプロキシジオメトリとの交差は円の半径\(R\)によって近似されます。この半径\(R\)から,我々はライトプローブの中心から計算を開始し,その中心から一致するラフネスを推定します。この完全連鎖操作は多くの項を排除することを可能とし,”距離に基づくラフネス”は単純な式:\(\alpha’ = \frac{distanceIntersectionToShaededPoint}{distanceIntersectionToProbeCenter} \alpha\) でラフネスに関連付けることが可能です。これは大雑把な近似であるということが重要です:近似された交差に加えて,スケールされたフットプリントとして事前畳み込みされた輝度を使用することを試みます。これは低いラフネス値に対してはきちんと動作しますが,高いラフネスに対しては不正確になります。この問題と避けるためと,この効果が低いラフネス値についてより目立つので,我々は線形に”距離に基づくラフネス”を元来のラフネスへと,ラフネス値に基づき補間します。また,線形なラフネスで動作することがより良い結果を与えることもわかりました。
後のセクション4.9.5で説明するように,SSRはSSRパスが与えられたピクセルに対する反射情報を求めるのを失敗したときにローカルライトプローブへと後退します。異なるライティング積分のため(SSRは適切にBRDFを積分し,完全に視差を考慮しますが,一方ローカルライトプローブは単一点から事前積分されており,視差は近似されます),この距離に基づくラフネスを考慮することはSSRとローカルライトプローブの間に合致するのを可能とし,結果として良い遷移になります。
4.9.4 Screen space reflections
スクリーン空間反射(SSR)は中距離に近い範囲の反射のキャプチャーを可能とし,正確なオクルージョンをもたらすので小さなオブジェクト/ディテールに対して間違いなく重要です。我々のテクニックは階層的Z構造を利用し,それはシーンの深度バッファ上に構築されます。これは高速に長いレイをトレースするのを可能とし,可能な限り利用可能なシーン情報を使用します。入射照明はこのとき,マテリアルのBRDFに対して積分されます。我々のアプローチは”Hi-Z Screen-Space Cone Tranced Reflections”[Ulu14]にてUludagによって述べられたアプローチです。
SSR and emissive: セクション4.8で見たように,エリアライトは2つの部分から構成されます:
● An analytical light はエミッションプロパティで記述され,BRDFで積分されます。
● An emissive surface は放射しているライトの実際の形状を記述します。
最初の部分は解析的なライティング評価パスの間で評価されます。第2の部分は純粋に見た目で,SSRパスまたはローカルライトプローブパスによってキャプチャーすることが可能です。この場合において,ライトは2倍の寄与となります:解析的な評価した時点と,画像に基づいた評価した時点は,ここではエミッシブ形状のキャプチャーのように入射照明として取り扱われます。残念なことに,これはこの問題を解決するための容易な方法ではありません。
4.9.5 Image based lights composition
各IBLタイプは異なる入射照明を表現し,制限を持ちます。その環境内で継続的にフィッティングするオブジェクトを持つのを可能とするために,我々は階層的な方法でそれらのIBL全てを結び付けます。
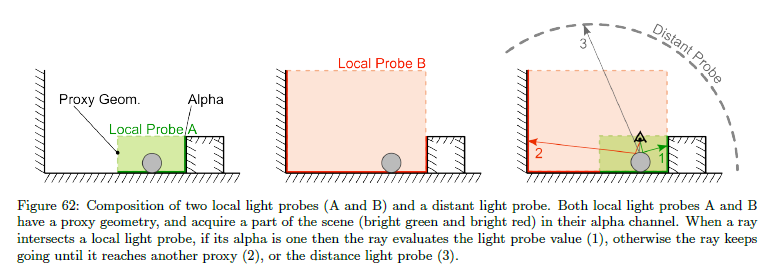
SSRは正確な反射を得るために良いテクニックですが,スクリーン空間の制限(現在の錘台と単一の深度レイヤー情報へと情報が制限される)のためにたまに失敗します。様々なヒューリスティック(シーン境界近傍,レイの方向,交差タイプなど)により主な失敗の場合を検知することが可能です。SSRが失敗したとき,ローカルライトプルーブ情報へと後退します。単一の視点からキャプチャーされる一方で,ライトプローブはSSRパスからの欠落した任意の情報をスムーズに埋めるためにプロキシジオメトリへとキャプチャーされた情報を再プロジェクションするのを可能とします。ローカルライトプローブはレベルについてすべて,アーティストによって手動で配置されます。ローカルライトプローブは反射情報が完全にリカバーされるまで小さなものから大きなボリュームへと階層的に評価され,アーティストがネストするの許可し,従って,ある位置において局所的に反射を改善します。反射情報がまだ欠落している場合は,ディスタントライトプローブが評価されます。
図62はこのコンポジションの概略を与え,異なるステップの疑似コードは次のようになります:
// 短距離反射
Evaluate SSR
RGB = SSR.rgb
Alpha = SSR.a
// 中距離反射
While local light probes And Alpha < 1 do
Evaluate local light probe
a = saturate(localLightProbe.a - Alpha)
RGB += localLightProbe.rgb * a
Alpha = saturate(a + Alpah)
// 長距離反射
If Alpha < 1 Then
Evaluate distance light probe
RGB += distantLightProbe.rgb * (1 - Alpha)
※図は,Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.74より引用
ローカルライトプローブのアルファチャンネルは与えられたピクセルが周囲環境の近いものに属するかどうかを示しています。このタグ付けはスカイピクセルを受け付けないことを可能とし,ディスタントライトプローブをフェッチすることを強制します。これはいくつかの利点を持ちます:ディスタントライトプローブは低いコストで動的なエレメント(例えば移動する雲)を含むことが可能です;ディスタントライトプローブはきっちりとした詳細を作成し,普通はローカルライトプローブよりも高い解像度となります。欠点はこのような方法で結び付けたときに入射照明の積分が完全に正確ではない結果になるということです。
中距離反射の重み計算について。我々は各ローカルライトプローブが重複して同じ可視情報を含むと仮定し,きっかり同じ方法でBRDFローブを遮蔽します。そのため,可視性0.1を持つ10の重複するローカルライトプローブを追加した場合に,0.1を得るべきです。このスキームはライトプローブの可視性の階層が1の場合に常にディスタントライトプローブの寄与を持ちます。このアルゴリズムはローカルライトプローブの順序に依存することに注意してください。
Planar reflections: 更に,平面反射の情報が利用可能なとき,フォーワードにおけるオブジェクトごとの基底,あるいはディファードにおいてタグ付けしているオブジェクトが受けるもののどちらか一方を適用することが可能です。平面反射は普通,シングルの深度レイヤーの制限と錘台の制限の両方を和らげ,より頑健にするのでフラットな面に対してSSRの良い代替えとなります。