こんこよ~。Pocolです。
今日は以前に読んだ,Generalized Resampled Importance Sampling: Foundations of ReSTIRの補足資料である
[Lin 2022] Daqi Lin, Markus Kettunen, Benedikt Bitterli, Jacopo Pantaleoni, Cem Yuksel, Chris Wyman, “Supplementary Document: Generalized Resampled Importance Sampling: Foundation of ReSTIR”, https://research.nvidia.com/publication/2022-07_generalized-resampled-importance-sampling-foundations-restir, 2022.
を読んでみます。
いつもながら,誤字・誤訳があるかと思いますので,ご指摘頂ける場合は正しい翻訳例と共に指摘して頂けるとありがたいです。
S.1 DERIVATION OF RESAMPLING MIS WEIGHTS
このセクションでは、まず、式19で与えられるリサンプリング重み\(w_i\)が有限の上界を持たなければならないという要件から、一般化されたTalbot MIS(式36)とペアワイズMIS(式37、式38)の重みを導出します。
次に、上記のMIS重みのスキームと、\({\hat p_i}\)の代わりに扱いやすいPDF\(p_i\)を使用するMISウェイトの変形について、リサンプリングウェイト\(w_i\)の上界を導出します。
\(M\)個の入力サンプル\(X_i\)のうち、集合\(R\)のインデックスが正準(定義5.2)、すなわち、そのドメインが\(\Omega\)、シフト・マッピングが恒等式、目標密度\({\hat p_i}={\hat p}\)であると仮定します。正準サンプルの集合を\(|R|\)とします。
S.1.1 Generalizing Talbot MIS Weights
我々はまず、リサンプリングウェイトが有界であることを要求し、この条件を満たすMISウェイト\(m_i\)を導出します。\(Y_i = T_i(X_i)\)とし、\(Y_i \in T_i({\rm supp}X_i)\)と仮定します。\(X_i\)のリサンプリングウェイトは、式19により,
\begin{eqnarray}
w_i = m_i(Y_i) \cdot {\hat p}(Y_i) W_i \cdot \left| \frac{\partial Y_i}{\partial X_i} \right| \tag{S.1}
\end{eqnarray}
\({\hat p_i}(X_i)W_i \leq C_i\)と仮定すると、上記の式は次のようになります。
\begin{eqnarray}
w_i &=& m_i(Y_i) \cdot \frac{ {\hat p}(Y_i){\hat p}_i(X_i)W_i }{ {\hat p}_i(X_i) } \left| \frac{\partial Y_i}{\partial X_i} \right| \tag{S.2} \\
& \leq & m_i(Y_i) \cdot \frac{ {\hat p}(Y_i) C_i }{ {\hat p}_i(X_i) } \cdot \left| \frac{\partial Y_i}{\partial X_i} \right| \tag{S.3}
\end{eqnarray}
これは最大でも何らかの \({\tilde C_i}\) である必要がありますが、適切な関数 \(m_i\) が見つかる限り、自由に選択できます。この場合、\(w_i \leq {\tilde C_i}\) も次のようになります。
\begin{eqnarray}
w_i \leq m_i(Y_i) \cdot \frac{ {\hat p}(Y_i)C_i }{ {\hat p}_i(X_i) } \cdot \left| \frac{\partial Y_i}{\partial X_i} \right| \leq {\tilde C_i} \tag{S.4}
\end{eqnarray}
後者の不等式は次の式と等価です。
\begin{eqnarray}
m_i(Y_i) \leq \frac{ {\tilde C_i} }{C_i} \frac{ {\hat p}_i(X_i) | \frac{\partial Y_i}{\partial X_i} |^{-1} }{ {\hat p}(Y_i)} \tag{S.5}
\end{eqnarray}
もし\(j\)が任意の正準インデックスであれば、\( {\hat p}(Y_i) = {\hat p}_j({T_j}^{-1}(Y_i)) \left| \frac{\partial {T_i}^{-1}}{ \partial Y_i} \right| \)となり、分子と分母が似てくることがわかります:
\begin{eqnarray}
m_i(Y_i) \leq \frac{{\tilde C_i}}{ C_i } \frac{ {\hat p}_i({T_i}^{-1}(Y_i)) \left| \frac{\partial {T_i}^{-1} }{ \partial Y_i} \right| }{ {\hat p}_j ({T_j}^{-1}(Y_i)) \left| \frac{\partial {T_j}^{-1} }{ \partial Y_i } \right| } = \frac{{\tilde C_i}}{C_i} \frac{ {\hat p}_{\leftarrow i}(Y_i) }{ {\hat p}_{\leftarrow} j(Y_i) } \tag{S.6}
\end{eqnarray}
\(Y_i = T_i(X_i)\)がサンプリングされた(したがって\(Y_i \in T_i({\rm supp}X_i\))ので、\({\hat p}_{\leftarrow i}\)と\({\hat p}_{\leftarrow j}\)で式を書くことは正当であり、これは\(Y_i \in {\rm supp}{\hat p}\)を意味します。\(j\)(は正準インデックスなので、\({\rm supp}{\hat p} \subset {\rm supp}X_j = {\rm supp} T_j({\rm supp}X_j)\)、そしてここでは\(Y_i \in {\rm supp}T_j(X_j)\)です。
\(m_i\)が上記の不等式を満たすが分母が大きくなるようなものであれば、それも上記の不等式を満たします。\(m_i\)の分母は、すべての添字\(j \in \{1, \cdots, M \}\)について合計することで対称にする。 さらに\({\tilde C_i} = C_i\)を選ぶと,次を導きます。
\begin{eqnarray}
m_i (y) = \frac{ {\hat p}_{\leftarrow i}(y) }{ \sum_{j=1}^M {\hat p}_{\leftarrow j}(y) } \tag{S.7}
\end{eqnarray}
これらの\(m_i\)は式20を満たし(\({\hat p}_{\leftarrow i}\)の定義、式35を参照)、有効で非負のリサンプリングMISウェイトとなります。
S.1.2 Generalizing Pairwise MIS Weights
一般化されたペアワイズMIS重みを導出するために、式S.5まで前と同様に進めます。
\begin{eqnarray}
m_i(Y_i) \leq \frac{{\tilde C}_i }{C_i} \frac{ {\hat p}_{\leftarrow i}(Y_i) }{ {\hat p}(Y_i)} \tag{S.8}
\end{eqnarray}
ただし、正準サンプル\(i \in R\)と非正準インデックス\(i {\notin} R\)は異なるものとして扱います。以前のようにすべてのインデックスを分母に含める代わりに、インデックス\(i\)に対応する項だけ分母を正の乗数\(\alpha_i\)で増加させる。非正準サンプルは
\begin{eqnarray}
m_i(y) = \frac{{\tilde C}_i}{C_i} \frac{{\hat p}_{\leftarrow i}(y) }{ {\hat p}(y) + \alpha_i {\hat p}_{\leftarrow}(y)} \quad {\rm for} \quad i {\notin} R \tag{S.9}
\end{eqnarray}
を選択し、この選択が式S.8を満たすことを観察します。式20を満たすためには、\(y\)を生成することができる\(i\)について\(m_i\)の和が1になる必要があるので、単純に余りを正規標本\(i \in R\)に一様に分割します。
\begin{eqnarray}
m_i(y) = \frac{1}{|R|} \left( 1 – \sum_{j \notin R} m_j(y) \right) \quad {\rm if} i \in R \tag{S.10}
\end{eqnarray}
\({\tilde C}_i\)と\(a_i\)の異なる選択により、MISの潜在的な重みの系列が得られます:\(\beta_i = {\tilde C}_i / C_i\)を表すと、次のようになります。
\begin{eqnarray}
m_i(y) &=& \frac{1}{|R|} \left( 1 – \sum_{j \notin R} \beta_j \frac{ {\hat p}_{\leftarrow j}(y) }{ {\hat p}(y) + \alpha_j {\hat p}_{\leftarrow j}(y) } \right) \tag{S.11} \\
&=& \frac{1}{|R|} \left( 1 – \sum_{j \notin R} \frac{\beta_j}{\alpha_j} + \sum_{j \notin R} \frac{\beta_j}{\alpha_j} \frac{ {\hat p}(y) }{ {\hat p}(y) + \alpha_j {\hat p}_{\leftarrow j}(y) } \right) \quad {\rm if} \in R \\
m_i(y) &=& \beta_i \frac{ {\hat p}_{\leftarrow i}(y) }{ {\hat p}(y) + \alpha_i {\hat p}_{\leftarrow i}(y) } \quad {\rm if} \, i \notin R \tag{S.12}
\end{eqnarray}
パラメータが\(i\)に依存しないことを条件としてこの族を制限し、\(\alpha_i= \alpha\)と\(\kappa = \sum_{i \notin R} \beta_i / \alpha_i = (M – |R|)\beta/\alpha\)とすると、次の族にたどり着きます。
\begin{eqnarray}
m_i(y) &=& \frac{1}{|R|} \left( 1 – \kappa + \frac{ \kappa }{ M – |R| } \sum_{j \notin R} \frac{ {\hat p}(y) }{ {\hat p}(y) + \alpha {\hat p}_{\leftarrow j}(y) } \right) \quad {\rm if} \, i \in R \tag{S.13} \\
m_i(y) &=& \alpha \frac{ \kappa }{ M – |R| } \frac{ {\hat p}_{\leftarrow i}(y) }{ {\hat p}(y) + \alpha {\hat p}_{\leftarrow i}(y) } \quad {\rm if} \, i \notin R \tag{S.14}
\end{eqnarray}
MISの重みは非負で和が1でなければならないので、すべての\(i\)と\(y\)に対して\(0 \leq m_i \leq 1\)でなければなりません。式S.13で\(m_i\)が負になる可能性があるので、一般に\(\kappa \leq 1\)でなければなりません。式S.14では\(\alpha \gt 0\)であり、\(m_i(y) \geq 0\)でなければならないので、\(0 \leq \kappa\)もなければなりません。我々は、\(0 \leq \kappa \leq 1\)とし、上記のMISの重みを、正準サンプル(\(\kappa = 0\), \(m_i=1/|R| \, {\rm for} \, i \in R\), \(m_i=0 \, {\rm for} \, i \notin R\))の1つを一様に選ぶことと、\(\alpha\)でパラメータ化された基本的なMISスキーム(\(\kappa=1\))の間の線形補間と解釈します:
\begin{eqnarray}
m_i(y) &=& \frac{1}{|R|} \left( \frac{1}{M – |R|} \sum_{j \notin R} \frac{ {\hat p}(y) }{ {\hat p}(y) + \alpha {\hat p}_{\leftarrow j}(y) } \right) \quad {\rm if} \, i \in R \tag{S.15} \\
m_i(y) &=& \alpha \frac{1}{M – |R|} \frac{ {\hat p}_{\leftarrow i}(y) }{ {\hat p}(y) + \alpha {\hat p}_{\leftarrow i}(y) } \quad {\rm if} \, i \notin R \tag{S.16}
\end{eqnarray}
The uniform case.
基本的なMISスキームのための\(\alpha\)の賢明な値を見つけるために,すべての\(X_i\)がi.i.d.である単純な場合を考察しました。すべての\(i\)に\({\hat p}_i = {\hat p}\)を指定します。この場合、サンプルのいずれかを優先する理由はなく、\(m_1 = \cdots = m_M = 1/M\)が生成されます。
\begin{eqnarray}
m_i(y) &=& \frac{1}{|R|} \left( \frac{1}{M – |R|} \sum_{j \notin R} \frac{1}{1 + \alpha} \right) = \frac{1}{M} \quad {\rm if} \, i \in R \tag{S.17} \\
m_i(y) &=& \alpha \frac{1}{M – |R|} \frac{1}{1 + \alpha} = \frac{1}{M} \quad {\rm if} \, i \notin R \tag{S.18}
\end{eqnarray}
上式から次を解きます。
\begin{eqnarray}
\alpha = \frac{M}{|R|} – 1 \tag{S.19}
\end{eqnarray}
基本的なケースである\(\kappa=1\)の場合、\(\alpha=M/|R| -1\)と置き換えると、次のようになります。
\begin{eqnarray}
m_i(y) &=& \frac{1}{M – |R|} \sum_{j \notin R} \frac{ {\hat p}(y) }{ |R| {\hat p}(y) + (M – |R|) {\hat p}_{\leftarrow j}(y) } \quad {\rm if} \, i \in R \tag{S.20} \\
m_i(y) &=& \frac{ {\hat p}_{\leftarrow i}(y) }{ |R| {\hat p}(y) + (M – |R|) {\hat p}_{\leftarrow i}(y) } \quad {\rm if} \, i \notin R \tag{S.21}
\end{eqnarray}
これを一様ペアワイズMISCと呼びます。
The defensive case.
代わりに、正準サンプルを他のサンプルよりも信頼できるものとして扱う場合は、\(\alpha = M/|R|-1\)を保持し、\(0 \leq \kappa \lt 1\)を選択することによって、常に正準サンプルのいずれかを選択するように前の解を補間することができます。そのようなヒューリスティックの1つは、正準サンプルのMISウェイトが常に他のサンプラーのそれと少なくとも同じ大きさであることを保証することです。\(\alpha = M/|R| – 1\)の場合、正準の\(m_i (y)\) は\((1 – \kappa)/|R|\) (式S.13の\({\hat p}_j(y) \rightarrow \infty\)を設定する)より小さくすることはできず、非正準の\(m_i\)は\( \kappa / (M – |R|)\) (式S.14の\({\hat p}_{\leftarrow j}(y) \rightarrow \infty\)を設定する)を超えることはできません。これらの境界は、\((1 – \kappa)/|R| = \kappa (M- |R|)\)、すなわち\(\kappa = (M – |R|)/M\)を選択することで等しくすることができ、これにより防御的な一般化されたペアワイズMISの重みが得られます。
\begin{eqnarray}
m_i(y) &=& \frac{1}{M} + \frac{1}{M} \sum_{j \notin R} \frac{ {\hat p}(y) }{ |R|{\hat p}(y) + (M – |R|) {\hat p}_{\leftarrow j}(y) } \quad {\rm if} \, i \in R \tag{S.22} \\
m_i(y) &=& \frac{M – |R|}{M} \frac{ {\hat p}_{\leftarrow i}(y) }{ |R| {\hat p}(y) + (M – |R|) {\hat p}_{\leftarrow i}(y) } \quad {\rm if} \, i \notin R \tag{S.23}
\end{eqnarray}
S.1.3 Resampling Weight Bounds
次に,一般化TalbotおよびペアワイズMISウェイトについてリサンプリングウェイトに対するより正確な境界を導出しました。すべての場合において、同じ境界\(C_i/|R|\)が得られます。ただし\({\hat p}_i(X_i) W_i \leq C_i\) です。
Generalized Talbot MIS
一般化されたTalbot MISウェイト(式S.7)を\(w_i\)の式(式S.1)に直接代入すると、\(Y_i\)が存在すると仮定して、以下のようになります(そうでなければ\(w_i=0\)です)。
\begin{eqnarray}
w_i &=& m_i(Y_i) \cdot {\hat p}(Y_i) W_i \cdot | \frac{\partial T_i}{\partial X_i} | \tag{S.24} \\
&=& \left( \frac{ {\hat p}_{\leftarrow i}(Y_i) }{ \sum_{j=1}^M {\hat p}_{\leftarrow j}(Y_i) } \cdot {\hat p}(Y_i) W_i \cdot | \frac{\partial T_i}{\partial X_i} | \right) \tag{S.25} \\
&=& \frac{ {\hat p}_i(X_i) | \frac{\partial {T_i}^{-1} }{ \partial Y_i} | }{ \sum_{j \in R} {\hat p}_{\leftarrow j}(Y_i) + \sum_{j \notin R}{\hat p}_{\leftarrow j}(Y_i) } \cdot {\hat p}(Y_i) W_i \cdot | \frac{\partial T_i}{\partial X_i} | \tag{S.26} \\
&=& \frac{ {\hat p}(Y_i) }{ |R| {\hat p}(Y_i) + \sum_{j \notin R}{\hat p}_{\leftarrow j}(Y_i) } \cdot {\hat p}_i (X_i) W_i \tag{S.27} \\
& \leq & \frac{1}{|R|} \cdot C_i = \frac{C_i}{|R|} \tag{S.28}
\end{eqnarray}
Generalized Pairwise MIS.
まず、\({\hat p}_i = {\hat p}\)を仮定して、実行可能なパラメータの組み合わせ\(\alpha \gt 0\)と\(0 \leq \kappa \leq 1\)を一気に説明します。正準サンプル\(i \in R\)の場合、\({\hat p}_i = {\hat p}\)と\(Y_i = T_i(X_i) = X_i\)があるので、式S.13を代入し、境界を得ます。
\begin{eqnarray}
w_i &=& m_i(Y_i) \cdot {\hat p}(Y_i) W_i \cdot \left| \frac{\partial Y_i}{\partial X_i} \right| \tag{S.29} \\
&=& \frac{1}{|R|} \left( 1 – \kappa + \frac{\kappa}{M – |R|} \sum_{j \notin R} \frac{ {\hat p}(Y_i) }{ {\hat p}(Y_i) + \alpha {\hat p}_{\leftarrow j}(Y_i) } \right) \cdot {\hat p}(Y_i) W_i \cdot 1 \tag{S.30} \\
& \leq & \frac{1}{|R|} \left( 1 – \kappa + \frac{\kappa}{M – |R|} \sum_{j \notin R} \frac{{\hat p}(Y_i) }{ {\hat p}(Y_i)} \right) \cdot {\hat p}(Y_i) W_i \tag{S.31} \\
& \leq & \frac{C_i}{|R|} \tag{S.32}
\end{eqnarray}
非正準サンプル\(i \notin R\)については、\({\hat p}_i(X_i) W_i \leq C_i\)を再び仮定し、式S.14を代入すると、次のような境界が得られます。
\begin{eqnarray}
w_i &=& m_i(Y_i) \cdot {\hat p}(Y_i) W_i \cdot \left| \frac{\partial Y_i}{\partial X_i} \right| \tag{S.33} \\
&=& \left( \alpha \frac{\kappa}{M – |R|} \frac{ {\hat p}_{\leftarrow i}(Y_i) }{ {\hat p}(Y_i) + \alpha {\hat p}_{\leftarrow i}(Y_i) } \right) \cdot {\hat p}(Y_i) W_i \cdot \left| \frac{\partial Y_i}{\partial X_i} \right| \tag{S.34} \\
&=& \alpha \frac{\kappa}{M – |R|} \frac{ {\hat p}_i(X_i) }{ {\hat p}(Y_i) + \alpha {\hat p}_{\leftarrow i}(Y_i) } \cdot {\hat p}(Y_i)W_i \tag{S.35} \\
& \leq & \alpha \frac{\kappa}{M – |R|} C_i \tag{S.36}
\end{eqnarray}
\(\alpha \leq M/|R|-1\)の場合、単純に次のようになります。
\begin{eqnarray}
w_i \leq \kappa \frac{C_i}{|R|} \leq \frac{C_i}{|R|} \tag{S.38}
\end{eqnarray}
S.14 Tractable Marginal PDFs
入力サンプル\(X_i\)のPDFが扱いやすい関数\(p_i\)であることがあります。その場合、MISの重み式の\({\hat p}_i\)の代わりにPDFの\(p_i\)を使用することができ、実質的に\({\hat p}_{\leftarrow i}\)を次の “\(i\)からの\(p\)”で置き換えることができます:
\begin{eqnarray}
p_{\leftarrow i}(y) = \begin{cases} p_i({T_i}^{-1}(y)) |{T_i}^{{-1}’}| (y), &\quad& {\rm if} \, y \in {\mathcal D}({T_i}^{-1}), \\
0 &\quad& {\rm otherwise} \end{cases} \tag{S.39}
\end{eqnarray}
その結果、一般化されたTalbot MISの式は以下のようになります:
\begin{eqnarray}
m_i(y) = \frac{ p_{\leftarrow i}(Y_i) }{ \sum_{j=1}^{M} p_{\leftarrow j}(Y_i) } \tag{S.40}
\end{eqnarray}
ペアワイズMIS式はさらに、正規化がPDF \(p_i\)の正規化と著しく異なる可能性のある項\({\hat p}(y)\)を含みます。そのため, MIS中の\({\hat p}(y)\)項を, \({\hat p}({\hat p}(y) \leq C_c p_c(y)\)を積分するのに妥当な固定正準重点サンプラー\(c \in C\)に置き換えることを提案します。既知のPDFへの変換の例として、一様な場合を示します。
\begin{eqnarray}
m_i(y) &=& \frac{1}{M – |R|} \sum_{j \notin R} \frac{p_c(y)}{ |R|p_c(y) + (M – |R|)p_{\leftarrow j}(y) } \quad {\rm if} \, i \in R \tag{S.41} \\
m_i(y) &=& \frac{ {\hat p}_{\leftarrow i}(y) }{ |R| p_c(y) + (M – |R|) p_{\leftarrow i}(y) } \quad {\rm if} \, i \notin R. \tag{S.42}
\end{eqnarray}
次に,これらの更新された式に対するリサンプリングウェイトの境界を導出しました。\(p_i\)はトラクタブルなので、アンバイアスドな寄与ウェイト\(W_i = 1 / p_i(X_i)\)を仮定します。また,正準サンプルは\({\hat p}\),すなわち,すべての\(i \in R\)に対して\({\hat p}(x) \leq C_i p_i(x)\)が合理的に重要であると仮定しました。
Talbot MIS
式S.40を式S.1に代入すると、\(p_{\leftarrow j}(y) = p_j(y)\)が正準\(j\)であることを思い出して、次式が得られます。
\begin{eqnarray}
w_i &=& m_i(Y_i) \cdot {\hat p}(Y_i) W_i \cdot \left| \frac{\partial T_i}{\partial X_i} \right| \tag{S.43} \\
&=& \left( \frac{p_ {\leftarrow i}(Y_i) }{ \sum_{j=1}^{M} p_{\leftarrow j}(Y_i) } \right) \cdot \frac{ {\hat p}(Y_i) }{ p_i(X_i) } \cdot \left| \frac{\partial T_i}{\partial X_i} \right| \tag{S.44} \\
&=& \frac{ p_i(X_i) }{ \sum_{j \in R} p_{\leftarrow j}(Y_i) + \sum_{j \notin R} p_{\leftarrow j}(Y_i) } \cdot \frac{ {\hat p}(Y_i) }{ p_i(X_i) } \tag{S.45} \\
&=& \frac{ {\hat p}(Y_i) }{ \sum_{j \in R} p_j(Y_i) + \sum_{j \notin R} p_{\leftarrow j}(Y_i) } \tag{S.46} \\
&\leq& \frac{ {\hat p}(Y_i) }{ \sum_{j \in R} p_j(Y_i) } \leq \frac{ {\hat p}(Y_i) }{ |R| {\rm min}_{j \in R} p_j(Y_i) } \tag{S.47} \\
&=& \frac{1}{|R|} \underset{j \in R}{\rm max} \frac{ {\hat p}(Y_i) }{ p_j(Y_i) } \leq \frac{1}{|R|} \underset{j \in R}{\rm max} C_j \tag{S.48}
\end{eqnarray}
Pairwise MIS.
ここで、\({\hat p}_i\)の代わりに\(p_i\)を用いて、\(0 \leq \alpha \leq M/|R|-1\)と\(0 \leq \kappa \leq 1\)の一般化ペアワイズMISウェイトの場合のリサンプリングウェイトの境界を導出します。
\(i\)が正準インデックスの場合、\({\hat p}_{\leftarrow j}\)を\(p_{\leftarrow j}\)に、\({\hat p}\)を\(p_c\)に置き換えて式S.13を用います。\(Y_i = T_i(X_i) = X_i\)となる正準インデックスはなく,次にたどり着きます。
\begin{eqnarray}
w_i &=& m_i(Y_i) \cdot {\hat p}(Y_i) W_i \cdot \left| \frac{\partial T_i}{\partial X_i} \right| \tag{S.49} \\
&=& \frac{1}{|R|} \left( 1 – \kappa + \frac{\kappa}{M – |R|} \sum_{j \notin R} \frac{p_c(Y_i)}{p_c(Y_i) + \alpha p_{\leftarrow j}(Y_i)} \right) \cdot \frac{ {\hat p}(Y_i) }{p_i(X_i)} \cdot 1 \tag{S.50} \\
&\leq& \frac{1}{|R|} \left( 1 – \kappa + \frac{\kappa}{M – |R|} \sum_{j \notin R} 1 \right) \cdot \frac{{\hat p}(X_i) }{p_i(X_i)} \tag{S.51} \\
&=& \frac{1}{|R|} \cdot \frac{ {\hat p}(X_i) }{ p_i(X_i) } \leq \frac{C_i}{|R|} \tag{S.52}
\end{eqnarray}
同様に、非正準の\(i\)については、同じ置換で式S.14を使い、次のようになります。
\begin{eqnarray}
w_i &=& m_i(Y_i) \cdot {\hat p}(Y_i) W_i \cdot \left| \frac{\partial T_i}{\partial X_i} \right| \tag{S.53} \\
&=& \left( \alpha \frac{\kappa}{M – |R|} \frac{ p_{\leftarrow i}(Y_i) }{ p_c(Y_i) + \alpha p_{\leftarrow i}(Y_i) } \right) \cdot \frac{ {\hat p}(Y_i) }{p_i(X_i)} \cdot \left| \frac{\partial T_i}{\partial X_i} \right| \tag{S.54} \\
&=& \left( \alpha \frac{\kappa}{M – |R|} \frac{ p_i(X_i) | \frac{\partial {T_i}^{-1} }{ \partial Y_i} | }{p_c(Y_i) + \alpha p_{\leftarrow i}(Y_i) } \right) \cdot \frac{{\hat p}(Y_i)}{p_i(X_i)} \cdot \left| \frac{\partial T_i}{\partial X_i} \right| \tag{S.55} \\
&=& \alpha \frac{\kappa}{M – |R|} \frac{ {\hat p}(Y_i) }{ p_c(Y_i) + \alpha p_{\leftarrow i}(Y_i) } \leq \alpha \frac{\kappa}{M – |R|} \frac{ {\hat p}(Y_i) }{ p_c(Y_i) } \tag{S.56} \\
&\leq& \alpha \frac{\kappa}{M – |R|} C_c \leq \left( \frac{M}{|R|} -1 \right) \frac{1}{M – |R|} C_c = \frac{C_c}{|R|} \tag{S.57}
\end{eqnarray}
上記の結果を、扱いやすいPDFで使用する場合に、任意の\(i\)および両方のMISウェイトファミリ (TalbotおよびPairwise) で動作する、1つの少し緩い境界にまとめることができます。
\begin{eqnarray}
w_i \leq \frac{1}{|R|} \underset{j \in R}{\rm max} C_j \tag{S.58}
\end{eqnarray}
S.2 CONVERGENCE WITH DEPENDENT SAMPLES
セクション5.7では,以下のような入力サンプルの依存を想定しています。
(1) 正規サンプルの比率\(|R|/M\)は、\(M\)が十分に大きい場合、正の定数\(\gamma\)を下回ることはありません。
(2) すべての\(i\)について\(w_i \leq C/|R|\)となるような\(C \gt 0\)が存在する。
(3) すべての\(i\)と\(b_k \rightarrow \infty\)について相関\(\rho_{i, i+k} \leq b_k\)が成り立つような非負の数列\(b_k\)が存在する。
このとき,
\begin{eqnarray}
{\rm Var} \left[ \sum_{i=1}^M w_i \right] = \sum_{i=1}^M {\rm Var}[w_i] + 2 \sum_{i=1}^M \sum_{k=1}^{M-i} {\rm Cov}(w_i, w_{i+K}) \tag{S.59}
\end{eqnarray}
はゼロに収束します:
最初の項の収束はセクション5.7で証明され,二つ目の項については次を得ます。
\begin{eqnarray}
\sum_{i=1}^{M} \sum_{k=1}^{M-i} {\rm Cov}(w_i, w_{i+k}) &=& \sum_{i=1}^{M} \sum_{k=1}^{M-i} \rho_{i, i+k} \sqrt{ {\rm Var}w_i {\rm Var}w_{i+k} } \tag{S.60} \\
&\leq& \sum_{i=1}^M \sum_{k=1}^{M-i} {\rm max}(0, \rho_{i, i+k}) \frac{C^2}{4|R|^2} \leq \sum_{i=1}^M \sum_{k=1}^{M-i} b_k \frac{C^2}{4M^2 \gamma^2} \tag{S.61} \\
&=& \frac{C^2}{4\gamma^2} \frac{1}{M^2} \sum_{k=1}^M \sum_{i=1}^{M-k} b_k = \frac{C^2}{4\gamma^2} \frac{1}{M^2} \sum_{k=1}^{M}(M – k) b_k \tag{S.64} \\
&\leq& \frac{C^2}{4\gamma^2} \left( \frac{1}{M} \sum_{k=1}^{M} b_k \right) \overset{M \rightarrow \infty}{\longrightarrow} 0 \tag{S.63}
\end{eqnarray}
式S.64に到達するために、Popoviciuの不等式を用いました:\(0 \leq w_i \leq C/|R|\)であるので,\({\rm Var}w_i \leq \frac{C^2}{4|R|^2}\)ということが分かります。次のステップでは\(|R|/M \geq \gamma\)を使用し、式S.62では合計の順序を逆にしました:\(\sum_{i=1}^{M} \sum_{k=1}^{M-i} = \sum_{k=1}^{M} \sum_{i=1}^{M-k}\) 。\(b_k\)はゼロに収束するので、\(b_k\)の平均はゼロに収束し、式S.63は以下を意味します。
\begin{eqnarray}
{\rm Var} \left[ \sum_{i=1}^M w_i \right] \overset{M \rightarrow \infty}{\longrightarrow} 0
\end{eqnarray}
この結果を少し一般化することができます。
\begin{eqnarray}
|R| \geq c_M M^{0.5} \sqrt{\sum_{i=1}^M b_i} \tag{S.64}
\end{eqnarray}
ここで、\((c_M)\)は無限大に近づく任意の非負数列です。そして、上記のように
\begin{eqnarray}
\sum_{i=1}^M \sum_{k=1}^{M-i} {\rm Cov}(w_i, w_{i+k}) &\leq& \sum_{i=1}^M \sum_{k=1}^{M-i} {\rm max}(0, \rho_{i, i+k}) \frac{C^2}{4|R|^2} \tag{S.65} \\
&=& \sum_{k=1}^{M} \sum_{i=1}^{M – k} {\rm max}(0, \rho_{i, i+k}) \frac{C^2}{4|R|^2} \leq \sum_{k=1}^M (M – k) b_k \frac{C^2}{4|R|^2} \tag{S.66} \\
&\leq& \left( \sum_{k=1}^M b_k \right) \frac{MC^2}{4|R|^2} \leq \left( \sum_{k=1}^M b_k \right) \frac{MC^2}{4 {c_M}^2 M (\sum_{i=1}^M b_i) } \tag{S.67} \\
&=& \frac{C^2}{ 4 {c_M}^2 } \overset{M \rightarrow \infty}{\longrightarrow} 0 \tag{S.68}
\end{eqnarray}
S.3 PRIMARY SAMPLE SPACE
モンテカルロ法における積分の実行は、通常、一次標本列、すなわち、\(U_i \in [0, 1)\)が一様に分布する乱数\({\mathbb {\bar U}} = (U_1, U_2, \cdots)\)のストリームから開始されます。各\({\mathbf {\bar U}}\)は寄与度F\({\mathbf {\bar U}})\)を推定するために使用され、モンテカルロ積分の結果は次のようになります。
\begin{eqnarray}
I = {\mathbb E}[ F({\mathbf {\bar U}})] = \int_{\mathcal U} F({\mathbf {\bar u}}) d{\mathbf {\bar u}} \tag{S.69}
\end{eqnarray}
一方向性のパストレーサーは、ランダム配列\({\mathbf {\bar U}}\)から異なる長さのパスシーケンスを構築する。多くの場合、パストレーサーは、各長さ\(d\)に対して、異なる戦略によって\(N\))個のパス\(X_{d, n} \in \Omega_d\)を生成します。ここで\(\Omega_d\)は、長さ\(d\)のすべてのパスの空間です。\(N\)は多くの場合2であり、異なる\(n\)を持つパス\(X_{d, n}\)は、ランダムなライトに接続されたnext-event-estimationパスと、BSDFに従って重点サンプリングされた方向に続くパスに対応します。パス\(X_{d, n}\)は\({\mathbf {\bar U}}\)の関数、すなわち\(X_{d, n} = x_{d, n}({\mathbf {\bar U}})\)です。
全パスの寄与は、固定長パスの寄与の積分の合計となります。
\begin{eqnarray}
I = \sum_{d=1}^{\infty} \int_{\Omega_d} f(x) dx \tag{S.70}
\end{eqnarray}
\(n\)個のサンプリング戦略のMISウェイト\(\omega_{d,n}\)を考慮すると、次のようになります。
\begin{eqnarray}
I &=& \sum_{d=1}^{\infty} \int_{\Omega_d} \left[ \sum_{n=1}^{N} \omega_{d, n}(x) \right] f(x) dx \tag{S.71} \\
&=& \sum_{d=1}^{\infty} \sum_{n=1}^N \int_{\Omega_d} \omega_{d, n} (x) f(x) dx \tag{S.72}
\end{eqnarray}
各項目について、密度\(p_{d, n}\)のパス\(X_{d, n} \in \Omega_d\)を生成する適切な重点サンプラーを仮定します。ここでは、が単一パーティションを保持するために\(p_{d,n}(x) = 0\)である場合は常に\(\omega_{d,n}(x) = 0\)と仮定します。これにより
\begin{eqnarray}
I = \sum_{d=1}^{\infty} \sum_{n=1}^N {\mathbb E} \left[ \omega_{d, n}(X_{d, n}) \frac{ f(X_{d, n} }{ p_{d, n} (X_{d, n}) } \right] \tag{S.73}
\end{eqnarray}
\(X_{d, n}\)は\(X_{d, n} = x_{d, n}({\mathbf {\bar U}})\)によって確率変数\({\mathbf {\bar U}}\)から生成されるので、次のように書くことができます。
\begin{eqnarray}
I = \sum_{d=1}^{\infty} \sum_{n=1}^N {\mathbb E} \left[ \omega_{d, n}(x_{d, n}({\mathbf {\bar U}}) \frac{ f(x_{d, n}({\mathbf {\bar U}}) }{ p_{d, n} (x_{d, n}({\mathbf {\bar U}}) } \right] \tag{S.74}
\end{eqnarray}
多くの\({\mathbf {\bar U}}\)が同じパス\(X_{d, n}\)につながるという事実は、この事実を複雑にするものではありません。期待値を積分として書くと、次のようになります。
\begin{eqnarray}
I &=& \sum_{d=1}^{\infty} \sum_{n=1}^{N} \int_{\mathcal U} \omega_{d, n} (x_{d, n}({\mathbf {\bar u}}) \frac{ f(x_{d, n}({\mathbf {\bar u}}) }{ p_{d, n} (x_{d, n}({\mathbf {\bar u}}) } d {\mathbf {\bar u}} \tag{S.75} \\
&=& \int_{\mathcal U} \sum_{d=1}^{\infty} \sum_{n=1}^N \omega_{d, n} (x_{d, n}({\mathbf {\bar u}}) \frac{ f(x_{d, n}({\mathbf {\bar u}}) }{ p_{d, n}(x_{d, n}({\mathbf {\bar u}})) } d {\mathbf {\bar u}} \tag{S.76}
\end{eqnarray}
これは,式S.69に対する\(F\)を算出します。
\begin{eqnarray}
F({\mathbf {\bar u}}) = \sum_{d=1}^{\infty} \sum_{n=1}^{N} \omega_{d, n} (x_{d, n}({\mathbf {\bar u}})) \frac{ f(x_{d, n}({\mathbf {\bar u}})) }{ p_{d, n} (x_{d, n}({\mathbf {\bar u}})) } \tag{S.77}
\end{eqnarray}
S.4 RESERVIOR STORAGE
アルゴリズム1に、我々のレゼバーデータ構造の概要を示します。再接続には、再接続頂点に対するオフセットパスの可視性と、ベースパスの次の頂点に対するBSDFを評価する必要があります。このリゼバーデータ構造は最適化されておらず、非常に圧縮されやすいことに注意してください。リアルタイムで使用する場合、性能を向上させるために非可逆圧縮が可能になりますが、プロトタイプの実装ではそれを行っていません。
S.5 PROOFS OF THEOREMS
S.5.1 Unbiased Contribution Weights (Theorem A.1)
定理A.1の証明。項目1:任意の積分可能な\(f\)について\({\mathbb E}[f(X)W] = \int_{{\rm supp} X} f(x)dx\)であるような\(W\)と\(X\)を仮定します。項目2:\(A \subset {\rm supp}(X)\)が可測であることを証明します。このとき,
\begin{eqnarray}
\int_A p_X(x) dx &=& \int_{{\rm supp}(X)} {\mathbb 1}_A (x) p_X(x) dx \\
&=& {\mathbb E}[{\mathbb 1}_A(X) p_X(X)W] = {\mathbb E}[ {\mathbb E}[ {\mathbb 1}_A(X) p_X(X)W | X]] \\
&=& {\mathbb E}[{\mathbb 1}_A(X) p_X(X) {\mathbb E}[W | X]] \\
&=& \int_A p_X(x)^2 {\mathbb E}[W | X = x] dx \tag{S.78}
\end{eqnarray}
これはすべての可測な\(A \subset {\rm supp}(X)\)に当てはまるので、\({\rm supp}(X)\)のほぼすべての場所にあるはずです。
\begin{eqnarray}
p_X(x) = p_X(x)^2 {\mathbb E}[W |X=x] \tag{S.79}
\end{eqnarray}
\({\rm supp}(X)\)上において\(p_X(x) \gt 0\)であるので,\({\rm supp}(X)\)上で\({\mathbb E}[W |X = x] = 1/p_X(x)\)を演繹します。
次に,項目2:\({\rm supp}(X)\)上で,\({\mathbb E}[W|X=x] = 1 / p_X(x)\)であるような\(W\)と\(X\)を仮定します。項目1:\(f: \Omega \rightarrow {\mathbb R}\)が積分可能であることを証明します。次を得ます。
\begin{eqnarray}
{\mathbb E}[f(X) W] &=& {\mathbb E}[ {\mathbb E}[ f(X)W | X]] = {\mathbb E}[f(X) {\mathbb E}[W|X]] \\
&=& {\mathbb E} \left[ \frac{f(X)}{p_X(X)} \right] = \int_{{\rm supp}(X)} f(x)dx \tag{S.80}
\end{eqnarray}
□
S.5.2 Asymptotic Sample Distribution (Theorem A.2)
式22から開始し、等式を導出します。
\begin{eqnarray}
\sum_{i=1}^{M} w_i = {\hat p}(Y) W_Y \tag{S.81}
\end{eqnarray}
そして、次のような少し一般的な結果を証明する: \((Y_M)_{M =M_0}^{\infty}\)が\({\hat p} \subset {\rm supp}Y_M\)(式57)を満たす確率変数の列であり、非負のアンバイアスドな寄与ウェイト\(W_{Y_M}\)を持ち(式58の一般化)
\begin{eqnarray}
{\rm Var}[{\hat p}(Y_M) W_{Y_M}] \overset{M \rightarrow \infty}{\longrightarrow} 0 \tag{S.82}
\end{eqnarray}
このとき,定理A.2の結論が成り立ちます:
定理A.2(項目1)の証明,式59。\(\epsilon \gt 0\)が与えられたとします。次を証明します。
\begin{eqnarray}
{\rm Pr} [ | p_Y(Y) – {\bar p}(Y) | \gt \epsilon] \overset{M \rightarrow \infty}{\longrightarrow} 0 :
\end{eqnarray}
任意の\(0 \lt \epsilon_2 \lt 0\)について,次を得ます。
\begin{eqnarray}
& & {\rm Pr} \left[ | {\bar p}(Y) – p_Y(Y) | \gt \epsilon \right] = A + B + C, \quad {\rm where} \tag{S.83} \\
A &=& {\rm Pr} \left[ (|{\bar p}(Y) – p_Y(Y) | \gt \epsilon) \land (p_Y(Y) \geq \frac{1}{\epsilon_2} ) \right] \\
B &=& {\rm Pr} \left[ (|{\bar p}(Y) – p_Y(Y) | \gt \epsilon) \land (1 \lt p_Y(Y) \lt \frac{1}{\epsilon_2}) \right] \\
C &=& {\rm Pr} \left[ (|{\bar p}(Y) – p_Y(Y) | \gt \epsilon) \land (p_Y(Y) \leq 1) \right]
\end{eqnarray}
\({\rm Pr}[ X \land Y] \leq Pr[Y]\)と\(p_Y\)は積分して1になるので、次のようになります。
\begin{eqnarray}
A \leq {\rm Pr} \left[ p_Y(Y) \geq \frac{1}{\epsilon_2} \right] \leq \epsilon_2
\end{eqnarray}
(そうではない場合, \(p_Y\)は積分されると\(\epsilon_2 \cdot 1 / \epsilon_2 = 1\)を超えてしまいます)。\(B\)の場合では\(1 / p_Y(Y) \gt \epsilon_2\)があるので、次のようになります。
\begin{eqnarray}
B &=& {\rm Pr} [ ( |{\hat p}(Y) – p_Y(Y)| \epsilon_2 \gt \epsilon \cdot \epsilon_2) \land (1 \lt p_Y(Y) \lt \frac{1}{\epsilon_2} )] \\
& \leq & {\rm Pr} [ ( \frac{ |{\bar p}(Y) – p_Y(Y)| }{ p_Y(Y) } \lt \epsilon \cdot \epsilon_2 ) \land (1 \lt p_Y(Y) \lt \frac{1}{\epsilon_2 )} \\
& \leq & {\rm Pr} [ | \frac{{\bar p}(Y) }{ p_Y(Y) } – 1 | \gt \epsilon \cdot \epsilon_2 ]
\end{eqnarray}
同様に、\(C\)の場合も\(1/p_Y(Y) \geq 1\)があるので,したがって
\begin{eqnarray}
C &=& {\rm Pr} \left[ ( |{\bar p}(Y) – p_Y(Y)| \gt \epsilon) \land ( p_Y(Y) \leq 1) \right] \\
&\leq& {\rm Pr} \left[ | \frac{ {\bar p}(Y) }{ p_Y(Y)} -1 | \gt \epsilon \right]
\end{eqnarray}
Chebyshevの不等式により,任意の\(s \gt 0\)について(例えば\(B\)については,\(s = \epsilon \cdot \epsilon_2\)で\(C\)については\(s = \epsilon\))次を得ます。
\begin{eqnarray}
{\rm Pr} [ | \frac{{\bar p}(Y) }{ p_Y(Y) } -1 | \gt s ] \lt \frac{1}{s^2} {\mathbb E} [ | \frac{ {\bar p}(Y) }{ p_Y(Y) } -1 |^2 ]
\overset{M \rightarrow \infty}{\longrightarrow} 0 \tag{S.84}
\end{eqnarray}
したがって,
\begin{eqnarray}
0 \leq \underset{M \rightarrow \infty}{\rm lim} A + B + C \leq \epsilon_2 + 0 + 0 \overset{\epsilon_2 \rightarrow 0}{\longrightarrow} 0 \tag{S.85}
\end{eqnarray}
すなわち,
\begin{eqnarray}
Pr [ |{\bar p}(Y) – p_Y(Y)| \gt \epsilon ] \overset{M \rightarrow \infty}{\longrightarrow} 0 \tag{S.86}
\end{eqnarray}
■
定理A.2(項目2)の証明、式60。仮定により、各\(M\)に対して\({\rm supp} {\hat p} \subset {\rm supp} Y_M\)が存在する。 簡潔にするためにインデックス\(M\)を省略すると、次のようになります。
\begin{eqnarray}
{\mathbb E} \left[ \frac{ {\hat p}(Y) }{ p_Y(Y) } \right] = \int_{{\rm supp}Y} {\hat p}(y) dy = || {\hat p} || \tag{S.87}
\end{eqnarray}
したがって、全分散の法則から次のように演繹されます。
\begin{eqnarray}
{\rm Var}[ {\hat p}(Y) W_Y ] &=& {\mathbb E}[ {\rm Var}[ {\hat p}(Y)W_Y | Y]] + {\rm Var}[{\mathbb E}[ {\hat p}(Y) W_Y | Y]] \\
&\geq& {\rm Var} [ {\mathbb E}[{\hat p}(Y) W_Y |Y]] = {\rm Var} [ \frac{ {\hat p}(Y) }{ p_Y(Y) } ] \\
&=& {\mathbb E} [ | \frac{ {\hat p}(Y) }{ p_Y(Y) } – || {\hat p} || |^2 ] \tag{S.88}
\end{eqnarray}
仮定により\({\rm Var}[{\hat p}(Y) W_Y]\)は0に向かうので、平均二乗において\(p_Y\)は\({\bar p}\)に収束します:
\begin{eqnarray}
{\mathbb E} [ | \frac{ {\bar p}(Y) }{ p_Y(Y) } – 1 |^2 ] &=& \frac{1}{ || {\hat p} ||^2 } {\mathbb E} [ | \frac{ {\hat p}(Y) }{ p_Y(Y) } – || {\hat p} || |^2 ] \\
&\leq& \frac{1}{ || {\hat p} ||^2 } {\rm Var} [ {\hat p}(Y) W_Y ] \overset{M \rightarrow \infty}{\longrightarrow} 0 \tag{S.89}
\end{eqnarray}
■
定理A.2(項目3)の証明、式61。コーシー・シュワルツの不等式により、平均2乗における確率変数の収束は平均の収束を意味します:
\begin{eqnarray}
{\mathbb E}\ | Z_i – Z_{\infty} |] \leq \sqrt{ {\mathbb E}[1^2] } \sqrt{ {\mathbb E} [ | Z_i – Z_{\infty}|^2 } \overset{i \rightarrow \infty}{\longrightarrow} 0 \tag{S.90}
\end{eqnarray}
式60より,\({\mathbb E} [ | \frac{{\bar p}(Y)}{p_Y(Y)} -1 | ] \overset{M \rightarrow \infty}{\longrightarrow} 0 \)。したがって\({\rm supp}{\hat p} \subset {\rm supp}Y\)を得るので,すべての\(M\)について\({\rm supp} Y\)の外側が \(p_Y(y) – {\hat p}(y) = 0 – 0\) であるので,
\begin{eqnarray}
\int_{\Omega} | p_Y(y) – {\bar p}(y) | dy = \int_{{\rm supp}Y} | p_Y(y) – {\bar p}(y) | dy \
= {\mathbb E}[ | \frac{ {\bar p}(Y) }{ p_Y(Y) } – 1 | ] \overset{M \rightarrow \infty}{\longrightarrow} 0 \tag{S.91}
\end{eqnarray}
■
定理A.2の証明(項目4)。\(p_{Y_M}(y)\)が収束する\(y \in \Omega\)の集合を\(G\)とし、極限を\(g(y)\)とする。すなわち,
\begin{eqnarray}
g(y) = \underset{M \rightarrow \infty}{\rm lim} p_{Y_M}(y) \quad {\rm for} \, {\rm all} y \in G \tag{S.92}
\end{eqnarray}
すべての部分列\(p_{Y_{a_k}}\)も、\(G\)において点状に\(g(y)\)に収束します。式61より,\(p_Y(y)\)はルベーグ\(L^1\)方向で\({\bar p}\)に収束します:
\begin{eqnarray}
|| {\bar p}(y) – p_{Y_M}(y) ||_{L^1} = \int_{\Omega} | {\bar p}(y) – p_{Y_M}(y) | dy \overset{M \rightarrow \infty}{\longrightarrow} 0 \tag{S.93}
\end{eqnarray}
\(p_{Y_M}\)は\(L^1\)-ノルムで\({\bar p}\)に収束するので、\(L^1\)-測度でも収束します[Bartle 2014.p69]。したがって、それはほぼどこでも\({\bar p}\)に収束する部分列\(p_{Y_{a_k}}\)を持ちます[Bartle 2014, p.69]。しかし,\(y \in G\)の場合,\(p_{Y_{a_k}}\)もまた\(g(y)\)に収束するので,\(G\)上のほぼすべての場所で\(g(y) = {\bar p}(y)\)を持たなければなりません。
■
定理A.2の証明(項目5)。\(X\)をPDF \(\bar p\)で分布させ、\(A\)を\(\Omega\)の任意の可測部分集合とします。このとき,定理A.2(項目3)により,
\begin{eqnarray}
| {\rm Pr} [Y \in A] – {\rm Pr}[X \in A] | &=& | \int_A p_Y(y)dy – \int_A {\bar p}(y) dy | \
& \leq & \int_{\Omega} | p_Y(y) – {\bar p}(y) | dy \overset{M \rightarrow \infty}{\longrightarrow} 0
\end{eqnarray}
■
S.5.3 Asymptotic Variance (Theorem A.3)
まず台を証明し、次に項目1から項目3を証明します:
定理A.3の証明、台。仮定(式57)により、すべての\(M\)に対して\({\rm supp}{\hat p} \subset {\rm supp} Y_M\)となります。また、ある\(C_f \gt 0\)に対して\(f \leq C_f {\hat p}\)を仮定します。したがって、\(f(x) \gt 0\)は\({\hat p}(x) \gt 0\)を意味し、\({\rm supp}f \subset {\rm supp}{\hat p} \subset {\rm supp} Y_M\)が得られます。
■
定理A.3(項目1)、式63、式64の証明。まず二乗平均の収束を証明します:
\begin{eqnarray}
&{\mathbb E}& \left[ \left| f(Y) W_Y – \frac{f(Y)}{{\bar p}(Y)} \right|^2 \right] = {\mathbb E} \left[ \left| \frac{f(Y)}{{\hat p}(Y)} \sum_{i=1}^M w_{M, i} – \frac{f(Y)}{{\bar p}(Y)} \right|^2 \right] \\
&=& {\mathbb E} \left[ \frac{ f(Y)^2 }{ {\hat p}(Y)^2 } \left| \sum_{i=1}^M w_{M, i} – \frac{ {\hat p}(Y) }{ {\bar p}(Y) } \right|^2 \right] = {\mathbb E} \left[ \frac{ f(Y)^2 }{ {\hat p}(Y)^2 } \left| \sum_{i=1}^M w_{M, i} – || {\hat p} || \right|^2 \right] \\
& \leq & {C_f}^2 {\mathbb E} \left[ \left| \sum_{i=1}^M w_{M, i} – || {\hat p} || \right|^2 \right] = {C_f}^2 {\rm Var} \left[ \sum_{i=1}^M w_{M, i} \right] \overset{M \rightarrow \infty}{\longrightarrow} 0
\end{eqnarray}
二乗平均の収束は、確率の平均の収束を意味します。例えば、チェビシェフの不等式により、\(\epsilon \gt 0\)が与えられると次のようになります。
\begin{eqnarray}
{\rm Pr} \left[ \left| f(Y) W_Y – \frac{ f(Y) }{{\bar p}(Y)} \right| \gt \epsilon \right] \geq \frac{1}{ {\epsilon}^2 } {\mathbb E} \left[ \left| f(Y) W_Y – \frac{ f(Y) }{ {\bar p}(Y) } \right|^2 \right] \overset{M \rightarrow \infty}{\longrightarrow} 0
\end{eqnarray}
■
定理A.3(項目2)の証明、式65。3つのステップを踏みます。
Step 1. 我々は次のことを示します。
\begin{eqnarray}
{\rm Var} \left[ f(Y) W_Y \right] – {\rm Var} \left[ \frac{f(Y)}{p_Y(Y)} \right] \overset{M \rightarrow \infty}{\longrightarrow} 0 \tag{S.94}
\end{eqnarray}
全分散の法則から次のようになります。
\begin{eqnarray}
{\rm Var}[ f(Y) W_Y ] = {\rm Var}[ {\mathbb E} [f(Y) W_Y| Y] + {\mathbb E}[ {\rm Var}[ f(Y) W_Y | Y]]
\end{eqnarray}
これを次のように書き直します。
\begin{eqnarray}
{\mathbb E}[ {\rm Var} [ f(Y) W_Y | Y]] &=& {\rm Var}[ f(Y) W_Y ] – {\rm Var}[ {\mathbb E}[f(Y) W_Y | Y]] \\
&=& {\rm Var} [ f(Y) W_Y] – {\rm Var} \left[ \frac{f(Y)}{p_Y(Y) } \right]
\end{eqnarray}
条件付き分散は非負であり、次のようになります。
\begin{eqnarray}
0 &\leq& {\rm Var} \left[ f(Y) W_Y \right] – {\rm Var} \left[ \frac{f(Y)}{p_Y(Y)} \right] = {\mathbb E} \left[ {\rm Var}[f(Y) W_Y | Y] \right] \\
&=& {\mathbb E} \left[ {\rm Var} \left[ \frac{ f(Y) }{ p_Y(Y) } \sum_{i=1}^M w_{M, i} | Y \right] \right] = {\mathbb E} \left[ \frac{ f(Y)^2 }{ {\hat p}(Y)^2 } {\rm Var} \left[ \sum_{i=1}^M w_{M, i} | Y \right] \right] \\
&\leq& {C_f}^2 {\mathbb E} \left[ {\rm Var} \left[ \sum_{i=1}^M w_{M, i} | Y \right] \right] \tag{S.95} \\
&\leq& {C_f}^2 \left( {\mathbb E} \left[ {\rm Var} \left[ \sum_{i=1}^M w_{M, i} | Y \right] \right] + {\rm Var} \left[ {\mathbb E} \left[ \sum_{i=1}^M w_{M, i} | Y \right] \right] \right) \\
&=& {C_f}^2 {\rm Var} \left[ \sum_{i=1}^M w_{M, i} \right] \overset{M \rightarrow \infty}{\longrightarrow} 0
\end{eqnarray}
Step 2. 我々は次のことを示します。
\begin{eqnarray}
{\rm Var} \left[ \frac{f(X)}{ {\bar p}(X) } \right] – {\rm Var} \left[ \frac{f(Y)}{p_Y(Y)} \right] \overset{M \rightarrow \infty}{\longrightarrow} 0 \tag{S.96}
\end{eqnarray}
ここで\(X\)は密度\({\bar p}(x)\)を持ちます。まず、次のように書きます。
\begin{eqnarray}
&& {\rm Var}\left[ \frac{f(X)}{ {\bar p}(X) } \right] – {\rm Var} \left[ \frac{f(Y)}{p_Y(Y)} \right] \\
&=& {\mathbb E} \left[ \frac{ f(X)^2 }{ {\bar p}(X)^2 } \right] – {\mathbb E} \left[ \frac{f(X)}{ {\bar p}(X)} \right]^2 – {\mathbb E} \left[ \frac{f(Y)^2}{p_Y(Y)^2} \right] + {\mathbb E} \left[ \frac{ f(Y) }{ p_Y(Y) } \right]^2 \tag{S.97} \\
&=& {\mathbb E} \left[ \frac{ f(X)^2 }{ {\bar p}(X)^2 } \right] – {\mathbb E} \left[ \frac{f(Y)^2}{p_Y(Y)^2} \right] \tag{S.98}
\end{eqnarray}
\({\rm supp}Y \subset {\rm supp}{\hat p}\)(式15)と\({\rm supp}{\hat p} \subset {\rm supp}Y\)を仮定すると、\({\rm supp}{\hat p} = {\rm supp}Y\)を得ます。\({\rm supp}{\bar p} = {\rm supp}{\hat p}\)を用いて、上記を次のように続けます。
\begin{eqnarray}
&=& \int_{{\rm supp}Y} {\bar p}(x) \frac{ f(x)^2 }{ {\bar p}(x)^2 } dx \, \, – \, \int_{{\rm supp}Y} p_Y(y) \frac{ f(y)^2 }{ p_Y(y)^2 } dy \\
&=& \int_{{\rm supp}Y} {\bar p}(y) \frac{f(y)^2}{{\bar p}(y)^2} \, \, – \, p_Y(y) \frac{ f(y)^2 }{ p_Y(y)^2 } dy \\
&=& \int_{{\rm supp}Y} p_Y(y) \left( \frac{ f(y)^2 }{ {\bar p}(y)^2 } \right) \left( \frac{ {\bar p}(y) }{ p_Y(y) } \, – \, \frac{ {\bar p}(y)^2 }{ p_Y (y)^2 } \right) dy \\
&=& {\mathbb E} \left[ \frac{ f(Y)^2 }{ {\bar p}(Y)^2} \left( \frac{ {\bar p}(Y) }{ p_Y(Y) } \, – \, \frac{ {\bar p}(Y)^2}{ p_Y(Y)^2} \right) \right]
\end{eqnarray}
従って,定理A.2(項目2)より
\begin{eqnarray}
& & \left| {\rm Var} \left[ \frac{f(X)}{{\bar p}(X)} – {\rm Var}[ \frac{f(Y)}{p_Y(Y)} \right] \right| \\
&\leq& {\mathbb E} \left[ \frac{f(Y)^2}{ {\bar p}(Y)^2} \left| \frac{ {\bar p}(Y) }{ p_Y(Y) } – \frac{ {\bar p}(Y)^2 }{ p_Y(Y)^2 } \right| \right] \\
&\leq& || {\hat p} ||^2 {C_f}^2 {\mathbb E} \left[ \left| \frac{ {\bar p}(Y) }{ p_Y(Y) } – \frac{{\bar p}(Y)^2}{p_Y(Y)^2} \right| \right] \\
&=& || {\hat p} ||^2 {C_f}^2 {\mathbb E} \left[ \left| 1 ( 1 – \frac{{\hat p}(Y) }{ p_Y(Y) } ) \right| \left| 1 – \frac{ {\bar p}(Y) }{ p_Y(Y) } \right| \right] \\
&\leq& || {\hat p} ||^2 {C_f}^2 {\mathbb E} \left[ \left(1 + \left| 1 – \frac{ {\bar p}(Y) }{ p_Y(Y) } \right| \right) \left| 1 – \frac{ {\bar p}(Y) }{ p_Y(Y) } \right| \right] \\
&=& || {\hat p} ||^2 {C_f}^2 \left( {\mathbb E} \left[ \left| 1 – \frac{{\bar p}(Y)}{p_Y(Y)} \right| \right] + {\mathbb E} \left[ \left| 1 – \frac{ {\bar p}(Y) }{p_Y(Y)} \right|^2 \right] \right) \\
&\leq& || {\hat p} ||^2 {C_f}^2 \left( \sqrt{ {\mathbb E} \left[ \left| 1 – \frac{{\bar p}(Y)}{p_Y(Y)} \right|^2 \right] } + {\mathbb E} \left[ \left| 1 – \frac{{\bar p}(Y)}{p_Y(Y)} \right|^2 \right] \right) \tag{S.99} \\
& & \overset{M \rightarrow \infty}{\longrightarrow} 0
\end{eqnarray}
となります。
Step 3. step 1 と 2を結び付け,次に帰着します。
\begin{eqnarray}
& &{\rm Var}[ f(Y) W_Y ] – {\rm Var} \left[ \frac{f(X)}{{\bar p}(X)} \right] \tag{S.100} \\
&=& \left( {\rm Var} [f(Y) W_Y] – {\rm Var} \left[ \frac{ f(Y) }{ p_Y(Y) } \right] \right) – \left( {\rm Var} \left[ \frac{f(X)}{{\bar p}(X)} \right] – {\rm Var} \left[ \frac{f(Y)}{p_Y(Y)} \right] \right) \\
& & \overset{M \rightarrow \infty}{\longrightarrow} 0
\end{eqnarray}
■
定理A.3の証明(項目3)。\({\hat p}(x) = Cf(x)\)、すなわち\({\bar p}(x) = f(x) / || f ||\)を前の結果に代入すると、次のようになります。
\begin{eqnarray}
{\rm Var}[ f(Y) W_Y ] – {\rm Var} \left[ \frac{ f(X)|| f || }{f(X)} \right] \overset{M \rightarrow \infty}{\longrightarrow} 0 ,
\end{eqnarray}
すなわち,
\begin{eqnarray}
{\rm Var}[f(Y) W_Y] \overset{M \rightarrow \infty}{\longrightarrow} 0
\end{eqnarray}
■
S.5.4 Variance in the Finite Case (Theorem 1)
定理1の証明。セクションS.5.3の定理A.3(項目2)の証明を続け、次を導出します。
\begin{eqnarray}
&& {\rm Var}[f(Y) W_Y] – {\rm Var}\left[ \frac{f(X)}{{\bar p}(X)} \right] \\
&=& {\rm Var}[f(Y) W_Y] – {\rm Var}\left[ \frac{f(Y)}{p_Y(Y)} \right] + {\rm Var}\left[ \frac{f(Y)}{p_Y(Y)} \right] – {\rm Var} \left[ \frac{f(X)}{{\bar p}(X)} \right] \\
&\leq& {\rm Var}[f(Y) W_Y] – {\rm Var} \left[ \frac{f(Y)}{p_Y(Y)} \right] + \left| {\rm Var} \left[ \frac{f(Y)}{p_Y(Y)} \right] – {\rm Var}\left[ \frac{f(X)}{{\bar p}(X)} \right] \right|.
\end{eqnarray}
\(V = {\rm Var}[\sum_{i=1}^M w_i ]\)とし、定理A.2の証明の式S.88から次を導出します。
\begin{eqnarray}
{\mathbb E} \left[ \left| 1 – \frac{{\bar p}(Y)}{p_Y(Y)} \right|^2 \right] \leq \frac{{\rm Var}[{\hat p}(Y) W_Y] }{ || {\hat p} ||^2 } = \frac{V}{ || {\hat p} ||^2 } \tag{S.101}
\end{eqnarray}
我々は,これを式S.99に代入し,次を得ます。
\begin{eqnarray}
& & \left| {\rm Var} \left[ \frac{f(X)}{{\bar p}(X)} \right] – {\rm Var}\left[ \frac{f(Y)}{p_Y(Y)} \right] \right| \tag{S.102} \\
&\leq& || {\hat p} ||^2 {C_f}^2 \left( \sqrt{ {\mathbb E} \left[ \left| 1 – \frac{{\bar p}(Y)}{p_Y(Y)} \right|^2 \right] } + {\mathbb E} \left[ \left| 1 – \frac{{\bar p}(Y)}{p_Y(Y)} \right|^2 \right] \right) \tag{S.103} \\
&\leq& || {\hat p} ||^2 {C_f}^2 \left( \sqrt{ \frac{V}{ || {\hat p} ||^2 } } + \frac{V}{ || {\hat p} ||^2} \right) = {C_f}^2 \left( || {\hat p} || \sqrt{V} + V \right) \tag{S.104}
\end{eqnarray}
式S.95を参照し,
\begin{eqnarray}
0 \leq {\rm Var}[f(Y) W_Y] – {\rm Var}\left[ \frac{f(Y)}{p_Y(Y)} \right] \leq {C_f}^2 {\rm Var} \left[ \sum_{i=1}^M w_i \right] = {C_f}^2 V
\end{eqnarray}
そして,次に帰着します。
\begin{eqnarray}
&& {\rm Var}[ f(Y) W_Y ] – {\rm Var} \left[ \frac{f(X)}{{\bar p}(X)} \right] \\
&\leq& {\rm Var}[f(Y) W_Y] – {\rm Var} \left[ \frac{f(Y)}{p_Y(Y)} \right] + \left| {\rm Var}\left[ \frac{f(Y)}{p_Y(Y)} \right] – {\rm Var}\left[ \frac{f(X)}{{\bar p}(X)} \right] \right| \\
&\leq& {C_f}^2 V + {C_f}^2 \left( || {\hat p} || \sqrt{V} + V \right) = {C_f}^2 \sqrt{V} \left( || {\hat p} || + 2 \sqrt{V} \right) \tag{S.105}
\end{eqnarray}
□
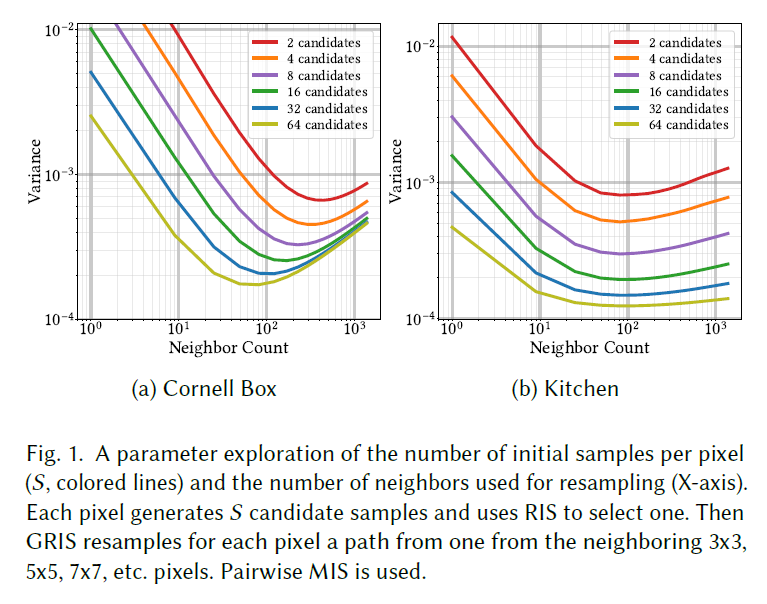
S.6 PARAMETER EXPLORATION
このセクションでは、オフラインレンダリングのためのReSTIR PTの近傍数、再利用窓サイズ、空間再利用パスの数などのパラメータの効果を分析し、デフォルトパラメータの選択を正当化します。単純なコーネルボックスとより複雑なキッチンの2つのシーンで実験を行い、結論を導きます。
まず、再利用するピクセル数と、ピクセルあたりの経路候補サンプル数を最適な数に増やすことで、サンプリングコストを償却できることを示します。最初の実験では、現在のピクセルを囲む正方形内の各ピクセルからのパスを密に再利用し、このケースを分析した後、より大きな近傍からランダムにサンプリングされた疎な近傍に結果を一般化します。
S.6.1 Parameters for Dense Block of Pixels
GRISを使用しない経路再利用(例えば、Bekaertら[2002]による経路再利用アルゴリズム)は、再サンプリングがゼロからサンプルを生成するよりも安価であるため、純粋な経路トレースよりも高いサンプリング効率を既に達成することができます。アンバイアスドな寄与重みを定義することで、我々のGRISはサンプリングコストのより積極的な償却をサポートします – レゼバーを使用することで、サンプル生成コストをさらに償却するために、初期RISの入力サンプル数を増やすことができます。\(S\)個の候補サンプルに対して、1個のサンプルを再利用する場合、およそ\(S\)個のサンプルを「獲得」します。サンプリング効率を分析するために、得られたレイ数と計算されたレイ数の比率を測定する単純化したモデルを作成します。全てのピクセルが一定の長さ\(L\)のパスを生成し、近傍のピクセルを再利用することでそのピクセルが生成する全てのサンプルを効果的に得るという単純化された理想的なケースを仮定すると、\(K\)個のピクセル(自己を含む)を再利用する場合の式は以下のようになります。
\begin{eqnarray}
\frac{\sharp \, {\rm rays \, gained}}{\sharp \, {\rm rays \, computed}} = \frac{KSL}{SL + \eta (K-1)}, \tag{S.106}
\end{eqnarray}
ここで,\(\eta\)は再サンプリングに対して我々が支払うレイのコストです(通常\(\eta \lt L\))。
\(S=1\)の場合、式は\(KL/(L + \eta(K-1))\)と評価されます。\(K \rightarrow \infty\)の場合でも、効率は\(L/ \eta\)に制限されます。もし\(S \rightarrow \infty\)があれば、効率は\(K\)によって制限されます。つまり、この単純化された理想的なケースでは、効率向上は理論的に無制限になります。実際には、レンダリング時間が等しいときの分散を比較することで、サンプリング効率を測定することができます。
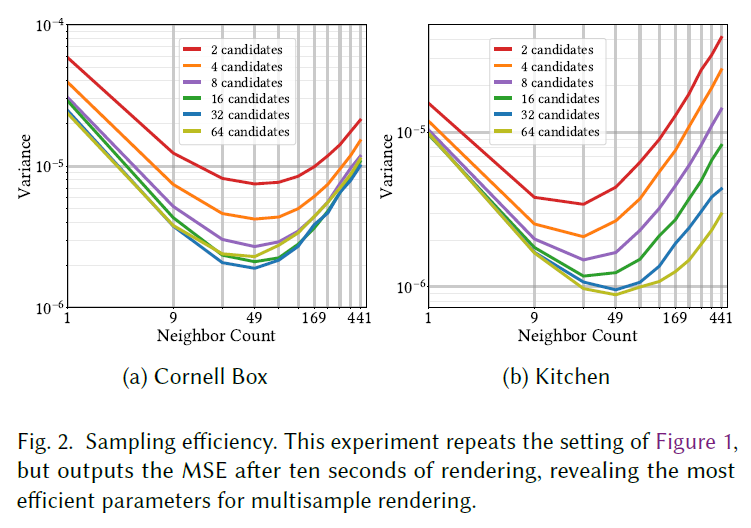
このことは、より高いサンプリング効率を達成するためには、比較的大きな\(S\)と比較的大きな\(K\)を使うべきであることを示唆しています。実際、図1を見ると、\(S\)と\(K\)を大きくすることは最終的に有害であることがわかります。近傍数\(K\)を大きくすると、近傍が十分に大きくなったときにMSEが減少する代わりにMSEが増加し、\(S\)を大きくするとさらに早く問題が発生します。これは、近傍サイズを大きくすると、より遠くにあるサンプルが追加され、パス空間の類似性は一般的に距離によって減少するためです。これは最終的にサンプル数の増加による利益を相殺します。図2に示すように、\(S\)(最初の再サンプリングの候補数)を大きくすることも、最終的には収穫逓増につながります。どちらのシーンでも、\(S=32\)と\(K=49\)の組み合わせ(つまり、\(7 \times 7\)の近傍)を使うと、サンプリング効率がほぼ最適になることがわかります。
S.6.2 Parameters for Sparse Neighbors
GRISのために多数の入力サンプルを使用するコストは、複数の空間再利用パスを連鎖させることによっても償却できます。注意点は、小さな固定近傍で空間再利用パスを連鎖させると、サンプル間に過度の相関が生じ、サンプリング効率が低下する可能性があることです。このことは、相関を最小化するために、大きな近傍領域からランダム化された疎な近傍領域を使用する動機付けとなります。
パラメータ探索の結果、ランダム再利用のサンプリング効率は、\(S=32\)(密集再利用の場合と同様)、半径5~10ピクセル(直径10~20ピクセル)に6~10個のランダムな近傍を持つ空間再利用を2~3ラウンド行うことで、ほぼ最適なサンプリング効率を達成できることがわかりました。両方のシーンでこのパラメータ範囲の視覚的品質を比較した後、半径10ピクセル、空間再利用の3ラウンド、ランダムな近傍6個のパラメータセットを選択します。最適に近いパラメータで密な再利用を行った場合と比較して、同等のレンダリング時間で分散がわずかに減少していることがわかります。疎な再利用は、サンプリングコストを償却することによる利点を部分的にキャンセルするために、より大きな近傍領域を必要とするため、サンプリング効率の改善は小さいです。しかし、ランダム再利用は近傍ピクセル間の視覚的相関を低減するため、視覚的な改善ははるかに大きくなります(図3)。複数フレームにわたって多くの再利用パスを連鎖させることで、より多くの相関関係が構築されるためです。リアルタイムレンダリングでは、レンダリング時間を短くするために、半径を20ピクセルにし、各ピクセルに1つの初期候補サンプルのみを使用し、現在のピクセルと他の3つのランダムなピクセルの間で1つの空間再利用パスを使用します。
S.7 MATHEMATICAL NOTES
S.7.1 Constrains on \(w_i\) for Zero Bias in Section 4.3
セクションに従い、次のように仮定します。
\begin{eqnarray}
g_i(x) = [ x \in {\mathcal D}(T_i)] c_i (y_i) \cdot f(y_i) | \frac{\partial T_i}{\partial x} |
\end{eqnarray}
ここで\(y_i\)は\(T_i(x)\)の省略形であり、\([\cdot]\)は\(\cdot\)が真のとき1、そうでないとき0です。
- (簡単な場合)\(X_i \in {\mathcal D}(T_i)\)と\(Y_i = T_i(X_i) \in {\rm supp}{\hat p}\)のときに正確に\(w_i \gt 0\)となり、それ以外は\(w_i = 0\)となります。
- (一般的な場合)\(w_i\)は、\(c_i(Y_i)=0\)または\(W_i=0\)のときにも0であることが許され、式17はすべての\(y \in {\rm supp}{\hat p} \cap {\cup}_{i=1}^M T_i({\rm supp}X_i)\)について成立します。
このとき,導出された推定量がアンバイスであることを示します。
\begin{eqnarray}
E [ g_s(X_s) \frac{ \sum_{j=1}^M w_j }{w_s} f(X_s) W_s] = \int_{{\rm supp}Y} f(y) dy, \tag{S.107}
\end{eqnarray}
そして,式15を用います。すなわち,
\begin{eqnarray}
{\rm supp}Y = {\rm supp}{\hat p} \cap {\bigcup}_{i=1}^M T_i ({\rm supp}X_i) \tag{S.108}
\end{eqnarray}
まず、どちらの場合も式S.108を証明してみましょう。
証明. 簡単な場合。\(x_i\)が正のPDFでサンプリングされうる場合、\(y \in {\rm supp}{\hat p} \cap \cup_{i=1}^M T_i({\rm supp}X_i)\)なら、\(z_i \in {\rm supp}X_i\)は\(y = T_i(x_i)\)です。\(y \in {\rm supp}{\hat p}\)にも\({\hat p}(y) = {\hat p}(T_i(x_i)) \gt 0\)があるので、仮定によって\(w_i \gt 0\)となります。したがって、正のPDf、\(w_i \gt 0\)、\(y=T_i(x_i)\)を持つ\(x_i\)があり、正のPDF、すなわち\(y \in {\rm supp}Y\)を持つ\(y\)をサンプリングする方法があります。我々は\({\rm supp}{\hat p} \cap \cup_{i=1}^M T_i({\rm supp}X_i) \subset {\rm supp}Y\)を示します。
一方、\(y \in {\rm supp}Y\)の場合、サンプリング\(y\)のPDFは正です。したがって、正のPDFを持ち、\(y=T_i(x_i)\)に対する正の選択確率を持つ\(x_i\)が存在します。したがって\(w_i \gt 0\)であり、これは\({\hat p}(y) \gt 0\)を意味し、したがって\(y \in {\rm supp}{\hat p} \cap \cup_{i=1}^M T_i({\rm supp} X_i)\)となります。前述と合わせると\(Y = {\rm supp}{\hat p} \cap \cup_{i=1}^M T_i({\rm supp}X_i)\)となります。
一般的な場合。\(y \in {\rm supp}{\hat p} \cap \cup_{i=1}^M T_i({\rm supp}X_i)\)とします。\(y \in T_i({\rm supp}X_i)\)を表すインデックスの集合を\(I\)とします。仮定により\(\sum_{i \in I} c_i(y) = 1\)であるから、\(c_i(y) \gt 0\)となるような\(i\)が少なくとも1つ存在し、したがって\(y = T_i(x_i)\)が\(p_{X_i}(x_i) \gt 0\)となるような\(x_i\)が存在します。\(0 \le p_{X_i}(x_i) = 1 / {\mathbb E}[W_i | X_i = x_i]\)であるので、\(W_i\)の条件期待値は正であり、ここでは\({\rm Pr}[W_i \gt 0 | X_i = x_i] \gt 0\)と\(p_Y(y) \gt 0\)、すなわち\(y \in {\rm supp}Y\)です。
次に\(y \in {\rm supp}Y\)を仮定します。\(y\)を生成するPDFは正であるため、\(p_{X_i}(x_i) \gt 0\)、\(y=T_i(x_i)\)、正の条件付き確率\(w_i \gt 0\)のように、\(i\)と\(x_i\)が存在する必要があります。もし\(w_i\)が正であれば、\(y \in {\rm supp}{\hat p}\)、つまり\(y \in {\rm supp}{\hat p} \cap \cup_{i=1}^M T_i({\rm supp}X_i)\)となります。
□
次に、式S.107を証明します。
証明。最初に
\begin{eqnarray}
& & {\mathbb E} \left[ g_s(X_s) \frac{ \sum_{j=1}^M w_j }{ w_s } W_s \right] \tag{S.109} \\
&=& {\mathbb E} \left[ \sum_{s=1}^M [w_s \gt 0] \frac{w_s}{\sum_{j=1}^M w_j} g_s(X_s) \frac{ \sum_{j=1}^M w_j }{w_s} W_s \right] \tag{S.110} \\
&=& {\mathbb E} \left[ \sum_{s=1}^M [w_s \gt 0] g_s(X_s) W_s \right] \tag{S.111}
\end{eqnarray}
次に、\(g_s\)の定義を置き換えて、次のようになります。
\begin{eqnarray}
= {\mathbb E} \left[ \sum_{s=1}^M [w_s \gt 0] [X_s \in {\mathcal D}(T_s)] c_s(Y_s) f(Y_s) \left| \frac{\partial T_s}{\partial X_s} \right| W_s \right] \tag{S.112}
\end{eqnarray}
両方の場合に成り立つ仮定を加え,\({\hat p}(Y_s) = 0\)の場合は\(w_s=0\)となり,次に帰着します。
\begin{eqnarray}
= {\mathbb E}\left[ \sum_{s=1}^M [ Y_s \in {\rm supp}{\hat p}][ w_s \gt 0 ] [ X_s \in {\mathcal D}(T_s)] c_s(Y_s) f(Y_s) \left| \frac{\partial T_s}{\partial X_s} W_s \right| \right] \tag{S.113}
\end{eqnarray}
次に、\([w_s \gt 0 ] = 1 – [w_s = 0]\)を代入すると、次のようになります。
\begin{eqnarray}
= {\mathbb E} \left[ \sum_{s=1}^M [ Y_s \in {\rm supp}{\hat p}][X_s \in {\mathcal D}(T_s)] c_s(Y_s) f(Y_s) | \frac{\partial T_s}{\partial X_s} | W_s \right] \\
– {\mathbb E} \left[ \sum_{s=1}^M [ Y_s \in {\rm supp}{\hat p}][w_s = 0][X_w \in {\mathcal D}(T_s)] c_s(Y_s) f(Y_s) | \frac{\partial T_s}{\partial X_s} | W_s \right] \tag{S.114}
\end{eqnarray}
アンバイアスドな寄与ウェイトの定義(\(W_s\)以外は\(X_s\)の関数)を用いると、第一項は次のようになります。
\begin{eqnarray}
& & {\mathbb E} \left[ \sum_{s=1}^M [Y_s \in {\rm supp}{\hat p}][X_s \in {\mathcal D}(T_s)] c_s(Y_s)f(Y_s) | \frac{\partial T_s}{\partial X_s} | W_s \right] \tag{S.115} \\
&=& \sum_{s=1}^M \int_{{\rm supp}X_s} [y_s \in {\rm supp}{\hat p}][x_s \in {\mathcal D}(T_s)] c_s(y_s)f(y_s) | \frac{\partial T_s}{\partial x_s} | d x_s \tag{S.116} \\
&=& \sum_{s=1}^M \int_{{\mathcal D}(T_s)} [y_s \in {\rm supp}{\hat p}][x_s \in {\rm supp}X_s] c_s(y_s) f(y_s) | \frac{\partial T_s}{\partial x_s} | d x_s \tag{S.117}
\end{eqnarray}
これは、各項の変数を\(y = T_s(x_s)\に変えて\(x_s = {T_s}^{-1}(y)\)とすると、次のように単純化されます。
\begin{eqnarray}
&=& \sum_{s=1}^M \int_{{\mathcal I}(T_s)} [ y \in {\rm supp}{\hat p}][ x_s \in {\rm supp}X_s] c_s(y) f(y) dy \tag{S.118} \\
&=& \sum_{s=1}^M \int_{{\rm supp}{\hat p}} [ y \in {\mathcal I}(T_s)] [ x_s \in {\rm supp}X_s] c_s(y) f(y) dy \tag{S.119} \\
&=& \int_{{\rm supp}{\hat p}} \left( \sum_{s=1}^M [y \in {\mathcal I}(T_s)[x \in {\rm supp}X_s] c_s(y) \right) f(y) dy \tag{S.120}
\end{eqnarray}
次に、括弧の積を和の条件として書くと、次のようになります。
\begin{eqnarray}
&=& \int_{{\rm supp}{\hat p}} \left( \underset{y \in T_s({\rm supp}X_s)}{ \sum_{s=1}^M } c_s(y_s) \right) f(y) dy \tag{S.121} \\
&=& \int_{{\rm supp}{\hat p} \cap \cup_i T_i({\rm supp}X_i)} \left( \underset{y \in T_s({\rm supp}X_s)}{\sum_{s=1}^M } c_s(y_s) \right) f(y)dy \tag{S.122} \\
&=& \int_{{\rm supp}Y} \left( \underset{y \in T_s({\rm supp}X_s)}{\sum_{s=1}^M} c_s(y) \right) f(y) dy \tag{S.123} \\
&=& \int_{{\rm supp}Y} f(y) dy \tag{S.124} \\
& & \tag{S.125}
\end{eqnarray}
\(f\)を\({\rm supp}Y\)上で積分する方法がアンバイアスドであるためには、次の二つ目の項がゼロになる必要があります。
\begin{eqnarray}
{\mathbb E}\left[ \sum_{s=1}^M [Y_s \in {\rm supp}{\hat p}][w_s = 0][X_s \in {\mathcal D}(T_s)] c_s(Y_s)f(Y_s) | \frac{\partial T_s}{\partial X_s} | W_s \right]
\end{eqnarray}
より簡単なケースでは、\(w_i \gt 0\)が\(X_i \in {\mathcal D}(T_i)\)と\(Y_i = T_i(X_i) \in {\rm supp}{\hat p}\)の場合に限ります。上記の第2項は、各\(s\)に対して次の係数を含みます。
\begin{eqnarray}
& & [Y_s \in {\rm supp}{\hat p}] [X_s \in {\mathcal D}(T_s)] [w_s = 0] \tag{S.126} \\
&=& [w_s \gt 0][w_s = 0] = 0, \tag{S.127}
\end{eqnarray}
したがって,第2項はゼロであり,推定器はアンバイアスドです。
一般的なケースでは、\(W_i = 0\)または\(c_i(Y_i) = 0\)のいずれかのときに、\(w_i\)はさらに0であることが許されます。しかし、もし\(w_s=0\)であれば、仮定により、\(X_s \notin {\mathcal D}(T_s)\)、\(Y_s \notin {\rm supp}{\hat p}\)、\(c_s(Y_s) = 0\)、\(W_s=0\)のいずれかとなります。これらのケースをチェックするのは簡単です:すべての場合において二つ目の項はゼロです。推定器はアンバイアスドとなります。
□
S.7.2 Non-Negativity for \(m_i\) and \(W_i\) in Section 4.4
ここでは、式19において、\(m_i \geq 0\)と\(W_i \geq 0\)が非負の確率を保証する必要があることを証明します。
証明。選択確率\({\rm Pr}[s = i] = w_i / \sum_{j=1}^M w_j\)はすべて非負でなければなりません。これらは同じ分母で除算され、\(w_i / \sum_{j=1}^M w_j\) の表現がどれも符号が反転しないか、すべて反転します。したがって、すべての\(w_i\)は同じ符号でなければならず、確率はすべて非負になる可能性があります。すべての\(i\)に\(w_i \gt 0\)がある場合、\(w_i\)の符号を反転させて\(w_i \geq 0\)にすることができます。一般性を失わずに、\(w_i \geq 0\)の場合に限定します。
もし\(w_i \geq 0\)であれば、次のような場合もあります。
\begin{eqnarray}
{\mathbb E}[w_i | X_i] \geq 0 \tag{S.128}
\end{eqnarray}
次に、式19を\(w_i\)に代入する。\(x \notin {\mathcal D}(T_i)\)であれば、\(w_i=0\)となります。そうでなければ、\(y = T_i(x)\)と\(Y_i = T_i(X_i)\)を表すと、次のようになります。
\begin{eqnarray}
0 \leq {\mathbb E}[w_i | X_i =x] &=& {\mathbb E}\left[ m_i(Y_i){\hat p}(Y_i)W_i \left| \frac{\partial T_i}{\partial X_i} \right| | X_i = x \right] \tag{S.129} \\
&=& m_i(y) {\hat p}(y) \left| \frac{\partial T_i}{\partial x} \right| {\mathbb E}[W_i | X_i = x] \tag{S.130} \\
&=& m_i(y) {\hat p}(y) \left| \frac{\partial T_i}{\partial x} \right| \frac{1}{p X_i(x)} \tag{S.131}
\end{eqnarray}
\({\hat p}(y)\), \(| \frac{\partial T_i}{\partial x} |\)と\(p X_i(X)\)はすべて非負であり、完全積は非負であるため、\(m_i(y)\)も非負でなければなりません。
式19を見ると、\(m_i \geq 0\)、\({\hat p}(y) \geq 0\)、\(|\frac{\partial T_i}{\partial x} | \geq 0\)があり、\(W_i\)との積は\(w_i \gt 0\)であるため、\(W_i \geq 0\)も必要となります。
□
S.7.3 Resampling MIS Must Be Positive in Support of \(c_i\) in Section 4.4
アンバイアスドな積分を保証するために、リサンプリングMISの重み\(m_i\)は、非負と式20に加えて、\(c_i(y) \neq 0\)のときはいつでも\(m_i(y) \gt 0\)を満たさなければなりません:
証明。\(g_i\)を式10の左辺に代入すると、次のようになります。
\begin{eqnarray}
& & {\mathbb E}\left[ g_s(X_s) \frac{ \sum_{j=1}^M w_j }{ w_s } W_s \right] = {\mathbb E} \left[ [w_s \gt 0]g_s(X_s) \frac{ \sum_{j=1}^M w_j }{ w_s } W_s \right] \tag{S.132} \\
&=& {\mathbb E}\left[ \sum_{s=1}^M [w_s \gt 0] \frac{ w_s }{ \sum_{j=1}^M w_j } g_s(X_s) \frac{ \sum_{j=1}^M w_j }{w_s} W_s \right] \tag{S.133} \\
&=& \sum_{s=1}^M {\mathbb E} [w_s \gt 0] g_s(X_s) W_s] \tag{S.134}
\end{eqnarray}
\(w_s\)(式19)が正であるのは、\(X_s \in {\mathcal D}(T_s)\)、\(m_s(Y_s) \gt 0\)、\({\hat p}(Y_s) \gt 0\)、\(W_s \gt 0\)、\(| \frac{\partial T_s}{\partial X_s} | \gt 0\)のときだけです。\(W_s \geq 0\)を仮定し、\(W_s=0\(の場合は係数\(W_s\)ですでに処理されています。\(T_i\)は両対称なので、ヤコビアン行列式は\({\mathcal D}(T_i)\)において確率1で非ゼロです。したがって、\(g_s\)を代入すると次のようになる。
\begin{eqnarray}
= \sum_{s=1}^M {\mathbb E} \left[ [X_s \in {\mathcal D}(T_s) ][m_s(Y_s), {\hat p}(Y_s) \gt 0] c_s(Y_s)f(Y_s) | \frac{\partial T_s}{\partial X_s} | W_s \right]
\end{eqnarray}
アンバイアスドな寄与ウェイト\(W_s\)から残るものはすべて\(X_s\)の関数となります。したがって、アンバイアスドな寄与ウェイトの定義により、次のようになります。
\begin{eqnarray}
= \sum_{s=1}^M \int_{{\rm supp}X_s} [x_s \in {\mathcal D}(T_s)] [m_s (y_s), {\hat p}(y_s) \gt 0] c_s(y_s) f(y_s) | \frac{\partial T_s}{\partial x_s} | d x_s
\end{eqnarray}
積分領域と\([x_s \in {\mathcal D}(T_s)]\)を入れ替えると、次のようになります。
\begin{eqnarray}
= \sum_{s=1}^M \int_{{\mathcal D}(T_s)} [x_s \in {\rm supp}X_s][m_s (y_s), {\hat p}(y_s) \gt 0] c_s(y_s) f(y_s) | \frac{\partial T_s}{\partial x_s} | d x_s
\end{eqnarray}
となり、変数\(y = T_s(x_s)\)を変えると次のようになります。
\begin{eqnarray}
= \sum_{s=1}^M \int_{{\mathcal I}(T_s)} [x_s \in {\rm supp}X_s][m_s (y), {\hat p}(y) \gt 0] c_s(y) f(y) dy
\end{eqnarray}
積分領域と\([{\hat p}(y) \gt 0]\)を入れ替えると次のようになります。
\begin{eqnarray}
= \sum_{s=1}^M \int{{\rm supp}{\hat p}} [x_s \in {\rm supp}X_s][y \in {\mathcal I}(T_s)][m_s(y) \gt 0] c_s(y) f(y) dy
\end{eqnarray}
これは積分の内側に和を移動させることができます:
\begin{eqnarray}
= \int_{{\rm supp}{\hat p}} \left( \sum_{s=1}^M [x_s \in {\rm supp}X_s][y \in {\mathcal I}(T_s)][m_s(y) \gt 0] c_s(y) \right) f(y) dy.
\end{eqnarray}
次に、最初の2つの指標を単純化して和の条件にします:
\begin{eqnarray}
= \int_{{\rm supp}{\hat p}} \left( \underset{ y \in T_s({\rm supp}X_s) }{ \sum_{s=1}^M} [m_s(y) \gt 0] c_s(y) \right) f(y) dy \tag{S.135}
\end{eqnarray}
和が少なくとも1つのインデックスを含まない限り、積分はゼロであり、それに応じて積分領域を縮小することができます:
\begin{eqnarray}
= \int_{{\rm supp}{\hat p} \cap \cup_{i=1}^M T_i({\rm supp}X_i)} \left(\underset{y \in T_s({\rm supp}X_s)}{ \sum_{s=1}^M} [m_s(y) \gt 0] c_s(y) \right) f(y)dy
\end{eqnarray}
式15により、この領域はまさに\({\rm supp}(Y)\)です:
\begin{eqnarray}
= \int_{{\rm supp}Y} \left( \underset{y \in T_s({\rm supp}X_s)}{ \sum_{s=1}^M [m_s(y) \gt 0] c_s(y) } \right) f(y) dy \tag{S.136}
\end{eqnarray}
最後に、\(c_s(y) \neq 0\)のときはいつでも,\(m_s(y) \gt 0\)を仮定すると、寄与MISウェイトの制約(式17)により、次のようになります。
\begin{eqnarray}
&=& \int_{{\rm supp}Y} \left( \underset{y \in T_s({\rm supp}X_s)}{\sum_{s=1}^M} c_s(y) \right) f(y)dy \tag{S.137} \\
&=& \int_{{\rm supp}Y} f(y) dy \tag{S.138}
\end{eqnarray}
もし\(m_s(y) = 0\)が\(c_s(y) \neq 0\)である確率がゼロでないと仮定した場合、式S.136の\(f(y)\)の前の乗数は\(c_i\)の制約で1に単純化されず、結果は間違いとなります。
□
REFEENCES
- Robert G Bartle. 2014. The elements of integration and Lebesgue measure. John Wiley & Sons.
- Philippe Bekaert, Mateu Sbert, and John H Halton. 2002. Accelerating Path Tracing by Re-Using Paths.. In Rendering Techniques. 125–134.