こんにちわ,Pocolです。
仕事で実装しているやつのアクネが酷く,Adaptive Depth Bias For Shadow Mapを読んでみたので,まとめておきます。
論文和訳
2. Adaptive Depth Bias
出発点として,従来のシャドウマップが持つ問題の解決をします。その他のシャドウマッピングアルゴリズムへの我々の手法の拡張は簡単で,以下のセクションで詳しく説明します。
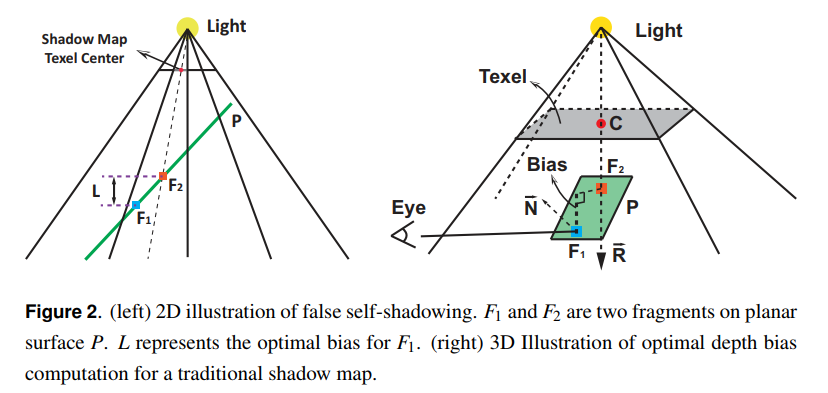
従来のシャドウマップにおけるシャドウアクネは主にシャドウマップ中におけるカメラビューからのシェーディング点のサンプルのミスマッチによって発生します。誤ったセルフシャドウイングを排除するために必要な深度バイアス量は,フラグメントによって異なります。図2に示すように,\(F_1\)と\(F_2\)が同じ平面にあると仮定します。\(F_1\)はシャドウマップ上でサンプルされた\(F_2\)によってシャドウになります。\(F_2\)は\(F_1\)のオクルーダーまたは,対応するテクセルのオクルーダーと呼ばれます。
\(F_1\)に対する間違ったシャドウイングを取り除くために必要とされる最小の深度バイアスあるいは最適な深度バイアスは\(L\)です。最適なバイアス以外に,オクルーダー\(F_2\)のぴったり真上に\(F_1\)を移動させるためには小さなイプシロン値が必要とされます。適応的深度バイアスを計算するための定式は単純に次のようになります。
\begin{eqnarray}
adaptiveDepthBias = optimalDepthBias + adaptiveEpsilon \tag{1}
\end{eqnarray}
2.1 Optimal Depth Bias
与えられたフラグメントに対して最適な深度バイアスを計算するために,最初に潜在的なオクルーダーを特定します。
平面的なオクルーダーであると仮定すると,フラグメント\(F_1\)が与えられると,その潜在的なオクルーダーは\(F_2\)は\(\vec{R}\)と\(P\)の交点として計算することができます。
ここで,ベクトル\(\vec{R}\)はテクセル中心Cを通して光源からレイトレースされるもので,\(P\)は\(F_1\)と法線\(N\)によって定義される接線平面です。
最適なバイアスは\(F_1\)と\(F_2\)の間の深度の差となります。実際には,optimalDepthBiasを明示的に計算するよりも,可視性をチェックするために接線平面のフラグメントとシャドウマップのテクセル中心を通る光線の交差点の深度を使用します。
平坦な平面上にフラグメントがあると仮定すると,多くの実際のシーンにおいて共通の状況に近い近似を得ることができます。
2.2 Adaptive Epsilon
潜在的なオクルーダー上でフラグメントをシフトさせるためには,最適な深度バイアスの代わりに適切なイプシロンの値が必要となります。しかしながら,定数イプシロンは深度値が大抵非線形に圧縮されるのでうまく動作しません。
従って,定数イプシロンを直接利用する代わりに,定数イプシロンを深度圧縮関数に基づいて適応的に変換します。
適応的イプシロンは次の深度圧縮関数と定数イプシロンに基づいて計算されます。
\begin{eqnarray}
\epsilon &=& f’ (x) \Delta x \tag{2} \\
\Delta x &=& sceneScale \times K \tag{3}
\end{eqnarray}
ここで,\(\epsilon\)はバイアスに使用するための適応的なイプシロンを示し,\(x\)はシェードされたフラグメントの正規化されていない深度値,\(\Delta x\)はワールド空間座標系における正規化されていないイプシロン値,\(f(x)\)はニア平面からファー平面への[0, 1]の深度値をマップする任意の深度圧縮関数,\(sceneScale\)は真のバウンディングボックスの対角線の長さを示し,\(K\)は定数となります。実際には標準的なOpenGLの深度圧縮関数
\begin{eqnarray}
a &=& – \frac{ lf + ln }{ lf – ln} \tag{4} \\
b &=& – \frac{ 2 \times lf \times ln }{ lf – ln } \tag{5} \\
f(x) &=& \frac{ -a \times x + b }{ 2 \times x } + \frac{ 1 }{ 2 } \tag{6}
\end{eqnarray}
ただし,\(ln\)と\(lf\)はライトのニア平面とファー平面の距離を表し,\(x\)は実数深度値\((x \in [-lf, -ln] )\)で,\(f(x)\)は圧縮された深度値\((f(x) \in [0, 1])\)を示します。
式(6)から,次を得ます:
\begin{eqnarray}
f(x)’ &=& \frac{ -b }{ 2 \times x^2 } \tag{7} \\
x &=& \frac{ b }{ 2f(x) + a – 1 } \tag{8}
\end{eqnarray}
式(2), 式(7), 式(8)をまとめ,適応的イプシロンのための定式を得ます:
\begin{eqnarray}
\epsilon = \frac{ ( 2f(x) + a – 1 )^2 }{ -2 \times b } \times \Delta x \tag{9}
\end{eqnarray}
\(a\)と\(b\)を式(4)と式(5)で置き換え,我々が提案する適応的イプシロンは以下のようになります:
\begin{eqnarray}
\epsilon = \frac{ (lf – depth \times (lf – ln) )^2 }{ lf \times ln \times (lf – ln) } \times sceneScale \times K \tag{10}
\end{eqnarray}
ここで,\(depth\)は与えられたフラグメントに対する正規化された深度値を表します。我々のすべての実験では,\(K = 0.0001\)を設定します。
3. Implementation
それでは,従来のシャドウマップ,放物面シャドウマップ,ボクセライズドシャドウボリュームについてのGLSL上での我々の手法の実装を説明します。
3.1. Adaptive Depth Bias for Traditional Shadow Map
従来のシャドウマップにおける各フラグメントに対して,潜在的なオクルーダーを特定し,適応的イプシロンを計算し,可視性チェックの前に潜在的オクルーダーのすぐ上にフラグメントをシフトします。
アルゴリズム1における疑似コードとリスト1に明確なGLSLの実装を詳細に示します。入力パラメータはライト空間におけるフラグメントの法線,ワールド空間におけるフラグメントの位置座標,そしてシャドウマップの解像度です。
3.2 Adaptive Depth Bias for Parabloid Shadow Map
半球上,および無指向性光源の場合は,全視野の光をマッピングする必要があります; キューブマップと放物面マップの2つは一般的なマッピングです。半球あるいは全方向位照明に対してキューブマップを使用するとき,セクション3.1で説明した適応的深度は直接使用することが可能です。放物面シャドウマップを用いた適用的バイアスについての可視性の疑似コードは従来のシャドウマップについての疑似コードと同じです。潜在的なオクルーダーの特定方法においてのみ違いがあります。
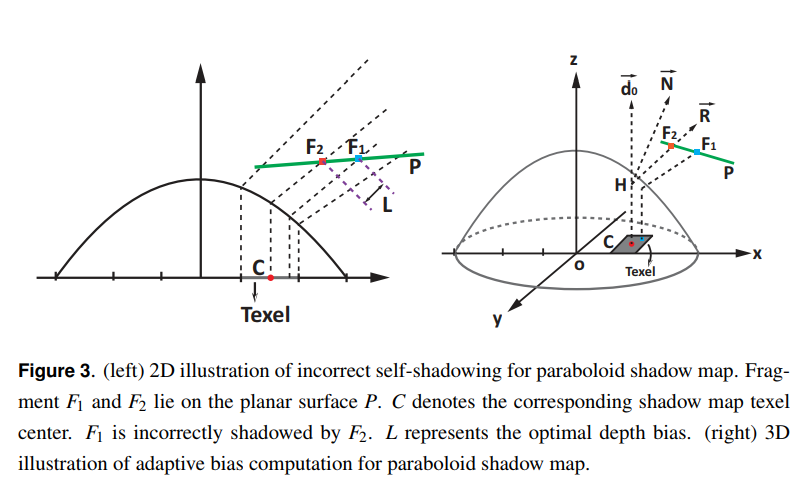
図3(右)に示すように,\(F_1\)は放物面シャドウマップ上の\(F_2\)によって間違ってシャドウになります。
\(F_1\)について,\(L\)は最適な深度バイアスです。従来のシャドウマップの場合と同様に,各フラグメントについて,放物面シャドウマップにおいて対応するテクセルを特定します。次に,フラグメントのローカル接線平面とそのテクセルのシャドウサンプルレイを交差させることによって,テクセル内の潜在的なオクルーダーを得ます。
下図に示すように,フラグメント\(F_1\)が与えられると,放物面シャドウマップへとそれを射影し,対応するテクセル中心\(C(x_c, y_c, 0)\)を特定します。\(H(x_h, y_h, z_h)\)は放物面上の衝突点を表します。\(N\)は\(H\)におけるサーフェイス法線を表します。次のようにサンプルシャドウレイ\(\vec{R}\)を得ることができます。
\begin{eqnarray}
\vec{ R } &=& 2 \times ( \vec{ d_0 } \cdot \vec{ N } ) \times \vec{ d_0 } – \vec{ d_0 } \\
\vec{ d_0 } &=& \lbrack 0, 0, 1 \rbrack ^{T} \\
\vec{ N } &=& \left\lbrack \frac{ x_c }{ z_h }, \frac{ y_c }{ z_h }, \frac{ 1 }{ z_h } \right\rbrack ^{T} \\
z_h &=& \frac{ 1 }{ 2 } – \frac{ 1 }{ 2 } \times ( x_{c}^{2} + y_{c}^{2} )
\end{eqnarray}
テクセル\(T\)内の潜在的なオクルーダーは\(F_2\)で,\(\vec{ R }\)と\(F_1\)のローカル接線平面\(P\)の交差点です。誤ったセルフシャドウイングを取り除くために,セクション2.2で説明した適応的イプシロンで\(F_2\)のぴったり真上に\(F_1\)を移動させます。以下はシェーダコードを示しています。入力パラメータは,フラグ面の位置,ライトの位置,シャドウマップの解像度です。従来のシャドウマップと同じように,放物面シャドウマップにおけるテクセル中心を横断するライトレイを事前計算することも可能です。
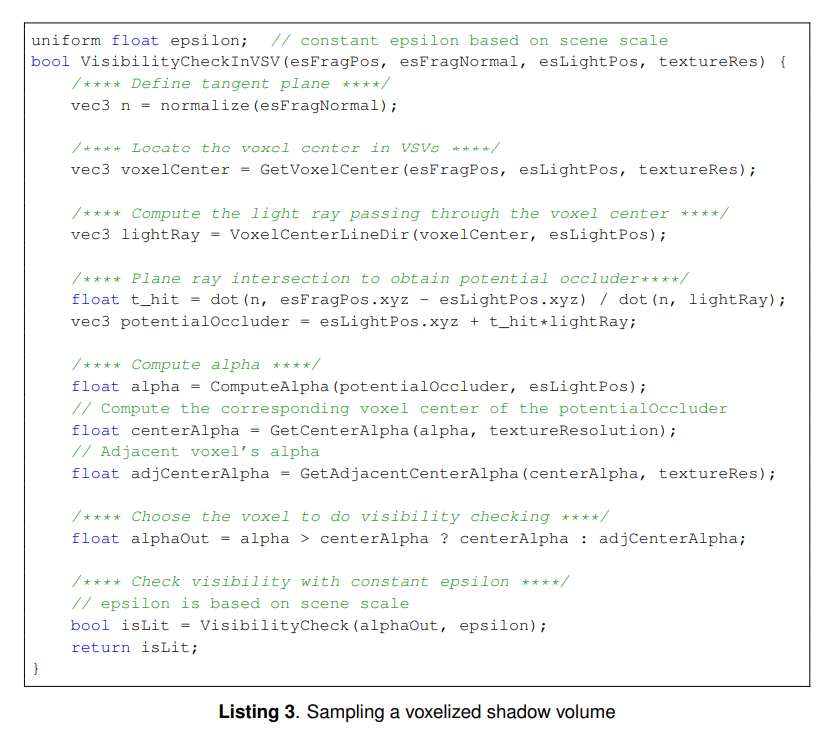
3.3 Adaptive Depth Bias for Voxelized Shadow Volume
ボクセライズドシャドウボリューム(VSV)は,関与媒質中におけるシャドウとサーフェイスのシャドウの両方を計算可能にします。従来のシャドウマッピングと同様に,VSVでサーフェイスのシャドウを計算するとジオメトリの離散化によって視覚的なアーティファクトが発生します。従来のシャドウマップとは異なりVSVはバイナリ情報を持つシャドウを表現します。ボクセルは,フラグメントが遮蔽されるか,ほかの遮蔽オブジェクトの影中に存在する場合のみ遮蔽されます。
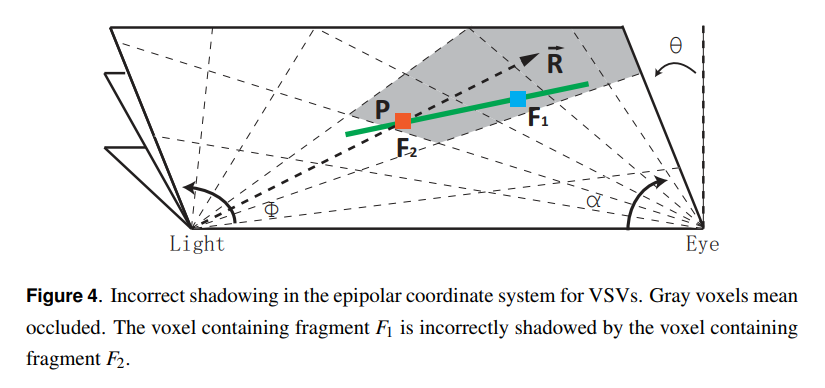
VSVは,バイナリのエピポラーボクセルグリッドを持つシャドウを表現します。図4に示すように,エピポラー空間は眼と光を結ぶ線であるエピポールに対して定義されます。
3つの角度がエピポーラ点を定義します。したがって,エピポーラ空間における点は:\( (\alpha\ \phi, \theta) \in ( \lbrack 0, \pi \rbrack, \lbrack 0, 2 \pi ), \lbrack 0, \pi \rbrack ) \)となります。角度\(\theta\)はあるベクトル(慣例的に,カメラのアップベクトル)に対するエピポーラ平面を定義します。エピポーラ平面上の点は視点とライト点に対して定義されます。角度\(\alpha\)はビューレイに平行な軸を決定し,角度\(\phi\)はライトレイに平行な軸を定義します。図4に示すように,フラグメント\(F_1\)が与えられると,与えられたフラグメントを対応するボクセル\(V_1(\alpha, \phi, \theta)\)に射影し,[Wyman 2011]で説明されるような\(V_1\)のボクセル中心\(C_{V_1} (\alpha_c, \phi_c, \theta_c) \)を得ます。シャドウサンプル例を生成するために\(C_{V1}\)をデカルト座標に変換する代わりに,シャドウサンプルレイを生成するために\(\theta_c\)によって定義される平面上でlightからeyeへのベクトルを変換します:
\begin{eqnarray}
\vec{ V } &=& Eye – Light \\
\vec{ R } &=& Rotate( \vec{ V }, \phi_c )
\end{eqnarray}
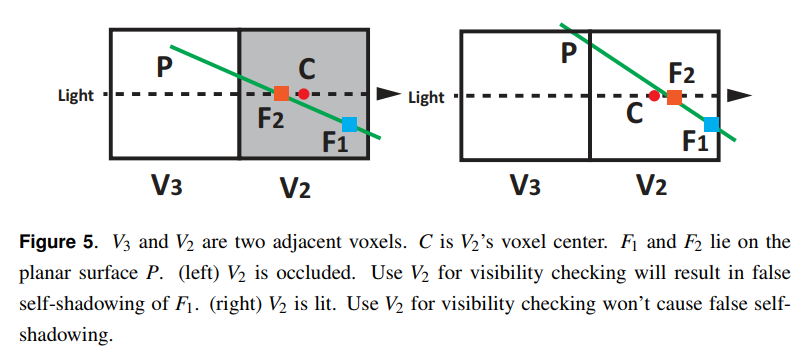
このとき,\(F_1\)の潜在的なオクルーダー\(F_2\)を得るために\(F_1\)のローカル接線平面\(P\)と\(\vec{ R }\)を交差させます。誤ったセルフシャドウイングを取り除くために,潜在的なシャドウをキャストするボクセルの真上に\(F_1\)をシフトする必要があります。ですが,潜在的なシャドウキャストとして\(F_2\)の対応するボクセル\(V_2\)を直接使用することは,図5に示すように偽陽性誤差を引き起こします。
疑似コードとGLSLシェーダは以下のようになります。入力パラメータはフラグメントの位置,フラグメントの法線,ライト位置そしてテクスチャの解像度で,それらはVSVが保持しています。すべてのパラメータはカメラ空間となります。
光源に近い\(V_2\)に隣接するボクセルが\(V_3\)であると仮定します。\(F_2\)がボクセル中心あるいは後ろにある場合に,可視性チェックのために\(V_2\)を使用します。\(F_2\)がボクセル中心の場合は,可視性チェックのために\(V_3\)を使用します。上記は明確にするための疑似コードを表しています。
4. Results and Discussion
我々はOpenGL/GLSLとC++で手法を実装しました。すべてのテストシーンはIntel(R) Cores(TM) i7 CPU at 2.93 GHzとNVIDIA GTX580のグラフィックスカードを装備するマシン上で描画しました。すべての画像の出力は1024×1024の解像度です。テストシーンにおいて,VSVはWymanらの研究のように[2011],シャドウマップのリサンプリングとプレフィックススキャンを適用することによって生成されます。
図6と図7は複雑なシーンにおいて従来のシャドウマップと法物面シャドウマップに対して定数バイアスとスロープスケール深度バイアス[King 2004]と我々の手法の比較となります。
我々は参考画像の生成に2層深度レイヤー手法[Weiskopf and Ertl 2003]を使用しました。定数バイアスと傾斜スケール深度バイアスでは,ライトに近いオブジェクトはシャドウアクネを持ちますが,ライトから遠いオブジェクトは強いシャドウの分離に悩まされます。テストシーンでは,本手法は2層深度シャドウマップに近い結果が得られますが,パフォーマンスは大幅に向上しています。
図9(右)に図示するように,遮蔽されたフラグメントのローカル接線平面がライトレイとほぼ平行である場合に,過剰なバイアスを被り適応的バイアスは予期しないノイズとなります。しかし,これはローカル接線平面がライトレイにほぼ平行である場合のみ発生し,LambertianやPhongのような一般的なマテリアルにおいて観測者にはほとんど輝度を与えません。ゆえに,この問題はシェーディングが適用された後に消えてしまいます。
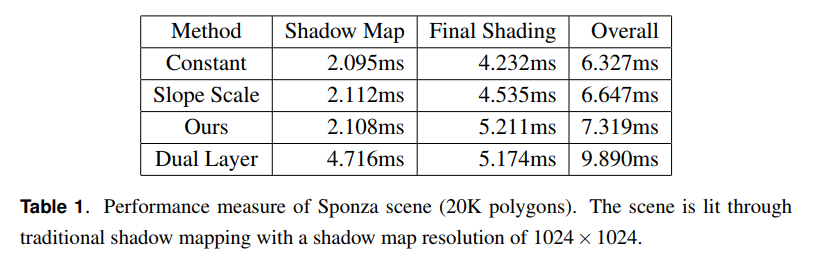
表1は図6に示したシーンに対応するパフォーマンスを示しています。
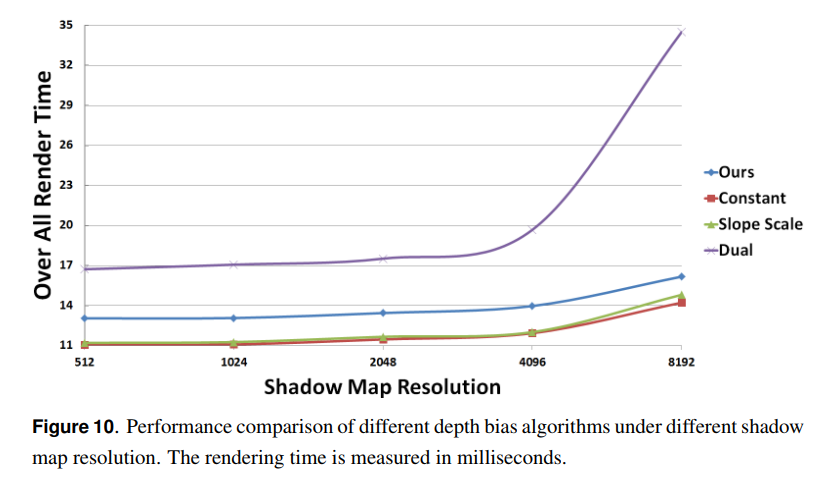
定数深度バイアスと傾斜スケール深度バイアスの両方はわずかなオーバーヘッドを追加します。2層深度バイアスは2つのレンダリングパスを持ち,シャドウマップの生成に2倍の時間がかかります。さらに,余分なテクスチャルックアップは0.6ms近くで,定数バイアスと比較するとレンダリング時間が18%も長くなります。シェーディングステージでは,本手法における適応的深度バイアスを計算するためのコストはデュアルレイヤーベースの手法における余分のテクスチャルックアップコストに近くなります。しかしながら,追加のレンダリングパス持つので2層ベースの手法は我々の手法と比べて50%近くレンダリング時間が長くなります。図10は図7におけるシーン(19Mポリゴン)のパフォーマンスチャートを示しています。シャドウマップの解像度が上がるにつれて,傾斜スケール深度のコストは定数バイアスと比較して約5%のレンダリング時間を要します。我々の手法は定数バイアスと比較すると20%近くレンダリング時間を要し,誤ったシャドウイングが大幅に少ないです。我々の手法と比較すると,2層深度マップは同等の画像品質を与えますが,シャドウマップ解像度が4096×4096未満の場合はレンダリング時間が50%長くなり,シャドウマップ解像度が増加し続ける場合はさらに50%以上のコストがかかります。
図8は,VSVに適応的バイアスを適用した結果を示しています。VSVは書くボクセル内にバイナリ値のみしか持たないので,スロープスケール深度バイアスや2層化のような他の深度バイアスアルゴリズムの拡張するという率直な方法はVSVに対してはうまく機能しません。そのため,適応的バイアスと定数バイアスの結果のみを比較します。VSVの非均一エピポラーボクセルグリッドと視点依存の性質は,定数バイアスをうまく働かせづらいものにしています。定数バイアスでは,アーチ上に間違ったセルフシャドウイングが残っていますが,離れた青いカーテンではシャドウの乖離を既に被っています。適応的深度バイアスは,間違ったセルシャドウイングを低減し,固定の定数バイアスよりも詳細なシャドウを保ちます。
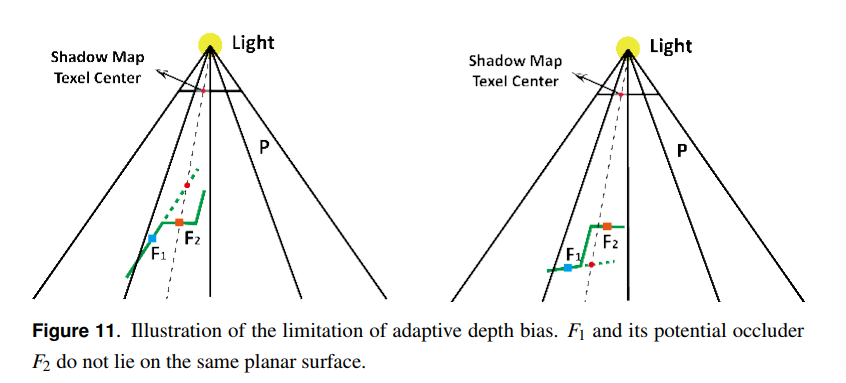
この技術の主な制限は,各フラグメントがその潜在的なオクルーダーと一緒に同じ平面上に存在するという仮定に由来します。図11は,単純なコーナーにおける場合を示しています。左側の画像では,フラグメントは過剰にシフトされていますが,誤ったセルフシャドウイングを削除することができます。しかし,右側の画像では,適応的深度バイアスは間違ったシャドウイングの削除に失敗します。
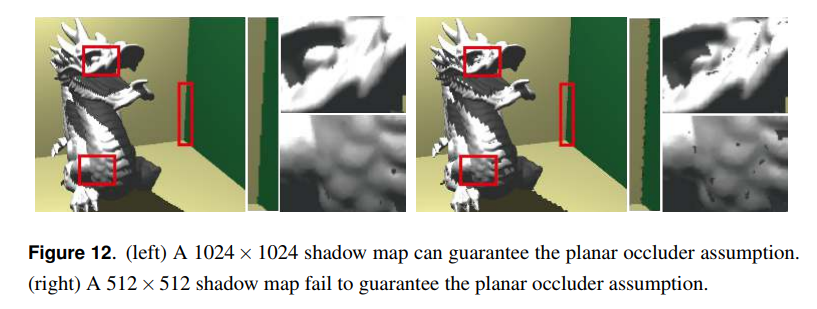
平面的なオクルーダーの仮定は,シャドウマップの解像度が低いあるいはオブジェクトが光源から非常に遠くに離れた大きなシーンスケールでは破綻する可能性があります。図12では,光源はオブジェクトから遠いです。1024×1024のシャドウマップでは,適応的バイアスは間違ったセルフシャドウの多くを排除することができます。512×512のシャドウマップでは,壁の隅やモデルの凹んだ領域において間違ったシャドウが現れ,ドラゴン上にシャドウの乖離が表示されます。
VSVの場合,エピポラーサンプリングの性質は,ライトが観測者の後ろにある場合に平面的なオクルーダーの仮定を維持することを困難にします。図13に示すように,1024×1024×512のバイナリボリュームを持つ適応的深度バイアスは多くの誤った背フルシャドウを排除することができます。ボリュームの解像度を512×512×512へと減らした際に,シャドウアクネが現れ始めます。
感想
読んだ感じだと,結構よさげに思いました。
やっていることとしては,上の和訳に書いた通り,きちんとしたピクセル中心をピクセルシェーダ内で演算して求めておき,そこからレイトレして正しいバイアス値を求めるという手法です。
図11にあるとおり,\(F_1\)と\(F_2\)が同一平面上にない場合は,誤った計算になります。特にシャドウマップの解像度が低い場合とか,こういった状況が発生しやすくなります。そのためか,論文の結果部分にも1024×1024の場合は殆ど誤判定を排除できるが,512×512にした場合は誤判定がでるという記述があります。
普通の定数バイアスとか深度傾斜バイアスなどの手法と比べるとコストが約20%増しというのが個人的には導入を悩むところですね。このコスト増が許容できるのであれば,積極的に取り入れるべきと個人的には思います。
大抵のアーティファクトが消えるのであれば,2割のコスト増でも導入するに値しそうな気がするのですが,同一平面上にあるという仮定を満たすことが手元で作っているゲームだと満たせそうにないのと,そもそもシャドウマップのコストが高すぎて,これ以上負荷を上げられないという問題があり,今やっているプロジェクトでは採用を見送りました。
PCや次世代機等では,コスト増は軽微で問題にならなそうな気がするので,シャドウマップを使っているのであれば採用してもよいのではないかなぁと思います。
参考文献
[Dou 2014] Hang Dou, Yajie Yan, Ehan Kerzner, Zeng Dai, Chris Wyman, “Adaptive Depth Bias for Shadow Maps”, Journal of Computer Graphics Techniques (JCGT), Vol.3, No.4, pp.146-162, 2014.