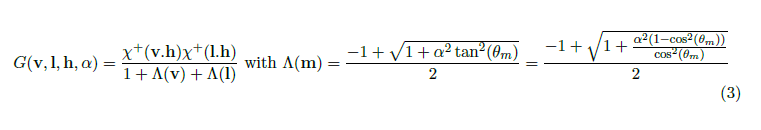投稿日: カテゴリー Paper, PBR

超雑訳 Moving Frostbite to Physically Based Rendering 2.0 (2)

前回は，Chapter1, 2を適当に和訳しました。
今回はマテリアルについての説明が記載されているChapter 3を和訳していくことにします。
毎度のことながら，誤訳等がありますので，予めご了承ください。
また，指摘して頂ける場合は，正しい翻訳例と共に指摘して頂けると有り難いです。

3 Material

3.1 Material models

3.1.1 Appearance

入射光とサーフェイスのマテリアル特性間の相互反射からの結果がサーフェイスの見た目です。複雑なレイヤー化されたシンプルな一様マテリアルから異成分から成るマテリアルに至るまで，実世界において観測できる見た目の多様性は非常に幅広いです。図4を参照。

Frostbite_Fig_4

※図は，Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.6 より引用

これらの異なる見た目は伝導率，平均自由経路，吸収などのようなある固有の物理特性によって分類分けすることが可能です。これらのマテリアル特性に基づき，フルスペクトルの中で見た目のある範囲で表現する能力がある様々マテリアルモデルを公開した文献があります。マテリアルモデルの文献は広大に及び，様々なトレードオフと精度を持った数多くの異なるモデルが存在します。BSDF(双方向散乱分布関数）として呼ばれるマテリアルモデルは，2つのパーツへと分解することが可能です：リフレクタンス部分(BRDF)と，トランスミッタンス部分(BTDF)です。このドキュメントでは，反射部分に焦点を当てます。具体的に言うとマテリアルモデルにおける”標準”の見た目を表現する能力，すなわち我々の日々の生活で出会う膨大な大多数のサーフェイスです。従って，短い平均自由経路を持つ反射，等方性，絶縁体/伝導体のサーフェイスに制限します。
 

3.1.2 Material models

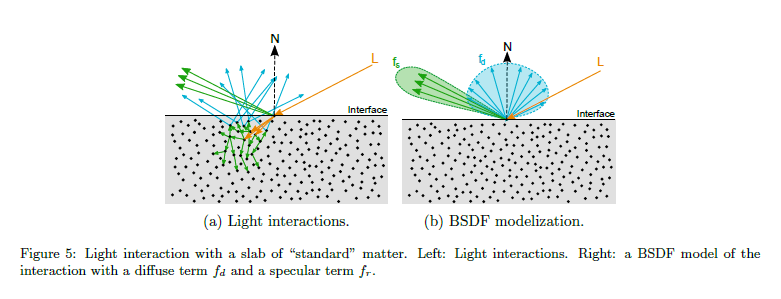
標準マテリアルモデルのコンテキストにおいて，サーフェイスレスポンス \(f\) はよく2つの異なる項へと分解されます：低周波シグナルで “diffuse” (\(f_d\)) と呼ばれるものと高周波部分で “specular” (\(f_r\)) と呼ばれるもので，図5を参照してください。インタフェースは2つの媒質に分かれます：空気と物質です。平らな界面で作られたサーフェイスは絶縁体と伝導体の両方に対して Fresnel の法則[Wikd] によって容易に表現することが出来ます。不均一な界面であるとき，図6参照，文献はマイクロファセットに基づくモデル[CT82]がこれらのサーフェイスタイプについてライトの相互反射を特徴づけるためうまく適用されるということを示しています。マイクロファセットモデルは式1によって記述され，導出の詳細について[Hei14]を参照してください：
\[
f_{d/r}({\bf v}) = \frac{1}{| {\bf n} \cdot {\bf v} || {\bf n} \cdot {\bf l}|} \int_{\omega} f_m ({\bf v}, {\bf l}, {\bf m}) \, G({\bf v}, {\bf l}, {\bf m}) \, D({\bf m}, \alpha) \langle {\bf v} \cdot {\bf m}\rangle \langle{\bf l} \cdot {\bf m}\rangle \, {\rm d}{\bf m} \tag{1}
\]

\(D\) 項はマイクロファセット分布（すなわち，NDF，正規分布関数）を形作ります。\(G\) 項はマイクロファセットのオクルージョン(シャドウマスキング）を形作ります。この定式化は diffuse項 \(f_d\) と specular項 \(f_s\) の両方に有効です。これらの2つの項にある違いはマイクロファセットBRDF \(f_m\) です。specular項について，\(f_m\) は完全鏡面で，したがって Fresnel \(F\) の法則でモデルされ，以下のよく知れた公式を導きます：
\[
f_r({\bf v}) = \frac{F({\bf v}, {\bf h}, f_0, f_{90}) \, G({\bf v}, {\bf l}, {\bf h}) \, D({\bf h}, \alpha) }{ 4 \langle {\bf n} \cdot {\bf v} \rangle \langle {\bf n} \cdot {\bf l} \rangle } \tag{2}
\]
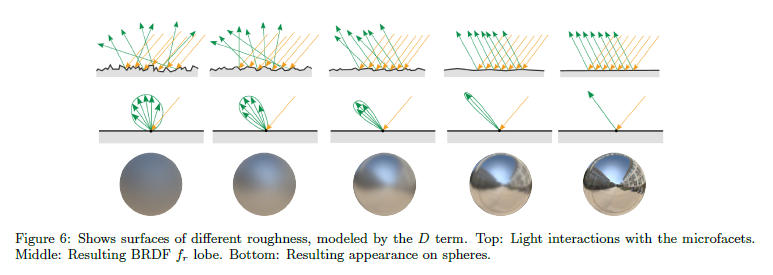
図6によって示されるように，\(D\) 項はサーフェイスの外見に重要な役割を担います。文献[Wal+;Bur12]は最近，GGX分布のような”長いテールの”NDFsを指摘しており，実世界のサーフェイスを捉えるのに良好です。\(G\) 項もまた高いラフネス値について重要な役割を担います。Heitz[Hei14]は最近Smithの可視関数が，\(G\) 項を使用するために正確でた正しいということを示しました。また彼は，Smithの可視関数の近似版を使用する傾向がよくあることを指摘する一方で，マイクロファセットの高さのためマスキングとシャドウイングの間の相互関係をより正確なマスキング-シャドウイング関数でモデル化しました。式3を参照して下さい。図7はシンプルなSmith関数と高さに相関性があるSmith関数の違いを示しています。

Frostbite_Equ_3

Frostbite_Fig_5

※図は，Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.7 より引用

Frostbite_Fig_6

※図は，Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.8 より引用

Frostbite_Fig_7

※図は，Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.8 より引用

diffuse項について，\(f_m\) は Lambertianモデルと式1に従い，次のように単純化できます：
\[
f_d({\bf v}) = \frac{\rho}{\pi} \frac{1}{|{\bf n} \cdot {\bf l}| |{\bf n} \cdot {\bf l}|} \int_{\Omega} G({\bf v}, {\bf l}, {\bf m}) \, D({\bf m}, \alpha) \langle {\bf v} \cdot {\bf m} \, \rangle \langle {\bf l} \cdot {\bf m} \rangle \, {\rm d}{\bf m} \tag{4}
\]
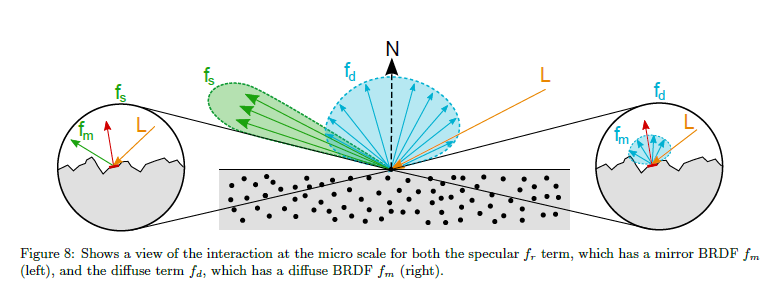
最近まで diffuse項 \(f_d\) はシンプルなLambertialモデルが当然であるとみなされていました。しかしながら，レイヤードマテリアルを除いて，diffuse 部分は specular項との一貫性が必要であり，サーフェイスの粗さを考慮しなければなりません（すなわち，specularとdiffuse項は同じroughness項が使用されるべき），図8を参照して下さい。式4は解析解を持ちません。Orenら[ON94]はOren-Nayarモデルとして知られているGaussian NDF分布とV-cavity G 項を用いたこの方程式の実験に基づいた近似を見つけました。正しく我々のモデルをサポートするために，五反田[Got14]に記載されているようなGGX NDFを持った式4に対する等価近似を作ります。Appendi Bはそのような diffuseモデルについて我々の解析のいくつかを詳細に述べていまが，さらなる研究が必要とされています。

Frostbite_Fig_8

※図は，Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.8 より引用

Burley[Bur12]は実世界のサーフェイスの観測上から構築された別のdiffuseモデルを提案しました。式5を参照。このモデルは経験に基づいている一方で，MERLのデータベースのマテリアルの主要な特徴を再現することができます。この理由と容易さのため，我々はFrostbite においてこのモデルを選択しました。diffuse項はマテリアルのroughnessが考慮され，グレージング角においてある再帰反射を生成します。
\[
f_d = \frac{\rho}{\pi} \left( 1 + F_{D90}(1 – \langle {\bf n} \cdot {\bf l} \rangle )^5 \right) \left( 1 + F_{D90} (1 – \langle {\bf n} \cdot {\bf v} \rangle )^5 \right) \hspace{0.2cm} {\rm where} \hspace{0.2cm} F_{D90} = 0.5 + \cos(\theta_d)^2 \alpha \tag{5}
\]

 

3.1.3 Energy conservation

エネルギー保存は受けたよりも多くのエネルギーを増やさないよう考慮するために重要です。さらに，diffuse項よりもspecular項によってより多く散乱される傾向がある光に対して，グレージング角における振る舞いを正しく取り扱うことができます。Frostbite では，計算を単純にすることを維持する選択をし，半球状の一定照明のために与えれた方向におけるリフレクタンスの総和がBRDF全体(diffuse + sepcular項）について1を下回る半球のディレクショナルリフレクタンスを保証することによって，エネルギー保存のみを保証します：
\[
\rho_{hd}({\bf v}) = \int_{\Omega} f({\bf v}, {\bf l}) \langle {\bf n} \cdot {\bf l} \rangle {\rm d}{\bf l} = \int_{\Omega} \left( f_r({\bf v}, {\bf l}) + f_d ({\bf v}, {\bf l}) \right) \langle {\bf n} \cdot {\bf l} \rangle {\rm d}{\bf l}　\leq 1 \tag{6}
\]

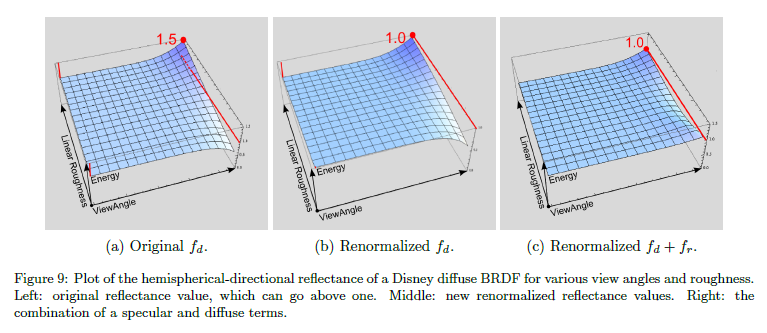
適切な導出を行うことはspecularとdiffuseモデル間での直接的な関係がないため難しいです（specularとdiffuse項の両方がマイクロファセットモデルに基づくこれらの場合についてはAppendix Cを参照）。Disney diffuseモデルを重要な注意点の1つはエネルギー保存が欠けているということです。図9はDisney diffuseモデルの半球方向のリフレクタンスを示しています。我々は，結果のリフレクタンス値が1を超えるので，明確にこのBRDFがエネルギー保存しないことを見ることができます。

Frostbite_Fig_9

※図は，Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.10 より引用

我々は，再帰反射特性を保ちながらエネルギーのゲインについて釣り合いを取るために，ほんのわずかに修正しました。リスト1は再正規化要素を持つDisney評価関数を示しています。図9cは半球方向の \(f\) を仕上げたリフレクタンスで，\(f_r\) についてspecularマイクロファセットモデルで \(f_d\) についてはDisney Diffuseモデルで構成されています。完全に1と一致しないですが，十分近くなります。図10はオリジナルのDisney diffuse項と再正規化バージョンの比較です。

Frostbite_List_1

※リストは，Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.10 より引用

Frostbite_Fig_10

※図は，Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.11 より引用

 

3.1.4 Shape characteristics

Specularマイクロファセットに基づくBRDFはある特性を持っています。それはよくバイパスされますが，最終的な見た目に強い影響力を持ちます。

● Half-angle parameterization： このパラメータはBRDFの形状の非線形変換を暗示し，法線における入射角の等方性からグレージング角度に向い異方性へとなります。

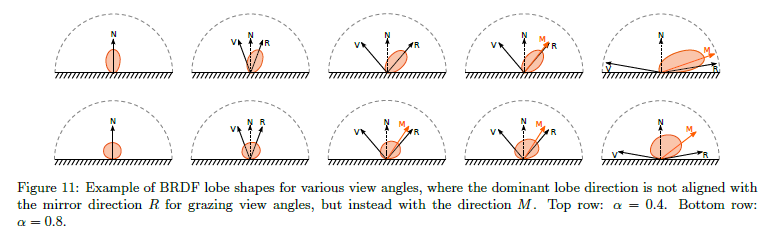
● Off-specular： BRDFのローブは反射された視線方向周りを中心としてよく考えられています（またミラー方向としても知られています）。しかしながら，\(\langle {\bf n} \cdot {\bf l} \rangle\) とシャドウマスキング項 \(G\) のため，BRDFのローブは roughnessが増加したときに法線方向に向かってシフトされて得られます。図11を参照。このシフトすることを “Off-specular peak”　と呼び，サーフェイスのおおまかな見た目に重要な役割を担っています。

Frostbite_Fig_11

※図は，Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.11 より引用

off-specular peak は高いroughness値について大きな違いを招きます。この重要な特徴を考慮するため，我々はエリアライトやイメージベースドライトの評価に使用される，この”支配的な方向”をモデル化しようと試みました。エリアライトはセクション4.7でイメージベースドライティングはセクション4.9を参照してください。

 

3.1.5 Frostbite standard model

要約すると，Frostbite の”標準的な”マテリアルモデルは他のゲームエンジン[Kar13; NP13; Bur12]によって使われたものに近いです。以下で構成されます：

● Specular term \(f_r\)： 可視関数とGGX NDFに関連があるSmithを用いたspecularマイクロファセットモデル（式2を参照）。
● Diffuse term \(f_d\)： エネルギーが再正規化された状態のDisney diffuse項。

両方のパーツについて，我々はライティングの積分をするときに支配的な方向の補正（off-specular peakハンドリング）を適用します。これらのモデルを操作するためのパラメータは次のセクションで説明します。Frostbite もまたクリアコート，表面下散乱を持つマテリアルのようなその他のマテリアルタイプをサポートしていますが，このドキュメントでは標準的なマテリアルモデルのみに焦点を当てます。

Frostbite_List_2

※リストは，Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.12 より引用

 

3.2 Material system

3.2.1 Material

Frostbite は，スポーツからレーシングまで，ファーストパーソンシューティングからオープンワールドのゲームまで幅広く様々ゲームに使用されます。これらのゲームが持つ異なる要件を満たすために，エンジンはライティングやマテリアルのサポートについて柔軟な制御を提供する必要があります。更に，PBRへの移行期間の制限の一つに移行を容易にするために古い非PBRライティングモデルとの互換性を保証することがあります。ライティングパスは制御可能です：ディファード，フォワードあるいはハイブリッド。このパスはセクション4.11で詳細に説明します。

Frostbite では，”マテリアル”は次のように定義されます：

●A lighting path： ディファード，フォワードあるいは両方。
●A set of input parameters： diffuse，smoothness，thicknessなど。
●A material mode： 粗いサーフェイス，半透明，肌，髪など，同様に非PBRの粗いサーフェイス。これはシェーダコードになります。
●A GBuffer layout： ディファードパスの支援に備えて。バッファの数は可変です。

与えれたライティングパスについて利用可能なマテリアルセットをゲームチームは選択することが可能です。各マテリアルはゲームについてのmaterialID属性をもって識別されます。基本のマテリアルは大部分をカバーする（我々は”標準”マテリアルと呼びます）ことで常に表示でき，その他のマテリアル（例えば roughness）と共有したパラメータを定義します。ディファードシェーディングについて，基本マテリアルは主にBurleyのモデル[Bur12]に述べられている”Disney”モデルが設定されます。しかしながら，我々もまた2つの他のマテリアルをサポートします：”2色”マテリアルと”古い”マテリアルです。

Disney base material： 我々のDisneyマテリアルは以下のパラメータを使用します：

Normal
標準の法線

BaseColor
Blurleyのプレゼンテーションによって提案されているように非金属オブジェクトについてディフューズアルベド，金属については法線における入射Fresnelリフレクタンス(\(f_0\))を定義します。金属オブジェクトについて，この属性のlower partはマイクロスペキュラーオクルージョンを定義します。

Smoothness
オブジェクトのroughnessを定義します。我々は roughness の代わりに smoothness を選択しました。これはなぜかというと滑らかな値に白くマッピングすることがアーティストにとってより直感的であり，Frostbite　の非PBRマテリアルモデルで既に使われているためです。Burleyのプレゼンテーションと同様で，smoothness は知覚的に線形な smoothness (\(1 – \alpha_{\rm lin}\)) へと再マッピングされます。

MetalMask
Burleyのプレゼンテーションのように”金属度”あるいはサーフェイスの伝導率（つまり，絶縁体/伝導体)を定義します。我々はアーティストにこの値の本質がバイナリであることを示唆するためにmetal maskと名付けました。

Reflectance
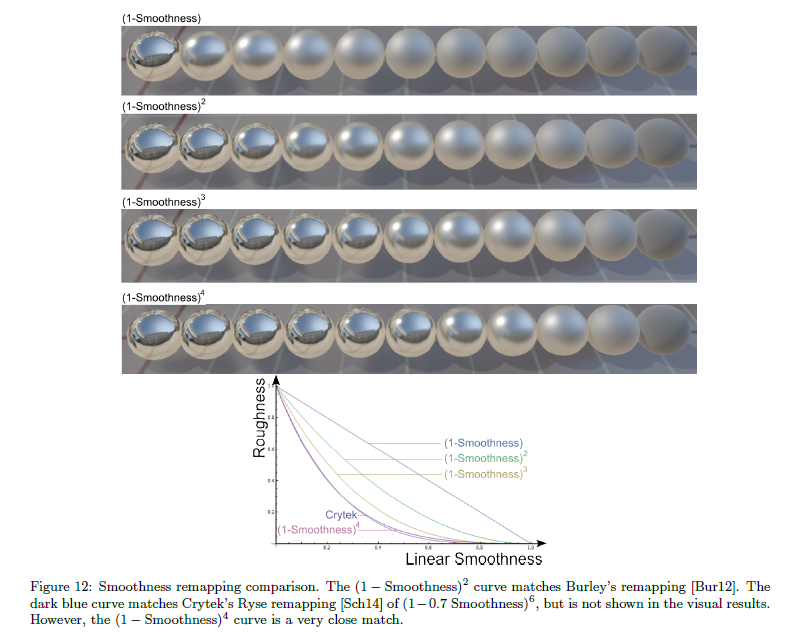
非金属マテリアルについてアーティストに親和性がある範囲へと（すなわち，MetalMask < 1)法線における入射Fresnelリフレクタンス(\(f_0\))を定義します。この属性のlower partは非金属マテリアルに対するマイクロスペキュラーオクルージョン項を定義します。 smoothnessの再マッピングについて，我々は異なる再マッピング関数を分析し，アーティストとそれらをテストしました。図12は異なる再マッピング関数のプロットと結果を示しています。Burleyのプレゼンテーションと同様に，アーティストについて最も好ましく見える”平方する”再マッピングを選択しました。reflectanceについては，以下の再マッピング関数を選択しました：

\[
f_0 = 0.16 \, reflectance^2
\]
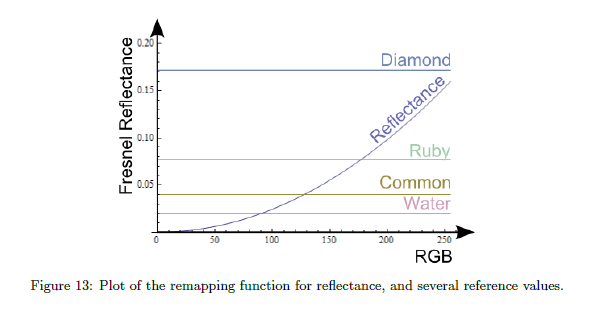
目的は，主に絶縁体4%のリフレクタンス上へとRGB 128を再マッピングする制限を持つ宝石の高いFresnel値を含む範囲へと\(f_0\)をマッピングすることです。宝石について，おおよそ\(f_0\) はルビーについて8%からダイアモンドついて17%までいきます。近似として16%へと関数を制限するよう選択しました。一般的な値との比較は図13で示されます。実際には，リアルタイムの制限を持つ状態で，\(f_0\)の1%あるいは2%の変換がかすかに知覚可能です。4%を超える値の急な上昇はこれとうまく合います。
非金属（Reflectange)と金属(BaseColor)オブジェクトの両方のケースでの法線における入射Fresnelリフレクタンスについて，マイクロスペキュラー制御（詳細についてはセクション4.10を参照）を提供するためにlower part\(< 2%\)を使用しました。我々の固有のエンコーディングのため非金属オブジェクトについて使用するためにマイクロスペキュラーオクルージョンの異なる範囲を暗示しているということが分かります。 Frostbite_Fig_12

※図は，Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.14 より引用

Frostbite_Fig_13

※図は，Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.15 より引用

Disneyマテリアルはセクション3.1で記述した”標準”マテリアルモデルを使用します。GBufferレイアウトとの関係は表2に示されます。このレイアウトは以下の制限に従います：

● すべての基本属性（Normal, BaseColor, Smoothnes, MetalMask, Reflectance）はディファードデカールをサポートするためにブレンド可能である必要があります。MaetrialIdのようなブレンドできない属性はアルファチャンネルへと格納されます。また，ブレンドの品質に影響を及ぼす圧縮とエンコーディングメカニズムを避けます。
● BaseColor属性の彩度サブサンプリングの使用を禁止するMSAAのサポート。
● 一般的に使用されるパラメータは同じバッファへと集約される必要があります。
● MaterialIdは全てのマテリアルにて同じ位置で格納される必要があります。
● パフォーマンス要件は基本/標準マテリアルについて4つのバッファのみが使用されるということが大切です（深度は含めません）。

Frostbite_Table_2

※表は，Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.15 より引用

MaterialIdはMaterialData(MatData)パラメータを解釈するのを可能とします。例として，ディファードスキンマテリアルについて，拡散プロファイルインデックスが格納されます。異方性マテリアルについては，異方性の強度が格納されます。AOパラメターはアンビエントオクルージョン項で，常に存在します（マテリアルタイプから独立）。詳細についてはセクション4.10を参照してください。RadiosityはGBufferの生成を通じて評価された間接diffuseライティングを格納するライティングバッファです。Normalは2つの部分に分けられ，依然として法線ブレンディングを可能とする損失の多いエンコーディング方法が使われます（このアルゴリズムは将来の話で説明される可能性があります）。
 

Two-color base material：
Disneyパラメータライゼーション（単一のbase color，metal mask，そしてreflectance 値を用いた）は混合されたマテリアルのスペキュラーハイライトを表現する時に不十分です。例えば，金属酸化物のような金属と絶縁体の調和など。この理由のため，我々は色付けされた \(f_0\) とdiffuseカラーを持つ”2色の”ディファードベースマテリアルをサポートします。関連したGBufferのレイアウトは表3に示されます。\(f_0\) 項はReflectanceに似たlower範囲におけるマイクロオクルージョンをサポートします。2つのパラメータライゼーション間の変換はコンテキストに依存して必要とされます。Disneyパラメータライゼーションからこの”2色の”パラメータライゼーションへの変換は定義によって自明であり，既にライティング計算上で使用されるためGBufferの解凍する間で行っています。反対の変換（すなわち，”2色の”パラメータライゼーションからDisneyのパラメータライゼーションへの変換）は非線形最適化を必要するのでよりややこしいです。これはアセットがあるエンジンモードから別へとコンバートするために必要とされるときのみに実行します。この変換の詳細をAppendix Dに掲載します。

Frostbite_Table_3

※表は，Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.16 より引用

Old base material： は非PBRエンジンに対する基本マテリアルで，[Cof10]で詳敷く述べました。レガシーなコンテンツをサポートするのと，PBRへの移行を容易にするため，我々は基本的なアーティスティックルールに基づき非PBRマテリアルとPBRマテリアル間の自動変換を追加しました。変換は入力パラメータを保存する前にシェーダ内で行われます。この自動変換は適切にオーサリングされたアセットと比べると低品質な結果を提供します。品質を保ちながらこれらのアセットを自動的に変換する方法がまだ見つかっていません。

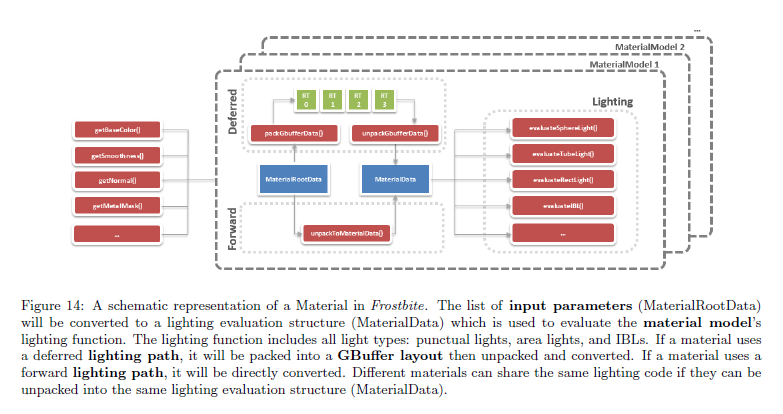
図14は異なるマテリアルパラメータの変換の主要部とマテリアルモードとライティング関数の間の依存を示しています。パフォーマンスについて，エリアライト（セクション4.7）とイメージベースドライト（セクション4.9）はマテリアルモードに依存する事前積分に頼っています。これはライティングとマテリアルモードがエンジン内部で連結されているということ暗示しています。PBRアプローチによって主張されるライティングとマテリアル間の分離はアセット作成のみに有効です：アーティストはシェーダ内の任意のライティング情報にアクセスする必要がありません。しかし，内部でこの分離は維持されず，新しいマテリアルは多くの場合，新しいライティングコードが追加することを暗示しています。

Frostbite_Fig_14

※図は，Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.17 より引用

 

3.2.2 Render loop

前のセクションはマテリアルの定義を提示しました。このセクションはどのようにマテリアルが描画されるかを記述したいと思います。フォワードライティングパスを用いたサーフェイスについて：マテリアルモデルのシェーダコードをセットアップし，パラメータリストを送信し，サーフェイスを描画します。ディファードシェーディングパスを用いたサーフェイスについては，より複雑になります。効率的にマテリアルセットを管理するために，ある考慮すべき事柄が存在します：

●　マテリアルモデルは小さな調整について動的分岐によって可能な限り同じライティングコードを共有しようと試みます。あまりにも違いがあるライティングコードはステンシルバッファを用いた異なるライティングパスを必要とします。
●　マテリアルは基本マテリアルのレイアウトの一貫性を保つのを試み，パラメータを格納する際の小さな調整について動的分岐を使います。あまりにも異なるマテリアルは異なるGBufferパスが要求され，再度ライティングパスの間，それらを認識するためにステンシルバッファを使用します。
●　”修正”を実行することによって異なるGBufferレイアウトを持つマテリアルを伴うライティングパスを共有しようと試みます。

ジオメトリが重いパスについては，GBuffer精製コストを減らしたいですが，まだ同じライティングパスが使われます。典型的なユースケースは植物で，基本GBufferレイアウトの最初のバッファ2つを埋めるためで，このときGBufferパラメータの不足をリスト3に示した”修正”パスで解決します。修正パスは同じハードウェアの同じバッファへの読み込みと書き込み能力に依存して複数パスで実行する必要がある恐れがあります。

Frostbite_List_3

※リストは，Sebastien Lagarde and Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 2.0”,
SIGGRAPH 2014 Course: Physically Based Shading in Theory and Practice, p.17 より引用

このとき描画ループは次のようになります：

// GBufferの生成
ForEach　異なるステンシルビット do
　　　　バッファ数分ディファードマテリアルについてのGBufferパスを描画する
　　　　　　　　必要であれば，シェーダ内の分岐を行う
　　　　(n + 1)個のバッファでディファードマテリアルについてのGBufferパスを描画する
　　　　　　　　必要であれば，シェーダ内での分岐を行う

// 修正パス
ForEach　ディファードシェーディングパスで共有することを必要とするディファードマテリアル
　　　　GBufferの修正パスを描画する

// デカール
一般的なパラメータに影響を与えるディファードデカールを描画する

// ディファードシェーディング
ForEach　個々の要求されたディファードシェーディングパス do
　　　　ディファードシェーディングを描画する
　　　　　　　　必要であればシェーダ内の分岐を行う
// フォワードレンダリングとライティング
ForEach　フォワードマテリアルモード do
　　　　フォワードライティングを描画する

デカールは次のセクションで説明したいと思います。実際には，マテリアルパラメータとライティング関数との間が関連するため全てをゲームチームがカスタマイズしようとするのはかなり困難です。MaterialIdはマテリアルをカスタマイズするためのシンプルな方法を提供していますが，ライティングコードの再利用と動的分岐を利用する制限を伴います。例として，ライティングを2度サンプリングする必要とするクリアコートモデルがゲームチームによって追加されました。このシステムは非PBRエンジンからの移行を実行し，異なる我々のユーザーのニーズに合いました。

 

3.3 PBR and decals

デカールはレイヤリングマテリアルの性質について動的なシステムとしてみることができ，見た目のリッチさと多様性を生成できるようになります。このコンテキスト内では，”正確な”デカールを持つことの重要性がPBRでは増大します。”正しさ”によって，複数がオーバーラップするデカールの場合においても，我々はライティングを行う前にデカールとサーフェイスのマテリアルパラメータを適切に組み合わせることができるようになることを意味します。Frostbite では，この目的のために我々は最初に描画するデカール（ディファードデカール）についてディファードシェーディングを使用しますが，ハードウェアとパフォーマンス制限下で正確に処理することはほぼ不可能です。物理ベースマテリアルの多様性を正確に考慮にいれたブレンディングデカールのための任意の良い解決方法は見つかっていませんが，網羅性の目標のため，いくつか大きな落とし穴と，Frostbiteでの選択を掲載します。

●　Correctness： ブレンディング操作の正確さは重要です。つまり，ブレンディング操作後の属性の復元が正確でなければなりません。例として，\(normal * 0.5 + 0.5\) あるいは \(normal.x, normal.y\) のみのコンポーネント，置換のみ(線形補間）のような通常のエンコーディングを持つNormalに対して法線を正しく復元できます。追加で詳述している[BBH12]ような妥当な操作は間違った結果を生み出します。これはプログラマブルにブレンディングすることには都合がよいですが，いくつかのプラットフォームは間違った結果を生み出す操作をサポートします。属性のいくつかが圧縮されるのを避けることを選択し，この場合においては線形に補間するアルファブレンディングにシンプルに頼りました。

●　Interaction： 正確にブレンディングするために，デカールとターゲットサーフェイスは同じモデルが使用されるべきです（つまりパラメータリストが同じである）。作品とパフォーマンスの観点の両方から，MaterailIDによってデカールをオーサリングする要求と各ケースに対してステンシルされたパスを行うので，これは扱いやすいです。我々はゲームによって選択されたマテリアルの間で一般的なパラメータセットへと厳密にデカールパラメータを選択しました。一般的には，Normal, BaseCodlor, Smoothnessです。MetalMask，Reflectance（あるいはf0 color）のような他のパラメータはDisney(あるいは2色）ベースマテリアルが選択された場合のみ考えます。しかしながら，これでは不足です。デカールはデフォルトよりもその他のMaterialIDsに影響をすることでアーティファクトを生み出します。MaterialDataとMaterialIDはブレンド可能なデータではなく，置換のみが可能です。１つのオプションは0のようなニュートラルな値に強いるためにアルファチャンネルの個別のブレンドファクターを用いることです。別のオプションはデカールがMaterialID = 0より大きい他のマテリアルに影響を与えるのを禁止することです。

●　Indirect lighting： ライティングを評価する前にデカールによってサーフェイスに影響を与える必要があります。しかしながら，Frostbiteでは，間接diffuseはGBuffer生成パス内で評価され，diffuseアルベドを除く，マテリアルプロパティの如何なる変更を禁止しています。1つの解決策はインスタンスに対してレベルをカーバするライトプローブボリュームテクスチャで[Val14]ディファードパス上で間接diffuseライティングを全て評価することです。別の解決方法はGBuffer生成前にバッファ内にデカール属性を格納するためにUE4[UE4]によって提案されているようにデカールのプリパスを使用することです。これはデカールを受けるオブジェクトを2回描画するのを必要とします。Frostbiteでは，そのような解決策によってオーバヘッドとなるためアーティファクトをそのままにする選択をしました。

●　Emissive： FrostbiteではGBufferストレージが制限されているため，emissive情報はあるときにパフォーマンスの理由のためにradiosityバッファと混合されます。セクション4.8を参照してください。radiosityバッファはその後アルベドと混合されます。デカールはアルベドを変更し，この場合におけるemissiveカラーを変更します。Frostbiteでは，emissiveとデカールを取り扱うアーティファクトを受け入れました。

●　Highlight shape preservation and specular aliasing： 任意の法線パラメータの変更はピクセルフットプリントの下でのNDFの変化を暗示しています。これが意味するのは，任意の形状を保存するバイアス（ToskvigあるいはLEANマッピングのような技法によって処理される）を意味しており，アプリケーションのデカールの前に実行されます。セクション5.3を参照してください。アプリケーションのデカール後にポストプロセスとして法線フィルタリングパスを実行することが解決方法です[Sch14]。

●　Forward rendered surfaces： ディファードデカールは半透明と相性が悪く，どれもフォワードレンダリングされたオブジェクトとなります。この場合における一般的な解決策はサーフェイスライティングでライティングした結果とブレンドするフォワードデカールに頼ることです。フォワード描画されたオブジェクトに対するデカールパラメータブレンディングをサポートすることは可能ですが，アートサイドに重い制約を必要とします（ブレンディングモードを制約する，テクスチャ配列に対するテクスチャサイズを制限する，など）。この問題はアプリケーションのライティングといくつかの類似点を共有します。タイルドディファードとタイルドフォワードデカールというライティングに対して既に見つかっている解決策の適用が利用できます。
 

コメントを残す

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

このサイトはスパムを低減するために Akismet を使っています。コメントデータの処理方法の詳細はこちらをご覧ください。