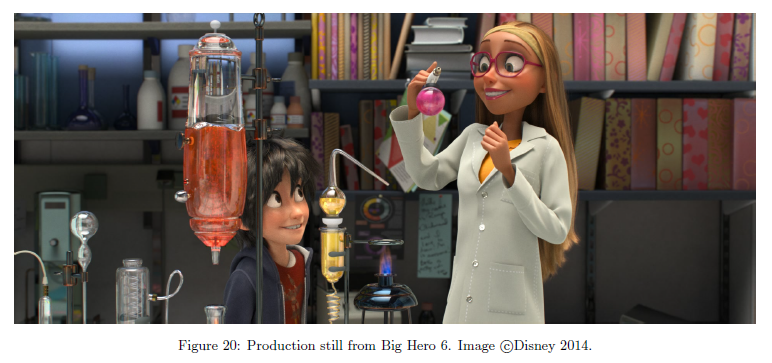前回ざっくりDisney BRDFを訳しました。
今回は，2015年に発表された”Extending the Disney BRDF to BSDF with Integrated Subsurface Scattering”のcourse noteをざっくり和訳していくことにします。
course note自体は，https://blog.selfshadow.com/publications/s2015-shading-course/#course_contentからダウンロードできます。
いつもながら，誤訳が多々あると思いますので，予めご容赦ください。

---

1 Introduction

シュガーラッシュ[Bur12]において，我々は新しい物理ベースシェーディングモデルを導入し，（髪の毛を除く）すべてのマテリアル上で多目的のBRDFを単一で使用しました。このモデルは，Disney BRDFとして知られるようになり，少ないパラメータのみで広範囲のマテリアルの再現を可能とします。我々の次の映画，アナと雪の女王では，このBRDFを修正せずに継続して使用しましたが，屈折や表面下散乱のようなエフェクトはBRDFとは別で計算され，間接照明は点群を用いて近似しました。これらのエフェクトすべては，追加的な方法でアドホックなシェーディングを通じて合成しました。
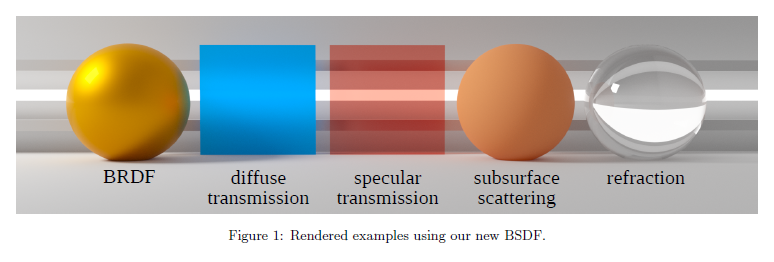
2014年はベイマックスで始まり，アドホックなライティングとシェーディングからパストレースされたグローバルイルミネーションに切り替えました。ここで，屈折，表面下散乱，そして間接照明はすべて単一の物理ベースフレームワーク上に統合されます。パストレースされたグローバルイルミネーションで，エネルギーが保存されないマテリアルはライトを増幅させ，イメージが収束するのを妨げるのでエネルギー保存則は重要になります。追加のアドホックシェーディングの本質は様々なコンポーネントが屈折されたエネルギーを冗長に表し，一般的にエネルギー保存されないことです。エネルギー保存則を保証するために，我々はBRDFを，そのような効果のすべてを一貫してエネルギー保存する方法を構成する統一されたBSDFモデルへと拡張します。新しいモデルの例は図1で示されます。

※図はBrent Burley, “Extending the Disney BRDF to a BSDF with Integrated Subsurface Scattering”,
SIGGRAPH 2015 Course: Physically Based Shading in Theory and Practice, p.1 より引用。

 

1.1 Representations of refracted energy

※図はBrent Burley, “Extending the Disney BRDF to a BSDF with Integrated Subsurface Scattering”,
SIGGRAPH 2015 Course: Physically Based Shading in Theory and Practice, p.1 より引用。

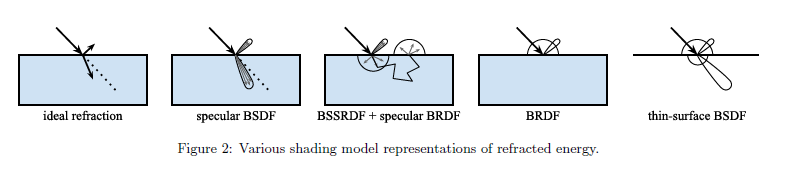
サーフェイスにレイがヒットしたとき，レイはあるエネルギーを持って反射されるものとサーフェイス中へと屈折するものに分割されます。レイの反射した部分はスペキュラーBRDFによって記述されます。しかしながら，レイの屈折した部分は，マテリアルに依存し，ほかのサイドの外へと伝達し続けるか，あるいは内部散乱とサーフェイス上の他の点において再放出される可能性があります。これらのケースは伝統的には図2に図示されるような別のシェーディングモデルとして扱われ，以下のように記述されます：
 

Ideal refraction: 滑らかな絶縁体サーフェイス（例えばグラス）は入射レイを反射される部分と屈折される部分に分割します。屈折されたレイは Snellの法則に従った方向に変化し，そしてFresnel方程式によって記述される反射あるいは屈折されたエネルギーの一部分となります。これは典型的にはデルタ超関数に関係するため特別な目的のシェーダとして取り扱われます。

Specular BSDF: サーフェイス境界において粗いサーフェイスは反射・屈折されたレイを散乱します。これはマイクロファセットBSDF，または双方向散乱分布関数[WMLT07]を用いた共通モデルです。そのようなBSDFはスペキュラー散乱を記述し，単一点においてのみです; 固体へと屈折するレイとそのほかのサイドに既存するレイは2つのBSDF散乱イベントとして表現されます。

BSSRDF + specular BRDF: 屈折されたレイはサーフェイス下で複数回散乱される可能性があり，入射点から遠く離れた任意の点において終了します。エネルギー量はBSSRDFあるいは双方向表面下散乱分布関数[JMLH01]によって記述されるサーフェイス上の2つの位置と方向の間での散乱によって伝達されます。特に，BSSRDFの実装は，一般的には厳密な幾何学的推定を行う拡散近似を用います。

BRDF: レンダリング精度に比べて散乱距離が小さいとき（例えば，射影されたピクセルよりも小さい），表面下散乱は ディフューズBRDF によって効果的に近似できる可能性があります。例えば，散乱はよく等方性であると想定されます。すなわち，Lambertianですが，これは Disney BRDF には当てはまりません。

Thin-surface BSDF: 薄く，半透明サーフェイスをシェーディングするとき（すなわち，非幾何学的にモデル化された内部ボリュームをもつもの），薄面のBSDFはディフューズとスペキュラー透過と同様にディフューズとスペキュラー反射の両方を表す可能性があります。

とりわけ，これらの各モデルは以前のモデルの近似です。従って，薄面のBSDFは近似の近似の近似の近似！これら近似のそれぞれはそれぞれの立場を持っており，我々の統合モデルはこれらのすべての特徴を包含します。
 

1.2 A unified scattering model

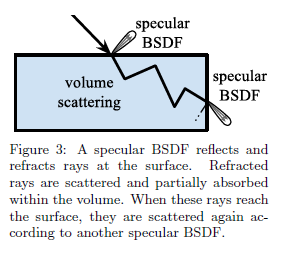
我々は，統合されたモデル内でスキャッタリングの全ての形式を表現したいです。最も一般的なモデルは，サーフェイスについて下の図3に示すような内部についてはボリュームメトリックスキャッタリングを組み合わせたスペキュラーBSDFに恐らくなるでしょう。そのようなモデルは物理的な効果全てを再現できる可能性がありますが，常にそうすることは実用的ではありません; 例えば，このモデル上のサーフェイスカラーは単にボリュームスキャッタリングする間の吸収からに由来しますが，散乱距離が無視できるときは，明らかにディフューズBRDFを使用するのがより効率的であり，十分です。

※図はBrent Burley, “Extending the Disney BRDF to a BSDF with Integrated Subsurface Scattering”,
SIGGRAPH 2015 Course: Physically Based Shading in Theory and Practice, p.2 より引用。

　ほぼ間違いなく，一つは最も一般的な統一された散乱の表現としてBSSRDFを考える可能性があり，したがって，少なくとも数学的に，任意の2点とサーフェイス上の方向間の全ての散乱を完全に記述します。しかしながら，BSSRDFは与えられた入射と出射点と方向は推測的に把握しなければならず，さらに出射点は普通はサーフェイスにおけるスキャッタリング後のオブジェクトを通じたトレーシングによって決定され非ディフューズスキャッタリングについては実現困難な表現です。BSSRDFの一般形式は卵とにわとりの問題を示します（あるいはより技術的には，放射輸送理論からのサーチライト問題の例です）。けれども，BSSRDFの拡散近似はこの問題を回避します。
　単一の一般的なモデルを使用しようとするよりもむしろ，我々の統合モデルは，我々の既存のBRDFとスペキュラーBSDFと表面下散乱モデルを組みあせたモデルのブレンドです。スペキュラーBSDFが選択され，内部的にボリュームシェーダと組み合わさったとき，我々は図3の一般的なスキャッタリングモデルを持ちますが，BRDFの効率的な近似をもったままで表面下拡散が利用可能です。
　我々の統合されたモデルをDisney BSDFとして呼びますが，表面下散乱を含む我々のモデルは厳密には正確ではないです。これはなぜかというと，我々はより公式に統合されたモデルを 表面下散乱を統合したDisney BSDF として呼ぶからです。
 

2 Disney BSDF

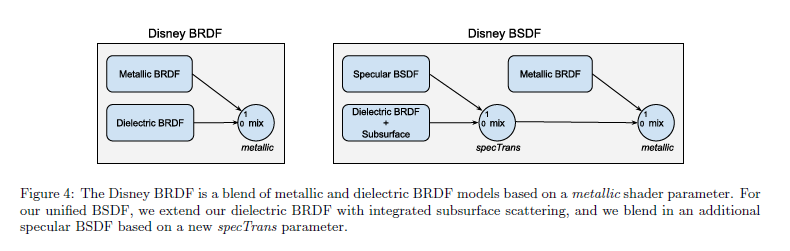
Disney BRDF はすでに金属と絶縁体モデルのブレンドであることを言及しておきます。屈折をサポートするために，我々はこれを図4に示すような追加のスペキュラーBSDFモデルをブレンディングすることによって拡張します。新しいパラメータであるスペキュラートランスミッションあるいは specTrans はブレンディングを制御します。図に見られるように，メタリックモデルは優先されますが，3つのモデル全てをすこしずつブレンドすることは可能です。各一貫性のあるモデルがエネルギーを保存する場合は，ブレンドもまた同様になります。

※図はBrent Burley, “Extending the Disney BRDF to a BSDF with Integrated Subsurface Scattering”,
SIGGRAPH 2015 Course: Physically Based Shading in Theory and Practice, p.3 より引用。

図2で示したような薄面については，特別な扱いが必要となります。表面下散乱を実行するためにボリューム内部を表現する内部体積が存在しないので，近似を使わねばなりません。また，屈折については，入力と出力の散乱事象の両方が同時にシミュレートされなければなりません。
　これらのモデルそれぞれは次のサブセクションで説明します。最初に，我々はDisney BRDF の特徴の要約をし，新しい追加分を述べます。
 

2.1 Disney BRDF Recap

Disney BRDF の大部分は主に MERL100マテリアル[MPBM03]からの，計測されたマテリアルの観測に基づいています。実験的にインスピレーションされましたが，アドホックな構築に従う既存の物理的由来のモデルは的確に計測されたマテリアルの結果を再現できません。
　我々のBRDFは2つのスペキュラーローブを含みます：異方性ラフネスを持つマイクロファセット反射ローブと随意的なクリアコート反射ローブです。マイクロファセット反射は標準モデル[Ct81, WMLT07]に従います。クリアコートローブは等方性であり，以下同様ですが，非物理的な構築です。
　我々のディフューズレスポンスは，指向性です（すなわち，非Lambertianです）。特に，グレージング再帰反射レスポンスは，粗いサーフェイスについて明るくするために滑らかなサーフェイスについてdarkeningする範囲とマイクロファセット反射の粗さに依存します。また，グレージングフォワード反射を追加する任意的なsheenコンポーネントを含みます。計測されたマテリアルにおいてこれらのモデルの両方で観測された効果は，微小面の機構を通じて複数回の散乱によって引きこされたと推測します。
　さらに，完全に別の（また指向性であり，また粗さに従属する）ディフューズモデルは表面下散乱の近似を含んでいます。これは BRDF のままであり，従って実際に表面下散乱は行われません。このモデルはユーザーパラメータに従って最初のディフューズとブレンドされます。我々は固体表面について正しい表面下散乱を選択して Disney BSDF からこのモデルを削除しましたが，それを薄面シェーディングで持ち続けています。
　BRDF のメタリック部分は単純に全てのディフューズリフレクタンスをなくし，指定された baseColor へと入射スペキュラーレスポンスを設定します。この baseColor パラメータは絶縁体（すなわち，非金属）ディフューズモデルで共有され，故に両方のモデルについてのアルベドを推定する近似として伝達します。我々はこの baseColor パラメータの補間をスペキュラー BSDF モデルへと拡張します。
　Disney BRDF は厳密にはエネルギー保存しませんが，理由についてはセクション5.1で述べることとし，典型的には1以下である妥当なアルベドから与えれられるエネルギー保存がもっともらしい結果を生み出すため，そのような方法でパラメータは定義されました。
 

2.2 Specular BSDF

　我々のスペキュラーBSDFは直接的に屈折に対するBRDFのマイクロファセット反射ローブをを拡張します。スペキュラーBSDFの例は図5に示すようなブレンドされたスペキュラートランスミッションになります。

※図はBrent Burley, “Extending the Disney BRDF to a BSDF with Integrated Subsurface Scattering”,
SIGGRAPH 2015 Course: Physically Based Shading in Theory and Practice, p.4 より引用。

　我々は Walterら[WMLTT07] の導出に従います。Snellの法則 \(\eta_i \sin \theta_i = \eta_0 \sin \theta_o\) に従ってレイは屈折します。ここで \(\eta_i\) と \(\eta_o\) は屈折面における2つの媒質の屈折率あるいは, IORs です。屈折は \(\eta = \eta_o / \eta_i\) の比率のみに依存し，主に 相対屈折率 と呼ばれるということに注意してください。空気中から来る場合（ここで \(\eta_i \approx 1.0003\) で，典型的には1と想定される）屈折率と相対屈折率は同じですが，オブジェクトの外へと屈折する時に値を逆転させることに注意する必要があります。
　Snellの法則はレイの曲がりを記述しますが，あまり明らかではないことに，レイの拡散も記述します。特に，屈折されたレイの見かけのラディアンスは \(\eta^2\) によってスケールされ，射影された立体角における変化に等しいことをVeachが示しています[Vea97]。
　BRDFとBTDFの総和 \(f_s({\boldsymbol i}, {\boldsymbol o}, {\boldsymbol n}) = f_r({\boldsymbol i}, {\boldsymbol o}, {\boldsymbol n}) + f_t({\boldsymbol i}, {\boldsymbol o}, {\boldsymbol n})\) としてマイクロファセットBSDFを導出するために，Walterらは最初に反射と屈性をのハーフベクトルを定義し，屈折の場合にSnellの法則を適用しました：

\begin{eqnarray}
{\boldsymbol h}_r &=& \frac{{\boldsymbol i}+{\boldsymbol o}}{\left\| {\boldsymbol i} + {\boldsymbol o} \right\|} \\
\tag{1} \\
{\boldsymbol h}_t &=& – \frac{{\boldsymbol i} + \eta {\boldsymbol o}}{\left\| {\boldsymbol i} + \eta {\boldsymbol o} \right\|}
\end{eqnarray}

このとき3つの補正要素を適用しました 1)微小面上へと入射ラディアンスを変換し，2)微小面へと散乱されたラディアンスを戻す変換をし，そして 3)立体角の変換を考慮して \( \left\| \frac{\partial \omega_h}{\partial \omega_o} \right\|\)を測定します。屈折について4つの目の要素は上述したように（Walterらによって省略された要素）屈折拡散するため立体角の変換を考慮する必要があるということです。これらの用を組み合わせた結果は次になります：

\begin{eqnarray}
f_r({\boldsymbol i}, {\boldsymbol o}, {\boldsymbol n}) &=& \frac{|{\boldsymbol i} \cdot {\boldsymbol h}_r|}{{\boldsymbol i} \cdot {\boldsymbol n}|} \cdot \frac{|{\boldsymbol o} \cdot {\boldsymbol h}_r|}{|{\boldsymbol o} \cdot {\boldsymbol n} |} \cdot \frac{1}{({\boldsymbol i} \cdot {\boldsymbol h}_r + o \cdot {\boldsymbol h}_r)^2} \cdot F({\boldsymbol i}, {\boldsymbol h}_r) G({\boldsymbol i}, {\boldsymbol o}, {\boldsymbol h}_r) D({\boldsymbol h}_r) \\
&=& \frac{F_r({\boldsymbol i}, {\boldsymbol h}_r)G({\boldsymbol i}, {\boldsymbol o}, {\boldsymbol h}_r)D({\boldsymbol h}_r)}{4|{\boldsymbol i} \cdot {\boldsymbol n}||{\boldsymbol o} \cdot {\boldsymbol n}|} \tag{2} \\
f_t({\boldsymbol i}, {\boldsymbol o}, {\boldsymbol n}) &=& \frac{|{\boldsymbol i} \cdot {\boldsymbol h}_t|}{|{\boldsymbol i} \cdot {\boldsymbol n}|} \cdot \frac{|{\boldsymbol o} \cdot {\boldsymbol h}_t|}{|{\boldsymbol o} \cdot {\boldsymbol n}|} \cdot \frac{\eta^2}{({\boldsymbol i} \cdot {\boldsymbol h}_t + \eta {\boldsymbol o} \cdot {\boldsymbol h}_t)^2} \cdot \frac{1}{\eta^2} \cdot (1 – F({\boldsymbol i}, {\boldsymbol h}_t))G({\boldsymbol i}, {\boldsymbol o}, {\boldsymbol h}_t)D({\boldsymbol h}_t)
\end{eqnarray}

　\(f_r\) における自明な項がキャンセルされたとき（\({\boldsymbol i} \cdot {\boldsymbol h}_r = {\boldsymbol o} \cdot {\boldsymbol h}_r\) に注意），使いやすい形式のマイクロファセットBRDFを得ます。注意： これらの式は半球上を積分することに関して定義されています。BRDFでは相反性がありますが，BTDFはそうではありません。なので，\({\boldsymbol i}\) と \({\boldsymbol o}\) を選択する時に注意しなければなりません。特に，カメラからのパストレーシングについて，\({\boldsymbol i}\) は視線ベクトルを表し，\({\boldsymbol o}\) はライト方向を表します。
　\(1/\eta^2\) の拡散要素は屈折固体を通過して大抵見えるインシデント無しで普通省略することが可能で，そこではある要素と逆要素が相殺されます。そしてそうすることで空気以外の媒質中にカメラセンサーが配置された時に好ましくないbrighteningを避けます（例．水中）; 一方で，例えば遷移が典型的にはモデルされていないような空気―水中―遷移のソートなしで水中にカメラを配置することは物理的に正しくありません。しかしながら，フォトンマッピングのような双方向手法は，エネルギ（フォトン）が屈折媒質内で保管することでき，正確な積分は要素が含まれるということを要求します。注意： フォトンをトレーシングするとき（立体角を持たない），拡散要素は使用されません。
　この基本モデルについて，以下を追加します：

●clearcoat： これは我々のBRDFから変化がなく，付随的な反射に寄与し，屈折に関係しません。

●surface absorption： サーフェイスカラーの平方根によって屈折を乗算し，入射と出射散乱イベントの両方が考慮された後で，期待されたアルベドを生成します。

●volumetric absorption： ボリュームメトリックな吸収を固体を通過した屈折パスの長さに基づき適用します。

●sheen： 非物理的ですが，BRDFからのsheenコンポーネントを含みます。Walterらによって提案された粗い絶縁体モデルがマイクロファセット相互反射/屈折による欠損のためエネルギーを失い，sheenコンポーネントはそれについて相殺できる可能性があり，そのような相殺はアーティストによって考えられる必要があるということに気付きました。この問題をさらにセクション5.1で説明します。

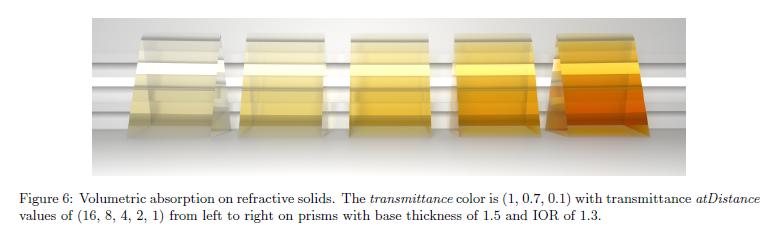
Volumetric absorption parameterization： Beer-Lambertの法則はボリュームを通過した透過率 \(T\)　は距離 \(d\) によって乗算された吸収係数 \(\sigma_a\) として表現することが可能な光学的深度に関係がある指数的であるということ，従って \(T = e^{-\sigma_a d}\) であるということを言明しました。これは実装するには素直でありますが，吸収係数は直感的ではありません。代わりに，2つの新しいパラメータを追加します：transmittance colorと，そして透過方程式：\(\sigma_a = -(\log T)/d\) の逆変換によって吸収係数を推測するものと一致する atDistance 要素です。例を図6に示します。

※図はBrent Burley, “Extending the Disney BRDF to a BSDF with Integrated Subsurface Scattering”,
SIGGRAPH 2015 Course: Physically Based Shading in Theory and Practice, p.6 より引用。

 

2.3 Dielectric BRDF with integrated subsurface scattering

表面化散乱を伴った絶縁体BRDFを拡張するために，我々は最初にディフューズローブを絶縁体微小面効果と非指向性（すなわち，Lambertian）サーフェイス効果へとリファクターします。このとき，ディフューズローブのLambertian部分を拡散モデルあるいはボリュームメトリックな散乱モデルのどちらかに置き換えます。これは微小面効果を保ち，散乱距離が小さいときにディフューズBRDFと同じ結果へと拡散モデルは収束します。
Disney BRDFについて，指向性ディフューズは以前に以下のように定義されました：
\begin{eqnarray}
f_d &=& \frac{baseColor}{\pi} \left( 1 + (F_{D90} – 1)(1 – \cos\theta_l)^5 \right) \left( 1 + (F_{D90} – 1)( 1 – \cos\theta_v)^5 \right) \\
{\rm where} \tag{3} \\
F_{D90} &=& 0.5 + 2\, roughness\, \cos^2\theta_d
\end{eqnarray}
　\(F_{D90}=0\) が使われた場合，この式は滑らかなサーフェイスのFresnel要素（ここではSchlickのFresnel近似を用います）を持つ標準のLambertianディフューズになりますが，2012のレポートで説明したように，これは不自然な暗いグレージングレスポンスを生み出します。ですので，グレージング角において0に行く代わりに，すなわち，ライトあるは視線方向がサーフェイス法線から90度であるとき，我々はエッジのdarkeningを0.5へと制限し，最大限に粗いサーフェイスについて2.5倍へと増やすことによって再帰反射におけるゲインを増やします。アドホックですが，この形状と粗さへの関係性は計測データの観測に基づいて選択されました。
　粗い面のFresnel要素と再帰反射ゲインを保持しながらLambertianディフューズと表面下散乱を交換可能にするためには，以下のようにディフューズモデルをリファクターします：
\begin{eqnarray}
f_d &=& f_{Lambert}(1 – 0.5F_L)(1 – 0.5 F_V) + f_{retro-reflection} \\
f_{Lambert} &=& \frac{baseColor}{\pi} \\
f_{retro-reflection} &=& \frac{baseColor}{\pi} R_R(F_L + F_V + F_L F_V(R_R -1)) \\
{\rm where} \tag{4} \\
F_L &=& (1 – \cos\theta_l)^5 \\
F_V &=& (1 – \cos\theta_v)^5\\
R_R &=& 2 \,roughness\, \cos^2\theta_d
\end{eqnarray}
　sheenコンポーネントは\(sheen \cdot (1 – \cos\theta_d)^5\) としてグレージングマイクロファセットトランスミッションの追加的なモデルであり， sheenTint パラメータに従って baseColor に向って随意的に色付けされます。これはすでに別々の追加されたコンポーネントとして与えれていて，表面下散乱とLambertianディフューズコンポーネントを交換する時に影響を与えません。
 

2.4 Subsurface diffusion

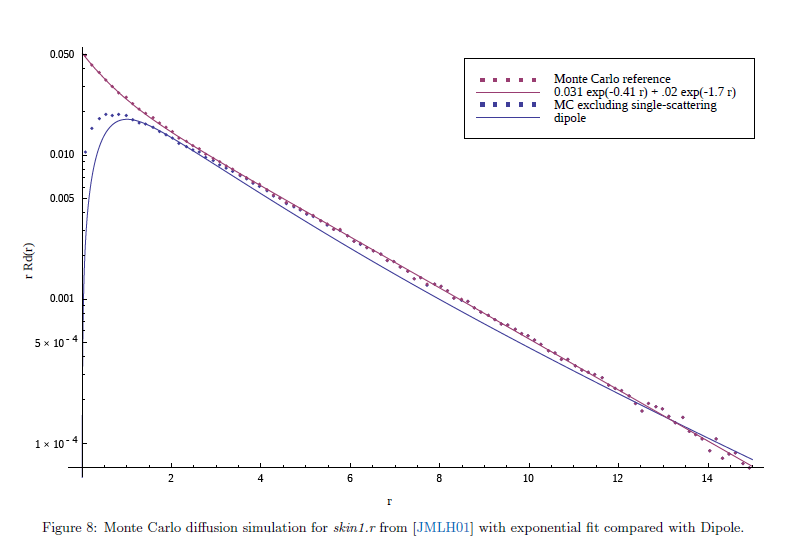
dipoleモデルの形式における表面下拡散はJensenら[JMLH01]による影響力のある論文でグラフィックスに導入されました。この研究において，サーフェイス境界はフラットであると仮定され，半無限スラブ -　すなわち，理想的な想定でこのとき散乱距離はサーフェイスの曲率と薄さに関して小さくなります。2点間のエネルギー伝達は放射輸送理論と図7で示した，単一散乱の独立な積分で決定された近似する複数の散乱拡散コンポーネントを用いて定義されます。後に続く研究はこの近似を改善しますが，幾何学的な仮定を保ち，評価コストが増加します[dI11, HCJ13]。

※図はBrent Burley, “Extending the Disney BRDF to a BSDF with Integrated Subsurface Scattering”,
SIGGRAPH 2015 Course: Physically Based Shading in Theory and Practice, p.7 より引用。

　アーティスティックな制御は拡散モデルではチャレンジとなりうる可能性があります。アーティストは拡散アルベドを指定することを好み，複数散乱距離を重要視し，しがって放射輸送の散乱係数は逆拡散方程式[JB02]によって推測されなければなりません; 例えば”アルベドの逆転”は典型的には反復あるいは表集計手法によってなさなければならず，それらの両方は高いアルベドと問題を持つ可能性があります。他のチャレンジは拡散プロファイルがよく典型的には複数散乱モデルのみにあまりにもブラーがかかり，アドホックな手法で組み合わされた2つあるいはそれ以上のプロファイルの使用を招くということです。
　我々の拡散モデルについて，異なるアプローチをとりました。最初にモンテカルロシミュレーションを通じて代表的な散乱パラメータについて単一散乱を 含む 拡散プロファイルが図8と9に示すような2つの指数の総和によってまく近似されるかを観察しました。シミレーションすることに基づいて，散乱パラメータの範囲をフィッティングし，我々は拡散プロファイルについて以下の原始的な形を選択しました：
\[
R_d(r) = \frac{e^{-r/d} + e^{-r/(3d)}}{8\pi dr} \tag{5}
\]
　拡散の寄与を評価するために，入射放射輝度がサーフェイス全てについて積分されなければいけません。特に，拡散モデルが定義される仮説的な無限平面について積分する時に，プロファイルは本質的に正規化されます：
\[
\int_0^{2\pi} \int_0^{\infty} R_d(r)r\,dr\,d\phi = 1 \tag{6}
\]
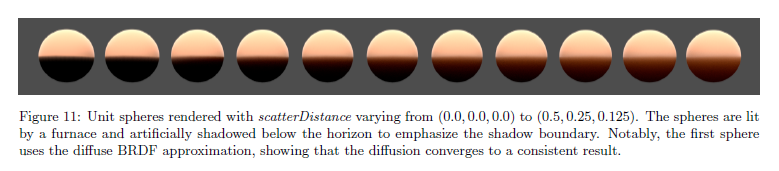
そして，正規化された拡散 とプロファイルを呼びます。我々のプロファイルは正規化されているので，我々は単純にbaseColor によって最後は積分された結果を乗算することによって求められたディフューズカラーを得ることができ，アルベドの逆転についての必要性を回避し，我々のディフューズBRDFとの一貫性を保証します。パラメータ \(d\) は赤，緑，そして青についてのコンポーネントを持った scatterDistance としてアーティストに直接的に提示します。scatterDistance が0の時，単純に我々のディフューズBRDFへと差し戻します。作品の結果画像は図10で示され，変化する scatterDistance の効果は図11で示されます。

※図はBrent Burley, “Extending the Disney BRDF to a BSDF with Integrated Subsurface Scattering”,
SIGGRAPH 2015 Course: Physically Based Shading in Theory and Practice, p.8 より引用。

※図はBrent Burley, “Extending the Disney BRDF to a BSDF with Integrated Subsurface Scattering”,
SIGGRAPH 2015 Course: Physically Based Shading in Theory and Practice, p.8 より引用。

※図はBrent Burley, “Extending the Disney BRDF to a BSDF with Integrated Subsurface Scattering”,
SIGGRAPH 2015 Course: Physically Based Shading in Theory and Practice, p.9 より引用。

※図はBrent Burley, “Extending the Disney BRDF to a BSDF with Integrated Subsurface Scattering”,
SIGGRAPH 2015 Course: Physically Based Shading in Theory and Practice, p.9 より引用。

より一貫性があり便利であることに加えて，Christensen[CB15]は我々のプロファイルもまた単一散乱（暗黙的に我々のプロファイルを含んでいる）で増大されたときでさえも最高水準の拡散プロファイルと比べてより適確であるということを示しました。Christensenは放射輸送理論からの自由パスを物理的に意味する我々のパラメータ \(d\) に関係があるシンプルな方程式を導出しました。そのような関係はその他のプロファイルとの比較を促進し，また我々のプロファイルも置換の落とし込みとして利用できるということを可能にしました。
　またプロファイルもより効率的です。比較的に単純な形式を持つことに加えて，単一散乱について離散積分を回避し，直接的かつ解析的にCDFと自明に導出できる逆CDFとして重点サンプル可能です。注意：そうするために各指数ロープが別々に必要とされますが，これは問題ではありません；3つのプロファイルは典型的には，赤，緑そして青について必要とされ，したがって6個のローブはマルチプルインポータンスサンプリングと容易に組み合わせることが可能であり，サンプルされなければなりません。
　拡散プロファイルは評価するのが効率的で，モンテカルロのリファレンスとうまく合致しますが，まだいくつかの難点があります：

　●　半無限スラブの仮定は図13で明らかなように散乱距離が大きいときにアーティファクトを生み出す。

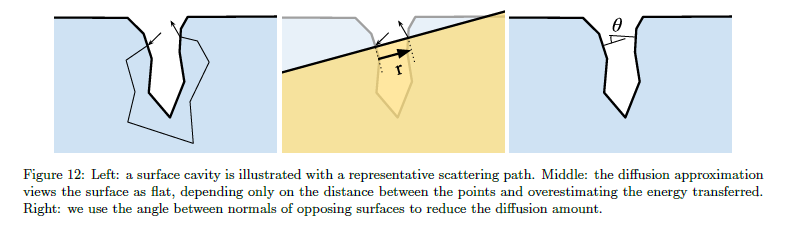
　●　サーフェイスのキャビティは図12で示した特有の問題があり，サーフェイスを反対にすることにより拡散結果をフェードアウトすることによって部分的に対処しています。

　●　拡散は小さなサーフェイス詳細を不鮮明にする傾向があります。これはなぜかというとサーフェイス法線が拡散プロファイルによって無視されるためです。

　●　サンプリングが困難で高価になる可能性があります。拡散の積分はなるべく拡散プロファイルに比例する密度を知った状態でサーフェイス全体について寄与を必要とします。平面内でそのようなサンプルを生成することが可能ですが，立体を通じて射影されたこの密度はサーフェイスのある部分でオーバーサンプルとその他の部分でアンダーサンプルになる可能性があります。複数平面間でのマルチプルインポータンスサンプル[KKCF13]を用いて，アンダーサンプルを防ぐの助けられますが，まだオーバーサンプルの問題があります。各平面のサンプルもまたサーフェイスに衝突するのを求めるためにレイの探索を必要とし，複数の交差があった場合に，各点への距離に基づき条件付きのCDFを構築します。このとき，サンプルのために点を確率的に選択します。1サンプルあたりのコストはかなりになります。

※図はBrent Burley, “Extending the Disney BRDF to a BSDF with Integrated Subsurface Scattering”,
SIGGRAPH 2015 Course: Physically Based Shading in Theory and Practice, p.10 より引用。

※図はBrent Burley, “Extending the Disney BRDF to a BSDF with Integrated Subsurface Scattering”,
SIGGRAPH 2015 Course: Physically Based Shading in Theory and Practice, p.11 より引用。

 

2.5 Path-traced subsurface scattering

我々は今，大部分のアーティファクトを回避しながら可能な限り効率的な拡散に近い実用的な代替え手段となりうるパストレースされた表面下を求めます。図13は複雑なジオメトリ上での拡散と一緒に生じる可能性があるアーティファクトを示しており，アーティファクトはパストレースされた表面下散乱と一緒になくなります。そして図14は実用的な作品での解決策となりうるパストレースされたサブサーフェイスを示しています。その画像は アナと雪の女王 エルサのサプライズ からの画像で，スノーマン，マシュマロ はパストレーシングでシームレスに統合された氷と雪の両方で構成されています。以前は，アーティストは特に裂け目において，アーティファクトを回避するために拡散描画された氷と悪戦苦闘しました。

※図はBrent Burley, “Extending the Disney BRDF to a BSDF with Integrated Subsurface Scattering”,
SIGGRAPH 2015 Course: Physically Based Shading in Theory and Practice, p.11 より引用。

 

2.6 Thin-surface BSDF

薄く，半透明のサーフェイスについて，我々の固体サーフェイスのシェーダに類似した方法でspecTrans と diffTrans によって制御されたスペキュラーとディフューズトランスミッションとして単一のシェーディング点における入射と出射散乱イベントの両方をシミュレートします。specTrans パラメータは完全ディフューズモデルと完全スペキュラーモデルの間をブレンドします。diffTrans パラメータはディフューズ反射ローブからのエネルギーをディフューズトランスミッションローブへと伝達します; 1の値は前と後ろのローブが等しくなり，値は2迄へと増加することが可能で，すべてのエネルギーを伝達するために与えられます。固体と一緒で，マイクロサーフェイスのディフューズ効果，sheen とディフューズ再帰反射は薄面の前面のディフューズモデルに含められ，ディフューズトランスミッションによって影響を受けません。さらに，ディフューズ形状に変わるものとしてオリジナルのBRDFからのサーフェイス近似を保持しています。これは正しい表面下散乱を持ち混乱をさせるために flatness に名前を変えた subsurface パラメータによって元来は制御されました。
　薄面上で屈折のため曲がるのをほぼキャンセルするということを観測し，したがってマイクロファセット分布を用いたモデルのスペキュラートランスミッションはBRDFのスペキュラーローブに等しくなりますが，その他のサイドへと反射されます。しかしながら，これは粗さがIORに依存し，屈折の曲がりが増加あるいは透過のボケを減衰のどちらかをする可能性があり効果的な伝達として完全に満たされません。実際に，\(\eta = 1\) の場合に，レイは正しく乱れなくマイクロファセットを通過します。図15に示されたようなIORに基づきスケールされた粗さ（トランスミッションのみについて）によってより一致するのを達成するのが可能となります。
　等方性のローブを持つ薄面のディフューズトランスミッションを近似します。これは表面下散乱のためトランスミッションが等方性であるという前提によって正当化されます。ディフューズとスペキュラートランスミッションは明らかに単純です。改善の可能性はセクション5.2で説明します。

※図はBrent Burley, “Extending the Disney BRDF to a BSDF with Integrated Subsurface Scattering”,
SIGGRAPH 2015 Course: Physically Based Shading in Theory and Practice, p.12 より引用。

 

3 Disney BRDF Revisited

3.1 Schlick Fresnel

BRDFについて，我々はSchlickのFresnel近似[Sch94]，\(F_{Schlick}(\theta_i) = F_0 + (1 – F_0)(1 – \cos\theta_i)^5\) を使用しました。これは妥当なIOR値について効率的で，満足がいく程度に正確です。しかしながら，屈折について使用する時には注意が必要で，特に臨界角\(\theta_c = \sin^{-1}\eta\) を超える角度でオブジェクトの外に屈折するときで，全反射をもたらします。
　臨界角を考慮してSchlickの近似を調整する簡単な方法は，単純に相対IORが1未満のときに入射角の代わりに屈折角\(F(\theta_t)\)を使用することです：
\begin{eqnarray}
F_0 &=& \left( \frac{1-\eta}{1+\eta} \right)^2 \\
\cos^2\theta_t &=& 1 \,-\, \frac{1-\cos^2\theta_i}{\eta} \tag{7} \\
F_{Schlick | \eta<1}(\theta_i, \eta) &=& \left\{ \begin{array}{l} F_0 + ( 1 - F_0)( 1 - \cos\theta_t)^5 &{\rm if} \, \cos^2\theta_t > 0 \\
1 &{\rm otherwise}\\
\end{array}
\right.
\end{eqnarray}

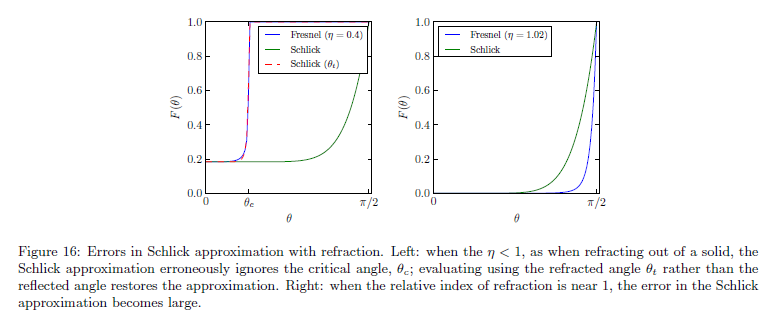
この補正は図16左側で示されます。Schlickの近似を用いた誤差のその他のソースは，図16右側に示されており，相対IORが1に近づいたときに発生します。これは例えば水中からの氷(\(\eta = 1.33/1.31 \doteq 1.02\))のように埋め込まれた固体を見る時に発生する可能性があります。結果として，氷上のスペキュラーハイライトは40倍近く明るくなる可能性があります。制限上，サーフェイスの反射は相対IROが1に向かうについて消えるべきですが，けれどもSchlickの反射は保たれたままです。

※図はBrent Burley, “Extending the Disney BRDF to a BSDF with Integrated Subsurface Scattering”,
SIGGRAPH 2015 Course: Physically Based Shading in Theory and Practice, p.13 より引用。

　BSDFについて，屈折方向を計算するために必要なものは既に与えらていて，\(\eta = 1\)付近で導入される重大な誤差を考え，我々は正確な（分極されていない，絶縁体）Fresnel方程式を選択しSchlick近似の使用を中止しました：
\begin{eqnarray}
F(\theta_i, \eta) = \left\{
\begin{array} {l}
\frac{1}{2} \left[ \left(\frac{\cos\theta_i – \eta\cos\theta_t}{\cos\theta_i + \eta\cos\theta_t} \right)^2 + \left( \frac{\cos\theta_t – \eta\cos_i}{\cos\theta_t + \eta\cos\theta_i}\right)^2 \right] &{\rm if}\, \cos^2\theta_t > 0 \\
\tag{8} \\
1 &{\rm otherwise}
\end{array}
\right.
\end{eqnarray}

　我々は既に\(\theta_t\) を計算しているので，Fresnel方程式の計算の追加コストは取るに足らないということを観測しました。
　メタリックBRDF，ディフューズローブ，クリアコート，そしてスペキュラーティントについて，我々はまだSchlick近似を使用します。後のセクション5.3でメタリックモデルの再検討を説明します。
 

3.2 Index of Refraction

BRDFについて，アーティストに対して非直感的に考えるのでパラメータとしては直接的にIORをむき出しにするのを避けました。代わりに，入射法線におけるFresnel方程式からのIORを推論し，親和性のある specular パラメータによって制御しますが，妥当な範囲を再スケールします：\(F_0 = 0.08 \, specular\)。暗黙的にIORは，\(\eta = 2 / (1 – \sqrt{F_0}) – 1\) になりますが，この値はSchlickの近似を使用する我々には必要ありませんでした。specular に対する[0, 1]の通常範囲は，これ故に[1, 1.8]のIORの範囲と一致し，とりわけ0.5は1.5のIORに一致し，ポリウレタンについての一般的な値となります。
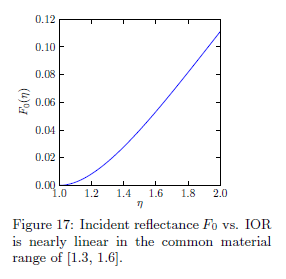
　BSDFについて，IORは屈折固体に対する曲げの度合いを制御します。エネルギー保存と妥当性を確保するために，我々は反射と屈折について同じIORを必要とし，アーティストが妥当な範囲を理解したときに直接的にIORでこれを直感的に制御することが分かりました。IORの値の範囲は空気については1からで，多くのマテリアルは1.3-1.6の範囲で，少数のみが極度に高密度なマテリアルで2を超えたり（例えばダイヤモンについては\(\eta \approx 2.5\))，[Pol08]という状態で，膨大な大多数のマテリアルについてはおそらく2の範囲です。アーティストは一般的なマテリアルが1.5に近いという状態で妥当な範囲である[1, 2]ということをただ単に理解する必要があります。
　BRDFの第2の目標はブレンディングを可能にするために線形あるいは知覚的に線形なパラメータを選択するということです。そのため，パラメータのブレンドの非等価はある程度マテリアルのブレンドの等価を近似します。幸いなことに，図17に示すように妥当な範囲においてIORは入射リフレクタンスに関してある程度線形です。これが意味するのは2つのIORの値を混合したものが補間された入射リフレクタンスとしてほぼ同じ結果を生み出すということです。

※図はBrent Burley, “Extending the Disney BRDF to a BSDF with Integrated Subsurface Scattering”,
SIGGRAPH 2015 Course: Physically Based Shading in Theory and Practice, p.14 より引用。

 

3.3 Smith G

2012のノートの付録[Bur12]に2014に記載し，そしてここで再度述べるように，Heitzの分析[Hei14]に基づき，我々は最重要なスペキュラーローブのためアドホックなSmith \(\rm G\)のラフネスのリマッピングを除去し，Heitzの異方性形式を適用しました。この結果は金属について一目瞭然でより良く，ほぼ間違いなく非金属について良いのですが，\(\rm G\)項はまだエネルギーを失ったままで，セクション5.1においてさらに問題を説明します。クリアコートのスペキュラーローブは修正されずにそのままです。
 

3.4 Parameter blending with pass-through

2012年のノートで，指定されたパラメータ値のまとまりが各レイヤーで定義され，これらのレイヤーは空間的に変化するマスクに従って”パラメータブレンドされる”というレイヤードマテリアルについてのユーザーインターフェイスを記述しました。ブレンドされた値は妥当な中間のマテリアル結果を生成し，高価な複数BRDFの組み合わせを回避します。これはアーティストにとって非常に直感的であることが分かり，マテリアルの仕様についての唯一のインタフェースはそのままです。
　元来，リフレクタンスのレイヤーにおいて10個のパラメータを持っていました。BSDFでは，固体について12個で，specTrans と scatterDistance，また薄面については13個で，前述したようにspecTrans，diffTrans，そしてflatnessを追加しました。非半透明レイヤーが追加されたときに，面倒ごとを減らすために，UIにパラメータのパススルーする新しい機能を追加しました。
　パラメータのパススルーで，アーティストはテーブルの入力空白から離れることが可能となります。パラメータブレンディングをする間，空白に出くわしたときに，以前のブレンドされた結果が維持されます。この単純な変はレイヤリングインターフェイスのユーザビリティ―を大きく改善しました。
　UIと値が連動するレイヤードマテリアルの作成例を図18に示します。

※図はBrent Burley, “Extending the Disney BRDF to a BSDF with Integrated Subsurface Scattering”,
SIGGRAPH 2015 Course: Physically Based Shading in Theory and Practice, p.14 より引用。

 

4 Production Results

新しいBSDFは髪を除きベイマックスの至るサーフェイスで使用され，全てのタイプの屈折効果は広範囲に使用されました。図19で示した作品スチールにおいて，ベイマックスはディフューズとスペキュラートランスミッションをブレンドした状態で薄面シェーディングが使用されており，彼が膨張したビニールで作らていることを納得のいく伝え方をしています。また薄面シェーディングは布や紙について様々に使用されています。窓は典型的には屈折固体としてモデルされています。図20はいくつかの屈折固体がある追加スチールを示します。全てのスキンやプラスチックのような多くの固体オブジェクトは正規化された拡散を用いて描画されます。

※図はBrent Burley, “Extending the Disney BRDF to a BSDF with Integrated Subsurface Scattering”,
SIGGRAPH 2015 Course: Physically Based Shading in Theory and Practice, p.15 より引用。

※図はBrent Burley, “Extending the Disney BRDF to a BSDF with Integrated Subsurface Scattering”,
SIGGRAPH 2015 Course: Physically Based Shading in Theory and Practice, p.16 より引用。

ベイマックスでの描画画像は各バウンスで完全BSDFレスポンスを持つ複数バウンスのパストレーシングが使われています。BSDFは全てのライティング状態において予測通りの結果を持ち，頑健で制御しやすいということを証明しました。実際に，アーティストは様々な屈折効果と，新しいパラメータのパススルーUIが，新しいレベルの生産性をアーティストが達成するとともに非常に簡単にレイヤリングを作成でき，途切れなくブレンドするのが容易であるということが分かりました。また，BSDFは平均的に1フレームに105億のシェーダ評価を有効にするために十分効率的であるということも証明しました。

 

5 Feature

5.1 Energy conversion

リフレクタンスモデリングにおけるエネルギー保存の原則は一般的には受けたエネルギーよりもより多くのエネルギーをサーフェイスが反射できないということを意味していますが，しかしながら，それはサーフェイスがエネルギーを失うことがないのとまったく同じように重要です。もちろん，サーフェイスはエネルギーを吸収し，色やアルベドの見える結果となりますが，サーフェイスが吸収しない状態でモデルされていた場合は，全てのエネルギーは反射されるべきです。
　いわゆるファーネステストは普通エネルギー保存を判定するのに使われます。一様ライディアンスの環境で描画したときに，1のアルベドを持つエネルギーを保存するマテリアルは”消失”しますが，一方で非エネルギー保存するマテリアルはビューイング角度に依存して明るくなりすぎるかあるいは暗くなりすぎるか，または両方のどれかが現れます。Heitzはマイクロファセットモデルが典型的には複数散乱をモデルせず，したがってファーネステストに合格しない[Hei14]ということに気付きました。マイクロファセット\(G\) 要素によってシャドウされたエネルギーは失われます。Heitzはマイクロファセットモデルを有効にする手法として”ウィークホワイトファーネステスト”を提案しました。そのテストは少なくともエネルギー保存は最初の散乱までで，マイクロファセット間の複数散乱からエネルギーがなくなるのみです。ウィークテストでは，シャドウイング項は省略され，最初の散乱イベント後で計測されたラディアンスを表現しますが，散乱される前のレイはマイクロファセットによりシャドウされます。Smithのシャドウイング関数はそのようなテストに通るということが示されていますが，根本的にエネルギーは失われたままです。
　マイクロファセットのエネルギー欠損の効果は図21で観測され，ここでは粗いグラスの球がファーネスで描画されたときにエッジ上で暗くなるのが見えます。複数バウンスパストレーシングは内部反射を使用しています。これは単に理論的な問題ではありません：この画像は，一様なライティング環境中で既存のマイクロファセットモデルで描画したときに粗いグラスがどのように見えるかという代表で，エッジ上で不自然に暗く見えます。

※図はBrent Burley, “Extending the Disney BRDF to a BSDF with Integrated Subsurface Scattering”,
SIGGRAPH 2015 Course: Physically Based Shading in Theory and Practice, p.16 より引用。

　図21に示すように，sheenを追加することはグラス球がファーネステストをほぼ合格することができるということをついでながらに気付きました。これは言うまでもなくsheenモデルは正確で，実際にはその他のroughness値については間違った形状を持ちますが，むしろそれを持つための 動機 は正当化されます。ディフューズ再帰反射についての動機は同様に正当化されます。
　今後の研究として，我々は再帰反射とsheenコンポーネントを再検討し，正しくエネルギー保存するコンポーネントでそれらを潜在的に置き換えるつもりです。例としてJakobら[JdJM14]らによる最近の研究はマイクロファセット相互反射から失われるエネルギーを置き換えるためのディフューズ補正項を提案しています。

 

5.2 Better thin-sheet model

前に説明したように，薄シートモデルはあまりにも単純で，定式化を再検討したいと思います。より厳密に定義され，薄シートを通じてスペキュラーとディフューズトランスミッションの両方に対して実験的に有効化されたモデルが近年の研究で提案されています[GQP15, PdMJ14]。
 

5.3 Better metallic model

我々のメタリックモデルはSchlickのFresnel近似を使用する上で正しい金属的なレスポンスから異なります。伝導体について正確Fresnel方程式は複雑な形を持ち，マテリアルのスペクトルの吸収係数\(k\) の追加のマテリアルパラメータに依存します。IOR，吸収係数，そして結果の色の間の関係性は直感的ではなく，任意のパラメータの組み合わせは怪しいです。
　Gulbarndsen[Gul14]による最近の研究は入射とエッジからの直接の仕様を用いて，(スペクトルの)IORと吸収係数の再パラメータ化によってアーティストに親和性のある制御を保証し，パラメータ化はアーティストと一緒に我々は調査することを望んでいます。
 

6 Conclusion

　我々は新しい Disney BSDFを提案し，屈折と表面下散乱が組み込まれたBRDFの拡張し，効率的で，正確で，制御性に利益をもたらす新たな拡散プロファイルを説明しました。作品例を示し，実装の問題と制限を説明しました。
　結論として，我々が確信するモデルの値は統合されたアプローチから由来しし―つまり，直感的で単一のモデルをもって，パラメータの最小セットがほぼすべてのマテリアルについて使用可能であり―そして，仕様の構成部品はより少ないということを強調したいです。我々はモデルの頑健性と妥当性の向上と我々のニーズを決定づける拡張を続けますが，我々のアプローチの簡素化と一般化への取り組みは残ったままです。
 

---

7 Achknowledgements　及び参考文献の和訳は省略しますので，各自で原文をご参照ください。