こんばんぐんぐん。
Pocolです。
今日は,
[Christensen and Burley 2015] Per H. Christensen, Brent Burley, “Approximate Reflectance Profiles for Efficient Subsurface Scattering”, Pixar Technical Memo #15-04, July, 2015.
を読んでみようと思います。
いつもながら誤字・誤訳等があるかと思いますので,指摘していただける場合は正しい翻訳例と共に指摘していただけると幸いです。
Abstract
経験的な反射率プロファイルに基づいたBSSRDFモデルのための3つの有用なパラメータ化を提示します。このモデルは非常にシンプルですが、適切なパラメータ化を行うことで、多くの一般的な物質について、最新の物理ベースのモデル(量子化拡散とフォトンビーム拡散)よりもブルートフォースモンテカルロ法の計算結果とよく一致します。各反射率プロファイルは2つの指数の和であり、指数の高さと幅は表面のアルベドと平均自由経路長に依存します。我々のパラメータ化により、同じパラメータを用いた物理ベースの拡散モデルとの直接比較が可能になりました。パラメータ化は、垂直照明、拡散表面透過率(照明の方向は関係ない)、散乱距離の代替指標について決定されています。我々の近似値は、レイトレースやポイントベースの表面下散乱のレンダリングに有用です。
1 Introduction
皮膚、肉、果物、植物、ワックス、大理石、ヒスイ、牛乳、ジュースなどの半透明な素材の画像を忠実にレンダリングするためには、表面下散乱をリアルにモデリングすることが重要です。コンピュータグラフィックス研究者は、単純なダイポール拡散モデル[Jensen et al. 2001]から量子化拡散モデル[d’Eon と Irving 2011]、フォトンビーム拡散および拡散単一散乱モデル[Habelら 2013]に至るまで、だんだん洗練された正確な物理ベースの表面下散乱モデルを開発してきました。ここでは、ダイポールと同じように単純でありながら、フォトンビーム拡散よりもブルートフォースモンテカルロ計算によくマッチする経験モデルの3つのパラメータ化を紹介します。
物理ベースのモデルを近似モデルに置き換える主な理由は、以下の通りです:
- ユーザーフレンドリーなサーフェイスアルベドと平均自由経路長の入力パラメータを、より直感的な体積散乱係数と吸収係数へと数値変換する必要がありません[Jensen と Buhler 2002; Habelら 2013]。
- 単一散乱項を備えています。
- 評価が高速化され、コードがシンプルになり、ルックアップテーブルが不要になりました。
- 理論をモンテカルロ法のリファレンスに適合させるためのアドホック補正係数\(\kappa(r)\)はありません [DonnerとJensen 2007; Habelら2013]
- 重点サンプリングのためのシンプルな累積分布関数
2 Background and related work
2.1 Monte Carlo simulation and BSSRDFs
表面下散乱を計算する最も一般的な方法は、物体を体積として扱い、ブルートフォースモンテカルロシミュレーションを実行することです[KalosとWhitlock 1986; Wangら 1995]。 しかし、これは特に複雑なシーンでは非常に時間がかかります。
光が物体に入射し、物体内部で散乱し、物体から出ていく様子を記述した関数がBSSRDF(双方向表面散乱反射率分布関数)です。Donnerら[2009]は、モンテカルロ粒子追跡を使用して、均質な半無限体積上の平面に対する経験的なBSSRDFモデルを集計しました。彼らは光の入射角,出射光の相対,物理パラメータ(ボリュームアルベド,平均自経路長,移送関数,屈折率)に応じた,サーフェイスから出る光の半球上の振舞いを表現しました。これらの表は計算に数ヶ月を要し、約250MBのデータを含んでいます。
2.2 Physically based reflectance profiles
BSSRDF \(S\)は、大抵、放射状に対称な(1D)拡散反射率プロファイル\(R\)、2つの方向性フレネル透過項\(F_t\)、および定数\(C\)の積として単純化されます[Jensenら 2001; d’EonとIrving 2011; Jimenezら 2015]:
\begin{eqnarray}
S(x_i, w_i; x_o, w_o) = C F_t (x_i, w_i) R(|x_o – x_i|) F_t(x_o, w_o) \tag{1}
\end{eqnarray}
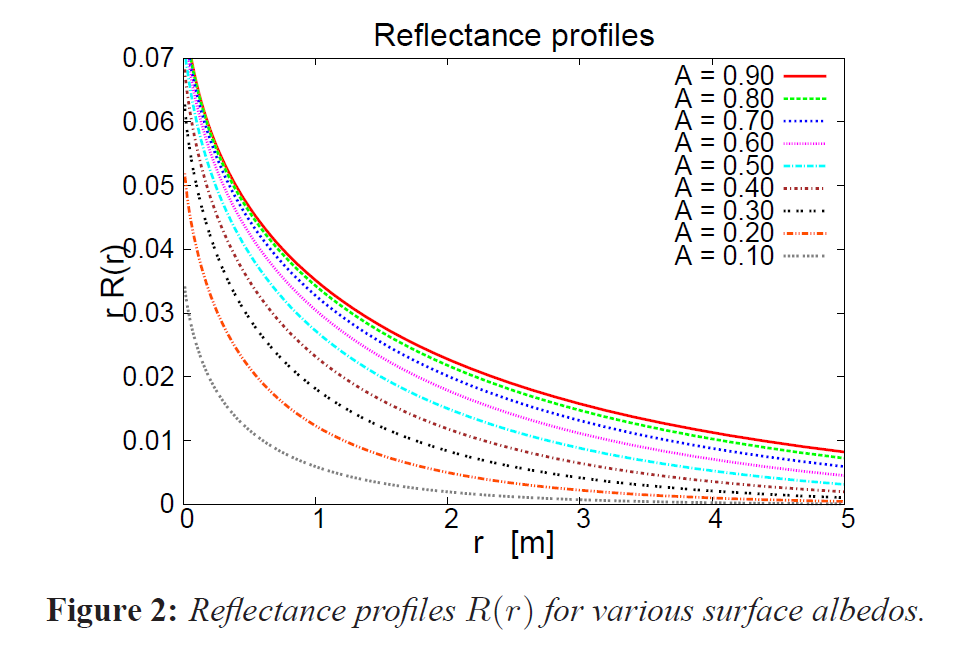
図2は、様々なサーフェイスアルベドに対する反射率プロファイルの例を示しており、これらの曲線はモンテカルロシミュレーションを用いて計算されています。縦軸は\(R(r)\)ではなく\(rR(r)\)を示していますが、これは\(R(r)\)が常に放射状に積分されているからです(\(r=0\)付近に鋭いピークを持っています)。
ダイポール拡散モデル[Jensenら 2001]は、多くの散乱イベントの後に拡散された表面下散乱の近似です。このモデルはシンプルで評価が速く、広く使われていますが、あまりにもぼやけすぎていて,ワックスのように見えてしまいます。散乱は、体積散乱係数と吸収係数の\(\sigma_s\)と\(\sigma_a\)(等価的には、体積散乱アルベド\(\alpha = \sigma_s / \sigma_t = \sigma_s/ (\sigma_s + \sigma_a)\),そして体積平均自由経路長\(\ell = 1 / \sigma_t = 1 / (\sigma_s + \sigma_a)\))によってパラメータ化されています。
Jensen と Buhler [2002]は、サーフェイスアルベド(拡散表面反射率)\(A = \int_0^{\infty} R(r) 2 \pi r dr \)と表面上の拡散平均自由経路長\(\ell_d\)という、より直感的な表面下散乱のパラメータ化を導入しました。我々の近似では、同様の直感的なパラメータを使用しています。(\(R_d\)は反射率プロファイルの拡散(多重散乱)部分にも頻繁に使用されるため、一般的に使用される\(R_d\)の代わりにサーフェイスアルベドの記号\(A\)を使用しています)。最近、Frisvadら[2014]は、放射状に対称な拡散プロファイルの仮定を解除した指向性ダイポールモデルを導入しました。これにより、例えば、滑らかな屈折面を持つ物体(牛乳、フルーツジュース、浮遊粒子を含む他の液体など)の非垂直(斜め)照明の精度が向上します。
d’Eon と Irving [2011]では、量子化された拡散が紹介されています:改良された拡散理論と、単なるダイポールの代わりに拡張された入力項です。この結果、よりシャープな特徴を持つより現実的な外観が得られますが、計算がより複雑で時間のかかるものとなります。結果として得られる拡散反射率プロファイルは、ガウシアンの和として近似されました。我々の近似は、より正確で、計算が非常にシンプルです。
Habelらによるフォトンビーム拡散の論文[2013]は、量子化された拡散と同等の精度を持ちながらも、より高速な評価が可能なフォトンビーム拡散モデル、正確な拡散単一散乱モデル、マテリアルへの斜め屈折のエレガントな取り扱い、という3つの主要な貢献をしています。我々の近似は、対称散乱(理想的な拡散面透過の垂直照明のいずれか)に対して、フォトンビーム拡散よりも高速で、より正確です。フォトンビームモデルには、中距離領域のモンテカルロ計算結果と理論結果をよりよく一致させるために、経験的な項\(\kappa(r)\)が含まれています。
上記のすべての拡散モデルは、明示的なレイトレーシングまたは個別の積分による単一散乱の個別の処理を必要とします。どちらの方法も時間がかかります。我々のモデルは単一散乱を含んでいるので、高価な計算は必要ありません。
2.3 Approximate reflectance profiles
図2のような反射率プロファイルは、表を用いて表現することができます。例えば、サーフェイスアルベド0, 0.01, 0.02, …1の距離\(r\)の関数としての反射率プロファイルのテーブルを格納することができ、与えられたサーフェイスアルベドと距離に対してそれらの間を補間することができます。
しかし、私たちのインスピレーションは、複雑な関数をより単純なもので近似するという、よく使われる手法に由来しています。その良い例がフレネル反射と屈折の公式です。フレネル反射と屈折は、物理学(マクスウェル方程式とエネルギー制約)に基づいて、垂直光と平行偏光の2つの項の和としてモデル化することができます。しかし、Schlick [1994]は、結果として得られる曲線は単純な多項式で近似できるという観測を行い、この近似はより単純で、評価が速く、目に見える違いを与えないので、コンピュータグラフィックスで広く利用されています。私たちは、表面下散乱についても同様の近似を行いたいと考えています。
反射率プロファイルは、ゼロ平均ガウシアンの和[d’Eonら 2007; Yanら 2012; Jimenezら 2015]を用いて合理的に近似され、単一ガウシアンまたは3次多項式[Kingら 2013]を用いてより粗く近似されてきました。
Burley [2013; 2015]は、拡散反射率プロファイルの形状は、2つの指数関数の和を距離\(r\)で割った形の曲線でかなりよく近似できることを指摘しています:
\begin{eqnarray}
R(r) = \frac{e^{-r/d} + e^{-r/(3d)}}{8 \pi d r} \tag{2}
\end{eqnarray}
\(d\)パラメータは曲線の高さと幅を形づくるもので、アーティスティックな好みに基づいて設定することも、物理的なパラメータに基づいて決定することもできます。\(R(r)\)のこの式では、\(d\)が正の値であれば、サーフェイスのアルベドは1になりますので、Burleyはこれを正規化拡散と名付けました。サーフェイスアルベド\(A\)を掛け合わせ、\(d\)の適切な値を選ぶことで、多くの一般的なマテリアルに対して非常に正確なフィットを得ることができます。このモデルは、ウォルト・ディズニー・アニメーション・スタジオのHyperionレンダラで実装されています。図3は、ディズニー映画「ベイマックス」でのこの散乱モデルの使用例を示しています。
以下のセクションでは、有効なサーフェイスアルベドの全範囲にわたってモンテカルロ法による計算結果と一致するように、正規化された拡散曲線をどのようにスケーリングし、伸張するのが最適なのかについての簡単な解析を紹介します。言い換えれば、物理パラメータから\(d\)への適切な “変換”を決定します。これにより、物理ベースの拡散モデルで使用されているのと同じ物理パラメータを散乱距離に使用することができ、それらのモデルとの直接比較が容易になります。
3 Searchlight configuration
まず、集光されたライトビームが平坦な表面の下にある半不定形の均質な媒体に入射する、いわゆるサーチライトの構成を考えてみましょう。フォトンは表面を透過し、媒体によって散乱され、最終的には吸収されたり、媒体から表面に戻ってきたりします。表面を出た光子の分布は反射率プロファイル\(R(r)\)を形成し、通常の入射光や拡散透過光では放射状に対称です。
このセクションでは、フォトンは最初に表面に垂直な方向に直進すると仮定しています。また、位相関数が等方的であると仮定します。異方的な位相関数は、多くの場合、縮小された散乱係数\(\sigma_s’ = (1 – g) \sigma_s\)を使用して、類似性のあるモーメントを使用して処理されますが、これについての詳細は第8節の将来の研究の下にあります。
3.1 Monte Carlo references
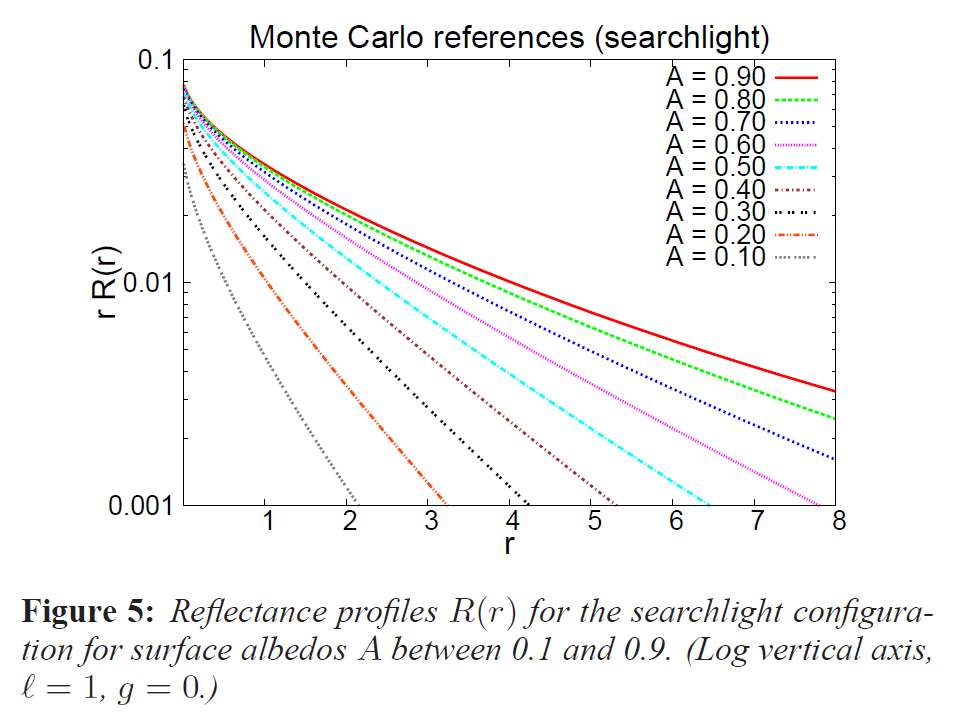
図5は、平均自由経路\(\ell = 1\)、異方性\(g = 0\)の場合のサーフェイスアルベド0.1から0.9の反射率プロファイル\(R(r)\)を示しています(実際には図2と同じデータですが、対数縦軸を使用しています)。これらのリファレンスプロファイルは, MCML [Wang et al. 1995] に似たブルートフォースモンテカルロシミュレーションを用いて計算され, 我々の近似目標曲線となっています。サーフェイスアルベドは、体積散乱・吸収係数\(\sigma_s\)と\(\sigma_a\)が平均自由経路長\(\ell = 1 / (\sigma_s + \sigma_a)\)が1(すなわち\(\alpha = \sigma_s, \sigma_a = 1 – \sigma_s = 1 – \alpha\))となるように選択され、\(R(r)\)を積分したときに所望のサーフェイスアルベド\(A\)に到達するように、フレネル項を用いずに\(A = \int_0^{\infty} R(r) 2 \pi r dr\)として計算されます。
3.2 Functional approximation
物理的に意味のある量に対応する適切な\(d\)の値を決定したいと考え、体積平均自由経路長\(\ell\)を選択しました。\(d\)と\(\ell\)の関係をスケーリングファクタ\(s\)で表現すると、式2に\(d = \ell/s\)を設定すると、次のようになります。
\begin{eqnarray}
R(r) = A s \frac{ e^{-sr/\ell} + e^{-sr/(3\ell)} }{ 8 \pi \ell r} \tag{3}
\end{eqnarray}
次に注意して欲しいのは、ある\(A\)のモンテカルロ参照曲線の形状は\(\ell : R(r, \ell) = R_{\ell=1}(\frac{r}{\ell}) / \ell^2\)に依存しないので、曲線フィッティングで\(s\)を決定するには\(\ell = 1\)を考慮すれば十分であるということです。したがって,曲線のフィッティングでは,考慮する必要があるのは:
\begin{eqnarray}
R_{\ell = 1}(r) = A s \frac{ e^{-sr} + e^{-sr/3} }{ 8 \pi r} \tag{4}
\end{eqnarray}
ここで、\(A\)の有効範囲に対して良い\(s\)値を決定する必要があります。\(s\)パラメータ空間のブルートフォースランダムサンプリングを使用して、\(r_i : \sum_i \frac{| R(r_i) – R_{MC}(r_i) | }{ R_{MC}(r_i) }\)に対する相対誤差を最小化し、\(A\)の任意の値に対する最適値\(s\)を決定します。
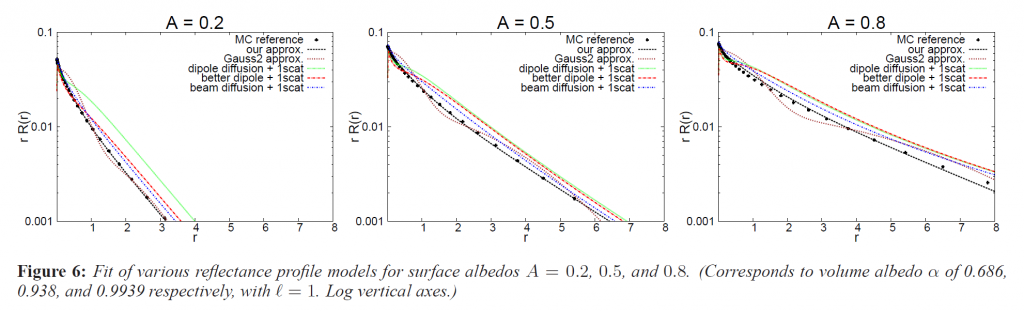
図6は、サーフェイスアルベド0.2、0.5、および0.8に対して、2つのガウシアン、フォトンビーム拡散+単一散乱、ダイポール拡散+単一散乱、およびより優れたダイポール拡散+単一散乱をベストフィットさせたモンテカルロ法と比較した反射率プロファイル近似の適合性を示しています。図は、2つのガウシアンは、我々の正規化された拡散のパラメータ化と同様に、参照曲線と一致しないことを示しています。また、我々の近似が、ダイポール、より良いダイポール、単一散乱を伴うフォトンビーム拡散のMC参照点に近いことを示しています。
\(A = 0.01, 0.02, \dots, 0.99\)の値に対する\(s\)値の表を単純に生成することができます;これらの値のいくつかは図7のデータポイントとしてプロットされています。これらの値を使用して、サーフェイスアルベドの中間の値を補間すると、モンテカルロ法の計算結果と比較して、平均相対誤差は4.9%となります。しかし、ここではさらにコンパクトで評価が簡単な関数を紹介します。
ちょっとした手動のカーブフィッティングで、スケーリング係数\(s\)の次の単純な式が最適値によくフィットすることがわかりました:
\begin{eqnarray}
s = 1.85 – A + 7 |A – 0.8|^3 \tag{5}
\end{eqnarray}
この関数を図7の曲線としてプロットします。この式を\(s\)とした場合、モンテカルロ法による反射率プロファイルの相対誤差は、サーフェイスアルベドの全範囲にわたって平均5.5%となります。これは、モンテカルロ法に暗黙のうちに組み込まれているすべての近似や仮定(半無限の均質体積、平坦な表面、サーチライトの配置など)と比較して、実際にはかなり小さな誤差となっています。
4 Diffuse surface transmission
前節では、光は表面に垂直な方向にまっすぐに体積内に入ると仮定しました。このセクションでは、表面での理想的な拡散透過後の表面散乱反射率プロファイルをモデル化します。これは、乾燥した(汗をかかない)肌、化粧品、ほとんどの果物、粗い(磨かれていない)大理石のような粗い表面物質や、入射する光の方向を無視する(あるいは知らない)状況には、より適切なモデルとなるかもしれません。
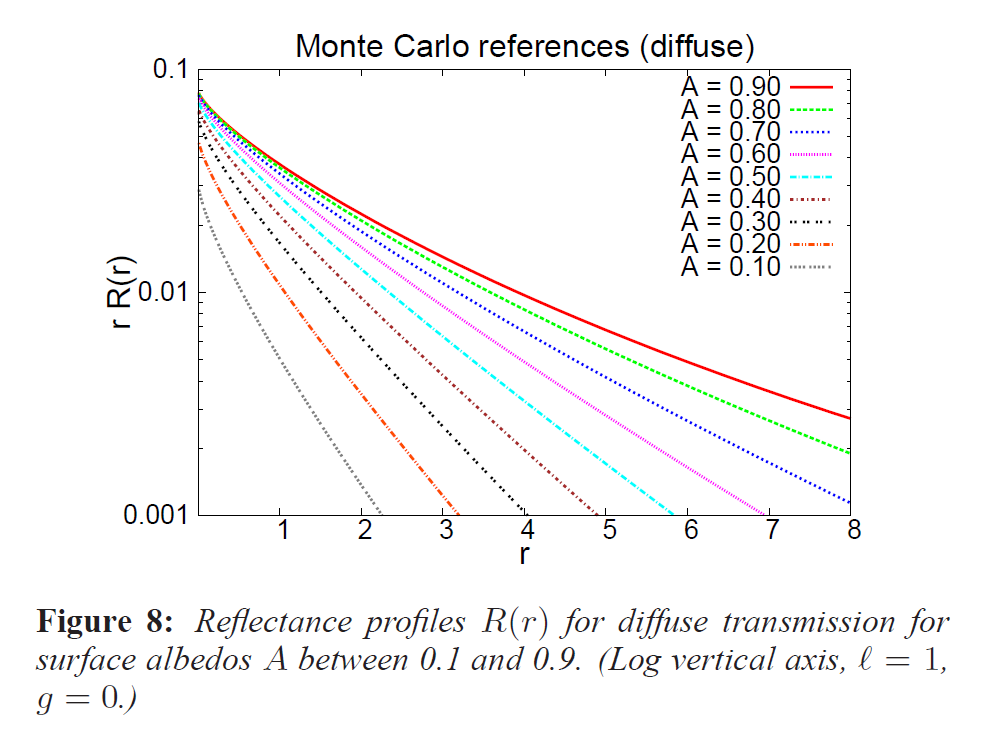
図8は、理想的な拡散表面透過(コサイン分布)後の表面下散乱の反射率プロファイル\(R(r)\)を示しており、再びモンテカルロシミュレーションを用いて計算されています。この場合の反射率プロファイルの一般的な形状はサーチライトの場合と似ているので、同じ関数近似式(式3)を使用しますが、新しい\(s\)値を計算します。最適な\(s\)値については、モンテカルロ法を用いて計算した場合と比較して、平均相対誤差は2.6%だけでした。
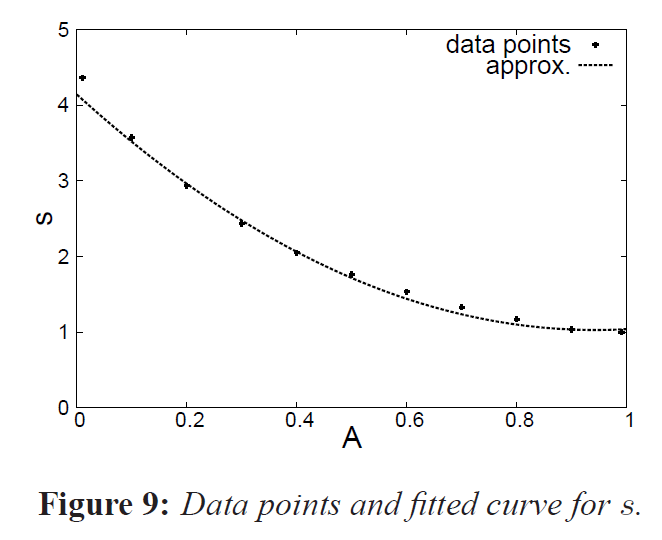
ここでも手動のカーブフィッティングを使用して、\(s\)の式が最適値によくフィットすることがわかりました:
\begin{eqnarray}
s = 1.9 – A + 3.5 (A – 0.8)^2 \tag{6}
\end{eqnarray}
図9は、データポイントと\(s\)のフィット曲線を示しています。この\(s\)の式を使うと、モンテカルロ法の参照に対する平均相対誤差はわずか3.9%です。
実際に使用してみると、サーチライト近似の見た目と拡散透過近似の見た目の差はあまりないことがわかりました。そのため、これらの抽象化は、2つの非常に異なるクラスのサーフェスを表現することを意図していますが、実用的なVFXやCGアニメーションの仕事では、この区別は特に重要ではないかもしれません。
5 dmfp as parameter
ここでサーチライトの設定に戻ります。散乱距離の別のパラメータ化を使用することが可能です。それは、体積\(\ell\)の平均自由経路(mfp)の代わりに、表面\(\ell_d\)上の拡散平均自由経路(dmfp)を使用することです。\(\sigma_s\)と\(\sigma_a\)に対応する拡散平均自由経路長を計算するために、まず拡散係数\(D\)を計算します。
\begin{eqnarray}
D = (\sigma_t + \sigma_a) / (3 {\sigma_t}^2) \tag{7}
\end{eqnarray}
\(D\)が与えられると、実効輸送消滅係数\(\sigma_{tr}\)と\(\ell_d\)を計算することができます。モンテカルロリファレンス曲線を計算するためには、\(\sigma_s\)と\(\sigma_a\)のどのペアの値が所望の\(A\)値と,\(\ell_d = 1\)を与えるを決定します:Aを与える\(\sigma_s\), \(\sigma_a\)の比を選択し、\(\sigma_s\)と\(\sigma_a\)を一緒に拡大縮小して\(\ell_d = 1\)を得ます。式3で\(\ell\)を\(\ell_d\)に置き換え、\(s\)についてこの簡単な式を使用することで、これらの曲線に良いフィットが得られることがわかりました:
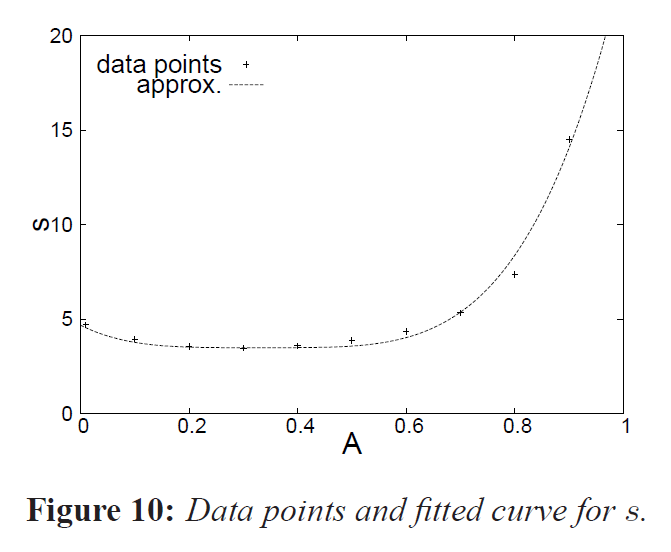
\begin{eqnarray}
s = 3.5 + 100 ( A – 0.33) ^4 \tag{8}
\end{eqnarray}
図10は、データポイントと\(s\)の適合曲線を示しています。平均誤差は、最適な\(s\)値の場合は6.4%、上記の式を使用した場合は7.7%となります。
6 Practical detail: importance sampling
入射点と出射点の半径方向の距離に比例する重点サンプリングには、\(R(r)\)と\(2\pi r\)の積に対応する\({\rm cdf}\)(累積分布関数)が必要です。物理ベースのBSSRDFの場合,この\({\rm cdf}\)は数値積分を用いて計算しなければなりませんが,これは煩雑であり,性能を低下させます。しかし,幸いなことに Burley の正規化拡散 \(R(r)\) × \(2\pi r\) は容易に積分できるので,この \({\rm cdf}\) が得られます:
\begin{eqnarray}
cdf(r) &=& \frac{\int_o^r R(t)2\pi t dt}{\int_0^{\infty}R(t) 2\pi t dt} \tag{9} \\
&=& \frac{A/2(4 – e^{-r/d}-3e^{-r/(3d)})}{A} \tag{10} \\
&=& 1 – \frac{1}{4}e^{-r/d} – \frac{3}{4}e^{-r/(3d)} \tag{11}
\end{eqnarray}
このシンプルな \({\rm cdf}\) は、私たちのパラメタライゼーションの両方で使用することができます:\(d = \ell /s\) または\(d = \ell_d / s\)。
\({\rm cdf}\) の逆関数 は \(r = {\rm cdf}^{-1}(\eta)\) であり、ここで \(\eta\) は 0 から 1 の間の確率変数です。 残念ながら \({\rm cdf}\) は解析的には可逆ではありませんが、(少なくとも)3 つの方法でこれを扱うことができます。1) 2つの指数のうちの1つをランダムに選び、その逆数を\({\rm cdf}\)として使用し、MIS(多重点サンプリング)を用いて結果を重み付けする;2) 数回のニュートン反復;3) \(d = 1\)の場合の\({\rm cdf}^{-1}\)の事前計算されたテーブルを\(d\)でスケーリングする。
※編集注:https://zero-radiance.github.io/post/sampling-diffusion/ にて可逆であることが示されています。
7 Discussion and reuslts
これらの簡単な計算式を使用することで、量子化拡散や単一散乱を伴うフォトンビーム拡散を計算するよりも何倍も高速に計算できます。実際、我々の計算式は単純なダイポール拡散モデルよりもさらに高速です。パラメータが同じなので、物理ベースの拡散モデルから我々の近似拡散モデルへの切り替えは簡単です。
物理ベースのモデルの実用的な使用では、レンダリング中に必要に応じて集計し、次のルックアップ中にテーブルを補間することができるので、実際には、我々の近似を使用して実行時間を節約することができます。それにもかかわらず、コードの簡素化はレンダリング作成者の視点から見ても重要です。特に、サーフェイスアルベドと平均自由経路長を体積散乱・吸収係数に数値的に逆にするコードは、完全に自明ではありません。このコードとテーブル生成とルックアップのための最適化コードを削除し、\(s\)と正規化された拡散\(R(r)\)のための非常にシンプルな公式で置き換えることは、有用で実用的な単純化です。おまけに,重要度サンプリングのための \({\rm cdf}\)は非常に単純です。
我々の近似拡散モデルは、レイトレースやポイントベースのサブサーフェス散乱に有用であり、検索用のmfpとdmfpのパラメータ化は、PixarのRenderManレンダラのサブサーフェス散乱モデルの2つとして実装されています。
図11は、スポットライトで照らされたサーフェイスを示しており、表面は、異なる皮膚のようなサーフェイスアルベドを持つ3つのストリップで構成されています。左はフォトンビーム拡散と単一散乱を加えたもので、右は同じパラメータを用いた我々の近似反射率プロファイル(セクション3のサーチライト構成)を用いたBSSRDFです。
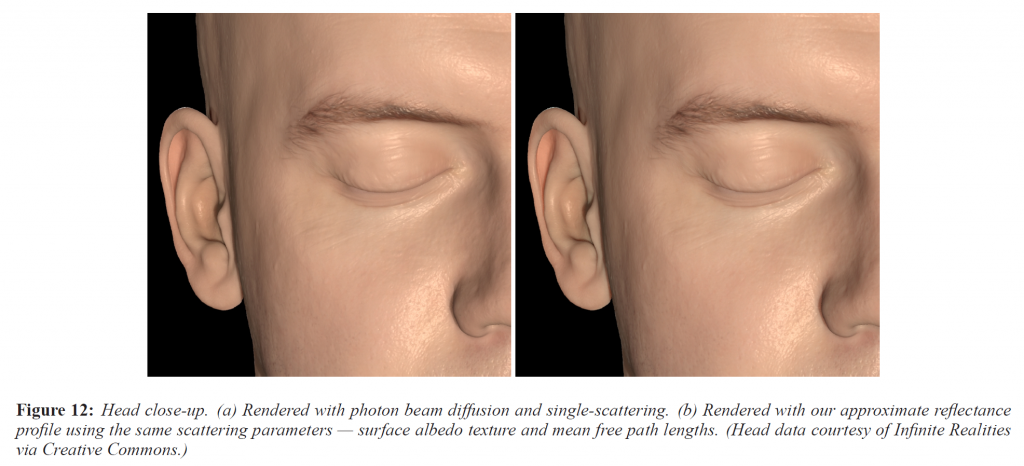
図12は、左がフォトンビーム拡散+単一散乱(表面に直接散乱)、右が同じパラメータを用いた我々の近似反射率プロファイルを用いたBSSRDFを用いた場合の人間の頭部のクローズアップ写真です。両方の画像で、バックライトで照らされた耳たぶを介して表面下散乱の特徴的な赤みを帯びた光を示していることに注目してください。
図1は、我々の近似反射率プロファイルを用いてレンダリングされた表面下散乱の他の例を示しています:大理石、人間の皮膚、プラスチック、果物、ろうそくのロウ、動物の皮膚です。
8 Conclusion and future work
本研究では、表面下散乱のシンプルで効率的なレンダリングのために、近似反射率プロファイルの3つのパラメータ化を提示しました。モンテカルロ法と比較した相対誤差は、サーフェイスアルベドの全範囲にわたって、それぞれ平均5.5%, 3.9%, 7.7%でした。我々は、より高い精度を目指しても、より深刻な無限スラブ仮定(平坦な表面を持つ半無限の均質体積)を維持したままでは、無駄になると確信しています。
今後の作業には、制限の少ない仮定のセットを見ることが含まれています。例えば、斜め入射方向と非放射対称散乱のための拡散プロファイルに単純な近似を適用することを試みることは非常に興味深いことでしょう。これは、スケール\(s\)が入射照明の極角と相対方位角に依存しているのと同じくらい簡単かもしれません(サーフェイスアルベドと同様に)。また、異方性散乱(\(g \neq 0\))を有する拡散性の表面下散乱物質は、しばしば、モーメントの類似性を用いて近似されます:\({\sigma_s}’ = (1 – g)\sigma_s\)。これは多くの散乱イベントの後では合理的な仮定かもしれませんが、単一散乱や低次散乱ではおそらくそうではありません。異方性散乱を用いて計算されたモンテカルロ法の計算結果に曲線をフィットさせることは興味深いことです。