こんにちわ，Pocolです。
今日は，Peter-Pike Solanによる”Deringing Spherical Harmonics”を読んでみようと思います。
いつものように誤字・誤訳があると思いますので，ご指摘いただける場合は正しい翻訳例と共に指摘して頂けると幸いです。

※図は，Peter-Pike Sloan, “Deringing Spherical Harmonics”, SIGGRAPH Asia 2017 Technical Briefs, No.11, pp.1-4, November 2017より引用。

ABSTRACT

球面調和関数(SH)は、照明と可視性が最も共通するコンピュータグラフィックスにおける様々な信号を表現するための便利な基底です。入力は厳密には正の値になる傾向がありますが、投影後に再構成された関数は負の値になることがあります。また、投影は、最小二乗によく見られる振動である「リンギング」アーティファクトを示すこともあります。本論文では、ビデオゲームの照度信号に有効な一変量多項式を最小化することで、厳密に正の関数となる窓関数を効率的かつ保守的に解くアルゴリズムを紹介します。

1 INTRODUCTION

球面調和関数(SH)は単位球上の正規直交基底です。これは、インタラクティブなコンピュータグラフィックス[7,8]やゲーム[1]で、照明、可視性、より一般的な光輸送を符号化するために広く使用されています[10]。ビデオゲームのライティングでは、他の基底も使用されていますが[4-6]、その場合でもSHは中間基底として使用されることが多いです[3]。ライティングや可視性のように厳密に正の関数を投影しても、結果的にはマイナスの値や振動になってしまうことがあります。振動は、高いダイナミックレンジを持つ物理ベースのライティングへの移行に伴って悪化します。一般的な解決策は、関数を「窓」にして [2, 8, 10]、エイリアシングとぼやけるのをトレードオフすることです。これまでの研究ではほとんど見落とされていたことですが、この論文では、与えられたシナリオで適用するウィンドウの量をどのように決定するかということに焦点を当てています。多くの場合、それは単に手で微調整されています。
この論文では、ゲームで最も一般的なケースである、二次球面調和関数として符号化された放射照度に焦点を当てています。これは、関数の最小値の保守的な境界を効率的に計算し、非負にするウィンドウパラメータを探索することによって行われます。

2 SPHERICAL HARMONICS

実数球面調和関数は球面座標で表すことができます：

\begin{eqnarray}
y_l^m = \begin{cases} \sqrt{2}K_l^m \cos(m \phi)P_l^m(\cos \theta) & m>0 \\
\sqrt{2}K_l^m \sin(|m|\phi)P_l^{|m|}(\cos \theta)& m<0 \tag{1} \\
K_l^m P_l^m (\cos\theta) & m=0 \end{cases}
\end{eqnarray}

ここで，\(P_l^m\)は関連するルジャンドル多項式で，\(K_l^m\)は正規化定数です.

\begin{eqnarray}
K_l^m = \sqrt{ \frac{(2l +1)(l – |m|)!}{4\pi(l + |m|)!} }
\end{eqnarray}

バンド\(l\)とバンド\(m\)の関数によってインデックス付けされます。ここで\(l\)は非負の整数であり、\(m\)はバンド\(l\)における\([-l, l]\)の整数とします。
次数\(O\)のSHは、\(0\)から\(O-1\)までのすべてのバンドから成り、\(O^2\)基底関数を持つ。関数\(f(s)\)は射影係数\(f_l^m\)を持ち、\(i = l(l+1)+m\)の単一インデックス\(f_i\)を使用します。この形式は記号計算や解析的積分の評価に便利ですが、実行時の評価にはコストがかかります。また、SHは単位球上の多項式としても効率的に評価できます[9]。基底は直交しており、回転下で閉じており、少数のバンドを用いて平滑関数を正確に表現できます。

2.1 Zonal Harmonics

バンドごとに1つの基底関数を持つ、帯域調和関数(ZH)のみへのZ投影で円対称性を持つ任意の関数。SH関数\(f\)とZH関数\(h\)は、以下の式を用いて閉形式で畳み込むことができます：

\begin{eqnarray}
(f \ast h)_l^m = \sqrt{ \frac{4\pi}{2l+1} } f_l^m h_l^0 = \frac{f_l^m h_l^0}{K_l^0} \tag{2}
\end{eqnarray}

ウインドウイング関数を議論する際には、バンドごとのスケーリング係数である係数\(h_l^0 / K_l^0\)を参照します。我々が注目するすべてのカーネルは，1に積分されるDCを持ち，球上の平均値を保持しています。

2.2 Relevant Properties of Spherical Harmonics

「最適な線形方向」[11]は、線形SH係数(\(-f_3, -f_1, f_2\))から計算するのが簡単です。「最適な直線方向」が\(Z\)軸と一致するようにSHを回転させると、非\(Z\)線形基底関数\(f_1^{-1}\)と\(f_1^1\)は消失します。
\(\pm m\)個の基底関数の任意の組は、\(90/m\)の位相シフトを持つ単一の関数の\(Z\)内での回転となります。\(l \lt 1\)と\(m \neq 0\) のとき、この関数もまた、任意の局所的な極大値に対して、同じ局所的な極大値が逆の符号を持つ\(Z\)の周りに回転があるため対称性を持ちます。図2を参照してください。

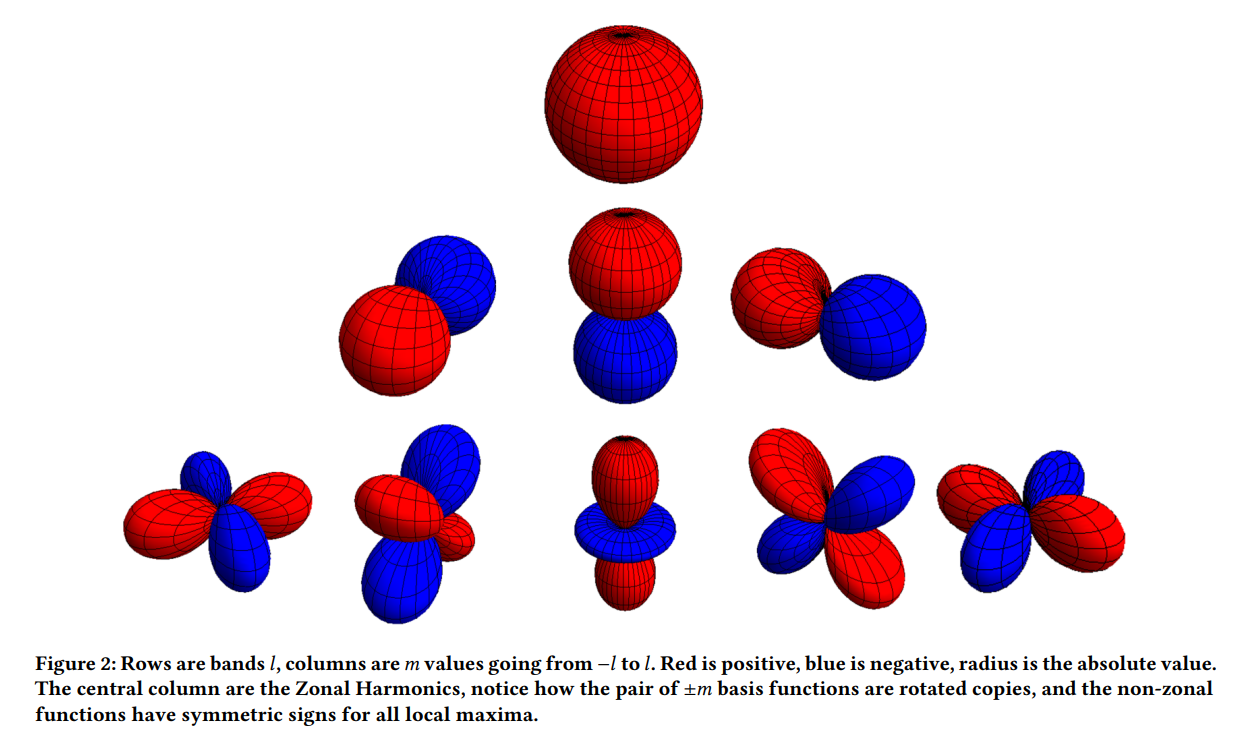
※図は，Peter-Pike Sloan, “Deringing Spherical Harmonics”, SIGGRAPH Asia 2017 Technical Briefs, No.11, pp.1-4, November 2017より引用。

関数\(f\)については，\(m\)個の係数のペアによる再構成は，基底関数のスケーリングされた回転を常にもたらします。つまり，\(f_2^{-2}Y_2^{-2} + f_2^2 Y_2^2 = a{Y_2^2}’\)です。ここで\({Y_2^2}’\)は基底関数の\(Z\)内での回転です。これは三角関数の加法定理から来ていて、位相シフト（回転）は使われていませんが、新しい振幅は\(a = \sqrt{{f_2^{-2}}^2 + {f_2^2}^2}\)となります。これは、固定周波数\(\omega\)の任意の正弦波が常に同じ周波数の正弦と余弦の線形合成として表現できるのと同じです。

2.3 Finding the minimum value of spherical harmonic

球面調和関数の最小値の正確な位置と値は、単位球に限定された\({\mathbb R}^3\)の2次多項式の根を見つける必要があります。これは複数の開始点と非線形ソルバー[8]を使用して行うことができますが、必要以上のものです。SH関数が負の値を持つかどうかを保守的に知りたいだけならば、境界を正確に計算することができます。
まず、SHを\(Z\)軸に沿った「最適な直線方向」の座標系に回転させます。これは一度で済み、反転させる必要はありません。これにより、\(Z\)が線形勾配に整列します。計算は、この座標系でZH基底関数を正確に評価し、残りの基底関数は、保守的な境界を使用して処理される2組の\(|m| \lt 0\)の基底関数のみです。\(|m| \lt 0\)基底関数については、\(|m| = n\)の任意の組は、\(Z\)における同じ関数の単純回転となります。これは、最大正の値を持ついくつかの位相角\(\phi\)があり、対称性のために負のコピーが存在することを意味し、この外形は\(Z\)の関数として最も負の位置を決定するために使用することができます。

2.3.1 Finding the mininum value of zonal harmonic

関数\(f\)の帯域調和関数は多項式です：

\begin{eqnarray}
\frac{f_0}{2 \sqrt{\pi}} + \frac{f_2 \sqrt{3}z}{2\sqrt{\pi}} + \frac{f_6\sqrt{5}(3z^2-1)}{4\sqrt{\pi}} \tag{3}
\end{eqnarray}

これはzの2次多項式であり、最小値は些細なことに見つけることができます。これをAから正則形式\(az^2 + bz + c\)に入れると、係数は\(a = \frac{f_6 \sqrt{5}3z^3}{4\pi}\),\(b = \frac{f_2 \sqrt{3}z}{2\sqrt{\pi}}\),\(c = \frac{f_0}{2\sqrt{\pi}} – \frac{f_6 \sqrt{5}}{4 \sqrt{\pi}}\)となります。この多項式の最小値を\(1 \leq z \leq -1\)とすると、計算は簡単です。\(a \lt 0\)の場合、最小値の位置は\(z_{min} = \frac{-b}{2a}\) にあり、\(1 \lt z_min \lt -1\)の場合は単にその位置で二次関数を評価します。それ以外の場合、最小値は値\(a + b + c\)と値(a – b + c\)を持つ終点のいずれかにあります。

2.3.2 \(|m|=2\)

外側の大部分の\(|m|\)も解析的に計算することができます。基底関数の多項式形式は：

\begin{eqnarray}
Y_2^2 = \frac{\sqrt{15}(x^2 – y^2)}{4 \sqrt{\pi}} \tag{4}
\end{eqnarray}

\(|m|=2\)となる基底関数の和のペアは、振幅\(q_2 = \sqrt{f_4^2 + f_8^2}\)を持ついずれかの基底関数の回転版になります。\(Y_2^2\)基底関数は\(y=0\)のときに最大となり、対称性の関係上、これの負が最小となります。多項式は球上にあり、\(x^2+y^2+z^2=1\)です。最大の等高線は、\(x^2 = (1-z^2)\), \(\frac{\sqrt{15}(1-z^2)}{4\sqrt{\pi}}\)なので\(y=0\)のときは\(z\)の関数として表現でき、最小値は単に負の値になります。これはZHの二次多項式に加算されます。ここでは\(a= a_{zh} + \frac{q_2 \sqrt{15}}{4\sqrt{\pi}}\)と\(c = c_{zh} – \frac{q_2\sqrt{15}}{4\sqrt{\pi}}\)であり、最小値は基底関数の\(|m| = 1\)ペア以外のすべてを含みます。

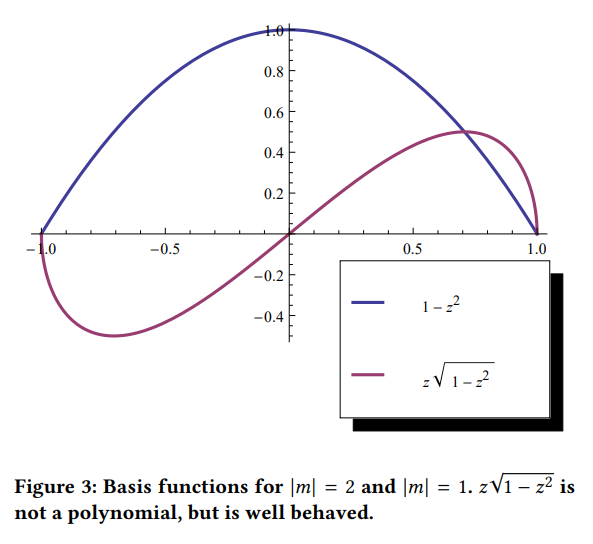
※図は，Peter-Pike Sloan, “Deringing Spherical Harmonics”, SIGGRAPH Asia 2017 Technical Briefs, No.11, pp.1-4, November 2017より引用。

2.3.3 \(|m| = 1\).

この時点までは、\(z\)と最小値は正確ですが、一方で位相は不明です。ですが，計算することができました。アルゴリズムが保守的な境界である理由は、\(|m|=2\)に関して最悪の位相にあると仮定して、\(|m|=1\)をどのように扱うかということです。

\begin{eqnarray}
Y_2^1 = – \frac{\sqrt{15}xz}{2\sqrt{\pi}} \tag{5}
\end{eqnarray}

\(xz\)基底関数は\(y=0\)のときに最大になりますが、その場合は\(x = \sqrt{1-z^2}\)なので、\(z\)の関数としては\(z\sqrt{1-z^2}\)になります。この基底関数の係数は\(\frac{ \sqrt{15} \sqrt{f_5^2 + f_7^2} }{2\sqrt{\pi}}\)で、この関数は滑らかで、\(-1/\sqrt{2}\)で-0.5の最小値を持ち、最小値は基底関数の最小値を最初に推測して、ニュートン法で求めることができます。
\(|m|=1\)基底関数の下界が-0.5であることを考えると、ニュートン法をスキップすることができる早期のアウトが存在します。\(|m|=1\)基底関数は上半球では正であるが, 実際には負の値は「最適直線方向」以下になる傾向があるので問題にはなりません。最適化は上半球と下半球の間で分割し、これが問題になる場合は強制的に両側の関数を負にするか、または係数の符号を負にして2回実行することができます。

2.4 Deringing

SHを用いたウィンドウウィングの詳細な議論は[8]で紹介されています。高いレベルでは、あるカットオフ周波数でバンドごとの係数が滑らかに減少してゼロになる必要があります。この論文では、ウィンドウ関数を明示的に評価するのではなく、ウィンドウ係数の表を使用しています。我々は、線形補間を用いた二値探索を行い、結果として得られる関数が負にならないような最小の窓関数を見つけます。テーブルの一方の端はデルタ関数なので窓関数はなく、もう一方の端には、クランプされた余弦との畳み込みの後、デルタ関数の投影を厳密に正にする窓関数があります。この関数を負にしないようにするために、線形帯域の余分な減衰を含めて \(sinc^4\) で窓化します。
ここで\(l\)はSHのバンドインデックス、\(w\)はウィンドウ関数がゼロになるバンドで、使用されるカットオフバンドよりも大きいことが望ましい。使用される明示的な値は以下の通りです：

※表は，Peter-Pike Sloan, “Deringing Spherical Harmonics”, SIGGRAPH Asia 2017 Technical Briefs, No.11, pp.1-4, November 2017より引用。

最も積極的な窓は、図4に見られるように、デルタ関数の放射照度を厳密に正の投影を持つようにします。正の信号は常にデルタ関数の線形の組み合わせとして解釈することができますが、もしそれらが厳密に正になるようにウィンドウされているならば、合計は正になります。

\begin{eqnarray}
\left( \frac{\sin \frac{\pi l}{w} }{ \frac{\pi l}{w} } \right)^4 \tag{6}
\end{eqnarray}

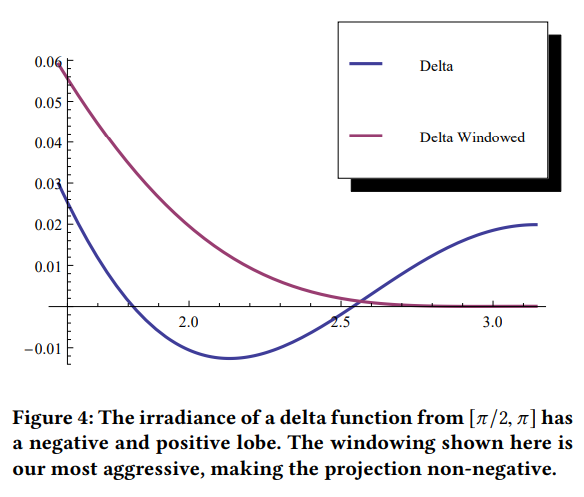
※図は，Peter-Pike Sloan, “Deringing Spherical Harmonics”, SIGGRAPH Asia 2017 Technical Briefs, No.11, pp.1-4, November 2017より引用。

3 DISCUSSION

ウィンドウイング値は RGB 係数ごとに別々に計算され、最小値が選択されて3つの色チャンネルすべてに適用されます。カラーチャンネルに異なるフィルタをかけると、色がずれる可能性があります。我々は，放射輝度関数を格納する傾向がありますが，クランプされたコサインカーネルで畳み込みを行った後に，それらが非負になるように，ウィンドウウィング値をそれらに適用します。
パンクチュアルライトは小さな正のリングを持つことができ、SHに追加する前にハンドチューニングされたコンボリューションが直接ライトに追加され、線形/二次関数のバンドあたりのスケーリング係数は0.92と0.73であり、間接光とスカイライトは標準アルゴリズムのみを実行します。このようにソースを分割し、それらを別々に一貫してウィンドウ化することは、実際には有用です。

※図は，Peter-Pike Sloan, “Deringing Spherical Harmonics”, SIGGRAPH Asia 2017 Technical Briefs, No.11, pp.1-4, November 2017より引用。

我々は、球面調和関数をリンギングを取り除くためにいくつかのアルゴリズムを経てきました。線形と二次エネルギーの比を使用して、同様の二値探索を行うことは、帯域調和関数の外側に多くのエネルギーを押し出す線形光源を追加するまではうまく機能しました。また、実行時に可視関数を用いてより多くの乗算を行うようになりましたが、照明に負の値があると、生の放射照度を見るだけの場合よりも深刻な問題を引き起こす可能性があります。

4 CONCOLUSIONS AND FUTURE WORK

球面調和関数のリンギングを取り除くのは難しいかもしれませんが、ここで紹介した解決策を思いつくまでに、いくつかの盲路を通ってきました。このアルゴリズムは高速で実装が簡単であり、複数のゲームで実際にロバストであることが証明されています。
これらの考え方は高次の球面調和関数にも拡張することができ、\(0 \gt |m| \gt 1\)を持つ関数は常に保守的な境界となります。\(|m|=1\)基底関数\(|m|=2\)基底関数の間の位相差を推論して、よりタイトな境界を生成することができます。すでパンクチュアルソースに対していくつかの余分なウィンドウイングを行っているので、これがどの程度有用なのかは不明です。
本研究は球面関数のみを対象としていますが、これらの考え方を拡張して半球関数をより良く扱うことは、今後の研究のための興味深い道筋となります。最後に，個別の成分（直接成分，間接成分，場合によっては強度など）をより注意深くウィンドウ化することで，方向性をよりよく考慮した非線形フィルタを実現することができます。直射光のための特別なウィンドウ処理は、これの大雑把なバージョンです。

5 ACKNOWLEDGMENTS

Michał iwanicki、Josiah Manson、Michał Drobot、Derek Nowrouzezahraは、この文書の以前のバージョンについてフィードバックをくれました。Shan Lingは、\(|m|=1\)基底関数の最小値に誤りがあることを発見してくれました。