こんにちわ，Pocolです。
今日はEurographics Symposium on Rendering 2020のSébastien Hillaireによる”A Scalable and Production Ready Sky and Atmosphere Rendering Technique”を読んでみようと思います。
論文はhttps://sebh.github.io/publications/からダウンロードできます。
いつも通り誤字・誤訳があると思いますので，ご指摘いただける場合は正しい翻訳例と共に指摘して頂けると幸いです。

Abstract

地上から宇宙に向かって惑星の大気をレンダリングするための物理的な手法を提案します。我々の方法は計算コストが安く、以前に成功した方法と比較して、高次元ルックアップテーブル（LUT）を必要としないため、高次元ルックアップテーブルに関連した視覚的なアーティファクトに悩まされることはありません。また、大気中の光の多重散乱をリアルタイムで評価するための新しい近似法を提案します。我々は、自然な大気効果をレンダリングすることが何を意味するのかを新たに検討し、空とその空の空気遠近法をレンダリングするためのシンプルなルックアップテーブルとパラメータ化のセットを提案しています。重度のLUT更新を必要とせず、アーティスティックなビジョンや天候の変化に合わせて、大気の構成を動的に変化させることができます。この完全な技術は、ゲーム、シミュレータ、建築物のプリビジュアライゼーションなどのリアルタイムアプリケーションで使用することができます。また、この技術は、電力効率の良いモバイルプラットフォームからハイエンドGPUを搭載したPCまで拡張可能で、パストレースの高速化にも役立ちます。

1. Introduction

信憑性のある世界を視覚的にシミュレーションするためには、自然現象のレンダリングが重要です。大気のシミュレーションとレンダリングは、1日の時間変化を持つ大規模なオープンワールドを必要とするアプリケーションや、宇宙から惑星を見るために重要となります。このようなアプリケーションには、ゲーム、建築物のビジュアライゼーション、フライトシミュレータやスペースシミュレータなどがあります。しかし、現在の手法には限界があります：それらは、地上からの眺めることに限定され、単一の大気タイプしか表現できず、大気特性が変更されたときにルックアップテーブル（LUT）の更新に計算コストがかかるか、視覚的なアーティファクトを示すことさえあります。
　大気の関与媒質の物理的な表現に基づいて、惑星の空と空気遠近法をリアルタイムでレンダリングする方法を提示します。本論文における我々の貢献は以下の通りです：

• 我々は、重要な視覚的特徴を維持しつつ、ライティング積分の高価な部分を低解像度で評価するために、LUTを利用した空と空気遠近法レンダリング技術を提案します。
• 本研究では、大気中の光多重散乱の寄与を評価する新しい方法を提案します。この方法は無限の散乱次数を近似することができ、パストレーシングの高速化にも利用できます。
• この技術は、ローエンドのApple iPhone 6sからコンソール、ハイエンドのゲームPCまで、幅広いデバイスで効率的にレンダリングしながら、大気特性の動的な更新に加えて、動的な時間変化をサポートしています。

このメソッドはEpic GamesのUnreal Engineで使用されています。本稿では、放射量単位(放射輝度/放射照度)ではなく、測光量単位(輝度/照度)を使用します。これは、最近のゲームエンジンではこれらの用語が普及しているためです[LdR14]。

　第2節で過去の研究の復習をした後、第3節では関与媒質レンダリング（大気の場合を中心に）について簡単に説明します。第4節では本論文で使用した大気マテリアルモデルを紹介し、第5節では我々の大気レンダリング技術を詳述します。第6節では、パストレースされたグラウンドトゥルースとの結果の比較，また以前のモデルとの結果の比較について議論します。最後に、第7節でパフォーマンスを報告し、結論を述べます。

2. Previous work

空のレンダリング技術の第一波は、視点から大気へのレイマーチングに焦点を当てていました。これは、西田ら[NSTN93]が地上・宇宙から大気をレンダリングする手法として最初に提案したものです。O’ Neil [ONe07]は、性能向上のために、頂点ごとの内散乱輝度を積分し、ピクセルごとに位相関数を適用して最終的な空の色をレンダリングすることを提案しています。Wenzel [Wn07]も同様のアイデアを提案していますが、コストを償却するために数フレームにわたって更新されるテクスチャに内散乱輝度を保存しています。これらのモデルの主な欠点は、光の多重散乱が空の外観に与える影響を無視していることです。

レイマーチのコストを削減し、多重散乱を含めるために、実測値[PSS99]またはスペクトル情報を用いたパストレース[HW12]を用いて生成された参照値に適合した解析モデルが提案されています。これらのモデルは非常に高速に評価でき、簡単なパラメータ化の恩恵を受けることができます：例えば、単一の濁度値は、空気中の煙霧質の量を表すために使用され、その結果、より密な外観の大気になります。しかし、これらは地上からの眺めと、パラメータが適合している単一の大気タイプに限定されます。例えば、モデルが地球の空にフィットしている場合、火星の空をレンダリングすることはできません。

地上から宇宙までを対象に、複数の散乱を用いて大気効果をレンダリングするためのより高度なモデルが提案されています。西田[NDN96]は、関与媒質をボクセルに細分化し、それらの間のエネルギー交換をシミュレーションすることを提案しました。ボクセル表現を削除したより手頃なモデルが提案されています。これらは、評価にコストがかかる積分の結果を、GPU上で実行時に簡単にクエリーできるルックアップテーブルに格納します。これらのLUTは、（ビュー、太陽、ワールド情報に応じて）実行時にピクセルごとにサンプリングされ、透過率と内散乱輝度を計算することができます。BrunetonとNeyret [BN08]は4D LUTを提案しましたが、Elek [Ele09]は1次元を捨てて、太陽が地平線のすぐ下にあるときに見える大気の影を効率的に無視しています。これらのモデルでは、ビューアからメッシュ面への散乱がLUTからサンプリングされた2つの値の減算として評価されるため、解像度とパラメータ化の精度の問題により、視覚的なアーティファクトが地平線に現れる可能性があります。Yusov [Yus13]は、より良いパラメータ化によってこの状況を改善し、地球のような大気に対してもうまく機能するようになりました。しかし、大気がより密な場合には、アーティファクトがまだ見える可能性があります。これらのLUTモデルのそれぞれについて，内散乱LUTを反復的に評価することで多重散乱を達成しています：新しいものを評価するために，前の散乱次数LUTから散乱された輝度をサンプリングします。すべてが一緒に加算されると、これは反復回数までの複数の散乱次数を持つ最終的な内散乱LUTを形成します。しかし、このようなLUTは、天候の変化やアートの方向性に合わせて、ゲームの大気特性を更新する必要がある場合には、更新が煩雑になります。タイムスライス更新を行うことは可能ですが、これは太陽の動きと空の色の間に視覚的な遅延をもたらすことになります[Hil16]。LUT ベースのモデルはオンラインでソースコードが入手可能で [Bru17b; Yus13]、いくつかのゲームで成功裏に使用されています [Hil16; dCK17; Bau19]。さらに進んで、Bruneton [Bru17a]はこれらのモデルを幅広く議論し、それぞれの利点と制限を比較しています。

大気をレンダリングする際の課題の一つは、丘や山によるボリューム感のあるシャドウイングを表現することです。エピポーラライン[Yus13]、シャドウボリューム[Bru17b]、またはシャドウマップ[Hoo16]からメッシュを押し出すシャドウボリュームの変形を利用することができます。これらの技術は高速ですが、不透明なメッシュからシャープな影を表現することしかできません。これらの技術は、雲の関与媒質や太陽ディスク領域のライトシャドウの半影から生じるソフトシャドウのレンダリングに失敗します。これは、このようなソフトなディテールをキャプチャする上で、レイマーチがまだ明確な優位性を持っている分野です。

3. Participating media rendering

関与媒質のレンダリングは、レイマーチやパストレーシングを使用して行うことができます。どちらの場合も、放射伝達方程式[FWKH17]で記述されているように、関与媒質を表すマテリアルパラメータ化を使用することに関係しています。このフレームワークでは、与えられた位置で、ある方向に進行するライトビームを考えると、波長あたりの吸収係数\(\sigma_{\mathbf a}\)と散乱係数\(\sigma_{\mathbf s}\)(\({\rm m}^{-1}\))は、それぞれ方向に沿って吸収された、または散乱された輝度の割合を表しています。消衰係数\(\sigma_{\mathbf t} = \sigma_{\mathbf a} + \sigma_{\mathbf t}\)は、吸収と外散乱により失われるエネルギーの総量を表します。さらに、散乱事象が発生した場合には、単位\({\rm sr}^{-1}\)の位相関数\(p\)で表される分布に基づいて散乱方向を決定する必要があります。
　強いリアルタイム制約の下で、我々のアプローチは、図2に示すように、最初に単一散乱を評価するためにレイ・マーチングを利用します。これは、\(N_{\rm light}\)ディレクショナルライトのセット、例えば太陽と月を想定しています。

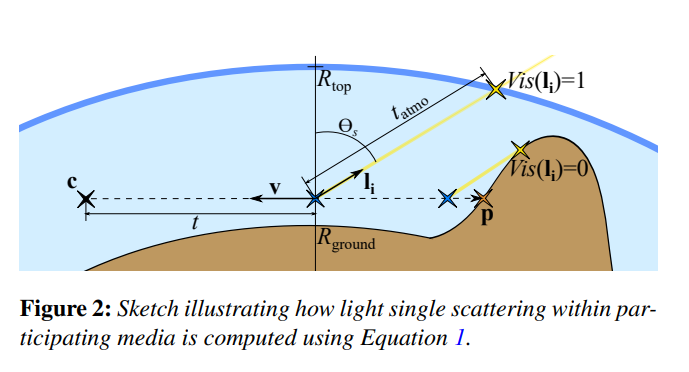
※図は，Sébastien Hillaire, “A Scalable and Production Ready Sky and Atmosphere Rendering Technique”, Eurographics Symposium on Rendering 2020, Vol.39, Number 4, 2020より引用。

また、アルベドの\(\rho\)に基づいた純粋な拡散応答を持つ仮想惑星も考慮に入れています。次の式を用いて、観測者に向かって散乱された輝度\(L\)を、媒質透過率\(T\)、シャドウファクター\(S\)（\(Vis\)は惑星からのシャドウイング、\(T\)は大気からのシャドウイング）、およびパスセグメントに沿って散乱された\(L_{\rm scat}\)の評価の関数として積分することを含みます。

\begin{eqnarray}
L ({\mathbf c}, {\mathbf p}) &=& T({\mathbf c}, {\mathbf p}) L_o({\mathbf p}, {\mathbf v}) + \int_{t=0}^{ \| {\mathbf p} – {\mathbf c} \| } L_{\rm scat}( {\mathbf c}, {\mathbf c} – t {\mathbf v}, {\mathbf v}) dt, \tag{1} \\
T({\mathbf x}_a, {\mathbf x}_b) &=& e^{-\int_{{\mathbf x} = {\mathbf x}_a}^{{\mathbf x}_b} \sigma_{\mathbf t}({\mathbf x}) \| {\mathbf dx} \| }, \tag{2} \\
L_{\rm scat}({\mathbf c}, {\mathbf x}, {\mathbf v}) &=& \sigma_{\mathbf s} ({\mathbf x}) \sum_{i=1}^{N_{\rm light}} T({\mathbf c}, {\mathbf x}) S({\mathbf x}, {\mathbf l}_{\mathbf i}) p({\mathbf v}, {\mathbf l}_{\mathbf i}) {\mathbf E}_i , \tag{3} \\
S({\mathbf x}, {\mathbf l}_{\mathbf i}) &=& Vis({\mathbf l}_{\mathbf i}) T({\mathbf x}, {\mathbf x} + t_{\rm atmo} {\mathbf l}_{\mathbf i}), \tag{4}
\end{eqnarray}

ここで、\({\mathbf c}\)はビューカメラの位置、\({\mathbf v}\)は現在位置に対するビューに向かう方向、\({\mathbf p}\) は交点の表面点、\(t_{\rm atmo}\) は大気の上端境界との光線の交点距離、\(L_o\) は \({\mathbf p}\)での輝度、例えば仮想惑星の地上の照明などです。\({\mathbf l}_{\mathbf i}\)、\(E_i\)は、\(i\)番目の光の方向と照度（指向性光源を考慮した場合）です。

　この論文では、我々の新しいレイマーチングアプローチとパストレーサーの結果を比較します。我々のパストレーサはGPU上に実装されており，インタラクティブなフレームレートでリアルタイムに洗練された結果を可視化できるようになっています。本論文では，関与媒質内でのデルタトラッキングと重要度サンプリングを用いたモンテカルロ積分を実装しています[FWKH17]。また、レシオトラッキング [NSJ]を活用することで、透過率を推定する際の収束速度を向上させています。これを我々のグラウンドトゥルースと考えています。

4. Atmospheric model

我々が使用している大気マテリアルモデルは過去の論文[BN08; Bru17a]に記載されています。我々は地球型惑星のシミュレーションに焦点を当てています。惑星の地上と大気の頂上境界は、地上の高度を表しています。地球の場合、地上半径を\(R_{\rm ground} = 6360 {\rm km}\)、大気トップ半径を\(R_{\rm top} = 6460 {\rm km}\)とすることで、\(100 {\rm km}\)の関与媒質層を表すことができます。地面は一様なアルベド\(\rho = 0.3\)[NAS]の純粋な拡散性物質と考えます。大気の関与媒質をレンダリングする際には、[Ele09]のような広いスペクトル表現は考慮していません。その代わりに、典型的なRGBベースのレンダリングに焦点を当てます。

大気は、地球や他の惑星の外観を達成するために考慮すべき重要ないくつかのコンポーネントで構成されています:

• レイリー理論は、空気分子と相互作用したときの光の挙動を表しています。光は決して吸収されず、周囲で散乱するだけであると仮定しています[BN08]。散乱事象後の光の方向分布を記述する位相関数は\(p_{\rm r}(\theta) = \frac{3(1+\cos(\theta)^2)}{16 \pi}\)です。ここで、\(\theta\)は入射散乱方向と出射散乱方向の間の角度とします。
• ミー理論は、塵や公害などのエアロゾルと相互作用したときの光の振る舞いを表しています。光は散乱されたり、吸収されたりします。位相関数はCornette-Shanks位相関数\(p_{\rm m}(\theta, g) = \frac{3}{8 \pi} \frac{(1-g^2)(1+\cos(\theta)^2)}{(2+g^2)(1+g^2-2g\cos(\theta))^{3/2}}\)を用いて近似され、ここで\(g\)は前方散乱と後方散乱の相対的な強さを決定する\(]-1, 1[\)の非対称性パラメータです。デフォルトでは、\(g=0.8\)です。より単純なHenyey-Greenstein位相関数を使用することも適切であることに注意してください。

簡単のために、本稿の残りの式では、これらの位相関数のパラメータを省略しています。また, 等方性位相関数を\(p_{\rm u} = \frac{1}{4\pi}\)として表現します。

　表1は、各成分[Bru17a]の散乱係数と吸収係数を示している。レイリー理論とミー理論に従う関与媒質は、それぞれ\(d^r(h) = e^{\frac{h}{1.2 {\rm km}}}\)と\(d^m(h) = e^{\frac{h}{8 {\rm km}}}\)の高度密度分布を持ちます。オゾンは、太陽が地平線にあるときに空色を実現する鍵を握っているため、地球の大気を表現するために重要な成分であることが確認されています[Kut13]。オゾンは散乱には寄与しません；光を吸収するだけです。Bruneton [Bru17a; Bru17b]に従い, \(d^o(h) = \max(0, 1- \frac{|h-25|}{15})\)の高度\(25{\rm km}\)を中心とした幅\(30 {\rm km}\)のテント関数として分布を表現します。

※表は，Sébastien Hillaire, “A Scalable and Production Ready Sky and Atmosphere Rendering Technique”, Eurographics Symposium on Rendering 2020, Vol.39, Number 4, 2020より引用。

5. Our rendering method

5.1 Dicussion: observing the sky

今、空と空気遠近法のビジュアルコンポーネントについて説明します。これは、LUTを構築する際に行った選択とレイマーチの使用を正当化するのに役立ちます。

　図3を見ると、地球のような空は、特に日中の視覚的周波数が低いように見えます。

• レイリー散乱は滑らかです。
• ミー散乱位相関数による太陽の周りのハロも、自然界で遭遇する現実的な位相\(g\)値に対してはかなり滑らかです。
• 多重散乱は、リアルな画像をレンダリングするための重要な要素です。図3（下段）に示すように、視覚的な周波数も低いです。
• 大気がすぐにそこで密度を高め、光がより多く加わるので、より高い周波数が地平線に向かって見えます。我々はそれを考慮しなければなりません。

※図は，Sébastien Hillaire, “A Scalable and Production Ready Sky and Atmosphere Rendering Technique”, Eurographics Symposium on Rendering 2020, Vol.39, Number 4, 2020より引用。

大気圏内の高周波の主な発生源は、惑星の影（日没時）と山からの影が式3の単一散乱事象を遮蔽しているためです。我々が提案する解は、2つのモードで大気をレンダリングすることができます：ボリューメトリックシャドウを無効にする、つまり高速レンダリングのためにSky-View LUTを利用する(5.4節参照)モード、あるいは有効にする。つまり，より正確ですが，より高価なレンダリングをする(7節参照)モードです。

5.2. Transmittance LUT

\(L_{\rm scat}\)を積分するためにレイマーチを実行する場合、シャドウイング項\(T\)(自分自身に投影される大気媒体を表す) を評価する必要があります。しかし、単一の散乱サンプルごとに太陽に向かって２回目のレイマーチを実行するには、コストがかかります。これを加速するために、BrunetonとNeyret [BN08]の4節に記載されているのと同じ表現を使用して、関数\(T\)をLUTとして格納します。

5.3. Sky-View LUT

大気を構成する関与媒質の全体的な低周波(5.1節参照)を考えると、少ないサンプル数でレイマーチするのに十分なはずです。しかし、各ピクセルに対してそうすることは、特に4Kや8Kのような高解像度では、高価になる可能性があります。空の全体的な視覚周波数が低いことを考えると、低解像度で空をレンダリングし、その後に高解像度にアップサンプルすることができるはずです。

　与えられた視点から、遠方の空を緯度経度テクスチャにレンダリングし、水平線が常にその中の水平線となるように惑星の地面上のカメラの局所的な上向きベクトルを基準にして方向付けを行います。この例については、図4を参照してください。上の部分が空、下の部分が仮想惑星の地面を表し、中央に地平線があります。5.1 節では、より高周波数の視覚的特徴が地平線に向かって見えることを述べました。これらの特徴をより良く表現するために、テクスチャ座標\(v \in [0, 1]\)を計算する際に緯度\(l\)に非線形変換を適用し、地平線付近でより多くのテクセルを圧縮しています。単純な二次曲線を使用しています:\(v = 0.5 + 0.5 \ast {\rm sign}(l) \ast \sqrt{\frac{|l|}{\pi /2}}\)で，\(l \in [-\pi/2, \pi/2]\)とします。

※図は，Sébastien Hillaire, “A Scalable and Production Ready Sky and Atmosphere Rendering Technique”, Eurographics Symposium on Rendering 2020, Vol.39, Number 4, 2020より引用。

これは、地平線に近いより多くのピクセルを効果的に圧縮し、そこに存在する詳細の量を向上させます。また、図5に示すように、大気が低解像度でレンダリングされているという事実を隠すのにも役立ちます。太陽のディスクは、解像度が低く、リニアマッピングではないため、テクスチャの一部としてレンダリングされていません。これは、Sky-View LUTを適用した後に合成されています。

※図は，Sébastien Hillaire, “A Scalable and Production Ready Sky and Atmosphere Rendering Technique”, Eurographics Symposium on Rendering 2020, Vol.39, Number 4, 2020より引用。

5.4. Aerial Perspetive LUT

シーンをレンダリングする際には、不透明な構造物（地形、山、建物など）と半透明な要素（ガラス、火、雲などの他の関与媒質）に対する空中透視効果を一貫性を持たせるためにレンダリングする必要があります。そこで、Hillaire [Hil16]と同様に、我々は、ビューカメラの錐台にフィットするボリュームテクスチャで、カメラへの散乱と透過率を評価します（図6を参照）。内散乱光はRGBチャンネルに蓄積され、透過率はAチャンネルに蓄積され、波長依存性のあるRGB透過率の平均値として蓄積されます。

※図は，Sébastien Hillaire, “A Scalable and Production Ready Sky and Atmosphere Rendering Technique”, Eurographics Symposium on Rendering 2020, Vol.39, Number 4, 2020より引用。

我々の場合において使用されているデフォルトの解像度は、画面の上に\(32 \times 32\)、深度32キロの範囲で32の奥行のスライスであり、ほとんどのアプリケーションやゲームには十分です。これはEpic GamesのFortniteの場合で、地球のような様式化された大気のセットアップで\(3 {\rm km}^2\)のワールドマップサイズを持っています。惑星の大気が遠くの物体が見えにくくなるポイントまで本当に密集している場合は、短距離での精度を高めるために、深度範囲をビューポイントに近づけて戻すことができます。

空気遠近法ボリュームテクスチャは、Sky-View LUTが画面上に適用されるのと同時に、ライティング評価後の後処理として不透明なオブジェクトに適用されます。フォワードレンダリングパイプラインの透明な要素に対しては、頂点ごとのレベルで空気遠近法を適用しています。これは、透明な要素は通常、大気中の視覚的変化に比べて画面空間が小さいためです。

5.5 Multiple scattering LUT

2節で述べたように、これまでの大気レンダリング技術[BN08; Ele09; Yus13]は、散乱次数ごとに1回の反復で、3Dまたは4D LUTを更新するための対話的な方法を利用しています。これは、現実的な空のビジュアルに到達するために5の多重散乱次数だけが必要とされる地球のような大気をレンダリングする場合には、許容可能な解決策です。しかし、厚い大気をレンダリングする場合、すなわち、より高い散乱次数が大気の外観に重要であり、LUTを何度も反復する必要がある場合には、すぐに非現実的になります。実際には、複雑な\({\mathcal O}(n)\) (ここで\(n\)は散乱次数)のこの操作は計算量が多すぎます。特に、アーティストがアートの方向性や天候の変化に合わせて、一日のうちの様々な時間帯に大気の特性を常に更新している場合には、このような傾向が見られます。計算はタイムスライス[Hil16]することができますが、これは更新の遅延をもたらし、リアルタイムでキャプチャされたグローバルイルミネーションや反射キューブマップのような他のシステムの反応性に影響を与える可能性があります。

　我々の目標は、散乱次数に依存しない、より安価で瞬時の\({\mathcal O}(1)\)メソッドを提案することであり、光の多重散乱の寄与を遅延なく各フレームごとに評価できるようにすることです。広範囲の雰囲気設定のための正確性と信頼性を維持することも必要条件であり、また、様々なデバイス（モバイルからハイエンドPCまで）で雰囲気をレンダリングできることも必要条件です。大事なことを言い忘れましたが、我々のアプローチは、物理ベースの関与媒質のパラメータ化を利用し、エネルギーを保存したいと考えています。

5.5.1. Building an intuition about our approximation

全体的に規模が大きく、平均自由行程が長く、大気中の関与媒質が滑らかに分布していることを考えると、空間内のある点に到達する照度\(E\)は、その周囲の大きな領域内のすべての点で同じであると考えることができます。このようにして、サンプル点の周囲の高次光散乱事象に起因する輝度の積分は、それらの点間の透過率を考慮しながら、同じ照度\(\rm E\)を受ける隣接点からの周囲の球体上の散乱光を積分することによって近似することができます。局所的なマテリアルデータを使用して多重散乱を評価するための入力として大域的な内散乱照度\(E\)を使用するこのアイデアは、毛髪における光の多重散乱を近似する二重散乱法[ZYWK08]に触発されています。

　媒質中で光が散乱すると、散乱方向の分布は急速に等方的になります [JMLH01; Yan97]。性能向上のためには、多重散乱LUTは低次元であることが望ましいです。この目的のために、我々は、2以上の散乱次数の光が等方的な位相関数に従って、すなわち、任意の方向性を持たないようにバウンスすることを想定しています。そのため、多重散乱近似の一部として、ミーとレイリー位相関数の設定を無視します。

レイリー位相関数がすでに滑らかであることを考慮すると、これは許容範囲内であると考えられます。ミー散乱の場合の近似についてより良い直観を得るために、Bouthors [Bou08]による散乱次数に対するBSDFの形状の解析を参照してください。

　さらに、2次散乱輝度とそれ以上の散乱次数との間に相関が存在することが示されています[HG13]。そこで本研究では、大気中の多重散乱の寄与を、各サンプルポイントに到達する散乱輝度の2次の関数として評価することを提案します。

　これらの過去の結果を基に我々の手法を構築します。これについては5.5.3節で詳しく説明します。ここではその概要と、多重散乱を評価する際の近似値を示します。

• 次数が2以上の散乱事象は、等方性位相関数\(p_{\rm u}\)を用いて実行されます。
• 現在シェーディングしている位置の近傍内のすべてのポイントは、同じ量の2次散乱光を受け取ります。
• 現在シェードする位置周辺の関与媒質から、2次散乱次数寄与量\(\mathbf{L_{\mathbf{2^{nd} order}}}\)と伝達関数\({\mathbf f_{\mathbf{ms}}}\)を計算します（透過率と高度に沿った媒体の変化を考慮しています）。
• 最後に、これらの因子から多重散乱寄与 \({\mathbf \Psi_{\mathbf{ms}}}\)を計算し、近傍点から現在のシェーディング位置に戻る伝達関数に対して等方的に2次光寄与の無限散乱をシミュレートします。
• 可視性\(Vis\)は多重散乱を評価する際に無視されます。これは、光が任意の山の周りで散乱するという事実に依存しています。例えば、平均自由行程が大きい自然大気の場合、可視性の影響は低いです。

5.5.2. LUT parameterization

空間内の任意の点について、LUTからの輝度に対する等方性多重散乱の寄与を保存し、クエリすることができるようにしたいと考えています。仮想惑星が完全な球体であること、多重散乱の寄与が等方的であること、大気中の媒体の分布が高度によってのみ変化することを考慮して、このLUTを小さな2Dテクスチャとして表現しています。\([0, 1]^2\)における\(u\), \(v\), のパラメータ化は、以下のようになります：

• \(u = 0.5 + 0.5 \cos({\rm \theta}_s)\)，ここで\({\rm \theta}_s\)は太陽の天頂角で，\({\rm \omega}_s\)はその方向を表します。
• \(v = \max(0, \min ( \frac{h – R_{\rm ground}}{R_{\rm top} – R_{\rm ground}}, 1))\)，ただし，サンプル位置\({\mathbf x}_{\mathbf s}\)は高度\(h\)です。

このようなLUTとそのパラメータ化の例を図7に示します。

※図は，Sébastien Hillaire, “A Scalable and Production Ready Sky and Atmosphere Rendering Technique”, Eurographics Symposium on Rendering 2020, Vol.39, Number 4, 2020より引用。

5.5.3. High scattering order LUT evaluation

位置\({\mathbf x}_{\mathbf s}\)と高度\(h\)のサンプル点を考慮して、図8（左）に示すように、点\({\mathbf x}_{\mathbf s}\)に向かって2次の散乱輝度\(\mathbf{L_{2^{nd} order}}\)を次式で積分します。

\begin{eqnarray}
{\mathbf L_{\mathbf{2^{nd} order}}} &=& \int_{\Omega_{4\pi}} L'({\mathbf x}_{\mathbf s}, – {\omega}) p_{\rm u} d\omega, \tag{5} \\
L'({\mathbf x}, {\mathbf v}) &=& T({\mathbf x}, {\mathbf p}) L_o ({\mathbf p}, {\mathbf v}) + \int_{t=0}^{\| {\mathbf p} – {\mathbf x} \|} \sigma_{\mathbf s}({\mathbf x}) T({\mathbf x}, {\mathbf x} – t {\mathbf v}) S({\mathbf x}, \omega_{\mathbf s}) p_{\rm u} E_{\mathcal I} dt \tag{6}
\end{eqnarray}

式6において、\(L’\)項は、構築中の現在のLUTエントリに一致する位置\({\mathbf x_s}\)に対して、照度\(E_{\mathcal I}\)と方向\(\omega_{\mathbf s}\)を持つ単一方向の光からの輝度寄与を評価します。また、\(L_o\)(アルベドに応じた拡散応答) を介して地上から反射した輝度寄与も含まれています。\({\mathbf L_{\mathbf{2^{nd} order}}}\)は、点\({\mathbf x}_{\mathbf s}\)に向かう2次の散乱光を輝度として与える必要があります。しかし、これは\(E_{\mathcal I}\)を使って評価されます：それは、ライトの照度\({\mathbf E}_{\mathbf i}\)のためのプレースホルダです。この場合、\({\mathbf L_{\mathbf{2^{nd} order}}}\)が輝度値を返さず、代わりに単位\({\rm sr^{-1}}\) の伝達関数として動作し、後に実際の指向性光の照度と乗算したときにのみ輝度を返すようにするために、単位のない係数\(E_{\mathcal I} = 1\)を指定しています。式5では、\(L_o\)も\(E_{\mathcal I}\)を使って評価していますが、簡単にするためにこれは省いています。

　次に、大気媒質の周りのすべてと位置\({\mathbf x}_{\mathbf s}\)における現在シェードされるサンプルに向かって発生するエネルギーの伝達を表す単位のない係数\({\mathbf f}_{\mathbf{ms}}\)を積分します。

\begin{eqnarray}
{\mathbf f}_{\mathbf{ms}} &=& \int_{\Omega_{4\pi}} L_f ({\mathbf x}_{\mathbf s}, -\omega) p_{\rm u} d\omega \tag{7} \\
L_f({\mathbf x}, {\mathbf v}) &=& \int_{t=0}^{\| {\mathbf p} – {\mathbf x} \|} {\mathbf \sigma}_{\mathbf s}({\mathbf x}) T({\mathbf x}, {\mathbf x} – t {\mathbf v}) {\rm l}dt \tag{8}
\end{eqnarray}

これを図8(右)に示します。球面上の方向積分は\({\mathbf f}_{\mathbf {ms}}\)として計算され、\(L_f\)は式8を用いて各レイに沿って積分されます。この式のシャドウイング項\(S\)と位相関数のサンプリングは、\({\mathbf L}_{\mathbf{2^{nd} order}}\)を評価する際に既に考慮されているため、スキップすることが重要となります。したがって、\({\mathbf f}_{\mathbf{ms}}\)は、\([0, 1]\)の範囲内で\({\mathbf x}_{\mathbf s}\)の周りと\({\mathbf x}_{\mathbf s}\)に向かって積分されたエネルギーの単位がない正規化された伝達係数です。この範囲を尊重するために、Hillaire [Hil15]によって提案された式8の積分の解析解を使用することが推奨されます。

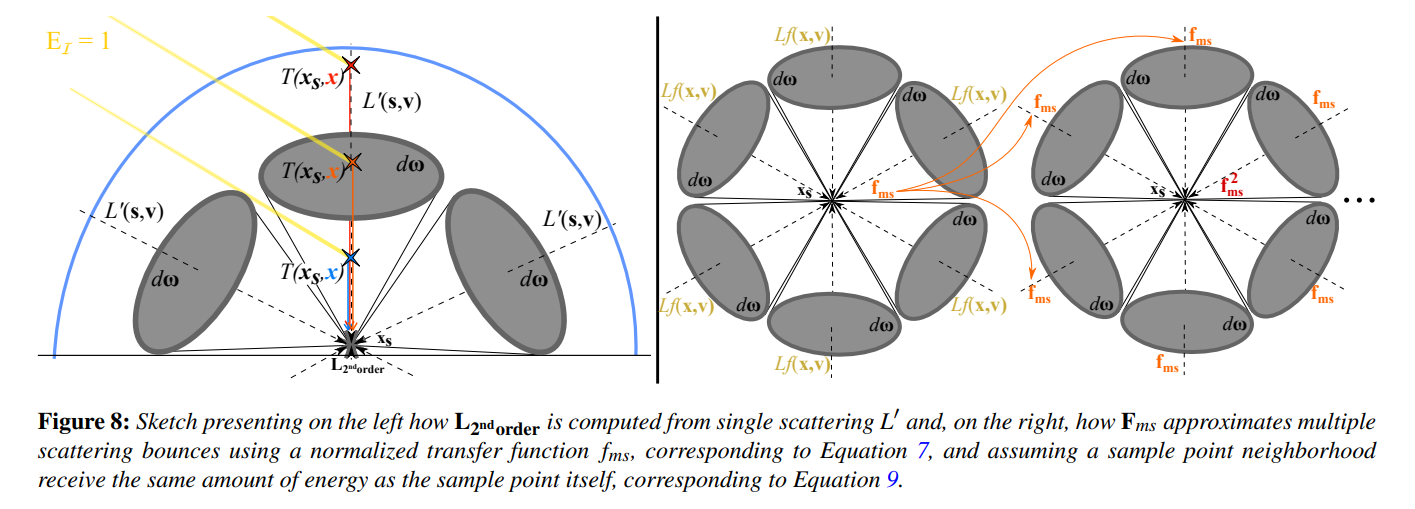
※図は，Sébastien Hillaire, “A Scalable and Production Ready Sky and Atmosphere Rendering Technique”, Eurographics Symposium on Rendering 2020, Vol.39, Number 4, 2020より引用。

　上述したように、散乱次数が2以上の場合、\({\mathbf x}_{\mathbf s}\)周辺の任意の点に到達する光は、\({\mathbf x}_{\mathbf s}\)自身に到達する光と同じであると仮定します。 この低い空間変動の仮定を用いて、多重散乱の寄与を解析的に評価することができます。二重散乱アプローチ[ZYWK08]にヒントを得て、無限の多重散乱光寄与係数\({\mathbf F}_{\mathbf{ms}}\)を幾何級数無限和として近似しました。

\begin{eqnarray}
{\mathbf F}_{\mathbf{ms}} = 1 + {\mathbf f}_{\mathbf{ms}} + {{\mathbf f}_{\mathbf{ms}}}^2 + {{\mathbf f}_{\mathbf{ms}}}^3 + \dots = \frac{1}{1 – {\mathbf f}_{\mathbf{ms}}} \tag{9}
\end{eqnarray}

最後に、散乱次数が無限大の方向性光の寄与度の合計は、次のように評価できます。

\begin{eqnarray}
{\Psi}_{\mathbf{ms}} = {\mathbf L}_{\mathbf{2^{nd} order}} {\mathbf F}_{\mathbf{ms}} \tag{10}
\end{eqnarray}

ここで、2次散乱寄与度\({\mathbf L}_{\mathbf{2^{nd} order}}\)は、多重散乱伝達関数\({\mathbf F}_{\mathbf{ms}}\)によって増幅されます。したがって、伝達関数\(\Psi_{\mathbf{ms}}\)（単位\(\rm{sr}^{-1}\)）は、任意のディレクショナルライト照度（\(\rm{cd}.\rm{sr}.\rm{m}^{-2}\)とするルクス）と単純に乗算され、画素に対する多重散乱寄与を輝度（\(\rm{cd}.\rm{m}^{-2}\)）として取り出すことができます。\(\Psi_{\mathbf{ms}}\)は、多重散乱LUTに格納されています。大気マテリアルのセットアップでは、このLUTは惑星の周りの任意の視点と光の方向に対しても有効です。

結論として、光の散乱式3は、我々の多重散乱近似を用いて拡張することができます。

\begin{eqnarray}
L_{scat}({\mathbf c}, {\mathbf x}, {\mathbf v}) = \sigma_{\mathbf s}({\mathbf x}) \int_{i=1}^{N_{\rm{light}}} (T({\mathbf c}, {\mathbf x}) S({\mathbf x}, {\mathbf{l_i}}) p({\mathbf v}, {\mathbf{l_i}}) + \Psi_{\mathbf{ms}}) {\mathbf E}_{i} \tag{11}
\end{eqnarray}

この単純化により、大気中の多重散乱の寄与を評価するための反復法への依存を避けることができます。我々のリアルタイム使用例では、単位球上の\({\mathbf f}_{\mathbf{ms}}\)と\({\mathbf L}_{\mathbf{2^{nd} order}}\)の積分は、\(64\)の一様分布方向を使用して達成されています。パフォーマンスの詳細については、7節を参照してください。

6. Results

我々は、Bruneton[Bru17a]によって提案されたモデルとボリュームメトリックパストレーサーの2つの最新技術と比較することによって、大気レンダリングに対する我々のアプローチを検証します。様々なシナリオを比較し、R、G、Bチャンネルのそれぞれについて、グラウンドトゥルースのパストレーサと比較した場合の画像の二乗平均誤差（RMSE）を出します。RMSEの測定に影響を与えないように、純黒のアルベドを使用した地形を持つ惑星と、太陽ディスクを使用しない惑星での結果を示します。このアプリケーションのコードはオープンソースです。

　まず、我々のモデルが地球の大気を忠実に表現できることを確認します（図9参照）。多重散乱を考慮に入れた場合の違いを示すために、単一散乱のみを使用したビューを示します。また、3つのモデルを示しています：そのモデルはBruneton(B)、我々のモデル(O)、リファレンスパストレーサー(P)です。日中における(B)と(O)のRSMEはそれぞれ\((1.43, 2.28, 6.07).10^{-3}\)と\((0.94, 1.74, 5.07).10^{-3}\)です。つまり、どちらも参照(P)に非常に近いです。夕焼けの場合、(B)は三重散乱によって伝播するオレンジ色を忠実に表現していないことに注意が必要です。これは、2つのRGB 4D散乱LUTを必要とするソリューションではなく、Aが無色のミー散乱を表す1つのRGBA 4D散乱LUTを使用しているためです。これは、メモリの割り当て量を減らし、パフォーマンスを向上させるためにリアルタイム・アプリケーションで使用される典型的なセットアップです（1つの散乱LUTだけを更新する必要があり、LUTデータを取得するために必要な帯域幅が少なくて済みます）。ミー散乱色は、BrunetonとNeyret [BN08]の4節で説明されているトリックを使用して回復されます。また、両方のモデルが大気中の地球の影に見える淡い散乱色を再現していることも興味深い点です。

※図は，Sébastien Hillaire, “A Scalable and Production Ready Sky and Atmosphere Rendering Technique”, Eurographics Symposium on Rendering 2020, Vol.39, Number 4, 2020より引用。

また、図10を参照して、空間ビューを実現するために、それらのモデルの精度を比較します。(B)モデルと(O)モデルはどちらも地球を忠実に再現しており, RSMEは\((0.58, 0.67, 1.61).10^{-3}\), \((0.95, 0.85, 1.23).10^{-3}\), RSMEは\((0.87, 0.97, 0.94).10^{-3}\), \((1.99, 0.91, 0.56).10^{-3}\)となっています。厚くて濃い大気を持つアーティスティックな小さな惑星に関しては、(B)では惑星の固い核からのボリュームメトリックなシャドウイングが再現できないようです。これはLUTのパラメータ化に起因しており、地表面の曲率が高い小さな惑星では精度が低くなっています。モデル(B)のこの制限は、4次元光散乱LUTの解像度を上げ、メモリと計算コストを追加することで解消される可能性があります。

※図は，Sébastien Hillaire, “A Scalable and Production Ready Sky and Atmosphere Rendering Technique”, Eurographics Symposium on Rendering 2020, Vol.39, Number 4, 2020より引用。

　地球の大気については、\(5^{th}\)までの計算でほとんどのエネルギーを捕捉できることが報告されており[BN08]、観測で確認できました。しかし、アーティストに大気の設定を制御させると、大気が濃くなり、より高い散乱次数を考慮することが重要になってきます。私たちの新しいモデル(O)はそれを自動的に考慮していますが、モデル(B)の場合はそうではありません。この場合，評価する必要のある散乱次数と同じだけの繰り返しが必要となり，タイムスライシングを行ってもすぐに非現実的になります。図11は、密度の高い大気では、高次散乱が正しい大気色を忠実に再現するために重要であることを示しています。我々のモデルはそのような振る舞いを表現することができますが、モデル(B)はより高い散乱次数では正しい色に収束せず、数値的にも爆発してしまいます（図11(右)）。これは、モデル(O)で十分な16ビットのfloat表現ではなく、モデル(B)の散乱LUTに32ビットのfloat表現を使用しているにもかかわらず、LUTをサンプリングする際の精度の問題が原因であると考えられます。

※図は，Sébastien Hillaire, “A Scalable and Production Ready Sky and Atmosphere Rendering Technique”, Eurographics Symposium on Rendering 2020, Vol.39, Number 4, 2020より引用。

　言及する価値のあるいくつかの問題があり、それぞれが多重散乱近似に起因するものです：

• 非常に高い散乱係数を使用している場合、色相が失われたり、グラウンドトゥルースと比較してドリフトし始めたりすることがあります。
• 2回目のバウンス直後は光の散乱方向が等方的であると仮定しています。これは実際には近似値であり、我々のモデルとリファレンスパストレーサーとの比較によって確認されています。ミー散乱のみの場合、\(g = 0.0\)と\(g = 0.8\)の場合、RMSEはそれぞれ\(0.0058\)と\(0.039\)です。

7. Peformance and Discussion

NVIDIA 1080 を搭載した PC 上では、図9 の昼間の状況を考慮すると、空と大気の遠近感の最終的な画面描画時間は 0.14 ミリ秒（\(\rm{ms}\)）です。より詳細なタイミングと本手法で生成した LUT の特性を表2 に示します。最終的に、解像度\(1280 \times 720\)の場合の合計レンダリング時間は\(0.31{\rm{ms}}\)です。同じビューの場合、Brunetonモデル[BN08]は\(0.22{\rm{ms}}\)でレンダリングされますが、これはすべてのLUTが更新されていない状態です。提供されたコード[Bru17b]を使用してすべてのLUTを更新すると\(250{\rm{ms}}\)かかりますが、このコストの99%は多重散乱を推定するのに必要な多くの反復に起因しています。Hillaire [Hil16]によって既に示されているように、更新をいくつかのフレームにわたってタイムスライスすることが可能です。しかし，高い散乱次数を評価する場合にはレイテンシが増加し，結果が画面に表示されるまでに長い時間がかかります。

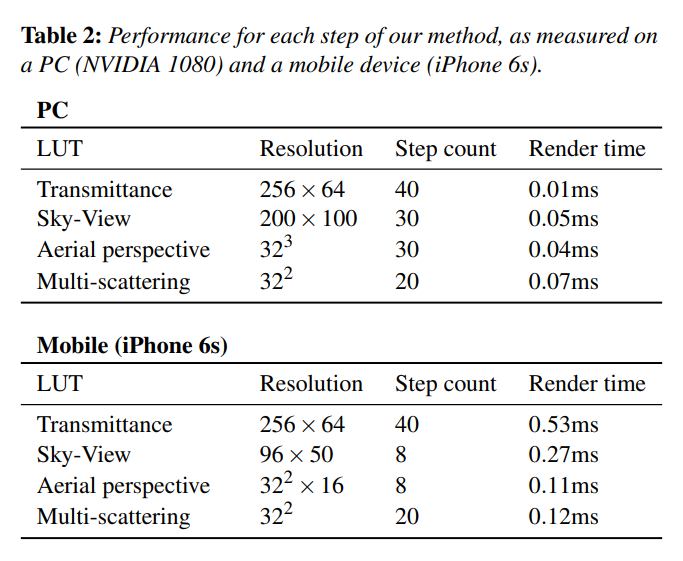
※表は，Sébastien Hillaire, “A Scalable and Production Ready Sky and Atmosphere Rendering Technique”, Eurographics Symposium on Rendering 2020, Vol.39, Number 4, 2020より引用。

5.3 節で説明した Sky-View LUT は、その大部分が空の空間をレンダリングするために無駄になるため、精度が悪くなります。この場合、画面上ではシームレスに単純なレイマーチに切り替えます。この場合、惑星と大気のレンダリング時間は0.33ミリ秒と高くなり、合計で0.5ミリ秒のレンダリングコストとなります。しかし、惑星の見た目は惑星自体に焦点を当てているので、レンダリング予算は高くなる可能性が高いため、これは許容できることが多いです。

　我々の技術は、デスクトップPCから比較的古いAppleのiPhone 6sのモバイルハードウェアにスケールすることができます。この場合、LUTの解像度とサンプル数は、結果のビジュアルに大きな影響を与えることなくスケールダウンすることができます。我々のセットアップとパフォーマンスの違いを表2に示し、ビジュアルの変化を図13に示します。LUT品質の低下による視覚的な違いは、肉眼では目立ちません。両プラットフォームで同様の透過率LUTを維持していることに注意してください。視覚的な違いをパフォーマンスと引き換えにすることができれば、モバイルではその均等性はさらに低下する可能性があります。Epic Gamesの「Fortnite」では、iPhone 6sでスカイレンダリングのトータルコストは約1ミリ秒でした。

※図は，Sébastien Hillaire, “A Scalable and Production Ready Sky and Atmosphere Rendering Technique”, Eurographics Symposium on Rendering 2020, Vol.39, Number 4, 2020より引用。

　再現するための重要な視覚効果は、例えば山から大気へのボリュームシャドウイングです。大気は均質な媒質ではないため、エピポーラサンプリング[BCR*10]を使用することはできません。また、私たちのLUTでは大気中のビューレイパス上の積分サンプリングができないため、シャドウボリュームアプローチ[BN08; Hoo16]を使用することもできません。最後に、これらの技術は、雲によるソフトシャドウキャストを表現することができません：レイマーチしなければなりません。Valient [Val14]やGjoel [GS16]と同様に、前のフレームからのサンプルを結合するためにパーレイサンプルジッタリングと再投影を使用することを推奨します。ジッタリングはブルーノイズ[GS16]に従って行うことができ、再投影は時間的アンチエイリアシング(TAA)アプローチ[Kar14]を介して自動的に達成することができます。これを図14に示します。このようなアプローチを使用すると、コンテンツに依存するサンプル数を必要とする。この例では、32個のサンプルを使用しているため、空と大気のレンダリング時間が1.0msになります。このコストを削減するために、より低い解像度でトレースし、結果を一時的に再投影してアップサンプルすることも可能です。これは、いくつかのゲームエンジンですでに使用されており、素晴らしい結果が得られています[Bau19; EPI18]。ボリュームシャドウを使用した結果は、図1のシャドウになります。

※図は，Sébastien Hillaire, “A Scalable and Production Ready Sky and Atmosphere Rendering Technique”, Eurographics Symposium on Rendering 2020, Vol.39, Number 4, 2020より引用。

※図は，Sébastien Hillaire, “A Scalable and Production Ready Sky and Atmosphere Rendering Technique”, Eurographics Symposium on Rendering 2020, Vol.39, Number 4, 2020より引用。

　さらに、我々が提案する多重散乱LUTは、5.5節と図12で説明した近似が許容できる場合には、大気関与媒質のパストレースを加速することもできます。この場合、単一の散乱事象のみをサンプリングする必要があり、例えばデルタトラッキング[FWKH17]を使用します。このような事象が発生した場合、トレースされたパスは直ちに停止され、その時点で単一散乱の寄与は次のイベント推定を用いて評価され、残りの散乱次数からの寄与は多重散乱LUTを用いて評価されます。このアプローチをリファレンス GPU パストレーサで使用すると，図9 に示すように，5 つの散乱次数（パスの深さ）を持つ日中の 702p フレームのコストは 0.74msから 0.29msに低下します。また，図 11 に示すように，50 の散乱次数を使用した日中のコストは 7.9ms秒から 0.6msに低下しました。

※図は，Sébastien Hillaire, “A Scalable and Production Ready Sky and Atmosphere Rendering Technique”, Eurographics Symposium on Rendering 2020, Vol.39, Number 4, 2020より引用。

8. Conclusion

要約すると、我々の手法は、光の多重散乱をシミュレートしながら、散乱次数ごとの煩雑な反復計算を必要とせずに、LUTを常に更新しながら、多くの視点から空と大気をリアルタイムで効率的にレンダリングすることができます。これは、照明アーティストが自分たちのビジョンを達成し、プロジェクトのアートディレクションに従うことができるようにするために重要であり、同時に一日の時間帯や天候の変化をシミュレートすることができます。我々は、正確な視覚的な結果を与え、密な大気や強い異方性の位相関数のためにグラウンドトゥルースからドリフトした場合でも、結果はもっともらしいままであることを示しました。物理ベースでエネルギー保存しているので、爆発することはありません。さらに、空と大気をレンダリングするパストレーシングアプリケーションを高速化するために使用することができます。

9. Future work

今後の研究では、異方性位相関数のルックアップテーブルの精度を向上させ、空間的に変化する大気条件をサポートする方法を検討することが考えられます。我々は、この方法の精度を向上させるために、ある時点でスペクトルレンダリングに切り替えることが重要であると考えています[EK10]。最後に、我々は、パストレーサとデノイザーを用いたリアルタイムの空と大気のレンダリングが有望な研究手段であると考えています。

Acknowlegements

有益なコメントを寄せてくださった匿名のレビュアーの方々、そして、Epic Games のレンダリングチーム全員、特に Krzysztof Narkowics 氏、Charles de Rousiers 氏、Graham Wihlidal 氏、Dmitriy Dyomin 氏をはじめとする、論文の校正を担当してくださった方々に感謝します。また、レベルアートの提供と技術の評価をしてくださった Jean-Sebastien Guasy 氏、Jordan Walker 氏、Ryan Brucks 氏、Sjored de Jong 氏、Wiktor Öhman 氏にも感謝したいと思います。最後に、論文の校正をしてくださったStephen Hill氏に感謝します。