D. Brandon Lloyd氏の博士論文である，Logarithmic Perspective Shadow Mapsを適当に訳していくことにします。
前回はChapter.3を何とか訳しました。今回はChapter.4を訳していきます。
誤訳があったりなど，日本語としては多々見苦しい点があるかと思いますが，そこはご容赦ください。

---

CHAPTER 4

Minimizing aliasing error

3章では，エイリアシング誤差の定量化の手法を説明しました。この章では，誤差を最小化するパラメータライゼーションを導くために使用することができるタイトな境界を導出します。最初にエイリアシング誤差を完全に排除する2次元上での理想的なパラメータライゼーションを計算するための手法を説明します。不運なことに，この説明は複雑さのため理論的な関心のみとします。代わりに透視エイリアシング誤差上のタイトな境界から出発し，最適に近いパラメータライゼーションを生み出す間隔分布 \({\delta}_b\) を計算します。これは視錐台の面に一致する領域へとシャドウマップを分割することを自然に導きます。3次元へと解析を拡張し，\({\delta}_b\) から導かれるパラメータライゼーションを解析します。これらのパラメータライゼーションもまた実際に使うにはあまりにも複雑すぎますが，次の章で，より単純なパラメータライゼーションを評価することに対する良い基準線を提供します。
 

4.1 The ideal parameterization

エイリアシング誤差 \(m\) は，ライト画像平面上の間隔分布 \(\delta_l\) と十分なシャドウマップ解像度 \(r_t\) を適切に選択することよって制御可能です。理想的には，特定のビューの可視可能な点のすべてについて \(m = 1\) となるような\(\delta_l\) と \(r_t\) を選択するのが望ましいです。この条件は，最小のシャドウマップ解像度を使用する間にエイリアシングを排除するのを保証します（我々は再サンプリングエイリアシングのみを処理するのを思い出してください。より大きいシャドウマップ解像度は初期サンプリングエイリアシングを処理しなければならない可能性があります）。式3.27から，\(m = 1\) は \(\delta_l / {r_t} = \delta_e / {r_j}\) を示しており，ひいては次を意味します：
\[
\frac{1}{r_t} \frac{dF}{dv} = \frac{1}{r_j} \frac{dj}{dv} \tag{4.1}
\]
式は \(F(v) = j(v)\) と \(r_t = r_j\) であるときに，満たされます。従って，理想的なパラメータライゼーションは，ライト画像平面上のシャドウマップクエリの位置が由来する画像中のピクセルに戻るようにマップする関数 \(j(v)\) です。理想的なシャドウマップ解像度は画像の解像度と同じです。
　シーンを構成する単一の平面について，\(j(v)\) は単一の射影変換から構成されます。複数または非凸面の存在は，\(j(v)\) が可逆であることを保証するためにパーティショニングを要求します。パーティションは連続である領域，視認可能である領域，そしてライトに向かう面によって定義されます（図4.1参照）。ライトに面していない視認可能な領域がシャドウ中にあることが保障されており，考慮する必要はありません。シャドウマップの解像度は画像内のピクセルに各テクセルがマッピングされるので画像よりも大きくする必要はありません。実際には，理想的なパラメータライゼーションはイレギュラーZバッファによって使用されるのと同じ様なサンプル位置を与えます。理想的なパラメータライゼーションはChongとGortlerのアルゴリズム(2004)の一般化です。彼らはシーン上においていくつかの重要な平面上でシャドウマップのテクセルと画像のピクセル間が1対1に対応することを立証しました。ポリゴンサーフェイスで完全に構成されるシーンについて，理想的なパラメータライゼーションは本質的には，各ポリゴンの可視できる部分に対してこのアルゴリズムを適用した結果となります。しかしながら，高次のサーフェイスに適用する可能性もまたあるので，理想的なパラメータライゼーションはより一般的になります。
　ついてないことに，理想的なパラメータライゼーションは完全に実現が困難です。複雑なシーンについて要求されるパーティションの数は非常に大きくなる可能性があります。パーティションに一致する領域を計算することは非常にコストが高いです。さらに，任意のサーフェイスに対するワーピング関数は非常に複雑あるいは閉形式では表現できない可能性があります。

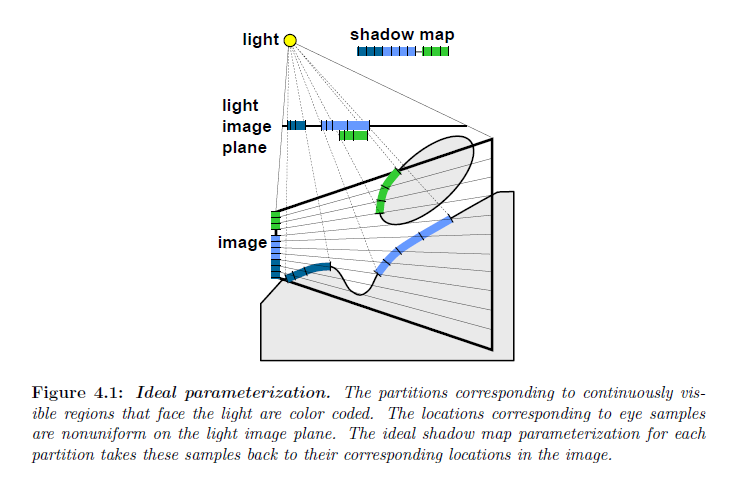
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.54 より引用。

 

4.2 Minimizing perspective aliasing error

理想的なパラメータによって潜在的に必要とされる多数のパーティションは，ライト画像上の \(v\) にすべての点についてマップする \(\delta_l(v)/r_t\) を \(\delta_e/r_j\) に一致させようとすることから生じます。単純なアプローチはこれらの点について \(\delta_l\) を \(\delta_e\) 上の下限に一致させようとする可能性があります：
\[
{\delta}_{e, \min}(v) = \min_{{\bf{p}} \in \cal{P}(v)} \left( \delta_{e} ({\bf{p}}) \right) \tag{4.2}
\]
\(\cal{P}(v)\) はライトとライト平面上の点 \({\bf{p}}_l(v)\) の両方を通過する線 \({\sf{L}}(v)\) を持つ視錐台内のサーフェイスの交差点の集合として定義されます。\(\delta_{e, \min}\) はシーンのジオメトリに依存するので，任意の複雑さになる可能性があります。透視因子 \(\tilde{\delta}_e\) 上の下限はシーンに依存した関数によって単純に得られます：
\[
\delta_b = \min_{ {\bf{p}} \in \{ {\sf{L}}(v) \cap {\sf{V}} \} } \left( \tilde{\delta}_e ({\bf{p}}) \right) \tag{4.3}
\]
\(\sf{V}\) は視錐台内部のすべての点の集合です。\(\delta_b\) を使用することで，\(v\) の関数として表現される透視エイリアシング誤差 \(\tilde{M}\) 上のタイトな上限を定義することができます：
\[
{\tilde{M}}(v) = \max_{ {\bf{p}} \in \{ {\sf{L}}(v) \cap {\sf{V}} \} } \left( {\tilde{m}}({\bf{p}}) \right) = \frac{r_j}{r_t} \frac{\delta_l(v)}{\delta_b(v)} \tag{4.4}
\]
与えられた \(\delta_l(v)\) について，視錐台上で透視エイリアシングが起こらないこと，すなわち \( {\max}_v ( {\tilde{M}} ) = 1\) を保証するために要求される最も低い解像度は \(r_t = R_t r_j\) です。ここで \(R_t\) は次式によって得られます：
\[
R_t = \max_{v} \left( \frac{\delta_l (v)}{\delta_b (v)} \right) \tag{4.5}
\]
\(R_t\) を 重要解像度因子 と呼ぶことにします。\(R_t\) は　\(\delta_l\) が \(\delta_b\) に比例するときに最も小さくなります。その場合では， \(R_t = \rho_b\) で，\(\rho_b\) は比例定数とします。一般には，\(\delta_b\) にぴったり一致する \(\delta_l\) を選択することはできません。なぜかというと，一定の拡大・縮小因子が通常は\([0,1]\)の範囲に正規化された \(\delta_l\) をパラメータライゼーション時に取り込むためです。
　任意の間隔分布関数 \(\delta(v)\) を与えると，パラメータライゼーション \(F\) は次によって計算可能な \(\delta_l \sim \delta(v)\) を算出します：
\begin{eqnarray}
\left( \frac{dF}{dv} \right)^{-1} \sim \delta(v) \\
\frac{dF}{dv} &=& \frac{1}{\rho \delta(v)} \tag{4.6} \\
F(v) &=& \frac{1}{\rho} \int_{0}^{v} \frac{1}{\delta(\nu)} d\nu \tag{4.7}
\end{eqnarray}
\(F\) を \([0,1]\) の範囲に正規化することは，比例定数を与えます。
\[
\rho = \int_{0}^{1} \frac{1}{\delta(v)}dv \tag{4.8}
\]
この過程は積分領域上の正で，有効な任意の \(\delta(v)\) で動作します。
 

4.2.1 Computing \(\delta_b\)

線 \(\sf{L}\) に沿った視錐台内部の点は図4.2で示されるようにパラメータライゼーションすることができます：
\[
{\bf p}(\mu) = {\bf l} + \mu {\hat {\bf v}}_l(v) \tag{4.9}
\]

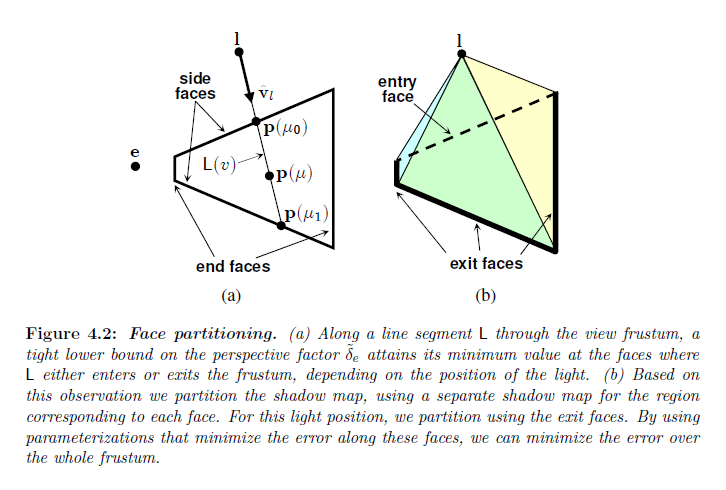
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.57 より引用。

式3.30から \(\tilde{\delta}_e(\mu)\) を計算します：
\begin{eqnarray}
\tilde{\delta}_e(\mu) &=& c \frac{d_e(\mu)}{d_l(\mu)} \cos\phi_e(\mu) \tag{4.10} \\
d_e(\mu) &=& – {\hat {\bf z}}_e \cdot ({\bf p}(\mu) – {\bf e}) = -\mu({\hat {\bf z}}_e \cdot {\hat {\bf v}}_l) – {\hat {\bf z}}_e \cdot ({\bf l} – {\bf e}) \tag{4.11} \\
d_l(\mu) &=& -{\hat {\bf z}}_l \cdot ({\bf p}(\mu) – {\bf l}) = -\mu( {\hat {\bf z}}_l \cdot {\hat {\bf v}}_l) \tag{4.12} \\
\cos\phi_e(\mu) &=& \frac{d_e(\mu)}{\parallel {\bf p}(\mu) – {\bf e} \parallel} \\
c &=& \frac{W_e}{W_l} \frac{n_l}{n_e} \frac{1}{\cos\phi_l}
\end{eqnarray}
値 \(c\) は \(\sf L\) 上で一定です。\(\delta_l\) もまた線に沿って一定であるので，任意のパラメータライゼーションについて \(\max(\tilde m)\) は \(\min({\tilde \delta}_e)\) と同じ場所で発生することに注意してください。我々は視錐台内の \(\mu \in [\mu_0, \mu_1]\)　の区間上で \({\min}_{\mu}( {\tilde \delta}_e (\mu) )\) を求めたいです。解析を単純にするために，対称な視錐台と \(\cos\phi_e\) の項を最も小さい可能値で置換することによって以下からの境界 \({\tilde \delta}_e(\mu)\) を仮定します：
\[
B(\mu) = c \frac{d_e(\mu)}{d_l(\mu)} \cos\theta \leq {\tilde \delta}_e(\mu) \tag{4.13}
\]
\({\tilde \delta}_e\) はよりも大きく \(1/\cos\theta\) 倍にすることができます。すなわち， \(\cos{\theta_e} = 1\)のときです。典型的な視野角について，\(B\) はかなりタイトな下限値です。例として，\(\theta = 30^{\circ}\) で，\(1/\cos\theta\) はわずか約\(1.15\) です。
　最小値に達したところを決めるために\(B(\mu)\)の微分をとります：
\[
\frac{dB}{d\mu} = (c \cos\theta) \frac{{\hat {\bf z}}_e \cdot ({\bf l} – {\bf e})({\hat {\bf z}}_l \cdot {\hat {\bf v}}_l)}{(\mu ({\hat {\bf z}}_l \cdot {\hat {\bf v}}_l) )^2 } \tag{4.14}
\]
最初の項と次の項の分母は完全に正であり，分子における\(({\hat {\bf z}}_l \cdot {\hat {\bf v}} )\) の項は完全に負です。従って，\(dB/d\mu\) の符号は， \({\hat {\bf z}}_e \cdot ({\bf l} – {\bf e})\) のみに依存します。\({\hat {\bf z}}_e \cdot ({\bf l} – {\bf e}) \) はすべての \(\mu\) について一定であるので，\(B\) の最小値，\(\mu_{\min}^{B}\) の位置は区間の境界で一つである必要があります：
\begin{eqnarray}
\newcommand{\argmin}{\mathop{\rm argmin}\limits}
\mu_{\min}^{B} = {\argmin_{\mu \in [\mu_0, \mu_1]}} (B(\mu)) = \begin{cases}
\mu_0 \hspace{1cm} {\hat {\bf z}}_e \cdot ({\bf l} – {\bf e}) > 0 \\
\mu_1 \hspace{1cm} {\hat {\bf z}}_e \cdot ({\bf l} – {\bf e}) < 0 \\ \end{cases} \tag{4.15} \end{eqnarray} \({\hat {\bf z}}_e \cdot ({\bf l} - {\bf e}) = 0\) のとき，\(B\) は全区間にわたって一定です。ディレクショナルライトについて， \(({\bf l} - {\bf e})\) の項はライトの方向 \({\hat {\bf l}}\) で置換されます。式4.15は カメラ視点に相対するライトの位置に依存して \({\sf L}(v)\) が視錐台に入るまた出るかのどちらかの一方の面上で \(\min (B)\) が発生することを示しています。\(\mu_{\min}^B\) が側面上のときに，\(B(\mu_{\min}^B)\) は \({\tilde \delta}_e\) について実際に最小となります。\({\tilde \delta}_e = B\) なので側面に沿って \(\cos\phi_e = \cos\theta\) であるとみなすことができます。\(B\) は決して \({\tilde \delta}_e\) より大きくなることはないので，区間上で \({\tilde \delta}_e\) の実際の最小値は，最小値 \(B\) より小さくなる可能性がなく，ゆえに同じでなければならないことを意味しています。この観点に基づき，\(\delta_b\) に対する \(\min(B)\) を得ます： \begin{eqnarray} \delta_b &=& {\min}(B) = B(\mu_{\min}^B) \\ &=& \frac{W_e}{W_l} \frac{n_l}{n_e} \frac{d_e}{d_l} \frac{\cos\theta}{\cos\phi_l} \tag{4.16} \end{eqnarray} ここで，\(d_e\) と \(d_l\) は適切な面に沿った点についての値です。\(\mu_{min}^B\) が面に入ってから出るまであるいは逆についても同様で遷移するライト位置において，\(\min(B)\) は面のセットの両方の上で同じになります。従って，ライトとカメラが周囲を動くような\(\mu_{\min}^B\)における突然の遷移は \(\delta_b\) において時間一貫性の不連続を引き起こしません。 　\(\delta_l(v)/r_t = \rho_b\delta_b(v)/r_j\) を選択することは，すべての \(v\) について \({\tilde M}(v) = 1\) であることを保証することができます。直感的には，これは交差する任意のアイビームの幅上の下限値より広いライトビームがないような \(\delta_l\) と \(r_t\) を選択することと考えることができます。  

4.3 Computing a parameterization in 3D

3次元上でパラメータライゼーションを計算するための1つのアプローチは，2次元について我々が使用した同じ積分式に単純に従うことです。ライト画像平面上でのサンプル間隔分布を記述する2×2行列である \(\delta(u, v)\)，\(\delta\) の逆行列，そして \({\bf F}(u, v)\) を得るために積分することから開始します。しかしながら，このアプローチにはいくつか複雑化させる要因があります。最初に，\({\tilde \delta}_e\)上の下限である \(\delta\) を計算する方法がはっきりとしていません。主な問題であるのは， 今 \(\delta\) が向きに関する情報を含んでいることです。それに対して2次元上では単純にスカラー値でした。\(\delta\) もまた可逆でなければなりません。第2に，たとえ \(\delta\) が可逆性を持つようになったとしても，\({\bf F}\) を得るために積分可能である保証がありません。\({\partial {\bf F}} /{\partial {\bf u}}\) の行は多変数関数 \(s(u, v)\) と \(t(u, v)\) の勾配です。従って，その行の要素の混合偏微分は次に等しくなければなりません。すわなち：
\[
\frac{{\partial}^2 s}{{\partial u}{\partial v}} = \frac{{\partial}^2 s}{{\partial v}{\partial u}} {\hspace 1cm} {\rm and} {\hspace 1cm} \frac{{\partial}^2 t}{{\partial u}{\partial v}} = \frac{{\partial}^2 t}{{\partial v}{\partial u}} \tag{4.17}
\]
もし，特定の \(\delta^{-1}(u, v)\) についてこの性質を持たない場合，関数 \({\bf F}(u, v)\) の勾配になることが出来ません。最後に, \(\delta^{-1}(u, v)\) が可逆であったとしても，シャドウマップによって覆われる領域のすべてについて1対1対応であることが保証されていません。
　我々のアプローチは，本質的には単純な2次元の問題における2つのインスタンスとしてパラメータライゼーション \(s\) と \(t\) を処理することです。式4.16からスカラー関数 \(\delta_{b,s}\) と \(\delta_{b, t}\) を選択し，\(s\) と \(t\) を得るために，\(u\) と \(v\) に関して，それぞれについてそれらの逆数を積分します。図4.3に示すような各面上での座標系を選択します。\(W_l\) の項について，適切な方向でパラメータライゼーションされた領域の幅を使用し，\(\cos\phi_l\) に関しては，\(XZ\) あるいは \(YZ\)平面それぞれの上の\({\hat {\bf z}}_l\) と \({\hat {\bf v}}_l\) の射影の間の角度である \(\cos\phi_{lx}\) または \(\cos\phi_{ly}\) を使用します。\(W_e\) と \(\cos\theta\) についてのスカラーを得るために，両方の方向における視野角は同じであると仮定します。そうではない場合は，保守的な境界を常にとることができます。すなわち，\(W_e = \min(W_{ex}, W_{ey})\) と，\(\theta = \min(\theta_x, \theta_y)\) です。またパラメータライゼーションを単純化するために，面と一致するライト画像平面を選択し，ゆえに \(d_l / n_l\)の項を排除します。今，各面のタイプについて \(\delta_{b,s}\) と \(\delta_{b, t}\) を計算する方法とそのときに一致するパラメータライゼーションを説明しました。もし，対称な視錐台を想定した場合，必要な時に \(W_e\) を展開するために以下の方程式を使用することができます：
\[
W_e = 2 n_e \tan\theta \tag{4.18}
\]

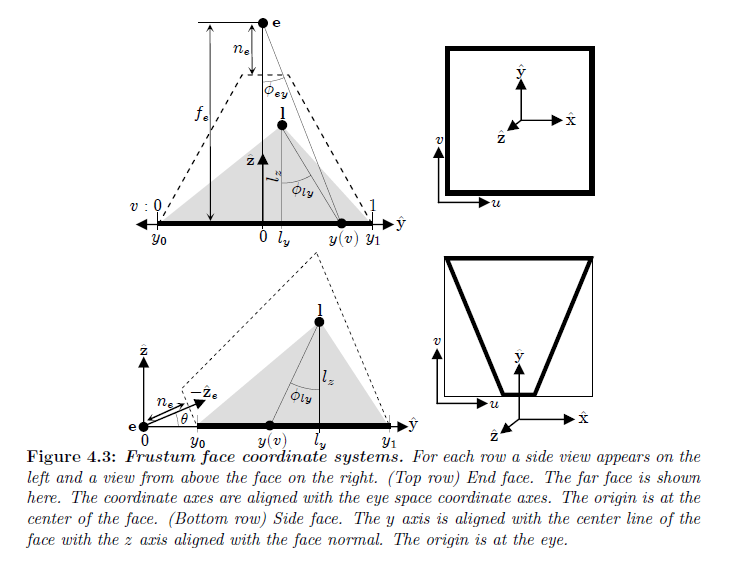
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.60 より引用。

 

4.3.1 \(\delta_b\) for end faces of the view frustum

最初に \(\delta_{b, t}^{\rm end}\) を見ます。近い面上で \(d_e = n_e\)，そして遠い面上で \(d_e = f_e\) とします。\(y\) 上の領域 \(v\) の幅は，面の幅 \(W_{ly} = (W_e d_e)/n_e \) と同じです。そのため，面上の位置は次のようにパラメータライゼーションできます：
\begin{eqnarray}
y(v) &=& (y_1 – y_0)v + y_0 \\
y_0 &=& – \frac{W_e}{2} \frac{d_e}{n_e}, {\hspace 0.5cm} y_1 = \frac{W_e}{2} \frac{d_e}{n_e}
\end{eqnarray}
\(v\) の項における \(\cos\phi_{ly}\) は次になります：
\[
\cos\phi_{ly}(v) = \frac{l_z}{\sqrt {(y(v) – l_y)^2 + l_z^2}} \tag{4.19}
\]
これらの式を式4.16に代入して次を得ます：
\[
\delta_{b,t}^{\rm end}(v) = \frac{\cos\theta}{\cos\phi_{ly}(v)} \tag{4.20}
\]
\(y\) と \(v\) 上の量が \(x\) と \(u\) 上に一致する量に交換されていることを除いて \(\delta_{b,s}^{\rm end}\) は \(\delta_{b,t}^{\rm end}\) と同じになります。
　図4.4はどのように \(\delta_{b,t}^{\rm end}\) が遠い面上でライト位置とともに変化するかを示しています。 \(\cos\phi_{ly}\) の項は関数の形状における変化の原因になっています。面の近くでは，\(\delta_{b,t}^{\rm end}\) は丸い先端を持つ絶対値関数に似ています。\(l_z \rightarrow \infty\)になるにつれて，\(\cos\phi_{ly}\) は一定に収束し，間隔は均一になります。\(y\) 上で移動するライトは単純に \(v\) 軸に沿った関数に変換します。

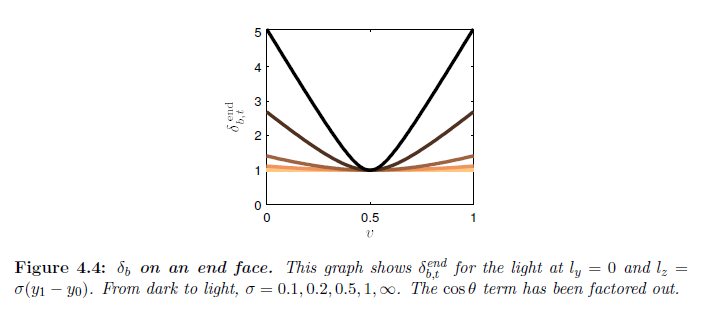
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.61 より引用。

 

4.3.2 \(\delta_b\) for side faces of the view frustum

側面の端点は \(n_e\) と \(f_e\) に関係があります：
\[
y_0 = \frac{n_e}{\cos\theta}, {\hspace 0.5cm} y_1 = \frac{f_e}{\cos\theta}
\]
側面上で，\(d_e\) は \(x\) 上で一定ですが，\(y\) で増加します。三角形の相似によって，\(\delta_b\) における \(d_e/n_e\) の項は次のように表されます：
\[
\frac{d_e}{n_e} = \frac{y}{y_0} \tag{4.21}
\]
側面は，\((u, v)\) の領域を完全に覆いません。\(x\) 上での範囲は次のようになります：
\[
x_0(y) = – \frac{W_e}{2} \frac{y}{y_0}, {\hspace 0.5cm} x_1(y) = \frac{W_e}{2} \frac{y}{y_0} \tag{4.22}
\]
\(x\) 上の領域の幅は \(y_1\)における面の幅 \(W_{lx} = (x_1(y_1) – x_0(y_1))\) です。\(y\) 上の幅 \(W_{ly}\) は \((y_1 – y_0)\) です。面上の位置を次のようにパラメータライゼーションします：
\begin{eqnarray}
x(u) &=& (x_1(y_1) – x_0(y_1))u + x_0(y_1) \tag{4.23} \\
y(v) &=& (y_1 – y_0)v + y_0 \tag{4.24}
\end{eqnarray}
これらの式すべてを一緒に加えることで次を得ます：
\begin{eqnarray}
\delta_{b,s}^{\rm side}(u, v) &=& \frac{y(v)}{y_1} \frac{\cos\theta}{\cos\phi_{lx}(u)} \tag{4.25} \\
&=& \frac{n_e + (f_e – n_e)v}{f_e} \frac{\cos\theta}{\cos\phi_{lx}(u)} \tag{4.26} \\
\delta_{b,t}^{\rm side}(v) &=& \frac{W_e}{(y_1 – y_0)} \frac{y(v)}{y_0} \frac{\cos\theta}{\cos\phi_{ly}(v)} \tag{4.27} \\
&=& \left( v + \frac{n_e}{f_e – n_e} \right) \frac{2 \tan\theta\cos^2\theta}{\cos\phi_{ly}(v)} \tag{4.28}
\end{eqnarray}
\(\delta_{b,s}^{\rm side}\) は \(u\) と \(v\) の両方の関数であり， \({\partial {\bf F}}/{\partial {\bf u}} \)の要素 \({\partial s}/{\partial v}\) は非ゼロであるため，厳密には2次元パラメータライゼーションの問題の別のインスタンスではありません。けれども示すのは些細であり，\(s = \delta_{b,s}^{\rm side}(u, v)\) であるとき，混合偏微分は等しくなります。パラメータライゼーション \(s(u, v)\) と \(t(v)\) は可逆であり，従って1対1対応します。なぜかというと， \(t^{-1}(v)\) を用いて，これを\(s(u, v)\) へ代入し，そして \(u\) を求めるために逆が求まるので， 常に \(v\) が求まるからです。
　図4.5は，面上の中心にあるライトに対する \(\delta_{b,s}^{\rm side}\) の形状を示しています。\(\delta_{b,s}^{\rm side}\) は本質的には \(x\) 上で \(\delta_{b,t}^{\rm side}\) によって調整された \(y\) における線形ランプであることに注意してください。

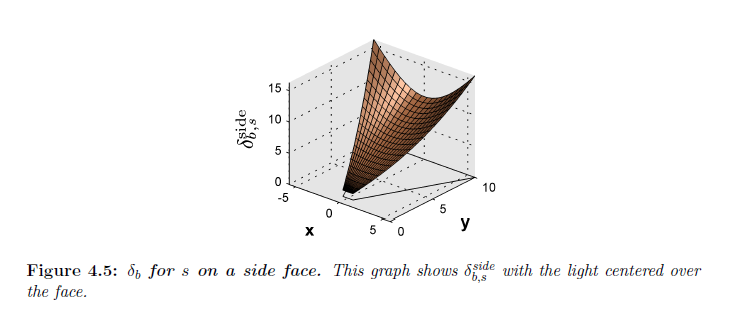
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.63 より引用。

　図4.6は，面上の変化する高さにおいてライトに対する \(\delta_{b,t}^{\rm side}\) を示しています。ライトが面に近づいたときに，間隔関数はライトと観測者の近くで高密度のサンプリングを持つうねった曲線です。\(y\) 上のライトを変換することは，関数のシフトとスケールされたバージョンを生成します。ライトが無限大に向かって離れるにつれて，間隔関数は線形ランプに収束します。再び，\(\cos\phi_{ly}\) の項は面にライトが近づくときに間隔関数の形状において変動することを考慮してください。ディレクショナルライトの位置が変化するときに，全体的なスケールのみは影響を受けます。

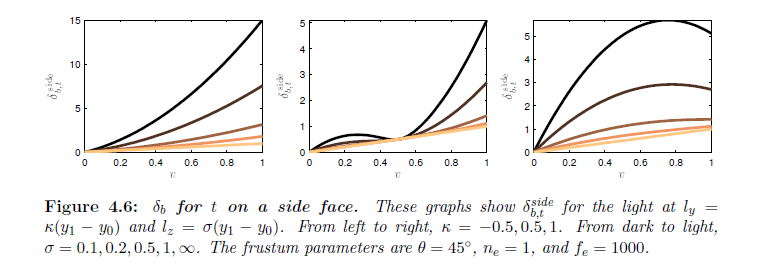
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.63 より引用。

 

4.3.3 \(\delta_b\) parameterizations

\(\zeta_b\) が \(1/\delta_b\) ，パラメータライゼーション \(F_b\) そして正規化された定数 \(\rho_b\) の 不定積分であるとする場合に　\(\delta_b\) の3つの種類について次のように計算することができます。：

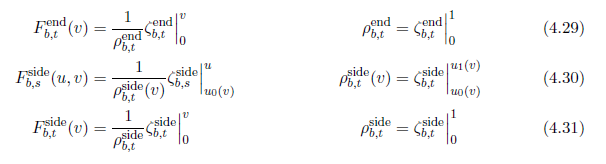
\begin{eqnarray}
\zeta_{b,t}^{\rm end}(v) &=& C_{b,t}^{\rm end} l_z \sinh^{-1} \left( \frac{y(v) – l_y}{l_z} \right) + C \tag{4.32} \\
\zeta_{b,s}^{\rm side}(u, v) &=& C_{b,s}^{\rm side} \frac{l_z}{y(v)} \sinh^{-1} \left( \frac{x(u) – l_x}{l_z} \right) + C \tag{4.33} \\
\zeta_{b,t}^{\rm side}(v) &=& -C_{b,t}^{\rm side} \frac{l_z}{\sqrt{l_y^2 + l_z^2}} \\
& {\hspace 0.1cm} & \log \left( \frac{2}{y(v)} \left( \frac{l_y(l_y – y(v)) + l_z^2}{l_z \sqrt{l_y^2 + l_z^2}} + \frac{1}{\cos\phi_{ly}(v) } \right) \right) \\
& {\hspace 0.1cm} & + C \tag{4.34} \\
C_{b,t}^{\rm end} &=& \frac{1}{(y_1 – y_0) \cos\theta} = \frac{1}{2d_e\tan\theta\cos\theta} \\
C_{b,s}^{\rm side} &=& \frac{1}{(x_1(y_1) – x_0(y_1))\cos\theta} = \frac{1}{2f_e\tan\theta\cos\theta} \\
C_{b,t}^{\rm side} &=& \frac{y_0}{W_e\cos\theta} = \frac{1}{2\tan\theta\cos^2\theta}
\end{eqnarray}
\(F_{b,s}^{\rm side}\) に対して，面によって覆われた領域の一部に一致する \(u \in [u_0(v), u_1(v)]\) 上を積分するということに注意してください。 \(u_0(v)\) と \(u_1(v)\) は \(u\) について \(x(u) = x_0(y(v))\) と \(x(u) = x_1(y(v))\) を解くことによって求まります：
\[
u_0(v) = \frac{y_1 – y(v)}{2y_1}, {\hspace 1cm} u_1(v) = \frac{y_1 + y(v)}{2y_1} \tag{4.35}
\]
　図4.7は 面をパラメータライゼーションするために\(F_b\) を使用してライトビームがどのように見えるかについて示しています。面にライトが近づいたとき，\(\cos\phi_l\) の要因のため，面を覆うにはより低い解像度が必要とされます。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.65 より引用。

 

4.4 Global error measures in 3D

我々は誤差の尺度として重要解像度因子 \(R\) (式4.5)を用いて2次元上でパラメータライゼーションを比較することができます。\(R\) は画像とシャドウマップ解像度が同じである場合に発生する視錐台上の最大透視エイリアシング誤差です。3次元上において \(s\) と \(t\) に対して重要解像度因子を組み合わせます：
\[
S = R_s \times R_t \tag{4.36}
\]
ピクセル単位での画像サイズに対する重要解像度シャドウマップのテクセルにおけるサイズについて表しているので \(S\) をストレージ因子と呼ぶことにします。\(R_s^{\rm side}\) の定義は次のように修正されます：
\[
R_s^{\rm side} = \max_{(u,v) \in {\cal F}} \left( \frac{\delta_l(u, v)}{\delta_{b,s}^{\rm side}(u, v)} \right) \tag{4.37}
\]
ここで，\(\cal F\)は面によって覆われた点の集合です。これは\(\delta_{b,s}^{\rm side}\) が \(u\) と \(v\) の両方の関数であるため必要です。全ての取りうるライトの位置の集合 \(\Omega\) について最大透視誤差の尺度を定義するために便利です：
\begin{eqnarray}
{\sf R} &=& \max_{\Omega} R \tag{4.38} \\
{\sf S} &=& \max_{\Omega} S \tag{4.39}
\end{eqnarray}
\(\sf R\) と \(\sf S\) は前述の面で直接的に無限遠におけるライトに関して \(R\) と \(S\) を計算することによって評価可能です。このライト位置について \(\delta_b\) の要素である \(\cos\phi_s\) は面全体について1になり，\(R\) と\(S\) は最大化されます。
 

4.4.1 Balancing error between shadow map partitions and directions

一般には，面に対してライトの位置は面の間で異なります。これはまた面の間で \(S\) が異なる原因となります。視錐台全体について最大誤差を最小化するために，利用可能なシャドウマップ解像度は最大誤差に比例して面の間で分配されるべきです。テクセルの総数 \(T\) の比率は各パーティション \(P_i\)　に対して \(\sigma_iT\) が確保されるべきです：
\[
\sigma_i = \frac{S_i}{\sum_{j=i}^k S_j} \tag{4.40}
\]
ここで，\(k\) はパーティションの数で，\(S_i\) はパーティション \(P_i\)のストレージ因子です。与えられたパーティションに割り当てられたテクセルは各方向における最大誤差を最小化するために \(R_s\) と \(R_t\) に比例したシャドウマップの方向 \(s\) と \(t\) の間に分けることができます：
\[
r_s = \sqrt{\frac{R_s}{R_t}\sigma T}, {\hspace 1cm} r_t = \sqrt{\frac{R_t}{R_s}\sigma T} \tag{4.41}
\]
 

4.5 Maximum error of \(\delta_b\) parameterizations

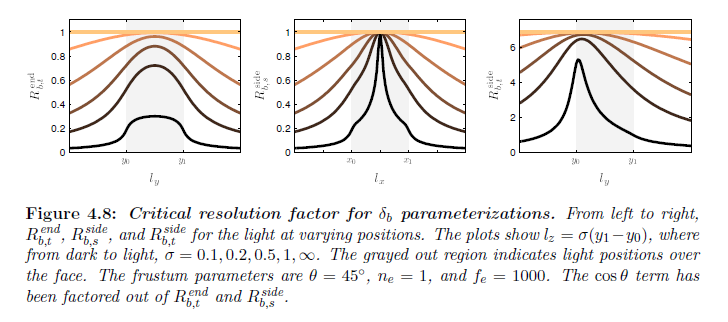
我々は今，重要解像度因子 \(R\) とストレージ因子 \(S\) の項において\(\delta_b\) のパラメータライゼーションの形式それぞれで最大誤差を計算することが可能です。以前に述べたように，\(R_b = \rho_b\) です。図4.8は \(\delta_b\) の3つの種類に対する \(R_b\) を示しています。一般には，\(R_b\) はライトが面を含む平面に近くなるときにより小さくなります。また，ライトがどちら側面へ動くにつれて低下します。最大重要解像度因子 \({\sf R}_b\) は次のようになります：
\begin{eqnarray}
{\sf R}_{b,t}^{\rm end} &=& \frac{1}{\cos\theta} \tag{4.42} \\
{\sf R}_{b,s}^{\rm end} &=& \frac{1}{\cos\theta} \tag{4.43} \\
{\sf R}_{b,t}^{\rm end} &=& \frac{y_0 \log (y_1/y_0)}{W_e\cos\theta} \\
&=& \frac{\log (f_e / n_e)}{2 \tan\theta\cos^2\theta} \tag{4.44}
\end{eqnarray}
\(s\) と \(t\) の両方の方向について \(R\) を一緒に乗算することで(\(\delta_{b,s}^{\rm end} = \delta_{b,t}^{\rm end}\) であるので，\({\sf R}_{b,s}^{\rm end} = {\sf R}_{b,t}^{\rm end}\) であることを思い出してください），ニア平面の距離の比に対してはるかに遠く，非常に広いあるいは狭い視野角を持つ視錐台について \(\sf S\) が最も大きいということがわかります。典型的な視野角はどこかの間で落ちるので，\((f_e/n_e)\) の比が支配的な要因となります。重要解像度因子は端面については大抵 \(O(1)\) で，側面については \(O(\log(f_e/n_e))\) です。これらのパラメータライゼーションは透視エイリアシングのタイトな境界に基づいているので，ほぼ最適値です。これらの誤差境界は最大誤差を最小化するための基準線を表しています。
　次の章では，最悪場合の誤差境界を持つLogPSMパラメータライゼーションが最適に近い \(\delta_b\) パラメータライゼーションとあらゆる点で等しいということを示します。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.67 より引用。