D. Brandon Lloyd氏の博士論文である，Logarithmic Perspective Shadow Mapsを適当に訳していくことにします。
前回はChapter.2をざっくり訳しました。今回はChapter.3を訳していきます。このChapter.3は論文のメインとなる4章のシャドウマップの解析に使うための数式を紹介する大事な所です。
誤訳があったりなど，日本語としては多々見苦しい点があるかと思いますが，そこはご容赦ください。

---

CHAPTER 3

Shadow map aliasing error

この章では，ギザギザなシャドウの境界を生じさせるエイリアシング誤差の定量化の方法を説明します。我々は，ここで次の章で様々なシャドウマップパラメータライゼーションを解析するために数式を用います。最初に2次元の環境におけるエイリアシング誤差について導き出します。我々が知る限りでは，一般的なライト位置における点光源に対する透視エイリアシング誤差の定量化を初めて解析するのが我々です。解析はディレクショナルライトにも拡張します。過去の研究における解析は典型的にはいくつかの特定の設定に対するディレクショナルライトに関して行われています(Stamminger & Drettakis, 2002; Wimmerら, 2004; Lloyedら，2006)。注目すべき特例(Zhangら，2006b)は角度の範囲上のディレクショナルライトについて透視エイリアシング誤差を計算していますが，視錐台を通じた単一直線に沿ったもののみです。我々は2次元解析を3次元にも拡張します。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.42 より引用。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.43 より引用。

 

3.1 Quantifying aliasing error

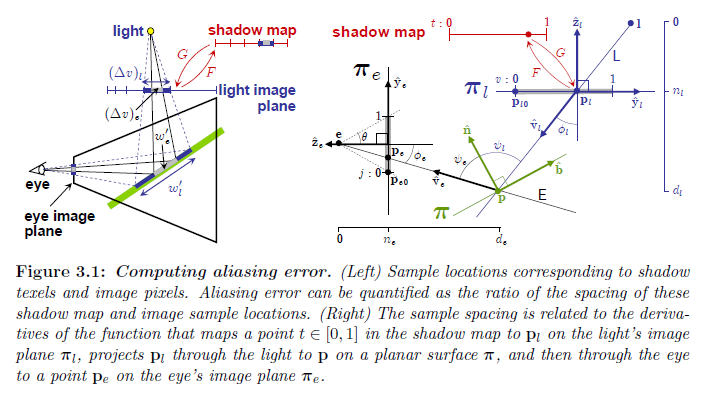
エイリアシング誤差は，ライトの視点からのシャドウマップ描画とカメラ視点からの画像のサンプル点間のミスマッチによって引き起こされます。理想的には，レイトレーシングやイレギュラーZバッファのようなものでライトサンプルとアイサンプルが正確に一致します。シャドウマップのワーピング手法は代わりにサンプリング比率に合うものを探します。我々の導出では，幾何学的でより直感的で理解しやすいのでサンプル間の空間で動作するものを選択します。図3.1は，単純な2次元のシーンにおける様々な場所においてアイサンプルとライトサンプルが一致するサンプル空間を示しています。エイリアシング誤差はアイサンプルよりもライトサンプルが大きくなったときに発生します。 \(j~{\in}~[0,1]\) と \(t~{\in}~[0,1]\) をそれぞれ正規化された画像座標とシャドウマップ座標として定義します。3次元の錐台の横からの視点で本質的には見ているため， \(j\) と \(t\) を座標として選択します。また，後で3次元についての方程式について考えるときに， \(i\) と \(s\) を座標として使用します。画像中のピクセルのサイズは \(1/{r_j}\) です。ここで，\(r_j\) は画像解像度とします。シャドウマップ中のテクセルのサイズは同様にして \(1/{r_t}\) になります。エイリアシング誤差は次のように定量化することができます：
\[
m = \frac{r_j}{r_t}\frac{dj}{dt} \tag{3.1}
\]
\(m>1\) のときにエイリアシング誤差が発生します。

※表はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.44 より引用。

 

3.2 Deriving the aliasing error equation

式3.1における \({dj}/{dt}\) を微分するために，シャドウマップから画像上の一致する場所へとサンプルをトレーシングすることによって図3.1からの関数 \(j(t)\) を計算します。最初に表記を紹介します。点 \(\bf{p}\) とベクトル \(\vec{\bf{v}}\) はアフィン座標系で列ベクトルとして表現され，最後の入力が点については1になり，ベクトルについては0になります。より簡単な式は完全同次座標系を用いることによって得られるかもしませんが，アフィン座標系で計算するのは簡単で，興味があるのは距離と角度の項でエイリアシングを直感的に定義することです。\(\vec{\bf{v}}\) は正規化されたベクトルです。平面 \(\pi\)（または2次元上の線）は行ベクトル \(({\hat{\bf{n}}}^{\sf{\top}}, -D)\) です。ここで，\(D\) は法線ベクトル\(\vec{\bf{n}}\)に沿った原点から平面（線）への距離とします。内積 \(\pi{\bf{p}}\) は平面 \(\bf{p}\) の符号付き距離を与え，内積 \(\pi\hat{\bf{v}}\) は \(\hat{\bf{n}}\cdot\hat{\bf{v}} = \cos\theta\) を得ます。ここで \(\theta\) は \(\hat{\bf{n}}\) と \(\hat{\bf{v}}\) の間の角度とします。
　関数 \(G\) は，シャドウマップパラメータライゼーション \(F\) の逆関数で，正規化されたライト平面座標 \(v \in [0, 1]\) へとシャドウマップ上の点 \(t\) をマップします。ライト画像平面 \(\pi_{l}\) 上の点 \({\bf{p}}_{l}\) は次によって与えられる \(v\) に一致します：
\[
{\bf{p}}_{l} = {\bf{p}}_{l0} + vW_{l}\hat{\bf{y}}_{l} \tag{3.2}
\]
　ここで，\(W_{l}\) はシャドウマップに覆われた \(\pi_{l}\) の一部分の幅です。ライト位置 \(\bf{l}\) を通る線 \(\sf{L}\) に沿った平面サーフェイス \(\pi\) 上の \(\bf{p}_{l}\) への射影は次式を得ます：
\[
{\bf{p}} = {\bf{p}}_{l} – \frac{\pi{\bf{p}}_{l}}{\pi({\bf{p}}_{l}-{\bf{l}})}({\bf{p}}_{l}-{\bf{l}}) \tag{3.3}
\]
このとき，この点はカメラ視点位置 \(\bf{e}\)を通る線 \(\sf{E}\) に沿ったaアイ画像平面 \(\pi_{e}\) へと射影されます：
\[
{\bf{p}_{e}} = {\bf{p}} – \frac{\pi_{e}{\bf{p}}}{\pi_{e}({\bf{e}} – {\bf{p}})}({\bf{e}} – {\bf{p}}) \tag{3.4}
\]
\(v\) によってライト画像平面がパラメータライゼーションされたのと同様にアイ画像平面は \(j\) によってパラメータライゼーションされます。座標 \(j\) は \(\bf{p}_{e}\) から計算することができます：
\[
j = \frac{\hat{\bf{y}}_{e} \cdot ({\bf{p}}_{e} – {\bf{p}}_{e0})}{W_{e}} = \frac{\hat{\bf{y}}_{e}^{\sf{\top}} ({\bf{p}}_{e} – {\bf{p}}_{e0})}{W_{e}} \tag{3.5}
\]
\(dj/dt\) を計算するために，連鎖律を使用します：

\begin{eqnarray}
\frac{dj}{dt} &=& \frac{{\partial}j}{{\partial}{\bf{p}}_e} \frac{{\partial}{\bf{p}}_e}{{\partial}{\bf{p}}} \frac{{\partial}{\bf{p}}}{{\partial}{\bf{p}}_l} \frac{{\partial}{\bf{p}}_l}{{\partial}v} \frac{dv}{dt} \tag{3.6} \\
\frac{{\partial}j}{{\partial}{\bf{p}}_e} &=& \frac{\hat{\bf{y}}_{e}^{\sf{\top}}}{W_e} \tag{3.7} \\
\frac{{\partial}{\bf{p}}_e}{{\partial}{\bf{p}}} &=& I + \frac{\pi_{e}\bf{p}}{\pi_{e}(e ~-~ {\bf{p}})}I ~ – ~ \frac{\pi_{e}{\bf{e}}}{(\pi_{e}({\bf{c}}_{e} ~ – ~{\bf{p}}))^2}(({\bf{e}}~- ~{\bf{p}}){\pi}_e) \tag{3.8} \\
\frac{{\partial}{\bf{p}}}{{\partial}{\bf{p}}_l} &=& I + \frac{\pi{\bf{p}}_{l}}{\pi({\bf{p}}_{l} ~-~ {\bf{l}})}I + \frac{\pi}{(\pi({\bf{p}}_{l}~-~{\bf{l}}))^2}(({\bf{p}}_l ~-~{\bf{l}})\pi) \tag{3.9} \\
\frac{{\partial}{\bf{p}}}{{\partial}v} &=& W_{l}{\hat{{\bf{y}}}}_l \tag{3.10} \\
\frac{dv}{dt} &=& \frac{dG}{dt} \tag{3.11} \\
\end{eqnarray}
式3.7から3.10はヤコビ行列で表現されています。\(I\) は単位行列です。導関数 \(dj/dt\) は単純な形へ整理することができます。まず最初に式3.9から3.11を一緒に乗算します：
\begin{eqnarray}
\frac{{\partial}{\bf{p}}}{{\partial}t} &=& \frac{{\partial}{\bf{p}}}{{\partial}{\bf{p}}_l} \frac{{\partial}{\bf{p}}_l}{{\partial}v} \frac{{\partial}v}{{\partial}t} \\
&=& W_l \frac{dG}{dt} \frac{\pi{\bf{l}}}{\pi({\bf{p}}_l ~-~ {\bf{l}})} \left( \hat{\bf{y}}_l ~-~ \frac{\pi{\hat{\bf{y}}}}{\pi({\bf{p}}_l ~-~ {\bf{l}})}({\bf{p}}_l ~-~ {\bf{l}})\right) \tag{3.12}
\end{eqnarray}
\(\pi{\bf{l}}\) と \(\pi({\bf{p}}_l ~-~ {\bf{l}})\) 項は \(d_l\) と \(n_l\) にそれぞれ比例するので，\(d_l/n_l\) の比に置き換えることができます。従って，\(\pi{\hat{\bf{y}}}_l = -{\sin}{\beta}_l\) です。\(({\bf{p}}_l ~-~ {\bf{l}}) = {\parallel}{\bf{p}}_l ~-~ {\bf{l}} {\parallel}{\hat{\bf{v}}}_l\) を代入します。ここで，\(-{\hat{\bf{v}}}\) はライトの方向ベクトルです。\( {\parallel}{\bf{p}}_l ~-~ {\bf{l}} {\parallel} \) 項はキャンセルされて\(\hat{\bf{v}}\) のみが残ります。このとき，\(\pi{\hat{\bf{v}}}\) は \(-\cos{\psi}_l\) で置き換えられます：
\[
\frac{{\partial}{\bf{p}}}{{\partial}t} = W_l \frac{dG}{dt} \frac{d_l}{n_l}\left(\hat{\bf{y}} – \frac{\sin\beta_l}{\cos\psi_l}{\hat{\bf{v}}}_l\right) \tag{3.13}
\]
　このとき，\(\hat{\bf{n}}\) と \(\hat{\bf{b}}\) の項で， \(\hat{\bf{y}}\) と \(\hat{\bf{v}}\) を展開します：
\begin{eqnarray}
\hat{\bf{y}}_l &=& \cos{\beta}_l{\hat{\bf{b}}} ~-~ \sin{\beta}_l{\hat{\bf{n}}} \tag{3.14} \\
\hat{\bf{v}}_l &=& – \sin{\psi}_l{\hat{\bf{b}}} ~-~ \cos{\psi}_l{\hat{\bf{n}}} \tag{3.15} \\
\end{eqnarray}
式3.13にこれらの式を置換し，\(\psi_l – \beta_l = \phi_l\) であることを用いて次式を得ます：
\begin{eqnarray}
\frac{dp}{dt} &=& W_l \frac{dG}{dt} \frac{d_l}{n_l} \frac{(\cos{\psi}_l\cos{\beta}_l + \sin{\psi}_l\sin{\beta}_l)}{\cos{\psi}_l}{\hat{\bf{b}}} \\
&=& W_l \frac{dG}{dt} \frac{d_l}{n_l} \frac{\cos({\psi_l – \beta_l})}{\cos{\psi}_l}{\hat{\bf{b}}} \\
&=& W_l \frac{dG}{dt} \frac{d_l}{n_l} \frac{\cos\phi_l}{\cos\psi_l}{\hat{\bf{b}}} \tag{3.16} \\
\end{eqnarray}
今，式3.7，3.8と3.16を一緒に乗算して，\(\pi_e {\bf{e}} = n_e \)，\( \pi_e ({\bf{e}} ~-~ {\bf{p}}) = d_e \) と \(({\bf{e}} ~-~ {\bf{p}}) = \parallel{{\bf{e}}-{\bf{p}}}\parallel\hat{\bf{v}}_e\) を置き換えます：
\[
\frac{dj}{dt} = \frac{W_l}{W_e} \frac{n_e}{n_l} \frac{d_l}{d_e} \left(\hat{\bf{y}}_e^{\sf{\top}}\hat{\bf{b}} – \frac{({\hat{\bf{y}}}_e^{\sf{\top}} {\hat{\bf{v}}}_e)( {\hat{\pi}}_e {\hat{\bf{b}}})}{\pi_e{\hat{\bf{v}}}_e}\right) \tag{3.17}
\]
\({\hat{\bf{y}}}_e^{\sf{\top}} {\hat{\bf{b}}} = \cos\beta_e\)，\({\hat{\bf{y}}}_e^{\sf{\top}} {\hat{\bf{v}}}_e = \sin\phi_e\)，\(\pi_e \hat{\bf{b}} = \sin\beta_e\)，そして \(\pi_e {\hat{\bf{v}}}_e = \cos\phi_e \) さらに， \(\beta_e – \phi_e = \psi_e \)であることを利用して，\(dj/dt\) の単純化された型を得ます：
\begin{eqnarray}
\frac{dj}{dt} &=& \frac{W_l}{W_e} \frac{n_e}{n_l} \frac{d_l}{d_e} \frac{(\cos\phi_e \cos\beta_e + \sin\phi_e\sin\beta_e)}{\cos\phi_e} \\
&=& \frac{W_l}{W_e} \frac{n_e}{n_l} \frac{d_l}{d_e} \frac{\cos(\beta_e – \phi_e)}{\cos\phi_e} \\
&=& \frac{W_l}{W_e} \frac{n_e}{n_l} \frac{d_l}{d_e} \frac{\cos\psi_e}{\cos\phi_e} \tag{3.18}
\end{eqnarray}
式3.1へと \(dj/dt\) を当てはめることで，エイリアシング誤差の最終的な表現を得ます:
\[
m = \frac{r_j}{r_t} \frac{dG}{dt} \frac{W_l}{W_e} \frac{n_e}{n_l} \frac{d_l}{d_e} \frac{\cos\phi_l}{\cos\phi_e} \frac{\cos\psi_e}{\cos\psi_l} \tag{3.19}
\]
 

3.2.1 Intuitive derivation.

式3.19におけるいくつかの直感の基になる項は同値を考えることによって得ることが出来ますが，シーン上のサーフェイスの関連するサンプル空間から \(m\) の厳密な導出よりも劣ります（図3.1参照)。ライト画像平面の領域を通るライトからのビームは幅 \({w_l}^\prime\) を持つサーフェイス上へと射影した単一のシャドウマップのピクセル一致します。幅 \({w_e}^{\prime}\) を持つサーフェイスへと射影したピクセルを通る眼からのビームもまた同じです。サーフェイス上のエイリアシング誤差は射影されたビームの幅の比によって与えられます：
\[
m = \frac{{w_l}^\prime}{{w_e}^\prime} \tag{3.20}
\]
相似な三角形によってカメラ視点からの距離 \(n_e\) における \(\pi_e\) 上のピクセルの幅は \(d_e\) の距離において，\({w_e}^{\perp {\hat{\bf{z}}}_e}\) になります。ここで，サーフェイスと交差するビームは以下になります：
\[
{w_e}^{\perp {\hat{\bf{z}}}_e} = \frac{W_e}{r_j} \frac{d_e}{n_e} \tag{3.21}
\]
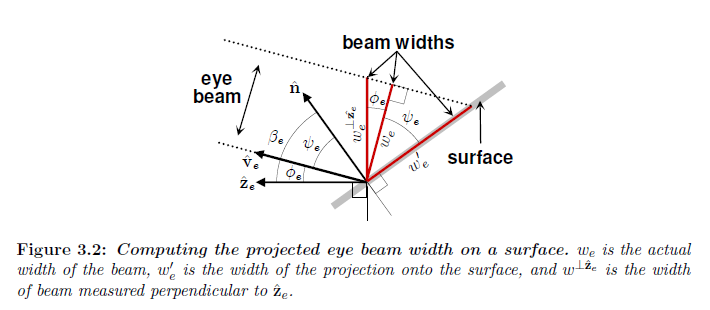
狭いビームに対しては，ビームのサイドが本質的には平行であるということを想定しています。図3.2から我々は \(\cos\phi_e\) によって \({w_e}^{\perp {\hat{\bf{z}}}_e}\) を乗算することが実際のビーム幅を与えることと， \(\cos\psi_e\) で除算することが射影した \({w_e}^\prime\) の幅を与えることがわかります：
\begin{eqnarray}
{w_e} &=& {w_e}^{\perp {\hat{\bf{z}}}_e} \cos\phi_e \tag{3.22} \\
{w_e}^\prime &=& \frac{w_e}{\cos\psi_e} = \frac{W_e}{r_j} \frac{d_e}{n_e} \frac{\cos\phi_e}{\cos\psi_e} \tag{3.23}
\end{eqnarray}
同様に，シャドウマップテクセルはサーフェイス上の射影されたライトのビーム幅を生成するライト画像平面上の \(\left(W_l/r_t\right) \left(dG/dt\right) \) のセグメント幅に一致します：
\[
{w_l}^{\prime} = \frac{W_l}{r_t} \frac{dG}{dt} \frac{d_l}{n_l} \frac{\cos\phi_l}{\cos\psi_l} \tag{3.24}
\]
式3.23と3.24を式3.20へと代入することで式3.19を得ます。
 

3.2.2 Directional lights

\(\bf{l}\) におけるポイントライトは方向 \(\hat{\bf{l}}\) に沿って無限大に向かって動くのでディレクショナルライトになります。式3.3は次にように収束します：
\[
{\bf{p}} = {\bf{p}}_l – \frac{\pi \bf{p}_l}{\pi \hat{\bf{l}}} \hat{\bf{l}} \tag{3.25}
\]
式3.9は次のようになります：
\[
\frac{{\partial}\bf{p}}{{\partial}\bf{p}_l} = {\bf{I}} – \frac{1}{\pi\hat{\bf{l}}} \hat{\bf{l}}\pi \tag{3.26}
\]
式3.19において，\(n_l/d_l\) の項は1に収束し，\(\cos\phi_e\) の項は定数になります。
　式3.19における \(m\) についての式は以前の研究のエイリアシングについて同じ類のものが使われました(Stamminger & Drettakis, 2002; Wimmerら, 2004; Zhangら, 2006b)。けれども，我々の定式の方がより一般的です。なぜかというと，ポイントライトとディレクショナルライトの両方について有効であり，\(\phi_e\) と \(\phi_l\) のそれぞれの関数として様々なアイビームとライトビームの幅を考慮しているからです。
 

3.3 Factoring aliasing error

我々の目標はエイリアシング誤差 \(m\) 上でタイトな領域を計算することで，このときに低い誤差のシャドウマップパラメータライゼーション \(F\)の定式化を使用します。便宜上，\(m\) を2つの主な部分に分解します：
\begin{eqnarray}
m &=& \frac{(\Delta v)_l}{(\Delta v)_e} \tag{3.27} \\
(\Delta v)_l &=& \frac{1}{r_t} \frac{dv}{dt} = \frac{1}{r_t} \delta_l \\
(\Delta v)_e &=& \frac{1}{r_j} = \frac{1}{r_j} \delta_e \\
\delta_l &=& \frac{dG}{dt} = \left( \frac{dG}{dv} \right)^{-1} \tag{3.28} \\
\delta_e &=& \tilde{\delta_e} \frac{\cos\psi_l}{\cos \psi_e} \tag{3.29} \\
\tilde{\delta_e} &=& \frac{W_e}{W_l} \frac{n_l}{n_e} \frac{d_e}{d_l} \frac{\cos\phi_e}{\cos\phi_l} \tag{3.30}
\end{eqnarray}
直感的に言えば， \((\Delta v)_l \) と \((\Delta v)_e\) はライトサンプルとアイサンプルに一致する間のスペースです（図3.1参照）。この因数分解は \((\Delta v)_e\) がライト，カメラ，そしてシーンの設定によって固定されるジオメトリ項をすべてカプセル化するので便利です。一方で，\((\Delta v)_l\) はエイリアシング制御を操作することができる2つの要素―すなわち，エイリアシングの分布を決めるパラメータライゼーションと全体のスケールを制御するシャドウマップ解像度―をカプセル化します。ポイントライトに関して，ライト画像平面の向きもまた，ライトのサンプル分布に影響を与えるので，エイリアシング誤差になります。シャドウマップを描画するために用いるライト画像平面とライト錐台のニア平面に区別をつけます。ニア平面は典型的には，そのほかの考えに基づき選ばれます。例えば，ライト錐台上のシーンジオメトリを適切に囲むようなものとして選択されます。1つのライト画像平面はパラメータライゼーションへと取り込むことができる射影変換によって互いに関係づけられているので(Appendix A参照)，計算について便利な”標準の”ライト画像平面を使用し，もう1つの画像平面は実際にシャドウマップを描画するのに使用します。解像度要素に依存するスペース関数と空間分布関数 \(\delta_l\) と \(\delta_e\) はそれぞれ単純に微分 \(dv/dt\) と \(dv/dj\) です。次の章では，エイリアシング誤差を最小化するための \(\delta_e\) を近似する \(\delta_l\) を生成するパラメータライゼーション \(F\) を微分します。この理由のため，我々はその逆関数の代わりに \(F\) の項で \(\delta_l\) を表現しています。
　StammingerとDrettakis(2002)に続くように，\(\delta_e\) は2つの構成要素へと因数分解することが可能です―すなわち，透視要素 \(\tilde{\delta_e}\) と射影要素 \(\cos\psi_e / \cos\psi_l \) です。透視要素は1点に関係のあるカメラ視点とライトの位置のみに依存します。視錐台上のすべての点上で透視要素は有界値になり，比較的スムーズ時に変化します。一方でシーン上のサーフェイスの向きに依存する射影要素は潜在的に有界値にならず，シーンに垂直に依存するものは複雑な方法で劇的に変化します。シーン依存の解析のような複雑なコストを負うことなくリアルタイムレンダリングに従順な単純なパラメータライゼーションを得るために，多くのアルゴリズムは射影要素を無視して透視エイリアシング誤差 \(\tilde{m}\) のみ解決します：
\[
\tilde{m} = \frac{r_j}{r_t} \frac{\delta_l}{\tilde{\delta_e}} = \frac{w_e}{w_l} \tag{3.31}
\]
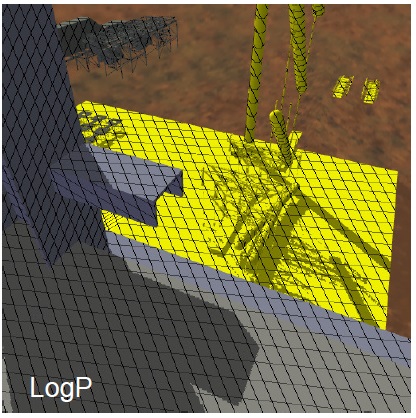
\(\tilde{m}\) は1点におけるライトビームとアイビームの幅の比率を測るものとして考えることができます。代わりに \(\tilde{m}\) は視線方向 \(\hat{\bf{v}_e}\) とライト方向 \(-\hat{\bf{v}_l}\) の間の中間に位置する法線を持つサーフェイス上のエイリアシング誤差として考えることができます。そのようなサーフェイスの射影要素は1です。画像における透視エイリアシング誤差を視覚化するために，このことを使用することができます。この論文を通じてエイリアシング誤差を視覚化するためにシーン上のシャドウマップからのグリッドを射影します。けれども，我々が見るのは射影エイリアシングと透視エイリアシングの組み合わせです。シーン上で適切に方向付けされた平面の”プローブ”周りに移動させることによって視錐台の差分領域に対して直接透視エイリアシングを視覚化することができます。
 

3.4 Aliasing error in 3D

これまでのところ，我々は2次元上でのエイリアシング誤差を解析しました。3次元上では，2次元座標 \({\bf{i}} = (i, j)^{\top}, {\bf{u}} = (u, v)^{\top} \) そして， \({\bf{s}} = (s, t)^{\top}\) それぞれによって，カメラ視点からの画像平面，ライト画像平面，そしてシャドウマップをパラメータライゼーションします。各座標は \([0,1]\) の範囲です。式3.2は次のようになります：
\[
{\bf{p}}_l = {\bf{p}}_{l0} + uW_{lx}\hat{x}_l + vW_{ly}\hat{y}_l \tag{3.32}
\]
式3.3と3.4は同じままです。式3.5における \(W_e\) を方向指定された \(W_{ey}\) で置換して，\(i\)　を計算するために式を追加します：
\[
i = \frac{\hat{x}_e^{\top}({\bf{p}}_e – {\bf{p}}_{e0} )}{W_{ex}} \tag{3.33}
\]
ライト画像平面のパラメータライゼーションは今2次元の関数 \({\bf{u}} = {\bf{G}}(s)\) です。これらの変更により，画像上のシャドウマップのテクセルの射影は今エイリアシング行列 \({\bf{M}}_a\) によって記述されます：
\begin{eqnarray}
{\bf{M}}_a &=&
\begin{bmatrix}
r_i & 0 \\
0 & r_j
\end{bmatrix} \frac{{\partial}{\bf{i}}}{{\partial}{\bf{s}}}
\begin{bmatrix}
\frac{1}{r_s} & 0 \\
0 & \frac{1}{r_t}
\end{bmatrix}
\tag {3.34} \\
\frac{{\partial}{\bf{i}}}{{\partial}{\bf{s}}} &=&
\begin{bmatrix}
\frac{\partial i}{\partial s} & \frac{\partial i}{\partial t} \\
\frac{\partial j}{\partial s} & \frac{\partial j}{\partial t}
\end{bmatrix} = \frac{\partial {\bf{i}}}{\partial {\bf{p}}_e} \frac{\partial {\bf{p}}_e}{\partial {\bf{p}}} \frac{\partial {\bf{p}}}{\partial {\bf{p}}_l} \frac{\partial {\bf{p}}_l}{\partial {\bf{u}}} \frac{\partial {\bf{u}}}{\partial {\bf{s}}} \tag{3.35} \\
\frac{\partial {\bf{i}}}{\partial {\bf{p}}_e} &=&
\begin{bmatrix}
\frac{\hat{\bf{x}}_e^{\top}}{W_{ex}} \\
\frac{\hat{\bf{y}}_e^{\top}}{W_{ey}}
\end{bmatrix} \tag{3.36} \\
\frac{\partial {\bf{p}}_l}{\partial {\bf{u}}} &=&
\begin{bmatrix}
W_{lx}\hat{\bf{x}}_l & W_{ly}\hat{\bf{y}}_l
\end{bmatrix}
\tag{3.37} \\
\frac{\partial {\bf{u}}}{\partial {\bf{s}}} &=& \frac{\partial {\bf{G}}}{\partial {\bf{s}}} \tag{3.38}
\end{eqnarray}
エイリアシング誤差の測定値を得るためには，\({\bf{M}}_a\) の要素の関数である測定基準 \(h\) を定義する必要があります。行列ノルム，例えば \(p\) ノルムやフロベニウスノルムや，行列式は画像中の射影されたシャドウマップテクセルの面積を近似するので \(h\) を含む可能性があります。
　3次元においては，空間分布関数 \(\delta_l\) と \(\delta_e\) は2×2のヤコビ行列です：　
\begin{eqnarray}
\delta_l &=& \frac{\partial {\bf{G}}}{\partial {\bf{s}}} = \left( \frac{\partial {\bf{F}}}{\partial {\bf{u}}} \right) ^{-1} \tag{3.39} \\
\delta_e &=& \left( \frac{\partial {\bf{i}}}{\partial {\bf{u}}} \right)^{-1} \tag{3.40}
\end{eqnarray}
\(\delta_e\) を透視と射影の要素に因数分解するのは2次元のように単純ではありません。いくつかの可能性が存在します。2次元の透視誤差の直感に基づく1つのアプローチは1点におけるライトビームとアイビームの微分断面積 \({\bf{X}}_e\) と \({\bf{X}}_l\) を計算することになる可能性があり，比率 \({\tilde m} = h({\bf{X}}_l) / h({\bf{X}}_e) \) として透視エイリアシング誤差を定義します。もう1つの可能性は \({\tilde m} = h({\bf{M}}_a)\) をとることです。 ここで，\({\bf{M}}_a\) を計算するために使われる平面サーフェイスの法線は \(\hat{{\bf{v}}}_e\) と \(- \hat{{\bf{v}}}_l\) の間の中間に方向付けされます。しかし2次元の場合とは異なり，これら2つのアプローチは同等であるとは限りません。
 

3.5 Summary

この章ではポイントライトとディレクショナルライトの両方について2次元と3次元の両方でエイリアシング誤差を計算する方法を示しました。次の章では，誤差を最小化するパラメータライゼーションを生成するためエイリアシング誤差上でタイトな領域を導出するために，これらの式を使用します。5章では，これらの領域を様々なパラメータライゼーションの分析をするために使用します。