こんにちわ、Pocolです。
今日は,
[Sloan 2008] Peter-Pike Sloan, “Stupid Spherical Harmonics (SH) Tricks”, GDC 2008
を読んでみようと思います。
いつもながら誤字・誤訳があるかと思いますので,ご指摘頂ける場合は正しい翻訳例と共に指摘していただけると幸いです。
概要
本論文は、GDC2008の同名の講演に付随するものです。球面調和関数(SH)の概要を説明し、インタラクティブ・グラフィックスにおけるSHの利用方法と発生しうる問題点をいくつか取り上げます。特に、次のような問題に焦点をあてています。SHを使用した照明モデルの効率的な評価方法、「リンギング」とは何か、それに対する対処法、SH productの効率的な評価とその使用場所、などです。最新版は、Webサイト(http://www.ppsloan.org/publications)でご覧いただけます。
導入
ラプラス方程式の解である調和関数[2]は、様々な分野で広く利用されています。球面調和関数は、球面に限定した場合の解です。熱方程式(温度の時間変化のモデル化[5][25])や重力場、電場[9]など、物理学の潜在的な問題の解決に利用されています。また、量子化学や量子物理学の分野では、原子の電子配置のモデル化、量子角運動量のモデル化などに用いられています[16][51]。よりグラフィックスに近いところでは、散乱現象のモデル化にも使われています[7][17]。コンピュータグラフィックスでは,初期の用途として,体積散乱効果のモデリング[18],グローバルシャドウのないマイクロファセットBRDFの環境反射[6],非拡散オフライン光輸送シミュレーション[40],BRDF表現[53],画像再照明[28],制御可能な照明での画像ベースのレンダリング[54][55],光源発光のモデリング[8]に広く使用されています。さらに最近の例としては,大気散乱[50]やコンピュータビジョン[3]におけるより多くの研究があります。
今回は、インタラクティブレンダリングに関するテクニックを中心に紹介します。ゲームに広く利用されている最初の論文は、球面調和関数を利用して放射照度環境マップを効率的に表現し、遠方照明下の拡散オブジェクトのインタラクティブなレンダリングを可能にすることを扱っています[35]。これは,同じ制約のもとでBRDFの限られたクラスを処理するために拡張されました[36]。PRT(Precomputed Radiance Transfer) [41][20][24] モデルは,拡散マテリアルや単純な光沢のあるマテリアルを持つソフトシャドウや相互反射のような複雑なグローバルイルミネーション効果を含む照明環境に対する静的オブジェクト/シーンの応答を,しばしばSHを用いて表現します。これは,より一般的な BRDF モデル [20][23][42] を扱い,表面下散乱を取り入れ [42],機械学習からの圧縮技術によってレンダリング効率を大幅に改善し [42],サーフェイスディテールのような「ローカル」テクスチャをモデル化する様々な技術 [43][44][45] に拡張されました。SH は遠方の照明環境からの単一散乱をモデリングするために使用されています [49]。他の用途としては,遠方照明の仮定を持ち上げるための勾配の使用[1],相互反射のサポートを含む動的オブジェクトを扱ういくつかのテクニック[56][37],一般的なBRDFモデルでオブジェクトの影をモデル化するための可視性の表現[12],変形可能オブジェクトから影をモデル化するためのスケーリング演算子の使用[52],屈折のパラメータ化 [11] 及び法線マップでの詳細度問題 [15] へのテクニックとして使われてきました。
より実用的な論文としては、PRTの実装の詳細[13]、これらの技術をエンジンに統合する方法[30]、放射照度ボリュームにSH+勾配を使用する方法[31][32]、投影に関する実用的問題とSH係数を効率的に量子化する方法 [21]、解析的スカイライトモデル [34] をSHに投影してグローバルポリノミアルフィットを使ってモデルパラメータの関数としてSHライトプローブを評価する素晴らしい論文 [14] が含まれます。また、SHを用いて半球上に定義された投影関数をより頑健にするための数値的手法も研究されています[22]。
リアルタイムグラフィックスでの用途の多くは、球面調和関数(視認性、照明、反射率)を表現する便利な方法としてだけです。使用できる基底関数は、ウェーブレット[39]、キューブマップ上のウェーブレット[27]、球面放射状基底関数[9]、その他[26]と多数ありますが、球面調和関数はこのドキュメントで説明するいくつかの素晴らしい特性を持っています。これらの他の基底関数がより適切であるシナリオがあることを強調することが重要です。
球面調和関数というと、なんだか難しそうなイメージがありますが、実は簡単なんです。球面調和は、単位円上のフーリエ基底の球面版であり、数値的に評価することが容易です。信号処理で使われるフーリエ基底と同様に、系列の切り捨てには注意が必要で(ビデオゲームでは必ず行われる)、発生しうる「リンギング」アーティファクトを最小限に抑えることができます。この記事では、球面調和関数を使用して効率的にライトを評価し表現する方法、SH表現から従来のライトを取り出す方法、「リンギング」とその影響を最小限に抑える緩和技術について説明し、球面調和関数を使用した関数の積について、それらが有用で最適化する価値のある特殊ケースを説明します。
背景
定義 球面調和関数は、球面S上の正規直交基底を定義します。以下のパラメータ化を使用します。
\begin{eqnarray}
s = (x, y, z) = (\sin\theta \cos\phi, \sin \theta \sin \phi, \cos\theta)
\end{eqnarray}
ここで、\(s\)はシンプルに単位球面上の位置です。基底関数は次のように定義されます。
\begin{eqnarray}
Y^m_l (\theta, \phi) = K^m_l e^{im\phi}P^{|m|}_l (\cos\theta), l \in {\mathbb N}, -l \leq m \leq l
\end{eqnarray}
ここで,\(P^m_l\) は関連するルジャンドル多項式,\(K^m_l\) は正規化定数で
\begin{eqnarray}
K^m_l = \sqrt{ \frac{(2l+1)(l-|m|)!}{4\pi(l+|m|)!} }
\end{eqnarray}
上記の定義は複素数形式(非グラフィックスの文献で最もよく使われる)に対するもので、実数値基底は変換によって与えられます
\begin{eqnarray}
y^m_l = \begin{cases}
\sqrt{2}{\rm Re}(Y^m_l) & m \gt 0 \\
\sqrt{2}{\rm Im}(Y^m_l) & m \lt 0 \\
Y^0_l & m = 0
\end{cases}
= \begin{cases}
\sqrt{2} K^m_l \cos m \phi P^m_l (\cos\theta) & m \gt 0 \\
\sqrt{2} K^m_l \sin |m| \phi P^{|m|}_l (\cos \theta) & m \lt 0 \\
K^0_l P^0_l (\cos\theta) & m = 0
\end{cases}
\end{eqnarray}
インデックス/は”帯”を表します。各帯はその次数の多項式と等価であり(つまり0は単なる定数関数、1は線形関数など)、ある帯には2/+1個の関数が存在します。球座標は積分を計算するときに便利ですが、積分を評価するときによく行われるように、多項式を使って表すこともできます(詳しくは付録A1 SH基底関数の評価の再帰規則と付録A2 SH基底の多項式形式を参照してください)。次数\(n\)のSH展開では、次数\(n-1\)までの基底関数を全て使用します。
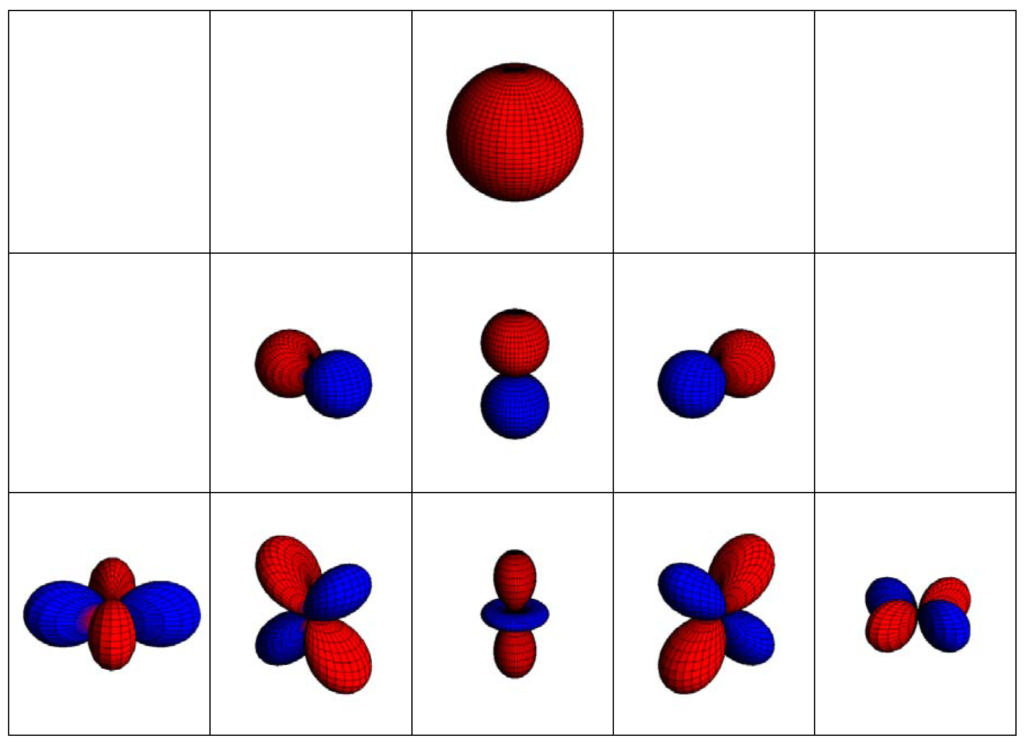
球面調和関数は、いくつかの方法で視覚化することができます。一つは、単位球を歪ませ、各点を関数の絶対値で放射状に拡大縮小し、符号に基づいて色付けする方法です(赤はプラス、青はマイナス)。
中央の列(\(l=0\))の関数は帯域調和関数(ZH)と呼ばれ、後述しますが、これらの関数はz軸まわりに回転対称であり、ゼロ(関数がゼロとなる位置)はXY平面に平行な球面上の等高線である。また、(\(l=|m|\))となる関数を扇状調和関数と呼び、その零点はリンゴの輪切りのような領域を定義します。
また、平面上に展開されたキューブマップのパラメター化を使って描くという方法もあります。キューブマップの展開図は以下の通りです。
ここでは、大きさを色で表現し(赤正、青負、緑ゼロ)、等濃度輪郭を均等に配置(白線)して、関数の勾配をより直感的に理解できるようにしました(束になると関数の変化が速くなる、など)。
投影と再構成 SH基底は直交正規分布なので、\({\mathbf S}\)上で定義されたスカラー関数\(f\)の最小二乗法による射影は、射影したい関数\(f(s)\)を基底関数に対して積分するだけです(付録A6 最小二乗法射影で証明します)。
\begin{eqnarray}
f^m_l = \int f(s) y^m_l (s) ds
\end{eqnarray}
これらの係数を用いて、関数\(f\)の近似値を再構成することができます。
\begin{eqnarray}
{\tilde f}(s) = \sum_{l=0}^n \sum_{m=-l}^l f^m_l y^m_l (s)
\end{eqnarray}
これは、帯の数\(n\)が増えるにつれて、ますます正確になっていきます。この論文では、低周波の\(f\)の近似に焦点を当て、高周波の表現には他の基底がより良い仕事をする傾向があります。\(n\)次への射影は\(n^2\)個の係数を生成します。投影係数と基底関数の両方に1つのインデックスを使用するのが便利な場合があります。
\begin{eqnarray}
{\tilde f}(s) = \sum_{i=0}^{n^2} f_i y_i (s)
\end{eqnarray}
ここで,\(i=l(l+1)+m\)です。この定式化により、近似関数の方向 \(s\) における評価は、\(n^2\) の係数ベクトル \(f_i\) と評価基底関数ベクトル \(y_i(s)\) との内積を意味することが分かります。最初の係数 (インデックス付けにより \(f^0_0\) または \(f_0\)) は球面上の関数の平均値を表し、DC項と呼ばれることもあります。
基本特性 SHの重要な特性の1つに、投影と回転の相互作用があります。関数 \(g(s)\) が、関数 \(f(s)\) を回転行列 \(Q\) で回転させたもので、 \(g(s) = f(Q(s))\) であるとすると、 \(g\) の射影は \({\tilde f}\) を回転させて再射影したものと同じになります。この回転不変性は、フーリエ変換の並進不変性と似ています。このことは、例えば、照明が回転しても安定で、エイリアシングアーティファクトや光源の “揺れ “が発生しないことを意味します。下図は、ディレクショナルライトによって照らされた球体の画像で、上段はSH、下段はValve[26]のアンビエントキューブ基底形式を使用したものです。最初の列はベストケースの方向で、2番目はワーストケースに近いものです。SHを用いた画像は不変量です。この基底については、付録A9 アンビエントキューブ基底で詳しく説明します。これは球面上で定義された他の基底でもある程度は起こることでしょう。
SH基底の直交性により、任意の2つのSH関数\(a\)、\(b\)が与えられた場合、その積の積分は単純に係数ベクトルの内積となります: \(\int {\tilde a}(s) {\tilde b}(s) = \sum_{i=0}^{n^2} a_i b_i\)
畳み込み 円対称性を持つカーネル関数\(h(z)\)があれば、そのカーネルと元の関数 \(f\) を畳み込んだ結果である新しい SH 関数を生成できます。畳み込んだ結果も回転群 \({\mathbf{SO}}(3)\) ではなく球面 \({\mathbf S}\) で表現するためには \(h\) は円対称でなければなりません。畳み込みは、次の式を用いて周波数領域で直接行うことができます:
\begin{eqnarray}
(h \ast f)^m_l = \sqrt{ \frac{4\pi}{2l+1} } h^0_l f^m_l
\end{eqnarray}
これは、\(f\)の各帯を\(h\)の対応する\(m=0\)の項で単純にスケーリングすることに等しいです。
回転 前述したように、SHは回転して閉じています。SHの回転行列はブロック構造になっており、各帯は回転独立で、\((2l+1) \times (2l+1)\)の密な部分行列を持ちます。この回転行列を計算する方法はいくつかありますが、非常に小さい次数(2次以下)では記号的に計算するのが最も効率的ですが、大きい次数では回転行列をzyz個のオイラー角に分解するのが効率的と思われます [19]。
帯域調和関数 軸を中心とした回転対称性を持つ関数の球面調和射影を帯域調和関数(ZH)と呼びます。この軸をZとするように向きを変えれば、関数のゼロは一定の緯度の線を形成し、関数は\(\theta\)にのみ依存します。この向きの係数ベクトルは、1帯につき1つの非ゼロしか持たないので、\(n\)次の関数は\(n^2\)ではなく\(n\)個の係数を持つことになります。帯域調和関数は伝達を近似するために使用されており[44]、散乱理論における位相関数の一般的な表現であり[7][17]、本論文では光源のモデリング時に広く使用されます。ZHの回転は一般的なSHよりも単純で、事実上対角行列で行うことができ、新しい方向\(d\)でSH基底関数を評価する必要があるだけです。関数のZH係数(SH投影からの\(m=0\)の項のみ)\(z_l\)があれば、この方程式を使って新しい方向\(d\)に回転することが可能です:
\begin{eqnarray}
f(s) = \sum_{l} z_l \sqrt{ \frac{4\pi}{2l+1} } \sum_{m} y^m_l (d) y^m_l(s)
\end{eqnarray}
そのため、結果的にSH係数は
\begin{eqnarray}
f^m_l = \sqrt{ \frac{4\pi}{2l+1} } z_l y^m_l(d)
\end{eqnarray}
となります。
SH Products \(n\)次SHを用いて表現された2つの関数\(f\)と\(g\)の積の\(k\)番目の係数をSHに射影すると、以下の形になります:
\begin{eqnarray}
p_k = \int y_k(s) \left( \sum_{i=0}^{n^2} f_i y_i(s) \right) \left( \sum_{j=0}^{n^2} g_i y_j(s) \right) ds = \sum_{ij} \Gamma_{ijk} f_i g_j
\end{eqnarray}
ここで,\(\Gamma\)はテンソル3重積です:
\begin{eqnarray}
\Gamma_{ijk} = \int y_i(s) y_j(s) y_k(s) ds
\end{eqnarray}
は、次数3の疎な対称テンソルです。SHは多項式なので、多項式積は最大次数\(2n-2\)となり、次数\(2n-1\)までの非ゼロの係数を持つことになります。これは乗算される関数の数が増えると広がらなくなるので、積を早めに切り捨てるのが一般的です[56][37]。\(n\)の関数としての非ゼロ係数の数は非常に大きいので[47][37]、効率的なコードを生成する際には注意が必要です。特殊なケースとして、関数 \(f\) が固定されている場合(つまり、遠方照明)、”積行列”\(M_f\) を計算することで、コストを大幅に削減できることが挙げられます。この行列は対称であり、以下の式を使って構築されます。
\begin{eqnarray}
(M_f)_{ij} = \sum_k \Gamma_{ijk} f_k
\end{eqnarray}
この場合の関数\(g\)との積の計算は、単純に行列のベクトル積となります。
放射照度環境マップ
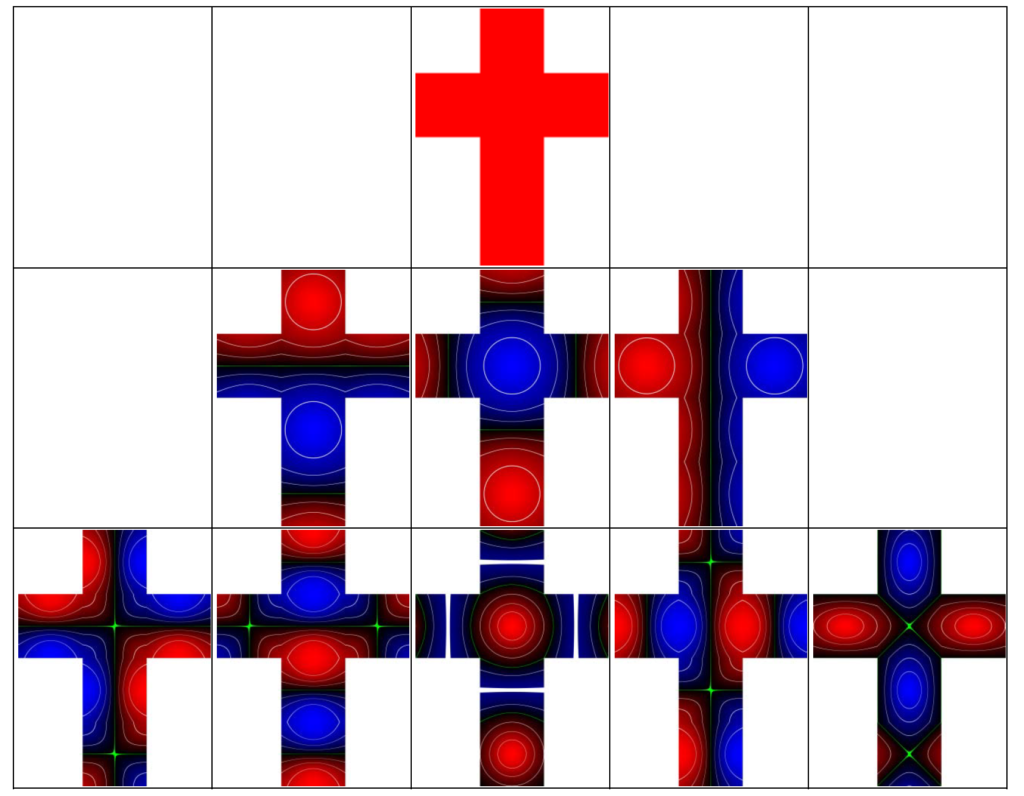
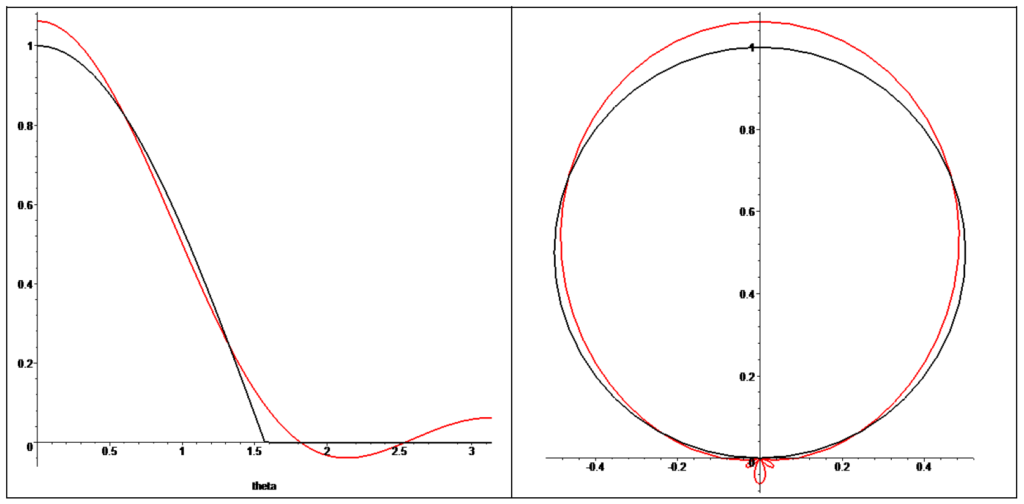
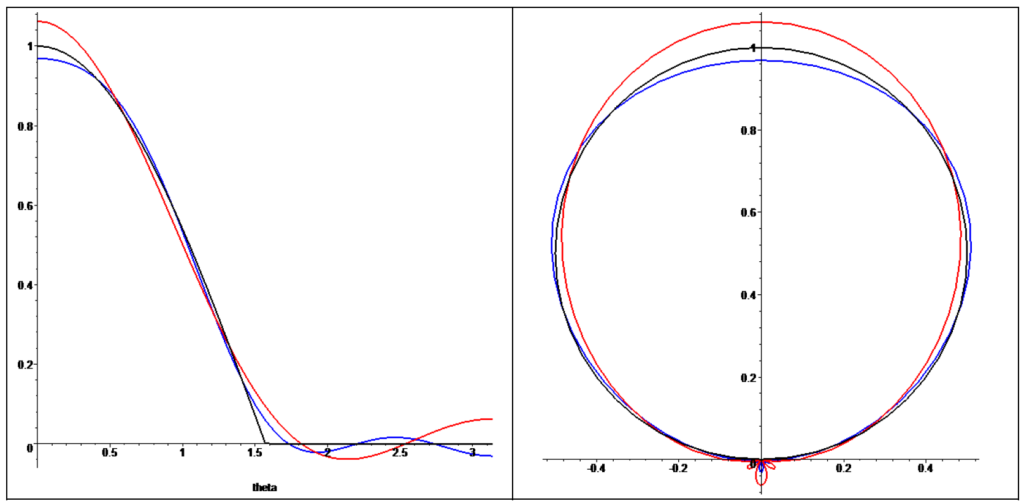
放射照度環境マップは、ライトプローブとクランプされたコサイン関数の畳み込みによって作成され、これを\(\pi\)で割って正規化することで放射輝度を表示します。この畳み込みはSH[35]を使って効率的に行うことができ、SHから直接レンダリングしても十分に効率的な精度が得られます。次数3のSHはこのカーネルをうまく近似しますが、HDR光源が使用される場合は、次数5の使用を検討することをお勧めします(次数4のZH係数はゼロなので、そのバンドはスキップできます)。下の図は、クランプされたコサインカーネルと次数3のSH近似のイメージです。赤いカーブがSH近似で、左の図は\(\theta\)の関数としてのプロット、右の図は関数の絶対値でスケーリングした極座標のプロットです。
以下は、次数5の投影(青)も含めたプロットです。
次数3のSH近似は、\(\theta=0\)(北極)で1/16の過剰推定となり、南極で1/16の大きさの誤ったローブを持ちます。法線が当たると17の値を反射するディレクショナルライトが、逆方向を向くと1の値を反射する(0を反射するはず)。次数5近似は負のローブを持ち、法線が真下を向いたときに31を反射するようなディレクショナルライトでは-1を反射することになります。これらの近似は正確ですが、特に非常に明るい光源を使用している場合、近似によって誤差が生じることがあります。
付録 A10 放射照度環境マップの為のシェーダ/CPUコードには、放射照度環境マップを効率的に評価するためのシェーダと CPU コードが含まれています。
ライティングモデル
SHで照明を表現する方法は様々です。最もシンプルなのはキューブマップから投影するだけですが、安価に評価できる解析モデルもあり、アーティストに公開するのに役立つ可能性があります。最近の論文[14]は、実用的なスカイライトモデル[34]をSHに投影し、モデルのパラメータ空間上でSH係数のグローバル多項式を適合させるという素晴らしい仕事をしています。
キューブマップからの射影
キューブマップから射影するには、キューブマップに対してSH基底関数を積分すればよいです。これは、テクセルの中心方向にSH基底関数を評価し、そのテクセルの差分立体角で重み付けし、結果を正規化することで数値的に行うことができます。擬似コードは次のようになります。
float f[], fs[];
float fWtSum=0;
Foreach(cube map face)
Foreach(texe)
float fTmp = 1 + u^2 + v^2;
float fWt = 4 / (sqrt(fTmp) * fTmp);
EvalSHBasis(texel, s);
f += t(texel) * fWt * s; // vector
fWtSum += fWt;
f *= 4 * Pi / fWtSum; // area of sphere
上のコードで、uとvは与えられた面上の座標で+/-1でない2つの座標を表し、t(texel)はテクセルの色を表します。EvalSHBasis は、入力座標(立方体の面上)を正規化し、その方向で SH 基底関数を単純に評価する必要があります。差分立体角の正規化された和は 4 * Pi になるはずなので、最後の正規化は省略できます(代わりにサンプル数で割ればよい)が、少しずれる傾向があります(特に低解像度のキューブマップを使用する場合)。
以下は、HDRライトプローブを1~6次までの球面調和関数に再構成した画像です。最後の画像は、投影されたライトプローブです。
解析モデル
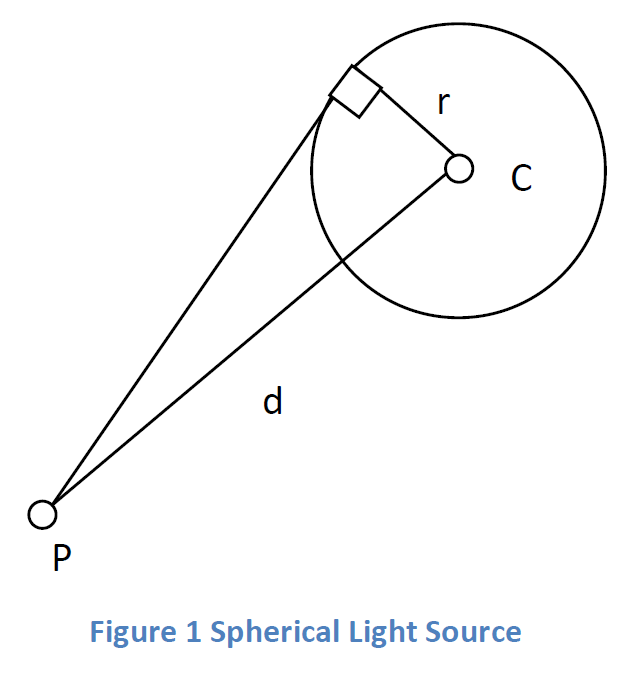
ディレクショナルライトは計算が簡単で、与えられた方向のSH基底関数を評価し、適切にスケーリングするだけです(正規化セクションを参照)。球状光源は、帯域調和関数を使って効率的に評価できます。中心C、半径rの球面光源がある場合、d単位離れた点Pに到達する放射輝度はどのようになるでしょうか? 光源の半角のsinはr/dですから、球面の適当な部分を差し引く光源を計算すればよいでしょう。ZH係数は、この角度の関数として閉じた形で計算することができます:\(z_l = \int_{\theta=0}^a \int_{\phi=0}^{2\pi} y^0_l d\phi d\theta\) ここで,\(a\)は半角に対する値です。6次までの式は付録A3 球状光源に対するZH係数を参照してください。
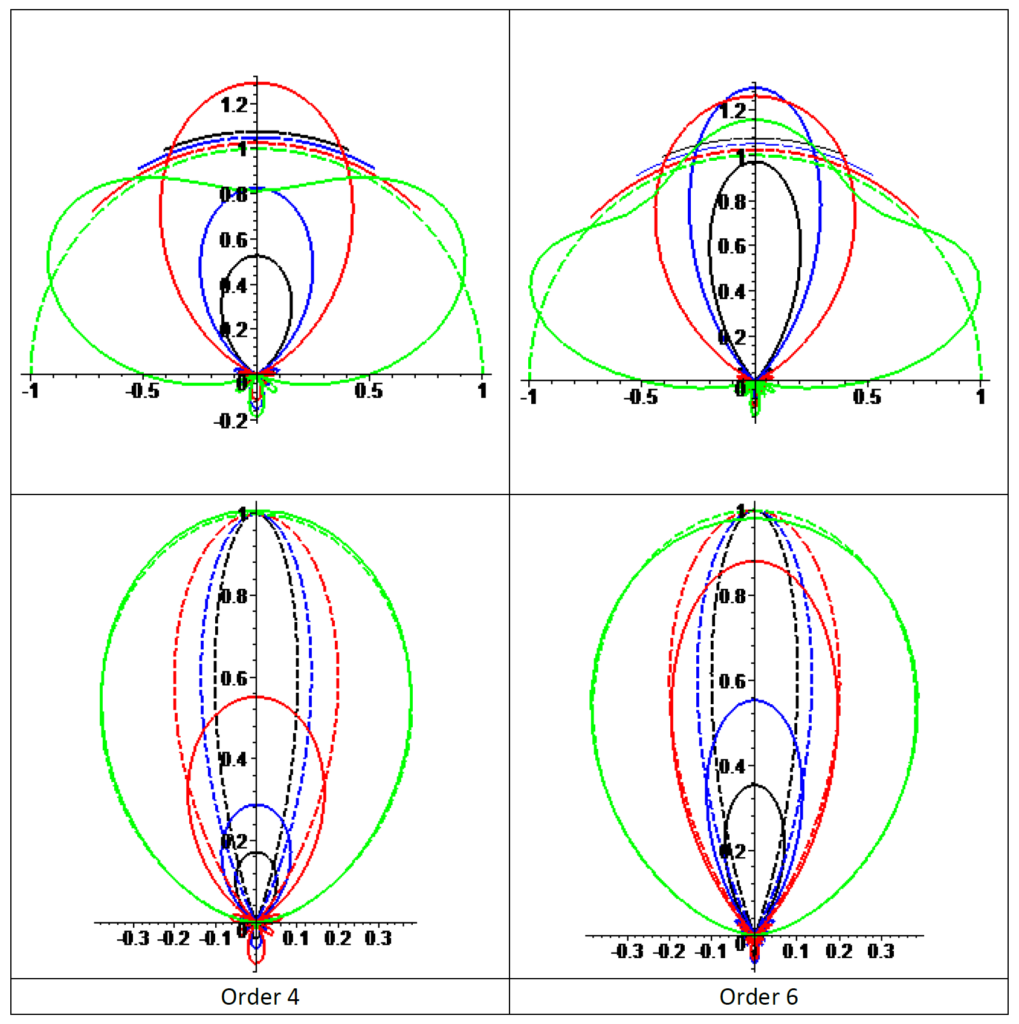
球面技法は、一定の発光を持つ円錐(無限遠の円盤と考えてください)をモデル化するためにも使用できます。より柔らかい円錐は、可視部分にわたって滑らかなフォールオフを持つようにモデル化することができます - 式は付録 A4 スムース円錐の為のZH係数を参照してください。
列はオーダー4と6のもので、上段は円錐の投影、下段は滑らかに落ちる円錐の投影です。角度は90(緑)、45(赤)、30(青)、12.5(黒)度です。破線は実際の関数(円錐の場合は重ならないように少しずらしてあります)、実線はSH近似です。一般にソフトコーンの方が良い挙動を示します。投影で発生するアーティファクトにどのように対処するかは、以下の”リンギング”のセクションの主題となっています。
正規化
[0, 1]の照明が使用されている場合、光源を直接指す法線を持つ影のないレシーバーの反射放射輝度が1.0となるように放射輝度ベクトルを正規化すると便利です。数学的には、照明ベクトルLに乗じたときに、非占有クランプコサインローブ(正規化クランプコサインのSHへの投影)を表すベクトル\(T\)に対して積分したときに単位反射放射輝度になるスケールファクター\(c\)を計算したいわけです。そのため,次を得ます:
\begin{eqnarray}
1 = \int cL(s) T(s) ds \overset{yields}\longrightarrow c = \frac{1}{dot(L, V)}
\end{eqnarray}
レンダリングに使用する帯のみ、正規化係数を計算する際に使用する必要があります。\(T\) を +Z に合わせると簡単な解析式が得られます。以下は、最初の 6 つのバンドに対する \(T\) の係数です。
\begin{eqnarray}
\frac{1}{2\sqrt{\pi}}, \frac{\sqrt{3}}{3\sqrt{\pi}}, \frac{\sqrt{5}}{8\sqrt{\pi}}, 0 \frac{-1}{16\sqrt{\pi}}, 0
\end{eqnarray}
解析的なライトについては、解析的な正規化項を使用することができます。角度\(a\)のコーンライトについては、次のようになります。
\begin{eqnarray}
\frac{1}{\sin^2 a}
\end{eqnarray}
しかし、クランプされたコサイン関数と光源の両方の投影誤差が考慮されないため、結果として得られる光は単位輝度を反映したものになりません。ディレクショナルライトの場合、正規化係数は\(\frac{16\pi}{17}\)で、”アンビエント”ライトの場合は\(2\sqrt{\pi}\)となります。
SHから畳み込みライトの抽出
SH照明ベクトルがある場合、1つのディレクショナルライトと環境光源として近似することが可能です。頂点シェーダをサポートしないハードウェアで利用されています。数学的には、任意のサーフェイス法線(\(N\))に対して、反射放射輝度の二乗誤差が最小になるように、ディレクショナルライトの強度(\(c\))と環境光源の強度(\(a\))を計算したいのです。光源の方向(\(d\))が固定されていると仮定すると、最小化したい誤差関数は次のようになります:
\begin{eqnarray}
E(c, a) = \int ( c H_N(d) + a – \int L_e(s) H_N(s) ds)^2 dN
\end{eqnarray}
ここで,\(H_N (x) = max(dot(N, x)/\pi, 0)\)は正規化されたクランプされたコサインです。照明\(L_e(s)\)をSHで表現した場合、これには簡単な解法があります。新しい照明環境が表す照度環境マップは、入力照度環境マップにできるだけ近いものであるべきです - この2つの環境マップの二乗誤差を最小化することは、すべての法線に対する反射放射輝度を最小化することと等価です。
\begin{eqnarray}
E(c, a) = \int (cL_d(s) \ast H_N(s) + aL_a(s) \ast H_N(s) – L_e(s) \ast H_N(s))^2 ds
\end{eqnarray}
ここで\(L_d(s)\)は方向\(d\)の正規化SHディレクショナルライト、\(L_a(s)\)は正規化SH定常光(DCに依存するだけ)です。最適な値\(a\)と\(c\)は次のようになります。
\begin{eqnarray}
c &=& \frac{867}{316\pi} dot_0({\hat L}_d, {\hat L}_e) \\
a &=& \left( {\hat L}_e[0] – c \frac{8 \sqrt{\pi}}{17} \right) \frac{\sqrt{\pi}}{2}
\end{eqnarray}
上記の照明ベクトルは、すべて正規化クランプコサインカーネルで畳み込み、放射照度環境マップに変換されます。上記の内積はDC項を無視し、\({\hat L}_e[0]\)は照明環境のDC項です。上記は既知の方向を想定していますが,良い候補は,照明環境の線形係数であるベクトル\((-{\hat L}_e[3], -{\hat L}_e[1], {\hat L}_e[2])\)を正規化して形成される「最適な線形」方向です[44].
複数ライトの抽出
また、SHライトプローブから複数の光を抽出することも可能です。これは、リンギング対策(解析ライトはネガティブローブを持たない)、光沢反射のモデル化(この方法で引き出された光源のみ)、または少数のシャドウZバッファー(BRDFの拡散部分と光沢部分の両方のライトsを引き出す)のために行うことができます。最適な線形方向は、ライトプローブが単一の光源によって支配されている場合にうまく機能します。そうでない場合は、ライトの方向と強度を何らかの方法で最適化する必要があります。関数の局所的な最大値を見つけるために「丘の上」を登るというのも一つの方法です。SHがいかに滑らかであるかを考えると、与えられた次数に対して、明確なピークからその距離だけ離れた点が、勾配上昇を使ってその点に到達することが保証される有限の距離が存在します。そのボロノイセルの中心から最も遠い球面上の点が、この距離より小さいという性質を持つ点の集合を生成することができます。これらの点のそれぞれから探索を開始すれば、すべての点の局所最大値を見つけることができるはずです。これらの距離は、デルタ関数の射影を見て、ピークとゼロの間の角度距離を計算することによって求めることができます。この半径の3分の2という控えめな見積もりを用いると、1次ごとに必要な点の数は、最初の6次について{1, 3, 6, 10, 15, 22}となります。
この点セットは、シミュレーションを計算することで算出することができます。すべての点は、ある種のフォールオフを持つ力(例えば\(1/d^2\)、\(d\)はそれらの間のユークリッド距離)を持ち、他のすべての点に作用します。各点に作用する正味の力を生成し、法線成分を差し引き(つまり単なる接線力)、この力によって点を重み\(w\)で動かします。力の正味の合計が増加したら、\(w\)を半分にしてもう一度試し、減少したら\(w\)を2倍にしてもう一度試します。これは、静電荷の和を最小にするような電子の集合を求める解法です。
SHの照明環境\(L(s)\)があるとき、球面上で局所最大となる点を探したいのですが、これは\(-L(s)\)の局所最小を見つけるのと同じことです。これは非線形最適化問題で、私の経験では少数のBFGS反復計算[29]でピークに収束します。最適化手法を使用する場合、基底関数の勾配を計算する必要があります。球面上の点に対しては多項式を微分するのは簡単ですが、直線探索を行う場合には球面から点を離す必要があるので、係数を正規化する記号入力(例えば、\(f(x, y, z)\)の代わりに\(f(\frac{x}{\sqrt{x^2+y^2+z^2}}, \frac{y}{\sqrt{x^2+y^2+z^2}}, \frac{z}{\sqrt{x^2+y^2+z^2}}\))を使用したいものです。これは、正規化された位置での勾配を単純に計算し、それに正規化関数のヤコビアンを乗じることで行われます。
\begin{eqnarray}
\begin{bmatrix}
\frac{L^2-x^2}{L3} & \frac{-xy}{L} & \frac{-xz}{L} \\
\frac{-xy}{L} & \frac{L^2-y^2}{L^3} & \frac{-yz}{L} \\
\frac{-xz}{L} & \frac{-yz}{L} & \frac{L^2-z^2}{L^3}
\end{bmatrix}
\end{eqnarray}
ここで,\(L\)は\(\sqrt{x^2+y^2+z^2}\)です。
3灯、2灯、1灯のディレクショナルライトと環境光で近似した場合の放射量(上段)と照度(下段)の比較画像です。最も重要なN個のピーク(大きさの点から)が与えられると、最小二乗法でディレクショナルライトと環境光の強度が解かれます。
2つのローブの光強度を計算する方程式は以下の通りです:
\begin{eqnarray}
\begin{bmatrix} c_0 \\ c_1 \end{bmatrix}
= \begin{bmatrix}
\frac{A}{A^2 – B^2} & \frac{-B}{A^2 – B^2} \\
\frac{-B}{A^2 – B^2} & \frac{A}{A^2 – B^2}
\end{bmatrix}
\begin{bmatrix}
L_e \circ L_{d0} \\
L_e \circ L_{d0}
\end{bmatrix}
\end{eqnarray}
ここで,
\begin{eqnarray}
A = L_{d0} \circ L_{d0}, B = L_{d0} \circ L_{d1}
\end{eqnarray}
です。
アンビエント項はこのとき:
\begin{eqnarray}
a = (L_e[0] – (c_0 L_{d0} [0] + c_1 L_{d1} [0])) \frac{\sqrt{\pi}}{2}
\end{eqnarray}
となります。
3つのライトに関して強度は:
\begin{eqnarray}
\begin{bmatrix} c_0 \\ c_1 \\ c_2 \end{bmatrix}
= \begin{bmatrix}
\frac{A^2-D^2}{E} & \frac{CD – AB}{E} & \frac{BD – AC}{E} \\
\frac{CD – AB}{E} & \frac{A^2-C^2}{E} & \frac{BC – AD}{E} \\
\frac{BD – AC}{E} & \frac{BC – AD}{E} & \frac{A^2 -B^2}{E}
\end{bmatrix}
\begin{bmatrix}
L_e \circ L_{d0} \\
L_e \circ L_{d1} \\
L_e \circ L_{d2}
\end{bmatrix}
\end{eqnarray}
となります。ただし,
\begin{eqnarray}
C = L_{d0} \circ L_{d2}, \quad D = L_{d1} \circ L_{d2}, \quad E = 2BCD + A(A^2 – B^2 – C^2 -D^2)
\end{eqnarray}
です。
この行列は対称で,アンビエント係数は:
\begin{eqnarray}
a = (L_e[0] + (c_0 L_{d0}[0] + c_1 L_{d1}[0] + c_2 L_{d2}[0])) \frac{\sqrt{\pi}}{2}
\end{eqnarray}
式の導出は、付録 A5 ディレクショナルライトとアンビエントライトでSH環境マップを近似するための係数の解法にあります。
すべての自由度(方向と強度)を追加し、非線形ソルバーを使用することで、より質の高い結果を得ることができます。
リンギング
ギブス現象とも呼ばれるリンギングは、信号処理でよく見られる問題です。不連続性を持つ信号を有限のフーリエ基底(連続関数しか表現できない)に射影すると、不連続性の周辺でオーバーシュートとアンダーシュートが発生します。不連続性を持たない関数も、射影が切り捨てられると同様の挙動を示すことがあります。このような問題は、照明モデルや照度環境マップの表現(クランプされたコサイン関数の射影)で既に見てきました。同様の問題は、サーフェイスデザインでも起こり、一連の幾何学的制約を満たそうとすると、不要な振動が発生することがあります。これらの問題に対する一般的な解決策は2つあります:
1) シグマ係数を用いた切断投影のウィンドウ化。これは信号処理で最も一般的な解法であり、球面調和関数 [8][41][37] でも些細なことで利用できます。
2) 標準的な最小二乗誤差ではなく、何らかの変分関数の最小化(例えば曲率の測定値の最小化)。これは、コンピュータ支援幾何学設計でよく行われることですが、球面調和関数[38]を使っても効率的に行うことができます。
ウィンドウイング
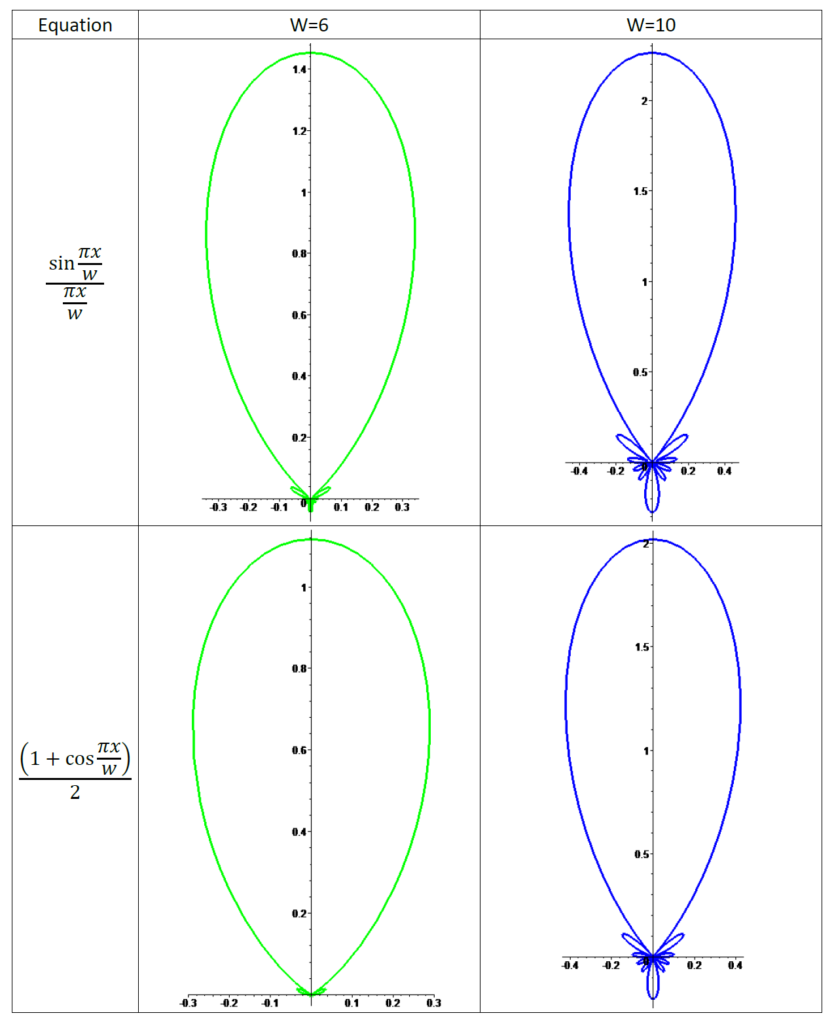
リンギングアーティファクトを最小化する一つの方法は、周波数領域での乗算(空間領域では畳み込み)と、カットオフ周波数に近づくほどゼロになる投影係数を持つカーネルとの乗算です。この関数が、切り捨てられた周波数帯域でゼロになるように引き伸ばされたsincである場合、Lanczonシグマ係数を使用して呼び出されます。直感的には、これは(1Dで)空間領域でタイトなボックス関数で畳み込むことで、関数を十分に滑らかにし、過度のリンギングなしに表現できるようにすることです。ギブス現象を攻略するもっと洗練された方法 [10][4] もありますが、それらはSH係数を用いて区分的解析関数を生成しており、ゲームにはあまり便利ではないでしょう。
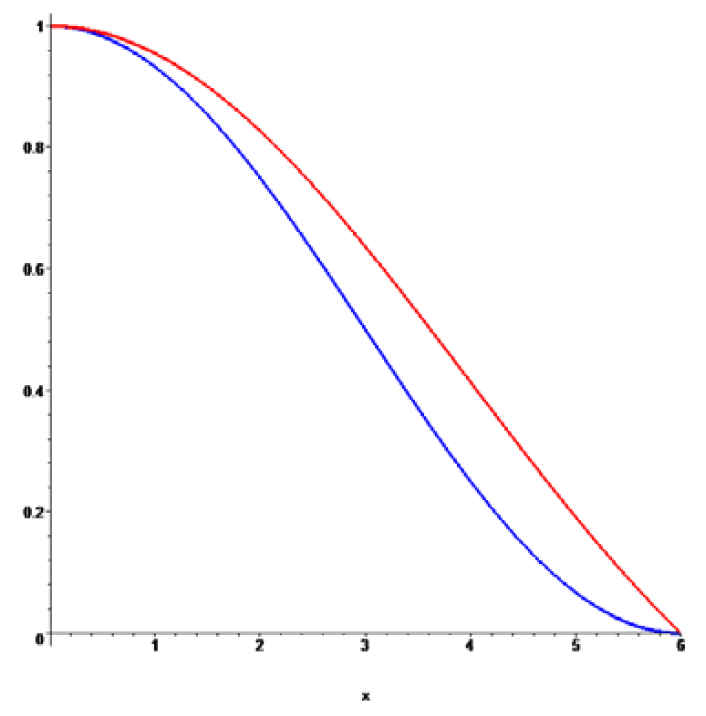
我々の経験では、ウィンドウ関数の選択は、リンギングとブラーがかかることのトレードオフを柔軟に行うことほど重要ではありません。左の画像は、2つの窓関数(赤はsinc、青はraised cosine lobe – Hanning windowと呼ばれる)を6次SH用にスケーリングしたものです(7次バンドでゼロになるように、最後に使用する値は5で評価し、関数は整数値でしか評価されないようにします)。Hanning関数はLancosz関数よりも減衰が速く、より積極的にブラーすることができます。
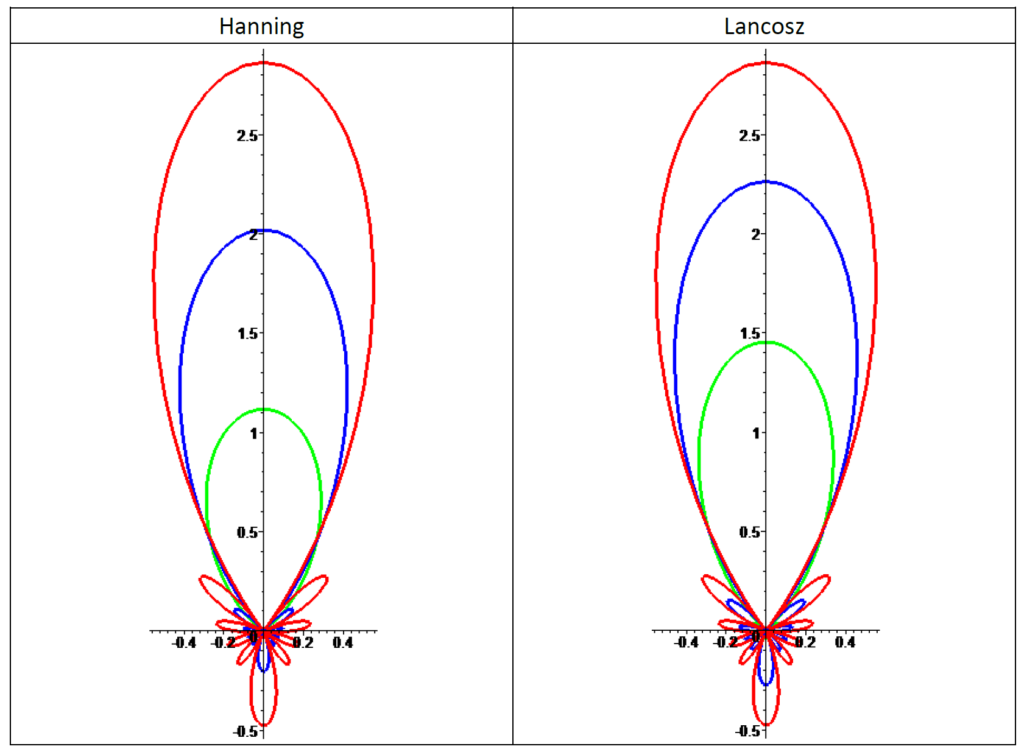
上記では、LanczonsとHanning sigma因子を用いた結果を示しました。投影される信号は次数6のデルタ関数で、SHに投影できる信号の中では「最もピーキー」なもので、リンギングアーティファクトが発生します。デルタ関数の投影はZHなので、球の断面を示していますが、phiは固定です。半径方向の大きさがプロットされ、ローブの符号が交互に変わります。
すべてのグラフを一緒に見ると(赤はデルタ関数の生の投影)、ウィンドウ処理によって信号がぼやけ、リング(図では原点付近に見える)が除去されていることがわかります。
関数の最小化
別のアプローチとして、二乗近似誤差以外の関数を最小化しようとする方法があります。この方法の1つは、制約条件(例えば、少数の点での正確な再構成など)を満たし、残った「スラック」変数(十分な自由度があると仮定)を使って、何らかの誤差関数を最小化する方法です[38]。ゲームやグラフィックでよく使われる低いSH次数を考えると、このアプローチはそれほど実用的とは思えないので、これ以上時間をかけるのはやめようと思います。代替案としては、大きな振動にペナルティを与えるノルムを最小化することを試みることです。これは球面調和関数で簡単に行うことができます。ラプラス演算子、またはラプラシアンは、スカラー関数の勾配の発散であり、等価的に非混合偏導関数の和であります。
\begin{eqnarray}
\Delta f = \frac{df^2}{dx^2} + \frac{df^2}{dy^2} + \frac{df^2}{dz^2}
\end{eqnarray}
単位球面上の球面座標では、次のようになります。
\begin{eqnarray}
\Delta f = \frac{1}{\sin \theta} \frac{d}{d\theta}( \sin \theta \frac{df}{d\theta}) + \frac{1}{\sin^2 \theta} \frac{d^2f}{d\phi^2}
\end{eqnarray}
二乗ラプラシアンの積分は、球面上で使用される曲率測定です[38]。我々が最小化しようとする関数は次のようになります:
\begin{eqnarray}
E(c) = \int \left({\tilde f}(s) – f(s) \right)^2 ds + \lambda \int \left( \Delta {\tilde f}(s) \right)^2 ds
\end{eqnarray}
我々はすでに生の投影係数\(f^m_l\)を知っているので、できるだけ最小二乗の結果に近い新しい係数\(c^m_l\)を見つけると同時に、加重二乗ラプラシアンを最小化したいのです。これは閉じた形で行うことができ[付録A6 最小二乗法による射影参照]、\(\lambda\)が与えられると次のような係数になる。
\begin{eqnarray}
c^m_l = \frac{f^m_l}{(1 + \lambda l^2 (l+1)^2)}
\end{eqnarray}
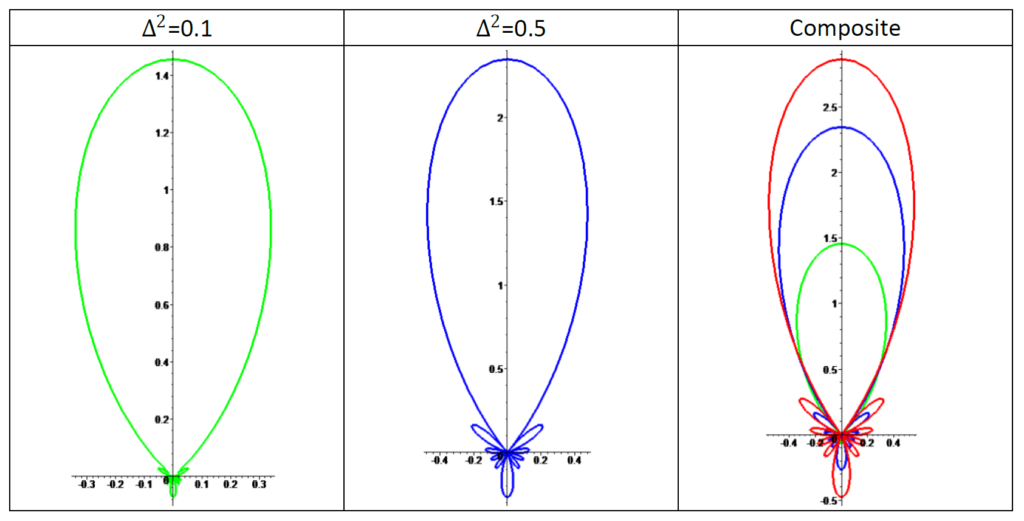
これは、\(\lambda\)に依存する窓関数に相当することに注意してください。ラムダがゼロのときは最小二乗係数が得られ、ラムダが無限大のときは曲率がゼロのDC項だけが得られます。ラムダを選択する一つの方法は、二乗ラプラシアンを固定量、例えば半分に減らすように解くことです。これは、標準的なルート探索のテクニックを使って行うことができます。Newtons法を使った方法については、[付録A7 二乗ラプラシアンを減らすためのラムダの解法]を参照してください。以下は、6次のデルタ関数で、2乗ラプラシアンが元の10% (\(\lambda\) = .004209 green) と50% (\(\lambda\) = .000632 blue)になるように解いた結果です。最終プロットでは、デルタ関数そのものと一緒にそれらを表示しています:
実際の照明環境を使った画像をご紹介します。1列目の画像は、2列目の画像の等高線プロット(青がネガティブ)です。広い(より滑らかな)ウィンドウでウィンドウ処理をしています。4列目の画像は3列目の画像の等高線プロットです – 狭い(ぼやけない)フィルターで平滑化します。一番上の列は元画像で、すべての結果は6次で表示されています。
ウィンドウイングは慎重に使用する必要があります。放射照度環境マップを使用する場合、クランプされたコサイン関数との畳み込みは高周波を積極的に減衰させるので、ウィンドウはほとんど必要ありません。また、法線の変化が大きいシーンでは、レシーバの法線が滑らかなシーンほど、リンギングアーティファクトが目立たない傾向があります。以下は、ウィンドウがシェーディング結果にどのように影響するかを示す、シンプルなシーン(「ドア」と「グランドプレーン」)の画像です。リンギングが発生する領域は、2行目でハイライトされています。
HDRや中程度の明るさの照明を使用する場合、リンギングはより深刻な問題となり、照度環境マップでもある程度のウィンドウ処理が必要となる場合があります。
リンギングで起こりうるもう一つの問題は、カラーアーティファクトです。以下の画像では、明るいディレクショナルイエローライト(右上からほぼリムライト、オーダー6)と適度な環境白色光で球体を照明しています。上段は照度環境マップ、下段は次数6のPRT(コサインカーネルのより正確な近似)を使用しています。1列目は窓なし、2列目は上段で次数5のハニング窓、下段で次数5のハニング窓を使用しています。窓なしバージョンはポジティブローブ(次数3、ネガティブ次数6)の両方を示し、青いバンドはディレクショナルライトのネガティブリングからのものです(周囲光から赤/緑を除去し、青だけを残します)。
コンテンツセンシティブウィンドウ
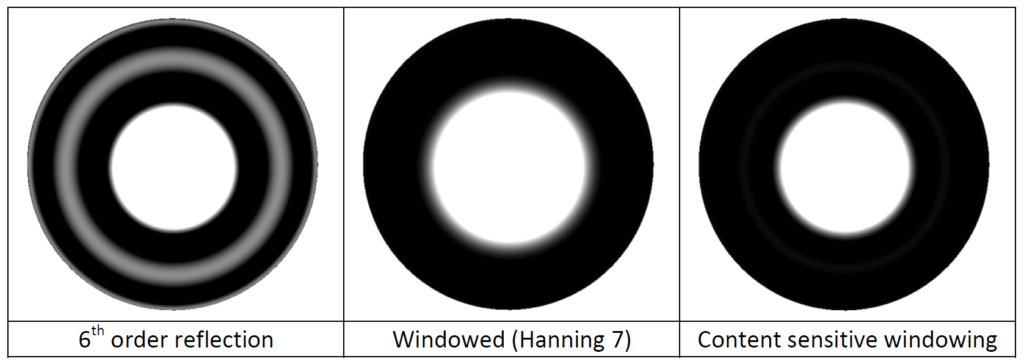
照明はグローバルにウィンドウ化できますが、リングが最終的なシェーディング画像に与える影響に応じてウィンドウ化することも可能です。以下に例を示します。明るいディレクショナルライト(ハイライトが飽和している)を使用して、ややマットな(しかし非拡散 – 指数10のphong)ボールをレンダリングしています。ウィンドウ処理を行わない場合、原則的なハイライトはより鮮明になりますが、リングによるアーティファクトは明確になります。照明がウィンドウ化された場合、リングは消えますが、原理的なハイライトもぼやけている。代わりに、反射ベクトルと支配的な光の方向の間の角度を見ることができます。これが小さい場合、ウィンドウ処理は必要なく、大きくなると、ウィンドウ処理された光源とウィンドウ処理されていない光源の間をブレンドし、リングアーティファクトを除去しながらシャープなハイライトを維持することが可能になります。この一連の画像を以下に示します:
ブレンドの制御に使われる方程式は:
\begin{eqnarray}
w_a = \left( {\rm max} \left( 0, \frac{( (n \circ r ) – c_t}{ 1 – c_t} \right) \right)^p
\end{eqnarray}
ここで、\(w_a\)はウィンドウなし光源のウェイト(ウィンドウありは\(1 – w_a\))、\(c_t\)はウィンドウあり光源を完全に使用するタイミングを決定する閾値、\(p\)はブレンドの遷移領域を制御します。この図では、\(c_t\)は0.07、\(p\)は0.8です。これらのパラメータを実験することができ,閾値はウィンドウの量とマテリアルプロパティに大きく依存します。
光源が指向性でない場合は、ディレクショナルライトでどの程度近似できるかを計算し、それを考慮してブレンドの程度を決めることができます(最も簡単な方法は、照明環境がディレクショナルライトでどの程度近似できるかと、法線/反射ベクトルが支配的光ベクトルにどれだけ近いかのテンソル生成を計算することでしょう)。より複雑なシェーディング、たとえば PRT の場合、支配的な伝達方向を使用することができ、それが伝達関数をどれだけよく近似しているかを、テンソル生成の別の要素とすることができます(したがって、いずれかの項がよく近似されていないときにウィンドウが表示されます)。
照明が非常に動的である場合、照明の変更に伴って発生する可能性のあるテンポラル・アーティファクトに注意する必要があります(例:影や反射がより鮮明になるなど)。静的なSHライトプローブのようなものでは、このテクニックはうまく機能するはずです。
SH Products
SHで表現された2つの関数の積のSH表現を計算することは、度々有用です。例として次のようなシナリオがあります。
3) 大きな飛翔体(視認性×光)、またはシーン(大きな建物など)の簡単な視認性モデルに基づいて、スカイライトモデルに穴を開けることができます。
4) 可視化関数の乗算。これは、動的な近似グローバルイルミネーションを行うときに発生します。
5) SHライトプローブの拡大縮小や修正。ゼロから1の間のある定数を掛けることで、例えば雲を近似的に表現することができます。
周波数領域での積の計算は非常に複雑で、2つのSHベクトルに「テンソル三重積」をかけることに集約されます。このコードは効率的に生成できるので[47]、この論文では説明しません。しかし、言及する価値のあるいくつかの特殊なケースがあります。
定数関数との積
SH関数の1つを多用する場合は、積行列と呼ばれる密な行列を作ることができます。これにより、三重積は単純な行列とベクトルの積になり、コストが大幅に削減されます。6次積の場合、[47]で生成されたコードでは2577回の乗算が必要でしたが、1296回になります。
変化する次数との積
特に、出力の次数が低い場合、例えば2次関数で、局所的な放射環境を表現できるようにするのが一般的です。このような場合のためにコードを特殊化することで、コードの複雑さを大幅に軽減することができます。例えば、2つの6次SHの積は、6次結果を計算するときは2527/1995の乗算/加算がありますが、3次結果を計算するときは933/676だけです。他の例としては、単純なアンビエントオクルージョンがあります。この場合、項の1つは単なるDCなので、単純にDC値で他のベクトルをスケーリングすればよいのです。最後に、2つの関数のうちの1つが低次(つまり、線形可視性を乗じるだけ)である場合も、コストを削減することができます。
帯域調和関数の積
関数の1つが帯域調和関数であれば、もう1つの関数をその同じフレームに回転させ(回転コストが低く、対称性のために2つのオイラー角で済む)、積を計算し、回転を戻します。ZH フレームのスパース性により、かなりの量の作業が不要になり、パフォーマンスを向上させることができます。2つの6次関数の積は、1つはz方向にZHであり、380/249の乗算/加算で済みます。任意のZHの場合、100万個の積(関数の1つは常に任意の方向にaである)の計算時間は約1.2秒であるのに対し、一般の6次積の計算時間は3秒強なので、この手法はほぼ3倍高速であることがわかります。
解析関数との積
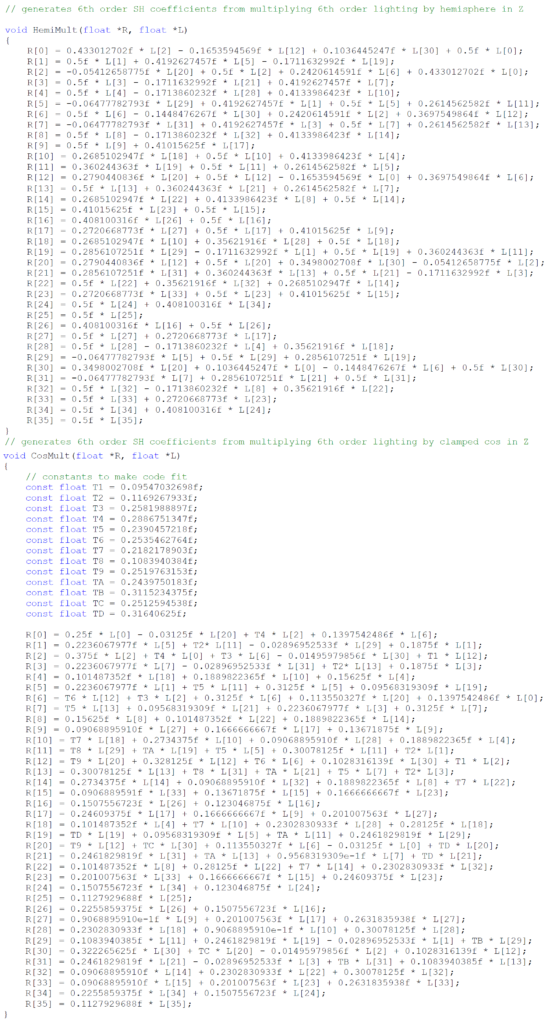
関数の1つが解析的な形式を持つ場合、積行列に相当するものを解析的に計算する方がより正確です。例えば、地平線の下をすべてゼロにしたり(地平線がある場合に有効)、クランプされたコサイン関数との積をとったりします。これを解析的に行うことは、解析関数の無限次展開を行うことと同じであり、一般に、このような場合、SH展開を用いるよりもはるかに高速になります。この2つの例のコードは付録A8「SHと解析関数の乗算コード」にあります。
結論
球面調和関数は、ゲームでは特にライティングに非常に有効なツールです。この記事では、球面調和関数をどのように使用するか、また、球面調和関数を使用する際に発生するいくつかの問題をどのように軽減するかについて、いくつかの光を当てることができればと思います。ネガ(またはポジ)ローブの大きさを最小にするようなウィンドウ係数(任意のウィンドウ関数を使用)を求めることもできますし、ゼロであるべき方向を向いているときの反射放射輝度の大きさを最小にすることもできます。ライトを抽出する場合、非線形最適化に基づくより厳密な技術を使用することができ[29][44]、より一般的な照明モデル(例えば、議論された光源を形成する円錐角を含む)を抽出することができます。また,フィッティングプロセスにウィンドウ処理を結びつけることも検討する価値があるかもしれません。最初は関数の平滑化されたバージョンでフィットし、その後、効果的により良いローカルミニマムへのステアリングを行うために、ウィンドウの量をダイヤルバックします。特にPRTのような手法と統合する場合、コンテンツセンシティブなウィンドウウィングのアイデアを具体化する必要があります。
球面調和関数で遊ぶときに重宝しているのが、記号演算プログラムです。私は Maple (http://www/maplesoft.com) を使っていますが、 Mathematica (http://www.wolfram.com) のような他のプログラムでも同様にうまくいきます。DirectX SDK (http://msdn.microsoft.com/directx) には、評価、回転、積、およびいくつかの分析的照明モデルの関数があり、PRTと放射照度の両方の環境マップを使用したサンプルもあります。
謝辞
特にJohn Snyderとは、私たちがMicrosoft Researchのグラフィックスグループで同僚だった頃から、長く実りある一連の論文を発表してきました。また、何人かのゲーム開発者と球面調和関数について議論することができたのも嬉しいことでした。Hao Chen(Bungie)、Arn Arndt、James Grieves、Clint Hanson(当時EA)、Loren McQuade(Blizzard時代)、Dan Baker(MSおよびFiraxis)、Alex Evans(当時Lionhead)、Tom Forsyth(Muchkyfoot)、Willem de Boer(Muckyfoot)、Mnchor Ko(Naughty Dog)、Naty Hoffman(SCEA)、Chris Oat(ATI)ら、何人かのゲーム開発者と球面調和について議論することができたのです。Jason Sandlin、Ben Luna、Jon Steedは、Microsoftでサンプル/テストコードに取り組みました。最後に、GDAlgorithms メーリングリストでの SH やその他のトピックに関する議論に参加できたことは、とても楽しかったです。
参考文献
[1] ANEN, T, KAUTZ, J, DURAND, F, SEIDEL, H. Spherical Harmonic Gradients for Mid-Range Illumination, Eurographics Symposium on Rendering 2004.
[2] AXLER, S, BOURDON, P, RAMEY, W. Harmonic Function Theory, Springer-Verlag, 2000.
[3] BASRI, R, AND JACOBS, D. Lambertian Reflectance and Linear Subspaces, ICCV 2001.
[4] BLAKELY, C, GELB, A, NAVARRA, A. An Automated Method for Recovering Piecewise Smooth Functions on Spheres Free from Gibbs Oscillations, Sampling Theory in Signal and Image Processing Vol 6, No. 3, Sep 2007.
[5] BYERLY, W. An Elementary Treatise on Fourier’s Series and Spherical, Cylindrical and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Phyisics, Dover, 1893.
[6] CABRAL, B, MAX, N, SPRINGMEYER, R. Bidirectional Reflection Functions from Surface Bump Maps, SIGGRAPH 1987.
[7] CHANDRASEKHAR, S. Radiative Transfer, Dover, 1960.
[8] DOBASHI, Y, KANEDA, K, NAKATANI, H, YAMASHITA, H. A Quick Rendering Method Using Basis Functions for Interactive Lighting Design, EUROGRAPHICS 1995.
[9] FREEDEN, W, GERVENS, T, SCHREINER, M. Construction Approximation on the Sphere, Clarendon Press, 1998.
[10] GELB, A. The Resolution of the Gibbs Phenomenon for Spherical Harmonics, Mathematics of Computation, Volume 66, Number 218, April 1997.
[11] GENEVAUX, O, LARUE, F, DISCHLER, J. Interactive Refraction on Complex Static Geometry using Spherical Harmonics, Symposium on Interactive 3D Graphics and Games 2006.
[12] GREEN, P, KAUTZ, J, DURAND, F. Efficient Reflectance and Visibility Approximation for Environment Map Rendering, Eurographics 2007.
[13] GREEN, R. Spherical Harmonic Lighting: The Gritty Details, GDC 2003.
[14] HABEL, R, MUSTATA, B, WIMMER, M. Efficient Spherical Harmonics Lighting with the Preetham Skylight Model. Eurographics 2008.
[15] HAN, C, SUN, B, RAMAMOORTHI, R, GRINSPUN, E. Frequency Domain Normal Map Filtering, SIGGRAPH 2007.
[16] INUI, T, TANABE, Y, ONODERA, Y. Group Theory and Its Applications in Physics, Springer-Verlag, 1996.
[17] ISHIMARU, A. Wave Propagation and Scattering in Random Media, IEEE Press, 1978.
[18] KAJIYA, J, von HERZEN, B. Ray Tracing Volume Densities, SIGGRAPH 1984.
[19] KAUTZ, J, SLOAN, P, SNYDER, J. Fast, Arbitrary BRDF Shading for Low-Frequency Lighting Using Spherical Harmonics, EUROGRAPHICS Workshop On Rendering, 2002.
[20] KAUTZ, J, LEHTINEN, J, SLOAN, P. Precomputed Radiance Transfer: Theory and Practice. SIGGRAPH 2005 course. http://www.cs.ucl.ac.uk/staff/j.kautz/PRTCourse/
[21] KO, J, KO, M, ZWICKER, M. Practical Methods for a PRT-based Shader Using Spherical Harmonics, Shader X6: Advanced Rendering Techniques, 2008.
[22] LANN, P, LEUNG, C, WONG, T. Noise-Resistant Fitting for Spherical Harmonics, IEEE Transactions on Visualization and Computer Graphics. 12(2) 2006.
[23] LEHTINEN, J, KAUTZ, J. Matrix Radiance Transfer, Symposium on Interactive 3D Graphics, 2003.
[24] LEHTINEN, J. A Framework for Precomputed and Captured Light Transport. ACM Transactions on Graphics 26(4) 2007.
[25] MACROBERTS, T. Spherical Harmonics, Dover, 1948.
[26] MCTAGGART, G. Half-Life 2 Source Shading, GDC 2004.
[27] NG, R, RAMAMOORTHI, R, HANRAHAN, P. All-Frequency Shadows Using Non-Linear Wavelet Lighting Approximation, SIGGRAPH 2003.
[28] NIMEROFF,J, SIMONCELLI, E, DORSEY, J. Efficient Re-rendering of Natural Environments, EUGROGRAPHICS Workshop on Rendering, 1994.
[29] NOCEDAL, J, WRIGHT, S. Numerical Optimization, Springer-Verlag 1999.
[30] OAT, C. Adding Spherical Harmonic Lighting to the Sushi Engine. GDC 2004. http://ati.amd.com/developer/gdc/Oat-GDC04-SphericalHarmonicLighting.pdf
[31] OAT, C. Irradiance Volumes for Games. GDC 2005. http://ati.amd.com/developer/gdc/GDC2005_PracticalPRT.pdf
[32] OAT, C. Real-Time Irradiance Volumes, ShaderX 5: Advanced Rendering Techniques, 2006.
[33] PAN, M, WANG, R, LIU, X, PENG, Q, HUJUN, B. Precomputed Radiance Transfer Field for Rendering Interreflections in Dynamic Scenes, Eurographics 2007.
[34] PREETHAM, A, SHIRLEY, P, SMITS, B. A Practical Analytic Model for Daylight, SIGGRAPH 1999.
[35] RAMAMOORTHI, R, AND HANRAHAN, H. An Efficient Representation for Irradiance Environment Maps, SIGGRAPH 2001.
[36] RAMAMOORTHI, R, AND HANRAHAN, H. Frequency Space Environment Map Rendering, SIGGRAPH 2002.
[37] REN, Z, WANG, R, SNYDER, J, ZHOU, K, SUN, B, SLOAN, P, BAO, H, PENG, Q, GUO, B. Real-Time Soft Shadows in Dynamic Scenes Using Spherical Harmonic Exponentiation, SIGGRAPH 2006.
[38] RUFFINI, G, MARCO, J, GRAU, C. Spherical Harmonics Interpolation, Computation of Laplacians and Gauge Theory, arXiv:physics/0206007, 2002.
[39] SCHROEDER, P, SWELDENS, W. Spherical Wavelets: Efficiently Representing Functions on the Sphere, SIGGRAPH 1995.
[40] SILLION, F, ARVO, J, WESTIN, S, GREENBERG, D. A Global Illumination Solution for General Reflectance Distributions, SIGGRAPH 1991.
[41] SLOAN, P, KAUTZ, J, SNYDER, J. Precomputed Radiance Transfer for Real-Time Rendering in Dynamic, Low-Frequency Lighting Environments, SIGGRAPH 2002.
[42] SLOAN, P, HALL, J, HART, J, SNYDER, J. Clustered Principal Components for Precomputed Radiance Transfer, SIGGRAPH 2003.
[43] SLOAN, P, LIU, X, SHUM, H-Y, SNYDER, J. Bi-Scale Radiance Transfer, SIGGRAPH 2003.
[44] SLOAN, P, LUNA, B, SNYDER J, Local, Deformable Precomputed Radiance Transfer, SIGGRAPH 2005.
[45] SLOAN, P. Normal Mapping for Precomputed Radiance Transfer, Symposium on Interactive 3D Graphics and Games 2006.
[46] SLOAN, P, GOVINDARAJU, N, NOWROUZEZAHRAI, D, SNYDER, J. Image-Based Proxy Accumulation for Real-Time Soft Global Illumination, Pacific Graphics 2007.
[47] SNYDER, J. Code Generation and Factoring for Fast Evaluation of Low-Order Spherical Harmonic Products and Squares, Microsoft Research Technical Report, MSR-TR-2006-53, 2006.
[48] SNYDER, J. Personal Communication, 2008.
[49] SUN, B, RAMAMOORTHI, R, NARASIMHAN, S, NAYAR, S. A Practical Analytic Single Scattering Model for Real Time Rendering, SIGGRAPH 2005.
[50] STAM, J. Multiple Scattering as a Diffusion Process, EUROGRAPHICS Workshop on Rendering, 1995.
[51] VARSHALOVICH, D, MOSKALEV, A, KHERSONSKII, V. Quantum Theory of Angular Momentum, World Scientific Publishing, 1988.
[52] WANG, J, XU, K, ZHOU, K, LIN, S, HU, S, GUO, B. Spherical Harmonic Scaling, The Visual Computer, 22(9-11), 2006.
[53] WESTIN, S, ARVO, J, TORRANCE, K. Predicting Reflectance Functions from Complex Surfaces”, SIGGRAPH 1992.
[54] WONG, T, HENG, P, OR, S, NG, W. Image-Based Rendering with Controllable Illumination, Eurographics Workshop on Rendering, 1997.
[55] WONT, T, FU, C, HENG, P, LEUNG, C. The Plenoptic Illumination Function, IEEE Transactions on Multimedia 4(3) 2002.
[56] ZHOU, K, HU, Y, LIN, S, GUO, B, SHUM, H-Y. Precomputed Shadow Fields for Dynamic Scenes, SIGGRAPH 2005.
付録 A1 SH基底関数を評価するための再帰律
SH基底関数の多項式形式を効率的に評価するために、再帰関係[48]を用いることができる。基底関数の公式を思い出してください。
\begin{eqnarray}
y^m_l = \begin{cases}
\sqrt{2} {\rm Re}(Y^m_l) & m \lt 0 \\
\sqrt{2} {\rm Im}(Y^m_l) & m \gt 0 \\
Y^0_l & m = 0
\end{cases} =
\begin{cases}
\sqrt{2} K^m_l \cos m \phi P^m_l(\cos \theta) & m \lt 0 \\
\sqrt{2} K^m_l \sin |m| \phi P^{|m|}_l (\cos \theta) & m \gt 0 \\
K^0_l P^0_l(\cos \theta) & m = 0
\end{cases}
\end{eqnarray}
単位球面上の点 \((x, y, z)\) が与えられると、連想レジェンドル多項式 (Zにのみ依存し、\(\sin \theta^m\) によって割る) は、これらの再帰を使って評価できます (\(P^0_0 = 1\)):
\begin{eqnarray}
P^m_m &=& (1 – 2m) p^{m-1}_{m-1} \\
P^m_{m+1} &=& (2m + 1) z P^m_m \\
P^m_l &=& \frac{(2l – 1)zP^m_{l-1} – (l+m-1)P^m_{l-2}}{l-m}
\end{eqnarray}
ここで,内側のループで\(l\)をインクリメントし、外側で\(m\)をインクリメントします。
三角加算式は、\(S(0)=0、C(0)=1\)である\(\phi\)依存項(球面上の\((x, y)\)座標から計算できるように\(\sin \theta^m\)を乗じたもの)を評価するために用いることができます:
\begin{eqnarray}
S(m) &=& x S(m-1) + yC(m-1) \\
C(m) &=& x C(m-1) + yS(m-1)
\end{eqnarray}
\(\sin|m| \phi\)を\(S(m)\)に、\(\cos m \phi\)を\(C(m)\)に置き換えることで、共通の部分式が自然に因数分解されるため、一般にこのような方程式に基づいてコードを生成する方が効率的です。
付録A2 SH基底関数の多項式形式
SH基底関数の多項式形式を以下に示す。\(L\)は帯の番号、\(M\)は基底関数です。なお、Mapleは\(L\)と\(M\)の順番をランダムに変えていることに注意してください。
\begin{eqnarray}
&\{ L=0, M=0 \},& \frac{1}{2 \sqrt{\pi}} \\
&\{ L=1, M=-1 \},& -\frac{\sqrt{3}y}{2 \sqrt{\pi}} \\
&\{ L=1, M=0 \},& \frac{\sqrt{3}z}{2\sqrt{\pi}} \\
&\{ L=1, M=1 \},& -\frac{\sqrt{3}x}{2\sqrt{\pi}} \\
&\{ L=2, M=-2 \},& \frac{\sqrt{15}yx}{2\sqrt{\pi}} \\
&\{ M=-1, L=2 \},& -\frac{\sqrt{15}yz}{2\sqrt{\pi}} \\
&\{ M=0, L=2 \},& \frac{ \sqrt{5}(3z^2 -1) }{4 \sqrt{\pi}} \\
&\{ M=1, L=2 \},& -\frac{ \sqrt{15} xz }{ 2\sqrt{\pi} } \\
&\{ M=2, L=2 \},& \frac{ \sqrt{15}(x^2 – y^2) }{ 4 \sqrt{\pi} } \\
&\{ M=-3, L=3 \},& -\frac{ \sqrt{2} \sqrt{35} y(3x^2 – y^2) }{ 8 \sqrt{\pi} } \\
&\{ M=-2, L=3 \},& \frac{ \sqrt{105}yxz }{ 2\sqrt{\pi} } \\
&\{ M=-1, L=3 \},& -\frac{ \sqrt{2}\sqrt{21}y(-1 + 5z^2) }{ 8\sqrt{\pi} } \\
&\{ L=3, M=0 \},& \frac{ \sqrt{7}z(5z^2 -3) }{ 4\sqrt{\pi} } \\
&\{ M=1, L=3 \},& -\frac{ \sqrt{2}\sqrt{21}x(-1 + 5z^2) }{ 8\sqrt{\pi} } \\
&\{ L=3, M=2 \},& \frac{ \sqrt{105}(x^2-y^2)z }{ 4 \sqrt{\pi} } \\
&\{ M=3, L=3 \},& -\frac{ \sqrt{2}\sqrt{35}x(x^2 – 3y^2) }{ 8 \sqrt{\pi} } \\
&\{ L=4, M=-4 \},& \frac{3 \sqrt{35} yx(x^2 – y^2)}{ 4 \sqrt{\pi} } \\
&\{ M=-3, L=4 \},& -\frac{ 3\sqrt{2}\sqrt{35} y(3x^2 – y^2)z }{ 8 \sqrt{\pi} } \\
&\{ M=-2, L=4 \},& \frac{3 \sqrt{5} yx(-1 + 7z^2) }{ 4 \sqrt{\pi} } \\
&\{ M=-1, L=4 \},& -\frac{3 \sqrt{2} \sqrt{5} yz (-3 + 7z^2)}{ 4 \sqrt{\pi} } \\
&\{ L=4, M=0 \},& \frac{ 3(35z^4 – 30z^2 +3) }{ 16 \sqrt{\pi} } \\
&\{ M=1, L=4 \},& -\frac{ 3\sqrt{2}\sqrt{5}xz(-3+7z^2) }{ 8 \sqrt{\pi} } \\
&\{ L=4, M=2 \},& \frac{ 3\sqrt{5}(x^2 – y^2)(-1 + 7z^2) }{ 8 \sqrt{\pi} } \\
&\{ M=3, L=4 \},& -\frac{ 3\sqrt{2}\sqrt{35} x(x^2 – 3y^2)z }{ 8 \sqrt{\pi} } \\
&\{ M=4, L=4 \},& \frac{ 3\sqrt{35}(x^4 – 6y^2x^2 + y^4) }{ 16 \sqrt{\pi} } \\
&\{ L=5, M=-5 \},& -\frac{ 3\sqrt{2}\sqrt{77}y(5x^4 – 10y^2x^2 + y^4) }{ 32 \sqrt{\pi} } \\
&\{ L=5, M=-4 \},& \frac{ 3\sqrt{385} yx(x^2 -y^2)z }{ 4 \sqrt{\pi} } \\
&\{ L=5, M=-3 \},& -\frac{ \sqrt{2}\sqrt{385}y(3x^2 – y^2)(-1 + 9z^2) }{ 32 \sqrt{\pi} } \\
&\{ M=-2, L=5 \},& \frac{ \sqrt{1155}yxz(-1+3z^2) }{ 4 \sqrt{\pi} } \\
&\{ M=-1, L=5 \},& -\frac{ \sqrt{165}y(-14z^2+21z^4+1) }{ 16 \sqrt{\pi} } \\
&\{ L=5, M=0 \},& \frac{ \sqrt{11}z(63z^4 – 70z^2 + 15) }{ 16 \sqrt{\pi} } \\
&\{ L=5, M=1 \},& -\frac{ \sqrt{165}x(-14z^2+21z^4+1) }{ 16 \sqrt{\pi} } \\
&\{ L=5, M=2 \},& \frac{ \sqrt{1155}(x^2 – y^2)z(-1+3z^2) }{ 8 \sqrt{\pi} } \\
&\{ L=5, M=3 \},& -\frac{ \sqrt{2}\sqrt{385}x(x^2 – 3y^y)(-1+9z^2) }{ 32 \sqrt{\pi} } \\
&\{ L=5, M=4 \},& \frac{ 3\sqrt{385}(x^4 – 6y^2x^2 + y^4)z }{ 16 \sqrt{\pi} } \\
&\{ L=5, M=5 \},& -\frac{ 3\sqrt{2}\sqrt{77} x(x^4 – 10y^2x^2+ 5y^4) }{ 32 \sqrt{\pi} }
\end{eqnarray}
付録A3 球面光源に対するZH係数
ラジアン単位の角度\(a\)を持つ光源が与えられた場合、最初の6バンドの記号積分は以下の通りです。
L=0 \(-\sqrt{\pi}(-1 + \cos(a)) \)
L=1 \(\frac{1}{2} \sqrt{3} \sqrt{\pi} \sin(a)^2\)
L=2 \(-\frac{1}{2} \sqrt{5} \sqrt{\pi} \cos(a)(-1 + \cos(a)) (\cos(a) + 1)\)
L=3 \(-\frac{1}{8} \sqrt{7} \sqrt{\pi}(-1 + \cos(a))(\cos(a)+1)(5\cos(a)^2 -1)\)
L=4 \(-\frac{3}{8} \sqrt{\pi} \cos(a)(-1 + \cos(a))(\cos(a) + 1)(7\cos(a)^2 -3)\)
L=5 \(-\frac{1}{16} \sqrt{11} \sqrt{\pi}(-1 + \cos(a))(\cos(a)+1)(21\cos(a)^4-14\cos(a)^2+1)\)
付録A4 スムース円錐に対するZ係数
ラジアン単位の角度 \(a\) を引く円錐があるとき、光源は北極で強度 1 を持ち、角度 \(a\) で 0 に落ちます。6次では、この関数は単精度で約8度未満の角度で評価してはいけません。平滑化関数の微分は北極と\(a\)で0となる。最初の6バンドは以下の通りです。
\begin{eqnarray}
\frac{ (a^3 + 6a -12 \sin(a) + 6\cos(a)a \sqrt{\pi} }{ a^3 }
\end{eqnarray}
\begin{eqnarray}
\frac{1}{4} \frac{ \sqrt{3}(a^3 -3\cos(a)\sin(a) + 3\cos(a)^2a \sqrt{\pi} }{ a^3 }
\end{eqnarray}
\begin{eqnarray}
\frac{1}{9} \frac{ (-6a – 2\cos(a)^2 \sin(a) -9\cos(a)a + 14 \sin(a)+3\cos(a)^3a) \sqrt{\pi} }{ a^3 }
\end{eqnarray}
\begin{eqnarray}
\frac{1}{256} \sqrt{7} (4a^3 + 15a – 108\cos(a)^2a -30\cos(a)^3\sin(a) + 63\cos(a)\sin(a) + 60\cos(a)^4 a) \sqrt{\pi} / a^3
\end{eqnarray}
\begin{eqnarray}
\frac{1}{1500} (-480a + 742\sin(a) + 596\cos(a)^2\sin(a) + 225\cos(a)a – 378\sin(a)\cos(a)^4 \\
– 1650\cos(a)^3a + 945\cos(a)^5a) \sqrt{\pi} / a^3
\end{eqnarray}
\begin{eqnarray}
\frac{1}{3072} \sqrt{11} (-63a + 12a^3 + 350\cos(a)^3 \sin(a) – 1260\cos(a)^4a – 15 \cos(a)\sin(a)\\
-224\cos(a)^5\sin(a) + 672\cos(a)^6a + 540 \cos(a)^2 a) \sqrt{\pi} / a^3
\end{eqnarray}
付録A5 ディレクショナルライトとアンビエントライトでSH環境マップを近似するための係数の解法
方向\(d\)のディレクショナルライトと元の照明環境との近似誤差を最小化する強度\(s\)を計算することができます。
\begin{eqnarray}
E(c) = (L_e – cL_d)^2
\end{eqnarray}
ここで、\(L_e\)は照明環境のSH表現、\(L_d\)は方向\(d\)における照明モデルのSH表現である。
\begin{eqnarray}
c = \frac{ L_e \circ L_d }{ L_d \circ L_d }
\end{eqnarray}
アンビエントライトを追加する場合、誤差関数を最小にする必要があります。
\begin{eqnarray}
E(c, a) = \int (cL_d(s) \ast H_N(s) + aL_a(s) \ast H_N(s) – L_e(s) \ast H_N(s))^2 ds
\end{eqnarray}
畳み込みをライティングへ取り込み、各変数に関して微分します。
\begin{eqnarray}
\frac{dE}{dc} &=& 2 \int (c{\hat L}_d(s) + a {\hat L}_a(s) – {\hat L}_e(s) ) {\hat L}_d(s) ds \\
\frac{dE}{da} &=& 2 \int (c{\hat L}_d(s) + a {\hat L}_a(s) – {\hat L}_e(s) ) {\hat L}_a(s) ds
\end{eqnarray}
ここで、2つの方程式を0まで解いて、最小値を求めます。\({\hat L}_a(s)\)はスカラー関数であり、SHの直交性により積分はすべてSHベクトルの単純な内積となります。このため、次のような方程式が残ります。
\begin{eqnarray}
cA + aB &=& D \\
cB + aC &=& E
\end{eqnarray}
ここで,
\begin{eqnarray}
A = \frac{508\pi}{867}, B = \frac{16}{17}, C = \frac{4}{\pi}, D= dot({\hat L}_d, {\hat L}_e), E = dot({\hat L}_a, {\hat L}_e)
\end{eqnarray}
\(c\)と\(a\)について解き,結果は次のようになります:
\begin{eqnarray}
c &=& \frac{867}{316\pi} dot({\hat L}_d, {\hat L}_e) – \frac{51}{79} dot({\hat L}_a, {\hat L}_e) \\
a &=& \frac{127\pi}{316} dot({\hat L}_a, {\hat L}_e) – \frac{51}{79} dot({\hat L}_d, {\hat L}_e)
\end{eqnarray}
しかし、同じ結果を得るには、もっと簡単な方法があることがわかりました。環境と光の両方がDC項を含まないディレクショナルライトの強度を解き、スケーリングされたディレクショナルライトを使用するときに環境のDC項を再構成するアンビエント項を計算することです。この結果、以下のようになります。
\begin{eqnarray}
c &=& \frac{867}{316\pi} dot_0({\hat L}_d, {\hat L}_e) \\
a &=& \left( {\hat L}_e[0] – c\frac{8 \sqrt{\pi}}{17} \right) \frac{\sqrt{\pi}}{2}
\end{eqnarray}
上記の式では、内積はDC項を無視し、\({\hat L}_e[0]\)は環境光のDC項となる。2 灯式、3 灯式でも同様の手法を用いる(ここで、\(a\) を光量と同時に扱うと、式がかなり厄介なことになります)。
複数のライトも同様に、まずすべてのライトベクトルからDCを除去し、2つのライトでこのエラー関数を得ることができます。
\begin{eqnarray}
E(c_0, c_1) = \int(c_0 L_{d0}(s) + c_1 L_{d1}(s) – L_e(s))^2 ds
\end{eqnarray}
次に、各係数に関して微分し、ゼロについて解きます。次の式で強度が求まります。
\begin{eqnarray}
\begin{bmatrix} c_0 \\ c_1 \end{bmatrix} =
\begin{bmatrix} \frac{A}{A^2 – B^2} & \frac{-B}{A^2 – B^2} \\
\frac{-B}{A^2 – B^2} & \frac{A}{A^2 – B^2} \end{bmatrix} \begin{bmatrix} L_e \circ L_{d0} \\ L_e \circ L_{d0} \end{bmatrix}
\end{eqnarray}
ここで,
\begin{eqnarray}
A = L_{d0} \circ L_{d0}, B = L_{d0} \circ L_{d1}
\end{eqnarray}
Aは方向とは無関係に一定であることは指摘に値する(次数とベクトルが畳み込まれているかどうかに依存する)。このとき、アンビエント項は
\begin{eqnarray}
a = (L_e[0] – (c_0 L_{d0}[0] + c_1 L_{d1}[0])) \frac{\sqrt{\pi}}{2}
\end{eqnarray}
3つのライトの強度は
\begin{eqnarray}
\begin{bmatrix} c_0 \\ c_1 \\ c_2 \end{bmatrix} =
\begin{bmatrix} \frac{A^2 – D^2}{E} & \frac{CD – AB}{E} & \frac{BD – AC}{E} \\
\frac{CD – AB}{E} & \frac{A^2 – C^2}{E} & \frac{BC – AD}{E} \\
\frac{BD – AC}{E} & \frac{BC – AD}{E} & \frac{A^2 – B^2}{E} \end{bmatrix}
\begin{bmatrix} L_e \circ L_{d0} \\ L_e \circ L_{d1} \\ L_e \circ L_{d2} \end{bmatrix}
\end{eqnarray}
ここで,
\begin{eqnarray}
C = L_{d0} \circ L_{d1}, D = L_{d1} \circ L_{d2}, E = 2 BCD + A(A^2 – B^2 – C^2 – D^2)
\end{eqnarray}
この行列は対称性があり,アンビエント係数は
\begin{eqnarray}
a = (L_e[0] – (c_0 L_{d0}[0] + c_1 L_{d1}[0] + c_2 L_{d2}[0])) \frac{\sqrt{\pi}}{2}
\end{eqnarray}
となります。
付録6 最小二乗法による射影
まず、直交基底関数の場合、最小二乗法による射影は、実際には基底関数に対して単純に積分することで実現できることを示します。この式を最小化するような係数ベクトル\(c\)を求めたい。
\begin{eqnarray}
E(c) = \int \left( \sum_i c_i y_i(s) – f(s) \right)^2 ds
\end{eqnarray}
これは、各係数に関して微分し、第一導関数をゼロで解くことで実現できます。
\begin{eqnarray}
\frac{dE}{dc_k} = s \int \left( \sum_i c_i y_i(s) – f(s) \right) y_k(s) ds
\end{eqnarray}
基底関数が直交関数であることから、この事実を利用し、ゼロについて解くと、\(\int y_i(s) y_j(s) ds = \delta_{ij}\)が得られることがわかります。
\begin{eqnarray}
\frac{dE}{dc_k} = 0 \overset{yields}\longrightarrow c_k = \int y_k(s) f(s) ds
\end{eqnarray}
つまり、直接積分すると、最小二乗の結果が得られます。
ここで、球面上で積分された二乗ラプラシアンに基づくペナルティを含む誤差汎関数を最小化する係数ベクトル\(g\)を導出します。純粋な二乗誤差を最小化する係数ベクトル\(c\)は上記からわかっています。インデックス付けを簡単にするための関数 \(h\) を導入します。
\begin{eqnarray}
\int (\Delta {\tilde f})^2 ds = \sum_{l=1}^n \sum_{m=-1}^l l^2(l+1) (f_l^m)^2 = \sum_{i=0}^{n^2} h_i(f_i)^2
\end{eqnarray}
このとき,誤差関数は
\begin{eqnarray}
E(g) = \left( \sum_i (g_i – c_i)^2 \right) + \lambda \sum_i h_i {g_i}^2
\end{eqnarray}
微分することで次を得ます。
\begin{eqnarray}
\frac{dE}{dg_k} = 2 (g_k – c_k) + 2 \lambda h_k g_k
\end{eqnarray}
ゼロについて解き,次を得ます。
\begin{eqnarray}
g_k = \frac{c_k}{(1 + \lambda h_k)}
\end{eqnarray}
付録A7 ラプラシアンの2乗の削減するためのラムダについての解法
これはニュートン法を使えば簡単に行えます。二乗ラプラシアンは
\begin{eqnarray}
\Delta^2 = \sum_{l=1}^n \sum_{m=-1}^l l^2(l+1)^2 (f_l^m)^2 = \sum_{l=1}^n l^2(l+1)^2 \sum_{m=-1}^l(f_l^m)^2 = \sum_{l=1}^n L_l B_l
\end{eqnarray}
\(L\)値の配列(\(L_l = l^2(l+1)^2\))は静的であり、\(B\)値の配列は\(B_l = \sum_{m=-1}^l(f_l^m)^2\)を計算することができます。Newtons 法は初期推測(この問題では 0 が有効)を取り、以下の再帰性を用いてそれを改善します。
\begin{eqnarray}
\lambda_{n+1} = \lambda_n – \frac{f(\lambda_n)}{f'(\lambda_n)}
\end{eqnarray}
ここで、\(f\)は根を求める関数、\(f’\)は一次導関数である。\(f_l^m\)を\(\lambda\)と因数分解を含む\(c_l^m\)に置き換えると、次のようになります。
\begin{eqnarray}
f(\lambda) = \Delta^2 – \sum_{l=1}^n \frac{L_l B_l}{(1 + \lambda L_l)^2} \\
f'(\lambda) = 2 \sum_{l=1}^n \frac{L_l^2 B_l}{(1 + \lambda L_l)^3}
\end{eqnarray}
ここで、\(\Delta^2\)は元の二乗ラプラシアンです。最大反復回数が発生するか、連続した近似値の絶対値が閾値以下になるまで反復します(実際には1e-6がうまく機能するようです)。これは次数 \((n-1)^2\) の多項式 (すべての分母の積を掛け合わせる) として表すことができ、\(n\) は次数です。これは2次以下の次数で、根の閉じた形の解が計算できる場合にのみ有効で、その場合でも反復解よりはるかに速いかどうかは不明です。
付録A8 解析関数によってSHを乗算するためのコード
以下は、半球上で定義された2つの関数です。1つ目は単純に一定で、グランドプレーンが支配的なシーンで有効です。2つ目は、Zのコサインをクランプしたものです。
付録A9 アンビエントキューブ基底
アンビエントキューブ基底は、Valve[26]で採用されています。この基底は6つの基底関数からなり、それぞれが半球上で定義されています。
\begin{eqnarray}
V0 &=& \begin{cases} x^2 & x \gt 0 \\
0 & x \leq 0 \end{cases}, \quad
V1 &=& \begin{cases} 0 & x \gt 0 \\
x^2 & x \leq 0 \end{cases} \\
V2 &=& \begin{cases} y^2 & y \gt 0 \\
0 & y \leq 0 \end{cases}, \quad
V3 &=& \begin{cases} 0 & y \gt 0 \\
y^2 & y \leq 0 \end{cases} \\
V4 &=& \begin{cases} z^2 & z \gt 0 \\
0 & z \leq 0 \end{cases}, \quad
V5 &=& \begin{cases} 0 & z \gt 0 \\
z^2 & z \leq 0 \end{cases}
\end{eqnarray}
この基底は直交していないため、基底関数に対して積分するだけでは係数は生成できません。最適な投影係数を計算するためには、線形最小二乗問題を解くことになります(付録A6 最小二乗法投影に似ているが、直交基底関数がない)。
\begin{eqnarray}
E(c) = \int \left( \sum_i c_i V_i (s) – f(s) \right)^2 ds
\end{eqnarray}
ここで、\(V_i(s)\)はアンビエントキューブ基底関数です。微分すると、以下のようになる。
\begin{eqnarray}
\frac{dE}{dc_k} = 2 \int \left( \sum_i c_i V_i(s) – f(s) \right) V_k(s) ds
\end{eqnarray}
積分は線形なので、項を並べ替えてゼロについて解くことができます。
\begin{eqnarray}
\sum_i c_i \int V_i(s) V_k(s) ds = \int f(s) V_k(s) ds
\end{eqnarray}
左辺は行列\(A\)の行を与え、\(A_{ij} = \int V_i(s) V_j(s) ds\)、右辺はベクトル(関数の積分とこの基底関数)を与える。これが連立一次方程式を導く:\(Ac=b\) \(A\)の逆行列は次のようになります。
\begin{bmatrix}
\frac{11}{4\pi} & \frac{1}{4\pi} & -\frac{3}{8\pi} & -\frac{3}{8\pi} & -\frac{3}{8\pi} & -\frac{3}{8\pi} \\
\frac{1}{4\pi} & \frac{11}{4\pi} & -\frac{3}{8\pi} & -\frac{3}{8\pi} & -\frac{3}{8\pi} & -\frac{3}{8\pi} \\
-\frac{3}{8\pi} & -\frac{3}{8\pi} & \frac{11}{4\pi} & \frac{1}{4\pi} & -\frac{3}{8\pi} & \frac{3}{8\pi} \\
-\frac{3}{8\pi} & -\frac{3}{8\pi} & \frac{1}{4\pi} & \frac{11}{4\pi} & -\frac{3}{8\pi} & -\frac{3}{8\pi} \\
-\frac{3}{8\pi} & -\frac{3}{8\pi} & -\frac{3}{8\pi} & -\frac{3}{8\pi} & \frac{11}{4\pi} & \frac{1}{4\pi} \\
-\frac{3}{8\pi} & -\frac{3}{8\pi} & -\frac{3}{8\pi} & -\frac{3}{8\pi} & \frac{1}{4\pi} & \frac{11}{4\pi}
\end{bmatrix}
この基底で表された関数をSHに投影するには、SHの基底に対して\(V\)を積分すればよく、2次球面調和では次のような行列になります。
\begin{bmatrix}
\frac{\sqrt{\pi}}{3} & \frac{\sqrt{\pi}}{3} & \frac{\sqrt{\pi}}{3} & \frac{\sqrt{\pi}}{3} & \frac{\sqrt{\pi}}{3} & \frac{\sqrt{\pi}}{3} \\
0 & 0 & -\frac{\sqrt{3}\sqrt{\pi}}{4} & \frac{\sqrt{3}\sqrt{\pi}}{4} & 0 & 0 \\
0 & 0 & 0 & 0 & \frac{\sqrt{3}\sqrt{\pi}}{4} & -\frac{\sqrt{3}\sqrt{\pi}}{4} \\
-\frac{\sqrt{3}\sqrt{\pi}}{4} & \frac{\sqrt{3}\sqrt{\pi}}{4} & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 \\
-\frac{\sqrt{\pi}\sqrt{5}}{15} & -\frac{\sqrt{\pi}\sqrt{5}}{15} & -\frac{\sqrt{\pi}\sqrt{5}}{15} & -\frac{\sqrt{\pi}\sqrt{5}}{15} & \frac{2\sqrt{\pi}\sqrt{5}}{15} & \frac{2 \sqrt{\pi}\sqrt{5}}{15} \\
0 & 0 & 0 & 0 & 0 & 0 \\
\frac{\sqrt{\pi}\sqrt{15}}{15} & \frac{\sqrt{\pi}\sqrt{15}}{15} & -\frac{\sqrt{\pi}\sqrt{15}}{15} & -\frac{\sqrt{\pi}\sqrt{15}}{15} & 0 & 0
\end{bmatrix}
2次以上の偶数次はアンビエントキューブ基底のヌル空間、2次以上の奇数次はクランプコサイン関数のヌル空間なので、照度環境マップを使用する場合はそれ以上の次数は必要ありません。アンビエントキューブ基底はDC項を正確に再構成し、線形項を近似し、2次基底関数のうち2つ\((y^0_2, y^2_2)\)を正確に再構成し、2次基底関数のうち3つがヌル空間\((y^{-2}_2, y^{-1}_2、y^1_2)\)になっています。
SHからアンビエントキューブベースに投影するには、この誤差関数を最小化する必要があります。
\begin{eqnarray}
E(c) = \int \left( \sum_i c_i V_i(s) – \sum_j l_j y_j(s) \right)^2 ds
\end{eqnarray}
ここで,\(l_j\) は SH ライティング係数(畳み込みと仮定)です。もう一度、未知の変数に関して微分します。
\begin{eqnarray}
\frac{dE}{dc_k} = 2 \int \left( \sum_i c_i V_i(s) – \sum_j l_j y_j(s) \right) V_k(s) ds
\end{eqnarray}
そして,ゼロについて解き
\begin{eqnarray}
\sum_i c_i \int V_i(s) V_k(s) ds = \sum_j l_j \int y_j(s) V_k(s) ds
\end{eqnarray}
この結果、\(Ac=Bl\)となり、\(A\)は先ほどと同じ\(B\)は\(B_{ij}=\int V_i(s) y_j(s) ds\)となる行列で、同様に線形系となります。行列\(A^{-1}B\)は、SHからアンビエントキューブ基底に移行するために使用することができます。
\begin{eqnarray}
\begin{bmatrix}
\frac{1}{2\sqrt{\pi}} & 0 & 0 & -\frac{5\sqrt{3}}{8\sqrt{\pi}} & 0 & 0 & -\frac{\sqrt{5}}{4 \sqrt{\pi}} & 0 &\frac{\sqrt{15}}{4\sqrt{\pi}} \\
\frac{1}{2\sqrt{\pi}} & 0 & 0 & \frac{5\sqrt{3}}{8\sqrt{\pi}} & 0 & 0 & -\frac{\sqrt{5}}{4\sqrt{\pi}} & 0 & \frac{\sqrt{15}}{4\sqrt{\pi}} \\
\frac{1}{2\sqrt{\pi}} & -\frac{5\sqrt{3}}{8\sqrt{\pi}} & 0 & 0 & 0 & 0 & -\frac{\sqrt{5}}{4\sqrt{\pi}} & 0 & -\frac{\sqrt{15}}{4\sqrt{\pi}} \\
\frac{1}{2\sqrt{\pi}} & \frac{5\sqrt{3}}{8 \sqrt{\pi}} & 0 & 0 & 0 & 0 & -\frac{\sqrt{5}}{4\sqrt{\pi}} & 0 & -\frac{\sqrt{15}}{4\sqrt{\pi}} \\
\frac{1}{2\sqrt{\pi}} & 0 & \frac{5\sqrt{3}}{8\sqrt{\pi}} & 0 & 0 & 0 & \frac{\sqrt{5}}{2\sqrt{\pi}} & 0 & 0 \\
\frac{1}{2\sqrt{\pi}} & 0 & -\frac{5\sqrt{3}}{8\sqrt{\pi}} & 0 & 0 & 0 & \frac{\sqrt{5}}{2\sqrt{\pi}} & 0 & 0
\end{bmatrix}
\end{eqnarray}
付録A10 放射照度環境マップの為のシェーダ/GPUコード
照明環境の2次関数SH表現があれば、シェーダーコードを生成するのは非常に簡単です。[35]では、行列表現が使用されていますが、これは、2次球面高調波をより直接的に評価する場合と比較して、より多くの命令(15対11)とより多くの定数(12対7)を必要とすることが判明しています。多項式の先行定数を照明係数に折り込み、\(y^{-2}_2\) 以外をチャンネルごとにグループ化し(float4 を使用)、\(y^{-2}_2\) を色として保持し、\(y^0_2\) の一部を DC に折り込んでいます。評価用のシェーダーコードと定数設定用のCPUコードを以下に示します。シェーダコードに渡される法線は正規化され、4チャンネル目は1.0にする必要があります。CPU コードは、2次放射輝度SH係数への3つのfloat ポインタの配列と、定数をバインドするための Effect を受け取ります。
// constants containing irradiance environment map
float4 cAr;
float4 cAg;
float4 cAb;
float4 cBr;
float4 cBg;
float4 cBb;
float4 cC;
float3 ShadeIrad(float4 vNormal)
{
float3 x1, x2, x3;
// Linear + constant polynomial terms
x1.r = dot(cAr, vNormal);
x1.g = dot(cAg, vNormal);
x1.b = dot(cAb, vNormal);
// 4 of the quadratic polynomials
float4 vB = vNormal.xyzz * vNormal.yzzx;
x2.r = dot(cBr, vB);
x2.g = dot(cBg, vB);
x2.b = dot(cBb, vB);
// Final quadratic polynomial
float vC = vNormal.x * vNormal.x - vNormal.y * vNormal.y;
x3 = cC.rgb * vC;
return x1 + x2 + x3;
}
//-------------------------------------------------------------
void SetSHEmapConstants(float* fLight[3], ID3DXEffect* pEffect)
{
// Lighting environment coefficients
D3DXVECTOR4 vCoeff[3];
static const float s_fSqrtPI = ((float)sqrtf(D3DX_PI));
const float fC0 = 1.0f / (2.0f * s_fSqrtPI);
const float fC1 = (float)sqrt(3.0f) / (3.0f * s_fSqrtPI);
const float fC2 = (float)sqrt(15.0f) / (8.0f * s_fSqrtPI);
const float fC3 = (float)sqrt(5.0f) / (16.0f * s_fSqrtPI);
const float fC4 = 0.5f * fC2;
int iC;
for(iC=0; iC<3; iC++)
{
vCoeff[iC].x = -fC1 * fLight[iC][3];
vCoeff[iC].y = -fC1 * fLight[iC][1];
vCoeff[iC].z = fC1 * fLight[iC][2];
vCoeff[iC].w = fC0 * fLight[iC][0] - fC3 * fLight[iC][6];
}
pEffect->SetVector("cAr", &vCoeff[0]);
pEffect->SetVector("cAg", &vCoeff[1]);
pEffect->SetVector("cAb", &vCoeff[2]);
for(iC=0; iC<3; iC++)
{
vCoeff[iC].x = fC2 * fLight[iC][4];
vCoeff[iC].y = -fC2 * fLight[iC][5];
vCoeff[iC].z = 3.0f * fC3 * fLight[iC][6];
vCoeff[iC].w = -fc2 * fLight[iC][7];
}
pEffect->SetVector("cBr", &vCoeff[0]);
pEffect->SetVector("cBg", &vCoeff[1]);
pEffect->SetVector("cBb", &vCoeff[2]);
vCoeff[0].x = fC4 * fLight[0][8];
vCoeff[0].y = fC4 * fLight[1][8];
vCoeff[0].z = fC4 * fLight[2][8];
vCoeff[0].w = 1.0f;
pEffect->SetVector("cC", &vCoeff[0]);
}