こんるる～。Pocolです。
今日は[Turquin 2019] Emmanuel Tureuin, “Practical multiple scattering compensation for microfacet models”
を読んでみようと思います。
いつもながら、誤字・誤訳があるかと思いますので，ご指摘頂ける場合は正しい翻訳例と共に指摘して頂けるとありがたいです。

Abstract

ゲームやアニメーション、VFX業界では、より物理的な根拠に基づいた光の輸送方法や材質の表現が採用されており、計算の数値的安定性と現実的な見た目の画像の両方を確保するために、エネルギーの保存に力が注がれています。しかし、この取り組みは、エネルギーを失わないことよりも、過度な発光を避けることに重点が置かれてきました。マイクロファセットモデルは、様々な粗さの鏡面成分を表現するためのサーフェイスマテリアルの標準的な構成要素となっています。しかし、マイクロファセットモデルは、説得力のある結果をもたらすだけでなく、多くの望ましい特性を持っていますが、その設計自体が、エネルギーの著しい損失を引き起こす重要な散乱の情報源を無視しています。具体的には、マイクロファセット上の単一散乱のみをモデル化し、ラフネスが大きくなるほど重要になる後続の相互作用を無視しています。ユーザーの立場からすると，粗いスペキュラーローブが予想外に暗くなってしまうため，通常はアドホックな方法を考慮する必要があります。このドキュメントでは、この欠点を解決し、エネルギー保存を確保するためのさまざまなアプローチを紹介し、比較します。このアプローチには、ILMにて開発されたものも含まれています。

1　Introduction

CookとTorrance[1982]によって導入されて以来，マイクロファセットモデルは，リアルタイムおよびオフラインのレンダリングにおいて，粗い鏡面反射や屈折を表現するための普遍的な方法となっています[Walter et al.2007]。鏡のように反射するファセットを考えると、マイクロファセットのBRDF \(\rho\)は、よく知られた公式を用いて表すことができます。

\begin{eqnarray}
\rho (\omega_o, \omega_i) = \frac{F(\omega_o, h) G(\omega_o, \omega_i, h) D(h)}{4 |\omega_i \cdot n| | \omega_o \cdot n|} \tag{1}
\end{eqnarray}

ここで、\(n\)は幾何学的な法線、\(h\)はマイクロファセットの法線、\(\omega_i\)、\(\omega_o\)は入射方向と出射方向、\(F\)はフレネル項、\(G\)はシャドーイング・マスキング関数、\(D\)はマイクロファセット分布関数である。この定式化は、他の利点に加えて、3つの項\(F\)、\(G\)、\(D\)のすべてを、異なる特性を持つ候補の中から選ぶことができるため、優れたモジュール性を備えています。

特に人気があるのは、粗い金属を再現するために、導体フレネル項とともに、\(D\)としてGGX分布（およびその関連項G；これらがどのように関係すべきかについては[Heiz 2014]を参照）を使用することです（図1の上段のように）。また、BTDFに誘電材質の\(F\)を組み合わせることで、すりガラスのような屈折する素材を再現することもできます。

※図は，[Turquin 2019]より引用

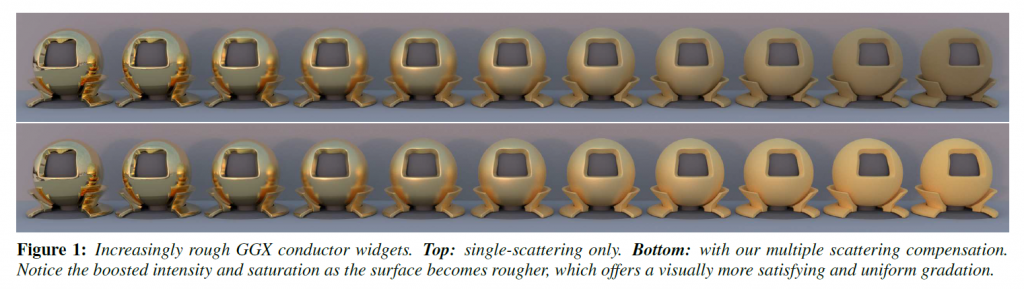
残念ながら、このモデルには重要な制限があります。それは、入射光線とマイクロファセットとの1回の相互作用しかシミュレートしておらず、その後の散乱光線は、\(G\)によって決定されるように、\(\omega_i/\omega_o\)から見えるか見えないかのどちらかになります。光線が見えない（つまり、別のマイクロファセットに当たる、1つまたは複数）場合に発生する多重散乱は考慮されていません（詳細は[Heitz 2014]のセクション3を参照）。予想されるように、ラフネスがゼロの場合、欠落したエネルギーはありません。これは、オクルージョンの可能性がない完全に平らな表面に対応しているからです。しかし，表面が粗くなるほど（あるいはマイクロファセットの向きの広がりが大きくなるほど），多重散乱エネルギーの欠如が顕著になります。図1の上段を見てみると、右端の物体は、光沢のある物体に比べて、過度に乾燥してくすんでいるように見えます。実際、GGXの場合、フレネル吸収を無視すると、ラフネスの値\(\alpha=1\)の場合、エネルギーの損失は約60%に達しています。GTR[Burley 2012]やSTD[Ribardiere et al. 2017]のような長いテールを持つ分布を使うとさらに悪くなり、図2に示すように、90%を超えることもあります。制作環境では、これはアルベドを目で見て手動で補正することを求めており、通常はルックの開発段階で適用され、他の方法でエネルギー保存を壊す可能性があります。ありがたいことに、より簡単で健全な方法が考案されています。

※図は，[Turquin 2019]より引用

2　Previous work

欠落していた多重散乱の寄与を再注入する方法は、発見的でアーティスティック制御されたものから、完全に物理的に基づいて自動化されたものまで様々です。また、複雑さ、実用性、スピードの点でも大きな違いがあります。

Burley [2015] は、Schlickのフレネルプロファイル\( (1 – \cos \theta_o)^5\) を使用した、シンプルで物理的に正当化された、ユーザー主導のSheenコンポーネントを導入しています。このコンポーネントは、観測された材質によりよくマッチするように、グレージングフォワード反射を追加し、[Burley 2012] で既に提案されている拡散後方反射を補完しています。この項の動機は、想定されていない「微小表面の特徴の間やそこを通る多重散乱効果」をほぼ補うためです。

残念ながら、この定性的な補正（図3）では、粗さの変化の影響などの重要な要素が考慮されていないため、BSDFの他の属性が編集されるたびに再調整する必要があります。同じコースノートの5.1節では、制作現場ではまだ実用的な問題であることが強調されており、より正確で自動化された方法が将来の課題として挙げられています。

※図は，[Turquin 2019]より引用

[Heitz 2014]の第7節の多重散乱のサブセクションでは、「エネルギー保存の知識と経験的な観察を組み合わせる」という提案がなされており、次のように表現される新しいBRDFモデルを検討しています：

\begin{eqnarray}
\rho(\omega_o, \omega_i) = \rho_{ss} (\omega_o, \omega_i) + \rho_{ms}(\omega_o, \omega_i) \tag{2}
\end{eqnarray}

ここで、\(\rho_{ss}\)は式1の通常の単一散乱のみの項であり、\(\rho_{ms}\)はすべての二次ローブを考慮した新たな多重散乱項です。\(\rho_{ms}\)に対する最初の重要な制約は、エネルギー保存によって自然に課せられるものです。アルベドを次のように導入します：

\begin{eqnarray}
E (\omega_o) = \int_{\Omega_i} \rho(\omega_o, \omega_i) | \omega_i \cdot n | d \omega_i \tag{3}
\end{eqnarray}

(同様に, \(E_{ss}\)と\(E_{ms}\)もです)。そして、一瞬フレネルを無視する（つまり、\(F=1\)と考える）と、以下の等式が成り立つはずです：

\begin{eqnarray}
E(\omega_o) = E_{ss}(\omega_o) + E_{ms}(\omega_o) = 1 \tag{4}
\end{eqnarray}

吸収することなく、すべての入射エネルギーがマイクロファセットで1回または複数回跳ね返ってくることを表現しています。別の言い方をすれば：

\begin{eqnarray}
E_{ms} (\omega_o) = 1 – E_{ss}(\omega_o) \tag{5}
\end{eqnarray}

\(E_{ss}\)が完全に定義されている場合、\(E_{ss}\)または\(E_{ms}\)を（事前に）計算するためのさまざまなオプションがあります。式(5)に従うことでエネルギーの損失を防ぐことができ、当然のことながら図2を完全に一定にすることができます。さて、残された課題は：

• \(\rho_{ms}\)の形状
• フレネル吸収の取り入れ方

です。Heitz[2014]はどちらの問題にも直接的な解決策を提示していませんが、次のように指摘しています:

「\(\rho_{ms}\)の形状は、例えば、粗いサーフェイスのサンプルでモンテカルロ・シミュレーションを行うことで調べることができます。」(Q1)

直後に次を追加しています：

「それが単純であることがわかれば、最初の近似として、分析関数でモデル化することができます（例えば、単一のローブとして）。」(Q2)

フレネルについては、1バウンス分の平均項\(F_{ss}\)をあらかじめ計算しておき、それによって\(E_{ms}\)を再スケールすることを提案しています。十分な精度が得られないと判断した場合は、「複数回バウンスした後の平均値\(F_{ms}\)も事前に計算できるかもしれない」としている。最後に、このような有望な意見で締めくくりました。

「多重散乱は我々の関数を滑らかにする傾向があるので、単純な解析関数や事前に計算された小さなルックアップテクスチャで効率的に表現され、保存されることが合理的に期待できます。」(Q3)

その後の取り組みとして、Heitzら[2016]は、Q1で示されたアイデアを追試し、体積にマイクロフレーク理論を用い、マイクロサーフェイス上でランダムウォークを用いて、多重散乱をシミュレートする本格的なストキャスティックモデルを提案しています。このモデルは、導体の反射だけでなく、誘電体の散乱に対しても非常に正確であることが示されており、既存のプロダクションレンダリングシステムにプラグインするのがそれほど簡単ではなく（特に、追加の乱数を使用する必要があります）、さらに重要なのは計算コストが非常に高いという、その複雑な性質がなければ、理想的なモデルです。

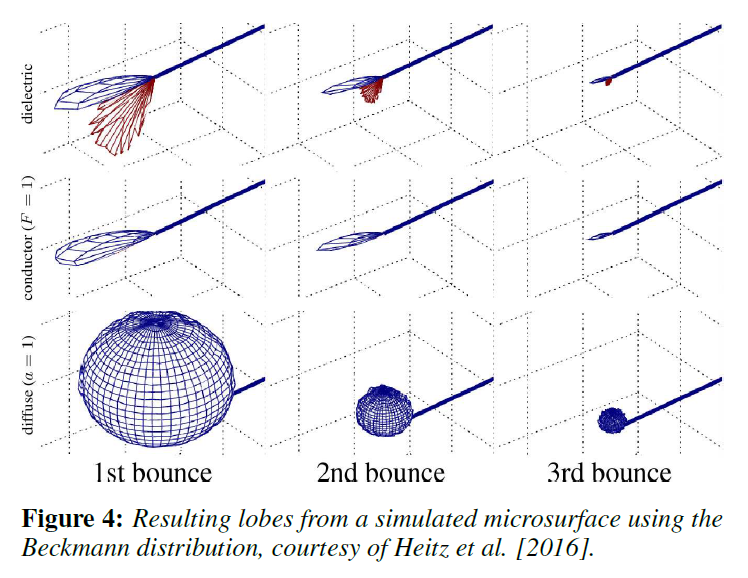
この研究では、二次ローブは拡散しているのではなく、一次ローブを縮小したもののように見えるという、興味深く、やや意外な結果が得られました（論文の図15に表示されていますが、ここでは便宜上、図4に部分的に再現しています）。

※図は，[Turquin 2019]より引用

我々と同様の取り組みとして、Kulla and Conty [2017]は、Q2とQ3で得られた観測結果を利用し、精度は著しく低いですが、はるかにシンプルで高速なソリューションを提案しています。彼らは、Kelemen and Szirmay-Kalos [2001]の研究を現在の問題に適応させ、式(5)について構築することによって拡散して見えるマットコンポーネントを多重散乱ローブとして使用しています：

\begin{eqnarray}
\rho_{ms}(\omega_o, \omega_i) = F_{ms} \frac{ (1 – E_{ss}(\omega_o)) (1 – E_{ss}(\omega_i)) }{ \pi (1 – E_{avg})} \tag{6}
\end{eqnarray}

フレネル項を用いることによって次のように定義されます：

\begin{eqnarray}
F_{ms} = \frac{F_{ss}E_{avg}}{1 – F_{ss}(1 – E_{avg})} \tag{7}
\end{eqnarray}

そして，\(F_{ss} = 2 \int_{0}^{1} F(\mu) \mu d\mu\)は拡散反射と仮定して計算され，\(E_{avg} = 2\int_{0}^{1} E_{ss}(\mu) \mu d\mu\)です。彼らは\(F\)と\(E_{ss}\)を\(\omega\)の代わりに\(\mu\)で再マッピングすることを選択したことに注意してください。これは両方の項が方位不変であるため、全く問題ありません。幾何級数を用いて得られる\(F_{ms}\)項の詳細な導出は、[Jakob et al 2014], Section 5.6に記載されています。この手法では、滑らかに変化する\(E_{avg}\)と\(E_{ss}\)のための小さな1D(\(\alpha\))および2次元(\(\alpha, \mu\))のルックアップテーブル（実装上の寸法はそれぞれ32および\(32 \times 32\)）に依存しており、これらは与えられたマイクロファセット分布ごとに事前に計算されなければなりません。ローブは相反(\(\rho_{ms}(\omega_o, \omega_i) = \rho_{ms}(\omega_i, \omega_o)\)) になるように設計されていますが、これは双方向で使用する場合に重要です。

さらに、\(F\)がIORにも依存する（導体の場合は2つの波長に依存する）ことから、様々なフレネル定式化（シュリック近似、導体、アーティストフレンドリー導体）に対する\(F_{ss}\)の簡単な解析的フィットを提供しています。また、粗い誘電体の反射と屈折もサポートしており、今回は2つのテーブルを使って、それぞれのタイプのインターフェイス（外部から内部へ、またはその逆）に対応しています。この場合、フレネルをエネルギーLUTに組み込む必要があります。フレネルは反射光と屈折光の比率を表すため、同等の解像度のテーブルに一次元を加えることになります。

全体として、この方法は非常に高速でロバストであり、BSDFに比較的小さな変更を加えるだけでレンダラーに追加することができます。しかし、この手法では拡散性のある\(\rho_{ms}\)ローブを使用しているため、Heitzら[2016]による二次ローブは一次ローブと似た形状であるという以前の結果とは矛盾しています。

3　Our methods

KullaとContyの主な関心事と設計上の制約は、相互性を維持することでしたが、我々の方法は、ローブ間の形状の類似性が観察されたことに由来していますが、同時に（複雑さがユーザーにとって有益であると証明されない限り）極端なミニマリズムを目指しています。そのため、単純にスケールアップした \(\rho_{ss}\) と \(\rho_{ms}\) を使用することにしました：

\begin{eqnarray}
\rho(\omega_o, \omega_i) = \rho_{ss}(\omega_o, \omega_i) + F_{ms} k_{ms}(\omega_o) \rho_{ss}(\omega_o, \omega_i) \tag{8}
\end{eqnarray}

\(k_{ms}\)は、失われたエネルギーを考慮して定義される係数です。

本章では、特に言及しない限り、GGX BRDFを使用します。

3.1　Conductors

3.1.1　Energy term

多重散乱項に対するフレネルの影響を脇に置くと、実際には\(\rho\)と、\(\rho_{ss}\)の正規化されたバージョンを見ることができます：

\begin{eqnarray}
\rho(\omega_o, \omega_i) = (1 + k_{ms}(\omega_o)) \rho_{ss}(\omega_o, \omega_i) = \frac{\rho_{ss}(\omega_o, \omega_i)}{E_{ss}(\omega_o)} \tag{9}
\end{eqnarray}

自然と次を得ます：

\begin{eqnarray}
k_{ms} (\omega_o) = \frac{1 – E_{ss}(\omega_o)}{E_{ss}(\omega_o)} \tag{10}
\end{eqnarray}

そのようなBRDFは式(4)を証明するので，構築することにより：

\begin{eqnarray}
E(\omega_o) = \int_{\Omega_i} \frac{\rho_{ss}(\omega_o, \omega_i)}{E_{ss} (\omega_o)} | \omega_i \cdot n | d \omega_i = \frac{E_{ss}(\omega_o)}{E_{ss}(\omega_o)} = 1 \tag{11}
\end{eqnarray}

\(E_{ss}\)は滑らかに変化するため、KullaやContyと同様に、出射角（または余弦）とラフネスでパラメータ化して事前に計算し（ここでも\(F = 1\)）、小さなLUTに格納できることがわかりました。我々の実装でも、\(\cos \theta_o\)と\(\sqrt{\alpha}\)を用いた\(32 \times 32\)のテーブルを使用しています（図5参照）。GTRやSTDのように、\(\gamma\)のテール長のパラメータが追加されている分布については、各分布に合わせた\(\gamma\)-マッピングを行い、テーブルを\(32 \times 32 \times 32\)に拡張しています。

※図は，[Turquin 2019]より引用

しかし、エネルギー項が全体の保存の中で最も重要な要素であるとはいえ、図6に示すように、マイクロファセットの各バウンスで起こるフレネル吸収は無視できません。そのため、満足のいく\(F_{ms}\)項を見つける必要があります。

※図は，[Turquin 2019]より引用

3.1.2 Fresnel term

先に進む前に、多重散乱を単一のローブでモデル化し、\(F_{ms}\)を可分で方向不変であると考える決定は、非常に粗い近似であることを認識しなければなりません。この設計では、せいぜい部分的な一致しか期待できません。しかし、単純な定性的な一致は、制作上のニーズには十分であると思われます。また、ユーザーにとっては、追加されるエネルギーの量に直接比例して飽和することで、補正の動作をより簡単に予測することができます。

\(F_{ms}\)には、式（7）で定義された項を再利用することができます。この関数は、\(\alpha=0\)(または\(E_{avg}=1\))のときに\(F_{ss}\)と完全に等しく、実際に単一散乱しかない場合に対応していますが、\(\alpha=1\)(または\(E_{avg} \approx 0.4\))のときには\(F_{ss}^2\)に近くなります。

図7の左図を見ると、\(F_{ss}^2\)はこの方式よりもわずかに彩度が高く、視覚的にもグランドトゥルースの結果に近いことがわかります（詳細はセクション4で説明します）。

※図は，[Turquin 2019]より引用

\(\rho_{ss}\)にはすでに方向性のある単一散乱フレネル係数\(F\)（式1参照）が組み込まれており、分子の\(F_{ss}\)を効果的に置き換えることができるため、若干の変更を加えて使用しています。これは、全体的な効果に指向性を与える方法として正当化でき、元の導出で行われた拡散の仮定と相殺されます。

\begin{eqnarray}
F_{ms} = \frac{E_{avg}}{1 – F_{ss} (1 – E_{avg})} \tag{12}
\end{eqnarray}

この関数の振る舞いは、Heiz [2016] モデルで行われた測定値を裏付けるもので、\(\alpha\)が0から1になると、平均的なランダムウォークの深さ（\(F_{ss}\)の指数と見なすことができる）が1からほぼ2まで変化することを示しています（図7右参照）。

これらの結果を利用して、\(F_{ms}\)に適した別の（さらに単純な）定式化を行います：

\begin{eqnarray}
F_{ms} = F_{ss}^{\alpha \sqrt{\alpha}} \tag{13}
\end{eqnarray}

フレネル項をさらに単純化するには、式(8)の\(k_{ms}\)の乗算値として、\(k_{ms}\)の値が大きいとき、つまりラフネス値が大きいときに、フレネル項の影響が大きくなることを観察する必要があります。

\(F_{ms}\)の影響は\(\alpha=1\)の時に最も顕著に現れるので、このようなラフネスにかかる値まで削ることができます：

\begin{eqnarray}
F_{ms} = F_{ss} \tag{14}
\end{eqnarray}

まだ完全に終わったわけではありません。最後に簡単な説明を加えます。\(F_{ss}\)は[Kulla and Conty 2017]で定義されているように，波長依存のパラメータ\(\eta\)と\(\kappa\)，あるいは交互に\(F_{0}\)と\(F_{edge}\)(\(F_{0}\)は法線方向の角度での色，このパラメータ化の詳細は[Gulbrandsen 2014]を参照)との多項式フィットで表されます。その評価にはコストがかかり、特にリアルタイムのアプリケーションを対象とする場合には、そのコストは大きいです。

我々のテストでは、金や銅のような強く着色された物理的に妥当な導体の場合、\(F_{ss}\)と\(F_{0}\)の値は非常に近く、結果に見た目の違いはなく、互換的に使用することができます。この観察結果は、物理的なフレネルを使用した場合にのみ成り立つことに注意してください。かすり傷の値が任意に着色できるようなアーティスト主導のフレネルを選んだ場合は、式(14)にこだわることをお勧めします。

これが最終結果の、素の状態での計算式につながります：

\begin{eqnarray}
F_{ms} = F_0 \tag{15}
\end{eqnarray}

また、式(8)で定義したBRDFをより明確に書き換えると

\begin{eqnarray}
\rho(\omega_o, \omega_i) = (1 + F_0 \frac{1 – E_{ss}(\omega_o)}{E_{ss}(\omega_o)}) \rho_{ss} (\omega_o, \omega_i) \tag{16}
\end{eqnarray}

これは、図1の下段の結果を生成するために使用された式です。興味深いことに、12、13、14、15のどのフレネル項を選択しても、視覚的に非常に近い結果が得られ、いずれも我々が本来求めていた飽和効果を実現しています。このように、高いラフネスに向かって\(F^2\)形状に近いものがあれば、我々の制作ニーズに応えることができると思われます。

3.2　Dielectrics

誘電体の場合、アプローチは似ていますが、いくつかの重要な違いがあります。フレネルは、反射\(E_{ss}^R\)と透過\(E_{ss}^T\)のエネルギーの比を示すものであり、単に反射と吸収の比を示すものではないので、式(9)の導体の場合と同様に、アルベドの正規化を決定する際にフレネルを無視することはできません。しかし、正規化できるのは、衝突するたびの\(E_{ss}^S = E_{ss}^R + E_{ss}^T\)の合計です。

我々の単一散乱誘電体BSDFを次のように定義します：

\begin{eqnarray}
\rho_{ss}^S(\omega_o, \omega_i) = \rho_{ss}^R (\omega_o, \omega_i) + \rho_{ss}^T(\omega_o, \omega_i) \tag{17}
\end{eqnarray}

そして、多重散乱にも同じ反射/透過率が適用されると考えると、エネルギー保存するBSDFが得られます：

\begin{eqnarray}
\rho^S(\omega_o, \omega_i) = \frac{\rho_{ss}^R (\omega_o, \omega_i) + \rho_{ss}^T(\omega_o, \omega_i)}{E_{ss}^S(\omega_o)} \tag{18}
\end{eqnarray}

図8を見ればわかるように、この補正の効果はかなり顕著で、もしかしたら導体の場合よりも顕著かもしれません。

※図は，[Turquin 2019]より引用

4　Comparison with other approaches

セクション3で紹介した方法は、Isotropix Clarisse、Pixar RenderManのRIS、Mitsubaパストレーサに実装されていますが、他のレンダラー（リアルタイムラスタライズエンジンを含む）にも簡単に追加することができます。

これはKullaとContyのものに近いですが、基本的には\(\rho_{ms}\)の形状の選択が異なります：私たちの場合は\(\rho_{ss}\)と同じローブであるのに対し、彼らの場合は拡散しています。前者の方がグランドトゥルースに近い（[Heitz et al. 2016]で示されている）ですが、相反性はないので、得られたBSDFを双方向の光輸送で使用する場合には、破綻する可能性があります。しかし、この正式な互恵性の欠如は、重大なアーティファクトを生み出す可能性は低いと考えています。

我々の手法は、\((\omega_o, \omega_i)\)ではなく\(\omega_o\)のみに依存しているため、クロージャー自体を変更するのではなく、クロージャーにゲインとして補正を適用することができ、既存のレンダラーへの組み込みがより簡単になります。よりシンプルになったことで、わずかながら高速化も実現しています。

もう一つの利点は、今回の結果は\(\rho_{ss}\)のスケーリングと見ることができ、その形状が完全に維持されているということです。対照的に、KullとContyのローブは、\(\rho_{ss}\)と方位不変のローブの混合物であり、最適な解析的重点サンプリングは達成できません。

どちらの手法も、理論的にはエレガントさや正確さに劣り、科学的には同じステップの前進を表すには程遠いものの、Heitzら[2016]に比べて実装が著しく容易で、実行時にははるかに高速です。彼らのオリジナルの実装を用いてMitsubaで行われたテストでは、単純な導体テストでは7倍、誘電体の透過テストでは15倍もの速度低下が観測されましたが、見た目の違いは最小限に抑えられているようです（図9の結果を参照）。

※図は，[Turquin 2019]より引用

最も注目すべき違いは、導体の飽和量で、リファレンスは、高ラフネスでわずかに飽和しているように見えますが、我々は、より正当化された式(12)の\(F_{ms}\)ではなく、式(15)の\(F_{ms}\)を使用しており、結果の飽和量は少し少なくなっています（図7左）。

いずれにしても、今回のように\(F_{ms}\)と\(\rho_{ms}\)を分離してはいけないし、方向性が異なることは間違いないので、完全に一致することは期待できません。しかし、このようなシンプルな手法を採用しても、十分に近い結果が得られると考えています。

最後に、[Kulla and Conty 2017]と私たちの方法は、単一散乱アルベド\(E_{ss}\)の計算にのみ依存しているため、どのような種類のBSDFにも対応できますが、[Heitz et al. 2016]はかなり強い制約を課しているため、BeckmannとGGX以外のモデルに使用することはさらに難しくなります。

すべての長所と短所の簡単なまとめは、表1を参照してください。

※表は，[Turquin 2019]より引用

5　Conclusion and future work

我々は、粗い反射や透過で欠落した多重散乱エネルギーを補うためのさまざまなアプローチを紹介しました。制作現場で使用する場合、最も適した候補は[Kull and Conty 2017]または今回紹介したもののどちらかであると思われますが、これは統合されるレンダラーにとって相互性がどの程度重要であるかによります。私たちは、どちらもアーティストにとって大きな助けとなり、よりエラーを起こしやすいアドホックな修正の必要性を取り除くことができると確信しています。

本レポートでの比較は、主に定性的な性質のものです。3つの主要な手法の違いをより詳細に定量的に分析することは、今後の課題とします。

さらに、すべてのスムースなルックアップテーブルの解析的な適合性を見つけることは興味深いことであり、コストのかかるテクスチャーアクセスを避けることができるという点で、リアルタイム実装に有益であるかもしれません。

また、もう導体用のフレネルを分離しないで、代わりにLUTを3D（IORの虚数部を本当に考慮したいなら4D）に拡張して、[Heitz eta al. 2016]のような参照アルゴリズムで計算することも考えられます（少なくともベックマン分布とGGX分布について）。

そういえば、将来的にはもっと野心的な試みとして、彼らの手法をより生産性の高いものに変える方法を見つけられたら素晴らしいと思います。

Acknowledgements

和訳省略。