知識というのは更新しないダメですね。
法線データのOctahedral Encodingをよく用いています。

※図は[Cigolle 2014]より引用。

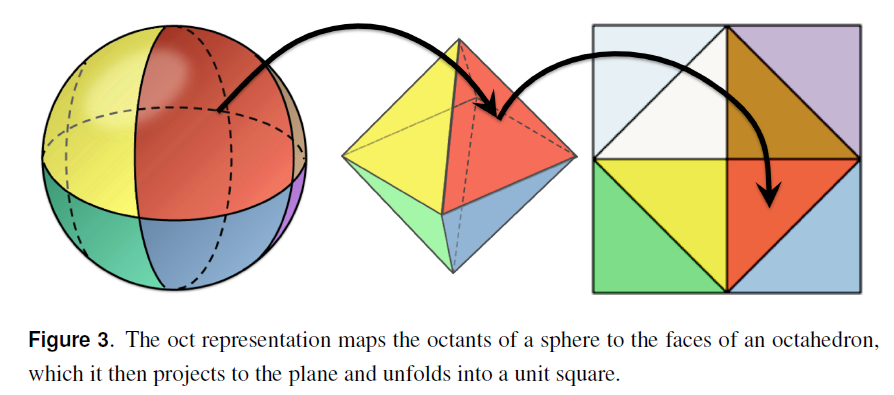
ここで，Octahedron を45度回転させて，符号をビットを別に持てば，表現する面積領域が増えるから精度が倍に上がるのと，OctWrap()の演算も無くなるので，デコードも高速できるそうです。

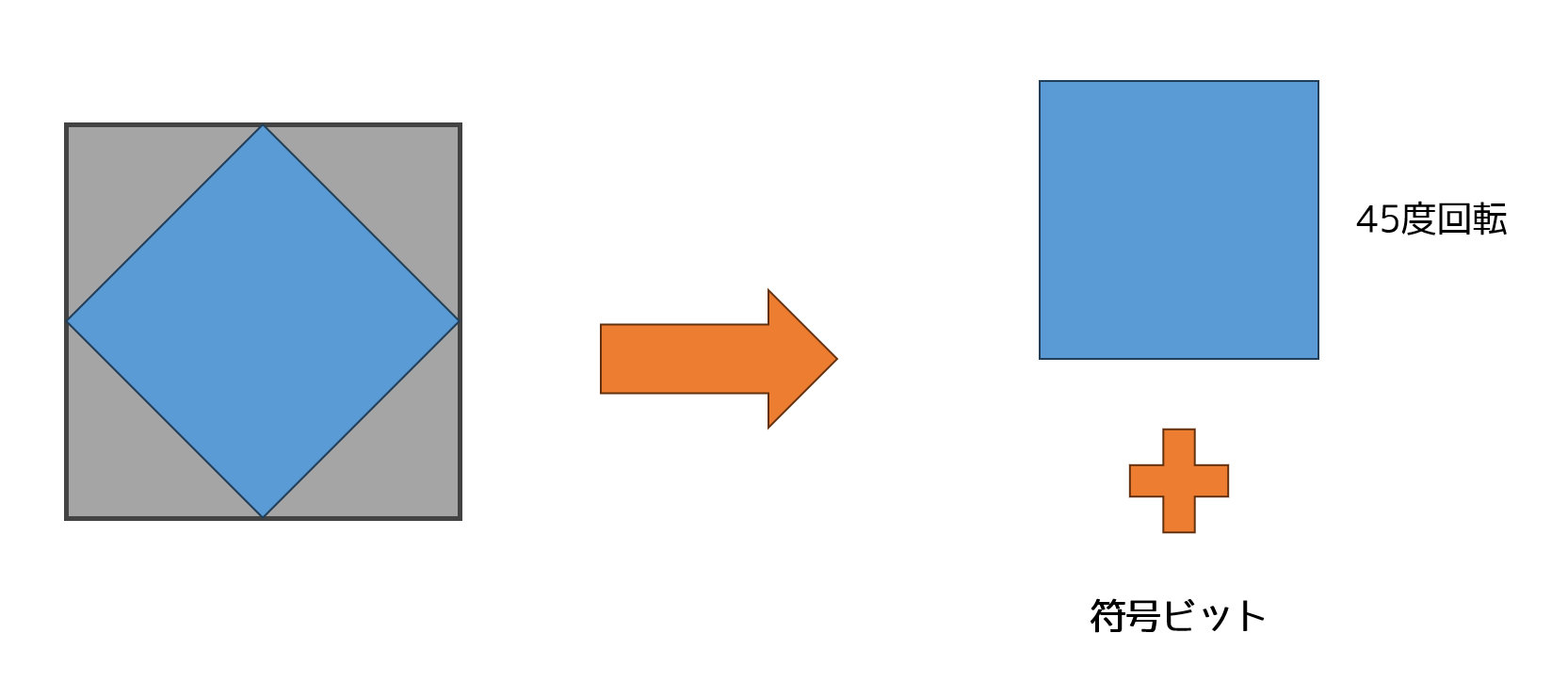
これが，John White 3Dというブログの，”Signed Octahedron Normal Encoding”という記事にのっていました。これをみて「ほぇぇ～」と感心しました。頭いい！
ただ、符号ビットを別に持つの何かやだなーと思っていたのですが，R10G10B10A2なら10bit分が残っているので，この32bitでNormal, Tangent, Bitangentを表現しちゃいたいところです。

以前に書いたかもしれませんが，SIGGRAPH 2020のDOOMで使っている，接線空間表現を使おうかなと思っていました。

※図は[Geffroy 2020]より引用。

しかし、今日もっといいやつを見つけました。
Jeremy Ongさんの”Tangent Spaces and Diamond Encoding”というブログ記事。この中でも上記のDOOMの方式が紹介されていますが，もっといいのがダイヤモンドエンコーディングというやつ。

※図は[Ong 2023]より引用

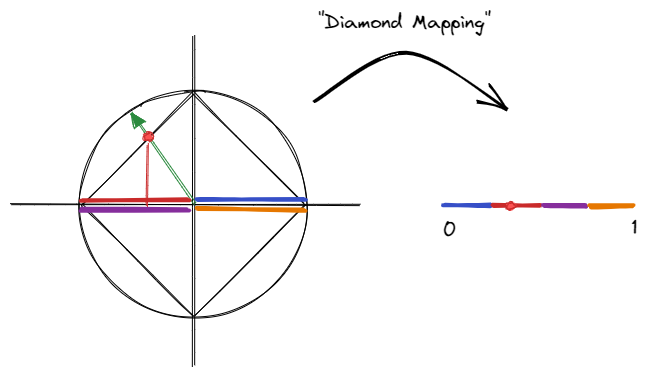
ここでも，Octahedronの考えを利用しています。ちなみにサンプルコードは下記の様です。

※コードは[Ong 2023]より引用

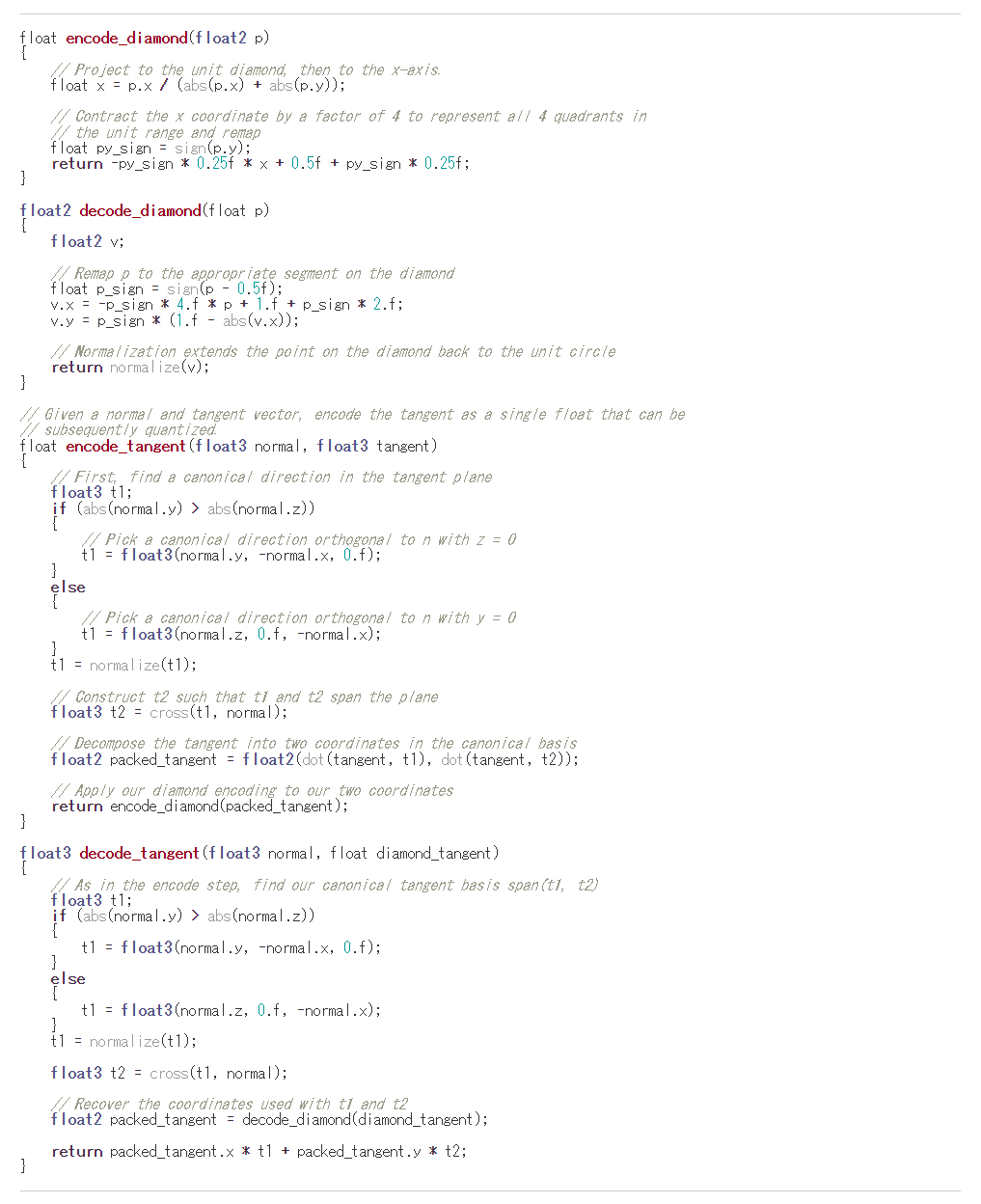
ダイヤモンドエンコードで得られた接線を表すデータを残りの10bit部分に入れてしまえば，うまくR10G10B10A2に収めることができます。

ちなみに，Octahedron Encodingですが，Z+の半球が約束されているのであれば符号ビットもいらないので，下記のHemi-Octで実現できるそうです。

※コードは[Cigolle 2014]より引用

…ということで接線空間データの圧縮についてでした。

参考文献

• [Cigolle 2014] Zina H. Cigolle, Sam Donow, Daniel Envangelakos, Michael Mara, Morgan McGuire, Quirin Meyer, “A Survey of Efficient Representations for Independent Unit Vectors”, Journal of Computer Graphics Techniques Vol.3, No.2, 2014.
• [JohnWhite3D 2017] John White 3D, “Signed Octahedron Normal Encoding”, https://johnwhite3d.blogspot.com/2017/10/signed-octahedron-normal-encoding.html, 2017.
• [Geffroy 2020] Jean Geffroy, Axel Gneiting, Yixin Wang, “Rendering The Hellscape of DOOM Eternal”, SIGGRAPH 2020 Advances in Real-Time Rendering course.
• [Ong 2023] Jeremy Ong, “Tangent Spaces and Diamond Encoding”, https://www.jeremyong.com/graphics/2023/01/09/tangent-spaces-and-diamond-encoding/, 2023.