わしゃがな！Pocolです。

今回は，Carmelo J. Fdez-Agüeraによる，”A Multiple-Scattering Microfacet Model for Real-Time Image-based Lighting”を読んでみようと思います。
論文は，http://jcgt.org/published/0008/01/03/からダウンロードできます。
いつもながら，誤字・誤訳があると思うので、ご指摘いただける場合は正しい翻訳例と共に指摘していただけるとありがたいです。

Abstract

この論文では、リアルタイムイメージベースドライティングモデルに多重散乱を組み込んだ拡張機能を紹介します。これは、実行時間コストが低いため、リアルタイムアプリケーションに適しています。主な洞察は、単一散乱項を計算するために使用される事前計算された積分が、残りの光のバウンスをシミュレーションするために必要なすべての情報をすでに含んでいることです。その結果、技法は単一散乱と比較するとわずかなオーバーヘッドが追加されますが、完全なエネルギー保護と保存を達成します。GGX双方向反射率分布関数(BRDF)のために導出されましたが、BRDF積分の事前計算や解析的フィットを見つけるために分離総和近似を使用することができる限り、他のモデルにも簡単に適用することができます。

1.　Introduction

この論文で紹介する技術は、リアルタイムアプリケーションのための一般的なイメージベースドライティングモデルをベースにしています。2節では、完全な反射面上でのエネルギー保存を強制することで、この技術の基礎を紹介します。3節では、フレネル反射率を考慮に入れて、この結果を任意の導体に一般化します。これは、単一散乱項に既に使用されていた事前計算データを再利用することによって行われます。最後に、4節では、この結果を誘電体マテリアルに拡張する方法を示し、その結果が、高いラフネスではエネルギーを保存し、低いラフネスでは過剰なエネルギーを防ぐことができ、完全なエネルギーの保護と保存をもたらすことを示します。図1に示すように、この欠落したエネルギーを取り戻すことで、特定の表面に強い視覚的インパクトを与えることができます。

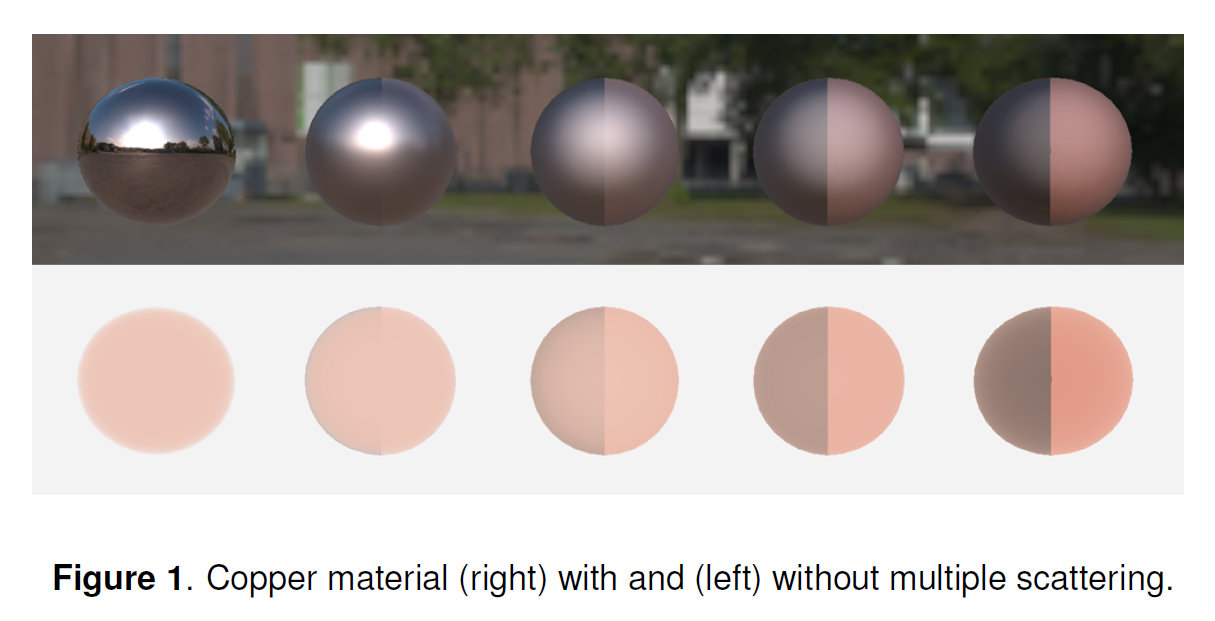
※図は，Carmelo J. Fdez-Agüera，”A Multiple-Scattering Microfacet Model for Real-Time Image-based Lighting”, Journal of Compute Graphics Techniques, Vol.8, No.1, 2019より引用。

1.1.　Related Work

Karis [2013]は、イメージベースドライティングのための単一散乱BRDF積分を事前計算する方法として、分離総和近似を導入しました。彼の方法は、BRDF応答のために事前に計算された積分を用いて、事前にフィルタリングされた輝度を使用します。この積分を2成分ルックアップテーブルとして保存し、フレネル項のスケールとバイアスとして使用します。
　Kulla と Conty [2017]は、ファーネステストを用いて単一散乱モデルの欠落エネルギーを補正し、その欠落エネルギーに基づいてBRDFに余分なローブを追加しています。推論はこの論文で紹介したものと類似していますが、彼らはいくつかの2Dおよび3Dルックアップテーブルを計算しており、彼らの結果はパストレースのためのものであり、リアルタイムのイメージベースドライティングのためのものではありません。
　Hill [2018a]は、KullaとContyによる手法を洗練し、幾何級数としての多重散乱事象におけるフレネル項の展開を探ります。さらに[2018b]、彼はパストレースシミュレーションを用いて、すべての散乱イベントで放出されるエネルギーを計算します。これはここで紹介したモデルよりも精度が高くなりますが、彼は多重散乱の各イベントのルックアップテーブルを事前に計算することになります。彼のアプローチは、解析的なライトを探索するだけで、イメージベースドライティングの一般化には対応していません。

1.2.　Furnace Test

反射面上でエネルギーが保存されるためには、任意の入射光の方向\(\omega_i\)について、視野半球に沿った反射光の積分が入射光の量に等しいことが真でなければなりません：

\begin{eqnarray}
\int_{\Omega} {\rm BRDF}(F_0, r, \omega_i, \omega_o) \cos \theta_o d\omega_o = 1
\end{eqnarray}

そして、相互関係を表すBRDFが与えられると、次のことも成り立つはずです：

\begin{eqnarray}
E(\omega_o, r) = \int_{\Omega} {\rm BRDF}(F_0, r, \omega_o, \omega_i) \cos \theta_i d\omega_i = 1 \tag{1}
\end{eqnarray}

　式(1)は、この論文で何度か使用するファーネステストを定義しています。関数\(E(\omega_o, r)\)は、BRDFの指向性アルベドとしても知られており、一様な白色環境に対してBRDFを積分することと等価です。

2.　Energy Preservation from Perfect Reflectors

多重散乱モデルを導出できる最も単純な表面は完全反射体であり、反射率\(F=1\)のサーフェイスです。これにより、BRDFのフレネル項がなくなり、積分が簡単になります。単一散乱BRDF (\(f_{ss}\))を白色の環境（式(2)）に対して積分すると、特定の方向に光が最初に跳ね返った後に表面から逃げるエネルギー、すなわち単一散乱の指向性アルベド\(E_{ss}\)が得られます。図2は、Epicの[2013]と同じBRDFを用いて、この積分の結果を示しています。実際には、彼らが提案しているスケールとバイアスの項を加えたものと同等です：

\begin{eqnarray}
E_{ss}(\omega_o, r) = \int_{\Omega} \frac{D(\omega_i, \omega_o, r)G(\omega_i, \omega_o, r)}{4 \cos \theta_i \cos \theta_o} \cos \theta_i d \omega_i \tag{2}
\end{eqnarray}

※図は，Carmelo J. Fdez-Agüera，”A Multiple-Scattering Microfacet Model for Real-Time Image-based Lighting”, Journal of Compute Graphics Techniques, Vol.8, No.1, 2019より引用。

エネルギーが保存されていれば、図2は真っ白になりますが、光の最初の跳ね返りだけを考慮しているので、一部の領域が暗くなっています。エネルギー保存(式(3)と(4))を適用すると、後のバウンスに対応するエネルギー\(E_{ms}\)が得られます：

\begin{eqnarray}
1 &=& E_{ss}(\omega_o, r) + E_{ms}(\omega_o, r) \tag{3} \\
E_{ms}(\omega_o, r) &=& \int_{\Omega} f_{ms} \cos \theta_i d \omega_i = 1 – E_{ss} (\omega_o, r) \tag{4}
\end{eqnarray}

不足しているエネルギーを考慮して、追加のBRDFローブを追加します：

\begin{eqnarray}
L_o = \int_{\Omega}(f_{ss} + f_{ms}) \cos \theta_i L_i d\omega_i = \int_{\Omega} f_{ss} \cos \theta_i L_i d \omega_i + \int_{\Omega} f_{ms} \cos \theta_i L_i d \omega_i \tag{5}
\end{eqnarray}

式(5)の右側の最初の積分式は従来の単一散乱項で，Kullaの分割総和を用いて計算することができます。そして，2つ目の積分は多重散乱ローブです。単一散乱項に対して我々がすることと同じく，分割総和(式(6))を用いてこの積分を近似することができます。分割の最初の項は正確には\(E_{ms}\)であり，2次散乱イベントに関与するエネルギーが一様に拡散されていると想定した場合，2つ目の項は余弦加重の放射照度で近似することができます。放射照度は通常，低解像度のテクスチャあるいは球面調和関数の係数へとベイクされるかのどちらかとして表現されます：

\begin{eqnarray}
\int_{\Omega} f_{ms} L_i \cos \theta_i d \omega_i \approx \int_{\Omega} f_{ms} \cos \theta_i d \omega_i \int_{\Omega} \frac{L_i}{\pi} \cos \theta_i d \omega_i \tag{6}
\end{eqnarray}

この近似値は、実際には一様な環境では正確であり、図3の完全なファーネステストを説明していることに注目してください。これは、スカイドームのようにエネルギーが多かれ少なかれ均等に分布している半球の大部分をカバーするライトにはまだ良い近似ですが、ほとんどのエネルギーが一方向から来る狭いライト（例えば、解析点や指向性のあるライト）には適していません。
　式(7)は完全なファーネステスト（イメージドライティング）の近似値であり、式(8)は完全反射体に対する分割総和の近似値です。

\begin{eqnarray}
\int_{\Omega} f_{ms} \cos \theta_i d \omega_i \int_{\Omega} \frac{L_i}{\pi} \cos \theta_i d \omega_i = (1 – E_{ss} ) \int_{\Omega} \frac{L_i}{\pi} \cos \theta_i d \omega_i \tag{7} \\
L_o = E_{ss} {\rm radiance} + (1 – E_{ss}) {\rm irradiance} \tag{8}
\end{eqnarray}

図3は、分割総和近似を用いた単一散乱イメージベースドライティングと、完全反射体について多重散乱を用いたモデルとの比較を示しています。アルベドの増加は、高いラフネス値に関してはかなり顕著です。

※図は，Carmelo J. Fdez-Agüera，”A Multiple-Scattering Microfacet Model for Real-Time Image-based Lighting”, Journal of Compute Graphics Techniques, Vol.8, No.1, 2019より引用。

3.　Generic Metals, Fresnel Term

一般的な金属については、フレネル項を考慮に入れる必要があります。完全反射体の分割総和近似(式(8))を再利用するために、一様なライティングの式は次のような形にしたいと思います：

\begin{eqnarray}
E = F_{ss} E_{ss} + F_{ms} E_{ms} \tag{9}
\end{eqnarray}

1回目のバウンス後は、光がランダムに四方八方に散らばります。このような二次バウンスの光の分布は、全方向に一様なエネルギーを持つものとしてモデル化することができるので、余弦加重放射照度の減衰形で表現することができます。この仮説のもとでは、すべての二次散乱イベントは最初のイベントと同じように振る舞いますが、この減衰された照度を光源とすることを除いては、最初のイベントと同じように振る舞います。この近似は、分割総和を使用した場合、入射光は多かれ少なかれ均等に分布していると仮定しているので、この近似は理にかなっています。
　Hill [2018a]とほぼ同じ方法で、\(F_{ms} E_{ms}\)を光のマルチバウンスのための幾何級数に発展させることができます。各光のバウンスでは、割合\(E_{avg}\)がサーフェイスから逃げ、\(1 – F_{avg}\)の割合が導体に吸収されるので、\((1 – E_{avg})F_{avg}\)だけが次のバウンスに残されます。ここで\(F_{avg}\)はフレネル項の余弦加重平均です。後者は視野角に依存しますが、前者は全方向から来た光の減衰を表し、方向性がないので、\(F_{ss}\)で\(F_{avg}\)を近似することはできないことに注意してください。しかし、\(F_{avg}\) は Schlick 近似を使うと解析的な解が得られます (式 (10), (11))。

\begin{eqnarray}
F_{avg} &=& 2 \pi \int_{0}^{\pi / 2} (F_0 + (1 – F_0)(1 – \cos (\theta)^5) \frac{\cos \theta}{\pi} \sin \theta d\theta \tag{10} \\
F_{avg} &=& F_0 + \frac{1}{21} (1 – F_0) \tag{11}
\end{eqnarray}

この時，\(F_0 = 1\)で，式12は

\begin{eqnarray}
E = F_{ss} E_{ss} + \sum_{k=1}^{\infty} F_{ss} E_{ss} (1 – E_{avg})^k F^{k}_{avg} \tag{12}
\end{eqnarray}

となります。
そして，式3に等しくなければならないので，

\begin{eqnarray}
1 &=& E_{ss} + \sum_{k=1}^{\infty} E_{ss} (1 – E_{avg})^k = \sum_{k=0}^{\infty} E_{ss} (1 – E_{avg})^k \\
1 &=& \sum_{k=0}^{\infty} E_{ss} (1 – E_{avg})^k = \frac{E_{ss}}{1 – (1 – E_{avg})} \\
& E_{avg} & = E_{ss}
\end{eqnarray}

となります。これは、\(E_{ss}\)のように、\(E_{avg}\)は見る方向に依存していることを意味しています。つまり、光がある方向に逃げるためには、他の方向よりも多くのバウンスが必要です。\(E_{avg}\)を式(12)に戻すと、次のようになります。

\begin{eqnarray}
E = F_{ss} E_{ss} + F_{ss} E_{ss} \frac{(1 – E_{ss}) F_{avg}}{1 – (1 – E_{ss})F_{avg}} \tag{13}
\end{eqnarray}

そして、式(9)と式(13)を組み合わせると、次のようになります。
\begin{eqnarray}
F_{ms} E_{ms} = F_{ms} (1 – E_{ss}) & = & F_{ss} E_{ss} \frac{(1 – E_{ss}) F_{avg}}{1 – (1 – E_{ss}) F_{avg}} \\
F_{ms} & = & \frac{F_{ss}F_{avg}E_{ss}}{1 – F_{avg}(1 – E_{ss})} \tag{14}
\end{eqnarray}

前の式の問題は、まだ\(F_{ss}\)の式がないことですが、単一散乱BRDFを積分することで\(F_{ss}\)を得ることができます。式(15)では、Schlickのフレネルへの近似を用いてそれを行います。

\begin{eqnarray}
F_{ss} E_{ss} = F_0 \int_{\Omega} \frac{f_{ss}(\omega_i, \omega_o)}{F(\omega_o, \omega_h)} \left( 1 – (1 – \omega_o \cdot \omega_h)^5 \right) \cos \theta_i d\omega_i \\
+ \int_{\Omega} \frac{f_{ss}(\omega_i, \omega_o)}{F(\omega_o, \omega_h)} (1 – \omega_o \cdot \omega_h)^5 \cos \theta_i d\omega_i \tag{15}
\end{eqnarray}

これは、Epic Gamesが単一散乱のイメージベースドライティング[2013]のルックアップテーブルに計算した積分であり、ベース反射率\(F_0\)のスケール(\(f_a\))とバイアス(\(f_b\))から構成されているので(図4参照)、次のように参照します。

\begin{eqnarray}
F_{ss} E_{ss} = F_0 f_a + f_b \tag{16}
\end{eqnarray}

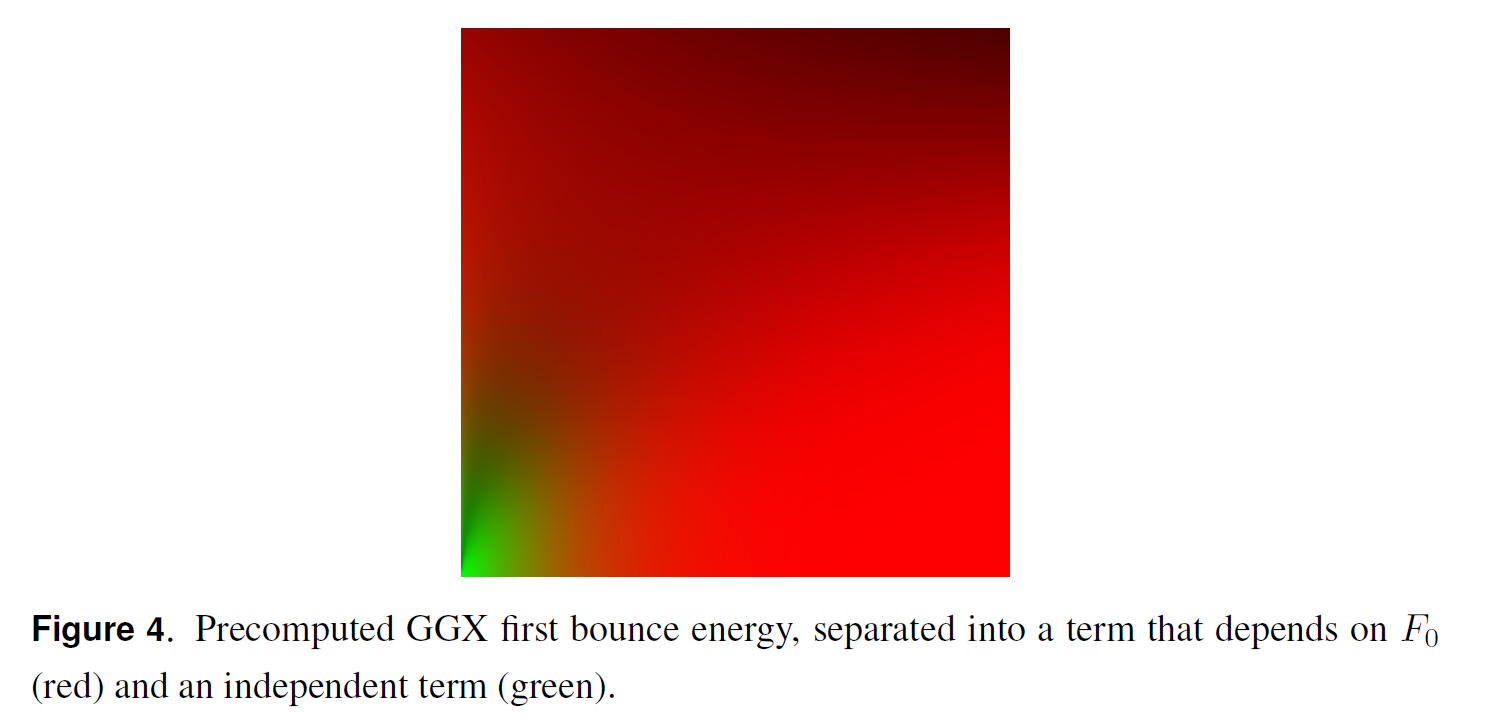
※図は，Carmelo J. Fdez-Agüera，”A Multiple-Scattering Microfacet Model for Real-Time Image-based Lighting”, Journal of Compute Graphics Techniques, Vol.8, No.1, 2019より引用。

式(16)を式(14)に代入すると、次のようになります。

\begin{eqnarray}
F_{ms} = \frac{(F_0 f_a + f_b)F_{avg}}{1 – F_{avg} (1 – E_{ss})} \tag{17}
\end{eqnarray}

そこで、金属の完全な式を以下のように表すことができます:

\begin{eqnarray}
L_o = (F_0 f_a + f_b) \, {\rm radiance} + \frac{(F_0 f_a + f_b)F_{avg}}{1 – F_{avg}(1 – E_{ss})} E_{ms} \, {\rm irradiance} \tag{18}
\end{eqnarray}

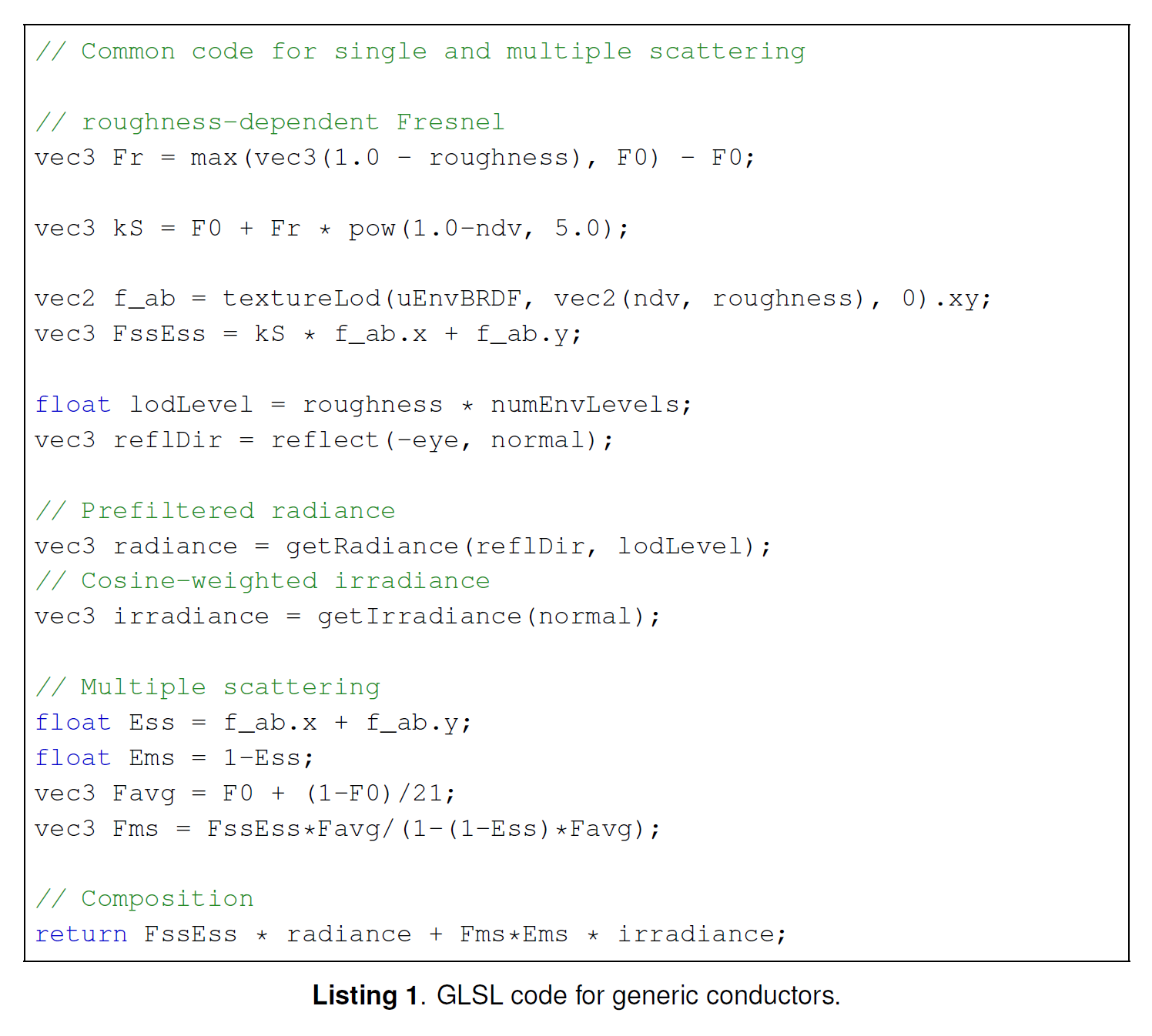
※リストは，Carmelo J. Fdez-Agüera，”A Multiple-Scattering Microfacet Model for Real-Time Image-based Lighting”, Journal of Compute Graphics Techniques, Vol.8, No.1, 2019より引用。

リスト1は、金属用のイメージベースドライティングの実装例を示しています。複数の散乱コードによって導入されるオーバーヘッドが非常に低いことに注目してください。結果は図5で比較することができます。

※図は，Carmelo J. Fdez-Agüera，”A Multiple-Scattering Microfacet Model for Real-Time Image-based Lighting”, Journal of Compute Graphics Techniques, Vol.8, No.1, 2019より引用。

4.　Dielectrics

誘電体では、フレネルで反射されないエネルギーがサーフェイスの下で拡散し、放射されて戻ってくる方法に対応する、さらなる項があります。\(K_d\)は、表面下でのエネルギー吸収をモデル化した表面の拡散アルベドであるとし、次のようにします。

\begin{eqnarray}
E = F_{ss} E_{ss} + F_{ms} E_{ms} + K_d E_d
\end{eqnarray}

\(E_d\)は\(1 – F_0\)として計算されることが多いです。しかし、入射光のグレージング角では、フレネル項はより高い(飽和度が低い)ので、拡散項ではより少ない光の量で終わるはずです。\(f_d\)のより良い近似を得るために、完全に白い誘電体(\(K_d = 1\))は光を吸収しないので、受け取ったエネルギーと同じだけのエネルギーを放射しなければならないことを観察することができます。

\begin{eqnarray}
1 = F_{ss} E_{ss} + F_{ms} E_{ms} + E_d \\
E_d = 1 – (F_{ss} E_{ss} + F_{ms} E_{ms})
\end{eqnarray}
　
　これは誘電体のエネルギー保存を修正し、多重散乱スペキュラーローブを考慮に入れています。これは拡散界面と鏡面界面の間を行ったり来たりする光散乱の影響を明示的にモデル化していませんが、誘電体の鏡面反射率は通常非常に低く、不飽和であるため、放射されたエネルギーは最終的にはそのまま表面を脱出することになるので、この近似は維持されます。
　図6は、灰色の背景に、ラフネスを変化させた単一散乱モデル（左）と多重散乱モデル（右）のファーネステストを示しています。ラフネスが大きい場合、多重散乱を導入することで、欠落していたエネルギーが回復し、滑らかな表面では、エッジに向かう余分なエネルギーが除去されます。これは図7にさらに示されており、両方のモデルが参考写真と比較されています。多重散乱の球体（中央）の暗い縁が、参照写真の光の分布とより密接に一致していることに注目してください。この効果は確かに金属の場合よりも微妙ですが、余分なエネルギーを除去することで、より自然な外観が得られます。リスト2は、誘電体のための適切な\(K_d\)項を計算するために必要なコードを示しています。繰り返しになりますが、従来の拡散IBLよりもオーバーヘッドは非常に小さいです。

※図は，Carmelo J. Fdez-Agüera，”A Multiple-Scattering Microfacet Model for Real-Time Image-based Lighting”, Journal of Compute Graphics Techniques, Vol.8, No.1, 2019より引用。

※図は，Carmelo J. Fdez-Agüera，”A Multiple-Scattering Microfacet Model for Real-Time Image-based Lighting”, Journal of Compute Graphics Techniques, Vol.8, No.1, 2019より引用。

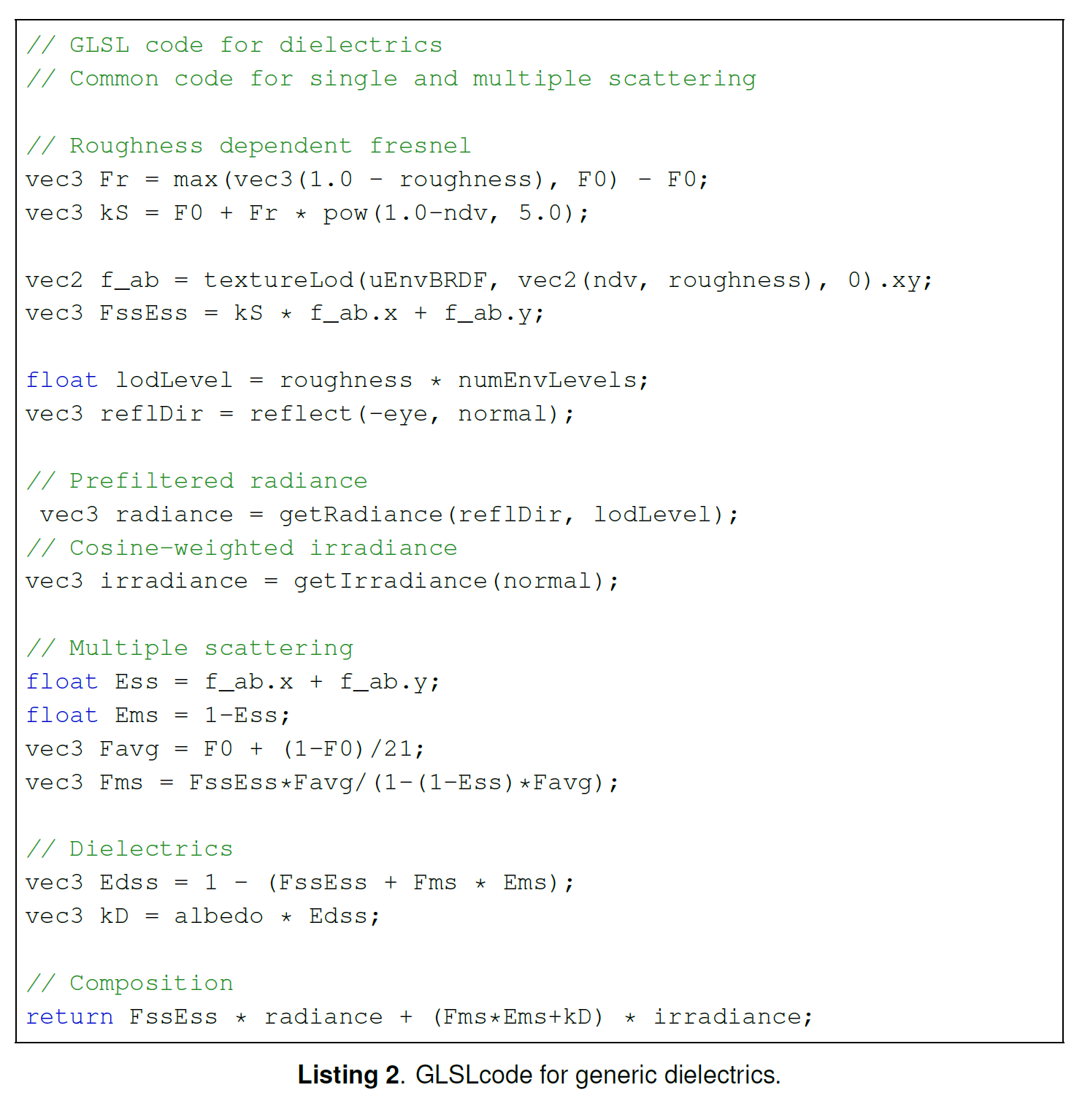
※リストは，Carmelo J. Fdez-Agüera，”A Multiple-Scattering Microfacet Model for Real-Time Image-based Lighting”, Journal of Compute Graphics Techniques, Vol.8, No.1, 2019より引用。

5.　Conclusions

多重散乱の効果をイメージベースドライティングに戻すことで、マテリアルの見た目に大きな影響を与えることができます。さらに、エネルギー保護と保存を保証することで、マテリアルは環境照明の変化に強くなり、これは一般的に物理ベースのレンダリングの利点の一つとなります。この論文では、わずかなオーバーヘッドでこの効果を達成することが可能であり、視覚的なインパクトはコストに見合う価値があることを示しました。