こんにちわ。Pocolです。
今日は,
[Hable 2007] Ralf Hable, Alexander Kustering, Michael Wimmer, “Physically Based Real-Time Translucency for Leaves”, EGSR’07: Proceedings of the 18th Eurographics conference on Rendering Techniques, June 2007, pp.253–263
を読んでみようと思います。
いつもながら誤字・誤訳があるかと思いますので,ご指摘頂ける場合は正しい翻訳例と共に指摘して頂けると有難いです。
Abstract
この論文では、植物の葉をリアルタイムでレンダリングするための新しいシェーディングモデルを紹介します。このモデルは、葉の重要な属性をすべて生成し、多数の葉をシェーディングすることができます。特に、直接照明された葉の半透明な面での正確な表面下散乱のために、物理的に基づいたモデルを使用しています。このモデルをリアルタイムでレンダリングするために、画像の畳み込み処理として定式化し、その結果を高速に評価できる効率的な方向性基底で表現しています。また、市販のデバイスを利用した葉のデータ取得方法を提案します。
1. Introduction
植物をリアルに表現することは、コンピュータグラフィックスの重要な研究テーマです。植物の幾何学的な複雑さに加えて、特に葉の内部での複雑な光の相互作用により、植物をリアルかつ効率的に表示することは非常に困難です。最近、Wangら[WWD*05]は、葉のリアルタイムレンダリングアルゴリズムに多くの照明効果を取り入れました。彼らのアルゴリズムは、反射率と半透明を扱い、間接照明と直射日光照明の両方について、樹木全体の放射伝達を事前に計算します。しかし、彼らの半透明モデルは基本的にLambertianであり、葉のサーフェイスに沿って変化する特性によって発生する多重散乱効果をすべて無視しています。BSSRDF[NRH*77]モデルでのみ表現可能なこれらの効果には、葉面上のセルフシャドウイング、葉の厚さの変化、葉面の色の変化などがあります。
本論文では、直射日光を浴びた葉の半透明な面を忠実に表現するためには、表面下の散乱効果が重要であることを示しています(図11を参照)。そこで,薄いスラブのための物理ベースのサブサーフェスシミュレーション[DJ05]を用いてこれらの効果を考慮し,入射光の方向に応じて変化するピクセルごとの半透明輸送関数を導出します。リアルタイム性を実現するために、最近開発された「Half Life 2基底」[McT04]を一般的な指向性基底として導入し、透光性輸送関数をこの基底に展開します。
この論文の主な貢献点は、植物の葉における半透明の表面下散乱を正確にリアルタイムで再現するモデルを初めて提案したことです。我々の半透明モデルは、Wangらのフレームワークに簡単に統合することができますが、葉に局所的であることから、ダイナミックで複雑なシーンで重要となるインスタンス化、アニメーション、シャドウマッピングとの組み合わせが容易です。また、市販のハードウェアを使用して、最も重要な葉の特性をキャプチャすることができる効率的な取得方法を示しています。図1は、物理ベースの半透明性をリアルタイムでレンダリングしたシーンの例です。
2. Related Work
葉の光の相互作用を計算するために、さまざまな手法が提案されています。HanrahanとKrueger[HK93]は,層状の表面下散乱を1次元輸送理論でモデル化し,後方散乱と透過の明示的な定式化を行い,モンテカルロ法を用いてBDFを評価しています。Baranoski[BR97]は,利用可能な生物学的情報に基づいたモデルを提案しました。Baranoskiは後に、反射率と透過率の値を事前に計算し、簡略化した散乱モデルを適用することで、この方法を拡張しました[BR01]。Ganapolら[GJH*98]によって提案されたLEAFMODモデルは、均質な光学特性を持つスラブ内の一次元放射伝達方程式を解き、葉の反射率と透過率の推定値を生成します。このモデルはWangら[WWD*05]も使用しています。これらの手法に共通しているのは、透光性に対して(8次元)BSSRDF[NRH*77]を用いた完全な表面下散乱レンダリング方程式を考慮しておらず、セルフシャドウイングや反射率パラメータの変化、厚さなどによる葉の表面の変化をシミュレートすることができません。そこで、これらのモデルでは、(4次元)BTDF(双方向透過率分布関数)を用いています。
葉っぱの散乱効果をすべて取り入れるための仮想的な方法として、葉っぱの半透明なBTF(bidirectional texture function [DvGNK99, MMS*05])を記録する装置を構築することができます。しかし、現在のBTFの手法では、メモリやレンダリングのコストが大きく、高解像度化もできません。また、Govaertsら[GVU96]によって提案された、葉の中の光の伝搬を正確にシミュレートする別の方法は、葉の組織の内部の3次元構造とその光学的特性を幾何学的に表現し、このモデルにレイトレーシングを適用することです。これは明らかに遅いです。均質な物質における表面下散乱を計算する最も実用的な方法は、Jensen[JMLH01]によって導入され、解析的な拡散ダイポール近似に基づいています。Franzkeら[FD03]は、この考えに基づいた葉の簡略化された単一散乱アルゴリズムを示しました。しかし、Jensenのダイポール近似は半無限のスラブに対してのみ有効であり、葉は除外されています。DonnerとJensen[DJ05]はこれを拡張し、多層の薄いスラブにおける表面下散乱を正確かつ効率的に計算しました。このマルチダイポールアプローチは、本稿で示した葉の透光性に対する効率的な事前計算プロセスの基礎となっています。
表面下散乱は活発な研究分野であり、例えば、皮膚のようなより一般的な材料[BL05]、より一般的な照明条件[WTL05]、あるいは変形可能なモデル[MKB*03]など、多くの結果が得られています。
3. A Leaf Model for Real-Time Rendering
3.1. Overview
このセクションでは、新しい半透明モデルの詳細を説明する前に、基礎となるリーフモデルとそれに伴う取得プロセスについて説明します。Wangら[WWD*05]と同様に、我々は葉を、粗い表面と裏面を持つ均質なマテリアルの薄いスラブとしてモデル化します。空間的に変化する反射率はアルベドマップ\(\alpha (\vec x)\)に、葉の厚さの変化は厚さマップ\(d(\vec x)\)にエンコードされます。新しいモデルで計算された透過色を指定するために、平均透過マップ\(\rho_t(\vec x)\)も保存します。最後に、法線マップ\({\vec n}(\vec x)\)を使用することで、高周波のスペキュラー反射を正確にシミュレートすることができます。これらのマップは、葉の表と裏の両方に存在します。
葉の中での光の相互作用は、いくつかの条件で決まります。
\begin{eqnarray}
L = L^{S_d} + L^{S_i} + L^{E}
\end{eqnarray}
つまり、直射照明、間接照明、環境照明の寄与を示すものです。直射照明の寄与は次のように分けられます。
\begin{eqnarray}
L^{S_d} = L_r + L_t
\end{eqnarray}
反射成分と半透明成分のうち、葉の法線と光の方向の内積に応じて、どちらか一方だけがゼロになりません。本論文では,直射光照明による透光性(\(L^{S_i}, L^E\))に着目し,これをアンビエント項で近似した結果を示します。これらの項はWangら[WWD*05]のモデルに従って計算することができますが、木全体の事前計算が必要になります。これはメモリの点で非常にコストがかかり、葉のアニメーションやインスタンス化もできません。
3.2節と3.3節では、反射率項\(L_r\)と取得について簡単に説明し、4節と5節では、本稿の主な貢献である\(L_t\)の葉の透光性モデルとそのリアルタイム評価に充てています。
3.2. Leaf reflectance
葉の構造は、主に直射日光の照射によるスペキュラー反射特性(\(L_r\))で認識され、その高周波構造が明らかになります。葉のBRDFには、微細な毛髪によるベルベット状のものから、厚いワックス層による高鏡面まで、実にさまざまな種類があります。多くの場合、葉の表側には広い鏡面性があり、葉の裏側には拡散性があります。木の葉に多いのですが、植物でもクレオソートブッシュのように葉の裏が鏡面になっているものもあります。
Bousquet[BLJM05]やWangら[WWD*05]に倣い、葉の表側にはCook-Torranceシェーディングモデル[CT82]を、裏側には拡散シェーディングを使用しています。反射性のある表面下の散乱に対してもBSSRDFアプローチを使用することを検討しましたが、表面下散乱による非方向性の寄与は取得プロセスからアルベドマップに含まれているため、標準的なBRDFモデルとの違いは無視できることがわかりました。これは、スキンレンダリングとは対照的に、非常に薄くて吸収率の高い媒体で表面下の散乱を計算し、光の拡散範囲を最大でも数ミリに抑えているためです。
我々は葉のBRDFを測定していないので、Bousquetの鏡面係数の測定値とフィッティング値を使用しています。有効屈折率は\(n=1.2〜1.7\)、粗さは\(\sigma=0.078〜0.5\)の範囲で、高いスペキュラーの葉(月桂樹など)からほぼ拡散したスペキュラーローブ(ハシバミなど)までをカバーしています(図2参照)。
我々の撮影プロセスでは、高解像度の法線マップが得られます。そのため、葉の反射率の解析的な表現を使用した従来の研究とは対照的に、ジオメトリ法線の代わりに、法線マップからのより正確な法線を使用してBRDFを評価します。また、拡散項はアルベドマップから取得しています。直射日光による反射の寄与は,光強度\(L_D\),光の方向\({\vec \omega}_D\),ディラック関数\(\delta\)を持つ指向性の光\(L(\omega) = L_D \delta ({\vec \omega} – {\vec \omega}_D)\)としてモデル化されるため,次のように評価されます。
\begin{eqnarray}
L_r({\vec x}, {\vec \omega}_o) = L_D \left( \frac{\alpha(\vec x)}{\pi} + f_s({\vec n}(\vec x), {\vec \omega}_D, {\vec \omega}_o \right) ({\vec n}(\vec x) \cdot {\vec \omega}_D) \tag{1}
\end{eqnarray}
ここで、\(\vec x\)はサーフェイスの点、\({\vec \omega}_o\)は出射方向、\(f_s\)はスペキュラーBRDFです。完全反射型BRDFは、このように\(f_r = \alpha + f_s\)となります。なお、拡散項を算出するためには、理論的には\(α(\vec x)\)を\(f_s\)のアルベドで減少させる必要がありますが、非グレージング角ではこの項は無視できます。
3.3 Data Acquisition
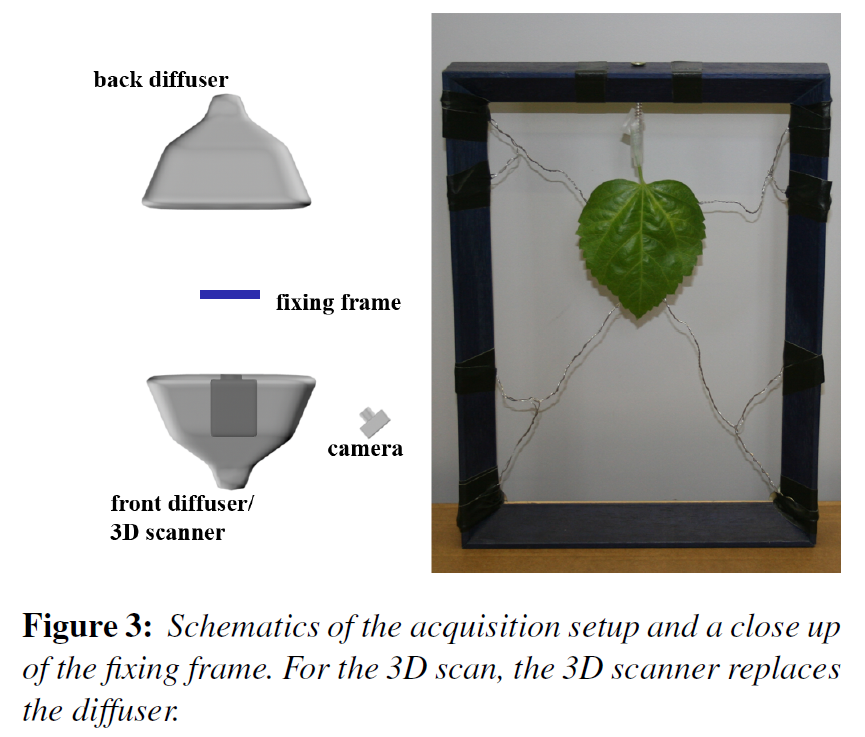
アルベド、法線、厚さ、平均透過度の必要なマップをどのように作成するかを簡単に説明します。私たちの取得方法は、簡単なプロセスと(少し高価な)市販のハードウェアを使って、高解像度(1mm未満)のマップを生成することができます。これは、高精度の3Dスキャナーを使用していることが主な理由です。
使用した機器は、有効解像度0.1mmの3Dスキャナー(Minolta VI-910)、露光時間を固定したデジタルカメラ(Canon ESO 20D)、大型ボックスディフューザーを備えた1,000Wの光源2台、葉っぱを固定するための簡単な構造のフレームです。大型の拡散板により、アルベドを捉えるために必要な半球状の照明に近づけることができます。固定フレームは、撮影中に葉が変化しないことを保証し、撮影データに一貫性を持たせています。リーフは、小さなクランプ付きのワイヤーブリッジを使ってフレームに固定されており、リーフがまっすぐかつ自然な位置に保たれるようになっています。3Dスキャナー、カメラ、ディフューザーを図3のように配置します。
葉っぱのサンプリングは、まず3Dスキャンを行い、次にスキャナーをディフューザーに替えてカメラでアルベドを記録し、次に背面のディフューザーに替えて透過度を記録します。固定フレームを慎重に回した後、葉の裏側にも同じ手順を繰り返します。
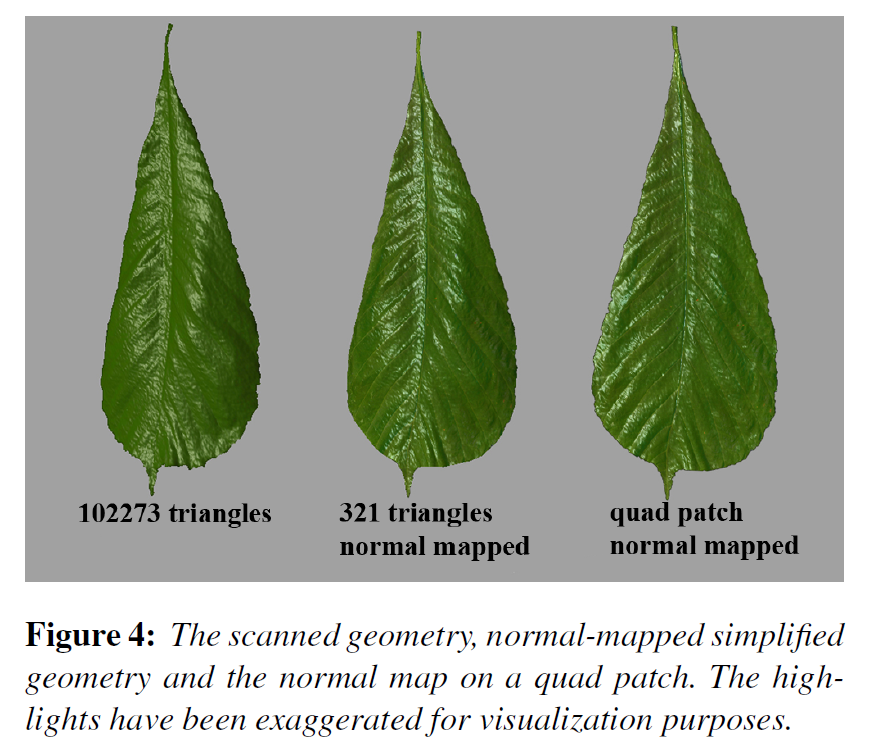
後処理にはGeomagicやMayaなどの標準的なツールを使用しています。いくつかのフィルタリングと、葉の高周波構造に影響を与えないような適度なスムージングを行い、撮影した画像をジオメトリに合わせた後、メッシュを幾何学的に単純化し、高周波の幾何学的構造を法線マップ[COM98]と各面の変位マップとしてエンコードします。厚みマップは、表側と裏側のスキャンの変位マップを差し引くことで生成され、ユーザーが定義した葉の最大厚さに正規化されます。このようにして生成された法線マップは、葉の異なる幾何学的な詳細レベルにマッピングすることができます(図4)。生成されたテクスチャは、使用されたリーフが強いスペキュラー特性を持つ場合、標準的な画像処理技術を用いてハイライトを除去する必要があるかもしれません。図5は、提案された方法で生成されたデータセットの一例です。
また、Wangら[WWD*05]の取得方法と比較して、カスタムメイドのリニア光源装置を必要とするピクセル単位のBRDFおよびBTDFデータを取得していません。そのため、空間的に変化する粗さや鏡面反射強度をエンコードすることができず、リーフ全体で1つのパラメータセットに頼らざるを得ません。一方、高解像度の法線マップを作成することで、葉の高周波構造に合わせて、より正確にハイライトを配置することができます。これは、葉の表側では直射日光による鏡面反射のハイライトが最も目立つため、重要なポイントです。
4. Leaf Translucency
この論文の主な洞察の1つは、表面下散乱は、葉の光が当たっている側の外観にはごくわずかな影響しか与えませんが、反対側の外観には圧倒的な影響を与えるということです。図11は、拡散BTDFに基づいたシンプルかつ最新の半透明モデルと、BSSRDFに基づいて本稿で提案したモデルの違いを示しています。葉の反射部分では高周波の特徴が法線マップを使って簡単にモデル化できるのに対し,透光部分では表面の変化による照明効果を導入する方法がまだないため,単純なモデルは葉の幾何学的な法線を使った単純な拡散シェーディングモデルに限定されています。一方、今回開発した手法では、入射光の角度に応じて、葉が滑らかに見えたり(急峻な角度)、立ち上がりや膨らみなどの葉の構造に起因する高周波のディテールが現れたり(グレージング角度)します。
BSSRDFモデルでは、光が葉の内部に入る前の葉の自己影、葉の厚さの変化、光が当たる葉の表面の反射率特性の変化などが主に考慮されています。これらの効果により、媒体に入射する光の量が変化し、反対側の葉の表面で影となる特定の点に向かって散乱することになります。なお,このモデルは葉の局所的なものであるため,他の葉などからの影による光の変化は,結果として得られる放射輝度を変化させるだけで,表面下散乱計算には影響を与えません(これらの効果は,標準的なリアルタイム影アルゴリズムを用いて処理されます).しかし、このような大規模な構造物が、はるかに小さなスケールで起こる葉の表面下の散乱に与える影響は、無視できる程度のものです。
最近,DonnerとJensen[DJ05]は,薄い均質なスラブにおける表面下散乱を計算する効率的な近似法を紹介しました.4.1節ではこの方法の主要な概念を紹介し、4.2節では画像の畳み込みとしての効率的な定式化を示します。
なお、すべての計算は簡略化されたジオメトリの接線空間で行われ、物理的な単位を維持するようにスケーリングされています。この接線空間は、BSSRDFモデルの前提条件である、散乱経路の典型的な長さと比較して、局所的に平坦であることを想定しています。
4.1. Background: Light Diffusion in Leaves
ここでは,吸収係数\(\sigma_a\),散乱係数\(\sigma_s\),散乱位相関数\(g\)の平均余弦で特徴づけられる葉を考えます。
透過マテリアルの散乱は、BSSRDF(Bidirectional Scattering Surface Reflectance Distribution Function)[NRH*77]で表されます。
\begin{eqnarray}
S({\vec x}_i, {\vec \omega}_i, {\vec x}_o, {\vec \omega}_o) = \frac{dL_o({\vec x}_o, {\vec \omega}_o)}{d\Phi ({\vec x}_i, {\vec \omega}_i} \tag{2}
\end{eqnarray}
ここで、\(L_o\)はライト向いていない側の出射光束、\(\Phi\)は葉のライトに面している側の入射光束です。\({\vec x}_i\)、\({\vec \omega}_i\)は入射位置と入射方向、\({\vec x}_o\)、\({\vec \omega}_o\)は出射位置と出射方向を表します。Jensenら[JMLH01]は、半無限の均質なスラブに対して、BSSRDFは拡散ダイポール、すなわち2つの仮想点光源で近似できることを示し、放射輸送の拡散近似を通して導き出しました。薄いスラブでは、2つの境界条件を考慮しなければなりません。葉の表側か裏側のどちらかに到達した光は決して戻りません。これらの境界条件を満たすために,複数のダイポールが必要になります[DJ05].この境界条件は,フルエンスとも呼ばれるスカラー・イラディアンス\(\phi\)で表されます(代数的な詳細は[DJ05]を参照)。
\begin{eqnarray}
\phi(r) – 2AD \frac{\delta \phi(r)}{\delta z} = 0 \quad at z=0, z = d \tag{3}
\end{eqnarray}
ここで、\(D = \frac{1}{2 {\sigma’}_t}\)は還元消光係数\({\sigma’}_t\)を持つ。式3は\(z=0\)の前面と\(z=d\)の深さの後面に適用され、項\(A\)は表面での内部反射によるフルエンスの変化を表します。
\begin{eqnarray}
A = \frac{1 + \rho_d}{1 – \rho_d} \tag{4}
\end{eqnarray}
葉は反射面が粗いので、フレネル項の代わりにサンプリングで評価できる反射BRDF \(f_r\)の平均拡散反射\(\rho_d\)を用いています。
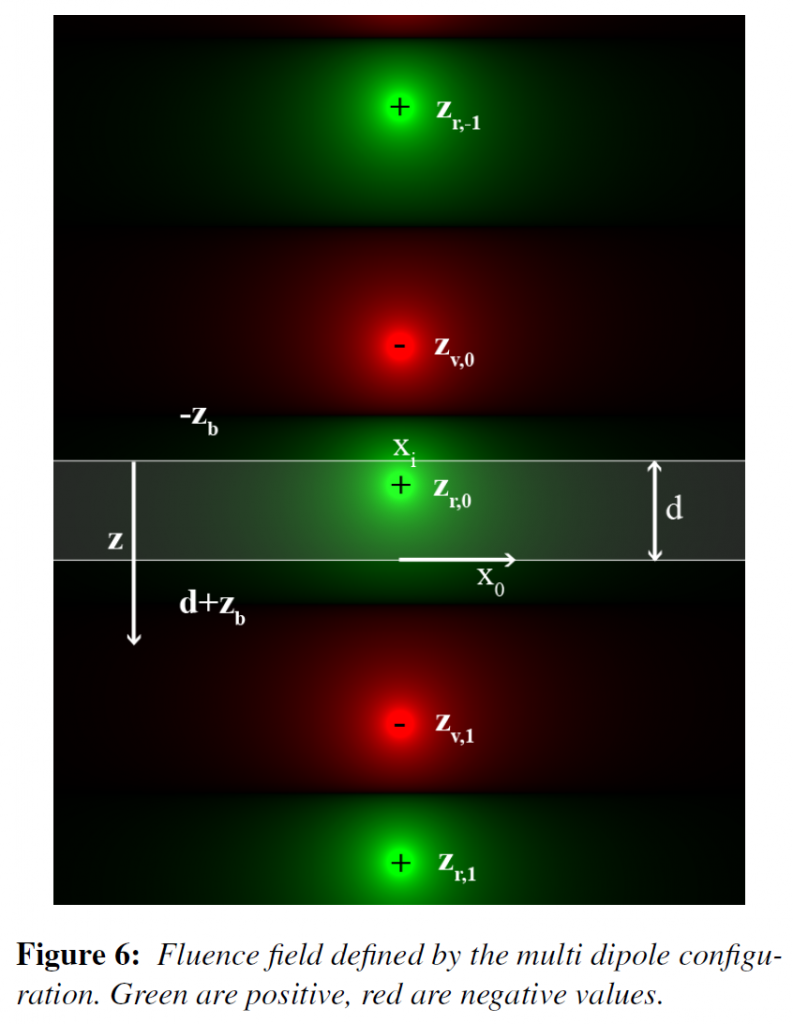
式3で与えられた\(z=0\)での境界条件に合わせるために、\({\vec x}_i\)の下に1平均自由行程\(l = 1 / {\sigma’}_t\)の深さで実正の点光源を配置します[PCW89]。\((1 + 4A / 3)/{\sigma’}_t = 2 z_b + l\)に負の仮想光源を配置すると,\(-z_b\)での正味のフルエンスが消失し,ダイポール配置からなる\(z = 0\)の第1境界条件[FP92]の良好な近似値が得られました。実光と仮想光の両方が関与媒質の内部にあるものとして扱われます。\(z=d\)で第2の境界条件を満たすためには、第2の境界条件の外挿距離にある既存のダイポールを\(z=d+z_b\)でミラーリングし、第1の境界条件に合わせるために\(z_b\)で再びミラーリングします。このプロセスは、両方の条件が同時に一致するように収束します[DJ05]。
正負の拡散ダイポールの極の位置\(z_{r, j}\)と\(z_{v, j}\)は、次のように表すことができます。
\begin{eqnarray}
z_{r, j} &=& 2 j(d + 2 z_b) + l \\
z_{v, j} &=& 2 j(d + 2 z_b) – l – 2 z_b, \quad j = -n \cdots n \tag{5}
\end{eqnarray}
結果のフルエンス場は次のように定義されます。
\begin{eqnarray}
\phi(r) = \sum_{j=-n}^n \frac{\Phi}{4 \pi D} \left( \frac{ e^{-\sigma_{tr}d_{r,j} }}{d_{r, j}} – \frac{e^{-\sigma_{tr}d_{v, j} }}{d_{v, j}} \right) \tag{6}
\end{eqnarray}
ここで、\(d_{r,i} = |{\vec x}_0 – {\vec x}_{r, j}| \)は\({\vec x}_0\)から実光源までの距離、\(d_{v,j} = | {\vec x}_0 – {\vec x}_{v, j}|\)は仮想光源までの距離、\(\sigma_{tr} = \sqrt{3 \sigma_a {\sigma`}_t}\)は実効輸送係数です。図6は,1つの入射放射点\({\vec x}_i\)に対するフルエンス場の\(z\)軸に沿った葉のスライスを示しています。
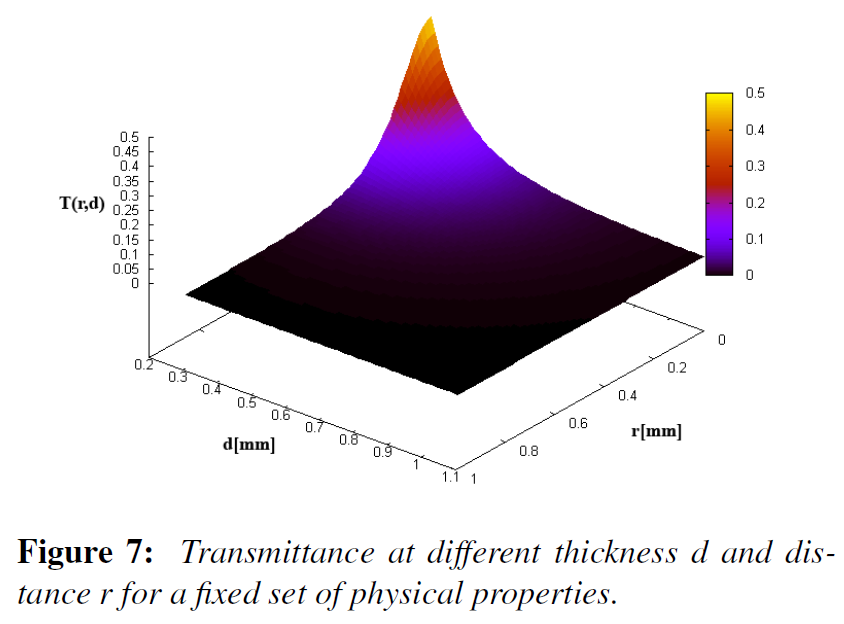
最後に、光が当たらない面での拡散透過率は、スラブの厚さ\(d\)と入射点からの距離\(r = |x_o – x_i|\)に応じて、フルエンス場の勾配と等しくなります:
\begin{eqnarray}
T(r, d) = -D \frac{{\vec n} c\dot {\vec \nabla}\phi({\vec x}_0)}{d\Phi({\vec x}_i, {\vec \omega}_i} \tag{7}
\end{eqnarray}
これは次のように評価されます
\begin{eqnarray}
T(r, d) = \sum_{j=-n}^n \frac{\alpha’}{4\pi} \left( \frac{ (d-z_{r,i})(1 + \sigma_{tr}d_{r,j} e^{-\sigma_{tr}d_{r,j}} ) }{ {d^3}_{r, j} } – \frac{ (d – z_{v,j})(1 + \sigma_{tr} d_{v,j}e^{-\sigma_{tr}d_{v,j}} ) }{ {d^3}_{v,j} } \right) \tag{8}
\end{eqnarray}
ここで、\(\alpha’ = {\sigma’}_s / {\sigma’}_t\)は減少されたアルベドです。図7は、一定の物理的特性に対する透過率を、厚さ\(d\)と距離\(r\)に応じて示したもので、厚さが増すと指数関数的に減衰し、距離が増すとガウス曲線のように滑らかに減衰することがわかります。
透過BSSRDFは、葉の内部の透過率に、葉の入射面と出射面の透過率をかけたものです。
\begin{eqnarray}
S({\vec x}_i, {\vec \omega}_i, {\vec x}_o, {\vec \omega}_o) = \rho_t({\vec x}_i, {\vec \omega}_i) T(r, d) \rho_t({\vec x}_o, {\vec \omega}_o) \tag{9}
\end{eqnarray}
ここでも、葉の表面が粗いため、フレネル項ではなく透過率を用いています。\(\rho_t\)の計算では、反射しない光はすべて透過すると仮定します。したがって、\(\rho_t({\vec x}, {\vec \omega}) = 1 – \rho_d({\vec x}, {\vec \omega})\)で,ここで\(\rho_d\)は反射アルベドです。表面と裏面では、BRDFが異なるため、アルベドも異なることに注意してください。
4.2. Light diffusion as an image convolution process
リアルタイムレンダリングに適した表面下散乱の定式化を実現するために、BSSRDFの評価を、撮影プロセスから得られるマップ上で動作し、高速な事前計算を可能にする画像畳み込みプロセスとして表現することを試みます。
式(2)を再構成すると、透過放射輝度の式が得られます:
\begin{eqnarray}
L_t({\vec x}_o, {\vec \omega}_o) = \int_{\Omega} \int_A L({\vec x}_i, {\vec \omega}_i) S({\vec x}_o, {\vec \omega}_o, {\vec x}_i, {\vec \omega}_i) ({\vec n}({\vec x}_i) \cdot {\vec \omega}_i) d{\vec x}_i d{\vec \omega}_i \tag{10}
\end{eqnarray}
ここでは,\(\omega_D\)方向に単位強度(\(L_D = 1\))の1つの指向性光を仮定し,ディラックインパルスで表現して事前計算を行います。その結果を実際の光の強さで変調し、インタラクティブな照明を実現しています。また,\({\vec x}_i\) に到達する放射輝度が次のようになるように,可視性項 \(V({\vec x}_i, {\vec \omega}_i)\) を通じて葉からの自己影を考慮します.
\begin{eqnarray}
L({\vec x}_i, {\vec \omega}_i) = \delta ({\vec \omega}_i – {\vec \omega}_D) V({\vec x}_i, {\vec \omega}_i) \tag{11}
\end{eqnarray}
これと(9)を(10)に代入すると
\begin{eqnarray}
L_t({\vec x}_o, {\vec \omega}_o, {\vec \omega}_D) = \rho_t({\vec x}_o, {\vec \omega}_o) \int_A T(r, d) E({\vec x}_i, {\vec \omega}_D) d{\vec x}_i \tag{12}
\end{eqnarray}
方向\({\vec \omega}\)からサーフェイス直下の点\(\vec x\)への光の輸送を記述する照度輸送関数\(E({\vec x}, {\vec \omega})\)を組み合わせたものです:
\begin{eqnarray}
E({\vec x}, {\vec \omega}) = \rho_t({\vec x}, {\vec \omega}) V({\vec x}, {\vec \omega})({\vec n}(\vec x) \cdot {\vec \omega}) \tag{13}
\end{eqnarray}
式12は、与えられた光の方向\(\omega_D\)に対して、薄いスラブ(葉)の\({\vec x}_o\)への透光性のある光の輸送を表しています。この式は、すでに信号\(E({\vec x}, {\vec \omega})\)とカーネル\(T(r, d)\)の連続的な畳み込みプロセスの形をしています。
厚みのばらつきを考慮するために、測定された厚み\(d\)を、透過率の項につながる境界条件の局所的な近似値としています。これにより、畳み込みカーネル\(T(r, d({\vec x}_i))\)は非定常になります。多重極モデルに固有のこの局所近似は、葉の場合、わずかに柔らかくなる粗い面側を除いて、実際の境界条件とよく一致します。任意の境界条件を正確に考慮することは、完全なモンテカルロ・シミュレーションと比較して、ダイポール近似の主な制限です[DJ05]。
最後に、空間的に変化する変数がすべて同じ解像度のマップで与えられているという事実を利用し、面積積分を離散化することで、連続的な畳み込みを離散的なものに変換します。面積要素としては、マップ内のテクセル\(A_p\)の一定の物理的面積を、スケーリングされた接平面に応じて使用します。
\begin{eqnarray}
L_t({\vec x}_o, {\vec \omega}_o, {\vec \omega}_D) = \rho_t ({\vec x}_o, {\vec \omega}_o) A_p \sum_{{\vec x}_i} T(r, d({\vec x}_i)) E({\vec x}_i, {\vec \omega}_D) \tag{14}
\end{eqnarray}
これで、\(L_t\)の計算は、アルベド、透過、厚さ、法線マップを入力として、画像の畳み込みとして実装することができます。なお、式14は画像の畳み込みを表していますが、距離などの変数はすべて葉上の物理的な長さであり、離散化を除けば、結果は式10を正確に表していることになります。
この結果は、リアルタイムレンダリングのための前処理に限らず、物理ベースのレイトレーサーでも使用でき、グローバルイルミネーションのために光の方向\({\vec \omega}\)の上で積分することができます。
5. Real-Time Translucency
このセクションでは、前のセクションで得られた画像の畳み込みを利用して、リアルタイムで評価できる形式を実現する方法を示します。式14により、葉の表面の各ピクセル\({\vec x}_o\)について、与えられた光の方向\(\omega_D\)に対する透光性を計算することができます。式を分離して,\(\omega_D\) にのみ依存する方向性の部分を得ます。
\begin{eqnarray}
L_t({\vec x}_o, {\vec \omega}_o, {\vec \omega}_D) = \rho_t({\vec x}_o, {\vec \omega}_o) {L_t}^D({\vec x}_o, {\vec \omega}_D) \tag{15}
\end{eqnarray}
ここで,
\begin{eqnarray}
{L_t}^D({\vec x}_o, {\vec \omega}_D) = A_p \sum_{{\vec x}_i} T(r, d({\vec x}_i)) E({\vec x}_i, {\vec \omega}_D) \tag{16}
\end{eqnarray}
リアルタイムで評価するためには、高価な画像の畳み込みを事前に計算しておきたいので、結果として得られる半球関数\({L_t}^D({\vec x}_o, {\vec \omega}_D)\)を効率的に保存し、ピクセルごとに評価する新しい手段が必要です。この目的のために、いわゆるHalf Life 2基底を導入します。
原則的には、関数\(L_t\)は波長に依存しているため、いくつかのスペクトルバンドに対して評価する必要があります。これは、葉の両面のアルベドと透過係数の測定値と色に依存する係数を用いて、3色の畳み込みで\(L_t\)を計算することで可能です。しかし、測定された平均透光度を使用すれば、結果ははるかに説得力のあるものになります。この透光度には、\(\rho_t({\vec x}_o)\)と、逆光の葉に現れる非常に複雑な分光吸収の挙動と微細構造の両方が含まれています。そこで、1つの支配的な波長(葉の場合は510nm、緑に相当)についてのみ指向性部分\({L_t}^D\)を評価し、基本的には表面下散乱によって生じる輝度への影響を捉えています。最終的な出射透過率\(\rho_t({\vec x}_o, {\vec \omega}_o)\)を、取り込んだ透光率\(\rho_t({\vec x}_o)\)に置き換えて、色調効果を加えます。このステップでは、実質的に拡散していると考えられる表面下散乱のビュー依存性も削除します[BR01]。
5.1. The Half Life 2 Basis
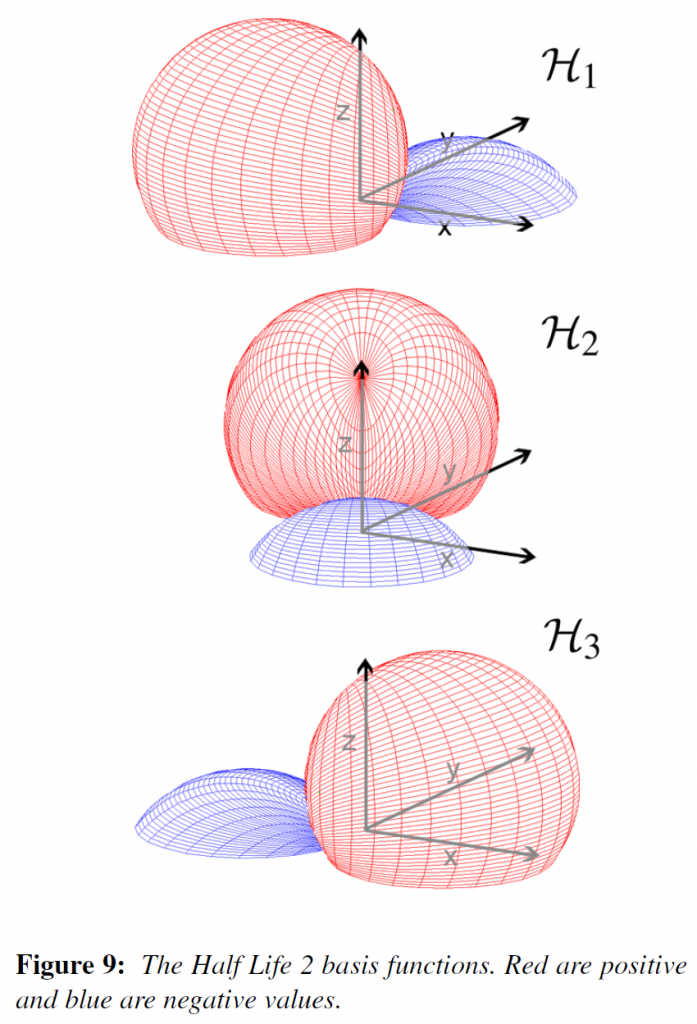
Half Life 2 Basis(HL2基底)は、Sourceエンジン[McT04]で導入されたベクトル基底で、法線マップをHL2基底で表現し、HL2基底のベクトルに対してライトマップを評価することで、ライトマッピングと法線マッピングを組み合わせたもので、あまり知られていません。これは例えばラジオシティにも有効で、法線ベクトルの線形関数として解釈することができます。また、球面調和ベースの事前計算された放射伝達と法線マッピングの組み合わせを実現するためにも使用されました[Slo06]この場合、ベクトルは内積の項の関数として解釈されます。
HL2基底は、接平面に投影された隣接するベクトル間の角度が等方的になり、接平面と各ベクトルの間の角度が同一になるように、接平面座標系に対して相対的に回転された直交する3つのベクトルによって生成されます(図8):
\begin{eqnarray}
{\vec H}_1 &=& \left( -\frac{1}{\sqrt{6}}, -\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{3}} \right) \\
{\vec H}_2 &=& \left( -\frac{1}{\sqrt{6}}, \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{3}} \right) \\
{\vec H}_3 &=& \left( \sqrt{ \frac{2}{3} }, 0, \frac{1}{ \sqrt{3} } \right)
\end{eqnarray}
これらのベクトルは、半球上の3つの余弦基底関数を定義します(図9)。
\begin{eqnarray}
{\mathcal H}_i({\vec \omega}) = \sqrt{ \frac{3}{2pi} } {\vec H}_i \cdot \omega \tag{17}
\end{eqnarray}
コサイン関数はクランプされないので、内積が負の値も含めて、すべての基底関数が半球全体に寄与します。HL2基底が半球の積分に対して直交していることは簡単に検証できます。
\begin{eqnarray}
\int_{\Omega} {\mathcal H}_i({\vec \omega}) {\mathcal H}_j({\vec \omega}) d{\vec \omega} = \delta_{ij} \tag{18}
\end{eqnarray}
であるため、半球状の関数\(f({\vec \omega})\)は容易に基底に投影することができます。
\begin{eqnarray}
f({\vec \omega}) = \sum_{i=1 \cdots 3} h_i {\mathcal H}_i({\vec \omega}) \tag{19}
\end{eqnarray}
この基底係数を用いて
\begin{eqnarray}
h_i = \int_{\Omega} f({\vec \omega}) {\mathcal H}_i ({\vec \omega}) d{\vec \omega} \tag{20}
\end{eqnarray}
なお、表される半球関数が常に正であっても、係数\(h_i\)の1つが負になることがあります。
HL2基底の利点は、ある半球方向の表現された関数を非常に安価に評価できることで、これはまさに直射日光の評価に必要なものです。これは他の半球基底(球面調和[SKS02]やウェーブレット基底[LSSS04]など)とは対照的で、光を基底に変換する必要があるため、照明自体が半球関数であり、単一の方向ではない状況でのみ好ましいと言えます。基底は3項しかないため,半球上の低周波信号しか表現できませんが,表面下散乱のぼかし特性のため,提案した方法ではこれで十分であり,第6節で数値的にも示しています。
5.2. Projecting Translucency into the HL2 basis
リーフ上の各位置\({\vec x}_o\)に対して、\({L_t}^D({\vec x}_o, {\vec \omega}_D)\)に対して式(20)を評価することにより、透過関数がHL2基底に投影されます。半球積分を評価するために、Shirleyの square to hemisphere mapping [SC97] を用いて、層状のランダムな点を半球にマッピングすることで、半球上の \(N_L\) の光の方向を一様に分布させてサンプリングします。
\begin{eqnarray}
h_i({\vec x}_o) = \frac{2\pi}{N_L} \sum_{m=1 \cdots N_L} {\mathcal H}_i({\vec \omega}_m) {L_t}^D({\vec x}_o, {\vec \omega}_m) \tag{21}
\end{eqnarray}
光の方向\(\omega_m\)ごとに、取得したマップを用いて、畳み込みカーネル\(T(r, d({\vec x}))\)による画像の畳み込み(式16)を行います。ただし、すべての画素とすべての画素をコンボリューションする必要はありません。カーネルの最大サイズとして、葉の最も薄い部分で式8を評価し、透過率が小さなしきい値以下になる半径を算出します。
投影の結果、HL2係数マップ(図10)が得られます(散乱のために1つの波長だけを計算することに再度注意してください、上記参照)。
興味深いのは、完全に拡散した透光性\({L_t}^D({\vec x}_o, {\vec \omega}_D) = {\vec n} \cdot {\vec \omega}_d\)の特殊なケースで、これは以前の研究で使用された拡散BTDFに対応するものですが、接線空間の\({\vec n} = (0, 0, 1)\)であるため、係数\(h_i = \sqrt{2 \pi} / 3\)を使って正確に表現できることです。
\begin{eqnarray}
\sum_{1 \cdots 3} \frac{\sqrt{2\pi}}{3} {\mathcal H}_i({\vec \omega}_d) = \sum_{1 \cdots 3} \frac{\sqrt{3}}{3} H_i{\vec \omega}_d = (\sum_{1 \cdots 3} \frac{\sqrt{3}}{3} H_i) {\vec \omega_d} = {\vec n} \cdot {\vec \omega}_d \tag{22}
\end{eqnarray}
この係数は、実際の物理ベースの透光性関数の、この特殊なケースからのずれを記録していると言えるでしょう。なお、実際にはどんな余弦関数もHL2基底で正確に表現できます。
5.3. Precomputing Visibility
画像の畳み込みには、可視性関数\(V({\vec x}_i, {\vec \omega}_k)\)の評価が含まれており、これは前処理でもコストがかかります。HL2基底への投影を高速化するために、\({\vec x}_i\)ごとの水平線マップの形で可視性項を事前に計算することで、可視性関数をルックアップに変え、隆起や膨らみの自己シャドウイングを捉えます。水平線の円を16のスライスに分割し、各スライスの平均水平線の高さを記録します。畳み込み時、つまり(16)を(21)で評価する際に、現在の光の方向\({\vec \omega}_m\)と線形補間された地平線の高さを比較し、\({\vec \omega}_m\)が地平線の上にあるか下にあるかを返します。
5.4. Rendering Translucency
レンダリング時には、ライトベクトル\({\omega}_D\)を接線空間に変換し、HL2基底係数を調べ、次のように半透明度を評価する必要があります。
\begin{eqnarray}
L_{r, rec}({\vec x}_o, {\vec \omega}_D) = L_D \rho_t({\vec x}_o) \sum_{i=1 \cdots 3} h_i({\vec x}_o) \sqrt{ \frac{3}{2\pi} } {\vec H}_i \cdot {\vec \omega}_D \tag{23}
\end{eqnarray}
その結果、2つのテクスチャ参照(\(\rho_t\)と\(h_i\)はそれぞれRGBテクスチャに格納されている)と、3つの加算および重み付けされた内積のみとなり、多数の葉の正確でダイナミックな半透明度をピクセル単位で計算することができます。
この計算は非常にシンプルでメモリ効率が良く、ピクセルシェーダーを使った最新のレンダリングパイプラインに組み込むことができます。ここでは1枚の葉に局所的なインタラクションのみを考慮しているため、葉をインスタンス化してアニメーション化することができ、多数の葉を持つ多くの木をアニメーション化してインタラクティブにレンダリングすることができます。
6. Implementation, Results and Discussion
提案された葉のモデルを実装してテストし、説明された撮影セットアップで取得された2つの葉のデータセットに適用しました。表面下光輸送\({L_t}^D\)は,表1にまとめた物理パラメータ([MIPK90]および[Woo71]からの平均値)と,事前計算のためのパラメータを使用しています。\({L_t}^D\)の評価は波長510nmで行っているため、パラメータはその波長に合わせて選択されています。
まず、図11に、拡散BTDF(我々の測定データによる)とジオメトリ法線\({\vec n}_g\)を用いて、提案する半透明法と現在の最新技術との比較を示し、次の式を与えます:
\begin{eqnarray}
{L_t}^{BTDF} ({\vec x}_0, \omega_D) = -L_D \rho_t({\vec x}_0) ({\vec n}_g \cdot {\vec \omega}_D) \tag{24}
\end{eqnarray}
図は、入射光の方向による透光性の変化を示したものです。例えば、急峻な角度では構造的な特徴がぼやけてしまいますが、かすかな角度では葉の高周波構造が観察できます。また、光が当たる面の変化(セルフシャドウイング、厚さ、反射率の変化など)による葉の散乱効果も正確にモデル化されています。対照的に、標準モデルは平坦で、光の方向の変化には余弦項でのみ対応しています。
次に、Half Life 2 Basisが多重極モデル[DJ05]の厳密な評価を近似的に行うことができる精度を分析します。そのために,地平線に対する3つの光の角度(\(\pi/2, \pi/4, \pi/8\))について,5で見たデータセットのすべてのテクセルについて,相対的な信号再構成誤差\(L_{t, rec}/L_t -1\)を計算し,その結果,リーフ上の誤差分布をヒストグラムとして図12にプロットしました。図13は、光の角度が\(\pi/8\)の場合の直接比較です。平均再構成誤差はわずか3%で、Half Life 2 Basisが半透明を表現するのに適していることがわかります。また,葉は入射光の約5~20%[ML51]しか透過しませんが,この効果は提案された方法で正確にモデル化されています.葉がトーンマッピングなしでレンダリングされた場合、HL2基底係数をスケーリングすることで、半透明の葉が暗くなりすぎないようにすることができます。
最後に、本手法の実装と性能について説明します。すべての結果は、Pentium4 3.2GHz と NVIDIA 8800 GTX グラフィックカード(DirectX 10)で得られたものです。ランタイムでは、半透明項の評価には、半透明マップと HL2 係数マップへの 2 つのテクスチャ検索と、いくつかの演算命令が必要となります。このコストはシェーディングモデルの他の部分に比べて非常に低く、例えばライトに面した面のCook-Torranceシェーディングモデルを評価するのに必要な演算があります。DirectX 10のシェーダコンパイラでは、シェーダ全体で約119の命令スロットが報告されていますが、そのうち半透明部分には約15の命令が必要です。このデータセットを使って,任意の数の葉をレンダリングすることができます.
6,392枚の葉を持つ木を,法線マップを用いたクワッドパッチとしてレンダリングしたインタラクティブなアプリケーションで,その性能を測定しました。各葉は動的にシェーディングされます.光が当たる側の葉には,セクション 3 で説明した Cook-Torrance シェーディングモデルを使用し,反対側の葉には物理ベースの半透明モデルを使用してシェーディングを行いました.シーンの高いダイナミックレンジを考慮して、ポストプロセスでReinhardのトーンマッピングアルゴリズム[RSSF02]とシンプルなブルーミングを適用しています。影は2048×2048のシャドウマップを用いて生成され、6つのポアソン分布サンプルを用いた近傍比率フィルター(PCF)[RSC87]で評価されます。木のアニメーションデータがないため,アンビエントオクルージョンを用いた単純な間接照明項を事前に計算することにしました。図1と図14(カラープレート)は、木全体のレンダリング品質を示すスクリーンショットですが、付属のビデオを見ると、より良い印象を受けます。木のフライスルーのフレームレートは、画面全体が断片で覆われた近景での66fpsから、前述のすべての効果を含む遠景での116fpsまで変化します。
アルベド、半透明、法線、厚さ、HL2基底係数マップからなる葉モデルのデータセットと、シェーダの例が[Hab07]に掲載されています。
7. Conclusion and Future Work
私たちは、植物の葉をリアルタイムでレンダリングするための、初めての物理ベースの半透明モデルを発表しました。このモデルでは,表面下散乱と葉の構造を完全に考慮しており,表面下散乱シミュレーションには,自己シャドウイング,空間的に変化する反射率,厚さなどの効果が含まれています。葉の光に面した面については、最新のシェーディングモデルに高解像度の法線マップを追加して、鏡面反射を改善しています。必要な入力マップはすべて、葉の上で1mm未満の解像度を実現する新しい取得プロセスによって作成されます。
我々の透過モデルは,DonnerとJensen[DJ05]によって導入された薄いスラブの表面下散乱に対するマルチダイポール近似に基づいている。半透明の寄与を画像の畳み込みプロセスとして再定式化し,効率的なレンダリングのためにHalf Life 2のベースに投影しました.将来的には,提案したデータ取得方法を自動化して,リアルタイムレンダリングと物理ベースレンダリングの両方に適したリーフのデータベースを作成できるようにしたいと考えています。
将来的には、完全なモンテカルロ法を用いてモデルを検証することは興味深いことです。また、DonnerとJensen[DJ05]が提案したような、葉に2つ以上の層を持つモデルと、我々のたった1つの層の近似値を比較するのにも使えるかもしれません。
8. Acknowledgements
和訳省略。