こんにちわ。
今日は,
[Wang 2005] Lifeng Wang, Wenle Wang, Julie Dorsey, Xu Yang, Baining Guo, Heung-Yeung Shum, “Real-Time Rendering of Plant Leaves”, SIGGRAPH 2005, July 2005, pp.712-719.
を読んでみようと思います。
いつもながら誤字・誤訳があるかと思いますので,ご指摘頂ける場合は正しい翻訳例と共に指摘していただけると幸いです。
Abstract
本論文では、グローバルイルミネーション効果を用いた植物の葉のリアルタイムレンダリングのためのフレームワークを紹介します。葉のリアルなレンダリングには、洗練された外観が必要であり、我々は、空間的に変化するBRDFとBTDFで葉を表現するパラメトリックモデルを紹介します。このBRDFとBTDFは、葉の組織内の表面下散乱と葉の表面上の粗い散乱の分析を組み込んだもので、実際の葉から測定することができます。さらに重要なことに、この記述はコンパクトであり、グラフィックスハードウェアにロードすることで、高フレームレートを実現するために不可欠なランタイムシェーディング計算を高速に行うことができます。照明計算については、PRT(Precomputed Radiance Transfer)アプローチを葉の全周波数照明に拡張したアルゴリズムを紹介しています。特に、低周波の環境光と高周波の太陽光による複合的な照明効果を処理します。これは,太陽光の局所入射輝度を直接成分と間接成分に分解することで実現しています.高周波数を多く含む直接成分は,PRT のように球面調和関数を用いて事前に計算するのではなく,事前に計算されたライトの可視性の畳み込みデータを用いてオンザフライで評価します.このフレームワークは、様々な葉やその集合体のレンダリングによって実証されています。
1 Introduction
植物や風景を表現するためには、樹木などの植物構造物をリアルに表現することが必要ですが、リアルに表現するためには、構造物の構成や外観に潜む多くの課題に直面します。特に葉は、その複雑な構造と、光との複雑で微妙な相互作用のため、再現が難しいとされています。特に、木のモデル全体が太陽光に照らされているシーンでは、影の効果を考慮するために、高度で時間のかかるトレーシング手法が必要になり、困難を極めます。しかし、環境アセスメントやゲームなどの様々な用途において、グローバルイルミネーション効果を持つ植物モデルのインタラクティブなレンダリングが望まれています。
本論文では、グローバルイルミネーション効果を用いて植物の葉をリアルタイムにレンダリングするフレームワークを紹介します。このフレームワークの基礎となるのは、リアルタイムレンダリングに適したリアルな葉の外観モデルです。このモデルは、葉の外観をいくつかのパラメトリックな双方向反射率分布関数(BRDF)および双方向透過率分布関数(BTDF)で表現します。これらの空間的に変化するBRDFおよびBTDFは、コンパクトなパラメータマップに格納されており、グラフィックスハードウェアにロードすることで、オンザフライで高速にシェーディング計算を行うことができます。これはリアルタイムレンダリングには欠かせない機能です。本システムでは、BRDFとBTDFのペアは、720×540 RGBAの2つのテクスチャとして格納されています。一般に、空間的に変化するBRDFは6次元の関数であり、この解像度(720×540)では、表形式で表現すると何ギガバイトものメモリを消費してしまいます。
現実的なレンダリングのために、葉の主な散乱挙動、すなわち葉の表面上の粗い表面散乱と葉の組織内の表面下散乱を考慮して、BRDFとBTDFを導き出します。さらに、これらのBRDFとBTDFを、実際の葉から測定できるように定式化しました。葉の組織内の表面下の散乱は、BTDFとBRDFの拡散項を決定する[Hanrahan and Krueger 1993]。我々の表面下散乱解析は、実際の葉からの測定データで実験的に検証された、均質材質のスラブのための放射伝達モデルであるLEAFMODに基づいています[Ganapol et al.] このモデルを用いて,葉の厚さ,葉の組織の散乱・吸収係数などをパラメータとして,BTDFとBRDFの拡散項のパラメトリックな形式を導き出しました。また,これらのパラメトリック形式を線形光源(LLS)装置で測定した反射率および透過率のデータに適合させることができることを示しました[Gardner et al.2003]。このモデルは葉の外観の重要な部分を含んでいるため,植物のレンダリングによく用いられる複雑な3層モデルを必要とせず[Baranoski and Rokne 2002],葉の外観を直感的に編集することができます.さらに、この表現はコンパクトであるため、リアルタイムでリアルなレンダリングが可能です。
葉の表面に光沢のある反射があるのは、表面の粗い散乱が原因です。グラフィックスの研究者たちは、BRDFの光沢項に対するいくつかのモデルを開発しました。しかし、これらのモデルは、無機材質の実験データに基づいています; しかし、これらのモデルのうち、どれがリーフレンダリングに適しているかは明らかではありません。我々は,葉の光沢反射をレンダリングするために,Torrance-Sparrowモデル[1967]の使用を提案する.この提案は、Maら[1990]の研究に基づいています。彼らは、単位面積あたりの正規化された散乱断面積に関するStogrynの公式[Stogryn 1967]が葉に適していることを確立するために、広範囲な実験を行いました。我々は、Torrance-Sparrowモデルが実際にStogrynの公式と同等であり、したがって葉のレンダリングに適していることを示します。BRDFの拡散項と同様に、このように定式化された光沢項もLLS装置を用いて測定することができます。
上記の外見モデルを用いて,PRT(Precomputed Radiance Transfer)法[Sloan et al 2002]に基づいた新しい2パスアルゴリズムを用いて,葉をレンダリングします.低周波照明を対象としたPRTとは異なり、本アルゴリズムでは、太陽によるソフトシャドウなどの高周波照明効果を取り込むことができます。これを実現するために,各地表点に入射する太陽光の放射輝度を直接成分と間接成分に分解し,それらを2回に分けて処理します.1回目の処理では、間接成分と低周波環境光をPRTで効率的に処理します。2回目の処理では,事前に計算された光と可視性の畳み込みデータを用いて,直射日光の寄与を迅速に評価します。これにより,PRT で必要とされる低次の球面調和関数基底を使用しないため,高周波の詳細情報が失われることはありません。最終的なレンダリング結果は、2つのパスの出力の合計となります。
本論文の残りの部分は、以下のように構成されています。次のセクションでは,既存の技術をレビューし,我々の技術と比較します。セクション3では、我々の葉のモデルと、実際の葉から取得した反射率と透過率のデータにこのモデルを適合させる方法について説明します。セクション4では,我々の2パスレンダリングアルゴリズムについて説明します.セクション5では,いくつかの結果を紹介し,セクション6では,今後の課題について述べます。
2 Related Work
Leaf Models: 葉の幾何学的形状を作成するには様々な手法があり,ヒンジ付きポリゴン[Bloomenthal 1985],フラクタル集合[Demko et al 1985],L-システム[Prusinkiewicz et al 1988; Prusinkiewicz et al 2001]などでモデル化することができます.私たちは、葉の質感と外観に焦点を当てています。葉の形状は、どのような技術でも入手できます。
グラフィックスの研究者の中には、葉の表面下散乱を研究している人もいます。HanrahanとKrueger[1993]は、葉を層状の表面としてモデル化し、モンテカルロ光線追跡法を用いてBRDFとBTDFを評価しました。Baranoski and Rokne [1997]は、葉における光の伝搬と吸収に影響を与える生物学的な要因を考慮したアルゴリズムBDFモデル(ABM)を提案しました。BaranoskiとRokne[2001]は、反射率と透過率の値を事前に計算し、簡略化された散乱モデルを適用することで、ABMよりも効率性を高めた葉面散乱モデル(FSM)を導入しました。ABMモデルもFSMモデルも、モンテカルロ光線追跡に基づいています。最近では,Franzke and Deussen [2003]が簡略化された表面下散乱モデルに基づいたレイトレーサーを用いて,良好なレンダリング速度(1フレームあたり数分)を実現しています.これらのレイトレーシングベースのモデルの難点は、リアルタイムレンダリングに必要な高速ランタイムシェーディング計算をサポートできないことです。また、これらのモデルのパラメータは、実際の葉から計測するのではなく、手で設定することが多いという問題もあります。
また,植物学やリモートセンシングのための葉の散乱モデルも開発されています [Vogelmann 1993; Jacquemoud and Ustin 2001; Baranoski and Rokne 2002]。これらのモデルは、一般的に、植物組織の生物学的情報を多用しています。例えば、[Govaerts et al. 1996]では、葉の組織の内部細胞構造(表皮、細長いパリセード細胞、スポンジ細胞)の3次元形状を明示的にモデル化し、モンテカルロ光線追跡法を用いて光の伝搬をシミュレーションしています。今回の葉のモデルは、葉の内部構造に関する詳細な知識に頼らず、実測の反射率や透過率のデータを利用してリアルな描画を行っています。一方、生物学的モデルは、葉の内部での光の伝播をシミュレーションすることで、計測データを予測することを目的としています。生物学ベースのモデルは、光輸送シミュレーションに時間がかかるため、リアルタイムのレンダリングに対応するのは困難です。
BRDFモデルには、等方性[Torrance and Sparrow 1967; Cook and Torrance 1982; Oren and Nayar 1994]や非等方性[Kajiya 1985; Ward 1992; Poulin and Fournier 1990; Ashikhmin et al 2000]のものがあります。これらのモデルはコンパクトで素早く評価できますが、ほとんどが有機材質ではなく、無機材質の実験データに基づいて設計されています。特に、植物組織にとって重要な表面下散乱を考慮したモデルはありませんでした。
Leaf Rendering: 植物や樹木のモデルをリアルに表現することは、コンピュータグラフィックスでは長い歴史があります(例えば、[de Reffye et al. 1988; Weber and Penn 1995; Max 1996; Deussen et al. 1998; Meyer et al. 2001; Qin et al. 2003; Reche et al. 2004])。PRT [Sloan et al. 2002; Sloan et al. 2003]や全周波数アプローチ [Ng et al. 2003; Ng et al. 2004]などの最近の技術は、リアルタイムレンダリングのためにハードウェアを事前に計算します。我々のレンダリングアルゴリズムは、ランタイムレンダリングを容易にするために光輸送情報を事前に計算するという点で、これらの最近の技術に似ています。ただし,オールフリークエンシー・アプローチは,一般的な環境の照明には有効ですが,今回のシナリオでは理想的ではないことに注意が必要です.今回のケースでは、全周波数アプローチは非常に高次元の信号を使用し、それをすべての面で非常に高密度にサンプリングする必要があるため、大きな葉の集合体をリアルタイムで処理するには現実的ではありません。
3 Parametric Leaf Model
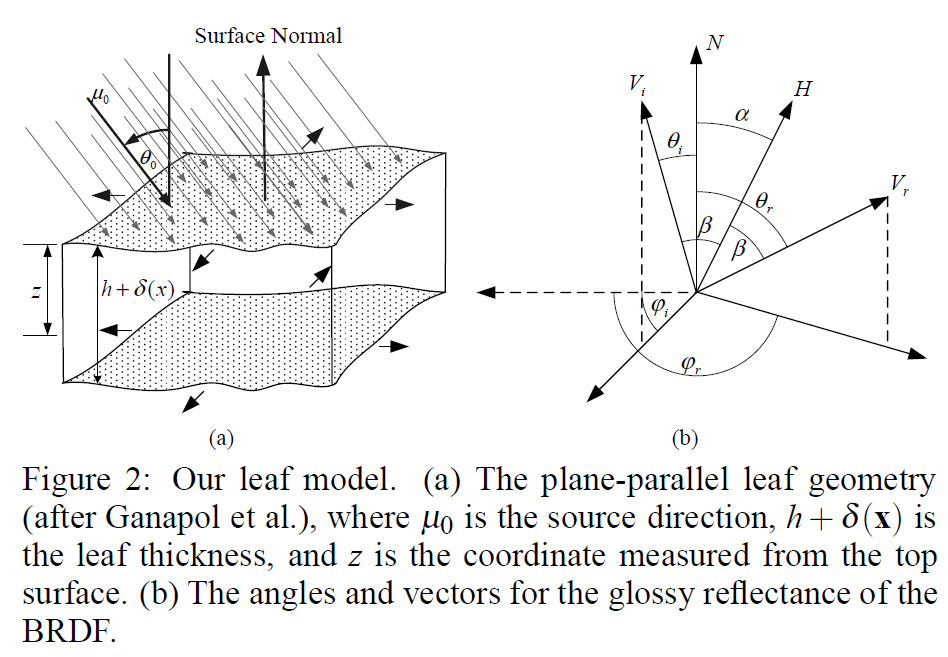
図2に示すように、葉を粗い表面を持つスラブとしてモデル化します。スラブの内部は均質であると仮定します。スラブの表面はアルベドマップ\(\gamma({\mathbf x})\)でテクスチャリングされており,空間的に変化する反射率特性を考慮しています.スラブの厚さは,\(h + \delta({\mathbf x})\)で表されます.ここで,\(h\)は葉の全体的な厚さをユーザが制御するための正の定数であり,\(\delta({\mathbf x})\)は葉のスラブの異なる部分における局所的な厚さの変化を表す関数です。\(\gamma({\mathbf x})\)と\(\delta({\mathbf x})\)は、実際の葉の反射率と透過率のデータから計算されます。以下では,まず葉のモデルを紹介し,次にモデルの各項がどのようにして導かれるかを示します。
葉スラブの各面(上面または下面)の反射率と透過率の特性は、6次元空間可変BRDF \(f_r({\mathbf x}, \theta_i, \phi_i; \theta_r, \phi_r)\)とBTDF \(f_t({\mathbf x}, \theta_i, \phi_i; \theta_r, \phi_r)\)で記述されます。
\begin{eqnarray}
f_t({\mathbf x}, \theta_i, \phi_i; \theta_t, \phi_t) &=& \frac{1}{\pi}e^{-(\sigma_a + \sigma_t)(h + \delta({\mathbf x}))} + \frac{B}{2\pi} \frac{\sigma_a}{\sigma_a + \sigma_s} \\
f_r({\mathbf x}, \theta_i, \phi_i; \theta_r, \phi_r) &=& \frac{A}{2\pi} \frac{\sigma_s}{\sigma_a + \sigma_s} \gamma({\mathbf x}) + \frac{\rho_s({\mathbf x})}{\cos \theta_i \cos \theta_r \cos^4 \alpha} \cdot \frac{ {\exp} -\frac{\tan^2 \alpha}{m({\mathbf x})^2} }{ 4 \pi m ({\mathbf x})^2} \tag{1}
\end{eqnarray}
ここで、\(A\)と\(B\)は定数、\({\mathbf x} = (x, y)\)は葉面上の位置、\((\theta_i, \phi_i)\)と\((\theta_r, \phi_r)\)は、図2に示すように、入射方向と反射方向を表しています。また,サブサーフェイスの光輸送に関するパラメータとして,葉スラブ内部の物質の吸収係数\(\sigma_a\)と散乱係数\(\sigma_s\),およびリーフの厚さ\(h\)があります。
BRDF \(f_r({\mathbf x}, \theta_i, \phi_i; \theta_r, \phi_r)\)は、拡散項と光沢項で構成されています。拡散項は,表面下散乱による拡散反射を考慮しています[Hanrahan and Krueger 1993]。拡散項は、入射方向と反射方向に依存しません。したがって,次のようになります。
\begin{eqnarray}
f_r({\mathbf x}, \theta_i, \phi_i; \theta_r, \phi_r) = \frac{1}{\pi} \rho_d({\mathbf x}) + f_s({\mathbf x}, \theta_i, \phi_i; \theta_r, \phi_r)
\end{eqnarray}
ここで、\(f_s({\mathbf x}, \theta_i, \phi_i; \theta_r, \phi_r)\)は表面の粗さによる光沢反射を表す光沢項です。後に、表面下光輸送の分析に基づいて、拡散反射率\(\rho_d\)の公式を導出します。BTDFは拡散項のみを持ち、マテリアルを透過した光が拡散するので,次のように書くことができます。
\begin{eqnarray}
f_t({\mathbf x}, \theta_i, \phi_i; \theta_t, \phi_t) = \frac{1}{\pi} \rho_t({\mathbf x})
\end{eqnarray}
Subsurface Scattering: ここで、拡散反射率\(\rho_d({\mathbf x})\)と透過率\(\rho_t({\mathbf x})\)の式を導き出します。\(\rho_d({\mathbf x})\)と\(\rho_t({\mathbf x})\)を明示的に表すことで、葉の厚さ\(h\)の変化に伴って葉のBRDFとBTDFがどのように変化するかなどの重要な問題に答えることができるようになります。明示的な表現のもう一つの利点は、これから説明するように、測定データからよりコンパクトなリーフモデルを導き出すことができることです。このモデルは、実際の葉から測定された反射率と透過率のデータで実験的に検証されています[Ganapol et al. 1998]。
一般に、放射伝達式は次のように書くことができます。
\begin{eqnarray}
\Omega \cdot \nabla I({\mathbf r}, \Omega) + \sigma_t I ({\mathbf r}, \Omega) = \sigma_s \int_{4\pi} d \Omega’ p(\Omega’, \Omega) I({\mathbf r}, \Omega’)
\end{eqnarray}
ここで\(\sigma_t = \sigma_a + \sigma_t\)で\({\mathbf r} = (x, y, z)\)です。均質なスラブ上の任意の点\({\mathbf x}=(x, y)\)において、この方程式を1次元形式で次のように書き換えることができます。
\begin{eqnarray}
\left[ \mu \frac{\partial}{\partial z} + \sigma_t \right] I(z, \mu) = \sigma_s \int_{-1}^{1} f(\mu’, \mu)I(z, \mu’)d\mu’
\end{eqnarray}
ここで、\(I(z, \mu)\)は方向\(\mu\)、\(\mu’\)における\(z\)での放射輝度で、\(f(\mu’, \mu)\)は一般的な位相関数\(p(\Omega’, \Omega)\)の方位角方向の平均値です。光路長を\(\tau = \sigma_t z\)とする。LEAFMODでは,生物学的な考察に基づいて,葉の内部は等方性の材質で満たされていると仮定しています[Ganapol et al.1998]。したがって、\(f(\mu’, \mu) = \frac{1}{2}\)で、次を得ます。
\begin{eqnarray}
\left[ \mu \frac{\partial}{\partial \tau} + I \right] I(\tau, \mu) = \frac{\omega}{2} \int_{-1}^{1} I(\tau, \mu’) d\mu’ \tag{2}
\end{eqnarray}
ここで,\(\omega = \frac{\sigma_s}{\sigma_t}\)です。
拡散反射率\(\rho_d\)と透過率\(\rho_t\)を得るためには、[Ganapol et al 1998; Siewert 1978]に従います。\(\mu_0 = \cos \theta_0\)、\(\theta_0 = 0\)とする。向軸性(表面)とア背軸(裏面)の境界条件は次のようになります。
\begin{eqnarray}
I(0, \mu) = \delta(\mu – \mu_0), \quad I(\Delta, -\mu) = 0 \tag{3}
\end{eqnarray}
ここで \(\mu \gt 0\), \(\Delta\) は物理的な厚さ \(h_0\) に対する \(\sigma_t h_0\) として定義される光学的な厚さです。境界条件\(I(\Delta, -\mu)\)は、背面の葉の表面に隣接する表面のランバート反射率\(r_s\)に依存し、ここでは\(r_s=0\)とします。
拡散反射率\(\rho_d = \int \mu I(0, -\mu)\)と透過率\(\rho_t = \int \mu I(\Delta, \mu) d\mu\)は、式(2)の\(I(0, -\mu)\)と\(I(\Delta, \mu)\)を境界条件式(3)で解くことで得られます。出射放射輝度をシフトしたルジャンドル多項式\(\psi_n(\mu)\)で展開すると、式(2)が解け、次のようになります。
\begin{eqnarray}
\rho_d = \int_{0}^{1} \frac{\omega}{2} \sum_{n=0}^{N-1} a_n \psi_n(\mu) \mu d\mu, \quad \rho_t = \int_{0}^{1} (e^{-\Delta} + \frac{\omega}{2} \sum_{n=0}^{N-1} b_n \psi_n(\mu)) \mu d\mu \tag{4}
\end{eqnarray}
ここで、\(a_n\)と\(b_n\)は定数であり、\(N\)は、連続する次数の2つの解が\(10^{-3}\)の相対誤差以内に収まるように選択されます。最終的には 次のようになります。
\begin{eqnarray}
\rho_d = \frac{A}{2} \frac{\sigma_s}{\sigma_a + \sigma_s}, \quad \rho_t = e^{-(\sigma_a + \sigma_s)h_0} + \frac{B}{2} \frac{\sigma_s}{\sigma_a + \sigma_s}
\end{eqnarray}
ここで、\(A\)と\(B\)は、式(4)の\(a_n\)と\(b_n\)で決まる定数です。
\begin{eqnarray}
A = \sum_{n=0}^{N-1} a_n \int_{0}^{1} \mu \psi_n (\mu) d\mu, \quad B = \sum_{n=0}^{N-1} b_n \int_{0}^{1} \mu \psi_n(\mu) d\mu
\end{eqnarray}
上の式はすべての点\({\mathbf x}=(x, y)\)で成立します。アルベドの変化と局所的な厚さの詳細を考慮して、それぞれ\(\gamma({\mathbf x})\)と\(\delta({\mathbf x})\)を加えることで、上の分析を葉全体に拡大して、次のように求めることができます。
\begin{eqnarray}
\rho_d({\mathbf x}) = \frac{A}{2} \frac{\sigma_s}{\sigma_a + \sigma_s} \gamma({\mathbf x}), \quad \rho_t ({\mathbf x}) = e^{-(\sigma_a + \sigma_s)(h + \delta({\mathbf x}))} + \frac{B}{2} \frac{\sigma_s}{\sigma_a + \sigma_s} \tag{5}
\end{eqnarray}
上式において、\(h\)は葉の厚さをユーザーが制御するための定数であり、局所的な厚さ変化関数\(\delta({\mathbf x})\)は、実際の葉から測定された透過率データにフィッティングすることで得られます。なお、\(\rho_d({\mathbf x})\)は葉の厚さ\(h\)の影響を受けません。
なお,\(r_s=0\)は,葉の反射率と透過率をLLS装置で測定していることに由来しています。LLS装置では,ライトボックスを拡散性のダークゲルで収束させることで,葉の軸方向に隣接する面をほぼ無反射にしています[Gardner et al 2003]。
Rough Surface Scattering:光沢項\(f_s({\mathbf x}, \theta_i, \phi_i; \theta_r, \phi_r)\)は、スラブモデルの粗い表面による光沢反射を表しています。粗い表面では、光がさまざまな方向に散乱します。葉の表面の粗さは入射光の波長に比べて大きく、また大きなスケールでうねっているので、キルヒホッフラフサーフェイス散乱理論[Beckmann and Spizzichino 1963]を適用することができます。Stogryn[1967]はキルヒホッフラフサーフェイス散乱理論を用いて、等方性粗面の単位面積当たりの正規化散乱断面積について次の式を導いています:
\begin{eqnarray}
\sigma^0_k = \frac{l^2(1 + \cos \theta_i \cos \theta_r + \sin \theta_i \sin \theta_r \cos(\phi_r – \phi))^2 }{ (\cos \theta_i + \cos \theta_r)^4 \sigma^2 } \cdot \exp\left( { – \frac{l^2(\sin^2 \theta_i + \sin^2 \theta_r + 2 \sin\theta_i \sin\theta_r \cos(\phi_r – \phi_i)) }{ 4 \sigma^2 (\cos \theta_i + \cos \theta_r)^2 } } \right)
\end{eqnarray}
ここで、\(l\)は相関長、\(\sigma\)はRMS高さであり、角度\(\theta_i\)、\(\theta_r\)、\(\phi_i\)、\(\phi_r\)は図2に示されています。Maらは、Stogrynの式が葉面上のラフサーフェイス散乱に適していることを実験的に立証しています[1990]。
点\({\mathbf x}\)におけるマイクロファセットの二乗平均平方根の傾きを\(m({\mathbf x}) = \frac{2 \sigma}{l}\)とすると、次のようになります。
\begin{eqnarray}
\sigma^0_k = \frac{1}{\cos^4 \alpha} \cdot \frac{ \exp(-\tan^2 \alpha/m({\mathbf x})^2 }{m({\mathbf x})^2} \tag{6}
\end{eqnarray}
ここで\(\alpha\)は、図2に示すように、表面の法線\(N\)と、入射光と反射光の方向の半分のベクトル\(H\)との間の角度です。このことから、光沢反射は次のように表すことができます。
\begin{eqnarray}
f_s({\mathbf x}, \theta_i, \phi_i; \theta_r, \phi_r) = \frac{\rho_s({\mathbf x})}{ \cos \theta_i \cos \theta_r \cos^4 \alpha} \cdot \frac{ e^{-\tan^2 \alpha/ m({\mathbf x})^2} }{ 4 \pi m({\mathbf x})^2} \tag{7}
\end{eqnarray}
ここで、\(\rho_s({\mathbf x})\)はスペキュラー強度マップ、\(m({\mathbf x})\)はスペキュラーラフネスマップと呼ばれます。式(7)は、\(\rho_s({\mathbf x})\)に幾何学的減衰係数とフレネル項を併合したCook-Torranceモデルです。導出の詳細については,学会DVDの付録Aをご覧ください。
Fitting BRDF and BTDF:これらの式(1)のパラメトリックモデルを、実際の葉から得られた反射率と透過率のデータにフィッティングすることで、最終的なBRDFとBTDFを得ることができます。[Gardner et al. 2003]を参考にして製作したLLS装置を用いて、このデータを取得しています。リーフスラブの上面と下面のそれぞれについて、2つのBRDF-BTDFペアを取得しました。LLS装置で取得した反射率データにディフューズローブとスペキュラーローブを当てはめ、拡散反射率\(\rho_d({\mathbf x})\)、スペキュラー強度マップ\(\rho_s({\mathbf x})\)、スペキュラーラフネスマップ\(m({\mathbf x})\)を得ます。また、各面の透過率\(\rho_t({\mathbf x})\)を測定します。
推定された葉の厚さ\(h\)と測定された\(\rho_d({\mathbf x})\)と\(\rho_t({\mathbf x})\)から、\(\sigma_a\)、\(\sigma_s\)、\(\gamma({\mathbf x})\)、\(\delta({\mathbf x})\)を以下のように計算することができます。まず、各点\({\mathbf x}\)における\(\sigma_a\)と\(\sigma_s\)の値を次の式を用いて解きます:
\begin{eqnarray}
\rho_d({\mathbf x}) = \frac{A}{2} \frac{\sigma_s}{\sigma_a + \sigma_s}, \rho_t({\mathbf x}) = e^{ -(\sigma_a + \sigma_s) h} + \frac{B}{2} \frac{\sigma_s}{\sigma_a + \sigma_s}
\end{eqnarray}
これらの値を葉面上で平均化し、2つのスカラー定数\(\sigma_a\)と\(\sigma_s\)を得る。\(\sigma_a\)と\(\sigma_s\)がわかれば、式(5)を使って\(\gamma({\mathbf x})\)と\(\delta({\mathbf x})\)を簡単に求めることができます。実際には、\(\sigma_a\)、\(\sigma_s\)、\(\rho_d({\mathbf x})\)、\(\rho_t({\mathbf x})\)はすべてRGBチャンネルを持っているので、上記の式を何度も繰り返す必要があります。
図3は、葉スラブの一面のパラメータマップです。パラメータ\(\gamma({\mathbf x})\)、\(\delta({\mathbf x})\)、\(\sigma_a\)、\(\sigma_s\)をフィッティングによって復元することには、2つの利点があります。まず、測定された拡散透過率\(\rho_t({\mathbf x})\)に含まれる冗長性を取り除き、リーフモデルをよりコンパクトにすることができます。測定された\(\rho_t({\mathbf x})\)は、RGBチャンネルを持っています。これに対して\(\delta({\mathbf x})\)は、BRDFパラメータに必要なテクスチャマップの1つのアルファチャンネルに格納できるグレースケールマップでしかありません。そのため、BTDFを格納するための別のテクスチャマップは必要ありません。もうひとつの利点は、\(\sigma_a\)、\(\sigma_s\)、葉の厚さ\(h\)などのパラメータを推定値から擾乱することで、葉の外観を意味のある形で編集できるようになったことです。編集例は図7をご覧ください。
4 Lighting Computation
本節では、グローバルイルミネーションを用いた植物の葉のリアタイムレンダリングのための2パスアルゴリズムを紹介します。我々のアプローチはPRTフレームワーク[Solen et al.2002]に基づいています。低周波数の照明を対象としたPRTとは異なり、我々のアルゴリズムは低周波数の環境マップと全周波数の光源である太陽の両方を含む照明を対象としています。
私たちの目標は、重要な高周波照明と太陽による詳細で柔らかい影の効果を含む、効率的なグローバルイルミネーションです。この目標を達成するために、私たちのアルゴリズムは、各サーフェスポイントにおける太陽の光の照明を直接成分と間接成分に分解し、2つのレンダリングパスで別々に処理します。最初のパスでは、間接成分と低周波の環境光をPRTで効率的に処理します。2回目の処理では,シーン内のすべての頂点で事前に計算された光と可視性の畳み込みデータを用いて,直接成分の寄与を迅速に評価します.第2パスでは、低次の球面調和関数基底を使用しないため、高周波のディテールの損失を避けることができます。最終的なレンダリング結果は、2つのパスの出力の合計となります。
Sunlight Decomposition:[Solan et al. 2002; Kautz et al. 2002]の定式化によれば、PRTは、シーン内のすべてのサーフェス点\({\mathbf p}\)において、線形演算子\(M_p\)を事前に計算し、保存しています。\(M_p\) は,光源照明ベクトル \(l\) を,\({\mathbf p}\) での局所的な入射輝度を表す \(l^{T}\) を持つ転写された入射輝度ベクトル \(l^{T}({\mathbf p}) = M_p l\) に変換します。\(M_p\) は,シャドウイングによって光源照明を減衰させ,相互反射によって増加させます。
葉が半透明であることを考慮して、各表面点でBRDFとBTDFの両方を評価するレイトレーサーを用いて、\(M_p\)を事前に計算します。与えられた視線方向 \({\mathbf v}_p\) に対する表面点 \({\mathbf p}\) での出射放射輝度 \(e({\mathbf p}, {\mathbf v}_p)\) は,内積 \(e({\mathbf p}, {\mathbf v}_p) = b({\mathbf v}_pl^{T}({\mathbf p}))\) として計算され,ここで \(b({\mathbf v}_p)\) は視線に依存する BRDF-BTDF ベクトルです。
私たちの光源照明ベクトル\(l=S+E\)、\(S\)は太陽光、\(E\)は低周波の環境光です。\(M_p\)は線形演算子なので、出射放射輝度は
\begin{eqnarray}
e({\mathbf p}, {\mathbf v}_p) = b({\mathbf v}_p) S^{T}({\mathbf p}) + b({\mathbf v}_p) E^{T}({\mathbf p}) \tag{8}
\end{eqnarray}
ここで、\(S^{T}({\mathbf p}) = M_p S\)で\(E^{T}({\mathbf p})= M_p E\)です。太陽が落とす柔らかな影の高周波の詳細を捉えるために、転送された太陽光の放射輝度\(S^{T}({\mathbf p})\)を、直接成分\({S^{T}}_d({\mathbf p})\)と、\({\mathbf p}\)における太陽から直接来る全ての太陽光の照明からなる間接成分\({S^{T}}_i({\mathbf p})\)に分解します。\({S^{T}}_i({\mathbf p})\)は透過や相互反射による\({\mathbf p}\)地点での間接的な全ての太陽光照明を含みます。したがって、式(8)は次のようになります。
\begin{eqnarray}
e({\mathbf p},{\mathbf v}_p) &=& b({\mathbf v}_p) {S^{T}}_d({\mathbf p}) + b({\mathbf v}_p) {S^{T}}_i({\mathbf p}) + b({\mathbf v}_p) E^{T}({\mathbf p}) \\
&=& b({\mathbf v}_p) {S^{T}}_d({\mathbf p}) + b({\mathbf v}_p) ({S^{T}}_i({\mathbf p}) + E^{T}({\mathbf p})) \tag{9}
\end{eqnarray}
最初の2つについてはすぐに説明します。2つ目の項については、PRTを用いて\({S^{T}}_i({\mathbf p}) + E^{T}({\mathbf p})\)を求めますが、その際、太陽光の間接成分のみを記録するように変更しました。伝達演算子 \(M_p\) はレイトレーサーを用いて事前に計算されており、直接照明は単に最初の光の跳ね返りであるため、この修正は簡単です。PRTは\(M_p\), \(S\), \(E\)を低次の球面調和関数基底に投影するので、式(9)の第2項には低周波の視覚効果しか得られません。これは、低周波であると想定される\(E\)については問題になりません。太陽光\(S\)については、PRTの制限により、\(S\)を含む相互反射は低周波数でしか捉えられません。
次に、式(9)の第1項を見てみましょう。ここでは、低次の球面調和基底を用いずに\(b({\mathbf v}_p){S^{T}}_d({\mathbf p})\)を直接計算することで、高周波の視覚効果を失わないようにしたいと考えています。定義は次のようになります。
\begin{eqnarray}
b({\mathbf v}_p) {S^{T}}_d({\mathbf p}) = \int_{\Omega} f_r({\mathbf s}, {\mathbf v}_p) S_d({\mathbf s}) V({\mathbf p}, {\mathbf s}) s_z d {\mathbf s}
\end{eqnarray}
ここで、\(f_r({\mathbf s}, {\mathbf v}_p)\)はBRDF、\(S_d({\mathbf s})\)は光の方向\({\mathbf s}\)の関数としての太陽光、\(V({\mathbf p}, {\mathbf s})\)は\({\mathbf p}\)における太陽の可視化関数、\(s_z\)は “余弦因子”(\({\mathbf s}\)の\(z\)成分)、\(\Omega\)は光の方向の半球を表しています。一般的な入射照明の場合、上の式の積分は評価するのにかなりのコストがかかります。太陽光という特殊なケースでは、シーン内のすべての頂点における光と可視性の畳み込みを事前に計算することで、この積分を素早く計算することができます。
Light-Visibility Convolution:私たちは、太陽を円盤状の面光源としてモデル化しています。太陽の円盤が広げる立体角を\(\Omega_0\)、太陽光の方向を\({\mathbf s}_0\)とします。\(S_d({\mathbf s})\)は\(\Omega_0\)の内側でのみ0ではありません。太陽は遠方にあるため、\(\Omega_0\)は非常に小さく、次のようになります。
\begin{eqnarray}
b({\mathbf v}_p) {S^{T}}_d({\mathbf p}) = \int_{\Omega_0} f_r({\mathbf s}, {\mathbf v}_p) S_d({\mathbf s})V({\mathbf p}, {\mathbf s}) s_z d{\mathbf s} \\
\approx f_r({\mathbf s}_0, {\mathbf v}_p) V_{{\mathbf s}_0}({\mathbf p}) \tag{10}
\end{eqnarray}
ただし,
\begin{eqnarray}
V_{{\mathbf s}_0}({\mathbf p}) = \int_{\Omega_0} S_d({\mathbf s}) V({\mathbf p}, {\mathbf s}) s_z d {\mathbf s} \tag{11}
\end{eqnarray}
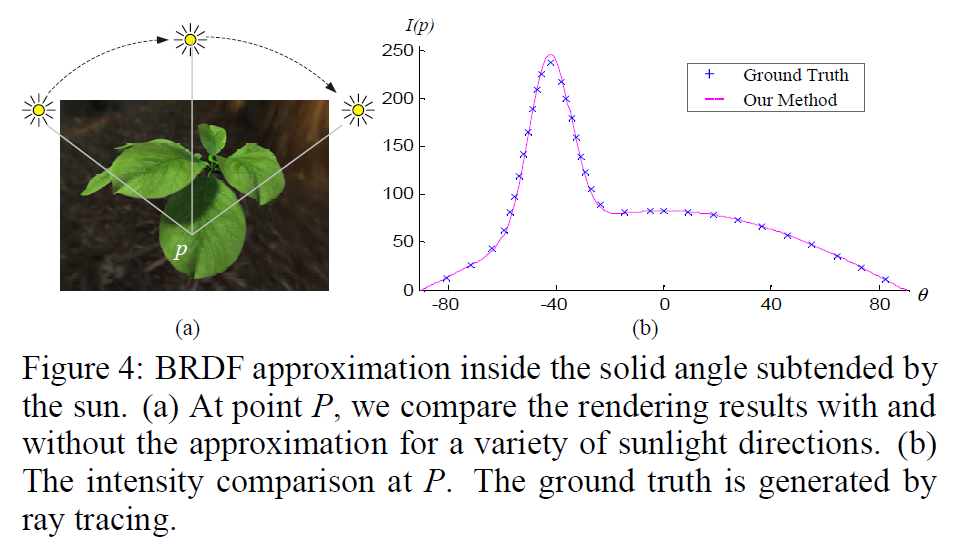
です。上式は\({\mathbf p}\)における光と可視性の畳み込み(LVC)と呼ばれています。\(V_{{\mathbf s}_0}({\mathbf p})\)は本質的には影の要素で、エリアソースによる\({\mathbf p}\)の照明を考慮します。式(10)では、太陽の円盤によって拡張された立体角\(\Omega_0\)の内側では、BRDFがほぼ一定であるとみなしています。図4が示すように、これはかなり正確な近似値であることがわかりました。
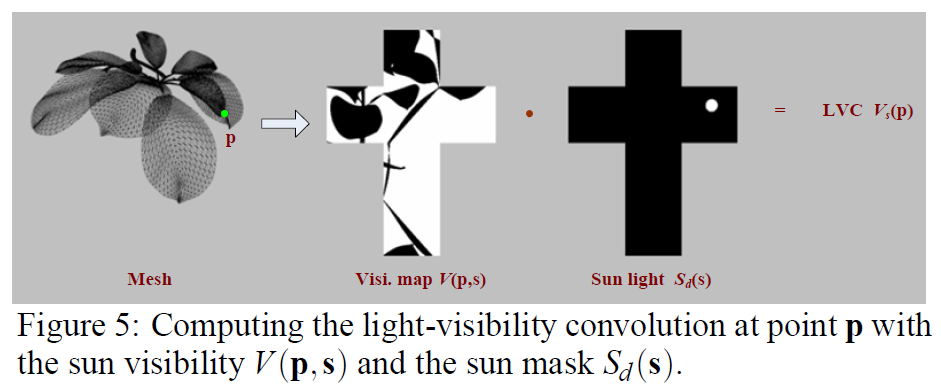
与えられた太陽光の方向\({\mathbf s}_0\)に対して、光の可視性マップ\(V_{{\mathbf s}_0}\)は、シーン内のすべての頂点\({\mathbf p}\)のLVC値\(V_{{\mathbf s}_o}({\mathbf p})\)で構成されます。図5は、光の可視性マップの計算方法を示したものである。ライトビジビリティマップの最も重要な点は、事前に計算することができるということです。\(V_{{\mathbf s}_0}({\mathbf p})\)が利用可能であれば、式(8)に従ってランタイムに素早く\(b({\mathbf v}_p){S^{T}}_d({\mathbf p})\)を評価することができます。ここでは、コンパクトでGPUにロードすることで高速に計算できるパラメトリックBRDFモデルを利用しています。
すべての光の可視性マップを事前に計算するために、まず、すべての太陽光の方向\({\mathbf s}_0\)について、すべての頂点\({\mathbf p}\)におけるLVC値\(V_{{\mathbf s}_0}({\mathbf p})\)を計算し、対応する光の可視性マップ\(V_{{\mathbf s}_0}({\mathbf p})\)を得る。与えられた頂点 \({\mathbf p}\) と太陽光の方向 \({\mathbf s}_0\) に対して、\(V_{{\mathbf s}_0}({\mathbf p})\) の評価はレイキャストプロセスとして考えることができます。一連のレイが \({\mathbf p}\) から太陽の円盤にキャストされ、各光線に対して、\(S_d({\mathbf s})\) と \({\mathbf p}\) における太陽の可視性を用いてライト可視性コンボリューション積分への寄与が計算されます。
\(V_{{\mathbf s}_0}({\mathbf p})\)の評価は前処理の一部であるため、システムのランタイム性能を気にすることなく、より高価な技術を使用する余裕があります。とはいえ、すべての太陽光方向\({\mathbf s}_0\)について\(V_{{\mathbf s}_0}({\mathbf p})\)を計算する効率的な方法があります。\({\mathbf p}\)の周囲にキューブマップを配置し、グラフィックスハードウェアを用いてシーンをキューブマップ上にレンダリングすることで、キューブマップのすべてのピクセルにおける\(S_d({\mathbf s})V({\mathbf p}, {\mathbf s})s_z\)の値を得ることができる。そして、すべての太陽光の方向\({\mathbf s}_0\)について、\({\mathbf s}_0\)に対応する太陽マスクとキューブマップのピクセル単位の内積として、ライト-可視性の畳み込み積分を得る。
Compression:すべての太陽の光の方向の光の可視性マップのコレクションはかなり大きいので、効率的な処理のために圧縮が必要です。32x32x6の環境マップと100kの頂点を持つシーンの場合、すべてのライトビジビリティマップのコレクションは約600MBを要します(ライトビジビリティマップの各ピクセルは1バイト)。幸いなことに、太陽光の方向はフレームごとに固定されているため、特定のフレームをレンダリングするためには、単一のライトビジビリティマップを解凍するだけで済みます。ライトビジビリティマップは小さく(上記の例では100KB)、すぐにデコードできます。ライトビジビリティマップをCPUで展開し、その結果を頂点属性としてGPUにアップロードします。圧縮には、各ライトビジビリティマップにランレングスエンコーディング(RLE)を適用します。RLEは、画質を維持しつつ、リアルタイムレンダリングにも対応できるロスレス方式です。上記の例では、600MBのライトビジビリティデータをRLEによって100MBに圧縮しています。もちろん、他の圧縮方式を用いて圧縮率を向上させることも可能です。
LVC値を太陽光の方向ごとに再ビニングすることは、圧縮のために重要です。頂点ごとにLVC値を再ビニングすると、各フレームのレンダリング時にこれらのデータにランダムにアクセスしなければなりません。その場合、ランダムにアクセスすることで、データの符号化・復号化が難しくなります。
Level of Detal:PRTレンダリングパスを高速化するために、葉のメッシュごとに離散ジオメトリのLODを構築し、すべてのLODメッシュの放射伝達マトリクスを導き出します。具体的には,まず,最も細かいレベルのメッシュの頂点における放射伝達マトリクスを事前に計算します。次に,ガウシアンウェイトを用いた単純な平均化スキームを用いて,粗いレベルのメッシュ頂点でのラジアンス伝達マトリックスを導出します。粗いメッシュ上の頂点を\({\mathbf p}\)とする。\({\mathbf p}\)における伝達行列は,最も細かいメッシュの頂点の伝達行列の加重和である(つまり,球状の近傍ではなく,表面の近傍でpから所定の半径r内にある頂点のみが対象となる)。各頂点の現在のメッシュLODレベルを決定し、対応する隣接するPRT LODからの放射伝達を計算するだけです。
Discussion:すべての頂点、すべての太陽光の方向に対するLVC値をあらかじめ計算して保存しておく代わりに、シャドウアルゴリズムを使って、その場でソフトシャドウを落としてみることができます。しかし、大規模な葉の集合体では、複雑な自己遮蔽が発生しやすいため、ソフトシャドウを計算するのは困難です。例えば,葉の集合体では,葉は同時に受光器でもありオクルーダーでもあることが多いので,コンボリューションシャドウテクスチャを使用することはできません[Sler and Sillion 1998].多数の葉では,[Assarsson and Akenine-Moller 2003]を含むシャドウ・ボリューム・テクニックは,実用的でないほど重いフィルレートに悩まされるでしょう。”Smoothies”は、葉に適用できると思われる高速のソフトシャドウテクニックですが、幾何学的に近似したシャドウは、特にクローズアップビューでは、破壊的なアーティファクトを引き起こす可能性があります[Chan and Durand 2003]。
今回の2パスアルゴリズムは太陽光を想定して開発しましたが、環境マップや複数の小さなエリアの光源で照らされる他の種類のシーンのレンダリングにも適用できます。面光源の形状に制限はありませんが、一定のBRDF近似が十分な精度を持つためには、光源が十分に小さい必要があります。
5 Results
2.8GHzのPentium ⅣプロセッサとATI Radeon 9800Proグラフィックスカードを搭載したPCに、OpenGLでシステムを実装しました。また,[Gardner et al.2003]を参考にしてLLSデバイスを作成しました。ここでは,LLS装置で取得した葉の反射率と透過率のデータを用いたレンダリング結果を報告します。
Leaf Model and Appearance Editing:リーフモデルは、リーフスラブの上面と下面の2組のBRDFとBTDFで構成されています。それぞれのBTDFには、厚みの詳細マップ\(\delta({\mathbf x})\)が格納されています。BRDFには、アルベドマップ\(\gamma({\mathbf x})\)、スペキュラー強度マップ\(\rho_s({\mathbf x})\)、スペキュラーラフネスマップ\(m({\mathbf x})\)の3つのマップを格納しています。これら4つのマップは,解像度720×540の2つのRGBAテクスチャとして格納されています。一方のテクスチャには,RGBチャンネルに\(\gamma({\mathbf x})\)が,アルファチャンネルに\(\delta({\mathbf x})\)が格納されています.もう一方のテクスチャは,RGBチャンネルに\(\rho_s({\mathbf x})\),アルファチャンネルに\(m({\mathbf x})\)を含んでいます.合計すると、リーフモデルは4つのRGBAテクスチャとして保存されます。
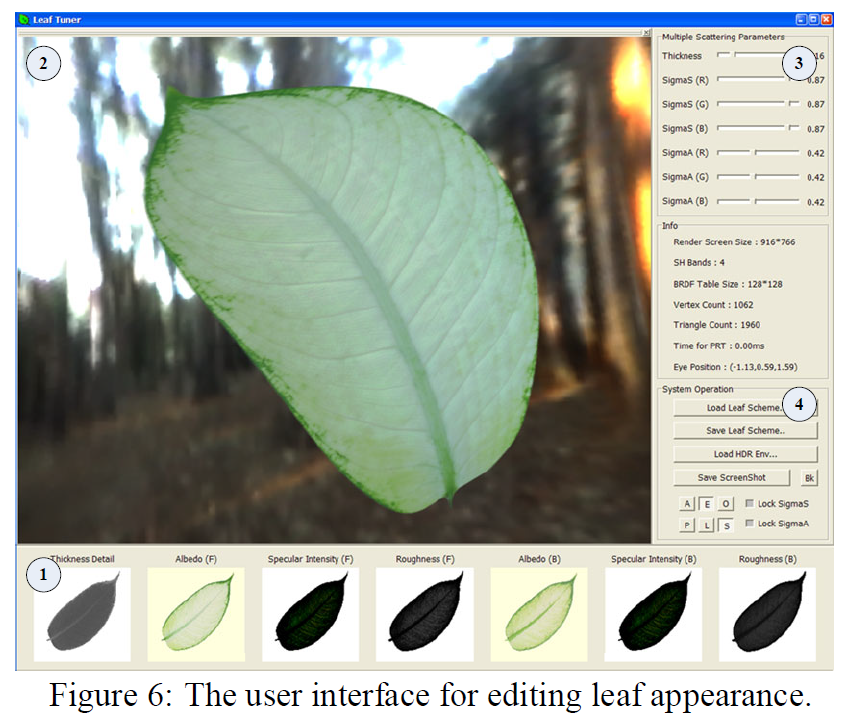
図6は、リーフの外観を編集するためのシンプルなユーザーインターフェースです。下のパネル(パネル#1)には,葉の上面と下面のアルベドマップ,スペキュラー強度マップ,スペキュラーラフネスマップなどのパラメータマップが表示されています。右上のパネル(Panel#3)では、葉の厚さや吸収・散乱係数のRGBチャンネルなど、表面下散乱パラメータを制御します。編集結果は、中央のウィンドウ(Window#2)にインタラクティブに表示され、ユーザーはすぐにフィードバックを得ることができます。図7は、リーフの外観編集の例です。その他の編集例については、会議DVDの付録Bに記載されています。
Rendering:図8は,本システムのレンダリング品質をPRTおよびレイトレーシングで生成したグランドトゥルースと比較したものである。私たちの結果は、グランドトゥルースと良好に比較されています。予想通り、PRTの結果では影の高周波のディテールが失われていますが、本システムではうまく捉えられています。
図1と図10は、様々な種類の葉をモデル化し、本システムでレンダリングした画像です。従来の手法では難しかった、ニレの葉のソフトエッジがうまく表現されていることがわかります。図1と図10の詳細情報を表1に示します。 レンダリング解像度は800×600。「SHデータ」の欄には、各モデルのメッシュの頂点数と、球面調和データのサイズ(メガバイト)が記載されています。このデータはPRTレンダリングパスに使用されており、25の係数を持つ5次の球面調和を使用しています。「LVCデータ」の欄には、モデルごとにメッシュの頂点数とライトビジブルコンボリューションデータのサイズが記載されています。球面調和データには低周波の情報しか含まれていないので、比較的疎なサンプリングで十分です。全周波数のLVCデータの場合は、より高いサンプリング密度が必要となります。
図11は、500k以上の頂点を持つバラタツリーのレンダリング結果です。このような大規模なモデルでも、本システムは約10fpsのレンダリングを実現しています。
図9では,本手法と全周波シャドウ法[Ng et al. 2003]を比較しています。2つの手法の画質は同等であり,主な違いはレンダリング速度です.動的視点,動的照明の場合,本手法は35fps以上を達成しています.葉の表面のような光沢のある表面では,動的視点を用いた全周波数アプローチは現在のところ利用できません.そのため,固定視点による全頻度アプローチ([Ng et al. 2003]では “image relighting “と呼ばれている)を用いており,5 fps 程度の速度で動作しています.イメージリライティングでは,32x32x6 の環境マップを使用し,約 1000 個のウェーブレット係数を保持します(16%).視認性の値は1バイトに量子化されています。圧縮率は約6.25です。画像サイズは800×600です。
6 Summary and Discussion
私たちは、グローバルイルミネーション効果を用いた植物の葉のリアルタイムレンダリングのためのフレームワークを発表しました。このフレームワークの重要な要素は,パラメトリックな葉のモデルであり,表面下散乱や粗い光源散乱を取り入れるのに十分な洗練されたモデルであると同時に,リアルタイムレンダリングをサポートするのに十分なコンパクトなモデルでもあります.このリーフモデルは、実際の葉からキャプチャすることができるため、非常にリアルな葉の外観モデルを簡単に作成することができます。このフレームワークのもう一つの重要な要素は、影の高周波の詳細を失うことなくグローバルイルミネーション効果をレンダリングする2パスアルゴリズムです。私たちは、さまざまな植物の葉をレンダリングすることで、このフレームワークを実証しました。
このシステムは、今後の研究に向けていくつかの興味深い分野を示唆しています。葉の構造を幾何学的にモデル化することは、コンピュータグラフィックスの分野で活発に行われています。今後の課題としては、我々の外観モデリング技術と、より精巧な幾何学的モデルを組み合わせることが挙げられます。我々の葉のモデルは、葉の上の髪の毛のような小さな特徴を考慮していません[Fuhere et al. 2004]。 これは、さらなる研究が必要なテーマです。最後に、私たちのフレームワークは、広葉樹の葉のレンダリングを目的としています。将来的には、針葉樹の葉のような他の種類の葉のレンダリングのためのアプローチを開発したいと考えています。
私たちは、実測データが利用可能な場合、レンダリング結果の品質を損なうことなく、むしろスピードと品質を大幅に向上させながら、よりシンプルな外観モデルを実現できることを示しています。さらに、光がマテリアルとどのように相互作用するかを詳細に予測するために必要なモデルと、その相互作用を記述するために必要なモデルは異なります。つまり、測定で得られる外観を予測するために、素材の内部をモデル化する必要はありません。これは、葉っぱなどの薄い物体の外観モデルを考える上で、従来の考え方や習慣とは異なる新しい考え方です。しかし、私たちは、このアプローチが実行可能であり、有望であることを示します。
コンピュータグラフィックスの分野では、近年、キャプチャーとリアルタイムレンダリングの分野が盛んに行われていますが、この2つの分野は互いに独立して発展してきたと言えます。今回、エンド・ツー・エンドのシステムを開発することで、一見バラバラに見えるこの2つの問題に関係性を持たせることに大きなメリットがあることを示しました。つまり、何をキャプチャし、どのように保存するかをレンダリングアルゴリズムに直接結びつけることで、非常に複雑な外観を持つマテリアルを効率的に高忠実にレンダリングできるようになるのです。
最後に、コンピュータグラフィックスでは、最終的には見る人が感じるレンダリング結果が重要になります。一方、生の計測データでは、ユーザーの意図とはかけ離れた結果になることがあります。ユーザーが望む結果を得るために、適切なハンドルを決めて提供することが、外観モデリングの重要な課題の一つです。そのためには、外見データを選択的に編集できることが重要です。本稿で紹介するリーフモデルは、直感的な制御パラメータを提供するモデルの一例です。今後の課題は、より多くの種類の材質に対応するモデルを開発することです。
Acknowledgement: LLSデバイスの構築にご協力いただいたJiaping Wang氏とAndrew Gardner氏に感謝いたします。また、葉の外観を編集するための初期システムを導入してくれたZhunping Zhang氏と、ビデオ制作に協力してくれたSteve Lin氏に感謝します。また、有益な議論をしていただいたPrzemysalaw Prusinkiewicz氏とXin Tong氏にも感謝いたします。葉や枝の形状モデルはMingdong Xie氏が作成しました。匿名の査読者の方々には,有益な提案とコメントをいただきました。