こんらみ。Pocolです。
今日は,Alan Wake 2で採用されているという…
[Münstermann 2018] Cedrick Münstermann, Stefan Krumpen, Reinhard Klein, Christophe Peters, “Moment-Based Order-Independent Transparency”, I3D 2018.
を読んでみようと思います。
いつもながら誤字・誤訳があるかと思いますので,ご指摘頂ける場合は正しい翻訳例と共に指摘して頂けるとありがたいです。
任意の順序でレンダリングされた透明なサーフェスを合成するには、order-independent transparencyのテクニックが必要です。オクルージョンを組み込むためには、各サーフェスカラーに視点に対する適切な透過率を乗算する必要があります。モーメントシャドウマッピングを基礎として、ピクセルごとにこの深度依存関数をコンパクトに保存し、高速に再構成するためのモーメントベースの手法を紹介します。対数透過率を用いることで、関数を乗算ではなく加算的に蓄積することができます。そして、すべての透明なサーフェイスに対して加法的なレンダリングパスを行うことで、モーメントが得られます。モーメントベースの再構成アルゴリズムは、元の関数の近似値を提供し、2回目の加算パスで合成に使用されます。我々は、4つまたは6つのべき乗モーメントを用いた既存のアルゴリズムを利用し、8つのべき乗モーメントまたは最大4つの三角モーメントを用いた新しいアルゴリズムを開発します。その結果、次数に全く依存せず、透明なサーフェイスだけでなく、関与媒質に対してもうまく機能し、さまざまなトレードオフを提供する多くのバリエーションがあります。また、透明なサーフェイスに対する影の計算という密接に関連した問題に対しても、同じアプローチを利用します。
1 INTRODUCTION
透明なサーフェイスをリアルタイムでレンダリングするのは難しいです。オーバーブレンディングとアンダーブレンディング [Porter and Duff 1984] は何十年もの間、ハードウェアでサポートされてきましたが、ジオメトリが保存されていない限り、正しい結果を提供することはできません。大規模な動的シーンですべての透明ジオメトリをソートするのはコストがかかり、交差がある場合はピクセルごとにフラグメントをソートしなければなりません[Carpenter 1984]。その結果生じる不規則な作業負荷は、超並列グラフィックスハードウェアとの相性が悪いです。
このオーバーヘッドを回避するために、多くのヒューリスティックが提案されてきました。レイヤーベースのアプローチは、透明なジオメトリを固定数のレイヤーに集積します[Maule et al.2013; Salvi et al.2011; Salvi and Vaidynanathan 2014]。この累積は、依然として実行順序に依存するため、実装には決定論的なパイプライン順序を保証するハードウェアが必要です。他のヒューリスティックは、実際の透明ジオメトリに依存しない同じ透過率関数を使用することで、完全な順序独立性を実現しています[MuGuire and Bavoil 2013; McGuire and Mara 2017]。このアプローチは高速で実装が簡単ですが、結果は不正確です。
我々は、モーメントベースの再構成における最近の進歩[Peters and Klein 2015; Peters et al 2017]に基づいて、プログラム可能なシェーダーと加法的ブレンドのみに依存する、order-independent transparency(OIT)のより正確な技術を導出します。乗算的に累積される必要がある透過率は、加法的累積を可能にするために、その対数で表されます。最初の加算レンダリングパスは、この深度依存関数のモーメントを決定します(セクション3.1)。モーメントが利用可能になると、モーメントベースの再構成は、任意の深さでの透過率の近似値を提供します(セクション3.2)。したがって、すべての透明なサーフェイスを合成するには、2回目の加算レンダリングパスで十分です。
透明なサーフェイスが多い場合、透過率関数は複雑になります。その適切な表現には、多数のモーメントが必要です。レンダリングにおける先行研究では、最大6つのパワーモーメントを使用しており、ほとんどのユースケースで十分な品質が得られています(セクション4.1)。より困難なケースのために、我々は8つのパワーモーメントを用いた実装を推し進めますが、三角モーメント、すなわち正信号のフーリエ係数に基づく数値的な不正確さを発見しました(セクション5)。この結果、演算量は多少増加するものの、よりロバストで表現力豊かな手法となります。
OITと同様、影のレンダリングは透過率の計算を意味します。したがって、フィルタリング可能なシャドウマップ(セクション6)を通じて透明なサーフェスの影をレンダリングするために、まったく同じアプローチを適用します。不透明なシャドウキャスターは別に扱われます。
我々の新しい技術は、関与媒質と他の透明サーフェイスとの間の複雑な相互作用を忠実に扱うことができることがわかりました(図1参照)。モーメントに基づく再構成は、少数の透明サーフェイスに対してはほぼ完璧であり、より複雑な状況に対しては連続透過率関数にスムーズに移行します。厳格な閾値がないため、結果は飛び出すようなアーティファクトが全くありません。パイプラインの順序が一貫していなくても、結果は変わりません。透明なサーフェイスの交差はより困難であり、モーメントの選択と存在するサーフェイスの数に依存して、ぼやける可能性があります。
2 RELATED WORK
OITは、色\(L_0, \cdots, L_{n-1}\)、不透明度\(\alpha_0, \cdots, \alpha_{n-1}\)、深度\(z_0, \cdots, z_{n-1}\)を持つ\(n \in {\mathbb N}\)個のフラグメントを合成するよう努めます。オーバー演算子[Porter and Duff 1984]を前後から順に適用すると、合成された色が得られます。
\begin{eqnarray}
\sum_{l=0}^{n-1} L_l \cdot \alpha_l \cdot \underset{z_k \lt z_l}{\prod_{k=0}^{n-1}} (1 – \alpha_k) \tag{1}
\end{eqnarray}
上記の積は透過率を表しています。オクルードしているサーフェイスへの依存性が重要な課題です。順序付きトラバーサルは問題を簡単にし、すべてのフラグメントを保存し、ピクセルごとに明示的にソートすることで達成できるかもしれません[Carpenter 1984]。ハードウェアによる高速化実装[Yang et al.2010]もありますが、コストがかなりかかります。デプスピーリングは、デプスバッファを使用して、一度に1つのサーフェスを順番にレンダリングします[Everitt 2001]。\(k\)-buffer [Bavoil et al. 2007]は、ピクセルごとに可変数のフラグメントを保存するのではなく、\(k \in {\mathbb N}\)個だけを保存します。これが不十分な場合、フラグメントはヒューリスティックにマージされます。Adaptive Volumetric Shadow Maps[Salviら2010]とAdaptive Transparency[Salviら2011]は\(k\)‐バッファに透過率関数への最適な近似を格納します。Adaptive Transparencyは、2番目のパスで合成されます。Deep Shadow Maps [Lokovic and Veach 2000] も似ていますが、より適応的な表現を使用しています。Mutli-layer alpha blending [SalviとVaidyanathan 2014] は\(k\)-bufferに直接コンポジットし、保存された深度値に応じてオーバーブレンディングとアンダーブレンディングを切り替えます。これらの経験則はすべて順序に依存せず,決定論的パイプライン順序を必要とします。Hybrid transparency[Mauleら2013]も同様に機能しますが、\(k\)個の最前面サーフェスのレイヤを明示的に使用します。したがって、これは真に順序に依存しませんが、多数のサーフェスが存在する場合に失敗します。
Stochastic transparency [Enderton et al. 2011]は、その不透明度に比例してフラグメントをランダムに棄却します。期待される値はグランドトゥルースですが、ノイズを減らすためにかなりのフィルタリングが必要です。同じアイデアが影にも使われています[McGuire and Enderton 2011; McGuire and Mara 2017]。ハッシュ化アルファテスト[Wyman and McGuire 2017]は、決定論的ハッシュによってノイズを時間的に安定させます。
様々な単層ヒューリスティックは、実際の形状に依存しない透過率関数の近似を使用します[McGuire and Bavoil 2013; McGuire and Mara 2017; Meshkin 2007]。Weighted blended OITでは、透過率はユーザー定義の有理関数に比例して低下します[McGuire and Bavoil 2013]。現象学的透明は、着色された透過率や他の様々な効果を追加します[McGuire and Mara 2017]。これらの技法は、非常に高速で、ロバストで、使いやすく、決定論的な順序を必要としません。しかし、結果はグランドトゥルースと大きく異なり、オクルージョンの手がかりは失われます。
Fourier opacity mapping [Jansen and Bavoil 2010] は透過率を深度の関数として捉え、それを対数で表しています。得られた吸光度は、乗法的蓄積ではなく加法的蓄積を可能にします。Convolution shadow maping[Annenら2007]と同様に,関数はフーリエ級数によって簡潔に表現されます。この手法は、対応する吸光度関数が低頻度であるため、関与媒質の影に対して特に有用です。Transmittance function mapping[Delalandreら2011]も同様のアプローチを取りますが、透過率を直接表します。レイマーチングによって計算されるため、順序の独立性は問題になりません。
Convolution shadow mapsのように、Moment shadow maps[Peters and Klein 2015]は、シャドウマッピングのための深度分布のコンパクトでフィルタリング可能な表現を提供します。各テクセルには深度の4乗が格納され,フィルタリングされたサンプルは4つのべき乗モーメントを提供します。そして,効率的な閉形式は,実際の累積分布関数に対する下界と上界を提供します。Convolusion shadow mapsとは異なり、Moment shadow mapsは疎な信号を正確に再構成することができます。
その後の研究[Peters et al. 2017]では、6つのパワーモーメントを使用するように技法を拡張し、透明なサーフェイスの影に使用しています。透明なサーフェスに対するアプローチは,不透明なサーフェスと透明なサーフェスを単一のモーメントシャドウマップにレンダリングするために,OITのための別のテクニックを使用します。別の最近の研究[Peters 2017]では,4つのパワーモーメントをよりコンパクトに保存し,より高速に再構成することを検討しています。
3 PIPELINE
我々の目標は、OITにFourier opacity mappingに似たアプローチを使用することです。フーリエ級数を使うのではなく、Moment shadow mappingのようにモーメントを使います。本節では、我々のレンダリングパイプラインを紹介し、モーメントベースの再構成をブラックボックスと見なします。セクション4と5では、再構成のさまざまなオプションについて詳しく説明します。
3.1 Representing Absorbance through Moments
多くのテクニックと同様に、透明なジオメトリは不透明なジオメトリとは別に扱います。すべての不透明ジオメトリは、深度バッファを使用して最初にレンダリングされます。この深度バッファは、目に見える透明ジオメトリのみをレンダリングするために保持されます。透明ジオメトリは2回レンダリングされ、1回はピクセルごとの透過率関数を決定し、もう1回はすべての透明サーフェスを合成します。
式(1)から、深度\(z_f \in {\mathbb R}\)のフラグメントの透過率は次式で与えられることを思い出してください。
\begin{eqnarray}
T(z_f) := \subset{z_l \lt z_f}{\prod_{l=0}^{n-1}} (1 – \alpha_l).
\end{eqnarray}
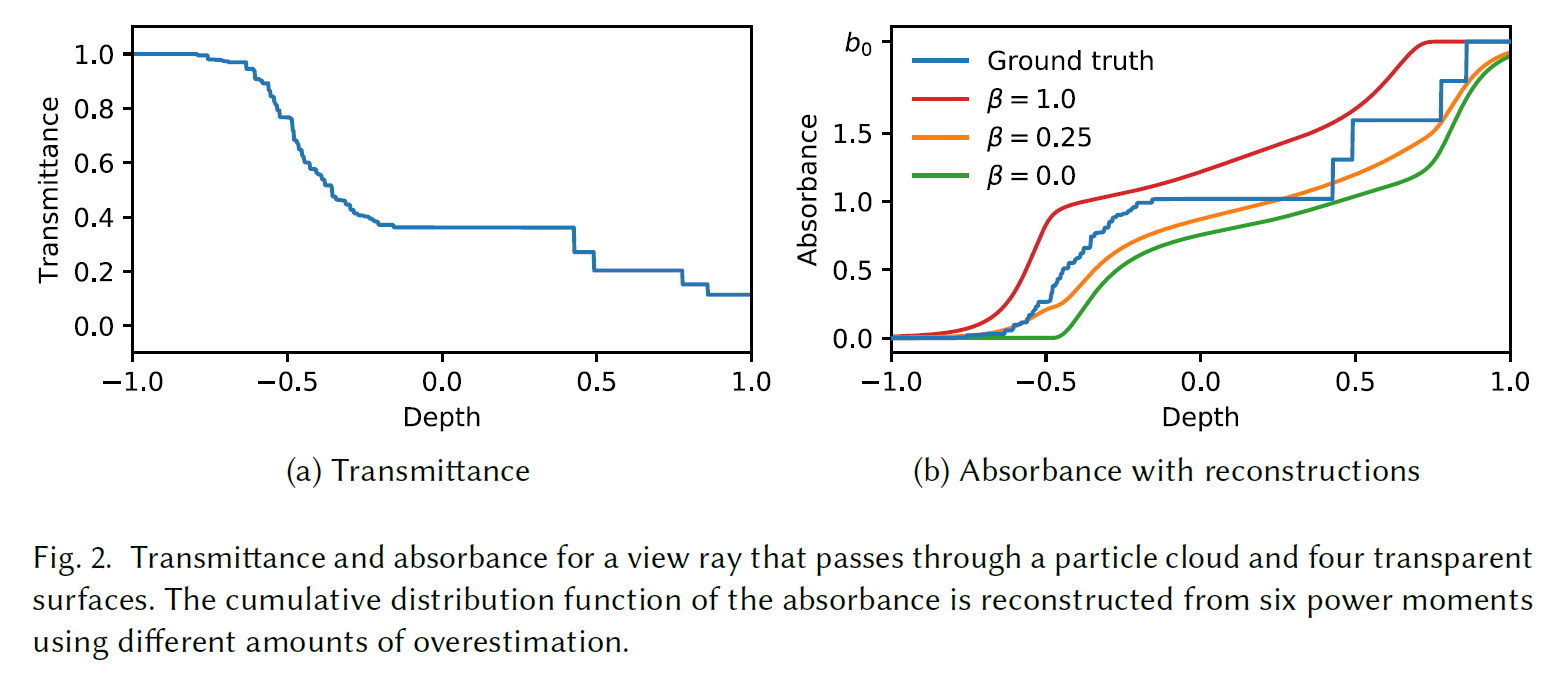
この乗算累積を直接実装するのではなく、対数領域で作業します(図2参照)。\(z_f\)に対する吸光度を次のように定義します。
\begin{eqnarray}
A(z_f) := – {\rm ln} T(z_f) = \subset{z_l \lt z_f}{\prod_{l=0}^{n-1}} – {\rm ln}(1 – \alpha_l).
\end{eqnarray}
\(0 \leq \alpha_l \lt 1\),よって \(0 \leq -{\rm ln}(1 – \alpha_l) \lt \infty\) に注意してください。したがって、吸光度は深度\(z_f\)とともに単調に増加し、有限尺度の累積分布関数として解釈することができます。
\begin{eqnarray}
Z := \sum_{l=0}^{n-1} -{\rm ln}(1 – \alpha_l) \cdot \delta_{z_l}
\end{eqnarray}
各サーフェイス深度に1つのDirac-\(\delta\)を持ちます。透過率を保存するには、この尺度を簡潔に表現する必要があります。Moment shadow mappingとその関連技術は、まさにそれを提供します。
Moment shadow mapping[Peters and Klein 2015]のように、モーメント生成関数\({\mathbf b}: [-1, 1] \rightarrow {\mathbb R}^{m+1}\)、例えば\({\mathbf b}(z) = (1, z, z^2, z^3, z^4)^{\top}\)を選びます。すると、透過率は次のように格納されます。
\begin{eqnarray}
b := \epsilon_Z ({\mathbf b}) := \sum_{l=0}^{n-1} -{\rm ln}(1 – \alpha_l) \cdot {\mathbf b}(z_l).
\end{eqnarray}
このベクトルを合計\(m+1\)チャンネルのレンダーターゲットに書き込むには、加算ブレンディングを使ったシンプルなレンダリングパスで十分です。
第0モーメントは全吸光度を格納します。
\begin{eqnarray}
b_0 = \sum_{l=0}^{n-1} -{\rm ln}(1 – \alpha_l).
\end{eqnarray}
したがって、\({\rm exp}(-b_0)\)は、最終的な合成中に不透明なサーフェスの輝度に係数として適用される総透過率です。負でない値を取る可能性があるため、明示的に格納する必要があります。これは、\(Z\)が確率分布であり、\(b_0=1\)を格納する必要がないMoment shadow mappingとは異なります。
3.2 Reconstructing the Transmittance
Moment shadow mappingの核となる再構成アルゴリズムは、\(b\)に基づいて\(Z\)の累積分布関数に鋭い下界を提供します[Peters and Klein 2015, Algorithm 2]。厳密に言えば、このアルゴリズムは\(b_0=1\)を仮定していますが、常に\(b\)を\(b_0\)で割り、最終結果に\(b_0\)を掛けることができます。詳細はセクション4と5で説明します。
同じ方法で、累積分布関数の上限を計算することができます[Peters et al. 2017, Section 5.3]。下界を使用することで、サーフェスがそれ自身をオクルードしないことが保証されますが、視認性の系統的な過大評価が犠牲になります。我々は、\(\beta=0.25\)付近の重みを使用して上限に向かって補間するとき、全体的な結果がより説得力のあることがわかりました(図2bを参照)。
したがって、任意の深度\(z_f\)における吸光度の近似値\(A(z_f, b, \beta)\)が得られます。そこから、次のように透過率を計算します。
\begin{eqnarray}
T(z_f, b, \beta) := {\rm exp}(-A(z_f, b, \beta)).
\end{eqnarray}
2回目の加算レンダリングパスでは、すべての透明なサーフェイスをレンダリングしてシェーディングし、吸光度を計算して、式(1)に従ってオフスクリーンのレンダーターゲットで合成します:
\begin{eqnarray}
\sum_{l=0}^{n-1} L_l \cdot \alpha_l \cdot T(z_f, b, \beta)
\end{eqnarray}
\(b_0=0\)のピクセルの場合、フラグメントはまったく不透明度を持たないので、早期リターンするのがベストです。
3.3 Warping Depth
理論的には違いはありませんが、深度範囲が不当に大きい場合、数値誤差が実際のモーメントベースの再構成の質を低下させます[Peters and Klein 2015]。そこで、シーン内のすべての透明なジオメトリを囲む保守的な境界球を計算し、この球から適度に鮮明な深度範囲\([z_{\rm min}, z_{\rm max}]\)を導き出し、それを\([-1, 1]\)にマッピングします。クリッピング平面に近いため、\(z_{\rm min} \gt 0\)であることに注意してください。このようにして、境界が急激に変化することはなく、結果は時間的に首尾一貫しています。
透過率は常に単調に減少するため、近くの透明なサーフェスは遠くのサーフェスよりも見えやすくなります。結果として,著者らはさらに,対数的に深度を歪めることによって近くの幾何学に対してより高い精度を割り当てました。これにより、表示品質が常に向上します。したがって、すべてのモーメントベースの計算に入る深さ値\(z\)は、次の方法で線形ビュー空間の深度値\(z_v \in {\mathbb R}\)から計算されます。
\begin{eqnarray}
z:= \frac{ {\rm ln}z_v – {\rm ln}z_{\rm min} }{ {\rm ln}z_{\rm max} – {\rm ln}z_{\rm min} } \cdot 2 – 1 \in [-1, 1].
\end{eqnarray}
3.4 Final Compositing
不透明なパスと透明なジオメトリの2つの加算パスの後、不透明なサーフェスと透明なサーフェスをそれぞれ示すターゲットをレンダーする必要があります。これらを合成するには、不透明なレンダーターゲットに総透過率\({\rm exp}(-b_0)\)を乗算し、透明なレンダーターゲットを追加します。不透明なサーフェスの出力放射輝度が\(L_n\)の場合、最終的な結果は
\begin{eqnarray}
{\rm exp}(-b_0) \cdot L_n + \sum_{l=0}^{n-1} L_l \cdot \alpha_l \cdot T(z_f, b, \beta).
\end{eqnarray}
しかし、この方法には問題があります。すべての放射量を合わせた総重量は必ずしも1ではありません。全体の透過率は正確でも、個々のサーフェイスの再構成された透過率はずれている可能性があり、これらの誤差が相殺される必要はありません。偏りの少ない結果を得るために、Weighted blended OIT[McGuire and Bavoil 2013]のように明示的に再正規化します:
\begin{eqnarray}
{\rm exp}(-b_0) \cdot L_n + \frac{ 1 – {\rm exp}(-b_0) }{ \sum_{l=0}^{n-1} \alpha_l \cdot T (z_f, b, \beta) } \cdot \sum_{l=0}^{n-1} L_l \cdot \alpha_l \cdot T(z_f, b, \beta) \tag{2}
\end{eqnarray}
分母の正規化値は、2回目の加算レンダリングパスの間にアルファチャンネルに書き込まれるだけです。
この再正規化には、ほとんど追加コストはかかりません。場合によっては、個々のサーフェイスの透過率の推定精度は低下しますが、全体的なアーティファクトは減少します(図7参照)。
4 POWER MOMENTS
これまでのところ、モーメント\(b \in {\mathbb R}^{m+1}\)のベクトルから吸光度\(Z\)の累積分布関数の再構成をブラックボックスとして捉えてきました。以下では、このステップの詳細を説明し、さまざまなトレードオフを提供する幅広い選択肢について議論します。
4.1 Four or Six Power Moments
\(m\)個のパワーモーメントを使う場合、すなわち
\begin{eqnarray}
{\mathbf b}(z) = (1, z, z^2, \cdots, z^m)^{\top}
\end{eqnarray}
ここで,\(m\)は偶数で,アルゴリズム1は望ましい再構成[Peters et al. 2017]を提供します。概念的には、計算された深度\(z_0, \cdots, z_{\frac{m}{2}} \in {\mathbb R}\)におけるDirac-\(\delta\)分布からなる特定の深度分布\(S\)を扱います。この深度分布は、与えられたパワーモーメント、すなわち\({\mathcal E}_s({\mathbf b}) = b\)を正確に実現します。同時に、\(z_f = z_0\)周りのその累積分布関数の値は、すべてのそのような深度分布の中で極値です[Peters and Klein 2015, Proposition 8]。従って、\(A(z_f)\)の望ましい下界と上界へのアクセスを提供します。我々の利用可能な知識は\(S\)の場合を排除しないので、これらの境界は達成可能な最良の境界です。
実際には、アーティファクトを避けるために数値的安定性が最も重要です。従って、ロバストな多項式ソルバーと線形ソルバーを使用することが重要です。\(m=4\)と\(m=6\)については、先行研究[Peters et al. 2017]から入手可能なロバスト実装に依存します。
上記のパイプラインでのこれらの実装の適用は、モーメントごとに1つの単精度浮動小数点を使用する場合に最も簡単です。アルゴリズム1は通常、特殊なケース\(b_0=1\)に対して実装されるため、\(b/b_0\)を入力し、最終結果に\(b_0\)を乗算します。丸め誤差を補正するバイアスも,この正規化ベクトルに適用しました。単精度で格納された6つのパワーモーメントについては、このバリアントが以前に使用されていないため、バイアス戦略[Peters et al. 2017]の最適化をやり直す必要があります。議論されたすべての技術に対する適切なバイアス戦略の詳細は、補足に記載されています。
Moment shadow mappingと同様に、帯域幅の要件を減らすために、モーメントあたり16ビットのみの量子化を使用することは価値があります。しかし、既存の量子化方式は\(b_0=1\)を利用しています。今回のアプリケーションではこの仮定が成り立たないため、値が範囲外で始まってしまう可能性があります。我々の解決策は、既存の量子化スキーム[Peters et al. 2017]を使用して正規化モーメント\(\frac{b_1}{b_0}, \cdots , \frac{b_m}{b_0}\)を格納し、\(b_0\)を別々に格納することです。\(b_0\)はダイナミックレンジが大きいため、半精度の浮動小数点が最適です。
加算ブレンディングの実装では、保存されたベクトルは加算前に\(b_0\)が乗算され、保存前に更新された\(b_0\)で除算される必要があります。このread-modify-write操作は、決定論的なパイプライン順序を必要としませんが、現在のハードウェアでは、対応する機能が最も実用的な実装を提供します。
16ビットのレンダーターゲットに対するこのような加算レンダーパスの問題は、フラグメントの数が増えるにつれて丸め誤差が蓄積されることです。通常のバイアス戦略は依然として効果的な対策ですが、必要なバイアスの強さはもはやシーンに依存しません。それでも、適切なバイアス値を見つけるのは簡単です。図1のような複雑なシーンでも、通常のバイアス値を1桁以上大きくする必要はありませんでした。
また、非線形量子化[Peters 2017]を使用して、より大きな帯域幅を必要とすることなく、丸め誤差の減少の恩恵を受けようとしました。しかし、非線形非量子化と量子化によってread-modify-write操作に追加されるコストは、この設定で正当化するには大きすぎることが判明しました。
4.2 Eight Power Moments
リアルタイムグラフィックスの先行研究では、6つ以上のパワーモーメントを使用したことはありませんでした。透明なサーフェイスは非常に複雑な構成で発生する可能性があるため、より高価ではあるが、より強力な手法のために、\(m=8\)への拡張を調査しています。線形ソルバーに関しては、アルゴリズム1の推奨は\(m=8\)でも有効です。
残された課題は、4つの実根を持つ4次多項式のロバストな多項式ソルバーを見つけることです。様々な反復解法、閉形式、ハイブリッド解法を試した結果、最もロバストな結果を効率的に与える閉形式解法[Neumark 1965]に落ち着きました。内部的には、このソルバーは、別のロバストソルバー[Blin 2007]を使って計算したレゾルベント3乗の最小の大きさの根を使います。そして、このソルバーは4次式を2つの2次多項式に因数分解します。その根が最終結果となります。数値的なキャンセルを避けるために、この因数分解に2つの異なるアプローチを適応的に使用します[Herbison-Evans 1995]。
最後に、16ビット量子化のための新しい量子化変換と、最適なバイアス戦略を導き出す必要があります。我々は、\(m=6\)の場合[Peters et al. 2017]と同様に、これらを正確に計算し、結果の行列とベクトルを、再構成アルゴリズムの補数コードとともに補足で提供します。
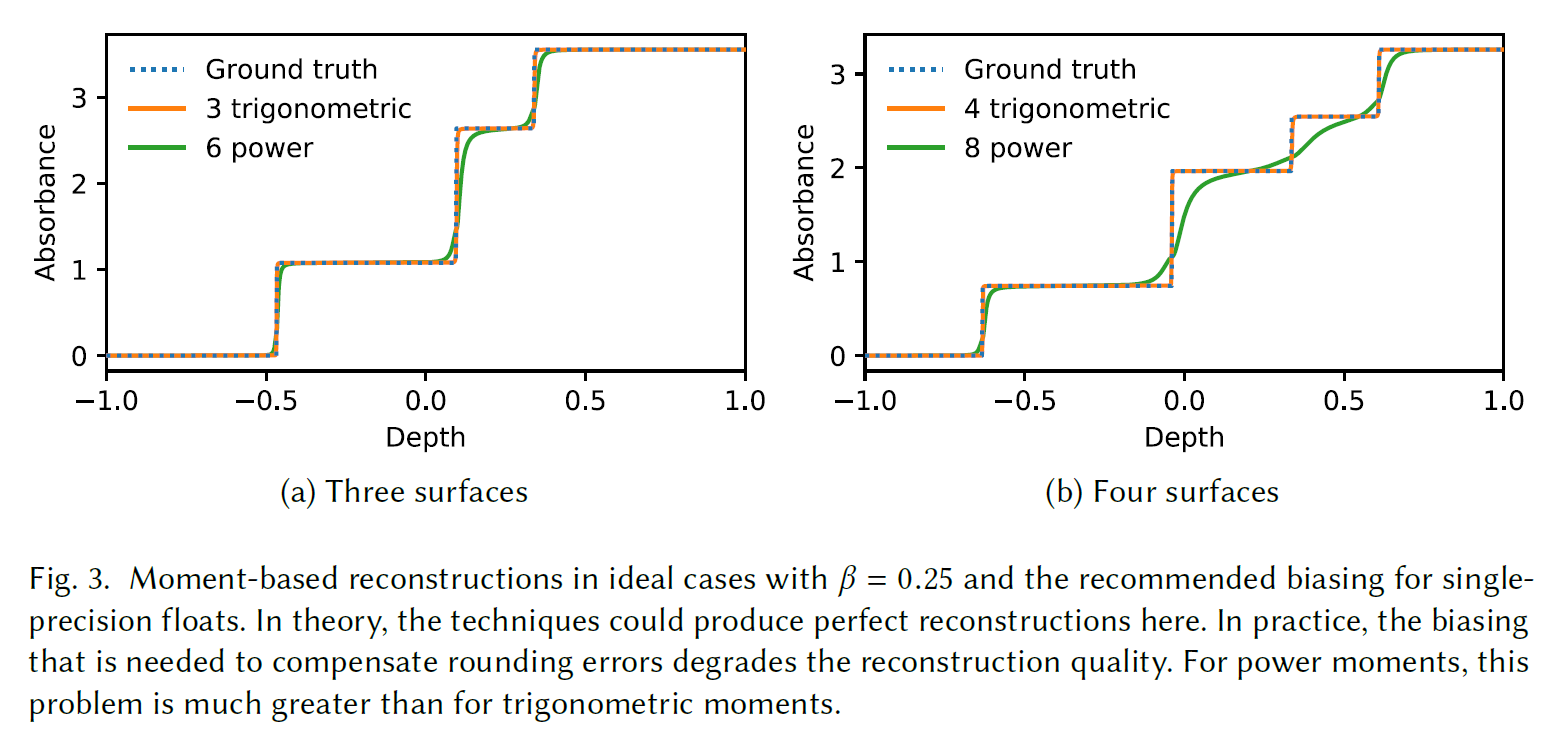
理論的には、8つのパワーモーメントは6つのパワーモーメントよりも複雑な分布を捉えることができます。最大4つの透明なサーフェイスを持つ分布を完全に再構成することができます。実際には、丸め誤差が大きな問題となります。単精度の浮動小数点数であっても、これらの誤差は、より多くのパワーモーメントの利点を減少させるバイアスを必要とします(図3を参照)。
5 TRIGONOMETRIC MOMENETS
Moment shadow mappingは、モーメント生成関数\({\mathbf b}\)としてフーリエ基底関数を使用する三角法モーメントシャドウマッピング[Peters and Klein 2015]と呼ばれる代替案とともに導入されています。しかし、鋭い下界の計算がはるかに複雑であるため、演算オーバーヘッドは法外となります。
5.1 Approximate Bounds
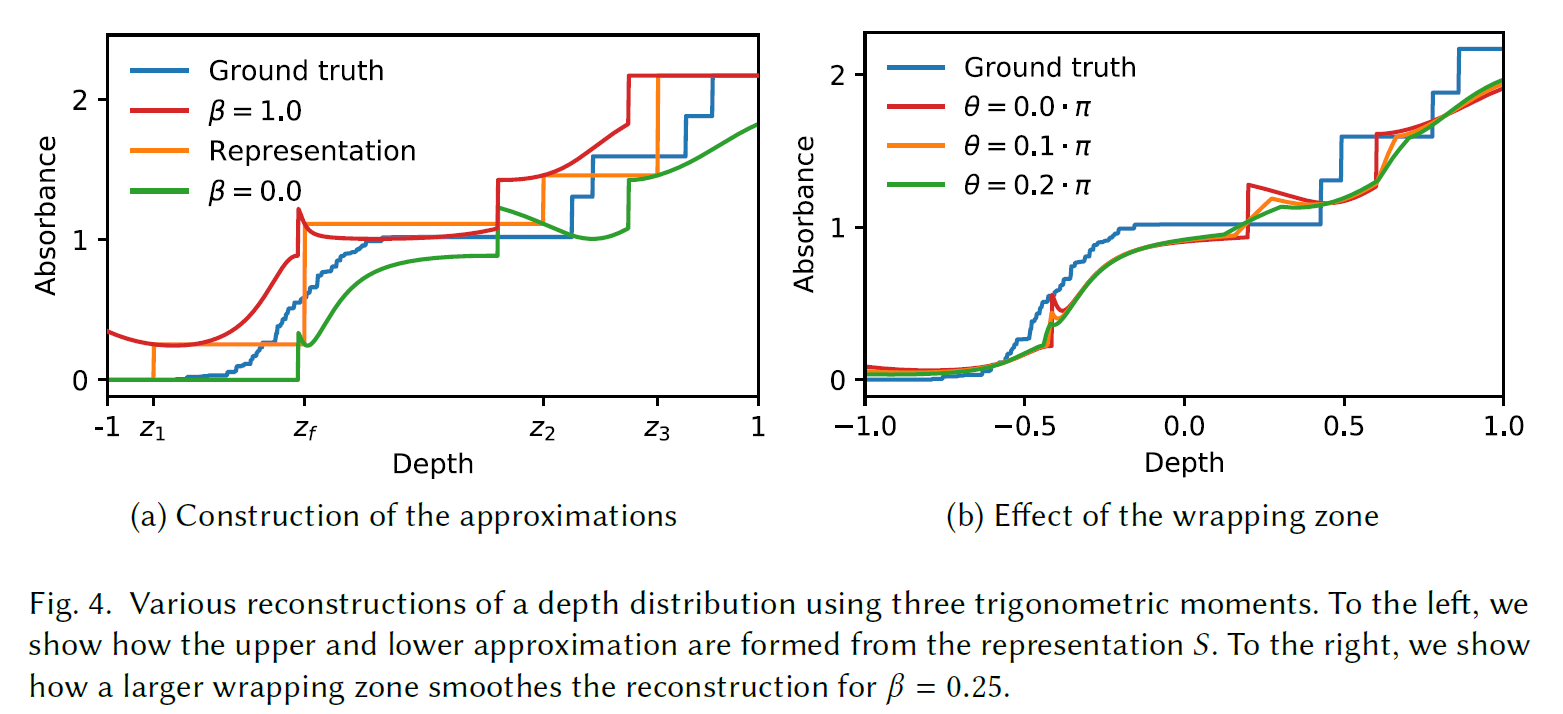
OITにとって、下限があることは重要ではありません。実際、系統誤差を減らすために、上限に向かって明示的に補間します。これを利用して、はるかに効率的なアルゴリズムを実現します。このアイデアは、アルゴリズム1と同じ原理を使って、与えられた三角法モーメントとDirac-\(\delta\) \(z_f\)を持つ疎な深度分布を見つけることです。\(z_f\)でのこの再構成による累積分布関数は、元の累積分布関数の近似を提供します(図4a参照)。
アルゴリズム2はこのアプローチを実装しています。すべてのステップはアルゴリズム1に類似しています。実数乗モーメントを扱うのではなく、複素三角モーメントを取ります。我々の深度範囲は、以下を通して複素単位円に関連しています。
\begin{eqnarray}
{\mathbf x}(z) := {\rm exp} \left( 2 \cdot \pi \cdot i \cdot \frac{z+1}{2} \right) \in {\mathbb C}. \tag{3}
\end{eqnarray}
モーメント生成関数は\({\mathbf x}\)のべき乗,すなわち\({\mathbf b}(z) = (1, {\mathbf x}^1(z), \cdots, {\mathbf x}^m(z))^{\top}\)からなり, \({\mathbf b} (z)\) は複素フーリエ基底関数のベクトルです。
アルゴリズム2は暗黙的に、与えられたすべての三角関数モーメントが正確に一致するように、\(z_l := {\mathbf x}^{-1}(x_l)\)と\(w_0, \cdots, w_m \lt 0\)を使用して一意の深度分布\(S := \sum_{l=0}^m w_l \cdot \delta_{z_l}\)を計算します[Peters and Klein, Propositions 15 and 16]。すなわち,すべての \(j \in \{0, \cdots, m\}\)について
\begin{eqnarray}
{\mathcal E}_S({\mathbf x}^j) = \sum_{l=0}^m w_l \cdot x^j_l = b_j.
\end{eqnarray}
これは、これらの三角モーメントを表す無限にある分布のひとつです。構造上、\(z_f\)において非ゼロの重み\(w_0\)を持ちます。アルゴリズム2の最後の3つのステップは、\(z_f\)での累積分布関数である\(w^{\top} \cdot v\)を評価します[Peters et al. 2017, Section 5.4.2]。この目的のために、各点の寄与を決定する必要があり、これは次式で与えられます。
\begin{eqnarray}
v_l = {\mathbf v}(x_l, x_0) := \begin{cases} 1 & {\rm if} \, {\mathbf x}^{-1}(x_l) \lt {\mathbf x}^{-1}(x_0) \\ 0 & {\rm otherwise} \end{cases} \tag{4}
\end{eqnarray}
パラメータ\(v_0 = \beta\)は、\(z_f\)におけるウェイト\(w_0\)の寄与を決定します。これが0の場合、結果は下限に近くなり、1の場合は上限に近くなります。いずれにせよ、適切な境界は得られませんが、少なくとも過小評価か過大評価かはある程度コントロールできます(図4a参照)。
5.2 The Wrapping Zone
適切な境界がないこと自体は問題ありませんが、いくつかの悪影響もある。最も顕著なのは、再構成が連続的でないことです。この問題は、深度値が回り込む\(x_l = 1\)に対する\({\mathbf v}(x_l, x_0) \)の不連続性に起因します。\(x_l = x_0\) についても不連続性がありますが、このケースは起こりえません [Krein and Nudel’mann 1977, Theorem Ⅳ.4.2]。このような不連続は結果的に見つけやすいので、\({\mathbf v}(x_l, x_0)\)を修正することで問題に対処します。
どの深度値にも対応しない領域のサイズを制御するラッピングゾーン角度\(0 \lt \theta \ll 2 \cdot \pi\)を導入します。これは、深度値を連続的に回り込ませるためだけに使用されます。したがって, 我々は次を再定義します。
\begin{eqnarray}
{\mathbf x}(z) := {\rm exp} \left( (2 \cdot \pi – \theta) \cdot i \cdot \frac{z+1}{2} \right). \tag{5}
\end{eqnarray}
\({\mathbf v}(x_l, x_0)\)を変化させるとき、逆三角関数を含むので\({\mathbf x}^{-1}\)を評価するのは非効率的であることに注意します。これを同じ意味で単調な区分線形関数で置き換えます。
\begin{eqnarray}
{\mathbf \psi}(x) := \begin{cases} – {\mathfrak R}_x + {\mathfrak J} & {\rm if} \, {\mathfrak R}_x \geq 0, {\mathfrak J}_x \geq 0, \\
2 – {\mathfrak R}_x – {\mathfrak J}_x & {\rm if} \quad {\mathfrak R}_x \lt 0, {\mathfrak J}_x \geq 0, \\
4 + {\mathfrak R}_x – {\mathfrak J}_x & {\rm if} \quad {\mathfrak R}_x \lt 0, {\mathfrak J}_x \lt 0, \\
6 + {\mathfrak R}_x + {\mathfrak J}_x & {\rm if} \quad {\mathfrak R}_x \geq 0, {\mathfrak J}_x \lt 0 \end{cases}
\end{eqnarray}
重みの連続係数は次のように計算できます。
\begin{eqnarray}
{\mathbf v}(x_l, x_0) :=
\begin{cases} 1 & {\rm if} \quad {\mathbf \psi}(x_l) \lt {\mathbf \psi}(x_0), \\
0 & {\rm if} \quad {\mathbf \psi}(x_0) \leq {\mathbf \psi}(x_l) \leq {\mathbf \psi}({\mathbf x}(1)), \\
\frac{ {\mathbf \psi}(x_l) – {\mathbf \psi}({\mathbf x}(1)) }{ 7 – {\mathbf \psi}({\mathbf x}(1))} & {\rm otherwise}. \end{cases} \tag{6}
\end{eqnarray}
ラッピングゾーン\(\theta\)のサイズを大きくすることは、滑らかさと深度の正確さを交換することになります。再構成はどの\(\theta \lt 0\)でも連続的ですが、それでも急速に変化することがあります(図4b参照)。我々の実験では、\(\theta = \frac{\pi}{10}\)を使用します。
5.3 Three or Four Trigonometric Moments
ほとんどの部分において、アルゴリズム2の実装はアルゴリズム1と非常によく似ています。大きな違いは、複素数がほとんどの実数に取って代わることです。したがって、\(m\)個の三角モーメントは\(2 \cdot m\)乗と同じだけのスペースを必要としますが、同程度の情報量を持ちます。実際、複素数の方が安定性が高いため、高次ではより良い再構成が可能です。しかし、複素数演算はより多くの演算命令を必要とします。2つの三角モーメントでは、安定性の向上による恩恵は小さすぎて、このコストを正当化することはできません。
高次の安定した実装に残された課題は、多項式ソルバーです。すべての根\(x_1, \cdots, x_m\)が単位円上にあることが知られているので、この問題は正常動作します。3つの三角モーメントについては、Blinnのソルバー[Blinn 2007]を分岐なしで複素数の場合にネイティブに一般化したものから始めましたが、アーティファクトはほとんどありませんでした。内部的には、このソルバーは2次多項式の根を計算します。残りのアーチファクトを取り除くには、より大きな二次関数の根を選んでキャンセルを避ければ十分です。Neumarkのソルバー[Neumark 1965]を複素数の場合にも同様に一般化すると、選ばれた窪んだ3乗の根が最小の大きさのものでなければ、ロバストに機能します。
バイアスは、\(b_1, \cdots, b_m\)に適切な定数\(1 – \alpha\)(補足参照)を乗算することにより、Trigonometric moment shadow mapping[Peters and Klein 2015]と同様に実装されます。三角モーメントは丸め誤差の影響を受けにくいので、それぞれ16ビットで保存する場合には量子化変換は不要です。
6 SHADOWS
OITが一次視界を扱うのに対し、影のレンダリングは二次視界に対応します。どちらの場合も、核となる問題は透過率の計算です。したがって、OITのほとんどのテクニックは影に使用でき、その逆も同様です。例えば、Stochastic transparency[Enderton et al. 2011]やColored stochastic shadow maps[McGuire and Enderton 2011]は、同じ基本原理を使用しています。ここでは、このモーメントベースのOITをシャドウに使用します。これは、Fourier opacity mapping[Jansen and Bavoil 2010]のためのモーメントベースの類似性を導きます。
OITと同様、不透明なシャドーキャスターと透明なシャドーキャスターを別々に扱います。不透明なシャドウキャスターには、どのようなシャドウ技法を用いてもよいです。我々はMoment shadow mapping[Peters and Klein 2015]を選択します。そして,加算パスによって,透明シャドウキャスターを別のモーメントシャドウマップにレンダリングし,セクション3.1で説明したように,吸光度の表現を蓄積します。異なる座標変換を除いて,これは全く同じ方法で動作し,セクション4と5のモーメントの任意の選択は有効です。この実装でも深度範囲は外接球から決定されますが、深度値は線形に定義されます。いずれにせよ、第0モーメントを保存する必要があります。これは無限深度までの透過率を表します。これを明示的に保存することは、地表面のような遠方の受光器上の影の品質に有益です。
エイリアシングを減少させるために、我々の実装では、両方のMoment shadow mapsを\(9 \times 9\)のガウシアンでフィルタリングし、バイリニア補間を使用しています。これは、モーメントが単精度の浮動小数点数で格納されている場合は問題なく機能しますが、モーメントごとに16ビットの場合は問題が発生します。除算は非線形であるため、正規化されたモーメントのベクトル\(\frac{b_1}{b_0}, \cdots, \frac{b_m}{b_0}\)は線形にフィルタリングされるべきではありません。そうすることで、場合によっては許容できる結果が得られますが、フィルタ領域が\(b_0\)が消失する透明サーフェイスのないテクセルに含まれる場合、明らかなアーティファクトが発生します。適切なフィルタリングを行うには、フィルタリングを行う前に正規化を元に戻す必要があります。我々の実装は、単精度浮動小数点を使用したものよりも遅い結果となりました。したがって、このコンテキストでは16ビット量子化を破棄しますが、特化したコンピュートシェーダが実用的になるはずであることに注意してください[Peters 2017]。
フラグメントをシェーディングするには、まず、通常通り、不透明なシャドウキャスターを通してフィルタリングされた透過率を計算します。次に、セクション3.2、4、5で説明したように、透明なシャドーキャスターを通した透過率の再構成を行います。両方の結果を組み合わせるために、後者の透過率はフィルター領域内で一定であると仮定します。この仮定の下では、適切な組み合わせ演算子は単純な乗算です。最後に、光からの入射放射照度にこの透過率積を乗じ、シェーディングを進めます。
不透明なシャドウキャスターの深度バッファを使用して透明なシャドウキャスターを破棄する場合、一定の透過率の仮定はすぐに破綻します。このため、不透明なシャドウキャスターのシルエットが透明なシャドウキャスターに影を落とすたびに、漏れが生じます。このアーティファクトは、透明シャドウキャスターに深度バッファを使用しないことで簡単に回避できます。
7 RESULTS
Direct3D 11.3を使用したフォーワードレンダラーで評価し,Adaptive transparency[Salviら2011],Multi-layer alpha blending[SalviとVaidyanathan 2014] およびWeighted blended OIT [McGuireとBavoil 2013] と比較しました。確定的なパイプライン順序が必要な場合は、ラスタライザオーダードビューを使用します。マルチレイヤアルファブレンドを含むすべての手法は、チャネルあたり16ビットのレンダーターゲットにカラーをレンダーします。Weighted blended OITの実装は現象学的透明性と同じ重み付け関数を使用します [McGuire and Mara 2017] 。
我々はFourier opacity mapping[Jansen and Bavoil 2010]と我々の影を比較しましたが、先行研究で品質が低いことが示されているため[Salvi et al.2010]、一次視認性にはこの手法は使いませんでした。モーメントベースのOITでは、常に\(\beta = 0.25\)の過大評価ウェイトを使用します。特に断りのない限り、64ビットのモーメントシャドウマップを使用して不透明シャドウをレンダリングし、224ビットに格納された6つのパワーモーメントを使用して透明シャドウをレンダリングします。シャドウマップの解像度は \(1024^2\) です。
7.1 Quality of OIT
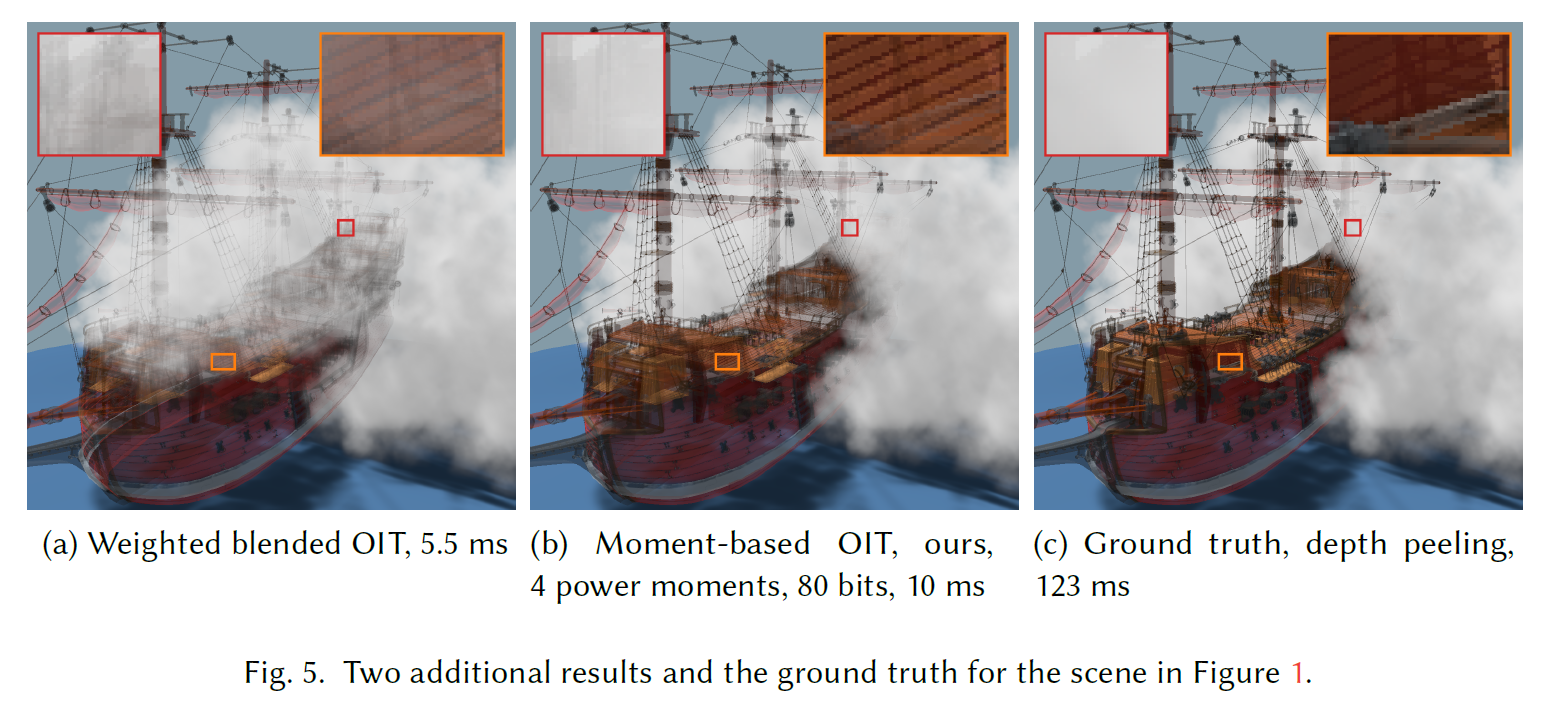
図1と図5は、大きなパーティクルクラウドと船の複雑な透明モデルを組み合わせた複雑なシーンで、選択したテクニックを比較したものです。パーティクルは単にカメラ指向のビルボードです。Multi-layer alpha blending[Salvi and Vaidyanathan 2014]は、船に対しては比較的うまく機能しますが、パーティクルを通した適切なオクルージョンを達成できず、パーティクルの境界に沿って不連続が生じます。すべてのパーティクルをソートし、船の後にレンダリングすることで、6つのレイヤーでうまく機能させることができます。Adaptive transparency[Salvi et al. 2011]の結果は悪く、ここでは示していません。Weighted blended OIT [McGuire and Bavoil 2013]は滑らかな結果をもたらしますが、霧と船の相互オクルージョンを正しく伝えることはできません。
我々のモーメントベースのOITは、オクルージョンをはるかに正確に捉えながら、滑らかな結果を生み出します。4つのパワーモーメントを使用した場合、結果は全体的にもっともらしいですが、いくつかのサーフェスは背景の近くのサーフェスによってオクルードされているように見えます。これは特にメインマスト周辺で顕著です。6つのパワーモーメントを使用すると、ほぼすべての場所でグランドトゥルースに近い結果が得られます。色が大きく異なるサーフェスが近い場所でのみ、若干の漏れがあります。単精度で保存された3つの三角モーメントを使用すると、これらの誤差はほとんどなくなります。我々の連続的に定義された再構成の優れた時間的安定性を示すために、補足ビデオにこのシーンのアニメーションを示します。
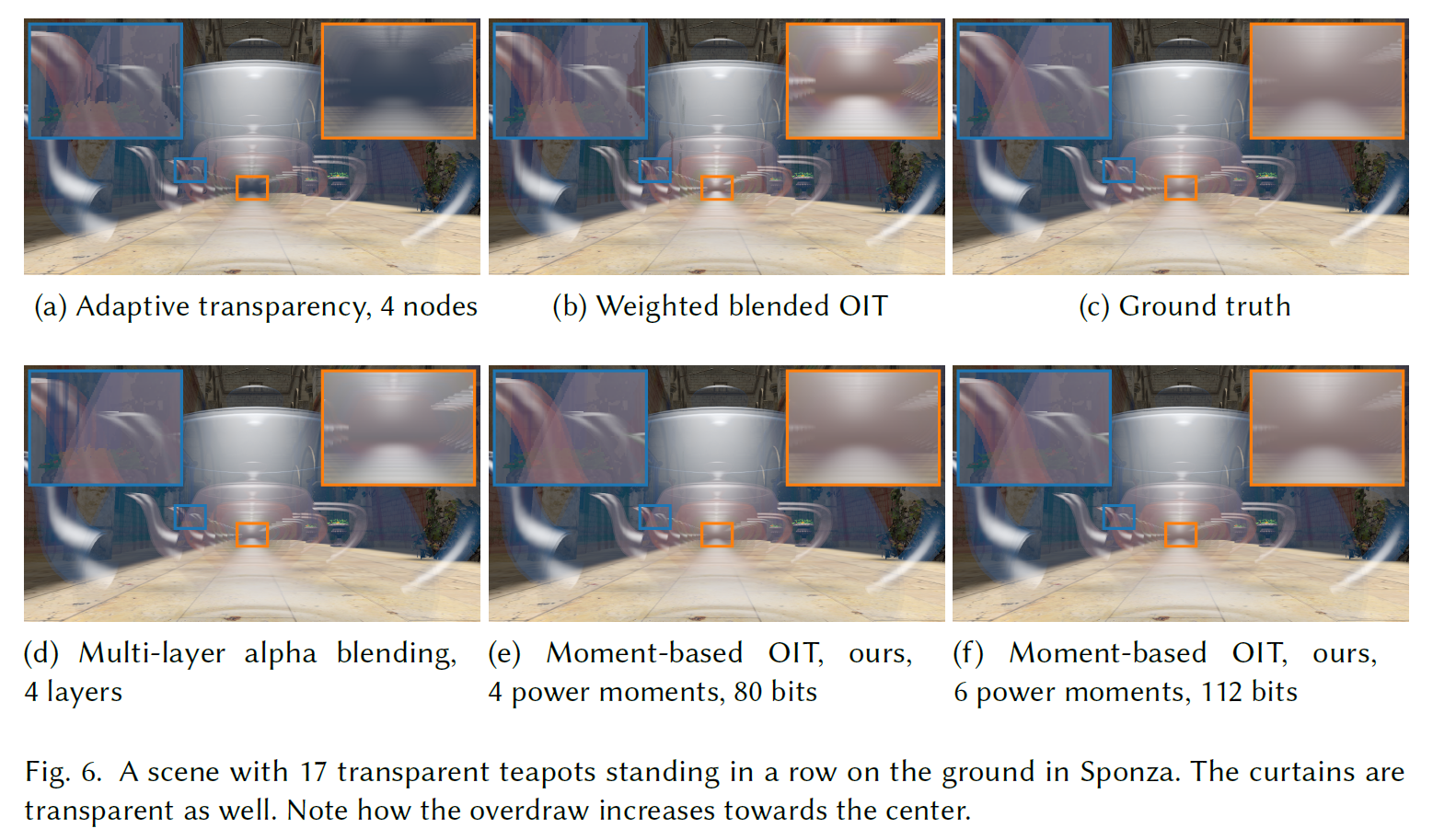
図6は難易度の低いテストケースです。Multi-layer alpha blendingは、カーテンが3つのティーポットによって不適切にオクルードされるいくつかのアーティファクトを除いて、うまく機能しています。Adaptive transparencyは同様のアーティファクトを共有しますが、さらに多くのティーポットが重なる中央領域では透過率を過小評価しています。Weighted blended OITは一般に、カーテンと一番後ろのティーポットが見えすぎてしまいます。4つのパワーモーメントを使ったモーメントベースのOITでは、カーテンの一部の可視性がわずかに過大評価されますが、結果は妥当です。6つのパワーモーメントを使うと、この状況はさらに改善されます。
図6では、葉にブレンドなしのアルファテストを使用しています。モーメントベースのOITを使用すると、図7に示すような失敗ケースが発生します。\(\beta=0.25\)の過大評価によって、葉の透明な部分が暗くなりすぎています。不透明な部分の次に、これは明らかなアーティファクトです。デフォルトでは、このアーチファクトを除去する式(2)の再正規化を使用します。しかし、誤差の一部が別の透明なサーフェイスに伝播してしまう可能性があります。Weighted blended OITは、同様のアーティファクトにつながる同様の再正規化を実行します。全体として、我々の手法は急速に変化するアルファマップには理想的ではありません。ハッシュ化アルファテストは、この場合に特化して設計されており、わずかなコストで介入することができます[Wyman and McGuire 2017]。
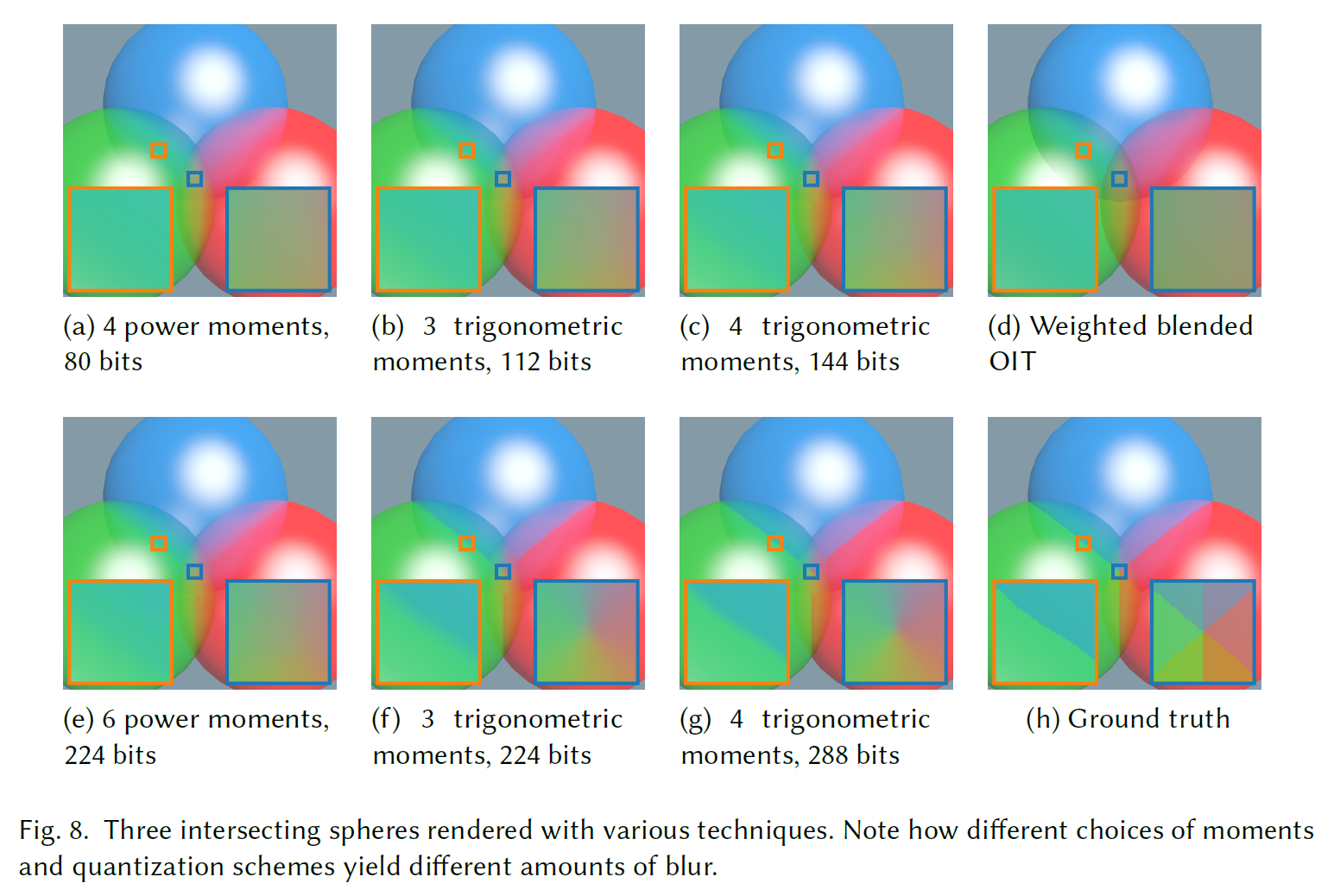
他の多くの手法とは異なり、我々のアプローチでは、透過率関数に不連続性をもたらす深度比較がありません。多くの場合、これは滑らかで安定した結果につながるため、利点となります。しかし、図8に示すように、交差する形状を扱う場合には問題になります。16ビットでモーメントを保存するすべての技法は、球が交差するシャープな線を生成できません。しかし、三角モーメントを使用するとシャープさが向上します。単精度浮動小数点に格納された4つの三角モーメントを使うと、2つの球の交点はシャープになりますが、この変形でも3つの球の交点はぼやけます。Weighted Blended OITはこのアーティファクトを共有しますが、2つのレイヤーを持つMulti-layer alpha blendingや、4つのノードを持つAdaptive Transparencyは完璧な結果を得ます。この例では、深度範囲を球の半径の10倍以上に人為的に拡大していることに注意してください。
7.2 Quality of Shadows
上に示したすべての結果と同様に、図1は、112ビットに格納された6つのパワーモーメントを持つモーメントベースのOITシャドウを透明シャドウに使用しています。パーティクル雲と影の組み合わせは単一散乱をもたらし、パーティクルはそれ自身を影にし、地面は予想通り部分的な影を受けます。若干のライトリークは発生しますが,透明な影の場合,Opaque shadows[McGuire and Mara 2017]よりも不快ではありません。
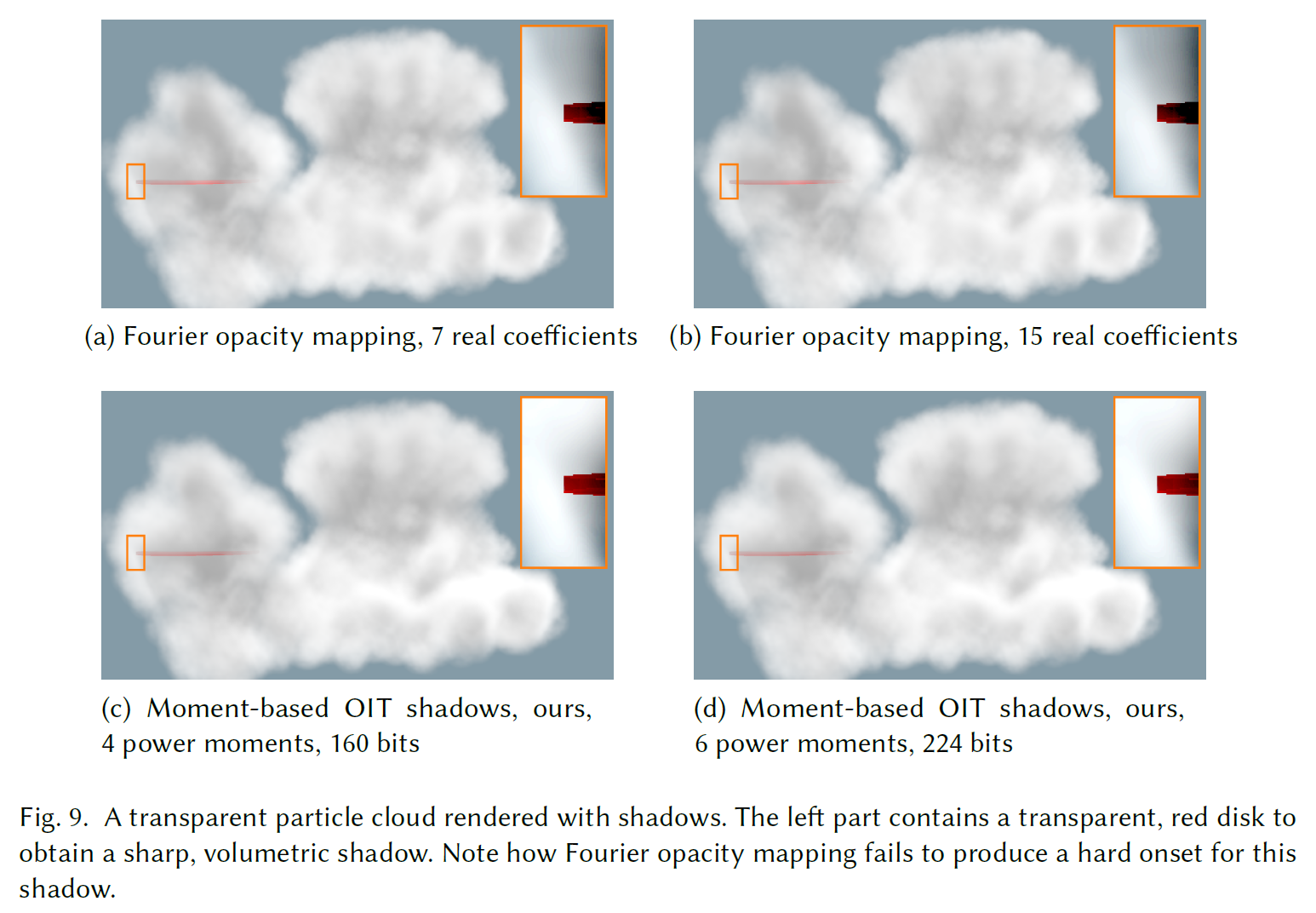
図9は、モーメントベースのOITシャドウに対する我々のアプローチと、Fourier opacity mapping[Jansen and Bavoil 2010]との比較です。我々の手法の他の結果は、透明なサーフェイス上の間違ったセルフシャドウイングを避けるために\(\beta=0\)を使用していますが、このシーンではより意味のある比較のために\(\beta=0.5\)を使用しています。全体的に、このシーンは深度範囲が小さく、透過率関数がパーティクル内で滑らかに変化しているため、Fourier opacity mappingの利点が発揮されています。それにもかかわらず、影はライト方向に沿って不鮮明になっています。直接光が当たっている雲の上部はすでにわずかに暗くなっています。この効果をより見やすくするために、雲の左部分に不透明度94%の赤い円盤を配置しました。モーメントベースのOITシャドウを使うと、シャドウは適度に硬いオンセットが得られますが、Fourier opacity mappingを使うと、シャドウはディスクの上にはっきりと見えます。
6つのパワーモーメントで誤ったセルフシャドウイングがわずかに減少したことを除けば、この例では、我々のテクニックの2つのバリエーションの結果は似ています。しかし、\(\beta=0\)の場合、4つのパワーモーメントを使用すると、透明なサーフェイスから生じる複雑な深度分布により、多くのリークが発生します。静止画像では、これらのアーティファクトを見つけるのは難しいですが、補足ビデオで示したように、アニメーションシーケンスでは明白になります。ロバスト性を向上させるために、6つのパワーモーメントを使用することを推奨します。単色シャドウのアーティファクトは、色がついたサーフェイスの OIT よりも目立ちにくいため、三角モーメントを使用するための余分なコストは正当化しにくいです。
7.3 Run Time
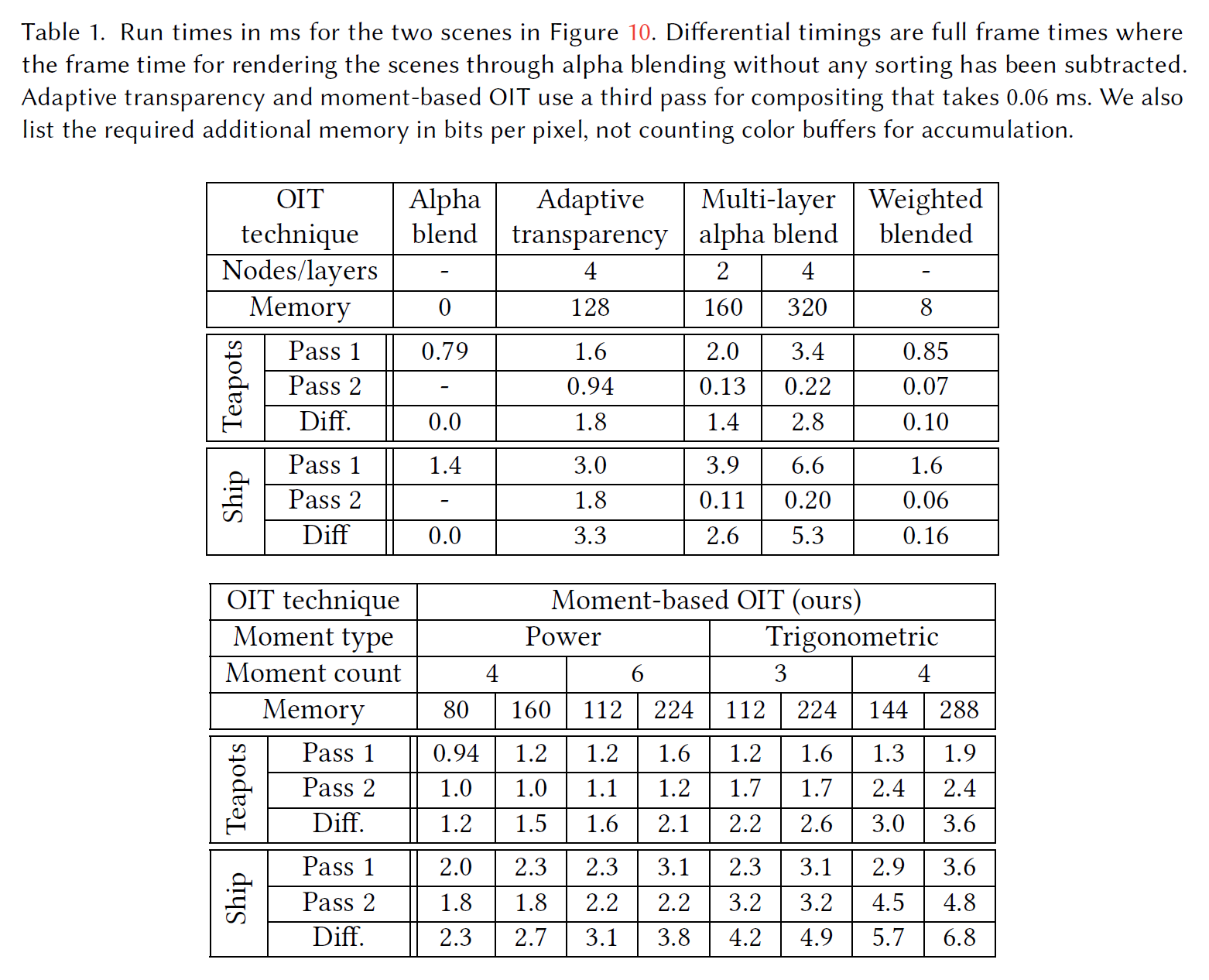
NVIDIA GeForce GTX 1080 TiとIntel Core i7-8700Kを搭載し、Windows 10を動作させたコンピュータで実行時間を測定しました。OIT テクニックを評価するために、ティーポットと、パーティクル雲を小さくした船のバージョンを使用します(図 10 を参照)。Adaptive transparencyとMulti-layer alpha blendingでは、良好な実行時間のためにメモリレイアウトが重要です。いくつかの実験の後、キャッシュのローカリティを向上させるために、モートンコードを通して\(16 \times 16\)タイル内のデータにインデックスを付けることにしました。これらのテクニックの深度値は、セクション3.3のワープされた深度を使用して、16ビットの固定小数点数で格納されます。表1に主な結果を示します。追加のタイミングは補足文書に記載されています。
4つのノードを持つAdaptive transparencyは、6つのパワーモーメントを持つモーメントベースOITよりも112ビットでわずかに多くかかります。4つのレイヤーを持つマルチレイヤーアルファブレンディングのタイミングは、224ビットで3つの三角モーメントを持つモーメントベースOITよりもわずかに長いです。2つのレイヤーの場合、実行時間は4つのパワーモーメントを持つ2つのバリエーションの中間となります。すべてのシーンに当てはまるわけではありませんが、3つのケースすべてにおいて、我々の技術は明らかに高い品質を提供します(図8など参照)。Weighted blended OITは、我々の全ての手法よりもかなり高速ですが、精度はかなり劣ります。
Multi-layer alpha blendingやweighted blended OITとは異なり、我々の技術は2回の透過パスを必要とすることに注意してください。我々の実装では、ジオメトリパイプライン全体が2回実行されます。このオーバーヘッドは、変換された頂点データを再利用することで削減できます。
我々の手法のバリエーションを比較すると、その実行時間は記載されている方法で完璧に保存されていることに気づきます。この進歩は、144ビットで保存された4つの三角モーメントを除いて、品質の向上とうまく一致しています。4つまたは6つのべき乗モーメント、あるいは3つの三角モーメントは賢明なトレードオフです。4つの三角モーメントを使用することによる品質の向上は比較的小さいので、追加コストを正当化するのは難しいかもしれません。補足文書では、8つのパワーモーメントを使用した場合の結果が、3つの三角モーメントに近いコストで、6つのパワーモーメントを使用した場合よりもわずかに優れていることを実証しています。
我々の技術のセカンドパスのタイミングは、使用する量子化に依存しないため、計算によって制限されるように見えます。このコストは、より多くのモーメントや三角モーメントを使用すると大幅に上昇します。一方、第1パスの所要時間は量子化に強く依存するため、帯域幅が制限されることが示唆されます。Adaptive transparencyの場合、2つ目のパスは比較的安価ですが、1つ目のパスは演算量が多いためコストが高くなります。
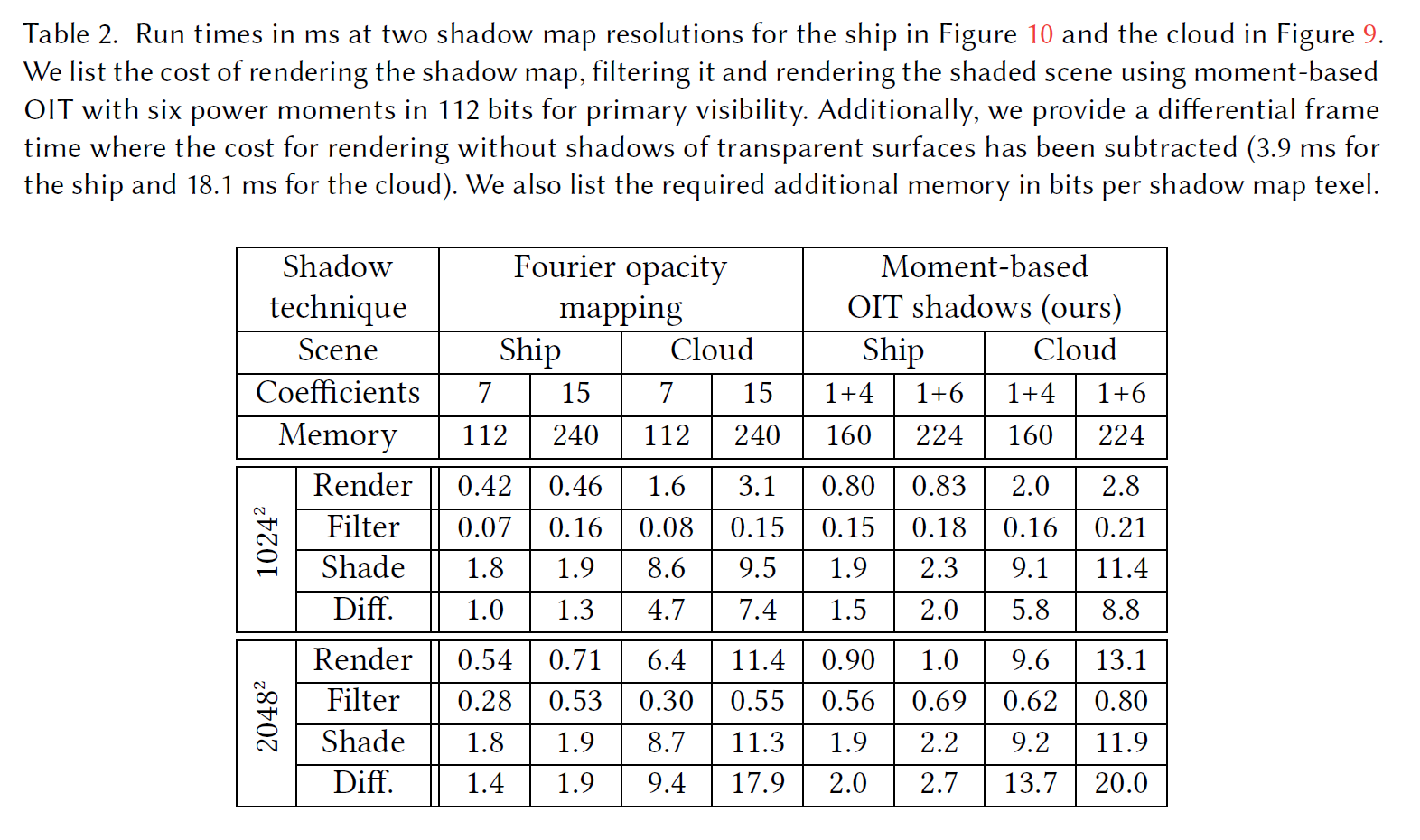
表2は、透明サーフェイスの影をレンダリングする際のフレーム時間です。Fourier opacity mappingは、7つの実係数で常に高速ですが、15係数を持つ変形は、多くの場合、4つまたは6つのパワーモーメントを持つ我々の技術の中間に位置します。帯域幅の使用量が少ないにもかかわらず、6つのパワーモーメントを持つシャドウマップの生成には、15個の係数を持つFourier opacity mappingよりも多くの時間がかかります。これは、テストしたハードウェアでは、半精度浮動小数点数と比較して、単精度浮動小数点数のスループットが低いためと思われます。シェーディングにかかるコストはモーメントベースのアプローチでわずかに高くなる傾向がありますが、これは演算負荷が大きくなることから予想されることです。しかし、上記の品質向上は、このコスト増を正当化するものです。
8 CONCLUSIONS
モーメントベースのOITは、興味深く有用な方法で既存のOIT技術を補完します。Weighted blended OITのように、完全に次数に依存せず、不透明度が滑らかな場合に滑らかな結果が得られます。しかし、ピクセルごとの透過率を表現するために実際のデータを使用するため、はるかに正確な結果が得られます。複雑な透明モデルと参加媒体を同時に扱う能力は、以前の技法とは比べものになりません。同時に、実行時間の点でも、これらの手法と競合することができます。GPUの計算能力がその帯域幅を凌駕する時代[Olsson et al. 2015]において、演算命令数が多いことは小さな懸念事項です。
モーメントには6つの選択肢があり、それぞれに2つの量子化スキームがあるため、多くのテクニックから選択することができます。4つのべき乗モーメントは、中程度の難易度のケースで問題なく安価な近似を提供しますが、単精度で保存された3つの三角モーメントは、最も困難なケースでさえも忠実に扱います(図1参照)。6つのパワーモーメントは、品質とコストの間の良いトレードオフを提供します。
結果の滑らかさが保証されているのは、透過率を連続的に表現しているからです。この特性は非常に望ましいですが、交差するジオメトリをレンダリングする能力に害を及ぼし、非常に大きな深度範囲を持つシーンでは問題になる可能性があります。対数で歪められた深度は、後者の問題に対する効果的な対策です。
影のための我々の新しい技術は、Fourier opacity mappingの品質を上回りますが、コストは増加します。将来的には、さらなる最適化を推し進めることができるでしょう。
ACKNOWLEDGMENTS
Micheal Weinmannのフィードバックと評価への協力に感謝したい。また 船の模型はGreg Zaal氏とChris Kuhn氏のご厚意によるものです。ティーポットのシーンは、Marko Dabrovic氏によってモデル化され、Frank Meinl氏によって改良されたAtrium Sponza Palaceを使用しています。