ども。Pocolです。
今日は,
[Garland 1997] Michael Garland, Paul S.Heckbert, “Surface Simplification Using Quadric Error Metrics”, SIGGRAPH 1997, pp.209-216.
を読んでみようと思います。
いつもながら誤字・誤訳があるかと思いますので,ご指摘頂ける場合は正しい翻訳例と共に指摘して頂けるとありがたいです。
Abstract
コンピュータグラフィックスの分野では、複雑で高精細なモデルを必要とするアプリケーションが多くあります。しかし、実際に必要とされる詳細度レベルは、かなり異なるものです。処理時間をコントロールするために、過度に詳細なモデルの代わりに近似値を使用することが望ましい場合があります。
我々は、ポリゴンモデルの高品質な近似値を素早く生成するサーフェイス簡略化アルゴリズムを開発しました。このアルゴリズムは、頂点ペアの反復的な縮約を用いてモデルを簡略化し、二次行列を用いてサーフェス誤差の近似値を維持します。このアルゴリズムでは、エッジだけでなく任意の頂点ペアを収縮させることで、モデルの未接続領域を結合することができます。これにより、視覚的にも幾何学的誤差に関しても、より優れた近似が可能になります。また、トポロジカルな結合を可能にするために、本システムは非多様体のサーフェイスモデルもサポートしています。
1 Introduction
コンピュートグラフィックスのアプリケーションの多くは、説得力を維持するために複雑で高精細なモデルを必要としたり、この必要性に対応するために非常に高い解像度で取得されます。しかし、複雑なモデルが必要とされる場合は少なく、また、モデルの計算コストはその複雑さに比例するため、複雑なモデルをよりシンプルにしたものがあると便利です。当然のことながら、我々はこの簡略化されたモデルを自動的に作成したいと考えています。最近のサーフェス簡略化アルゴリズムの研究は、この目標に焦点を当てています。
この分野の他の多くの研究と同様に、ここでは多角形モデルの簡略化に焦点を当てます。ここでは、モデルが三角形のみで構成されていると仮定します。元のモデルのすべてのポリゴンは、前処理の一部として三角形にすることができるので、これは一般性の損失を意味しません。より信頼性の高い結果を得るためには、2つの面の角がある点で交差する場合、その面は、たまたま空間的に一致した2つの別々の頂点を使用するのではなく、1つの頂点を共有するものとして定義されるべきです。
我々は、このようなポリゴンモデルを簡略化して作成するアルゴリズムを開発しました。このアルゴリズムは、頂点ペアの反復的な縮退(エッジ縮退の一般化)に基づいています。アルゴリズムが進行すると、現在のモデルの各頂点で幾何学的な誤差近似が維持されます。この誤差近似は、二次行列を用いて表現されます。我々のアルゴリズムの主な利点は以下の通りです。
- 効率性:このアルゴリズムは、複雑なモデルを非常に高速に単純化することができます。例えば、私たちの実装では、70000個の面を持つモデルから100個の面を持つ近似モデルを15秒で作成することができます。また,この誤差近似は非常にコンパクトで,1つの頂点につき10個の浮動小数点数しか必要としません.
- 品質: このアルゴリズムで生成された近似値は、元のモデルに高い忠実性を保っています。大幅に単純化しても、モデルの主要な特徴は維持されています。
- 普遍性:他の多くのサーフェス簡略化アルゴリズムとは異なり、我々のアルゴリズムは、モデルの連結されていない領域を結合することができます。オブジェクトのトポロジーを維持することが重要でない場合には、これにより、多くの切断されたコンポーネントを持つモデルの近似が容易になります。このためには、我々のアルゴリズムが非多様体モデルをサポートする必要がある。
2 Background and Related Work
ポリゴンサーフェイスの簡略化の目的は、ポリゴンモデルを入力とし、簡略化されたモデル(すなわち元のモデルの近似値)を出力として生成することです。ここでは、入力モデル(\(M_n\)が三角形化されていると仮定します。目標とする近似値(\(M_g\))は、望ましい面数または最大許容誤差のいずれかである与えられた目標基準を満たします。我々が興味を持っているのは、多解像度モデリング(現在の状況に応じて適切なレベルの詳細を持つモデルを生成すること)のためのレンダリングシステムで使用可能な、サーフェイス簡略化アルゴリズムです。
モデルのトポロジーが維持されなければならないとは考えていません。しかし、医用画像などの特定のアプリケーション分野では、オブジェクトのトポロジーを維持することが不可欠な場合があります。しかし、レンダリングのようなアプリケーション分野では、トポロジーは全体的な外観よりも重要ではありません。我々のアルゴリズムは、トポロジーの穴を塞ぐだけでなく、つながっていない領域を結合することもできます。
これまでの多くの簡略化アルゴリズムは、暗黙のうちに、あるいは明示的に、入力サーフェスが多様体サーフェスであることを前提としていましたが、現在ではそのようなことはありません。しかし、我々はこのような仮定をしていないことを強調しておきたいです。実際には、集約の過程で非多様体の領域が生じることはよくあることです。
2.1 Surface Simplification
近年、サーフェスの単純化の問題、さらには多解像度モデリングの問題が注目されています。サーフェスを単純化するために、いくつかの異なるアルゴリズムが策定されています。私たちの研究に最も関係のあるアルゴリズムは、大きく3つのクラスに分類されます。
Vertex Decimation.
Schroederら[9]は、頂点デシメーションと呼ばれるアルゴリズムを説明しています。彼らの手法は、除去すべき頂点を繰り返し選択し、隣接するすべての面を除去し、結果として生じる穴を再三角形化します。Soucy と Laurendeau [10]は、より洗練された、しかし本質的には同様のアルゴリズムを記述しました。これらの手法は適度な効率と品質を提供しますが、我々の目的にはあまり適していません。どちらの手法も、頂点の分類と再三角形化のスキームを使用していますが、これは本質的に多様体表面に限定されており、モデルのトポロジーを慎重に維持しています。これらは一部の領域では重要な機能ですが、マルチレゾリューションレンダリングシステムでは制限があります。
Vertex Clustering.
RossignacとBorrel[8]のアルゴリズムは、任意の多角形の入力を処理できる数少ないアルゴリズムの一つです。元のモデルの周りにバウンディングボックスを配置し、グリッドに分割します。各セル内では,そのセルの頂点が1つの頂点にまとめられ,それに応じてモデルの面が更新されます。このプロセスは非常に高速であり、モデルのトポロジーを劇的に変化させることができます。しかし、グリッドセルの大きさによって幾何学的な誤差を抑えることができますが、出力の質は非常に低いものになります。さらに、面の数は指定されたグリッドの寸法によって間接的に決定されるだけなので、特定の面の数を持つ近似式を構築することは困難です。また、生成される正確な近似値は、周囲のグリッドに対する元のモデルの正確な位置と向きに依存します。この画一的な手法は、オクツリーなどの適応的なグリッド構造を使用するように簡単に一般化できます[6]。これにより、簡略化の結果を改善することができますが、私たちが望む品質と制御にはまだ対応していません。
Iterative Edge Contraction.
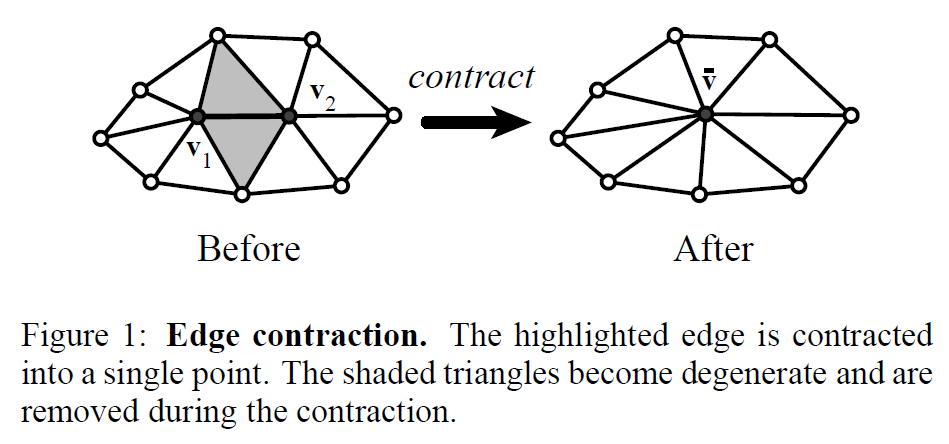
エッジを反復的に収縮させることでモデルを単純化するアルゴリズムがいくつか発表されています(図1参照)。これらのアルゴリズムの本質的な違いは、収縮させるエッジの選択方法にあります。Hoppe [4, 3],Ronfard と Rossignac [7], Gueziec [2]などのアルゴリズムが有名です。これらのアルゴリズムは、いずれも多様体表面での使用を想定して設計されているようですが,エッジ収縮は非多様体表面でも利用可能です。辺の収縮を連続して行うことで、物体の穴を塞ぐことはできますが、連結していない領域を結合することはできません。
近似モデルが元のモデルからある程度の距離に収まり、そのトポロジーが変わらないことが重要な場合は、Cohenら[1]の簡略化エンベロープ法と上記の簡略化アルゴリズムのいずれかを併用することができます。モデルに加えられる修正がエンベロープ内に収まるように制限されている限り、グローバルエラー保証を維持することができます。しかし、この方法は強力な誤差制限を提供する一方で、本質的に配向可能な多様体表面に限定されており、モデルのトポロジーを慎重に保存します。繰り返しになりますが、これらは多くの場合、レンダリングを単純化する目的での制限です。
これまでに開発されたこれらのアルゴリズムは、私たちが求める効率、品質、汎用性を兼ね備えたものではありません。頂点デシメーションアルゴリズムは、モデルのトポロジーを維持することに注意を払い、通常は多様体のジオメトリを想定しているため、我々のニーズには適していません。頂点クラスタリングアルゴリズムは非常に一般的であり、非常に高速です。しかし、これらのアルゴリズムは、結果の制御が不十分であり、結果はかなり低い品質になる可能性があります。エッジ収縮アルゴリズムは集約をサポートしません。
私たちは、集約と高品質な近似の両方をサポートするアルゴリズムを開発しました。このアルゴリズムは、頂点クラスタリングの一般性と、反復型縮退アルゴリズムの品質と制御性の両方を備えています。また、いくつかの高品質な手法よりも高速に簡略化することができます[3]。
3 Decimation via Pair Contraction
我々の簡略化アルゴリズムは、頂点ペアの反復的な収縮に基づいており、以前の研究で使用されたインタラクティブなエッジ収縮技術を一般化したものです。ペア収縮は、\(({\mathbf v}_1, {\mathbf v}_2) \rightarrow {\bar {\mathbf v}}\)と書きますが、頂点\({\mathbf v}_1\)と\({\mathbf v}_2\)を新しい位置\({\bar {\mathbf v}}\)に移動させ、それらのすべての入力エッジを\({\mathbf v}_1\)に接続し、頂点\({\mathbf v}_2\)を削除します。その後、縮退したエッジや面を取り除きます。縮退の効果は小さく、非常に局所的なものです。\(({\mathbf v}_1, {\mathbf v}_2)\)がエッジであれば、1つ以上の面が削除されます(図1参照)。それ以外の場合は、モデルの2つの独立したセクションが\({\bar {\mathbf v}}\)で結合されます(図2参照)。
この収縮の概念は実際には非常に一般的で、頂点のセットを単一の頂点\(({\mathbf v}_1, {\mathbf v}_2, \cdots, {\mathbf v}_k) \rightarrow {\bar {\mathbf v}}\)に収縮させます。この一般化された縮退の形式は、ペアの縮退だけでなく、頂点のクラスタリングのようなより一般的な操作も表現できます。しかし、我々はペア収縮をアルゴリズムのアトミックな操作として使用しています。
初期モデル\(M_n\)から始まり、単純化の目標が満たされるまで、一連のペア収縮が適用され、最終的な近似値\(M_g\)が生成されます。各収縮は現在のモデルの局所的な増分修正に対応するため、このアルゴリズムは実際には一連のモデル\(M_n, M_{n-1}, \cdots, M_g\)を生成します。そのため,1回の実行で,多数の近似モデルや,プログレッシブメッシュなどの多重解像度表現を生成することができます[3]。
3.1 Aggregation
一般的な頂点ペア収縮を利用することで得られる主な利点は、モデルの以前は接続されていなかった領域を結合するアルゴリズムの能力です。副次的な利点としては、元のモデルのメッシュの接続性に対するアルゴリズムの影響が少なくなることが挙げられます。実際に2つの面が重複している頂点で出会う場合、その頂点ペアの収縮は、初期メッシュの欠点を修復します。
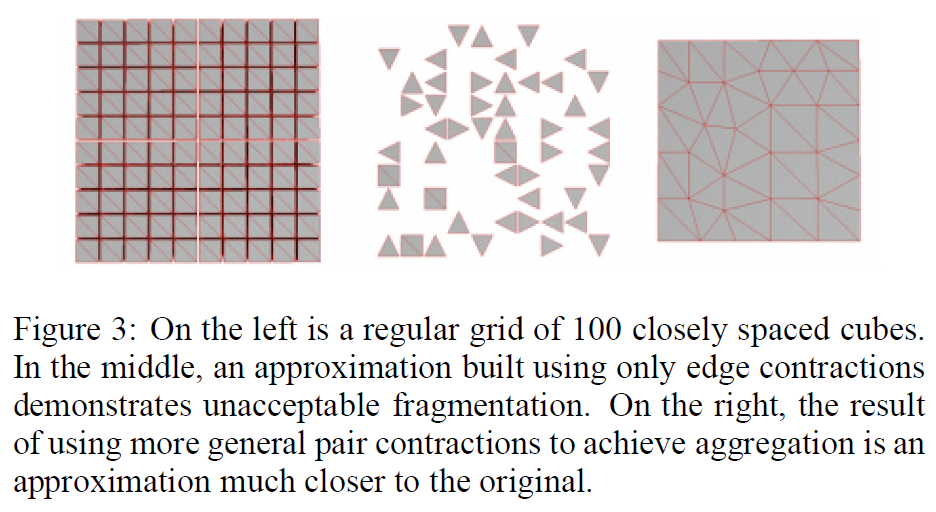
レンダリングなどの用途では、全体の形状よりもトポロジーが重要でない場合もあります。図3のように、100個の立方体を規則的なグリッドに配置した形状を考えてみましょう。左側のモデルの近似モデルを作成して、遠くからのレンダリングを行いたいとします。辺の収縮を利用したアルゴリズムは、オブジェクトの穴を塞ぐことはできますが、切断されたコンポーネントを結合することはできません。辺の縮退のみを利用したアルゴリズムでは、中央のモデルのように、個々の構成要素が個々に単純化されて何もない状態になります。ペア収縮を用いれば、右のモデルのように、個々のコンポーネントを1つのオブジェクトに統合することができます。その結果、より忠実な近似値が得られます。
集約を可能にするためには、非多様体の表面をサポートする必要があります。2つの別々の領域が結合される瞬間に、非多様体の領域がかなりの確率で作られます。実行できる収縮の種類を大幅に制限することなく、収縮によって非多様体領域が作られないようにするには、多大な注意と努力が必要です。
3.2 Pair Selection
ここでは、初期化時に有効なペアのセットを選択し、アルゴリズムの実行中はこれらのペアのみを考慮することにしました。この決定は、良好な近似では、点は元の位置から遠くに移動しないという仮定に基づいています。
ここでは、次のいずれかの場合に、ペア\(({\mathbf v}_1, {\mathbf v}_2)\)が縮退に有効なペアであると言います。
- \(({\mathbf v}_1, {\mathbf v}_2)\)はエッジである。
- \(|| {\mathbf v}_1 – {\mathbf v}_2 || \lt t\)とする。ただし,\(t\)は閾値パラメータとします。
閾値を\(t=0\)とすることで、シンプルなエッジ収縮アルゴリズムが得られます。より高い閾値では、非連結の頂点をペアにすることができます。この閾値が高すぎると、モデルの大きく離れた部分が接続されてしまう可能性があり、これはおそらく望ましくないことで、\(O(n^2)\)個のペアを作ることになります。
反復収縮の過程で、有効なペアのセットを追跡する必要があります。各頂点には、その頂点がメンバーであるペアのセットを関連付けます。縮退\( ({\mathbf v}_1, {\mathbf v}_2) \rightarrow {\bar {\mathbf v}}\)を実行すると、\({\mathbf v}_1\)は\({\mathbf v}_2\)にリンクしていたすべてのエッジを獲得するだけでなく、\({\mathbf v}_2\)からのペアのセットを自分のセットにマージします。有効なペアの\({\mathbf v}_2\)のすべての出現は、\({\mathbf v}_1\)に置き換えられ、重複するペアは削除されます。
4 Approximating Error With Quadrics
あるイテレーションで実行する縮退を選択するためには、縮退のコストに関する何らかの概念が必要です。このコストを定義するために、各頂点でのエラーを特徴づけることを試みます。これを行うために、各頂点に対称的な\(4 \times 4\)の行列\({\mathbf Q}\)を関連付け、頂点\({\mathbf v} = \begin{bmatrix} v_x & v_y & v_z & 1\end{bmatrix}^{\top}\)での誤差を二次形式の\(\Delta({\mathbf v}) = {\mathbf v}^{\top} {\mathbf Q} {\mathbf v}\)と定義します。セクション5では、初期行列の構築方法について説明します。なお、\({\mathbf Q}\)に対する誤差が\(\epsilon\)となるすべての点の集合である水準面\(\Delta({\mathbf v}) = \epsilon\)は、二次曲面であることに注意してください。
与えられた収縮\(({\mathbf v}_1, {\mathbf v}_2) \rightarrow {\bar {\mathbf v}}\)に対して、\({\bar {\mathbf v}}\)での誤差を近似する新しい行列\({\bar {\mathbf Q}}\)を導出しなければなりません。ここでは、単純な加法規則\({\bar {\mathbf Q}} = {\mathbf Q}_1 + {\mathbf Q}_2\)を使用することにしました。
縮退\({\bar {\mathbf v}}\)を行うためには、\({\bar {\mathbf v}}\)の位置も選ばなければなりません。単純に考えれば、\({\mathbf v}_1\)、\({\mathbf v}_2\)、\(({\mathbf v}_1 + {\mathbf v}_2)/2\)のうち、\(\Delta({\bar {\mathbf v}})\)の値が最も小さくなるものを選択すればよいです。誤差関数\(\Delta\)2次関数なので、その最小値を求めることは線形問題となりますが、\(\Delta({\bar {\mathbf v}})\)を最小化する\({\bar {\mathbf v}}\)の位置を見つけることができればよいと思います。そこで、\(\partial \Delta/ \partial x = \partial \Delta / \partial y = \partial \Delta / \partial z = 0\)を解くことで\({\bar {\mathbf v}}\)を求めます。これは次を\({\bar {\mathbf v}}\)について解くことと同じです:
\begin{eqnarray}
\begin{bmatrix}
q_{11} & q_{12} & q_{13} & q_{14} \\
q_{12} & q_{22} & q_{23} & q_{24} \\
q_{13} & q_{23} & q_{33} & q_{34} \\
0 & 0 & 0 & 1
\end{bmatrix} {\bar {\mathbf v}} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix}
\end{eqnarray}
\({\bar {\mathbf v}}\)は同次ベクトルであり、\(w\)成分は常に1であるため、行列の最下行は空です。この行列が可逆であると仮定すると、次のようになります。
\begin{eqnarray}
{\bar {\mathbf v}} = \begin{bmatrix}
q_{11} & q_{12} & q_{13} & q_{14} \\
q_{12} & q_{22} & q_{23} & q_{24} \\
q_{13} & q_{23} & q_{33} & q_{33} \\
0 & 0 & 0 & 1 \end{bmatrix}^{-1} \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix} \tag{1}
\end{eqnarray}
この行列が可逆でない場合は、セグメント\({\mathbf v}_1 {\mathbf v}_2\)に沿って最適な頂点を見つけるのを試みます。これも失敗した場合は、端点と中点の中から\({\bar {\mathbf v}}\)を選ぶことになります。
4.1 Algorithm Summary
我々の簡略化アルゴリズムは、ペア収縮と2次関数誤差に基づいて構築されています。現在の実装では、隣接グラフ構造を用いてモデルを表現しています。つまり、頂点、辺、面はすべて明示的に表現され、互いにリンクされています。有効なペアのセットを追跡するために、各頂点は自分がメンバーとなっているペアのリストを保持しています。アルゴリズム自体は以下のように簡単にまとめられます。
- 初期頂点すべてに対して\({\mathbf Q}\)行列を計算します。
- 有効なペアすべてを選択します
- 有効なペア\(({\mathbf v}_1, {\mathbf v}_2)\)ごとに、最適な縮退目標\({\bar {\mathbf v}}\)を計算します。この対象となる頂点の誤差\({\bar {\mathbf v}}^{\top}({\mathbf Q}_1 + {\mathbf Q}_2) {\bar {\mathbf v}}\)は、そのペアを収縮するためのコストになります。
- すべてのペアを、コストをキーにしたヒープに配置し、最小コストのペアを一番上にします。
- コストが最も低いペア\(({\mathbf v}_1, {\mathbf v}_2)\)をヒープから繰り返し削除し、このペアを収縮させ、\({\mathbf v}_1\)を含むすべての有効なペアのコストを更新します。
唯一残された課題は、誤差指標\(\Delta\)を構築するための初期の\({\mathbf Q}\)行列をどのように計算するかということです。
5 Deriving Error Quadrics
2次関数誤差を構築するためには、幾何学的エラーを特徴づけるヒューリスティックな手法を選択する必要があります。ここでは、Ronfard and Rossignac [7]が示したものとよく似たヒューリスティックを選択しました。[7]によると、オリジナルのモデルでは、各頂点は平面のセットの交点の解であることがわかります。つまり、その頂点で出会う三角形の平面です。各頂点に平面のセットを関連付けることができ、このセットに対する頂点の誤差を、その平面への二乗距離の合計として定義することができます:
\begin{eqnarray}
\Delta({\mathbf v}) = \Delta( \begin{bmatrix} v_x & v_y & v_z & 1\end{bmatrix}^{\top}) = \sum_{{\mathbf p} \in {\rm planes}({\mathbf v})} ({\mathbf p}^{\top} {\mathbf v})^2 \tag{2}
\end{eqnarray}
ここで、pは方程式\(ax + by + cz + d = 0\)で定義される平面を表します。ただし,\(a^2 + b^2 + c^2 = 1\)とします。この近似誤差指標は[7]と似ていますが、平面の集合に対する最大値ではなく、総和を使用しています。ある頂点の平面のセットは、その頂点であう三角形の平面であるように初期化されます。なお、[7]のように、これらの平面集合を明示的に追跡する場合は、次のルールを用いて収縮\(({\mathbf v}_1, {\mathbf v}_2) \rightarrow {\bar {\mathbf v}}\)の後に平面を伝播させることになります:\({\rm planes}({\bar {\mathbf v}}) = {\rm planes}({\mathbf v}_1) \cup {\rm planes}({\mathbf v}_2)\)。そのため、膨大な量のストレージが必要になりますが、簡素化が進んでもその量は減りません。
(2)で与えられた誤差指標は、二次形式として書き換えることができます。
\begin{eqnarray}
\Delta({\mathbf v}) &=& \sum_{{\mathbf p} \in {\rm planes}({\mathbf v})} ({\mathbf v}^{\top} {\mathbf p})({\mathbf p}^{\top} {\mathbf v}) \\
&=& \sum_{{\mathbf p} \in {\rm planes}({\mathbf v})} {\mathbf v}^{\top}({\mathbf p}{\mathbf p}^{\top}) {\mathbf v} \\
&=& {\mathbf v}^{\top} \left( \sum_{{\mathbf p} \in {\rm planes}({\mathbf v})} {\mathbf K}_{\mathbf p} {\mathbf v} \right)
\end{eqnarray}
ここで,\({\mathbf K}_{\mathbf p}\)は行列で次のようになります:
\begin{eqnarray}
{\mathbf K}_{\mathbf p} = {\mathbf p}{\mathbf p}^{\top} = \begin{bmatrix} a^2 & ab & ac & ad \\
ab & b^2 & bc & bd \\
ac & bc & c^2 & cd \\
ad & bd & cd & d^2 \end{bmatrix}
\end{eqnarray}
この基本2次関数誤差\({\mathbf K}_{\mathbf p}\)は、空間上の任意の点から平面\({\mathbf p}\)までの二乗距離を求めるのに使用することができます。これらの基本二次式をまとめて、平面の全体像を1つのマトリック\({\mathbf Q}\)で表すことができます。
和集合(\({\rm planes}({\mathbf v}_1) \cup {\rm planes}({\mathbf v}_2)\))を計算する代わりに、2つの2次形式(\({\mathbf Q}_1 + {\mathbf Q}_2)\)を加算するだけです。元のメトリックの\({\mathbf Q}_1\)と\({\mathbf Q}_2\)で表される集合が不連続である場合、二次関数の加算は集合の結合と同等です。多少の重なりがある場合は、1つの平面を複数回カウントすることができます。しかし、各平面は最初はその定義三角形の頂点にのみ分布しているので、1つの平面は最大3回まで数えることができます。この方法は,誤差の測定に多少の不正確さをもたらすかもしれませんが,大きな利点があります。平面集合を追跡するために必要なスペースは,\(4 \times 4\)対称行列(10個の浮動小数点数)に必要なスペースだけであり,近似値を更新するためのコストは,そのような行列を2つ追加するためのコストだけです。多少のストレージの追加を犠牲にしても構わないのであれば、包含-排除式を用いてこの多重カウントを排除することも可能です。
したがって、ペア収縮アルゴリズムに必要な初期\({\mathbf Q}\)行列を計算するためには、各頂点がその頂点で一致する三角形の平面を蓄積する必要があります。各頂点について、この平面のセットは、いくつかの基本的な2次関数誤差\({\mathbf K}_{\mathbf p}\)を定義します。この頂点の2次関数誤差\({\mathbf Q}\)は、基本的な2次関数の合計です。各頂点の初期誤差推定値は0であることに注意してください。なぜなら、各頂点は、その頂点に入射するすべての三角形の平面内にあるからです。
5.1 Geometric Interpretation
これからわかるように、この平面ベースの2次関数誤差は、かなり高品質の近似値を生成します。さらに、これらは幾何学的な意味を持っています。
これらの四角形の水平面は、ほとんどの場合、楕円体です。場合によっては退化していることもあります。例えば、平行な平面(例えば、平面状の表面領域の周り)は、2つの平行な平面であるレベル・サーフェイスを生成し、すべてが直線に平行な平面(例えば、直線状の表面のしわの周り)は、円筒状のレベル・サーフェイスを生成します。最適な頂点の位置を求めるための行列(式1)は、水準面が非縮退楕円体である限り、可逆です。この場合、\({\bar {\mathbf v}}\)は楕円体の中心に位置することになります。
6 Additional Details
これまでに紹介した一般的なアルゴリズムは、ほとんどのモデルで良好な性能を発揮します。しかし、いくつかの重要な改良点があり、特定のタイプのモデル、特にオープンな境界を持つ平面モデルでの性能を向上させることができます。
Preserving Boundaries.
前述の2次関数誤差では,開境界を考慮していません。テレインハイトフィールドのようなモデルでは、境界曲線を保存しつつ、その形状を単純化する必要があります。また、離散的な色の不連続性を保持したい場合もあります。このような場合には、最初に各エッジに法線または「不連続」のいずれかのラベルを付けます。特定の不連続なエッジを囲む各面に対して、そのエッジを通る垂直面を生成します。そして,これらの拘束面を2次関数に変換し,大きなペナルティファクターで重み付けして,エッジの端点の初期2次関数に追加します.これは非常に効果的であることがわかりました。
Preventing Mesh Inversion.
ペアの収縮では、収縮した部分の面の向きは必ずしも維持されません。例えば、エッジを収縮させると、隣接する面が互いに折り重なってしまうことがあります。通常、このようなメッシュの反転は避けた方がよいでしょう。ここでは、他の研究者が行っているのと基本的に同じ方式を採用しています([7]など)。収縮の可能性を検討する際には、収縮前と収縮後の各隣接面の法線を比較します。もし法線が反転した場合、その収縮は大きなペナルティを課すか、あるいは許可しないことができます。
6.1 Evaluating Approximations
このアルゴリズムで生成された近似値の品質を評価するためには、アルゴリズム自体が採用しているヒューリスティックな誤差測定よりも、もう少し厳密な誤差測定が必要です。ここでは、近似値とオリジナルモデルの間の平均二乗距離を測定する指標を選択しました。これは、Hoppeら[4]が使用した\(E_{dist}\)エネルギー項と非常によく似ています。我々は、簡略化されたモデル\(M_i\)の近似誤差\(E_i = E(M_n, M_i)\)を次のように定義します・
\begin{eqnarray}
E_i = \frac{1}{|X_n| + |X_i|} \left( \sum_{v \in X_n} d^2 (v, M_i) + \sum_{v \in X_i} d^2 (v, M_n) \right)
\end{eqnarray}
ここで、\(X_n\)と\(X_i\)は、それぞれモデル\(M_n\)と\(M_i\)上でサンプリングされた点の集合です。距離\(d(v, M) = {\rm min}_{p \in M} || v – p ||\)は、\(v\)から\(M\)の最も近い面までの最小距離です( \(|| \cdot ||\)は通常のユークリッドベクトル距離操作です)。この指標は、評価のためだけに使用しており、実際のアルゴリズムには関与していません。
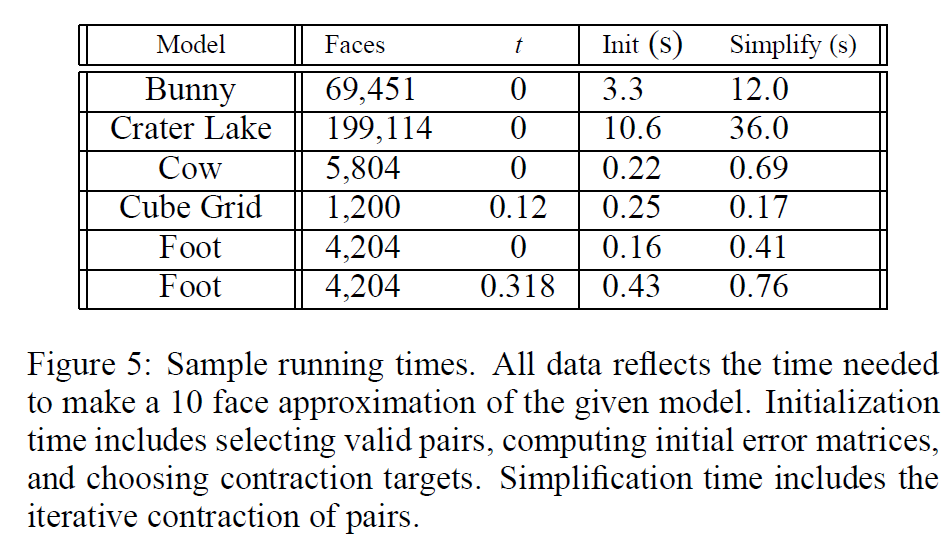
7 Results
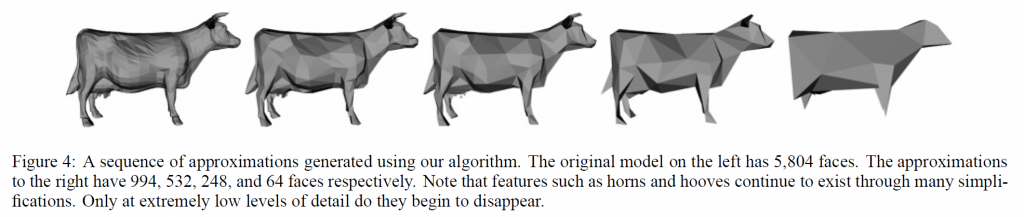
私たちのアルゴリズムは、高忠実度の近似値をかなり短い時間で生成することができます。図5は、本稿で紹介したモデルを用いた現在の実装の実行時間をまとめたものです。図4は,我々のアルゴリズムによって生成された近似値のシーケンスの例です.この一連の牛の隊列は、約1秒で構築されました。角やひづめなどの特徴は、多くの簡略化を経ても認識可能であることに注目してください。極めて低いLODでのみ、これらの特徴が消えていきます。
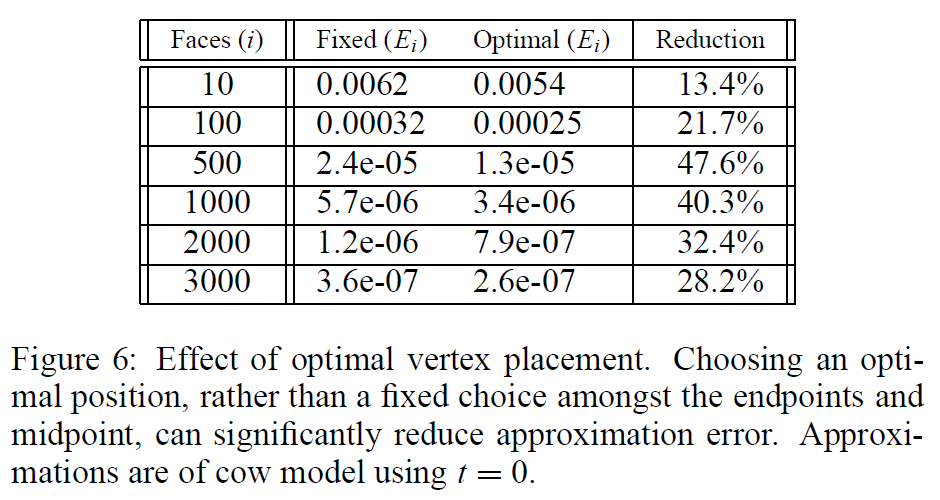
前述したように、我々のアルゴリズムは収縮後の頂点の配置を最適化しようとします。図6は、代表的なモデル(図4の牛のモデル)の近似値に対するこの方針の効果をまとめたものです。非常に低いLODでは、その効果はわずかなものです。頂点の配置を最適化することで、全体的な誤差を50%程度まで減らすことができます。また、実験では、最適な頂点配置を行うことで、より形状の整ったメッシュが得られる傾向があることもわかりました。
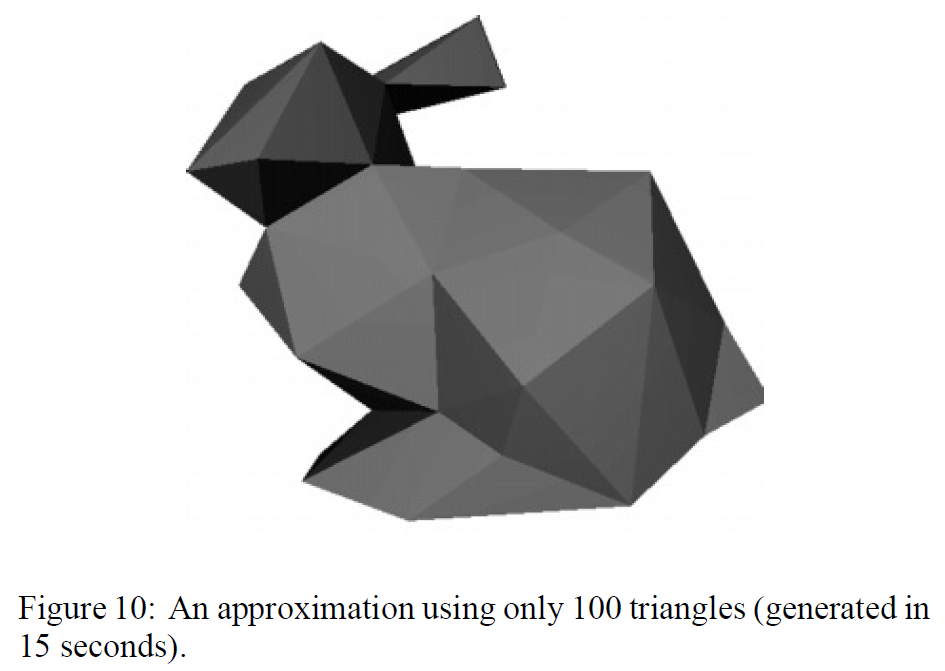
図8-13は、より大規模なモデルに対する我々のアルゴリズムの性能を示しています。図9は、元のモデルを大幅に単純化(1.4%)したものですが、元のモデルの主要な部分はすべて残っていることに注目してください。特に、耳の内側の輪郭と、実際の脚の周りの大きな輪郭が維持されていることに注目してください。図10は、さらに大幅に近似したものです。100面、オリジナルサイズの0.14%です。モデルの細部はほとんど失われていますが、物体の基本的な構造は損なわれていません。頭、脚、尻尾、耳などの主要な特徴は、非常に単純化されてはいるものの、明らかになっています。図12は非常に緻密にテッセレーションされた地形モデル、図13は非常に簡略化されたモデルです。地形の小さなスケールのテクスチャーはほとんど消えていますが、地形の基本的な特徴はすべて残っています。また、開いた境界線が適切に保存されていることもわかりません。先に述べた境界の制約がなければ、境界は大きく侵食されていたでしょう。
図11は、単純化の際に蓄積された誤差の四角形の性質を示しています。各頂点には、水平面の\({\mathbf v}^{\top}{\mathbf Q}{\mathbf v}= \epsilon\)が示されています。各レベルのサーフェスは、対応する頂点を中心とした楕円体です。これらの楕円体の解釈は、頂点がその楕円体の範囲内であればどこにでも移動できるということであり、モデル表面の形状に非常によく適合しているということです。楕円体は、後脚の中央部のようなほぼ平面的な部分では大きく平らであり、耳を通る輪郭や脚の下部に沿った輪郭のような不連続線に沿って細長くなっています。これらの楕円体は、ある意味では、その頂点付近の局所的な表面の形状に関する情報を蓄積していると考えることができます。
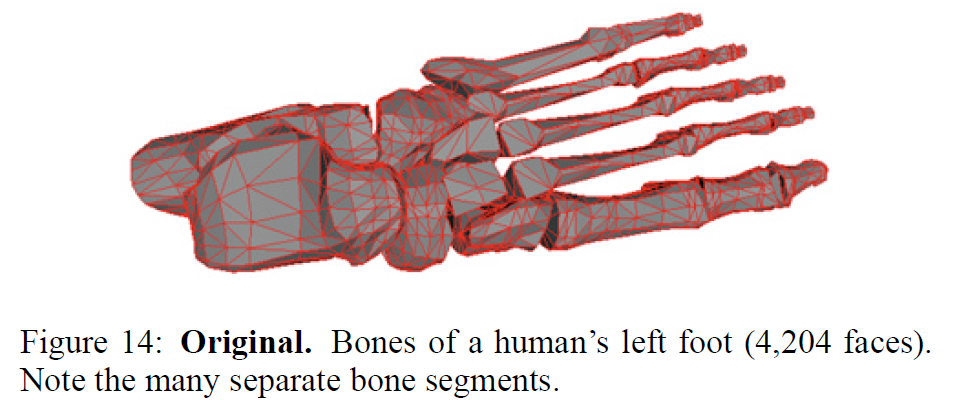
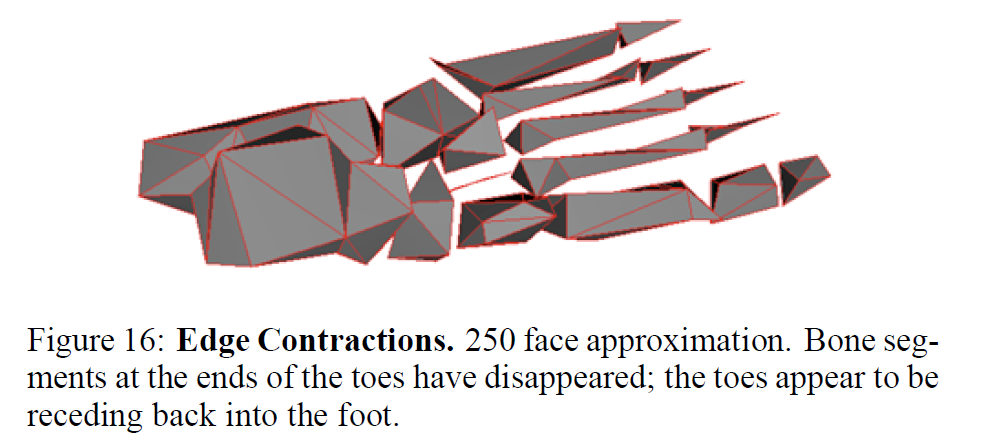
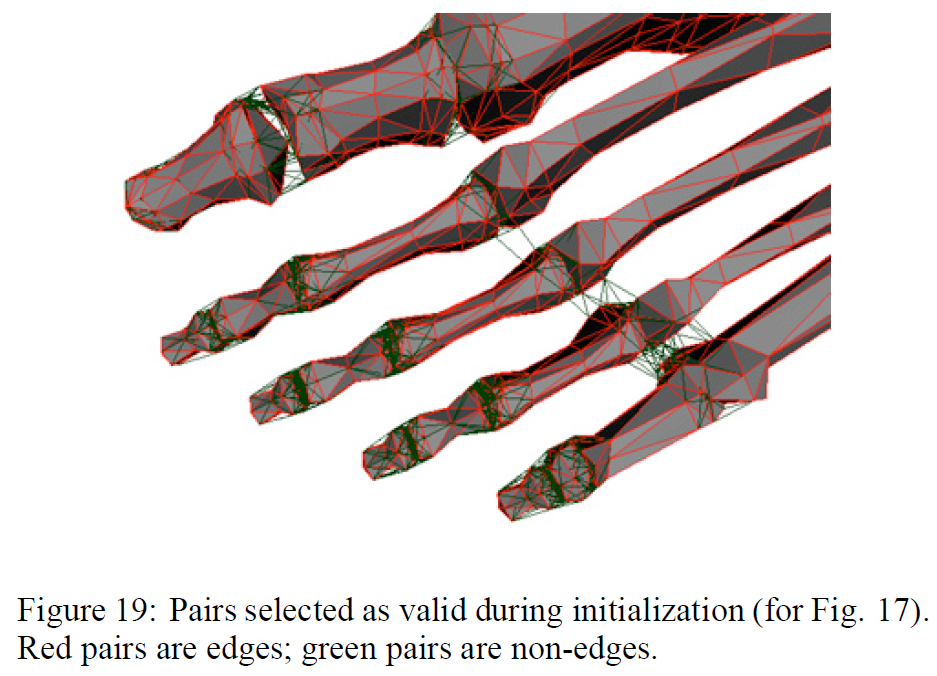
図14-17は、ペア収縮による集約がもたらす真のメリットを示しています。元のモデルは、人間の左足の骨で構成されています。多くの独立したボーンセグメントがあり、中には相互に干渉しているものもあります(明らかにモデル再構築のエラーです)。3つの近似モデルを比較しました。1つは均一な頂点クラスタリングによって作られたもの、もう1つはエッジ収縮のみで作られたもの、そしてもう1つはペア収縮で作られたものです。エッジ収縮のみを用いた場合、足指の端の小さなセグメントが単一の点に崩れ、足指がゆっくりと足の中に後退していくような印象を与えます。一方、より一般的なペア収縮を使用すると、別々のボーンセグメントを結合することができます。図17を見ると、足の指が1つの長いセグメントに統合されているのがわかります。図19は、最初に有効とされたペアのいくつかを示しています。それらがどのようにボーンセグメント間のギャップを越えているかに注目してください。最後に、図18は、簡略化の際に蓄積されたエラー四角形の水平面を示す別の図です(これは図16で見たモデルです)。
アグリゲーションのメリットは視覚的なものだけではありません。アグリゲーションは、近似誤差を客観的に小さくすることもできます。図7は,様々なtの値を用いて足のモデルの面を250個近似したときの誤差\(E_{250}\)を示しています.かなり広い範囲の値で,エッジ収縮のみの近似(\(t=0\))よりも客観的に良い近似が得られています.しかし、\(t\)を増加させても近似値が改善されるとは限らないことに注意してください。これは、2次のエラー指標の性質によるものです。局所的には、平面の集合への距離は、面の集合への距離の妥当な近似となります。しかし、平面には無限の広がりがあり、面にはそれがないため、遠くに行くほど誤差指標の信頼性は低くなります。
8 Discussion
私たちのアルゴリズムは、これまでのアルゴリズムにはない、効率性、品質、汎用性を兼ね備えています。ある種の他のアルゴリズムは、我々のアルゴリズムよりも高速であったり、高品質の近似値を生成したりしますが、通常、3つの分野すべてにおいて我々のアルゴリズムの能力を満たしていません。任意のポリゴンモデルを単純化できる唯一のアルゴリズムである頂点クラスタリング[8]は、高品質の近似値を確実に生成しません。また、高品質な手法である[2, 7, 3]は、いずれも集約をサポートしていません。また、[2]と[3]はいずれも我々のアルゴリズムよりも大幅に時間がかかるようです。[7]の結果は、非常に似た誤差近似を使用しているため、我々の結果と最も似ています。しかし、我々のシステムは、平面集合を追跡するために、より効率的な手段を使用しており、また、境界保存などのいくつかの拡張機能を組み込んでいます。
アルゴリズムには、まだまだ改善すべき点があります。私たちは、有効なペアを選択するために、かなり単純なスキームを使用しました。より洗練された適応策を用いれば,よりよい結果が得られる可能性があります.色のような表面の特性の問題は扱っていません。1つの可能な解決策は、各頂点をベクトル\((x, y, z, r, g, b)\)として扱い、\(7 \times 7\)の四角形を構築し、単純化することです。この方法はうまくいくと思いますが、サイズと複雑さが増すため、基本的なアルゴリズムよりも魅力的ではありません。
概ね良好な結果が得られましたが、このアルゴリズムにはいくつかの明確な弱点があります。まず、先に述べたように、平面のセットへの距離として誤差を測定することは、適切にローカルな近傍でしかうまくいきません。第二に、2次関数に蓄積された情報は基本的に暗黙的なものであり、これが問題になることがあります。例えば、2つの立方体を結合し、現在は消滅している内側の面に関連する平面を削除したいとします。どの面が消滅したのかを判断するのは一般的に難しいだけでなく、適切な面を確実に2次関数から削除する明確な方法はありません。その結果、私たちのアルゴリズムは、集約による単純化を思うように行うことができません。
9 Conclusion
私たちは、ポリゴンモデルの忠実度の高い近似値を迅速に生成することができる表面簡略化アルゴリズムを説明しました。このアルゴリズムでは、反復的なペア収縮を用いてモデルを簡略化し、二次の誤差尺度を用いて、簡略化されたモデルの近似誤差を追跡します。また、最終的な頂点に格納されている二次曲線は、サーフェスの全体的な形状を特徴付けるために使用することができます。
私たちのアルゴリズムは、かなり高い品質の結果を維持しながら、モデルの連結されていない部分を結合する能力を持っています。これまでのアルゴリズムの多くは、本質的に多様体の表面に限定されていましたが、我々のシステムは非多様体のオブジェクトを扱い、単純化することができます。最後に、我々のアルゴリズムは、頂点クラスタリング[8]のような非常に高速で低品質な手法と、メッシュ最適化[3]のような非常に低速で高品質な手法の間の有用な中間点を提供します。