この記事はレイトレ Advent Calendar 2016の22日目の記事です。
コンニチワコンバンワオハヨウゴザイマス。
Pocolデス。
栄養ドリンクなしでは生きていけない身体になりつつあります。わーい。
さて,今回はレイトレを勉強するために,SIGGRAPH 2013の”Physically Based Lighting at Pixar”を読んでみようと思います。
いつも通り,誤訳等が多々あるかと思いますので,ご指摘いただける場合は正しい翻訳例と共に指摘していただけると助かります。
SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.1 より引用
1 Intoroduction
モンスターユニバーシティと最新のブルー・アンブレラに関して,Pixarにおけるライティングパイプラインは完全に書き直しされ,物理ベースでレイトレ―スされるシステムに移行しました。レイトレーシングはあるケースでは既に使われています(例えば,カーズの映画中)。我々はまだポイントライト,シャドウマップ,アドホックなシェーディングモデルなどを使っていました。長年にわたって,元来のパイプラインは物凄く複雑になり,各映画のショット毎に数千のライトとシェーダの微調整をします。その考えは,コンピュータにこの複雑さのすべてを取り扱わせ,アーティスティックな面に集中するためにライト担当者を解放することです。
物理ベースシェーダへ移行し,現在の主な焦点はレンダリング方程式を解くことです:
\begin{eqnarray}
L(x, \omega_o) = \int_{\Omega} f(x, \omega_i, \omega_o) L(x, \omega_i) \cos(\theta) d\omega
\end{eqnarray}
この方程式には更新することが必要なコンポーネントが2つあり,それらは物理的な照明を作成する上でうまく働きます:ライト\(L\)はシーンにおける放出されたエネルギーを表し,BRDF\(f\)は,シーンにおいてライトがどのような反応をするかを表します。両方ともタンデムではたらくことは重要です; 物理的に正しいライトと非正規化されたBRDFが相互作用する,または正確なBRDFが不正確なライトと相互作用することは,それほど意味をなしません。実際に,最終的には潜在的な利益を完全に見ることなく,より多くの不利益を持つ可能性があります。
我々は通常一般的に場合において,この方程式を解くためにモンテカルロレイトレーシングを使用しますが,馬鹿正直な実装は耐え難いレンダリング時間を招きます。これを避けるために,収束時間を最適化するために考えられる光路に依存した,異なる戦略が使用されます。方程式は,サブコンポーネントへと分割され,それらの各々は積分器と呼ぶ指定されたコシェーダによって解かれます。
\begin{eqnarray}
L(x, \omega_o) & = & \int_{\Omega} f(x, \omega_i, \omega_o) (L_{direct}(x, \omega_i) + L_{indirect}(x, \omega_i)) \cos(\theta) d\omega \\
L(x, \omega_o) & = & \int_{\Omega} f(x, \omega_i, \omega_o) L_{direct}(x, \omega_i) \cos(\theta) d\omega \\
& + & \int_{\Omega} (f_{diffuse}(x, \omega_i, \omega_o) + f_{specular}(x, \omega_i, \omega_o)) L_{indirect}(x, \omega_i) \cos(\theta) d\omega \\
L(x, \omega_o) & = & \int_{\Omega} f(x, \omega_i, \omega_o) L_{direct}(x, \omega_i) \cos(\theta) d\omega \\
& + & \int_{\Omega} f_{diffuse} (x, \omega_i, \omega_o) L_{indirect}(x, \omega_i) \cos(\theta) d\omega \\
& + & \int_{\Omega} f_{specualr} (x, \omega_i, \omega_o) L_{indirect}(x, \omega_i) \cos(\theta) d\omega
\end{eqnarray}
これは次のようになります:
\begin{eqnarray}
L(x, \omega_o) = L_{direct} + L_{indirectDiffuse} + L_{indirectSpecular}
\end{eqnarray}

SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.2 より引用
\(L_{direct}\)は\(\sf directLighting\)積分器によって求められます(光路 = \(\rm E\{D, S\}L\),[Heckber 1990]経路表記法を使用)。\(L_{indirectDiffuse}\)は\(\sf indirectDiffuse\)積分器によって求められ(光路 = \(\rm ED\{D, S\}^*L\)),\(L_{indirectSpecular}\)は\(\sf reflection\)積分器によって求めらます(光路 = \(\rm ES\{D, S\}^*L\))。RenderManの機能を利用するため,\(\sf indirectDiffuse\)積分器は,サブパーツへと分割されます。コースティック積分器は,ディフューズバウンス(\(\rm EDS^*L\))で終わるスペキュラーパスを解くことになります。複数のディフューズバウンスについて,フォトン積分器か再帰的に間接積分器(\(\rm EDD^*L\))のどちらかを使用することが可能です。フォトンとコースティック積分器は,フォトンマッピングの機能を利用します[The RenderMan Team 2013b];\(\sf indirectDiffuse\)積分器はラジオシティキャッシュ([Christensenら, 2012]に記述がある)とイラディアンスキャッシング技術の一部を使用します。
\begin{eqnarray}
L_{indirectDiffuse}(x, \omega_o) &=& \int_{\Omega} f_{diffuse} (x, \omega_i, \omega_o) L_{indirect}(x, \omega_i) \cos(\theta) d\omega \\
&=& \int_{\Omega} f_{diffuse}(x, \omega_i, \omega_o) \left( \int_{\Omega} f_{specular}(x, \omega_i, \omega_o) L_{specular} (x, \omega_i) \cos(\theta) d\omega
+ \int_{\Omega} f_{diffuse}(x, \omega_i, \omega_o) L_{diffuse}(x, \omega_i) \cos(\theta) d\omega \right) \cos(\theta) d\omega \\
\end{eqnarray}
reflection積分器に対しても同様の再帰アルゴリズムを適用します。
コシェーダ積分器によって解かれる部品へと式を分解することで,何もリビルドすることなく部品を変更可能な非常に多用途で拡張できるシステムを作成できます。例えば,つい最近はvolumetric積分器を追加しました; システムにプラグインする際に,同様の問題を持つオーバーラップしない部分を解決したので全てが最小の変化で動作しました。我々が現在無視しようとしている難しい光路が存在することにあなたは気づいたかもしれません; 将来,双方向パストレーシングや頂点マージ技法を使用してこれらを解くことを計画しています。最終的に4つの積分器を持ちます:
- \(\sf directLighting\)積分器
- \(\sf indirectDiffuse\)積分器
- \(\sf reflection\)積分器
- \(\sf photonCaustic\)積分器
これらコースノートにおいて,大域照明の場合であっても,ライティングの主要な部分を表現する\(\sf directLighting\)積分器の実装に焦点を当てることにします。それは最も最適化可能な部分でもあります; (光線を入射する前に)シーンの推測的な知識については通常持たない間接光積分とは逆で,直接光積分器は光源について把握しています。
直接光の計算は主に3つの部分へと分解することが可能です:
- Lightコシェーダ
- BRDFコシェーダ
- 積分器コシェーダ
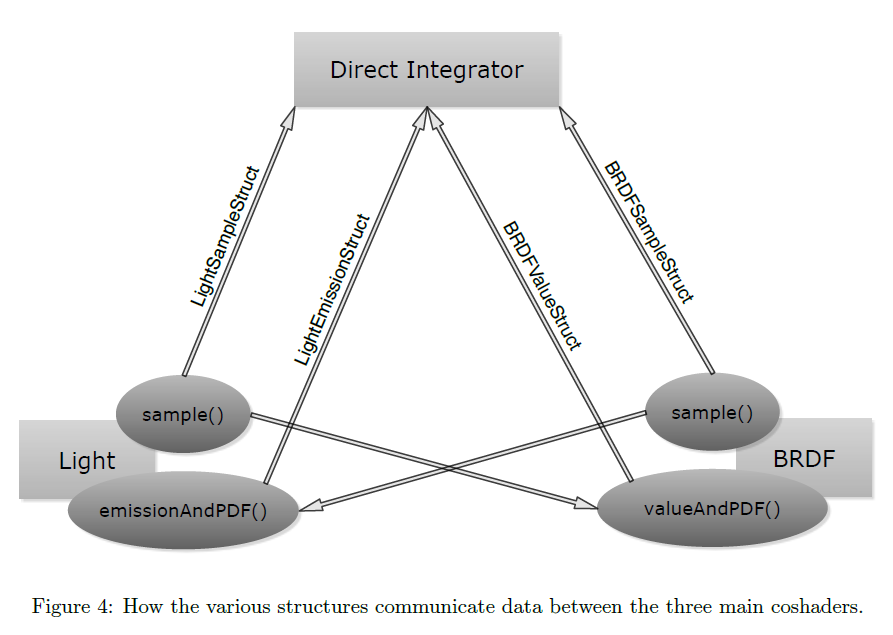
積分器コシェーダは多重重点サンプリング([VeachとGuibas 1995]参照)を用いて最終的なライティング結果を計算する主なシェーダです。ライトとBRDFシェーダはサンプリング戦略に関連を持つサンプルと重みのすべてを提供するための責務を担っています。これらには2つの間で良い対称性を持ちます: 自身の戦略を使用するサンプルを生成するための\(\sf sample\)関数と,そのほかの戦略に合致する値を生成するための\(\sf emissionAndPDF\)と\(\sf valueAndPDF\)関数の両方を持ちます。
ライブラリ上に多くのライトとBRDFシェーダを提供しています。いくつか名前をあげると:\(\sf lambertianDiffuse\), \(\sf orenNayarDiffuse\), \(\sf kajiyaHairDiffuse\), \(\sf beckmannIsotropicSpecular\), \(\sf beckmannAisotoropicSpecular\), \(\sf gtrIsotropicSpecular\), \(\sf ggxAnisotropicSpecular\)と,\(\sf marschnerHairSpecular\)です。ライトについて,\(\sf dome\), \(\sf portal\), \(\sf rect\), \(\sf disk\), \(\sf sphere\)そして\(\sf distant\)型を持ちます。コシェーダについて,システム上でそれらの全ては抽象化されており,シーン記述子において取り換え可能です。
SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.4 より引用
SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.4 より引用
データの要素(サンプル)は配列の構造体を用いたこれらコシェーダ間で渡されます:
- \(\sf LightSampleStruct\)はライトのサンプリング結果を含みます:
- ライト上の位置\(\sf P\)をサンプル
- シェーディング点から\(\sf P\)への正規化されたベクトル\(\sf Ln\)
- カラー\(\sf Cl\)のサンプル
- 確率密度関数\(\sf pdf\)のサンプル
- \(\sf BSDFSampleStruct\)はBRDFのサンプリング結果を含みます:
- 重みづけされたサンプル値(値/確率密度関数)\(\sf weight\)
- 確率密度関数\(\sf pdf\)のサンプル
- 方向\(\sf dir\)のサンプル
- \(\sf LightEmissionStruct\)はBRDFサンプリングのライト側の値を含みます:
- ライト上の位置\(\sf P\)のサンプル
- カラー\(\sf Cl\)のサンプル
- 確率密度関数\(\sf pdf\)のサンプル
- \(\sf BSDFValueStruct\)はライトサンプリングのBRDF側の値を含みます:
- 値\(\sf value\)のサンプル
- 確率密度関数\(\sf pdf\)のサンプル
SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.5 より引用
このドキュメントは,最初の2つの例ととそれらの実装に詳述します:2章で\(\sf sphere area light\),そして3章で\(\sf beckmannIsotropicSpecular\) BRDF。\(\sf marschnerHairSepcular\)アプローチに興味ある方は,[HeryとRamamoorthi 2012]をご確認ください。後の4章で,直接光積分器内でサンプリングデータが一緒に引き合わされる方法を正確に示します。
2 Sphere Area Light
SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.6 より引用
スフィアエリアライトは我々の最も単純な照明オブジェクトであり,サンプリングとこの特定照明器具の評価について以下のアルゴリズムを提供します。元来は,これらの関数はRenderManのシェーディング言語([The RenderMan Team 1987-2013])で書かれていました; パフォーマンスの局大化のため,後で,それらの位置をC++へとポート([VilleminとHery 2012]を参照)し,Intelの新しい\(\sf ispc\)コンパイラを利用しました―ここでは自由に利用可能です[PharrとMark 2012]
2.1 Sphere Area Light Sampling
最初に(行7から9),我々はシェーディング点\(\sf P\)から観測される立体角に基づくヒューリスティックを持つ理想的なサンプル数を計算します。また,レイの重要性から(コード中の\(\sf rayWeight\)),再帰におけるサンプル数を減らします。このとき,サンプリングに対して我々は大まかに[Shirleyら,1996]に従います―つまり,単純なアプローチ,ここでは立体角内の分布サンプルです。行14かと16のアルゴリズムにおいて,我々は2つの乱数に依存します:\(\xi_1\)と\(\xi_2\)です。\(\sf P\)がライト内場合(行3と26を参照),有効なサンプルはありません。
SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.7 より引用
2.2 Sphere Area Light Evaluation
ここでは,ライトの評価手法は,入力としてBRDFサンプルの配列が与えられます。我々は単純な2次公式を使用します。行15-19は,潜在的なライトへ衝突を判定しています。与えらたBRDFのサンプル方向がライトが見えない場合(この交差ルーチンを通じて),PDF値0を持つ記録をマークします(行30)。
SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.8 より引用
2.3 Sphare Area Light Diffuse Convolution
この関数は制御変数法(4.5で述べます)についての積分器において使用されます。[Snyder 1996]に従います。注意してほしいのは,我々が提供可能な有効な畳み込みかどうかを決定するためのサーフェイスタイプをチェックすることです。
SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.9 より引用
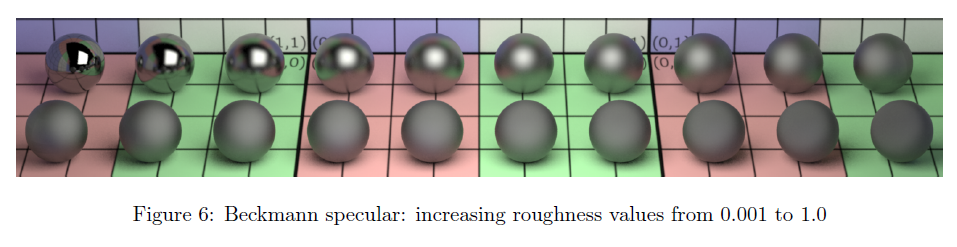
3 Bechkmann BRDF
この特定のスペキュラーモデルは簡潔さと効率性の観点から導かれました。[Walterら 2007]によって大きくインスピレーションを受けており,またすべての最もたるモデル[CookとTorrance 1982]と多くの共通する点を持ちます。
我々はラフネス項\(\alpha\)(0と1の間)を持つ信頼できるBeckmann分布を採用することを決定しました。任意のマイクロファセット法線\(\bf m\)について,この\(\bf m\)の方向とマクロなサーフェイス法線\(\bf n\)を角度\(\theta_m\)を用いて,分布を次のように表現します:
\begin{eqnarray}
D_b(\bf m) = \frac{e^{-\tan^2 (\theta_m) / \alpha^2}}{\pi \alpha^2 \cos^4 (\theta_m)} = \frac{e^{\frac{({\bf n} \cdot {\bf m})^2 -1}{\alpha^2 ({\bf n} \cdot {\bf m})^2 }}}{ \pi \alpha^2 ({\bf n} \cdot {\bf m})^4}
\end{eqnarray}
[Hoffman 2013]で見られたように,マイクロファセットBRDFは常にライト方向\(\bf l\)と視線ベクトル\(\bf v\))のからハーフベクトル
\(\bf h\)における法線分布を評価します。[Walter 2005]は\(D_b\)における支配的な項,すなわち指数についてのサンプリング戦略を導出しました。このスキームにおいて,各サンプルは次の確率で選ばれます:
\begin{eqnarray}
pdf = \frac{D_b(\bf h)({\bf n} \cdot {\bf h})}{4({\bf v} \cdot {\bf h})}
\end{eqnarray}
我々は完全なBRDFモデル(\(D_b\)に多くの項を加える)を想定しており,与えられた\(\bf l\),\(\bf v\)と\(\bf n\)(そして結果的に\(\bf h\))の集合に対しての評価を意味する”値”を使用します。放射輝度とサンプリングの定義により,次を得ます:
\begin{eqnarray}
color = \frac{value ({\bf n} \cdot {\bf l})}{pdf}
\end{eqnarray}
制作環境において望ましいBRDFの性質は可能な限りエネルギーを保存することです。一般的な検証方法は”ホワイトファーネス”テストで,それは一様に白い結果を生み出すはずです。数学的には,これは次のように解釈されます:
\begin{eqnarray}
\frac{value({\bf n} \cdot {\bf l})}{pdf} = 1
\end{eqnarray}
別の表現をすると:
\begin{eqnarray}
f_{\mu}({\bf l}, {\bf v}) = value = \frac{pdf}{{\bf n} \cdot {\bf l}} = \frac{\frac{D_b(\bf h)({\bf n} \cdot {\bf h})}{4 ({\bf v} \cdot {\bf h})}}{{\bf n} \cdot {\bf l}} = \frac{D_b(\bf h)({\bf n} \cdot {\bf h})}{4({\bf n} \cdot {\bf l})({\bf v} \cdot {\bf h})}
\end{eqnarray}
フレネル\(F\)について考慮すると,これは我々のBRDFを与えます:
\begin{eqnarray}
f_{\mu}({\bf l}, {\bf v}) = \frac{F({\bf l}, {\bf h}) D_b(\bf h) ({\bf n} \cdot {\bf h})}{4 ({\bf n} \cdot {\bf l})({\bf v} \cdot {\bf h})}
\end{eqnarray}
実際には,この定義からフレネル項を引き出し,正の\({\bf n} \cdot {\bf l}\)をコサインの変わりに組み込みます。これは打消しされて,次のようになります:
\begin{eqnarray}
f^{*}_{\mu}({\bf l}, {\bf v}) = \frac{D_b(\bf h)({\bf n} \cdot {\bf h})}{4 ({\bf v} \cdot {\bf h})} = pdf
\end{eqnarray}
これは非常にシンプルで(かつ速い)表現であるという利点を持ち,また少なくともBeckmann分布が進む限りファーネステストの合格を保証します。\(\alpha \leq 0.1\)の小さなラフネス値で,\(D_b\)(そして,これゆえ\(f_{\mu}\))はファーネス要件によって確かに順守します。大きな値について,グレージング角においていくつ分かエネルギー損失がまだあります。これはフレネル項を外に出す理由です:アーティストは損失を相殺するために使います。まとめると,我々のBRDF(ビルドインコサインを持つ)は次のようになります:
\begin{eqnarray}
f^{*}_{\mu}({\bf l}, {\bf v}) = \frac{ e ^{\frac{({\bf n} \cdot {\bf h})^2 – 1}{{\alpha}^2 ({\bf n} \cdot {\bf h})^2}} }{4 \pi \alpha^2 ({\bf n} \cdot {\bf h})^3 ({\bf v} \cdot {\bf h})}
\end{eqnarray}
完全な分布に基づくBRDFです!([AshikhminとPremoze 2007]を参照)
SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.11 より引用
3.1 Beckmann BRDF sampling
今,ターゲットの分布が得られたので,分布を使用してBRDFサンプルが生成される方法を示します。様々なローブ間でエネルギー保存を強制しないことに注意してください:これはシェーディングアーティストのための”練習”として残されますが,アーティストは\(\rm K\)項の総和が\(\leq 1\)であること(あるいは,そうでないことを)を保証しなくていけません。以下のアルゴリズムにおいて,フレネルは\(\sf specColor\)へと外部にベイクされ,面比率テスト\(V \cdot N_g\)は,呼び出し前に実行されます。行8と14は[Walter 2005]からの指示です。
SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.11 より引用
3.2 Beckmann BRDF evaluation
我々のBRDFはライティング分布のから生成されたサンプルの寄与を評価することもしなければいけません。あるライトサンプルは零の寄与を解くかもしれません。なぜかというと,それらは間違った方向に向いているからです(行17)。また,行13における返却値が実際にはコサインによるBRDFの結果ということを思い出してください。
SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.12 より引用
4 Direct lighting integrator
\(\sf directLighting\)積分器はBRDFコシェーダ,ライトコシェーダからのサンプルをすべて集め,最終結果を計算します。頑健性のため,多重重点サンプリング(MIS)を用いてこれら2つのサンプリング戦略を組み合わせます。導入部で記述したように,この積分器は直接光のみに着目しており,そのため間接光の効果すべてを完全に無視し,唯一のタスクに対して最適化された計算となります。BRDFのサンプリングはライトに非依存なので,ライトループの外側で1度行われます。ここで,\(\sf BSDFSampleStruct\)を2つ返却することに注意してください。1つはエリアライトの”法線”で,もうつは無限遠ライト用です。ライトの種類に応じて,\(\sf bs\)あるいは\(\sf bsbvh\)を使用します。\(\sf bsbvh\)は少なくとも交差した1つのライトのサンプルのみを含みます。任意の方向で潜在的にこうする可能性がある無限遠ライトについて元々のサンプルのセットが必要なままです。このとき,すべてのライトに対する結果は最終結果へと蓄積されます。ここでの1つ重要な点は,エリアライトがあるにも関わらず,デフォルトでシーンにおいて任意の幾何形状を持たないので,それら自身は可視出来ないことです。これは,それらのライトについて別々のアクセラレーション構造を持つ理由でもあります。
SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.13 より引用
4.1 BSDF Struct
\(\sf BSDFStruct\)は与えられたマテリアルに対するBRDFのローブすべてを含む構造体です。コードを明確するためとパフォーマンス上の理由のため,この構造体に合併させています。ディフューズコンポーネントについて,計算を最適化するため,(ローブが標準的なLambertianディフューズの場合に)すべてのローブを複数の異なるアルベドの代わりにマージされたアルベドを使用することによって1つへと”平たくします”。より複雑な(潜在的には視線依存)ディフューズを持つ場合であっても,我々は単一戦略―例として,均一あるいはコサイン加重されたもの―を用いて全てのローブを一度にサンプリングすることによって利得をまだ得られます。スペキュラーローブについては,異なる戦略(独特なBRDFのセットあるいは異なるラフネスを持つ場合のどちらかのため)を使用するので,それぞれ別にサンプルする必要がありますが,我々はまだ共通の構造体上にすべてのサンプルを保存します。一旦すべてのサンプルと,それらに一致する値とPDFを持つと,どこでどのような方法で計算されたかを知る必要はなくなります:MISを実行するためには値で十分です。\(\sf valueAndPDF\_Spec\)はここで示され,\(\sf valueAndPDF\_Diff\)と同等です:
SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.14 より引用
SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.14 より引用
4.2 Light integrator
これは単一のライトに対する積分コードです。BRDFサンプリングは既に外部で実行されているものと仮定し,ここでは入力パラメータとして渡します。最初に,ライト戦略に従ってサンプルを計算します。これは,ライトコシェーダ内の(2.1節上のように)\(\sf sample\)関数を使って行われます。このとき,MISを使用するため,我々はBRDFサンプリングに対して対応する値とPDFを計算します。これは,\(\sf emissionAndPDF\)関数を通じして実行され,BRDFコシェーダのそれぞれについて\(\sf valueAndPDF\)関数が行われます。これらは我々に最初の値のペアを与えます。次に,入力として渡されたBRDFサンプルについて対応するライト値を計算します。BRDFサンプリングは既に外部で行われているので,ライトコシェーダ側上では\(\sf emissionAndPDF\)を呼び出すことがのみが必要となります。これは,BRDFの入力サンプルと結びついて,MISに対する2つ目の値のペアを与えます。
\(\sf computeMIS\)関数は,このときそれらの各サンプルについての重みと最終的な値を計算します。この段階において,我々は任意の可視性を考慮することなく結果を保持します。最終的なステップは,サンプリング結果のすべてについて可視性の項を計算することです。シャドウイングの実行は通常最もコストがかかるステップなので,カットオフ(あるいは案バイアスのままにしたい場合にはロシアンルーレット)を用いて計算を最適化するために各サンプルの最終的な重みづけを使用することがすべて可能になった後で実行されます。リサンプリングを有効にしている場合も同じです:最終的なサンプル数はシャドウイング計算を実行する前に減らされます。
SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.15 より引用
4.3 BRDF integrator
BRDFの積分は一度にすべてのスペキュラーローブに対して実行されます。ローブの数は\(\sf numSpecLobes\)で返却され,各ローブごとのサンプル数は\(\sf numLobSamples\)の配列で返却されます。各BRDFはその性質(ラフネスなど)に基づいて可変のサンプルを持つことができます。このス段階において最適化は実行されます:すべてのサンプルがエリアライトのすべてを含むアクセラレーション構造についてテストされます。BRDFサンプルが任意のライトと交差しない場合は,棄却されます。この最適化は必須ではありませんが,シーン中にライトが数千ある場合にサンプリングは非常にコストがかかるので最適化が推奨されます。無限遠ライト(特に\(\sf dome\,area\,light\)について使用するために元々のサンプルのセットをまだ保持します;直接光積分器はタイプに応じて適切なライトのセットを渡す責務を担います。
SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.16 より引用
SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.16 より引用
4.4 MIS integrator
2つの戦略―ライトとBRDF―からサンプルをすべて得たら,MISを実行します(我々はディフューズローブについて,通常はライトサンプリングのみを使用します)。我々の積分器もまたMISの場合に,リサンプリングステップあるいはリサンプルされたMIS([Talbotら 2005]でのように)を実行する可能性があります。これは時々,特にライトのエミッションにおける高周波パターンを解決するのために多くのサンプルが必要な場合に,シャドウレイをトレースする数を減らすのに有益です。
SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.17 より引用
SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.17 より引用
4.5 Shadow integrator
ライトのシャドウイングは可視性を計算するためのみに最適化された透過(表に出てこない)のレイトレーシングを用いて実行されます。これはここでは示されませんが,特別なシャドウイング戦略がここで実装することが可能です。戦略が互いに重ならない限り(つまり,2重影を生成しない),異なるシャドウ付けするものを複数回呼び出すことが出来ます。例えば,シーン内の標準的なオブジェクトに対するシャドウトレーシングの後、重いベジテーションのために特別な球面調和の可視性スキームを使用するや,大きなヘアオブジェクトに対してシャドウマップ内を例マーチする([The RenderMan Team 2011]を参照)ことが可能です。
シャドウ付けしないライティングの解析解を提供することが出来る場合に制御変量を用いて追加ステップが実行されます。これは通常,閉曲線積分計算あるいはテクスチャマップの事前畳み込みに依存しています。一般的な手法は,何らかの形で近似であるが,ディフューズ畳み込みを得るために球面調和関数表現([RamamoorthiとHanrahan 2001],そして[Mehtaら 2012])を利用することが出来ます。スフィアエリアライトについての例は2.3で述べています。
ここでのアイデアは入射放射輝度とBRDFと可視性項\(v\)の積\(f\)を持つ次式を計算しようとすることです:
\begin{eqnarray}
I = \int fv
\end{eqnarray}
任意の変化がない場合,\(I\)は次のように書くことができます:
\begin{eqnarray}
I = \int fv + \alpha \left( \int f \,\, – \int f \right), \forall \alpha
\end{eqnarray}
解析的に\(G = \int f\)を計算する方法がある場合に,次が導かれます:
\begin{eqnarray}
I = \int fv + \alpha \left( G \,\, – \int f \right)
\end{eqnarray}
例えば,平均可視\(\alpha = {\bar v}\)を取ることが出来ます。利点はもし\({\bar v}\)が1である場合に,\(I\)は厳密に\(G\)であることです。一方で,\({\bar v}\)がちょうど0である場合に,\(I\)が元のサンプリングになります。\({\bar v}\)が0と1の間である場合,\(f\)と\(fv\)間の相関が十分に高い限り,分散はもっと減少します。ここで:
- \(G\)はディフューズ事前畳み込みされた解\(\sf diffConv\)
- \(\int fv\)は\(\sf diffPerLight\)
- \(\int f\)は\(\sf diffPerLightNoShad\)
です。我々は読み手に[ClarbergとAkinin-Möller 2008]を案内します。それには近似と効果的な\({\bar v}\)項についての戦略が記載されています。
SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.19 より引用
SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.19 より引用
BRDFのシャドウイングは素直です:ここでは特別なトリックは存在せず,シャドウレイすべてを単にトレースし,スペキュラーアキュムレーションへと結果を加算します。複数シャドウイング戦略(SH,シャドウマップなど)を使用したい場合に,同じ手法が適用されます。すなわち,ここでそれらを実行します。
SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.20 より引用
5 Conclusion
RenderManの多機能性によりシェーダを書く人は独自の積分器,ライトそしてBRDFを生成することが出来ます。したがって完全に物理ベースのシステムを(例えば,このドキュメントで概説したように)レンダラーの邪魔にならずに開発をすることが出来ます。しかしながら,このレベルのカスタマイズが必要ない場合や,レンダリングエンジンですべての実装の詳細とパフォーマンスの最適化を処理したい場合は,RenderMan 17.0のビルトイン積分器[The RenderMan Team 2012]を利用することでき,RenderMan 18.0[The RenderMan Team 2013a]上で新しいジオメトリックエリアライトAPIを利用することができます。
モンスターズユニバーシティとブルー・アンブレラにおいてシェーディング,ライティングそしてレンダリングアーティストの全ての作業をここで感謝したいです。そして,特にそれぞれの写真監督に感謝します(モンスターズユニバーシティのJean-Claude Kalache,そしてブルー・アンブレラのBrian Boyd)。また、RenderManの全チームと”GI”プロジェクトの一部であるTDのグループに感謝の意を表します。
モンスターズユニバーシティの照明写真監督Jean-Claude Kalacheからの引用:
“物理ベースライトは我々の設定を劇的に簡単にしました。当社の主照明の生産性は倍増し,ショットの照明効率は55%までアップしました。対話的でバッチレンダリングに対してはマルチスレッドを使用しました。私たちが照明担当者から得た圧倒的なフィードバックは,新しいライトが使いやすかったことと芸術的探索のためのより多くの時間を提供したということでした。またセットのシェーディング部門に対して有意義なプレビズライティングを作成するために物理ベースライトを使用しました。すべての主なセットは平均で1-2日でこれらのライトをプレビズしました。両方の部門の照明設定が規格化され,どの照明条件でもより堅牢なシェーダ動作になりました。”
モンスターズユニバーシティのセットシェーディングリードのChris Bernardiからの引用:
“物理シェーディングでは,シェーディング側からSpecularとReflectionを統合する必要がありました:私たちは長年に渡る多くのアプローチを考え直さなくてはなりませんでしたが,その結果,セット全体で鏡面反射をより一貫して表現することができました。ライティングの事情で必要とされる調整が少なくなり,結果としてマテリアルはより移植可能になりました。第2の結果は,ライティングリグがより簡単に操作できるようになったため,個々のセット向けにカスタマイズされたライティング設定を提供するためにライティングが容易になりました。これにより,意味のある照明のコンテキストでシェーダを調整する機会が与えられました。これは,よりクリーンなシェーディング目録を返すのにも役立ちました。HDRとのレンダリングとスペキュラーモデルのエネルギー保存を組み合わせることで,より多様な素材にあたりやすくなりました。そのほとんどは,主にラフネス制御です。”
SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.21 より引用
SIGGRAPH 2013 Course: Physically Based Shading in Theory and Practice, p.21 より引用