D. Brandon Lloyd氏の博士論文である，Logarithmic Perspective Shadow Mapsを適当に訳していくことにします。
前回は5.2まで和訳しました。今回はその続きからです。
誤訳があったりなど，日本語としては多々見苦しい点があるかと思いますが，そこはご容赦ください。

---

5.3 Comparisons

このセクションでは，対数ラスタライゼーションのためのシミュレータ（詳細は6章を参照）を用いて得たLogPSMsについての実験に基づいた結果を示します。また我々はいくつか異なるシャドウマップアルゴリズムについていくつか比較も行いました。我々は以下の略語を異なるアルゴリズムとして分類するために使用します：

● \(\sf P\)： 透視ワーピング。特に断りがない限り，LiSPSMパラメータと新しいワーピングパラメータ形状関数を使用します。
● \(\sf P_o\)： LiSPSMsによって使用される元来の \(1/\sin \gamma\) のフォールオフを持つ透視ワーピング。
● \(\sf LogP\)： 対数＋透視ワーピング。
● \({\sf ZP}k\)： \(k\)パーティションを用いた\(z\)パーティショニング。このセクションにおいては\(\sf ZP_{log}\)パーティショニングのみ使用します。
● \(\sf FP\)： フェースパーティショニング。
● \(\sf FP_c\)： シアリングを取り扱うための座標フレーム調整を用いたフェースパーティショニング。
● \(\sf FP_{cs}\)： 座標フレーム調整と面分割を用いたフェースパーティショニング。

パーティショニングスキームはワーピングと組み合わせることが可能です。例えば\(\sf ZP5 + P\) は5つのパーティションを持つ\(z\)パーティショニングと透視ワーピングを示し，\(\sf FP_c + LogP\) は座標フレーム調整を用いたフェースパーティショニングと対数＋透視ワーピングを示します。\(\sf FP_c + ZP2 + P\) は側面について透視ワーピングを用いた \(z\)パーティショニングを持つフェースパーティションを意味します。\({\sf ZP}k\) がワーピングなしの単独を表す時はユニフォームパラメータライゼーションが使用されます。

5.3.1 Experimental results

単一の別画像に対する1つのシャドウマップアルゴリズムの品質を示すことは困難であることが多いです。最大誤差の領域はアルゴリズム間で異なることがあります。最大誤差を確認するためには，これらの領域内にシャドウエッジを含むサーフェイスがなければなりません。エイリアシング誤差をより簡単に視覚化するために，シーン上へとシャドウマップからのテクセルグリッドを射影します。加えて，エイリアシング誤差の色分けがされた画像を生成します。画像中の射影されたテクセルの領域（ピクセルで測定された）をエイリアシング尺度として使用します。領域はシャドウマップの両方向における誤差を結合して測定される一方で，射影されたテクセルグリッドは射影の形状を伝えるのに役立ちます。図5.31に示した色分けされたカラーマッピングは赤が高い誤差を示し，緑は誤差がないこと，そして青はオーバーサンプリングを示します。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.115 より引用。

　図5.32は様々なシャドウマップアルゴリズム間の比較を示しています。エイリアシングは標準のシャドウマップについては観測に近いところで非常に高いですが，離れたところでは低くなります。\(\sf FP_c + P\)アルゴリズムはPSMパラメータの代わりにワーピングについてLiSPSMパラメータが使用される点を除いては，透視ワープドキューブマップアルゴリズムに相当します。LiSPSMパラメータはシャドウマップの方向 \(s\) と \(t\) 間の誤差のより均一な分布を与えます。\(\sf FP_{cs} + LogP\) はより良いパラメータライゼーションのため \(\sf FP_{cs} + P\) より低い誤差になります。\(\sf ZP5 + P\) はカスケードシャドウマップ(Engle, 2007)に似ていますが，さらに誤差低減のためのワーピングが追加されています。\(\sf ZP5 + P\) は常に5つのシャドウマップを描画する一方で，\(\sf FP_{cs} + LogP\) は 1 ～ 7 の任意の場所に描画することが可能です。この観点から，\(\sf FP_{cs} + LogP\)は3つのみ描画します。\(\sf FP_{cs} + LogP\)は誤差分布が最も均一です。

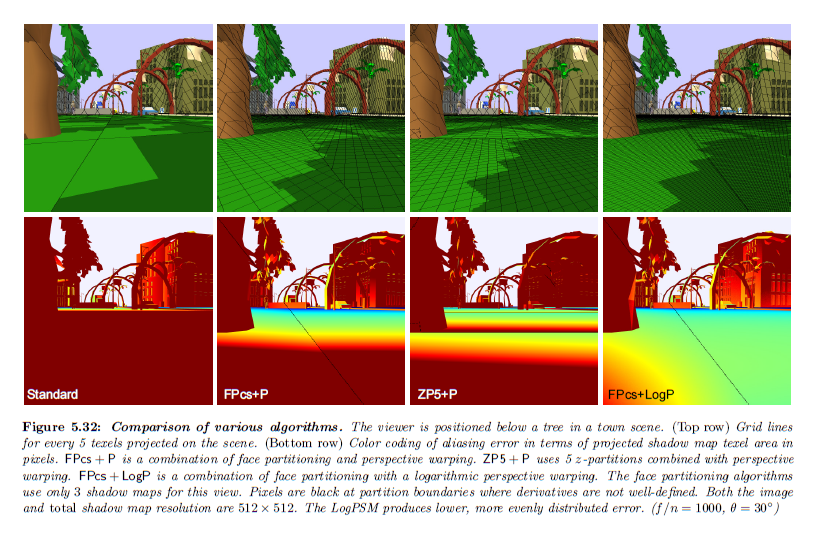
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.116 より引用。

　図5.33は特にシングルシャドウマップで取り扱うのが難しい向かい合う錐台状況を示しています。ここで，\(\sf FP_c + LogP\) は\(\sf ZP5 + P\) よりも少ない誤差を生み出します。ライト方向周囲の画像の部分は観測者から遠く離れたサーフェイスについてオーバーサンプルされています。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.117 より引用。

　図5.34はシングルシャドウマップを用いた比較です。ライトはほぼ\(\sf P\) と \(\sf LogP\) の両方について最適な位置にあります。ライトが
観測者の後ろまたは前側にあるとき，これらのアルゴリズム双方は標準のシャドウマップへと劣化します。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.118 より引用。

　図5.35はポイントライトを用いた\(\sf FP + LogP\) を示しています。Kozlovの透視ワープドキューブマップ(Kozlov, 2004)に対してアルゴリズムを比較します。\(\sf LogP\) パラメータライゼーションもまたポイントライトに対して低い誤差を与えます。

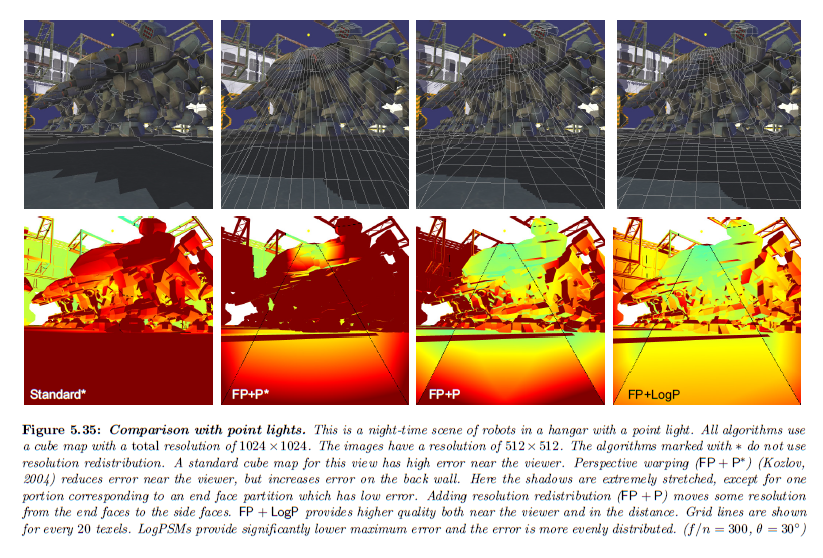
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.119 より引用。

5.3.2 Analysis

表5.4は様々なアルゴリズムについてすべてのライト方向についてのストレージ要因によって測定した透視エイリアシング誤差の変化を示しています。標準のシャドウマップは最も高い誤差を持ちますが，全てのライト方向にわたっての誤差の変化はかなり小さいです。
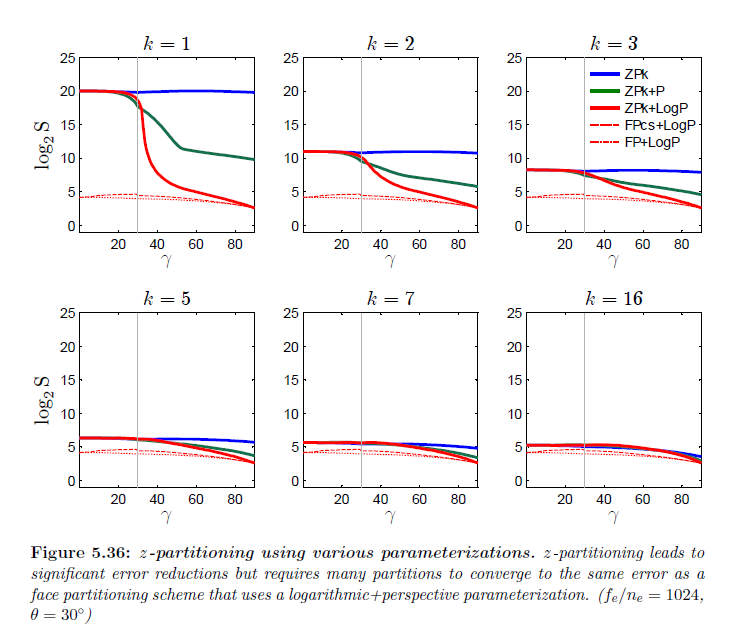
シングルシャドウワーピングアルゴリズム\(\sf P\)，\(\sf P_o\)，そして\(\sf LogP\) は俯瞰についてより低い誤差を提供しますが，ライトが観測者の後ろまたは前に移動するときに標準のシャドウマップへと劣化します。これはこれらのアルゴリズムを使用することをより困難にし，誤差の大規模な変化につながります。表が示しているのは，\(\sf P_o\)とは対照的に，我々の改善したワーピングパラメータに対する形状関数が標準のシャドウマップを下回る\(\sf P\) の最大誤差を保持するということです。\(\sf LogP\)が\(\sf P\)よりもはるかに低い最小誤差を持っているにも関わらず，\(\sf P\) よりわずかに早くユニフォームパラメータライゼーションへとランプオフし，ユニフォームパラメータライゼーションの非常に高い誤差は平均を支配します。しかしながら，図5.36から見られるように\(\sf LogP\)は \(\gamma \in [\theta, 90^{\circ}]\) のほぼ全域について\(\sf P\) を超える重要な改善を提供します。

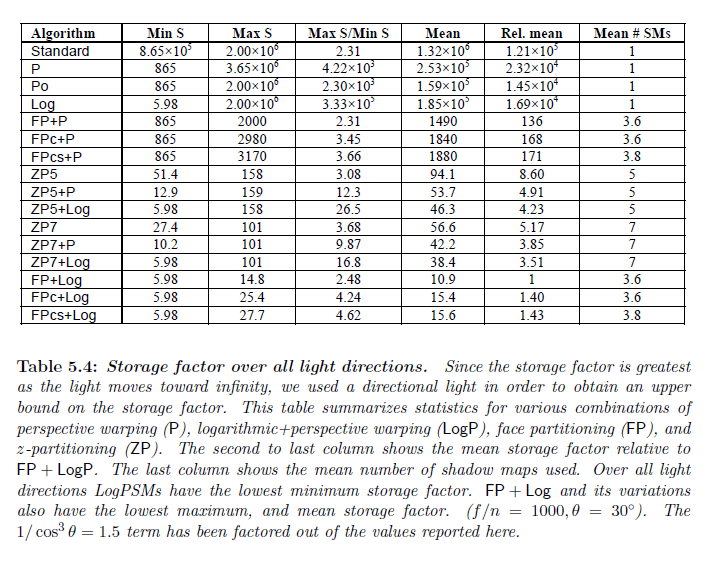
※表はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.120 より引用。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.121 より引用。

　フェースパーティショニングは全てのライト方向にわたって誤差の変動がより少なくなるように導きます。座標フレーム調整と面分割はストレージ要因によって考慮されないシアリング誤差を減らします。ストレージ要因上のシアリング誤差はわずかに増加しますが,
全体の実際の誤差は減ります。\(\sf FP* + LogP\) アルゴリズムはより良いパラメータライゼーションのために\(\sf FP* + P\) アルゴリズムよりもより少ない誤差になります。
　シングルシャドウマップを用いたように，ユニフォームパラメータライゼーションを伴う\(z\)パーティショニングは全てのライト方向について誤差の変化が最小限となります。\(\gamma \in [\theta, 90^{\circ}]\) についての誤差を減らすワーピングを追加します。俯瞰のディレクショナルライトについて発生する\({\sf ZP}k + {\sf LogP}\) についての最小誤差は任意の \(k\) について同じとなります。このライト位置で，\(z\)パーティションの数を増加させることはパラメータライゼーション上では効果がありません。これはユニフォームと透視パラメータライゼーションについては当てはまりません。図5.36はその他のライト位置について，\(k\)を増加する時に誤差の劇的な低減を生み出し，その時に次第に小さくなることを示しています。ワーピングの利益もまた減らされます。比較すると，\(\sf FP + Log\) と\(\sf FP_{cs} + LogP\) についての誤差もまた図5.36に示されます。\(\sf FP_{cs} + LogP\) における小さな上昇は新しいフェースパーティションが現れ，分割される\(\gamma = \theta\) で見ることができます。\({\sf ZP}k\) アルゴリズムについて \(k=5\) と\(k= 7\) を示しました。これはなぜかというと\(\sf FP\) と\(\sf FP_c\) そして，\(\sf FP_{cs}\) アルゴリズムそれぞれについて必要とされるシャドウマップの最大数であるからです。\(z\)パーティションの数が増加するにつれて，誤差は\(\sf FP + LogP\) の誤差に近づき始めます。しかしながら，平均的には \(\sf FP\)と\(\sf FP_c\) によって使用されるシャドウマップの数は3.6 しかなく，\(\sf FP_{cs}\) についての平均数はたったの3.8です。
　表5.4で説明した統計は全てにライト方向についてシーンに非依存の最大透視エイリアシング誤差を示しています。実際のシーンについて画像中の実際のエイリアシング誤差とどのぐらい相関があるかという考えを得るために，上述のシーンでライトの方向を均一に半球サンプルし，画像中の誤差のヒストグラムを生成しました。曲線上の点\(x\) における値は\(x\)未満のピクセルを有する割合です。誤差分布は視錐台内のサーフェイスの位置に依存します。シングルシャドウマップアルゴリズムはより広い範囲について広がっている高い誤差を持つ傾向であることがわかります。視点から遠く離れたサーフェイスの時は，図5.37に示した最初のビューのように，あらゆる種類のワーピングとパーティショニングは標準シャドウマップを超えるほとんどの利益をもたらします。実際には，ワーピングアルゴリズム \(\sf P\) はこのビューについて標準シャドウマップよりも大いに悪い誤差を生成します。2番目のビューのようにサーフェイスが視点に近づいたときは，\(\sf FP_c + LogP\) はその他のパラメータライゼーションよりも著しく低い誤差を生み出します。

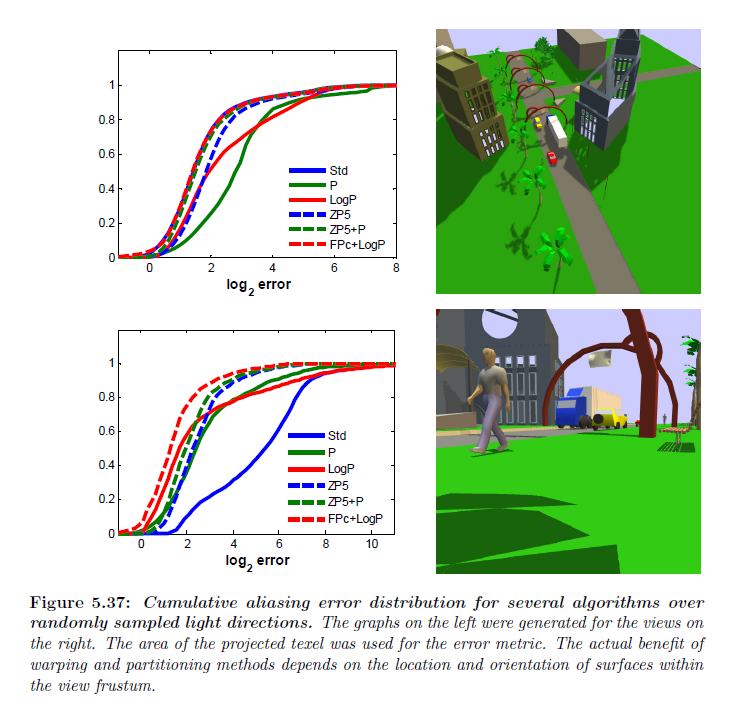
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.123 より引用。

5.3.3 Benefits of LogPSMs

この分析では，3つの種類のLogPSMsを検討しました：\(\sf LogP, ZP + LogP\) そして\(\sf FP + LogP\)です。我々は今から，誤差低減の項とシャドウマップの数で既存のアルゴリズムと比較した各アルゴリズムの利点を説明します。理想的には，シャドウマップの数が最も少ない状態でもっとも低い誤差を与えるアルゴリズムにしたいです。
\(\sf LogP\)。\(\sf LogP\)アルゴリズムは最もシャドウマップが少ない状態（1のみ）で，任意のテクニックで最もよく誤差を低減しますが，ライトの位置の範囲のみが制限されます。高い\(f_f /n_e\)比率に対して，\(\sf LogP\)の最大誤差はその他のシングルシャドウマップワーピングスキームよりもかなり低いです。視線方向に垂直に近いライト方向については，\(\sf ZP\)スキームは誤差のレベルを同じに近づけるために数多くのパーティションを必要とします。\(\sf LogP\)アルゴリズムはライト方向が視線方向に近づくアプリケーション（例えば，ドライビングシミュレータで昼間の太陽からの影など）に最も有益です。しかし全てのライト位置について，\(\sf LogP\)はそのほかのシングルシャドウマップアルゴリズムのように同じ高い誤差を共有します。
\(\sf ZP + LogP\)。\(\gamma < \theta\) について\(\sf LogP\)の高い誤差はいくつかの\(z\)-パーティションで劇的に減らすことができます。しかしながら，\(z\)-パーティションの数が増加するにつれて，\(\sf ZP\)または\(\sf ZP + P\) に対比した\(\sf ZP + LogP\) の相対利益が減ります。したがって，アプリケーションは2～4のシャドウマップの描画を利用可能にすればよいだけなので，\(\sf ZP + LogP\)はアプリケーションにとって最もよいです。けれども\(\sf FP + LogP\)は同じ範囲でシャドウマップの平均数を用いて低い誤差を得ることが可能ですが，\(\sf ZP + LogP\)は実装するのがより簡単です。 \(\sf FP + LogP\)。同じ数のシャドウマップを用いてその他のアルゴリズムと比較すると，\(\sf FP + LogP\)は全てのライト方向について最も少ない誤差を生み出します。\(\sf FP + LogP\)は同じ最大数のシャドウマップ（5または7で，面分割が使われるかどうか依存する）を用いた\(\sf ZP\)スキームよりも低い誤差を持ちますが，誤差は劇的に低くなりません。\(\sf LogP\)の平均は同一のシャドウマップ数(3.6～3.8)で\(\sf ZP\)スキームと比較した場合より多少は重要になります。\(\sf ZP\)アルゴリズムを超える\(\sf FP + LogP\)の本当の利点は全方位ポイントライトを伴う状態であることです。全方位ライトはすべてのライト方向を覆うために複数のシャドウマップが必要とされます。例としてキューブマップ。各キューブマップの面に\(z\)-パーティショニングを追加することはシャドウマップの数の激増を招きます。しかしながら，\(\sf FP + LogP\)はディレクショナルライトの場合と比べて全方位ポイントライトに対してより多くのシャドウマップを必要としません。

5.3.4 Limitations of LogPSMs

LogPSMはその他のサンプル再分布技法の制限のいくつかを継承します。ワーピングは非均一分布の深度値を生成し，適した定数バイアスを選択するのを困難にします。これはスロープスケールされたバイアスに対する問題よりも少ないです。またワーピングはライトに平行に近くなるサーフェイス上のテクスチャ座標の導関数計算の不安定性を増加する傾向があります（いくつかのノイズが図5.32上で見られる）。またフィルタリングはワーピングのためにより複雑になります。これはなぜかというと，フィルターカーネルがワーピングによって導入されたゆがみを考慮する必要があるからです。フェースパーティショニングによってシアリングアーティファクトを取り扱うことは２つの余分なシャドウマップを必要とし，複雑性が追加されます。またフェースパーティショニングは俯瞰の実装を必要とする可能性があり，可変数のシャドウマップを使用します。最も重要なのは，対数ラスタライゼーションは現在のGPU上で利用できないことです。フラグメントプログラムでシミュレートすることができますが，線形ラスタライゼーションよりも大幅に遅いです。なぜかというと，GPUの最適化に重要な深度書き込みを無効にする必要があるためです。

5.3.5 Lowest error for perspective warping: \(z\)-partitioning for faces or frustum?

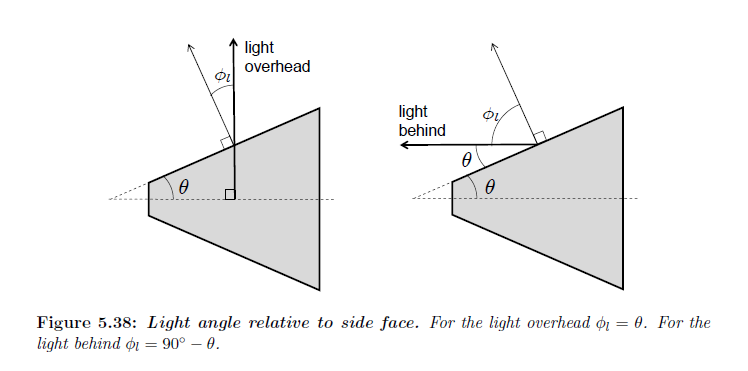
我々は今，対数ラスタライゼーションなしで現在のハードウェア上で最も低い誤差を得るための方法を考えます。我々は，透視ワーピング，フェースパーティショニングそして\(z\)-パーティショニングの組み合わせを考えます。フェースパーティショニングは全てのライト方向へのワーピングする利点を拡張します。さらなる誤差低減を得るために，\(z\)-パティショニングは面に対して適用されなければなりません。また，\(z\)-パーティショニングはフェースパーティショニングを使用することなく視錐台に直接適用することができます。どのアプローチが最も少ないシャドウマップの数について最も大きい誤差低減を与えるのか？エイリアシング誤差における各パーティショニングタイプの効果を分析するために，観測者に対して2つのライト方向を考えます：ライトが頭上にある場合(\(\gamma = 90^{\circ}\))と，ライトが背後にある場合(\(\gamma = 0^{\circ}\)と同じ誤差を持つ）。
　\(z\)-パーティショニングは視錐台をサブ錐台へと分割するので，我々はライト方向に垂直に向いたライト画像平面を使用し，セクション5.2において使用された基本誤差分布のために同じ式を使用します。また，\(\cos \phi_l\) と\(W_e = 2 \tan \theta\) 項を \({\tilde {\rm M}}^{\rm side}_t\) へと移動させます。側面上の \(t\) における誤差量から錐台に対する \(t\) 方向の項へと変換するために，\(\cos \phi_l / (2 \tan \theta )\) で乗算します。基本ストレージ因子 \(\rm S\)は同じ因子によって乗算されることによって変換することができます。\(\cos \phi_l / (2 \tan \theta )\) によって\(\rm S\) を乗算した後で，\(\cos \phi_l \cos^2 \theta\)の因子による面上での \(\sf S\) とは結果が異なります。すべてのパラメータライゼーションについて\(\sf S\) を明示的に計算しているので，この因子を用いて変換を行います。図5.38から面に相対する\(\cos \phi_l\) 項は頭上のライトと背後のライトについてそれぞれ \(\cos \theta\) と \(\cos (90^{\circ} – \theta) = \sin(\theta)\) になることがわかります。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.125 より引用。

Light overhead. 頭上にライトがある状態で，1つの面のみがライトに見えます。面誤差値から変換をすることで次を得ます：
\[
{\rm S^{over}} = {\sf S}^{\rm side} \cos^3 \theta . \tag{5.79}
\]
この式を\({\sf S}^{\rm side}_{un, k}\) (式5.55)へと適用することで，\(k\)パーティションを持ち，ワーピングがない \(\sf ZP\) に対する基本ストレージ因子を得ます：
\[
{\rm S}_{\sf ZP}^{\rm over} = k(f_e/n_e)^{1/k} \frac{\left( (f_e/n_e)^{1/k} – 1 \right)}{2 \tan \theta }. \tag{5.80}
\]
同様に，\({\sf S}_{p, k}^{\rm side}\)(式5.56)から透視ワーピングを持った状態の\(z\)-パーティショニングにういての基本ストレージ因子を計算することができます：
\[
{\rm S}_{\sf ZP + P}^{\rm over} = k \frac{\left( (f_e/n_e)^{1/k} -1 \right)}{2 \tan \theta}. \tag{5.81}
\]
このライト位置について，\(\sf FP + ZP + P\) は\(\sf ZP + P\) と同じ正確な結果を与えます：
\[
{\rm S}_{\sf FP + ZP + P}^{\rm over} = {\rm S}_{\sf ZP + P}^{\rm over}. \tag{5.82}
\]
対数透視パラメータライゼーションについて，ストレージ因子は\({\sf S}_{lp}^{\rm side}\)（式5.57)から計算することができます：
\[
{\rm S}_{\sf LogP}^{\rm over} = {\rm S}_{\sf FP + LogP}^{\rm over} = \frac{\log(f_e/n_e)}{2 \tan \theta}.
\]
これが比較に対する基準線を与えます。

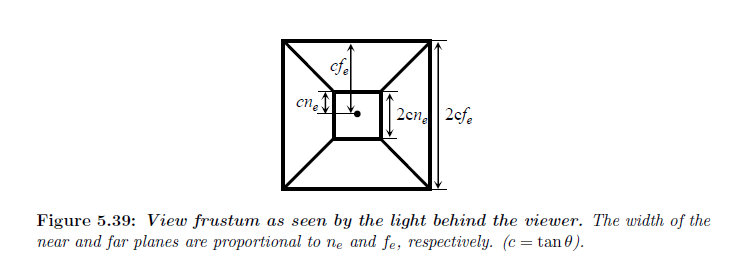
Light behind. 図5.39は観測の背後にあるライトから見られるような視錐台を示しています。\(\sf ZP\) スキームは視錐台が正方形であるのでワーピングを使用することができません。シャドウマップの重要解像度は画像と同じテクセル間隔になります。それゆえストレージ因子は画像によって覆われた領域へとシャドウマップによって覆われる領域の単純な比です：
\begin{eqnarray}
{\rm S}^{\rm behind}_{\sf ZP +P} = {\rm S}^{\rm behind}_{\sf ZP} &=& \frac{(2 \tan \theta f_e)^2}{(2 \tan \theta n_e)^2} = (f_e /n_e)^2 \hspace{2cm} &{\rm with} \hspace{0.25cm} k=1& \\
&=& k(f_e /n_e)^{2/k} &{\rm with} \hspace{0.25cm} k \geq 1&. \tag{5.83}
\end{eqnarray}
フェースパーティショニングを追加した場合，ワーピングを使用することができます。4つの側面とニア平面のそれぞれにシャドウマップを使用します。基本ストレージ因子は端面については1になります。ライト背後に対する面誤差値からの変換は次のように与えられます：
\[
{\rm S}^{\rm behind} = 4 {\sf S}^{\rm side} \sin \theta \cos^2 \theta + 1. \tag{5.84}
\]
この式を\({\sf S}_{p,k}^{\rm side}\) へと適用することで次を得ます：
\[
{\rm S}_{\sf FP + ZP + P}^{\rm behind} = 2k \left( (f_e /n_e)^{1/k} -1 \right) + 1. \tag{5.85}
\]
\(\sf FP + LogP\)に対するストレージ因子は次と同様になります：
\[
{\rm S}_{\sf FP + LogP}^{\rm behaind} = 2\log(f_e/n_e) + 1. \tag{5.86}
\]

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.127 より引用。

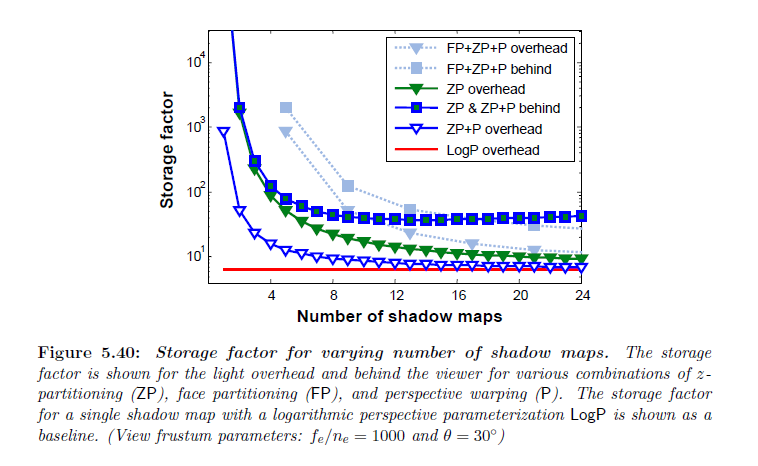
　図5.40はシャドウマップの数の変化に対する\(\sf ZP\)，\(\sf ZP + P\) そして，\(\sf FP + ZP + P\) を示しています。ワーピングなしの\(\sf ZP\) でさえ，俯瞰の場合においては \(\sf FP + ZP + P\) よりも良くなります。ポッピングを避けるためにすべてのライト方向について固定数の\(z\)-パーティションを使用しなければならないので，\(\sf FP + ZP + P\)スキームは4つのシャドウマップ毎に1つの\(z\)-パーティショニングのみを得ます。\((f_e/n_e)\)の大きな値について次を得ます：
\begin{eqnarray}
{\rm S}^{\rm over}_{\sf ZP} &\sim& k(f_e/n_e)^{2/k} \tag{5.87} \\
{\rm S}^{\rm over}_{\sf FP+ZP+P} &\sim& k(f_e/n_e)^{4/k} \tag{5.88}
\end{eqnarray}
ここで，\(k\) はシャドウマップの数とします。ストレージ因子はシャドウマップの数が増加するにつれて\(\sf FP + ZP + P\) についてよりも\(\sf ZP\)についてより急激に減ります。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.128 より引用。

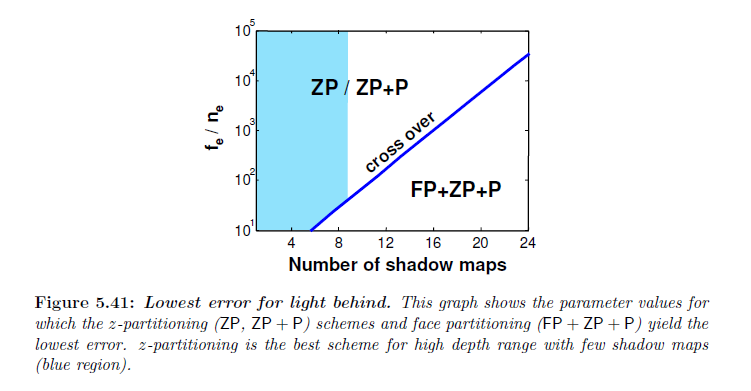
　ライトが背後にある状態で，\(\sf ZP\)スキームの誤差は急激に減少し，その後ゆっくりと大きくなっていきます。この増加はこのライト方向で発生するシャドウマップの大幅なオーバーラップの量によって引き起こされます。実際には，\(k \rightarrow \infty\)につれて，\({\rm S}_{\sf ZP}^{\rm behind}\) は \(\infty\) へと発散します。\(\sf FP + ZP + P\) スキームは非常に小さなオーバーラップがあり，シャドウマップの数が増加するにつれて，最終的には\(\sf ZP\)スキームよりも低い誤差になり，\({\rm S}_{\sf FP + LogP}^{\rm behind}\) と同じ誤差に収束します。図5.41は2つのスキームの間で交差が発生する場所を示しています。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.129 より引用。

　我々の分析に基づき，ワーピング\((\sf ZP + P)\)を持つ \(z\)-パーティショニングは高い深度範囲を持つシーンにおいて少ない数のシャドウマップでシャドウを描画するにはもっとも良いスキームです。利益の大部分は，\(z\)-パーティショニングから来ています。全てのライト方向について，最大誤差はワーピングによってあまり影響を受けません。これはなぜかというと，視線ベクトルに沿ったライト方向であるところで高い誤差設定において使うことができないからです。しかしながら，ワーピングは平均最大誤差を減らします。ワーピングの効果は各パーティションの深度比が減少するのでパーティションの数が増加すると減少します。
　我々は2つのライト方向のみを分析しました。一般的な場合における誤差の閉形式表現の定式化は難しいです。なぜかというと変化するパラメータもつ任意の方向づけされた視錐台へとワーピング錐台をフィットさせる操作の複雑さのためです。図5.42は半球上のライト方向を密にサンプリングすることによって計算されたすべてのライト方向についての最大ストレージ因子を示しています。ワーピング，パーティショニング，そしてパーティションの数の組み合わせすべてについて，最悪の場合 \(\rm S\) はライトが背後にある場合について解析的に計算すると2～3倍であることが分かりました。

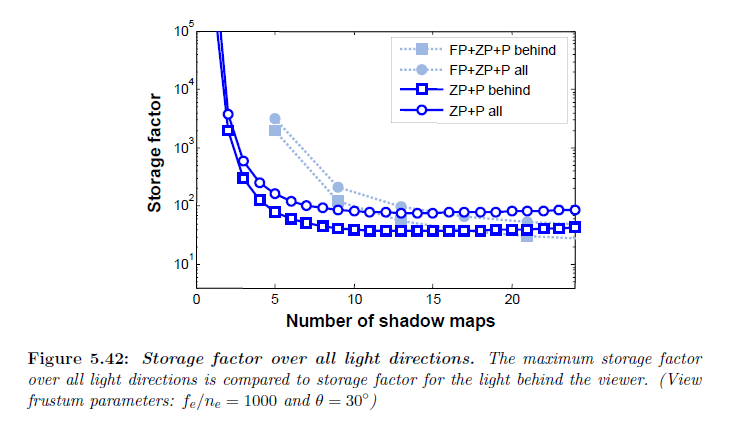
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.130 より引用。

5.3.6 Approximating logarithmic warping with \(z\)-partitioning

この章における分析は指定された値内でLogPSMと比較して\(z\)-パーティションの最大誤差を減らすためにどのくらい多くのパーティションが必要とされるかを決定するために使うことができます。\({\sf ZP}k\)の誤差を\(\sf FP + LogP\)の誤差の\(\epsilon\) の因子内にしたいとしています。誤差の比率はライト位置が変化するとともに変化します。保守的に我々は双方のアルゴリズムからの全てのライト方向についての最大誤差を比較をします。最大誤差のための閉形式を微分するのは面倒です。しかしながら，視錐台の背後にライトについて前の導出を使うことができます。これはなぜかというと，全てのライト方向についての最大誤差がライトが背後にある場合について定数倍であるからです（ \(f_e/n_e \in [10^1, 10^5]\) の範囲について全ての方向とライトが背後にある場合の誤差間の相異が\({\sf ZP}k\) については2, \(\sf FP + LogP\) については1で，\(\sf FP_c + LogP\) については1.5で，\(\sf FP_{cs}+LogP\) について1.7であることを数値的な実験が示しています）。式5.83と5.86を組み合わせて次を得ます：
\[
\epsilon = \frac{{\rm S}_{\sf ZP}^{\rm behind}}{{\rm S}_{\sf FP + LogP}^{\rm behind}} = \frac{k(f_e/n_e)^{2/k}}{2\log(f_e/n_e) + 1}. \tag{5.89}
\]
\({\rm S}_{\sf FP_c + LogP}^{\rm behind}\) と \({\rm S}_{\sf FP_{cs} + LogP}^{\rm behind}\) は \({\rm S}_{\sf FP + LogP}^{\rm behind}\) に等しいです。
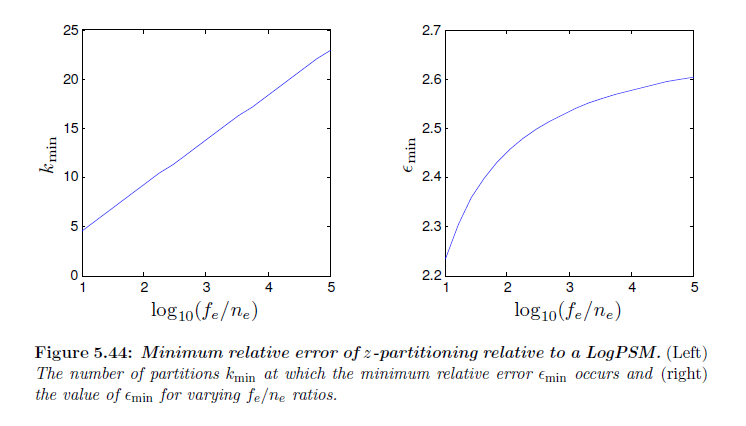
　図5.43は\(f_e/n_e\) と \(k\) のいくつかの値に対する相対誤差 \(\epsilon\) を示しています。以前に見たように，誤差曲線は収束しませんが，それらは比較的に局所的最小値に達して，そしてその後ゆっくりと大きくなります。図5.44は典型的な\(f_e/n_e\) の範囲についての\(\epsilon\) と最小値\(k\) を示しています。ライトが背後にある状態で，この範囲について\(z\)-パーティショニング単独ではLogPSMの誤差から2倍程度よりも近づいてないということに気が付きました。パーティションの数を決定することは\(k\) について式5.89を解きこの最大値よりも大きな\(\epsilon\) を得る必要があり，以下の解析解を得ます：
\[
k = – \frac{2\log(f_e/n_e)}{W_{-1}\left( \frac{2 \log(f_e/n_e)}{\epsilon + 2 \log( f_e /n_e )} \right)} \tag{5.90}
\]
ここで，\(W\)は　ランベルトのW関数(対数積とも呼ばれます）(Corlessら，1996)です。\(W_{-1}\) は\(W\)のブランチで，-1未満の実数を生成します。\(W_{-1}\)関数は一般的には標準ライブラリに含まれません。級数展開また反復アルゴリズムを用いて計算されます。しかしながら，\(W_{-1}\)を正確に計算するルーチンは必要ありません。なぜかというと，我々は\(k\)の整数値にのみに関心があり，一般的な\(f_e/n_e\) の比率について\(k\)の取りうる範囲は特に大きくなく，指定された閾値を\(\epsilon\) が下回るか増加し始めたときに停止することで，ただ\(k\) の連続値をイタレートすることによって実行可能です。

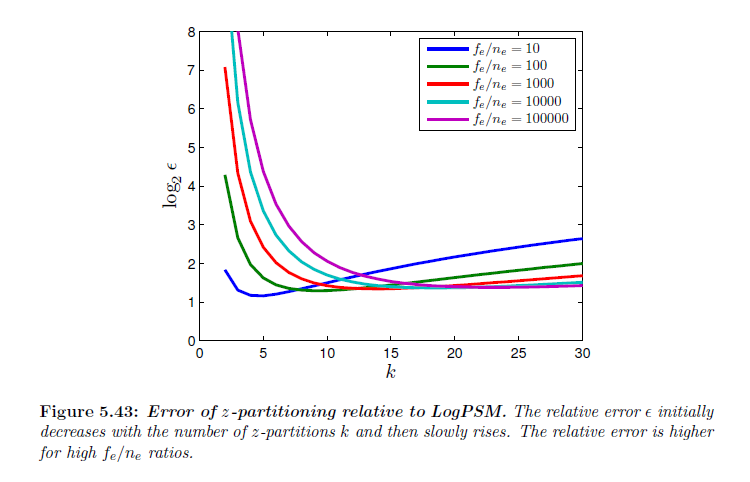
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.131 より引用。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.131 より引用。

5.4 Summary

この章では，我々は様々なワーピングとパーティショニングの組み合わせを分析しました。我々はLogPSMsがほぼ最適なパラメータライゼーションに近く，同じ全てのライト方向について誤差範囲を与えることを示しました。疑似ニア平面，改善されたワーピングパラメータ形状関数，LogPSMsのシングルシャドウマップ についての疑似\(\gamma\) パラメータの使用を含む，シャドウマップを改善するためのいくつかの手法を提案しました。我々はLogPSMsの利点を強調するために様々なアルゴリズム間の詳細な比較を行い，対数透視パラメータライゼーションが利用できない時に誤差の低いシャドウマップを得るためのガイドラインを提供しました。次の章では，これらの種類のシャドウマップを実装する時に上がる問題のいくつかとトレードオフを見ていきます。