D. Brandon Lloyd氏の博士論文である，Logarithmic Perspective Shadow Mapsを適当に訳していくことにします。
前回はChapter.5の途中まで和訳しました。今回はその続きからです。
誤訳があったりなど，日本語としては多々見苦しい点があるかと思いますが，そこはご容赦ください。

---

5.2 Frustum parameterization

このセクションでは，視錐台全体を覆うパラメータライゼーションについての誤差を解析します。頭上のディレクショナルライトから，視錐台はちょうど側面のように見え，分析は非常に類似します。これは以前の研究で解析された設定です（Stamminger & Drettakis, 2002; Wimmerら, 2004)。一般的な位置におけるライトについて，特にポイントライトですが,分析はより退屈なものになります。エイリアシング誤差式はライトの位置に依存していくつかの形式を持ちます。これについての主な理由は，ワーピング錐台をタイトフィッティングを制限する視錐台の頂点のサブセットがライト位置が変化するにつれて変化するからです。可能な限り単純な式を保つためにいくつかの簡略化を行います。視錐台の \(y\) と \(z\) 軸によって形成される平面上のライト位置について注意を制限します。更に，ここではディレクショナルライトのみを考えます。解析はポイントライトへと拡張することが可能ですが，式はより複雑になります。錐台パラメータライゼーション手法は典型的には，どうゆうわけかとにかくディレクショナルライトについて使用されるか，あるいは非常にディレクショナルライトのように振る舞う視野角のかなり狭いスポットライトについて使用されます。
　錐台パラメータライゼーションは通常は視線方向に垂直なライト方向について最も低い誤差となります。しかしながら，ライト方向が平行あるいは視線方向に反平行に近づくにつれて，パラメータライゼーションは高い誤差を避けるためにユニフォームへと戻さなくてはなりません。このセクションにおける解析の主な目的の1つは，低い誤差を保つ間，最適なワーピングからワーピングなしへとスムーズな推移する方法を決めることです。
　図5.24はライト画像平面と視錐台周囲のワーピング錐台を示しています。ライトと視線方向の間の角度 \(\gamma\) によってライト方向をパラメータライズします。\( \gamma \in [0^{\circ}, 90^{\circ}]\) のみ考えます。この範囲について，最大透視誤差は視錐台の背面上で発生します。\(\gamma < 90^{\circ}\)のすべてについてニア平面はバックフェースとなります。両側面は \(\gamma < \theta\) のときにバックフェースとなりますが，側面のうち１つのみとなるのは \(\gamma > \theta\) です。ライト画像平面をライトに垂直な方向に合わせます。透視エイリアシングエラー上の領域を計算するために，適切な面に沿った点について \(\delta_b\) (式4.16)を計算できる必要があります。\(\delta_b\) の項の変化は単純なジオメトリを用いて式5.24から計算することが可能です：


ディレクショナルライトを使用しており，またライト画像平面がライト方向に垂直であるので，\(n_l / d_l\) と \(\delta_b\) の \(\cos \theta_l\) 項は1になります。これらの値をもって，透視エイリアシングエラーの領域についての式は次のように書き直すことができます：

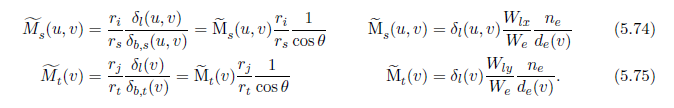
\({\rm {\tilde M}}_s\) と \({\rm {\tilde M}}_t\) の式はセクション5.1のはじめに定義したものとは微妙に異なります。錐台パラメータライゼーションについて完全に \(\theta\) から独立した \({\rm {\tilde M}}\) を定義するのが不可能であるので，\({\rm {\tilde M}}_s\) と \({\rm {\tilde M}}_t\) において \(W_e/n_e = 2 \tan \theta\) の項を含めるように決めました。我々は \({\rm {\tilde M}}_{p,s}\) と \({\rm {\tilde M}}_{p,t}\) が Zhangら(2006) によって透視ワーピングの解析において使われた式に似ているということに気が付きました。主な違いは彼らは視線方向に沿って誤差を解析し，我々は面に沿って誤差を評価するということです。
　図5.25は異なる \(\gamma\) について透視と対数パラメータライゼーションの \({\rm {\tilde M}}\) を示しています。すべての \(\gamma \in [0^{\circ}, 90^{\circ}]\) について，最大誤差はニア平面のエッジと \(v = v_{s2}\) において \(v=0\)　から最も離れた側面上で発生します。\(\gamma \in [\theta, 90^{\circ}]\) について，特に \(f_e/n_e\) の比が高い場合には，\({\rm {\tilde M}}\) はほとんど変化しません。\(\gamma = 0^{\circ}\) のとき，最大誤差は \(\eta = -1\) におけるすべてのパラメータライゼーションについて最小化されます，これはなぜかというとシングルシャドウマップワーピングアルゴリズムはこのライト方向についてユニフォームパラメータライゼーションにすべて劣化するからです。

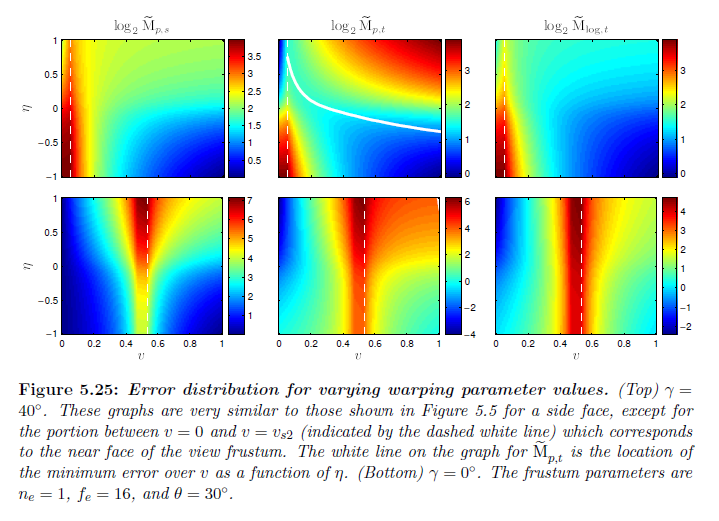
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.106 より引用。

 

5.2.1 Warping parameter shaping functions

低いエラーを維持する間 \(\gamma \rightarrow 0^\circ\) としてユニフォームパラメータライゼーションへと滑らかな減衰を与える関数を計算するために，図5.26上の変化する \(\gamma\) 上の \(\tilde{\rm M}\) の振る舞いを分析します。図5.25の分析に基づき，\(v = v_{s2}\)，\(v = 1\) においてと 最小の \(v = v_{\min}\) の位置における \(\tilde{\rm M}_{p,t}\) についての誤差をプロットします。頭上のライトについて，\(\rm R\) と \(F_{p,s}\) と \(F_{lp, t}\) について \(\tilde{\rm M}\) 上の変化の両方について \(\eta = 1\) において最小となります。 \(\gamma\) が減るにつれて，誤差上の変化は \(\eta = 1\) においてわずかに増加しますが，実際に\(\rm R_{lp, t}\) を保つ間，\(\rm R_{p,s}\) はわずかに上昇します。\(\gamma\ = \theta\) において，\(\eta \in [0,1]\) について \(\rm R\) 上の急激な変化があります。この範囲において \(\eta\) について \(v = v_{s2}\) について\(\tilde{\rm M}_{p,s}\) もまた急激な変化が見えますが， \(\rm R_{p,t}\) における変化はより段階的です。なぜかというと，最大誤差はすでに高いからです。\(\gamma\) が減少するにつれて，すべての \(\eta \neq 0\) についてユニフォームパラメータライゼーションの最大誤差より高くなるまで，すべての関数についての最大誤差は着実に増加します。このことから，\(\gamma\) が減少すると \(\gamma = \theta\) のときに \(\eta\) は \(0\) に近づくということが重要であることがわかります。\(\gamma\) が減少し続けると，\(\eta\) は最終的には，\(-1\) まで減少します。

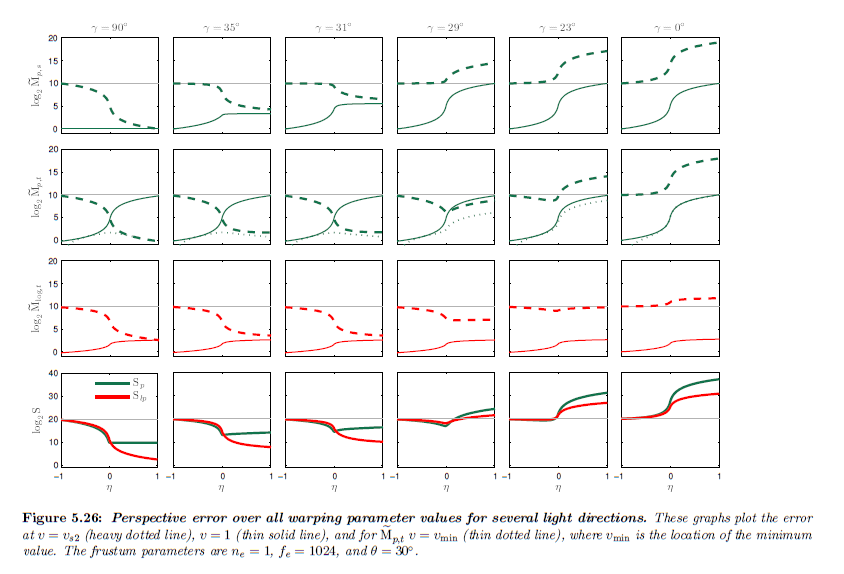
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.107 より引用。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.108 より引用。

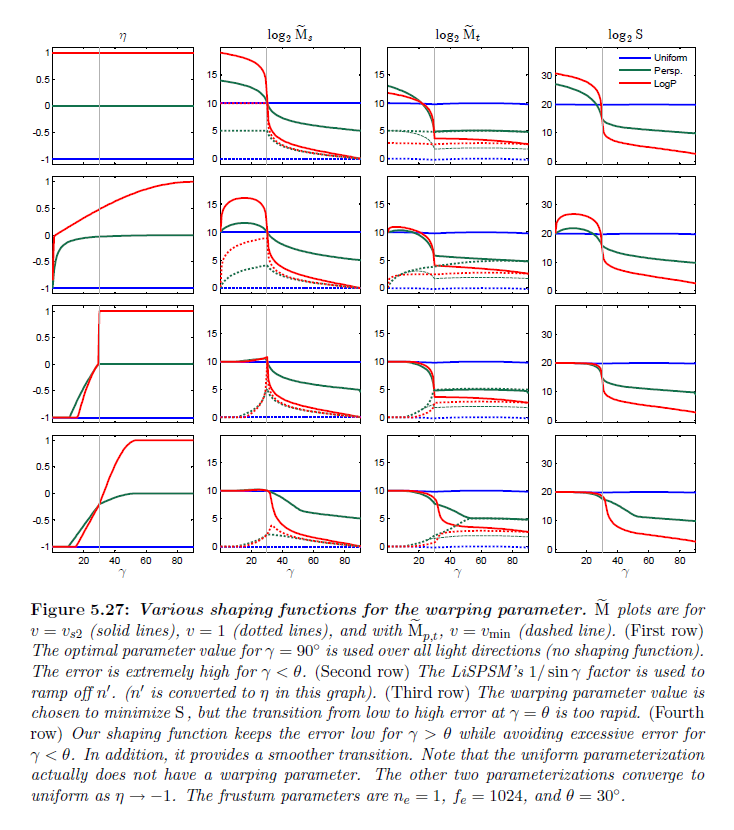
　図5.27はワーピングパラメータについてさまざまな形状関数を用いて，\(\gamma \in [0^{\circ}, 90^{\circ}]\) についての誤差を示しています。任意の形状なしで各パラメータライゼーションが最適なパラメータを使用するとき，\(\gamma < \theta\)について誤差は高くなります。LiSPSMアルゴリズムは最適なパラメータを調整するために \(1/\sin \gamma\) を使用します。図は，この形状関数は誤差を低く維持することに望ましい \(\gamma \in [\theta, 90^{\circ}]\) について比較的に小さな効果であるということを示しています。しかし，\(\gamma \in [\theta, 90^{\circ}]\) について，減衰は\(\eta \neq -1\) に対して \(\tilde{\rm M}_{p,s}\) 上の誤差が増加するのを回避するためには十分に速くありません。\(\eta_{\log}\) は \(-1\) から遠いので，\(\tilde{M}_{\log, s}\) は \(\eta_{p}\) よりもさらに高い誤差を持ちます。したがって，移行するのになお一層長い時間がかかります。\(\rm S\)　を最小化する最適なパラメータを計算する場合，\(\gamma \in [\theta, 90^{\circ}]\) について，\(\eta\) が形状をまったく持たない状態と同じであるということがわかります。\(\gamma = \theta\) において，\(\eta\) は突然 \(0\) に飛び，そしてそのとき，\(\gamma\) が\(0\) と \(\theta\) の間のある点に近づくにつれてほとんど線形に \(-1\) へと減少します。最適な \(\rm S_{p}\) と \(\rm S_{lp}\)　は決して \(\rm S_{un}\) より上に増加しません。\(\rm S\)最適なワーピングパラメータを持つ１つの問題は \(\rm S\) が \(\gamma = \theta\) 近くで非常に急激に変化する可能性があることです。 　\(S_{p}\) と \(S_{lp}\) を最小限に抑えることよりもパラメータについての方程式を計算することはやや複雑になります。代わりに，以下の単純な形状関数を提案します：
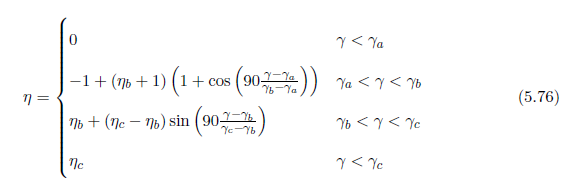
式5.76はほぼ\(\rm S\)-最適なワーピングパラメータの曲線を複製するだけでなく，ユーザーに誤差の形状をより良好に制御することを与えます。この関数は\(\gamma \in [\gamma_{a}, \gamma_{b}]\) の区間上で \(-1\) から \(\eta_{b}\) へと線形変化を提供します。そこから，\(\gamma \in [\gamma_{b}, \gamma_{c}]\) について \(\eta_{c}\) へと滑らかな推移を提供します。典型的な \(\theta\)と \(f_e/n_e\) の範囲についてついて最適な\(\rm S\) 曲線の観測と，ある実験に基づき，透視パラメータライゼーションと対数透視パラメータライゼーションについて以下の値を選択します：

\(\gamma_b = \theta\)を選択します。これはなぜかというと誤差関数が急激に変化し始める時点では \(\eta\) を細かく制御できるからです。\(\gamma = \theta\) 付近であまりにも急激にならないように高い誤差へと推移を伸ばしている間 \(\gamma > \theta\) について誤差を低く保つのを保証する \(\gamma_c\) についての値を選択します。\(\eta_b\) は \(S\)-最適な曲線の振る舞いを置き換えるために 0 にすべきです。しかしながら，これが起こるのは，\(v = 1\) における \(\tilde{\rm M}_{p,s}\) の値が \(v = v_{s2}\) においてと同じ値へと増加するためです。少しの量 \(\eta_b\) を減少することによって\(\rm S\) への影響をそれほど多くなくこの効果を軽減することが可能です。このワーピング形状関数を使用する \(\rm S\) の振る舞いは変化する \(\theta\) と \(f_e/n_e\) 上でかなり一貫性があります。
　我々の形状関数は誤差尺度として \(\rm S\) を用いた最適なワーピングパラメータ値に基づいています。\(\rm S\) は唯一の可能性がある誤差尺度であり，すべてのアプリケーションについて適合しないかもしれません。我々の形状関数はその他の尺度について良いフィットを提供できないかもしれません。この理由のため，ユーザーがスプラインのような何かを用いて対話的に形状関数を構築できるようなより柔軟なシステムを生成したいです。この章で使用したものと同様のグラフをユーザーに提供することによって，特定のニーズを見たする形状関数を対話的に生成することができます。

 

5.2.2 Error over all light directions

図5.28は錐台パラメータライゼーションに対して変化するライト方向についての誤差分布を示しています。ユニフォームパラメータライゼーションを用いた標準のシャドウマップは小さな変化を示しています。\({\bf F}_p\) を用いたときの変化は \({\bf F}_{lp}\)　よりも少ないです。\({\bf F}_{lp}\) と比較した \({\bf F}_p\) についての誤差のグラフは \(\gamma < 30^{\circ}\) については大まかに同じですが，\({\bf F}_{lp}\) の誤差は \(\gamma > 30^{\circ}\) については非常に高いです。誤差の変化は低い \(f_e/n_e\) の比に対して大きく減少します。

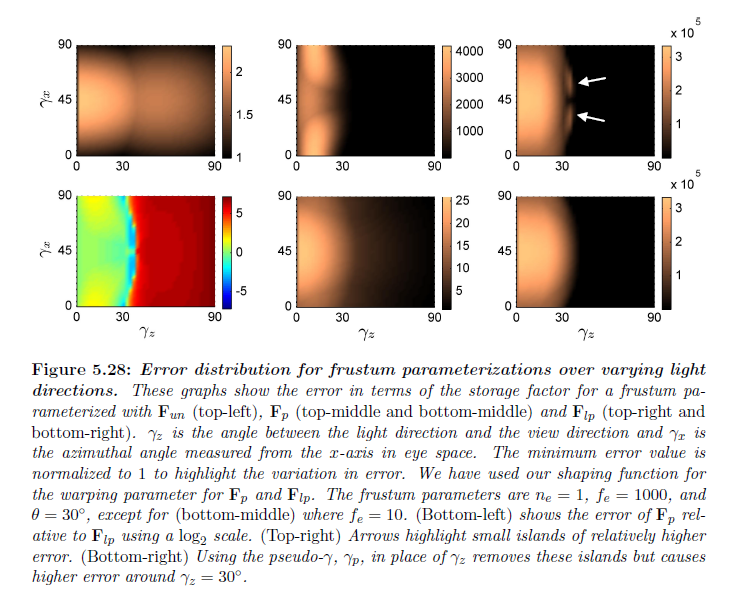
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.111 より引用。

 

5.2.2.1 Using pseudo-\(\gamma\) for \({\bf F}_{lp}\)

\({\bf F}_{lp}\) に関するエラー分布は \(\gamma = 30^{\circ}\) 付近で高いエラーの小さな島部分を示しています。このエラーの大半は \(R_s\) に集中しています。ライトの方向がこれらの領域を横断する時に，影の品質において急激な変化は非常に目立つ可能性があります（図 5.29参照）。図5.30はどのように問題が発生するかを示しています。このライト方向について視錐台を回転させる方法のため，ファー平面からの頂点は視点位置の下に下がります。この状況は，図5.24で図示された \(\gamma < \theta\) のケースに似ています。我々の解析に従って，ワーピングはこのケースについては比較的に弱くなり，結果としてユニフォームパラメータライゼーションに近くなります。しかしながら， \(\gamma\) は実際には \(\theta\) より大きいので，ワーピングはかなり強くなり，高いエラーへと至ります。この問題を避ける一つの方法は，疑似\(\gamma\)，すなわち\(yz\) 平面上のライト方向について \(\gamma \) に似た振る舞いをする \(\gamma_p\) を定義することですが，疑似 \(\gamma\) はファー平面の範囲に相対する視点位置の項で定義されます。図5.30から \(d_0 = f_e \tan \gamma \) と，\(d_1 = f_e \tan \theta \) であることが分かります。相似三角形の性質により \(d'_0 / d'_1 = d_0/d_1\) 。これから以下のように結論付けることができます： \[ \gamma = \tan^{-1} \left( \frac{d'_0}{d'_1} \tan \theta \right) \tag{5.77} \] ここで，\(v_{f0}\) と \(v_{f1}\) はライト画像平面へと射影されたファー平面の領域と定義し，\(d'_0 = v_e - v_{f0}\) と　\(d'_1 = (v_{f1} - v_{f0}) /2\) を定義する場合，疑似\(\gamma\) は次のように計算することが出来ます： \[ \gamma_p = \tan^{-1} \left( \frac{|v_e - v_{f0}|}{v_{f1} - v_{f0}} \tan \theta \right). \tag{5.78} \] 絶対値は，全てのライト方向について有効な \(\gamma_p\) を生成するために必要となります。ライト方向が \(yz\) 平面上にある場合は，\(\gamma_p = \gamma\) となります。その他の場合 \(\gamma_p > \gamma\) であり，ワーピングパラメータ形状関数の \(\gamma\) の代わりに \(\gamma_p\) を使用すると，ユニフォームパラメータライゼーションへの変化はわずかにより早く発生するため，したがって高いエラーの島部分を排除します（図5.28と図5.29を参照）。

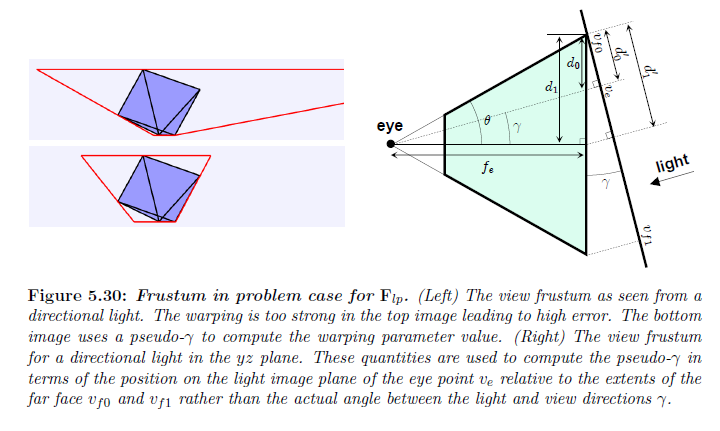
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.113 より引用。

 

5.2.3 \(z\)-partitioning

すべてのグローバルワーピング手法は \(\gamma \in [0, \theta]\) について高いエラーを持ちます。\(z\)パーティショニングはこのエラーを劇的に減らすために使用することができます。また，\(z\)パーティショニングは \(\gamma \in [\theta, 90^{\circ}]\) について実質的なエラー削減を提供します。次のセクションでは，フェースパーティションニングと比べたときの効果的な\(z\)パーティションニングのより詳細な分析を示します。