投稿日: カテゴリー Paper, Program

超雑訳 Point Light Attenuation Without Singularity

こんにちわ，Pocolです。
今日は，
[Yuksel 2020] Cem Yuksel, “Point Light Attenuation Without Singularity”, SIGGRAPH 2020 Talks.
を読んでみようと思います。
いつもながら，誤字・誤訳があるかと思いますので，間違いを指摘して頂ける場合は正しい翻訳例と共に指摘して頂けると有難いです。


※図は，[Yuksel 2020]より引用

ABSTRACT

コンピュータグラフィックスでは、逆二乗の減衰関数を持つ点光源がよく使われます。本論文では、点光源を球面光源の簡略形として扱うことで、点光源減衰の代替定式化を提案します。これにより、逆二乗減光関数の特異性が解消され、点光源を実際に扱うことが容易になります。また、逆2乗式の典型的なアドホックな修正が、我々の定式化に基づいてどのように改善されるかを紹介します。

1　INTRODUCTION

コンピュータグラフィックスでは、ポイントライトは当たり前のように使われています。リアルな光源を表現しているわけではありませんが、そのシンプルさから物理ベースのレンダリングにも使用されています。また、グローバルイルミネーションを近似するための仮想光源としても利用されています。
　逆二乗減衰は点光源では正しい定式化ですが、光量が無限大になるゼロ距離での特異点が現実的な問題を引き起こします。一般的なソリューションでは、シーンに依存する「ライトに近すぎる」位置の特異点を回避するアドホックな減衰関数を使用しています。
　問題の主な原因は、減衰関数そのものではなく、そもそも光源を点として扱っていることにあることを特定しました。実際、ほとんどの場合、点光源はサイズがゼロでない小さな光源を近似するために使用されます。
　我々は、点光源を球形光源の簡略形として扱い、特異点を完全に排除した光源減衰の代替導出を提案します。この定式化は、点光源の単純性を維持しつつ、球状光源からの近接照明の近似を提供します。

2　POINT LIGHT ATTENUATION

サーフェイス点からの出射光（反射光）\({\mathbf L}_o\)の方向\(\omega_o\)に対するレンダリング方程式は、次のように書かれます。

\begin{eqnarray}
{\mathbf L}_o(\omega_o) = \int_{\Omega} {\mathbf L}_i(\omega_i) f_r(\omega_o, \omega_i) \cos \theta d \omega_i \tag{1}
\end{eqnarray}

ここで，ここで、\({\mathbf L}_i\)は方向\(\omega_i\)に沿った入射光、\(f_r\)は材質の双方向反射率分布関数（BRDF）、\(\cos\theta = \omega_i \cdot {\mathbf n}\)はサーフェイス法線\({\mathbf n}\)を持つ幾何学項、\(\Omega\)はすべての入射光方向を表す半球です。強度\({\mathbf I}\)の一点光に対して、式1は次のように書くことができます。

\begin{eqnarray}
{\mathbf L}_o(\omega_o) = {\mathbf I} V(\omega_i) f_a(d) f_r(\omega_o, \omega_i) \cos \theta \tag{2}
\end{eqnarray}

ここで，\(V(\omega_i)\)は2値の可視関数(ポイントライトシャドウを考慮している），\(d\)はライトへの距離，\(f_a(d) = 1/d^2\)は減衰関数です。
　\(d=0\)における\(f_a(d)\)の特異点をなくすために、ライトを半径\(r\)の小さい球状のランバートエミッターとして扱い、式1を異なる減衰関数を持つ式2と同じ形に簡略化します。同じ放射強度を放つ球状の光は、そのライトが見えるすべての\(\omega_i\)に対して\({\mathbf L}_i(\omega_{\mathbf i}) = {\mathbf I}/\pi r^2\)に相当します。したがって、式1は次のように書くことができます。

\begin{eqnarray}
{\mathbf L}_o (\omega_o) = \frac{\mathbf I}{\pi r^2} \int_{\Omega} V(\omega_i) f_r(\omega_o, \omega_i) \cos \theta d \omega_i \tag{3}
\end{eqnarray}

BRDF評価用の光源を点光源とし扱い、ライトの方向\(\omega_i\)を一定とする幾何学項として取り扱うと、次のようになります。

\begin{eqnarray}
{\mathbf L}_o(\omega_o) \approx \frac{\mathbf I}{\pi r^2} f_r(\omega_o, \omega_i) \cos \theta \int_{\Omega} V(\omega_i) d \omega_i \tag{4}
\end{eqnarray}

※図は，[Yuksel 2020]より引用

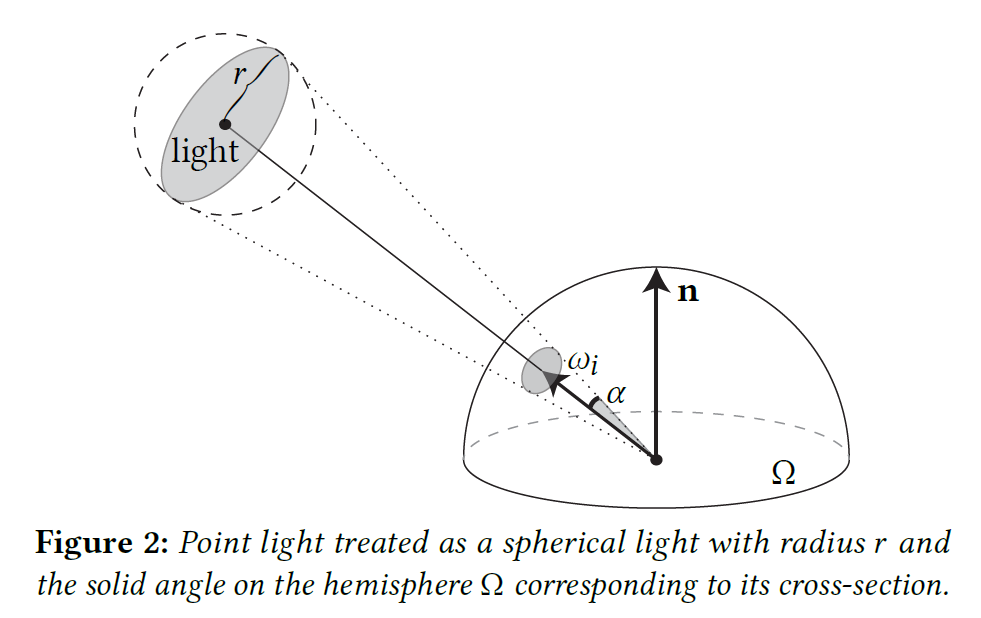
ライトがシャドウされない場合、可視関数の積分は単位球面上で光が見える立体角の面積に等しくなります（図2）。立体角全体が半球\(\Omega\)に含まれると仮定すると、次のように書くことができます。
\begin{eqnarray}
\int_{\Omega} V(\omega_i) d\omega_i \approx 2 \pi (1 – \cos\alpha) V(\omega_i) \tag{5}
\end{eqnarray}

これらの仮定の下で、\({\mathbf L}_o(\omega_o)\)は式2と同じ形で、異なる減衰関数を用いて書くことができます。

\begin{eqnarray}
f_a(d) = \frac{2\pi(1- \cos\alpha)}{\pi r^2} \tag{6}
\end{eqnarray}

球状の光源の場合、\(d \lt r\)では\(\cos\alpha\)は定義されません。その代わりに、図2のようにライト方向\(\omega_i\)に並べた円盤状の光源で近似すると、\(d \gg r\)で同一の照明になります。こうして、光の減衰の最終的な定式化が得られます。

\begin{eqnarray}
f_a(d) = \frac{2}{r^2} \left(1 – \frac{d}{\sqrt{d^2 + r^2}} \right) \tag{7}
\end{eqnarray}

　式7における我々の減衰の定式化は、Lambertian球状光源に対する以下の単純化に依存しています：

  • BRDF，ジオメトリ項，ライトの影は，単一のライト方向\(\omega_i\)を用いて計算されます(式4)。
  • 立体角は、半球\(\Omega\)に完全に含まれると仮定します(式5)。
  • 立体角は、ライト断面（＝ディスクライト）の投影面積で近似されます(式7)。

したがって、上で説明した減衰の定式化は、単純に点光源を球状光源に変換するのではありません。代りに，ポイントライトをその減衰を計算するためだけに球状半径を持つポイントライトとして取り扱います。なお、\(r\)がゼロになる極限では、これらの単純化はすべて完全に正当化され、予想通り\(f_a(d)\)は\(1/d^2\)に近づいていきます。

3　COMMON AD HOC SOLUTION

逆2乗減衰関数の特異性を解消するには、分数の分母に定数係数を加えるだけでよいのが一般的です。この方法の唯一の難点は、妥当な定数値を選ぶことです。この問題を解決するには、ユーザーが指定したライトの半径\(r\)を使用して、減衰関数が次のようになるようにします。

\begin{eqnarray}
{\tilde f}_a(d) = \frac{1}{d^2 + \frac{r^2}{2}} \tag{8}
\end{eqnarray}

となり、式7と同じ\(d=0\)での減衰値が得られます。なお、\({\tilde f}_a\)は我々の減衰関数と逆二乗減衰で境界が決まっています。しかし、式7と異なり、このアドホックな解の物理的な意味は不明です。

4　EVALUTATION

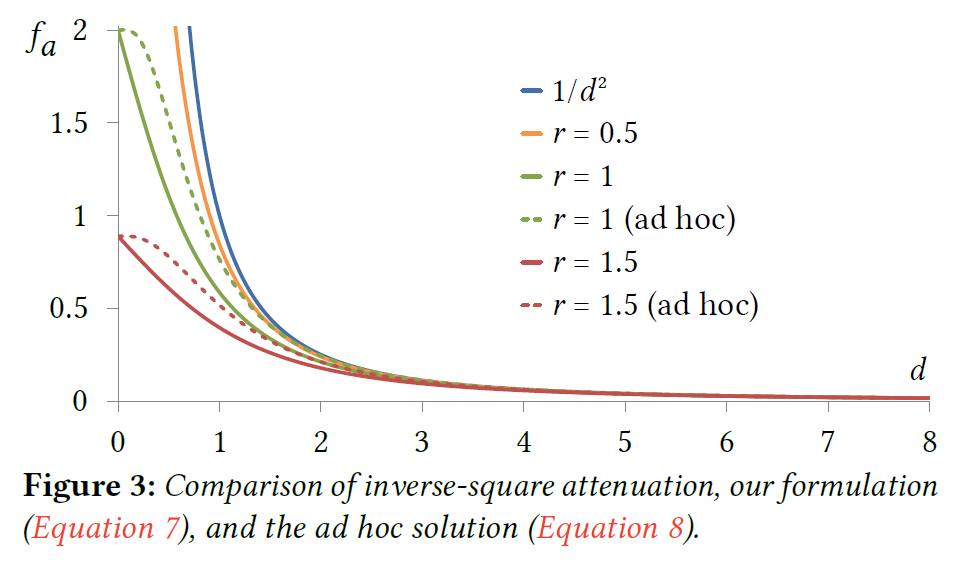
予想通り、この定式化は遠く離れた照明については(d \gg r\)\(r\)が\(0\)になると逆二乗減衰に近づきます。そのため、実際には、光源に近すぎる物体が含まれない限り、我々の減衰計算式は逆二乗減衰とほぼ同じ結果を得ることができます。図3は、我々の減衰関数とその単純な近似値、および点光源に対する正しい逆二乗減衰を比較したものです。

※図は，[Yuksel 2020]より引用

　我々の定式化は，ユーザが定義した半径値を持つシーンに手動で配置された点光源用に設計されていますがが，より単純な定式化で仮想球面光源 [Hašan et al. 2009] を形成するために用いることもできます。図1は，ストキャスティックライトカット[Yuksel 2019]を用いてレンダリングされたような例です。

5　CONCLUSION

我々は、点光源に非ゼロの半径パラメータを加えるだけで、典型的な逆二乗減衰関数の特異性を排除する代替定式化を提示しました。これは概念的には球状光源を形成しますが、特に近距離の場合、球状光源に忠実ではありません。

REFERENCES

  • Miloš Hašan, Jaroslav Křivánek, Bruce Walter, and Kavita Bala. 2009. Virtual Spherical Lights for Many-light Rendering of Glossy Scenes. ACM Transactions on Graphics (Proceedings of SIGGRAPH Asia 2009) 28, 5, Article 143 (Dec. 2009), 6 pages. https://doi.org/10.1145/1618452.1618489
  • Cem Yuksel. 2019. Stochastic Lightcuts. In High-Performance Graphics (HPG 2019). The Eurographics Association. https://doi.org/10.2312/hpg.20191192

Notes

ここで、減衰関数\(f(d)\)を簡略化して表記すると、\(d\)は光源からの距離、\(r\)は光の半径パラメータです。

\begin{eqnarray}
f(d) = \frac{2}{d^2 + r^2 + d\sqrt{d^2 + r^2}}
\end{eqnarray}

この式は、数学的には私の講演のものと同じですが、見た目がよりシンプルで、数値的な特性も良いので、こちらのバージョンを使うことをお勧めします。元の減衰関数の導出については、講演を参照してください。講演の式から上記のバージョンに移行するには、いくつかの代数的な修正を行うだけです。

面白いことに、平方根の中の\(r^2\)項を省略すると、一般的なアドホットソリューションになるのです。

私の講演で用いた減衰関数が、\(d\)が大きくなるにつれてより良い数値精度をもたらすこの単純な形式で書くことができることを発見してくれたYuki Ozawa氏とYuki Ito氏に感謝します。