こんにちわ。Pocolです。
今日は,
[Schied 2017] Chirstoph Schied, Anton Kaplanyan, Chris Wyman, Anjul Patney, Chakravarty R. Alla Chaitanya, Johon Burgess, Shiqiu Liu, Charsten Dachasbacher, Aaron Lefohn, Macro Salvi, “Spatio Temporal Variance-Guided Filtering: Real-Time Reconstruction for Path-Tarced Global Illumination”, HPG 2017,
を読んでみようと思います。
いつもながら誤字・誤訳があるかと思いますので,ご指摘頂ける場合は正しい翻訳例と共に指摘して頂けるとありがたいです。
ABSTRACT
ピクセルごとに1パスのグローバルイルミネーションから、時間的に安定した画像シーケンスを生成する再構成アルゴリズムを紹介します。このようなノイズの多い入力を処理するために,時間的な蓄積を利用して有効なサンプル数を増やし,時空間の輝度分散推定値を利用して,階層的な画像空間ウェーブレットフィルタ[Dammertz ら 2010]を駆動します。この階層化により,局所的な輝度分散を用いて,複数のスケールでノイズとディテールを区別することができます。
物理法則に基づく光輸送を再現することは、リアルタイムコンピュータグラフィックスの長年の目標でした。最近のゲームでは、限られた形のレイトレーシングが使用されていますが、物理法則に基づくモンテカルログローバルイルミネーションでは、30Hzの最小性能要件を満たすことができません。完全に動的なリアルタイム・パストレーシングを実現するためには、ピクセルあたり少数のパスを使用しなければならないと考えています。そのため、パストレーシングをリアルタイムに行うには、少ないサンプル数での画像再構成が鍵となります。従来のインタラクティブな再構成フィルターと比較すると,本研究では,時間的に約10倍安定した結果が得られ,参照画像とのマッチングが5~47%向上しました(SSIMによる).また,\(1920 \times 1080\)の解像度で最新のグラフィックスハードウェアを使用した場合,わずか10ms(\(\pm\)15%)で動作します。
1 INTRODUCTION
近年、映画や視覚効果のレンダリングアルゴリズムとして、パストレーシング[Kajiya 1986]が登場しました[Kellerら2015]。これにより,モンテカルロ・サンプリングの避けられないノイズを低減する高度なフィルタや再構成カーネルの開発に拍車がかかっています(例えば,Zwickerら[2015]参照)。これらのカーネルは,1ピクセルあたり数十から数百のサンプルを持つ画像をノイズなしで再構成することができます。アルゴリズムがさらに進化すれば、リアルタイムグラフィックスにおいても、パストレース型グローバルイルミネーションへの移行が視野に入ってくると考えられます。
ビデオゲームも映画も、最近では経験モデルから物理法則に基づくシェーディングに移行していますが[McAuley and Hill 2016]、ラスタライズで利用できる簡略化された光輸送は、正確な影と反射のためのレイトレーシング[Whitted 1980]や、マルチバウンスグローバルイルミネーションの検討を開発者に促し続けています。しかし、現在のレイトレーシングの性能は、約200~300Mrays/sec [Binder and Keller 2016; Waldら2014]に制限されており、\(1920 \times 1080\)、30Hzの場合、ピクセルあたりわずか数本の光線しか得られません。この数値は、動的な加速機構、大規模なシーン、可変のCPU/GPU性能を持つプロダクション用途ではさらに低くなります。したがって、1パスあたり複数のレイが存在し、解像度とリフレッシュレートがより高くなる傾向にあることから、実用的なパフォーマンスが1ピクセルあたり1パスを超えることは当面ないと考えられます。この制約を考慮した再構成フィルタを開発することで、リアルタイムのパストレーシングをより早く実現することを目指します。
Dammertzら[2010]の階層型ウェーブレットベースの再構成フィルターを拡張し,1ピクセルあたり1サンプル(spp)の画像ストリームから,拡散反射や光沢反射,ソフトシャドウを含む,時間的に安定したグローバルイルミネーションを出力しました(例:図1)。
非常に低いサンプリングレートでの再構成には多くの課題があります。サンプリングが不十分なために分散が大きくなり、高周波信号が不明瞭になったり、たった1つのサンプルではノイズの原因を見分けることが困難になります。例えば、高周波のサーフェイステクスチャを空間的にサンプリングしたときに発生するノイズと、光輸送や可視性のイベントによってもたらされる分散が混ざり合ってしまいます。
リアルタイム性を重視し、前のフレームのサンプルを利用することで、アニメーションシーンであっても細かいディテールを分離し、ノイズ源を切り離すことができます。現在、\(1920 \times 1080\)の環境では、現行のGPUで約10msで動作しており、将来のリアルタイム・パストレース・グローバルイルミネーションへの道を開いています。我々の具体的な貢献は以下の通りです。
- 空間および時間領域の分散推定によってガイドされるフィルターの組み合わせを使用して、1ピクセルあたりのシングルパス入力からリアルタイムで再構成するための効率的で時間的に安定したアルゴリズムを構築します
- 過去のフレームからの情報を使用してピクセルごとの分散推定値を計算するテンポラルパスで、遮蔽されないものやその他の時間的アンダーサンプリングイベントの際には、空間推定値にフォールバックします。
- 先行研究(Dammertzら[Dammertzら2010])に基づいて、複数のウェーブレットの反復によって入力カラーをフィルタリングする空間パスです。この空間パスは,分散の一時的な推定値を使用して開始されますが,信頼性を向上させるために各反復の間にそれを更新します.
- シーンを選ばないジオメトリのエッジストッピング関数。
このフィルタは,シーンに依存するパラメータや光輸送アルゴリズムの知識を必要としませんが,ノイズのないG-Buffer [Saito and Takahashi 1990]の入力を前提としています.つまり、被写界深度やモーションブラーのための確率的にサンプリングされた可視性には対応していません。しかし,今日のゲームは,ポストプロセス技術を用いてこれらの効果をうまく近似しています。
2 RELATED WORK
リアルタイムのグローバルイルミネーションは、長年にわたって研究者たちを悩ませてきました。現在の近似法は,サーフェイスやスパース的にサンプリングされたボリューム上の光輸送計算を事前に計算したり,キャッシュしたりすることに依存しています。キャッシュされた光を調整するために,アンビエントオクルージョン,光沢のあるスクリーン空間の反射,ソフトシャドウイングなど,特定の望ましい効果を含めることができる技術が追加されています[Ritschelら2012].しかし、このようにして得られた照明は、現実的なものとは程遠いものになります。リアルタイムで真のリアリズムを得るためには,開発者は物理法則にもとづくモンテカルロ光輸送に切り替える必要があると考えています。
パストレーサーは,確率的なサンプリングによって光輸送を考慮し,被写界深度,モーションブラー,コースティクス,ソフトシャドウ,グローバルイルミネーションなどの寄与効果[Cookら1984]を正確にレンダリングすることができます。また,パストレーシングによって,エフェクトごとのレンダリングアルゴリズ ムを使用しなくて済むため,コードの複雑さが軽減される可能性があります。このような移行は、オフラインレンダリングではすでに行われており[Kellerら2015], Zwickerら[2015]は、これらの技術の優れたサーベイを提供しています。
Monte Carlo Denoising.
デノイジングフィルタは,複数の画素ごとのモンテカルロ推定量を組み合わせることで,バイアスを犠牲にして分散を低減します.このフィルタは、エッジやサーフェイスのディテールなど、画像のシャープな特徴を維持しながら、出力を滑らかにすることを目的としています。オフラインのノイズ除去フィルタの多くは,ピクセルあたり数十から数百のサンプルを用いて入力画像を空間的にフィルタリングしており,計算時間は数秒から数分程度です.
回帰ベースのアプローチ[Bitterliら2016; Moonら2014, 2015, 2016; Rosselleら2012]は、高いサンプルレート(\(\geq 128\))で良好な結果が得られることが示されていますが、これらのフィルターは外れ値に関して敏感であるため、低いサンプルレートでは確実に機能しません。さらに,これらのフィルタは計算量が多いため,リアルタイムレンダリングには適用できません。
Munkbergら[2016]は、テクスチャ空間で動作することで、空間的および時間的な再利用の恩恵を受けるフィルタをよりシンプルにできることを示しています。しかし、このアプローチをリアルタイムレンダリング用の大規模なアセットに拡張することは、容易ではありません。フィルタリングはパス空間でも行うことができますが[Kellerら2016]、これは高価なkNN探索を使用し、レンダリングとフィルタリングのアルゴリズムを結合します。画像空間フィルタのブラックボックス性は、リアルタイムアプリケーションにとって魅力的な機能です。パス空間メトリクスは画像空間フィルタリングを改善することができますが[Gautronら2014]、これらのメトリクスは依然としてコストが高く、極めて低いサンプル数で多くのフレームにわたって漸進的に収束するだけです。
前述のいくつかの手法は、局所的に品質を向上させる適応型サンプリングを行うことを目的としていますが、我々の要求は異なります。安定した予測可能な性能を維持するためには、適応型サンプリングを避け、サンプリングレートを固定し、バイアスを変動させることが望ましいです。
Interactive Monte Carlo Denoising.
Durandら[2005]は、モンテカルロ法でサンプリングされたライトフィールドの周波数解析により、最適なフィルターフットプリントを導き出しました。その後,ソフトシャドウ,モーションブラー,デフォーカスブラー,線形シアーフィルターを用いた間接照明(Eganら[2011a; 2011b; 2009]),軸合わせフィルター(Mehtaら[2012; 2013; 2014])などの拡張が行われています.分離可能なシアードフィルターを使用すると、より高い性能が得られますが[Hasselgrenら2015; Munkbergら2014; Vaidyanathanら2015; Yanら2015]、周波数分析は総コストを増加させ、良好な結果を得るためには一般的に少なくとも4~16ppが必要となります。さらに、高周波領域の周波数空間フィルタでは、フィルタのフットプリントが小さな領域に縮小されるため、適応型サンプリングを行わないと分散が大きくなってしまいます。
非線形フィルタは、フィルタのフットプリントを縮小するのではなく、フィルタの重みを調整して顕著な特徴を維持します。非線形モンテカルロ法によるノイズ除去の先駆的な研究では,外れ値の除去[Lee and Redner 1990],スムーズなエネルギー再配分[Rushmeier and Ward 1994],異方性拡散[McCool 1999]などが行われています。また、エッジを保持するバイラテラル・フィルタ[Tomasi and Manduchi 1998]をモンテカルロ・デノイジングに適用することができます[Xu and Pattanaik 2005]。再構成されたクロス(またはジョイント)バイラテラルフィルタ[Eisemann and Durand 2004; Petschniggら2004]は、各ピクセルを距離、色、その他の違いに対する加重平均で置き換え、エッジストッピング関数によって画像を誘導する。幾何学的な情報をエッジストッピング関数に含めることで,クロスバイラテラルフィルタの入力ノイズに対するロバスト性が向上します.
エッジストッピング関数の成分を画素ごとに重み付けすることで、空間的に変化するサンプリングノイズに対するロバスト性がさらに向上します。Liら[2012],Rousselleら[2013],Kalantariら[2013],Bauszatら[2015a]は,フィルタ候補のバンクを作成し,推定された入力分散やフィルタ誤差に応じて,画素ごとにフィルタを選択または補間しています.Kalantariら[2015]は、小さなニューラルネットワークを適用して、クロスバイラテラルフィルターのピクセルごとの特徴重みを制御することを提案しています。これらのフィルターは、比較的低いサンプリングレートでも適用できますが、かなりの前処理や平滑化の誤差の推定に依存しており、現在のところリアルタイムでは実行されません。
クロスバイラテラルフィルターの高速近似は,ガイド付き画像フィルター[Bauszatら2011; Heら2013],エッジを考慮したもの[Dammertzら2010; Fattal 2009],適応/線形マニフォールド[Bauszatら2015b; Gastal and Oliveira 2012]など,いくつか存在します.一般的に,これらの近似法はリンギングやハローイングのアーチファクトを引き起こします.粗くサンプリングされた入力(4spp以下)では、画像の構造を推論することができない場合があるため、ぼかしすぎやディテールの損失を防ぐためには、フィルターガイド画像を介して重要な特徴を確立することが重要です。
Temporal Filtering.
複数のフレームにまたがる時間的情報を利用することで、空間フィルターの欠点を解消し、低サンプリングレートでの時間的安定性を向上させることができます。Delbracioら[2014]は、フリッカーを減らすために、複数のフレームにわたるレイのヒストグラムを考慮し、MeyerとAnderson[2006]は、時間的な安定性を向上させるために、重要でないベースを破棄して、すべてのフレームにわたるPCAを計算します。Zimmerら[Zimmer et al. 2015]は,動き推定のために経路空間分解を使用し,複数のバッファにノイズ除去を適用しています。しかし、これらの方法は、リアルタイムに必要とされるような、前のフレーム上でのみ時間的にフィルタリングするのではなく、事前に計算されたフレームの入力セットを必要とします。
インタラクティブフィルタは,モーションベクトルに基づいてサンプルをフレーム間で再投影することが多いです[Nehab et al 2007; Walter et al 1999].これは,事前にレンダリングされた画像群からサンプルを再投影して新しい視点を生成する視点補間(view interpolation)[Chen and Williams 1993]と似ています.近年,再投影は,時間的アンチエイリアシング(TAA)の広範な採用によって人気を博しています[Karis 2014].TAAは,時間的に償却されたスーパーサンプリング[Yang et al.2009]からヒントを得ていますが,古くなったサンプルを廃棄するのではなく,再投影された位置の色と一致するように条件付けられています.Patneyら[2016]は、色の統計的分布を推定することでこれを改良している。
Maraら[2017]は、直接光と間接光を別々にフィルタリングするのではなく、フルパスで動作するノイズ除去法を独立して同時期に開発しており、今後の課題として比較を期待しています。
3 RECONSTRUCTION PIPELINE
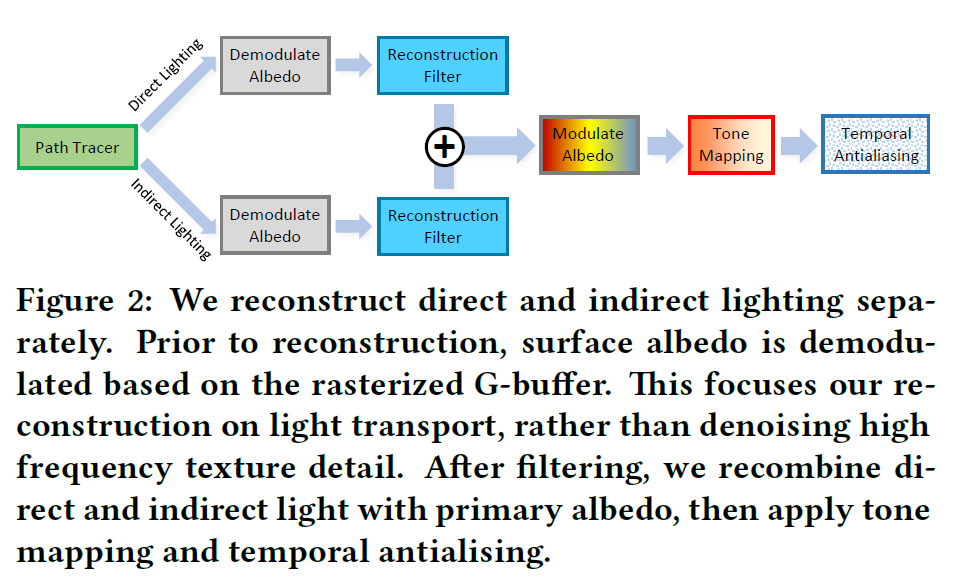
以下に、再構成パイプラインの概要を示します(図2参照)。ラスタライズとパストレーシングの入力、コンポーネントを分離してノイズ源を分離する方法、再構成フィルター、後処理の手順などを説明します。セクション4では,再構成アルゴリズムの詳細を説明します.
Path Tracing.
再構成フィルターへの入力として,次のイベントを推定する標準的なパストレーシングを用いて,一般的な1 sppのカラーサンプルを取得します。このパストレーサーには,利用可能なGPUリソースをより有効に活用するための最適化が施されており,ラスタライザを使用して一次光線を効率的に生成するなどの工夫がなされています.これにより、再構成フィルターのステアに使用される追加の表面属性を含むノイズフリーのGバッファー[Saito and Takahashi 1990]が得られます(セクション4参照)。
光源と散乱方向のサンプリングには,低ディスクレパンシーのHaltonシーケンス[Halton and Smith 1964]を使用しています。これは,時間フィルタの指数移動平均が数フレーム後に以前のサンプルからの寄与を失うためです.パスの最初の散乱イベントの後の非拡散面に対しては,パススペースレギュラリゼーション[Kaplanyan and Daschsbacher 2013]を適用します.レギュラリゼーションは、二次散乱イベントにおけるサーフェイスのラフネスを本質的に増加させ、非常に光沢のあるマテリアルであっても、パストレーサーが光源に接続して間接的なバウンスの寄与を見つけることを可能にします。これにより,光輸送のロバスト性が高まり,パスがより均一に寄与するようになります.また、パスの長さを1パスあたり1つの追加散乱イベントに制限することで、計算コストを抑えています。そのため,間接的に見えるサーフェイスを見つけるために1本の光線をトレースし,さらにプライマリおよびセカンダリのヒットポイントを光源に接続するために2本のシャドウ光線をトレースします.
パストレーサーは、直接光と間接光を別々に出力します。これにより、フィルターは両方の成分で独立して局所的な滑らかさを考慮することができ、サンプル数の少ないシャドウエッジの再構築が可能になります。分離するとコストが2倍になるように見えますが、多くのステップでラスタライズされたGバッファーを使用するため、重要な作業が共有されます。
Reconstruction.
まず、直接見えるサーフェイスのアルベド(テクスチャーや空間的に変化するBRDFを含む)を、サンプルカラーから復調します。これにより、フィルターで高周波のテクスチャの詳細がぼやけるのを防ぐことができます。言い換えれば、テクスチャのない照明成分をフィルタリングし、再構成後にテクスチャを再適用します。テクスチャの詳細がぼやけないようにする必要がなくなるだけでなく、隣接するサンプルの空間的な再利用の可能性が高まります。マルチレイヤーマテリアルの場合には、サンプリング確率で重み付けされたレイヤーごとのアルベドを追加します。
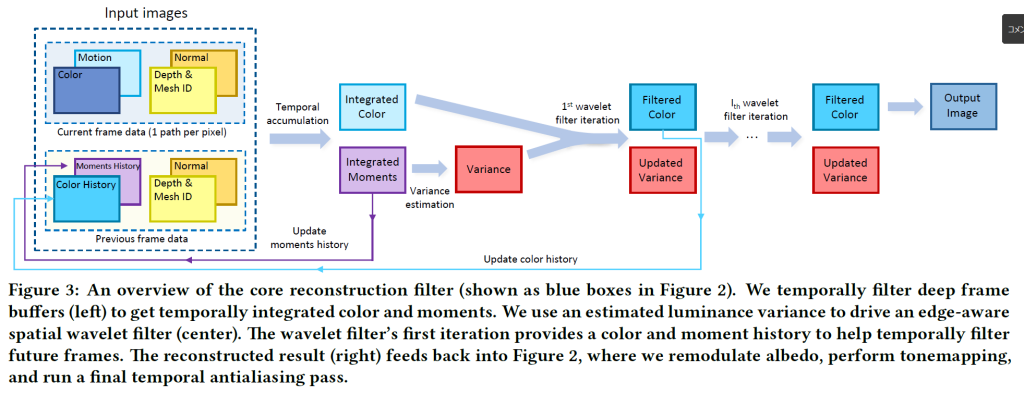
この再構成は主に3つのステップで構成されています。1ppのパストレースされた入力を一時的に蓄積して有効なサンプリングレートを増加させ、この一時的に増強されたカラーサンプルを使用して局所的な輝度の分散を推定し、この分散推定値を使用して階層的なà-trousウェーブレットフィルターを駆動します。図3に概要を示し、セクション4ではこれらのステップをさらに詳しく説明します。再構成後、フィルターの出力をサーフェイスのアルベドで(再)変調します。
Post Processing.
再構成後は、現在の多くのリアルタイムレンダラーと同様の後処理を行います。フィルタリングされた結果は、高いダイナミックレンジを処理するためにトーンマッピング処理にかけられます。最後に,時間的な安定性を高めるためにテンポラルアンチエイリアシング[Karis 2014]を行い,再構成フィルタが保持する幾何学的エッジに沿ってエイリアシングをフィルタリングします.
4 SPATIOTEMPORAL FILTER
再構成フィルターは,1 sppのパストレースされたカラーバッファと,ラスタライズされたGバッファ[Saito and Takahashi 1990],および前フレームの再構成によるヒストリーバッファを入力とします.再構成された画像と次のフレームのヒストリーバッファを出力します。
Gバッファーには、深度、オブジェクト空間とワーク空間の法線、メッシュID、プライマリービジビリティのためのラスタライズパスから生成されたスクリーン空間のモーションベクトルが含まれています。ヒストリーバッファには、時間的に統合されたカラーとカラーモーメントデータ、および前フレームの深度、法線、メッシュIDが含まれています。ロバスト性を高めるために、光の位置や形状などのシーン固有の情報は意図的に使用せず、特定の光輸送方法も想定していません。
図3は、フィルタリングパイプラインの主なステップを示しています。4.1節では,時間的なサンプルの蓄積について,4.2節では,輝度分散の時空間的な推定について,4.3節では,分散ガイド付きウェーブレットフィルタについて詳しく説明しています。セクション4.4では、フィルタの重みを制御するエッジストッピング関数を提供しています。
4.1 Temporal filtering
TAA(Temporal Antialiasing)[Karis 2014]がビデオゲームの償却済みスーパーサンプリングに広く採用されていることから、これをリアルタイムのパストレーシングに適用するのは自然なことだと思われます。しかし残念ながら,カラーベースのテンポラルフィルタリングは,非常にノイズの多い入力に適用するとアーティファクトが発生します.我々は、Nehabら[2007]とYangら[2009]のアイデアに触発されたジオメトリベースのテンポラルフィルタを採用することで、これらのアーティファクトを最小限に抑え、有効なサンプル数を増加させます。
TAAと同様に,フレームiの各色サンプル\(C_i\)に関連する2次元の動きベクトルが必要です。これは,前のフレームからの幾何学的な動きを表しており,\(C_i\)を前のフレームのスクリーン空間の位置に逆投影することができます。前のフレームでフィルタによって出力されたカラーヒストリーバッファにアクセスすることで、複数のフレームにわたってカラーサンプルを継続的に蓄積することができます。各\(C_i\)に対して、カラーヒストリーバッファからサンプル\(C_{i-1}\)を逆投影して見つけ、2つのサンプルの深度、オブジェクト空間の法線、メッシュIDを比較して、それらが一貫しているかどうか(つまり、同じ表面上にあるかどうか)を判断します。これらの一貫性テストには,先行研究のフラグメントマージヒューリスティックスに似た経験的な類似性メトリクスが用いられている[Jouppi and Chang 1999; Kerzner and Salvi 2014].一貫性のあるサンプルは、指数移動平均によって新しい統合色\({C’}_i\)として蓄積されます:
\begin{eqnarray}
{C’}_i = \alpha \cdot C_i + (1 – \alpha) \cdot {C’}_{i-1}
\end{eqnarray}
ここで\(\alpha\)は時間的なフェードをコントロールし、時間的な安定性とラグを交換します。\(\alpha=0.2\)が最も効果的であることがわかりました。モーションベクターは現在、カメラとリジッドオブジェクトの動きに対応していますが、ヒストリーバッファにデータを追加したり、一貫性のテストを行うことで、より複雑な変換が可能になります。
動きのある場合の画質を向上させるために、\(2 \times 2\)タップバイリニアフィルタを用いて\(C_{i-1}\)を再サンプリングします。各タップは、逆投影された深さ、法線、メッシュIDを個別にテストします。タップに一貫性のないジオメトリが含まれている場合、そのサンプルは破棄され、その重みは一貫性のあるタップに一様に再分配されます。一貫性のあるタップがない場合は、葉のような薄いジオメトリを見つけやすくするために、より大きな\(3 \times 3\)フィルタを試します。それでも一貫性のあるジオメトリが見つからない場合、そのサンプルはdisocclusionとなり、時間的な履歴を破棄して\({C’}_i = C_i\)を使用します。
4.2 Variance estimation
à-trousウェーブレット・フィルターを信号に合わせて局所的に調整するために、ノイズを検出するための効率的なプロキシとして、時間的な蓄積を用いてカラー輝度のピクセルあたりの分散を推定します。ここで重要なのは,ノイズがほとんどない領域(例えば,完全に影になっている領域)ではサンプルが少なくならないようにする一方で,サンプルが少なくノイズが多い領域ではより多くのフィルタリングを行うことです。異なるサンプルを時間軸で分析することで、フィルタは特定のサンプルの信頼性を検出します。なお,空間的に計算された分散推定値は,ノイズの不完全な代用にしかなりません.ノイズは分散を増加させますが,ノイズがなくても分散は発生します.
色の輝度の第一、第二の生のモーメントである\(\mu_{1_i}\)と\(\mu_{2_i}\)を用いて、ピクセルごとの輝度分散を推定します。意味のある推定値を得るために十分な数のサンプルを収集するために、幾何学的整合性テストを再利用して、これらのモーメントを時間的に蓄積します。次に、サンプル式\({\sigma’}^2_i = {\mu’}_{2_i} – {{\mu’}_{1_i}}^2\)を用いて、積分されたモーメント\({\mu’}_{1_i}\)と\({\mu’}_{2_i}\)から時間的な分散を推定します。
カメラの動き,アニメーション,ビューポートの境界などがDisocclusionイベントの原因となり,分散推定値の品質に影響を与えます.時間的な履歴が限られている場合(Disocclusionから4フレーム未満),代わりに深度とワールドスペースの法線によって重み付けされた\(7 \times 7\)のバイラテラルフィルタを使用して,分散\({{\sigma’}^2}_i\)を空間的に推定します。基本的に、Disocclusion後の数フレームの間、我々のフィルタは、時間的な蓄積が安定した推定に十分なデータを収集するまで、分散の空間的な推定に依存しています。
4.3 Edge-avoiding à-trous wavelet transform
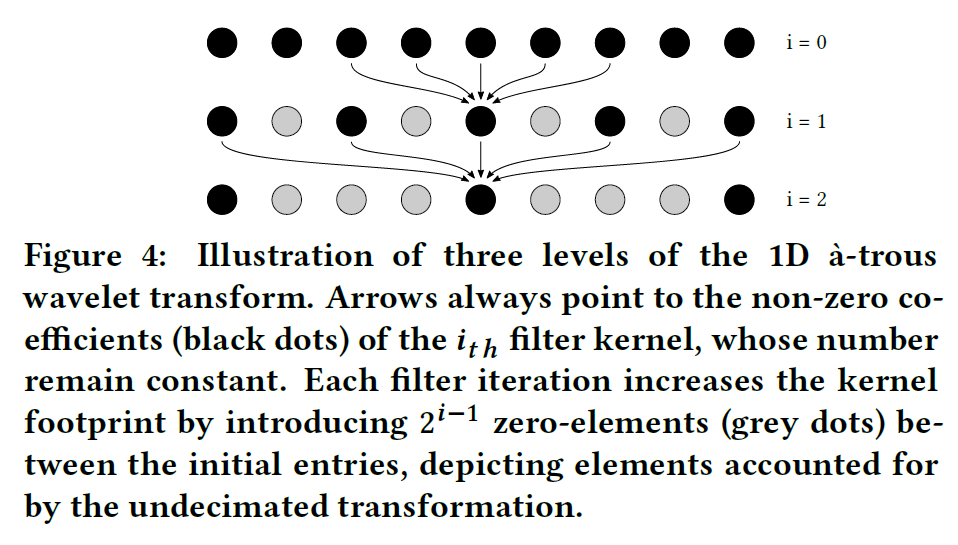
à-trousウェーブレット変換は、フットプリントは増加しますが、非ゼロの要素の数は一定である複数の反復を繰り返して、階層的にフィルタリングを行います(図4参照)。詳細な係数を破棄することで入力を滑らかにする一方、エッジストッピング関数により、境界でのフィルタ範囲を制限することでシャープなディテールを維持します。
ラスタライズされたG-bufferには確率的なノイズが含まれていないため、G-bufferのアトリビュートを用いて共通のサーフェイスを特定するエッジストップ関数を定義することができます。Dammertzら[2010]は、ピクセル\(p\),\(q\)間の重み関数\(w(p,q)\)を持つ\(4 \times 4\)クロスバイラテラルフィルタを用いて、エッジを考慮したアトラスウェーブレット分解の各ステップを実現していますが、我々の実装はこれに倣っています:
\begin{eqnarray}
{\hat c}_{i+1}(p) = \frac{ \sum_{q \in \Omega}h(q)\cdot w(p,q) \cdot {\hat c}_i(q) }{ \sum_{q \in \Omega} h(q) \cdot w(p, q) } \tag{1}
\end{eqnarray}
ここで、\(h = \left( \frac{1}{16}, \frac{1}{4}, \frac{3}{8}, \frac{1}{4}, \frac{1}{16} \right) \)はフィルターカーネル、\(\Omega\)は集められたフィルターフットプリントです。
重み関数\(w(p,q)\)は,通常,幾何学的なエッジストッピング関数と色に基づくエッジストッピング関数を組み合わせたものです[Dammertz et al 2010].我々の新しい重み関数は,フィルタ入力の輝度に加えて,深度,ワールド空間法線を利用しています.
\begin{eqnarray}
w_i(p, q) = w_z \cdot w_n \cdot w_l \tag{2}
\end{eqnarray}
ウェーブレット・フィルターを適用する前に、輝度分散の局所的な推定値に基づいて、輝度エッジストッピング関数を調整します(セクション4.4参照)。次に、式1のように時間的に積分された色にウェーブレットフィルターを適用し、分散のサンプルが無相関であると仮定して、以下のようにフィルターをかけます。
\begin{eqnarray}
{\rm Var}({\hat c}_{i+1}(p)) = \frac{ \sum_{q \in \Omega} h(q)^2 \cdot w(p, q)^2 \cdot {\rm Var}({\hat c}_i(q)) }{ ( \sum_{q \in \Omega} h(q) \cdot w(p,q) )^2 }
\end{eqnarray}
この結果を利用して、次のレベルのà-trous変換のためのエッジストッピング関数を操縦します。今回の再構成では、5レベルのウェーブレット変換を使用し、\(65 \times 65\)ピクセルのフィルターフットプリントを実現しています。
ウェーブレット変換の一環として、最初のウェーブレット反復でフィルタリングされた色を、将来のフレームと時間的に積分するためのカラーヒストリーとして出力します(図3参照)。他のウェーブレットレベルでフィルタリングされた色を使用することもできますが、経験的に、時間的積分に第1ウェーブレット反復を使用することで、時間的安定性の向上と空間フィルタリングによるバイアスのバランスが最もよくなることがわかりました。
4.4 Edge-stopping functions
リアルタイム性が求められる中、時間的な安定性とロバスト性を最大限に高めるために、空間的な偏りが大きくなる可能性を考慮して、式2の3つのエッジストッピング関数を選択しました。各関数のサンプルを拒否する能力は,パラメータ\(\sigma_z\),\(\sigma_n\),\(\sigma_l\)によって個別に制御されます.これらのパラメータは様々な値が有効ですが、実験の結果、\(\sigma_z = 1\)、\(\sigma_n = 128\)、\(\sigma_l = 4\)が、テストしたすべてのシーンでうまく機能することがわかりました。そのため、これらのパラメータはユーザーに公開していません。
Depth.
リアルなシーンでは、特にオープンなランドスケープにおいて、幾何学的スケールの大きな変化が見られることが多いです。そのため、グローバルなエッジストッピング関数の制御が難しくなっています。そこで、サーフェイスの深度に対して局所的な線形モデルを仮定し、そのクリップ空間平面からの偏差を測定します。ローカルな深度モデルは、クリップスペースの深度のスクリーンスペースでの偏微分を用いて推定します。これにより、次のように定義される重み関数が得られます。
\begin{eqnarray}
w_z = {\rm exp} \left( – \frac{ |z(p) – z(q)| }{ \sigma_z | \nabla z(p) \cdot (p -q)| + \epsilon } \right) \tag{3}
\end{eqnarray}
ここで、\(\nabla z\)はスクリーン空間の座標に対するクリップ空間の深度のグラデーションであり、\(\epsilon\)はゼロによる除算を避けるための小さな値です。
Normal.
ワールド空間の法線に対するエッジストッピング機能にはコサイン項を採用しています。
\begin{eqnarray}
w_n = {\rm max}(0, n(p) \cdot n(q))^{\sigma_n} \tag{4}
\end{eqnarray}
上式は、画像平面上の点\(p\)における入力法線\(n(p)\)についてです。 メッシュの簡略化やアンチエイリアシングのアルゴリズムでは、同様の項を用いて2つの面をマージするかどうかを制御しています。
Luminance.
輝度エッジストッピング機能は、輝度を局所的な標準偏差に基づいて再正規化することで、あらゆるスケールに自動的に対応することができる点が特徴です。しかし、サンプル数が少ないと、分散や標準偏差の推定値が不安定になり、アーティファクトが発生する可能性があります。これを避けるために、\(3 \times 3\)のガウスカーネルを用いて分散画像を事前にフィルタリングすると、再構成の品質が大幅に向上します(図5参照)。輝度エッジストッピング関数はガウスカーネル\(g_{3 \times 3}\)と位置\(p\)の輝度\(l_i(p)\)について次のようになります。
\begin{eqnarray}
w_l = {\rm exp} \left( – \frac{ | l_i(p) – l_i(q) | }{ \sigma_l \sqrt{ g_{3 \times 3} ( {\rm Var}(l_i(p))) } + \epsilon } \right) \tag{5}
\end{eqnarray}
輝度のばらつきはフィルターの繰り返しで小さくなる傾向があるため、\(w_l\)の影響は繰り返しごとに大きくなり、ぼかしすぎを防ぐことができます。
なお,このガウス型プレフィルターは,輝度エッジストップ機能を駆動するためにのみ使用され,ウェーブレット変換の次の反復に伝搬される分散画像には適用されません。
5 RESULTS AND DISCUSSION
この新しい時空間分散ガイド付きフィルターを,最終的な画質,性能,時間的安定性など,多くの指標で評価しました.この評価では,1 sppの画像に焦点を当てていますが,これは我々の設計上の決定がすべてこのサンプリングレートをターゲットにしているからです.プロトタイプでは,OpenGLを用いてプライマリ・ビジビリティを生成し,SVGFを実装しています.二次光線と影の光線は,OptiX(Parker et al.2010)を用いてトレースしています.報告されているパフォーマンス結果はすべて,NVIDIA TITAN X(Pascal)を使用しています.
5.1 Comparison With Existing Work
本研究では,それぞれの論文をもとに,共通のフレームワークで独自に実装された様々なノイズ除去技術と比較しています.一般的な画像空間のフィルタリングについては、Dammertzら[2010]によるedge-avoiding à-trous wavelet filter (EAW)、Liら[2012]によるSURE-based filter (SBF)、およびKalantariら[2015]によるlearning-based filter (LBF)と比較します。また、直接照明(影)については、Mehtaら[2012]による軸合わせフィルタ(AAF)とSWGFを比較しています。
この再構成フィルターは、時間的なフィルタリングに依存しているため、時間的なヒストリーバッファを使用すると、より高い有効サンプル数で動作します。これにより、SVGFは、視覚的にも(図6参照)、RMSEとSSIMの観点からも(表1)、先行研究よりも大幅に優れた品質を実現しています。
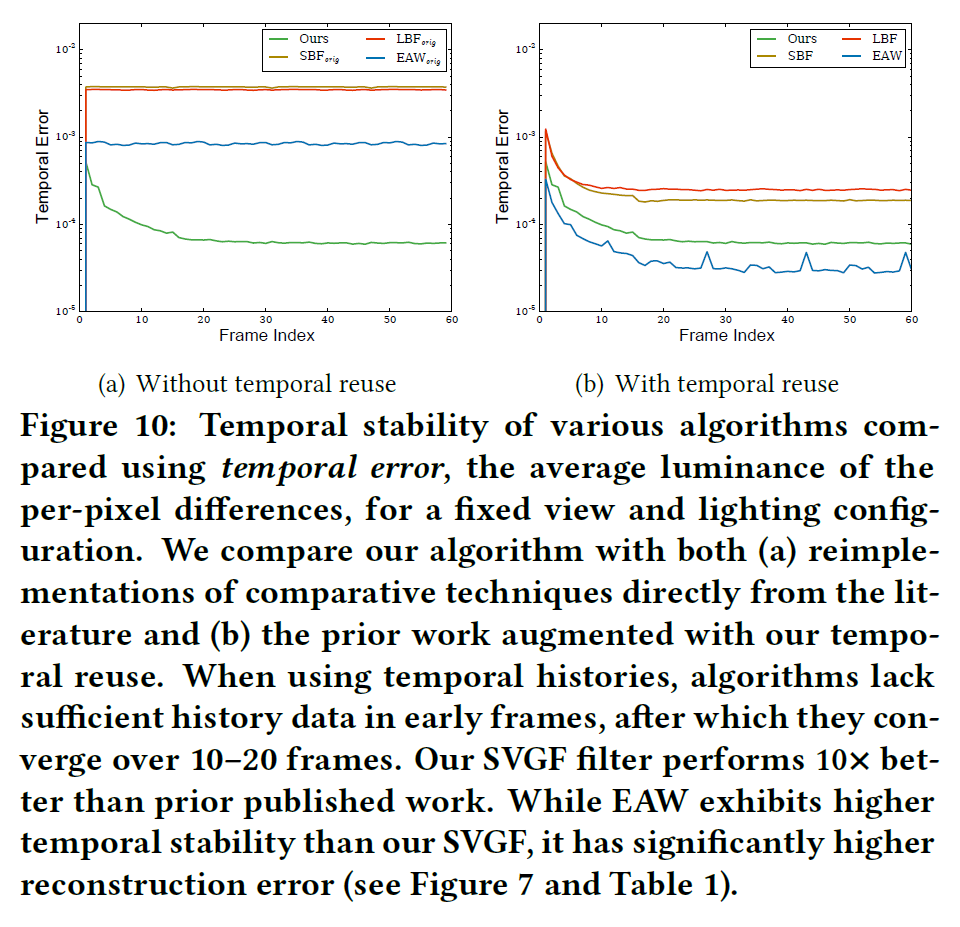
また、図10(a)では、SVGFはフレーム間の変動が10倍少なく、時間的な安定性が非常に高いことがわかります。視覚的な時間的安定性の比較については、補足のビデオを参照してください。
残りの比較評価では、我々の時間的蓄積と後処理の時間的アンチエイリアシングを用いて先行研究を補強しています。時間的な蓄積は有効なサンプル数を増加させるので、分散誘導型再構成フィルターを比較するための公平な場を提供できると考えています。オリジナルのEAW、SBF、LBF、AAFのアルゴリズムは、テンポラルアキュムレーションを使用していませんが、画質(表1)と時間的安定性(図10(b))の両方で大幅な改善が見られました。わかりやすくするために,テンポラルアキュムレーションを行わない実装を\({\rm EAW}_{orig}\),\({\rm SBF}_{orig}\),\({\rm LBF}_{orig}\)と呼ぶことにします.
AAFはMehtaら[2012]の記述に従っています。我々のレイバジェットではピクセルあたり1本の影の光線しか使用できないため,固定された空間ウィンドウで最小および最大のオクルージョン距離を収集します。推定されたオクルージョン距離には,可視性の入力と同様に時間的フィルタリングを適用します。
我々のSBF [2012]の実装では、適応型サンプリングを行っていません。画素ごとに1つのサンプルしかないので,小さな空間的な窓関数を使って色分散を推定します.著者のアドバイスに従い,ノイズのない特徴量の距離関数(例:深度,法線,アルベド)の繰り込みをスキップします.直接照明と間接照明の両方を含む、時間的に蓄積された復調されたサンプルに対してフィルタを実行します。
LBF[2015]では、サンプルコードで提供されている事前に学習されたネットワークの重みを使用しています。私たちのシーンでは再学習を行わず、ネットワークの入力はすべて彼らの論文に記載されている通りに計算しました。我々は,直接照明と間接照明の両方を含む,時間的にフィルタリングされたカラー入力をフィルタに与えます.ネットワークへの入力には,直接および間接のアルベドと,ファーストバウンスの可視性情報が含まれているため,サンプルには復調を適用しませんでした.
このフィルターは、空間的にフィルタリングされたサンプルをテンポラルアキュムレーションの入力としているため(図3参照)、空間フィルターは技術的には比較フィルターと同じ入力を使用していません。しかし,すべての結果は決定論的にレンダリングされるため,すべてのフィルタは,同一のサンプル位置で同一のパストレースされたサンプルのセットに対して実行されます.
5.2 Image Quality
複数のシーンでの画質を評価します。SPONZAとGLOSSY-SPONZAでは、孤立した拡散照明と高光沢照明を評価しています。
REDROOM、SANMIGUEL、CLASSROOMでは、実世界の環境に似た複雑な幾何学的・物質的なインタラクションを実現しています。アニメーションには、REDROOMとSPONZAでのライトの動きや、SPONZA、GLOSSYSPONZA、SANMIGUEL、CLASSROOMでのカメラの動きなどがあります。アニメーションシーケンスを60Hzでレンダリングし,各再構成手法に1ppのパストレース入力を与えました.
図7は、これらのアニメーションのフレームを選択して詳細に比較したもので、結果の主な違いを示すために挿入図を使用しています。この図では、他の結果と同様に、先行研究を時間的に補強したものを使用しています。表1は,Roo-Mean Square Error(RMSE)とStructural Similarity Index(SSIM)[Wang et al.2004]という指標を用いて,4096種のリファレンスとの差異を定量化したものです.また,補足資料として,最終的なアニメーションの比較映像を掲載しています.
質的には、我々の再構成結果は、過去の研究よりもリファレンスに忠実です。また、SANMIGUELの葉の部分など、幾何学的なディテールが多く、ディスクロージョンが多い領域でも、もっともらしい結果が得られています。RMSEとSSIMは、SVGFが先行研究と比較してより良い、または同等の結果を与えることを示し、これらの観察をサポートしています。先行研究で再構成された画像のSSIMは、我々のアルゴリズムよりも2%から25%低い値を示しています。
グローバルに調整されたエッジストップ機能のため、EAQフィルターでは目立つディテールを保持できません。SPONZAの柔らかな影やGLOSSYSPONZAの艶やかな反射などに顕著に現れています。また、EAQフィルターは、ジオメトリベースのエッジストップ関数が最適でないため、再構成出力にハローが発生します(図7、SPONZA、シアン色の挿入図)。LBFは、表面の質感が失われ、影の部分にノイズが発生します。SBFは、多くの重要な特徴を捉えていますが、強い中周波ノイズが見られます。
Effectiveness of temporal variance estimation. SVGFのディテール保持能力を検証するために、サンプリング密度を変化させた構造化ノイズを含む合成テストシーンを設計しました。図9は、このテストの入力を示しており、空間フォールバックと時空間フィルタの結果をリファレンスと比較しています。テストパターンの入力は、各画素が以下の分布からサンプリングされた画像です。
\begin{eqnarray}
f(x, \alpha) = \begin{cases} 0 & {\rm if} \quad x \lt \alpha \\ \frac{1}{1-\alpha} & {\rm otherwise} \end{cases}
\end{eqnarray}
\(\alpha \in [0, 1)\)で積分値\(\int_0^1 f(x, \alpha) dx = 1\)を推定します。左から右に向かって、\(\alpha\)を変化させながら、徐々に分散を大きくしていきます。
時間的な再投影に失敗した場合、再構成フィルタは統計量を推定するための履歴を持たず、空間的な推定値に頼らざるを得ません。時間的分散の推定値は、フィルタがノイズの少ない領域でシャープネスを維持することを可能にしますが、空間的分散は画像全体に高い量のバイアスがかかります。我々のフィルタは、あるサンプリング確率を超えると、構造を忠実に再現できなくなりますが(図9の右側)、時間的分散推定はその限界点をさらに押し上げることになることに注意してください。
5.3 Performance
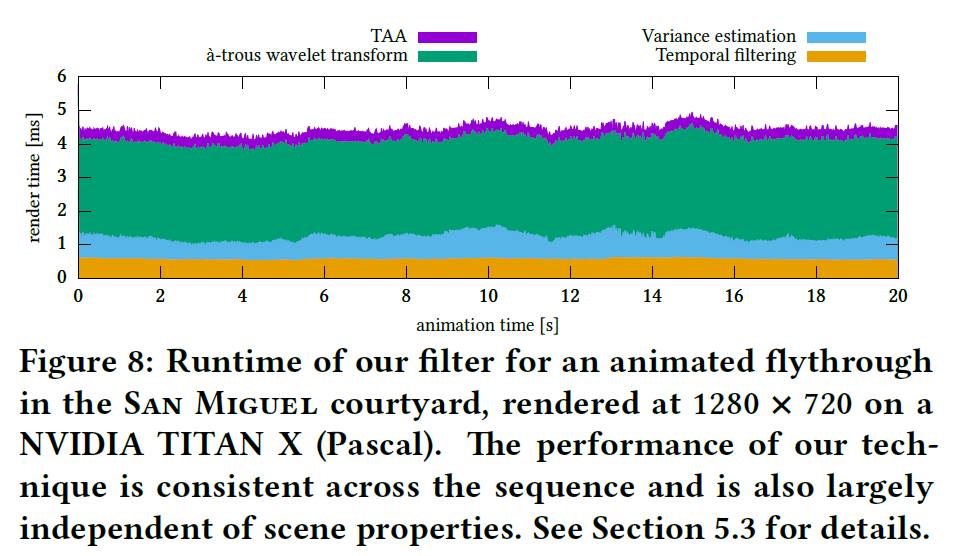
SVGFはリアルタイムでの再構成を想定して設計されていますので、ここではその性能を評価してみます。図8は、SANMIGUELの中庭を\(1280 \times 720\)でフライスルーしたときのフレーム実行時間を示しています。この中庭には、現実的な量の薄いディテールとディスクルージョンが含まれていると考えられます。SVGFのコストは4.1msから5.8msの間で変化しています。最初のフレームを除くと、パフォーマンスのばらつきは平均4.4msのコストの15%以下です。この変動はすべて分散推定(4.2項)によるもので、時間的な再投影に失敗した場合、分散推定のためにクロスバイラテラルフィルタに差し戻ります。フレームコストは、葉の多いフレームなど、排除された部分の数に応じて増加します。最悪のケースのフレームは稀で、通常はアプリケーションの起動時やカメラパスの不連続時に発生し、フレーム全体に渡って離散が発生します。このような場合(図8には示されていません),我々の実装はベストケースのパフォーマンスよりも約50%悪くなります。
SVGFの性能は、解像度に応じてリニアに変化します。フレームあたりの平均コストは\(1280 \times 720\)で4.4ms、1920×1080で10.2msとなり、約200MPixels/secの処理が可能となります。
5.4 Temporal Stability
図10(b)は、我々の時間的安定性を先行研究と比較したものです。SPONZAの60フレームのシーケンスに対して、静的な照明、カメラ、シーンを使用し、連続したフレーム間の差の平均輝度を測定することで、時間的安定性を定量化しています(これを時間的誤差と呼びます)。フィルターの時間的な収束を示しています。
どのアルゴリズムも、最初は十分な履歴がないために時間的誤差が大きくなりますが、すぐに収束し、すべての変動がサンプルパターンの繰り返しから生じるようになります。EAQは時間的誤差が最も小さいものの,再構成時に細部が大きく失われます(図7参照)。EAWは空間的な偏りが大きいため(エッジを止める機能が不十分なため),より多くのピクセルを結合し,高い偏りと時間的な安定性を両立させています。SVGFはEAWに近い時間的誤差を与えますが、画質ははるかに高くなります。
5.5 Applicability
SVGFはシーンの光輸送に関する特別な知識を必要としないため、レイトレーシングが必要とされる様々な状況に適用できます。図12は、光沢反射の正確な再構成(図7参照)に加え、SVGFが1 sppの入力からアンビエントオクルージョンを再構成できることを示しています。さらに、1つのサンプルから複数のライトからのイルミネーションを再構築することができます。これは、各ライトに対してシャドウマップを照会するラスタライズよりも大きな改善です。いずれの場合も、4096sppのリファレンスに近い形で再構成されています。
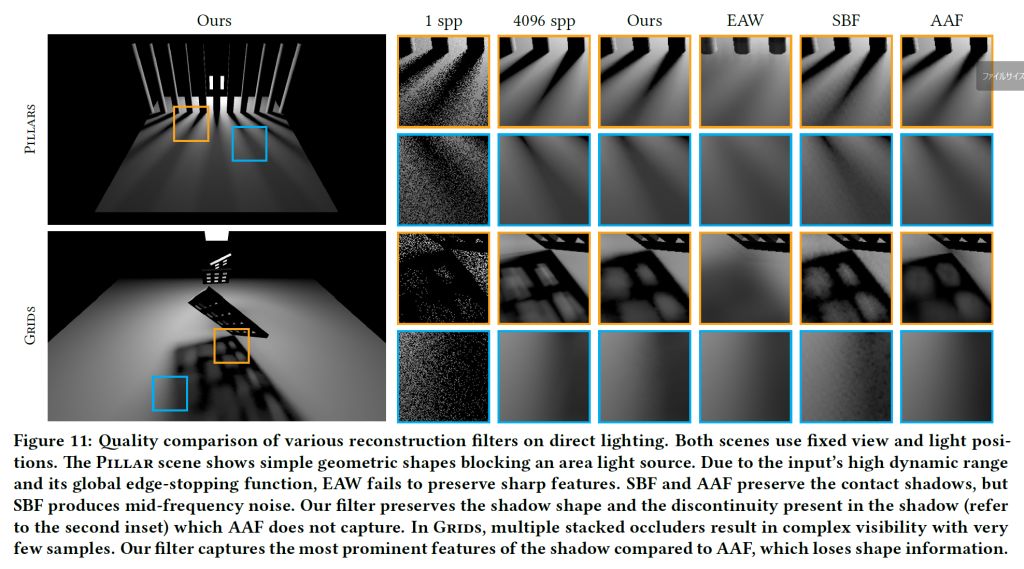
図11は、直接照明を再構成したときの品質を比較したものです。このシーンには、明るいエリアライトによる複雑な影が含まれています。EAQは非適応的なエッジストップ機能によりディテールが失われ、SBFは大きなノイズを残しています。AAFも多くの影のディテールを保持していますが、微妙な影の形状を失うという代償を払っています。全体として、SVGFはドメイン固有の知識を使わずに、正確な再構成を行います。図11は、間接照明がない場合でも先行研究の結果が悪いことを示しており、直接照明と間接照明を分けて別々にフィルタリングすることが、我々の再構成品質向上の唯一の原因ではないことを強調しています。
5.6 Filter Scalability with Additional Samples
私たちは、今日では1spp以下でしか成立しないリアルタイム・パストレーシングのための高品質なフィルターの開発を目指しました。この目標とするサンプリングレートによって、多くの設計上の決定がなされました。この決定は、現在のフィルター設計の範囲外である、より高いサンプリングレートでの作業を考慮して見直す必要があります。
例えば、1 sppの場合、従来の分散の推定は、各ピクセルからの単一のサンプルでは意味がありません。4.2節では、分散を推定するために、時間的アンチエイリアシングでよく見られるように、指数移動平均を用いて、時間的に分散を蓄積します。算術平均を使用しない場合、この推定値はサンプルを追加しても実際の分散に収束しません。そのため,サンプル数の多い画像を使用する場合には,より伝統的な分散計算を行うべきかどうかを再検討する必要があります。
6 LIMITATIONS
このフィルターは、非常にノイズの多いモンテカルロ画像を時間的に安定してリアルタイムで再構成することができますが、このアルゴリズムを改善できるシナリオがあります。
Over-Blurred Chrominance. エッジストッピング関数では輝度の分散のみを計算して追跡しているため、このフィルターではクロミナンスが過剰にぼやけてしまうことがあります。例えば、図7のGLOSSYSPONZAの下の挿入図にある多色の反射を見てください。リファレンスやSBFと比較して、本フィルタは色付きの反射をぼかしすぎていることに注意してください。この問題は、色成分ごとに分散を推定することで解決できますが、メモリや計算のコストが増えてしまいます。
Detached Shadows in Motion. 光源の近くを高速で移動するジオメトリには、離された影ができることがあります(図13(a)のパイプの影を参照)。これは、時間的な蓄積が、物体の動きによる照明の変化を意識していないためです。
Temporally Unstable Noise in Extremely Low-Light. このアルゴリズムでは、間接光で薄暗い地域など、光の移動によってサンプル数が非常に少なくなる場合に、時間的に不安定なノイズが発生することがあります。Diffuse SPONZAの映像では2階の廊下の端、図13(b)ではこの映像シーケンスの露光強調画像、図9では右端の領域を参照してください。サンプル密度がゼロに近づくと、分散の推定値の信頼性がますます低くなり、フィルタはもっともらしい画像を復元できなくなります。
Our-Blurred Specular Reflections. 理想的な条件では、このアルゴリズムは鏡面反射を正しく再現することができます(図13(c)参照)。しかし、間接照明を確率的にサンプリングしているために反射光にノイズがある場合は、フィルターによってノイズが除去され、反射光がぼやけてしまいます(図13(d)参照)。
Incompatible with Stochastic Primary Ray Effects. 我々のフィルタは、プライマリレイヒットのバッファ(G-buffer)からの分散を測定することに依存しています。そのため,一次光線にモンテカルロノイズが含まれていないことが条件となり,stochastic transparency,stochastic depth-of-field,stochastic motion blurなどのstochastic primary ray effectとは互換性がありません。
7 CONCLUSION
本論文では、リアルタイムレンダリングに適した新しい再構成アルゴリズムを紹介しました。我々のフィルタの性能と品質が達成されたことで、リアルタイムグラフィックスにおけるパストレーシングの使用を制限していた性能の差を大幅に縮めることができ、ピクセルあたり単一のパスだけで動作する初の実用的なリアルタイム再構成フィルタであると確信しています。
SVGFの品質向上は、画素ごとの分散の不完全な代理として使用する時空間分散推定値に依存しています。この推定値を用いて、空間ウェーブレットベースのフィルタを制御し、分散推定値と同様に色を階層的にフィルタリングしています。そのため,分散推定値が不正確な場合に最大となる再構成誤差は,局所的なものにとどまり,再構成の信頼性は反復ごとに向上します.
その結果、SVGFは従来と比べて格段に高い品質の再構成を実現しています。私たちの研究は、非線形時空間再構成という大きなデザインスペースを探求する上で重要なステップであると考えています。私たちは、この分野において、より高速で、より高品質で、セクション6で説明したアーティファクトのないアルゴリズムの探求を続けていきたいと考えています。
8 ACKNOWLEDGEMENTS
執筆に協力してくれたPetrik Clarberg氏、Falcorフレームワークに協力してくれたNir Bently氏、そしてシーンを我々のレンダラーに合わせてくれたNicholas Hull氏に感謝します。また、多数の匿名の査読者の方々には、本稿の改善に向けて貴重なご意見をいただきました。