前回に引き続き，“Progressive Photon Mapping : A Probabilistic Approach”のものすごーく適当でいい加減で雑な和訳をやっていきます。今回は４章からです。

 

4.  PROBLEM FORMULATION

---

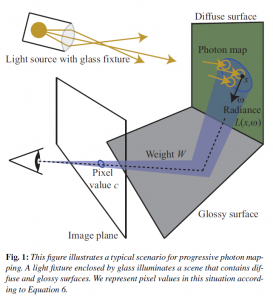
このセクションでは，プログレッシブフォトンマッピング(PPM)と確率的PPMの新しく，より一般的な導出を紹介します。我々は，フォトンの放射輝度推定において特定のカーネルに依存しない確率的なフレームワークを使用します。それはまた，ローカルの統計量をメンテナンスすることに依存しません。我々の目標は，図１で描かれたような以下の式のピクセル値\(c\)を計算することです。
\[
c = \int W(x, \omega)L(x, \omega)dxd\omega
\tag{6}
\]
シーンのすべての表面点上と各点半球の各点における方向を渡って積分します。ここで\(L(x, \omega)\)はシーンの表面上に廻って反射された放射輝度の分布です。我々のアルゴリズムでは，フォトンマッピングを用いて\(L\)を近似します。さらに，\(W\)は重みづけ関数で，各表面位置\(x\)と方向\(\omega\)のピクセル値への\(L\)の寄与として記述されます。この重みは，アンチエリアシングのためのピクセルフィルタを含むことができ，モーションブラーや，被写界深度，光沢のある反射のような特殊効果を含むこともできます。一般的には，視経路追跡によって\(W\)を評価します。

※図は論文より引用

 

4.1 Monte Carlo Approximation and Photon Maps

従来のフォトンマッピングの主な問題は，放射輝度推定において分散やノイズと期待誤差あるいはバイアス間のトレードオフが存在することです。分散を低くすることか期待誤差を低くすることのどちらか一方を達成することが可能でありますが，両方達成はできません。プログレッシブフォトンマッピングの主な洞察は，極限において分散をなくし，多数のフォトンマップの結果を平均化することによって期待する解を得られるということです。これがどのように可能であるかを説明するために，モンテカルロ推定として式6の評価を定式化します。我々は反射された真の放射輝度の近似値を得るためにフォトンマップを使用します。\(L(x, \omega) + \epsilon\)として近似を記述します。ここで，\(\epsilon\)は放射輝度推定によって導入された誤差を示しています。簡潔のために，省略表現\(\epsilon_{i}=\epsilon(x, r_{i})\)を用いて，誤差の独立変数を省略します。このモデルを用いて，モンテカルロ推定は以下になります。
\[
\bar{c}_{N} = \frac{1}{N}\sum^{N}_{i=1}\frac{1}{p_{e}(x_{i}, \omega_{i})}W(x_{i}, \omega_{i})(L(x_{i}, \omega_{i})+\epsilon_{i})
\tag{7}
\]
ここで，\(\bar{c}_{N}\)は，視経路で\(N\)個のサンプルを用いてピクセルの値を推定することを示しています。サンプル\((x_{i}, \omega_{i})\)は目から開始したレイトレーシングによって生成されたパスの面と交差する位置と方向を示しており，それらの確率密度は\(p_{e}(x_{i}, \omega_{i})\)です。\(\epsilon_{i}\)によって\(i\)番目のサンプルの放射輝度推定誤差を示します。

今，我々のアルゴリズムの目標は，期待値\({\rm E}[\bar{c}_{N}]\)が真のピクセル値\(c\)に収束し，サンプル数\(N\)が増加するにつれて分散\({\rm Var}[\bar{c}_{N}]\)がゼロに近づくような推定値\(\bar{c}_{N}\)を得ることです。プログレッシブフォトンマッピングの極めて重要な性質は，各サンプルが新しいフォトン分布，つまり新しいフォトンマップを用いて評価されるということです。したがって，放射輝度推定の誤差はランダムなフォトンの分布に依存するので，ランダム変数のサンプルとして\(\epsilon_{i}\)を解釈します。以下の式によって\(N\)個上のフォトンマップの放射輝度推定値の平均誤差を示すとしましょう。
\[
\bar{\epsilon}_{N}=\frac{1}{N}\sum^{N}_{i=1}\epsilon_{i}
\tag{8}
\]
Appendix CとDにおいて分散と平均誤差の期待値が同時にゼロになることを確証することによって我々の目的を達することが可能であることをします。つまり，
\[
N \rightarrow \inftyで，\nonumber \\
{\rm Var}[\bar{\epsilon}_{N}] \rightarrow 0 \Rightarrow {\rm Var}[\bar{c}_N] \rightarrow 0 \nonumber \\
{\rm E}[\epsilon_{N}] \rightarrow 0 \Rightarrow {\rm E}[\bar{c}_{N}] \rightarrow c
\tag{9}
\]
ここで，
\[
{\rm Var}[\bar{\epsilon}_{N}]=\frac{1}{N^2}\sum^{N}_{i=1}{\rm Var}[\epsilon_{i}]　であり， {\rm E}[\bar{\epsilon}_{i]}] = \frac{1}{N}\sum^{N}_{i=1}{\rm E}[\epsilon_{i}]
\tag{10}
\]
とします。
これらの収束条件をすべて満たす戦略を次に提示します。

 

4.2 Achieving Convergence

先ほどの式から明らかになるのは，各誤差の分散\({\rm Var}[\epsilon_{i}]\)が定数のままである場合に，平均誤差の分散\({\rm Var}[\bar{\epsilon}_{N}]\)がゼロになるということです。しかしながら，この場合においては平均誤差の期待値\({\rm E}[\bar{\epsilon}_{N}]\)は消えません。プログレッシブフォトンマッピングの主なアイデアは各ステップにおいて小さな係数によって放射輝度推定の分散させることですが，平均においては消失したままです。今度は，式4に示すようにカーネル半径の減少に従って分散を増加させると，式5に示すような期待誤差を減らします。この考えの基づき，我々は分散の消滅と平均誤差の期待値を同時に得ることができます。

平均誤差の分散。
元来のプログレッシブフォトンマッピングの定式化と同様にして，各サンプルにおいて以下の因子によって誤差の分散を増加させます。
\[
\frac{{\rm Var}[\epsilon_{i+1}]}{{\rm Var}[\epsilon_{i}]} = \frac{i+1}{i+\alpha}
\tag{11}
\]
ある定数値\(\alpha\)について\(0 < \alpha < 1\)とします。パラメータ\(\alpha\)は各イタレーションにおいてどれくらい速く分散を増加させるかを制御するものです。\(\alpha\)は効果的に分散の消失と平均誤差の期待値の間のトレードオフを決定するものとみなします。最初のサンプルの初期の分散が\({\rm Var}[\epsilon_{1}]\)であると仮定すると，\(i\)番目のサンプルに関する式は次のようになります。 \[ {\rm Var}[\epsilon_{i}] = {\rm Var}[\epsilon_{1}](\prod^{i-1}_{k=1}\frac{k}{k+\alpha})i \tag{12} \] Appendix Eにて，この数列を用いて，平均誤差の分散\({\rm Var}[\bar{\epsilon}_{N}]\)が以下のようになることを示します。 \[ {\rm Var}[\bar{\epsilon}_{N}] = \frac{{\rm Var}[\epsilon_{1}]}{N^{2}}(1 + \sum^{N}_{i=2}(\prod^{i-1}_{k=1}\frac{k}{k+\alpha})i) \tag{13} \] また，この式の漸化解析が示すのは，\(O(1/N^{\alpha})\)のオーダで分散が消失することを示しています。 \[ {\rm Var}[\bar{\epsilon}_{N}] = O(1/N^{\alpha}) \tag{14} \] ここで，\(N\)はサンプルの数です。 平均誤差の期待値。
式4から分散は半径の2乗に半比例することを思い出してください。上述の分散の数列を与えられると，カーネル半径の数列に一致するものを取得します。
\[
\frac{r^{2}_{i+1}}{r^{2}_{i}} = \frac{{\rm Var}[\epsilon_{i}]}{{\rm Var}[\epsilon_{i+1}]} = \frac{i+\alpha}{i+1}
\tag{15}
\]
式12と同様にして，初期半径\(r_{1}\)が与えれると，半径\(r_{i}\)に関する式を得ます。
\[
r^{2}_{i} = r^{2}_{1}(\prod^{i-1}_{k=1}\frac{k+\alpha}{k})\frac{1}{i}
\tag{16}
\]
期待誤差は半径の2乗に比例するので(式5), \(i\)番目のサンプルの期待誤差は以下のようになります（ただし，\(i > 1\)とする)
\[
{\rm E}[\epsilon_{i}] = {\rm E}[\epsilon_{1}](\prod^{i-1}_{k=1}\frac{k+\alpha}{k})\frac{1}{i}
\tag{17}
\]
そして，平均誤差の期待値は次のようになります。
\[
{\rm E}[\bar{\epsilon}_{N}] = \frac{{\rm E}[\epsilon_{1}]}{N}( 1 + \sum^{N}_{i=2}(\prod^{i-1}_{k=1}\frac{k+\alpha}{k})\frac{1}{i})
\tag{18}
\]
Appendix Fに示すように\(O(1/N^{1-\alpha})\)のオーダになると消滅します。すなわち，
\[
{\rm E}[\bar{\epsilon}_{N}] = O(1/N^{1-\alpha})
\tag{19}
\]
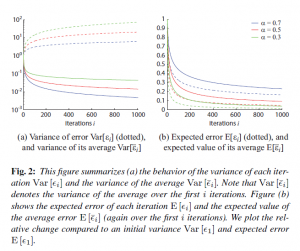
です。図2aにおいて，各イタレーションにおける誤差の分散の振る舞い（式12)と平均誤差の分散(式13)の目に見えるようにまとめます。図は，各イタレーションにおける分散がどのように増加するかを示しています。その一方で，平均の分散は減少する一方です。同様にして，図2bでは各イタレーションにおける期待誤差(式17)と平均誤差の期待値(式18)をプロットします。要約すると，分散と平均誤差の期待値は\(0 < \alpha < 1\)の場合に消滅します。ここで\(\alpha\)は減少の相対比率を制御します。

※図は論文より引用。

また，Appendix Gで証明するように蜂須賀ら[2008]によって提案された半径減少スキームはローカルのフォトン密度が一定であるということを仮定している式15によって与えられるような半径の同じ数列を導きます。これは驚くべきことかもしれません。なぜかというと，彼らのアプローチはローカルの統計量を収集し，収集されたデータに基づき半径を減少させるからです。我々の証明が示すのは，減少された半径の比率がローカルのフォトン密度に非依存であり，集められた統計量は不要であるということです。

ボリューメトリックプログレッシブフォトンマッピング。我々の導出の主な利点の1つは，ボリュームメトリックなプログレッシブフォトンマッピングに拡張するのが軽微であるということです。式6からのピクセル値を計算する我々のモデルは加入している媒体に対して同じということです。この場合では，放射輝度\(L\)は表面上の代わりとして体積で定義でき，ボリュームメトリックなフォトンマップを用いて近似します。加えて，重みづけ関数\(W\)は視光線に沿った減衰を含んでいます。最終的に，積分は表面上を廻る代わりに3次元の空間に廻ったものになります。

平均誤差の分散の消失を得るために式12と同じようなスキームを使用することができます。これは式15に似た半径の数列を導き出します。
\[
\frac{r^{3}_{i+1}}{r^{3}_{i}} = \frac{{\rm Var}[\epsilon_{i}]}{{\rm Var}[\epsilon_{i+1}]} = \frac{i+\alpha}{i+1}
\tag{20}
\]
付録からの我々の漸近線解析は体積がある場合に同様にしてすぐさま適用します。結果として，平均誤差の分散\({\rm Var}[\bar{\epsilon}_{N}]\)に対して\(O(1/N^{\alpha})\)で，平均誤差の期待値\({\rm E}[\bar{\epsilon}_{N}]\)に対して\(O(1/N^{1-\alpha})\)と同じ収束オーダを得ます。