D. Brandon Lloyd氏の博士論文である，Logarithmic Perspective Shadow Mapsを適当に訳していくことにします。
今回はChapter.7を訳していくことにします。
誤訳があったりなど，日本語としては多々見苦しい点があるかと思いますが，そこはご容赦ください。

---

CHAPTER 7

Logarithmic rasterization hardware

影の重要性はベンダーにハードウェア機能の導入と具体的には影のレンダリング(NVIDIA Corp., 2004)のコストを減らすことにおいての最適化を導きました。この章では，高品質なシャドウマップを描画することのサポートするためのハードウェア機能拡張の追加について紹介します。シャドウマップは現在のGPUの莫大なフィルレートを生かします。例えば，GeForce 8800は1クロックあたり192サンプルを\(z\)-onlyレンダリングのために生成します(NVIDIA Corp., 2006)。575MHzのGPUクロックレートでは，1秒当たり1100億ピクセルの驚異的なフィルレートに相当します。これらのフィルレートは深度バッファ圧縮と連動してラスタライゼーションを使用することによって得られます。ラスタライゼーションは並列性を多用し，計算とメモリアクセスの両方の高度な一貫性を有効に使います。圧縮は利用可能なメモリ帯域の効率的な使用を与えます。現在のGPUもまた高速なメモリインタフェースを持っています。それにも関わらず，メモリ帯域はまだ高解像度なシャドウマップについてボトルネックになる可能性があります。また，高解像度なシャドウマップは高いストレージコストと制限があるGPUメモリについて競合を増加させます。
　LogPSMsはこれらの問題を軽減に役立つ可能性があります。競合するシャドウマップアルゴリズムと同じ誤差については，LogPSMsはより低い解像度で済みます。不運なことに，LogPSMsによって必要とされる対数ラスタライゼーションは現在のGPU上ではサポートされていません。この章では，グラフィックスハードウェアへの追加の修正を通じて対数ラスタライゼーションを実装する方法について説明します。我々が提案する機能拡張の主な利点は既存のハードウェア設計を利用することです。我々の低コストな機能拡張は、以前の機能を損なうことなく，既存のシャドウマップアルゴリズムを超える有意な改善を可能にします。対数ラスタライゼーションは追加の少量の計算力を必要とし，著しい帯域幅とストレージの節約を生み出すことが出来ます。それゆえ，これらの機能拡張はオンチップの計算のためのコストと比較的に高いオフチップの帯域幅についてのコストを減らす現在のハードウェア傾向とうまく整合します。
この章では，ややシンプルな記法を採用しています。透視変換後の座標を示すために,
\((x, y) \in [0, 1]^2\) を使用します。\(y’\) は対数変換 \(F\) 適用後の \(y\) 座標を示します：
\[
y’ = F(y) = c_0 \log(c_1 y + 1) \tag{7.1} \\
c_0 = \frac{-1}{\log (f/n)}, \hspace{1cm} c_1 = \frac{1-(f/n)}{(f/n)},
\]
ここで，\(n\) と \(f\) は透視変換に使われるニア平面とファー平面の距離です。
　LogPSMパラメータライゼーションの透視部分は標準のグラフィックスパイプラインを用いて処理することが出来ます。しかしながら，対数ラスタライゼーションに必要とされる対数部分は平面のプリミティブを曲線にします。平面プリミティブと同様のレートで湾曲したプリミティブをラスタライズするためには，ハードウェアコンポーネントの2つの固定機能を修正をします―それは，ラスタライザーと深度圧縮です。エッジ方程式に基づくラスタライゼーションを軽く見た後で，修正の説明をします。

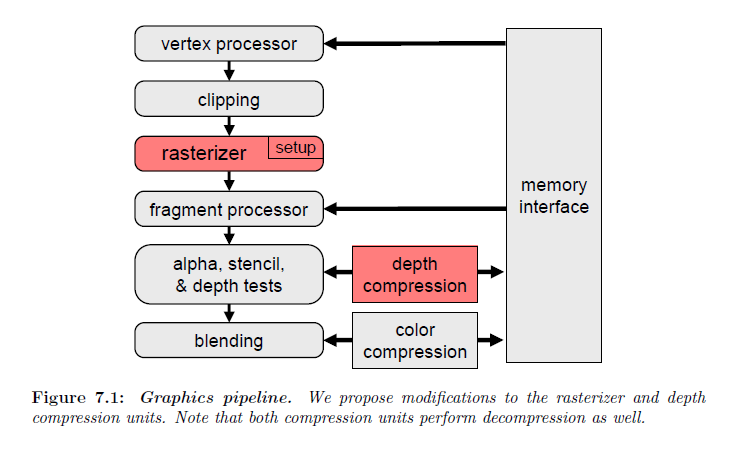
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.149 より引用。

7.1 Rasterizing with edge equations

ラスタライザーは主に2つの機能を実行します。最初に，プリミティブによって覆われているピクセルがどれであるかを決定します。次に，ピクセルに覆われている頂点からのアトリビュートを線形補間します。現代の高パフォーマンスグラフィックスハードウェア上での範囲決定は普通，以下の一般形式の暗黙的なエッジ方程式を使用することで行われます：
\[
E(x, y) = Ax + By + C. \tag{7.2}
\]
点 \((x, y)\) における記号 \(E\) は点があるエッジ側を示します。凸包プリミティブ内の点は全てエッジの正側にあります。エッジ方程式を用いたラスタライゼーションの主な利点の一つは多くのピクセルについて \(E\) の方程式を並列化しやすいということです。現在のGPUは並列でタイルサンプル（例えば 4×4のブロック）についてエッジ方程式を評価します。ハードウェアの使用を最も効率的にするために，GPUは画像を階層的なトラバーサルを行います。粗いステージでは，少なくとも潜在的にプリミティブによって覆われるタイルを特定します。タイルはページされたメモリとキャッシュコヒーレンスを最大化するのに良い方法でトラバースされます(Pineda, 1998; McCormack & McNamara, 200; McCoolら, 2001)。洗練されたステージはタイル内の個々のサンプルについて範囲を計算します。例えばカラーや深度，テクスチャ座標のようなピクセルについてのアトリビュートは式7.2と同様の形式の式を用いて頂点から線形補間されます。OlanoとGreer(1997)はこれらの方程式を効率的に計算する方法を示しました。係数はラスタライザのセットアップの段階において計算されます。
　エッジ方程式は大抵，固定小数点制度で計算されます。浮動小数から固定小数への頂点位置の変換はユニフォームグリッド上の離散的な座標へ頂点を”スナッピング”することとして考えることができます。離散的な座標を用いたエッジ方程式は打ち切り誤差を避けるために十分な数のビットを用いて任意のグリッド位置で正確に評価することが出来ます。これは数値的に頑健な問題から生じる可能性があるダブルヒットまたはピクセル欠けなしの水密なラスタライゼーションを提供します。

7.2 Logarithmic rasterization

対数ラスタライゼーションはユニフォームグリッド上の湾曲したプリミティブをラスタライズすることまたは1次元のみ非均一のグリッド上の線形プリミティブをラスタライズすることとして考えることができます（図7.2参照）。我々は対数ラスタライゼーションをサポートするために線形ラスタライゼーションがどのように拡張可能であるかを説明するのを楽にするため後者の観点を採用します。我々のアプローチはサンプルを明確に表現するために十分細かい均一グッドに内在する位置へ非均一のグリッドサンプルへスナップすることです。このとき，エッジ方程式は水密なラスタライゼーションを提供するために固定小数の算術演算を用いて正確に評価することができます。
　これから修正したエッジ方程式，範囲を計算する方法，評価するために必要とされる精度の量，そして自己シャドウアーティファクトを処理するための一般化されたポリゴンオフセットについて説明します。

7.2.1 Modified edge and interpolation equations

対数ラスタライゼーションについてのエッジ方程式は歪んだ空間上の変換した \(y’\) を式7.1の逆関数を用いて線形空間上の \(y\) へと戻すによって計算することができ，式7.2を用いた結果から成ります：
\begin{align}
E'(x, y’) = E(x, G(y’)) = Ax + BG(y’) + C \tag{7.3} \\
G(y’) = F^{-1}(y’) = \frac{e^{(y’/c_0)}-1}{c_1} = \frac{(f/n)(1-(f/n)^{-y’})}{(f/n)-1}. \tag{7.4}
\end{align}
同様にして補間式は処理されます。注意してほしいのは，これらの方程式の係数はLogPSMパラメータライゼーションの透視部分から結果として生じる線形空間上の頂点位置に基づいていることです。頂点位置を用いてタイルトラバーサルを初期化するラスタライゼーションアルゴリズムは開始点を得るために三角形をセットアップする間，式7.1を頂点の \(y\) 座標へ適用することが出来ます。
　ラスタライズに使用されるアルゴリズムのいくつかは全てのタイルにわたってタイルコーナーにおいて計算されたそれらの量に対する保守的な境界を提供するという事実に依存している。例えば，タイルコーナーにおけるエッジ方程式の値はタイルトラーバサルを操作するために使われます。タイルコーナーから得られる保守的な深度境界は例えば階層的な \(z\)-バッファあるいは，\(z\)-最小と \(z\)-最大カリングとしてカリング最適化のために使われます。歪んだエッジと補間式はタイルコーナーにおける値はまだ保守的な境界を提供するので単調のままです。これが意味するのは，この性質に依存するアルゴリズムは修正なしで対数ラスタライゼーションのために使うことができるということです。

7.2.2 Converage determination

サンプルのタイルについての範囲は各サンプルのタイルについての範囲はエッジ方程式評価機の配列によりブルートフォースで計算することが出来ます。しかしながら，\(x\) 次におけるエッジ方程式をインクリメンタルに計算するために \(E’\) の線形性を活用することによってダイの領域を一定に保ちます：
\[
E'(x_0 + \Delta x, y’) = E'(x_0, y’) + A \Delta x. \tag{7.5}
\]
我々は最初に，タイルの最初の列のサンプルに対して並列でエッジ方程式を完全な評価するすることを行います。このとき，残った列に対する値を最初の列に定数を単純に足すことによって並列に計算します。これらの計算はパイプライン化できるので，1クロックあたり4×4のタイルサンプルのレートで持続して計算することが出来ます。ダウンストリームバッファリングの数サイクルは各タイルと一緒に集計し，ダウンストリームユニットにブロードサイドを表示するために各タイルに対してビット範囲を割り当てます。このアプローチによって負担される追加のレイテンシ―は現在のGPUパイプラインの深度に比較して小さいです。対数ラスタライゼーションモードはシャドウマップのみについて使用されることを想定しているので，エイリアシングのマルチサンプリングについてのサンプル配置を考慮する問題は関係しません。
　エッジ方程式を評価することについてのその他の可能性が存在します。また１つの可能性は最初に列に沿ってインクリメンタルに \(G(y’)\) 項を計算することです。最初の行について \(G(y’)\) の完全な評価した後で，行 \(k\) に続く \(y’=y_0’\) の値は積和演算で並列に計算することができます：
\begin{align}
G(y’_0+ k\Delta y’) = G(y’_0)P_k + Q_k \tag{7.6} \\
P_k = (f/n)^{-k\Delta y’}, \hspace{0.5cm} Q_k = (f/n) \frac{(1 -(f/n)^{-k\Delta y’})}{(f/n)-1}. \tag{7.7}
\end{align}
定数 \(P_k\) と \(Q_k\) はパラメータライゼーションに依存し，シャドウマップ中の全てのプリミティブいついて使用されます。余分なステップを必要とし，余分なレイテンシーを生成するので最初の列について \(G(y’)\) をインクリメンタルに計算することはやや複雑です。他の可能性はスキャンラインにおいて \(G(y’)\) の値を事前計算し，テーブルに格納しておくことです。テーブルは頂点／フラグメントプロセッサについて既に利用可能な浮動小数ハードウェアを用いて構築できる可能性があります。タイル上での最初の列についてのエッジ方程式の評価はテーブルのルックアップと内積のみを伴います。所定の順序でトラバースされたタイルであるので，タイルに使用されるテーブルの各値はプリフェッチされます。テーブルは高解像度バッファについてかなり大きくする必要があります。サイズはタイルの最初の行のみについて \(G(y’)\) を事前計算をし，その他の行をインクリメンタルに計算することによってすこし減らすことができます。

7.2.3 Percision requirements

エッジ方程式を正確に評価するために \(G(y’)\) 値の固定小数が必要となります。少なくとも任意の2つの値 \(G(y’)\) と \(G(y’+\Delta y’)\) が明確に表現できる十分な固定小数精度を使用しなければなりません。言い換えると，最下位ビットは　\(\Delta G_{\rm min} = {\rm min}_{y’} | G(y’) – G(y’+\Delta y’)|\) よりも少ない量を表現すべきです。与えられた \(G\) の範囲は \([0,1]\) で，必要とされるビットの最小値は次になります：
\[
b_{\rm min} = \lceil \log_2 (1/\Delta G_{\rm min}) \rceil \tag{7.8}
\]
\(\Delta G_{\rm min}\) はニア平面に対するファー平面の深度比 \((f/n)\)　に依存するので，ビットの固定値を使用することは正確に描画できる深度比の範囲において制約を置くことになります。ラスタライザーに要求される \(2^{b_x} \times 2^{b_y}\) のバッファを想定しています。\(y’ \in [0,1]\) におけるユニフォームサンプル間の距離は \(\Delta y’ = 1/2^{b_y} = 2^{-b_y}\) です。図7.2から \(y=G(y’)\) 上の非均一空間の結果は \(y’=1\)　における最小であることが分かります。したがって，\(\Delta G_{\rm min} = G(1) – G(1-2^{-b_y})\) です。これを式7.8へと代入することで，\((f/n) \in [1, 10^5]\) についてかなりしっかりと境界付けされた表現を得ることが出来ます：
\[
b_{\rm min} < b_y + 0.8 \log_2 (f/n). \tag{7.9} \] エッジ方程式のセットアップに使われた頂点は32bit浮動小数の仮数部が24bit精度に制限されています。それゆえ，\(y\) 座標と \(G(y')\) の固定小数を表現するために24bitを選択しました。式7.9に \(b_{\rm min} = 24\) を代入し，最も大きな \((f/n)\) を的確に扱うことが出来る表現を得ます: \[ (f/n)_{\rm max} = 2^{\frac{(24-b_y)}{0.8}} \tag{7.10} \] \(4K \times 4K\) バッファに対して，\(b_y = 12\) で \((f/n)_{\rm max} \approx 3.3 \times 10^4\) です。この深度比はかなり大きいです。高い深度比をもつ視錐台について，\(z\)-パーティショニングは個々の分割された深度比を減らすために使用することが出来ます。既存のシャドウマップ手法とは違って，この\(z\)-パーティショニングはエイリアシングエラーを制御するためのものではなく，精度制限を処理するためのものです。幸いなことに，必要であれば任意の数に分割できます。例えば，シングルのLogPSMが1mから33,000m 離れたレシーバー上にシャドウを正確に描画することができます。シングル正方形分割はこの範囲が1,000,000mに近いです。 　標準のラスタライゼーションは普通，精度を上げるためにサブピクセルグリッドへと描画します。\(y\) 上のサブピクセル解像度を追加することは，\((f/n)_{\rm max}\) 上の制限をさらに強いる \(b_y\) を効率的に増加させます。しかしながら，我々のアプローチはすでに \(y\) 上のサブピクセル解像度に与えているので，これは必要ないかもしれません。\(\Delta G\) は \(y=1\) における \(\Delta G_{\rm min}\) から \(y=0\) における \((f/n) \Delta G_{\rm min}\) へと線形に増加します。深度比が \((f/n)_{\rm max}\) に等しくなったとき，観測者付近の範囲はサブピクセル解像度の有り余る量に恵まれます。より低いサブピクセル解像度が遠く離れた領域に対して利用可能になるとき，これは問題にならないかもしれません。なぜかというと，遠く離れた領域は重要性が低いという傾向があるからです。低い深度比については，サブピクセル解像度は近いところと遠く離れた領域の両方について利用可能となります。

7.2.4 Attribute interpolation

アトリビュート補間は \(E’\) と同じ形式の式を用います。補間式はエッジ方程式と同様の方法で評価することができます。唯一の違いは，正確に評価される必要がないので，浮動小数あるいはより低い精度の固定小数表現が使われる可能性があるということです。次のセクションにおいて説明するようにポリゴンオフセットの処理するために若干深度補間を修正します。

7.2.5 Generalized polygon offset

ポリゴンオフセットは間違った自己シャドウイングを避けるために生成する深度バイアスとしてたびたび使用されます。標準のオフセットは \(s \cdot m_z + u\) です。ここで \(s\) はスケール係数で， \(m_z\) はポリゴンの深度傾斜で，\(u\) は定数です。OpenGLの仕様(Segal & Akeley, 2006)は 深度傾斜の近似 \(m_z\) を次のように定義しています：
\[
m_z = {\rm max} \left( \left|\frac{\partial z}{\partial x}\right|, \left|\frac{\partial z}{\partial y}\right| \right). \tag{7.11}
\]
線形ラスタライゼーションについてのポリゴンオフセットはセットアップの段階で計算することができ，深度補間式へと畳み込みできます。対数ラスタライゼーションについて，連鎖律を用いて線形空間上で歪んだ空間の \(|\partial z \partial y’|\) の値を計算します：
\[
\left|\frac{\partial z}{\partial y’}\right| = \left|\frac{\partial z}{\partial y}\right| \left|\frac{\partial y}{\partial y’}\right| = \left|\frac{\partial z}{\partial y}\right| \left|\frac{c_1y + 1}{c_0 c_1}\right|. \tag{7.12}
\]
\(|(c_1 y + 1)/(c_0 c_1)|\) 項は \(y\) で減少します。線形ラスタライゼーションとは違って \(m_z\) は \(|\partial z/ \partial x|\) また \(|\partial z/ \partial y|\) のどちらもポリゴン全体についてではなく，対数ラスタライゼーションでの \(m_z\) は \(|\partial z/ \partial y’|\) から \(|\partial z/ \partial x|\) へと切り替わる可能性があります。これを扱うための1つの方法は，2つの深度補間式を使用することであり，\(|\partial z/\partial x|\) と \(|\partial z/ \partial y’|\) それぞれについてのポリゴンオフセットを組み合わせることです。 このとき，最大値演算はピクセルごとに実行します。もう一つの可能性は切り替えが発生する場所においてスキャンラインに沿ったポリゴンを分割することです。各ポリゴンの半分はこのときに適切な深度補間式でラスタライズさせます。しかしながら，最も単純なアプローチは \(m_{z0}\) を計算することであり，\(m_{z1}\) はポリゴンの下限 \(y\) \(y_0\) においての \(m_z\) と 上限 \(y_1\)　における \(m_z\) の値であり，単一の式 \(m_z(y)\) はそれらを使用して線形に変化します：
\[
m_z(y) = \frac{m_{z0}(y_1 – y) + m_{z1}(y-y_0)}{(y_1 – y_0)} \tag{7.13}
\]
この式を用いて計算されるオフセットは単一の深度補間式へと畳み込むことができます。ポリゴン上の最大深度傾斜方向に切り替わりがないときは，式7.13は正しい結果を与えます。切り替えがあるときは，保守的な近似を与えます。近似式における相対誤差の最大値は約1の値を持つ \(y_1 – y_0 = 1\) の時に最も大きくなりますが，短い範囲のためこの違いははるかに小さくなります（この近似の誤差解析についてはAppendix Bを参照）。気を付けてほしいのは，テストシーンを通じたパスで実際に発生する切り替えはポリゴンの1%未満です。切り替えを持つこれらのポリゴンについて，実際の値と我々の近似の間の相対誤差の最大値の平均は0.001未満です。

7.3 Depth buffer compression

深度バッファ圧縮はラスタライゼーションに必要とされるメモリバンド幅を減らすための重要な最適化です。我々は読者に素晴らしい調査と既存の深度圧縮スキームの詳細説明について Hasselgren　と Möller(2006) を紹介しました。多くの現在のアルゴリズムは可逆圧縮を高速にするためタイル深度値の平面性を利用しています。対数ラスタライゼーションは平面のプリミティブが曲線になるため，既存のアルゴリズムの多くが良い圧縮比率になりません。
　\(y\) 方向における曲率をより良く捕捉することができる2次圧縮スキームを生成するために2つの既存の1次スキームから成り立ちます。アルゴリズムは図7.3に要約されています。最初に，完全な24bit精度でタイルの左上の角にベース値を保存します。残りの値については１階微分を計算します（DeRooら, 2002)。右側の緑の\(4 \times 3\) ブロックについては，\(x\) 上でエッジ方程式が線形であるので微分はかなり小さくなります。このとき，アンカー符号化スキームのバリエーションを使用します(Van Dyke & Margeson, 2005)。アンカー値に関してオフセットが計算されます。線または残りの位置については予測値が使われる平面からのオフセットとアンカー値を一緒にします。また予測値に対する補正項も計算されます。アンカー，オフセットそして補正項の値が割り当てされた大きなバジェット内に全て収まる場合，タイルは圧縮することができます。その他の場合は非圧縮が保存されます。解凍は単純に逆プロセスです。我々のスキームは3:1の圧縮比を持つ可逆圧縮にするため128bitのアロケーションを使用します。

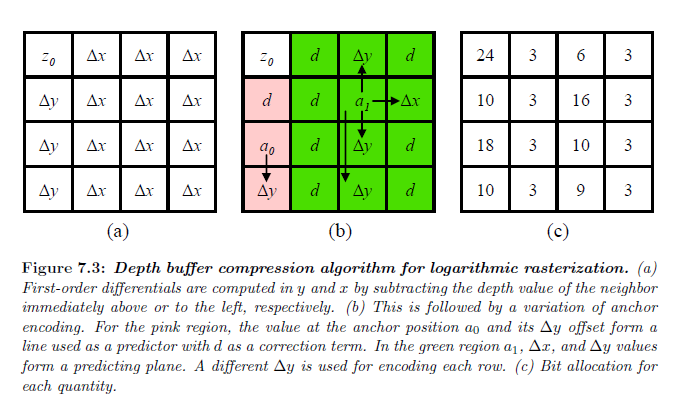
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.156 より引用。

7.3.1 Result

HasselgrenとAkenine-Möller(2006)に類似した方法で深度圧縮スキームを評価しました。異なる４つの解像度を用いて複雑さが変化する３つのモデルを通じたカメラパスについてデータをキャプチャーしました。また同様の圧縮アルゴリズムをいくつか使用しました（Van Dyke & Margeson, 2005; DeRooら, 2002; Ornsteinら, 2005; Hasselegren & Akenine-Möller, 2006)。深度オフセットアルゴリズムはテストできませんでした。なぜかというと，これは\(z\)-最小と\(z\)-最大値を必要とし，我々のシミュレータによって提供できないからです。各フレームに対して描画された深度バッファを（シーンラスタライゼーションの間に触れられていないタイルを除いて）\(4 \times 4\) のタイルへと完全に分割し，圧縮アルゴリズムを介してそれらを実行しました。より詳細なシミュレーションは部分的に完成したタイルのバンド幅を取り込みます。図7.4に示す結果はアルゴリズムのパフォーマンスの関係性を示しています。線形深度圧縮スキームを用いたアルゴリズムの視覚的な比較は図7.5で示されます。
　線形ラスタライゼーションを用いて描画した深度バッファ上で，我々の圧縮スキームはその他のアルゴリズムいくつかと同等です。対数ラスタライゼーションついて，その他のアルゴリズムは不十分です。我々の圧縮スキームは特により高解像度において，もっと良い圧縮比になる可能性がありますが，線形ラスタライゼーションについてはその他のよりも圧縮比が若干少なくなります。

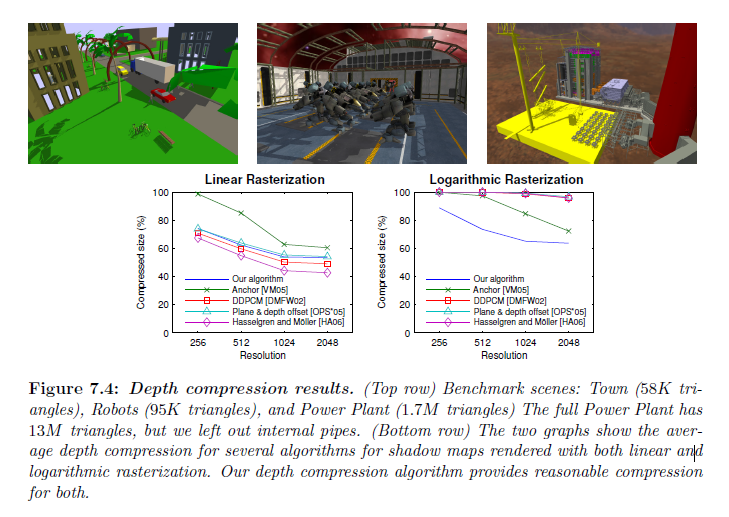
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.158 より引用。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.159 より引用。

7.4 Feasibility

以下のリストは対数ラスタライゼーションをサポートするために必要とされる修正をまとめています：
● \(y\)座標の24bit固定小数をサポートするためにラスタライザー上のビット幅を増加させる。現在のGPU上のビット幅の詳細は一般的には利用できない。4bitのサブピクセル精度を持つ \(4K \times 4K\) バッファをサポートするGPUが少なくとも16bit固定小数座標をサポートする必要がある。
● エッジにおいて指数を計算し，補間式を計算するための評価機。
● セットアップ段階で \(y\) 座標へ対数パラメータライゼーションするアプリケーション。
● セットアップ段階で一般化されたポリゴンオフセットの計算
● 新しい深度圧縮ユニット
残りのグラフィックスパイプラインは同じままです。
　我々はこれらの機能拡張が実現可能であると信じています。なぜかというとこれらはインクリメンタルで，既存のハードウェア設計を活用できるからです。修正はGPUパイプライン上の２つの固定機能要素のみに分離されています。ラスタライザーへの変化はインクリメンタルです。我々のアルゴリズムを使用する新しい深度ユニットはその他のアルゴリズムと同等の複雑さを持ちます。所望の場合，深度圧縮ユニットは線形ラスタライゼーションに使用する既存のものと一緒に置くことができます。また我々のアルゴリズムは線形ラスタライゼーションについて同等の圧縮比を提供するので，我々の深度圧縮ユニットは既存のユニットを置き換え可能であり，したがって線形と対数ラスタライゼーションの両方を処理できる単一のユニットを可能にします。
機能拡張はオンチップでの少量の増加を必要としますが，帯域幅とストレージ要件の大幅な削減を実現します。帯域幅を節約するために増分計算を使用することは現在のハードウェア傾向にうまく合います。なぜかというと，同じコストについて帯域幅は大幅な遅れをとる一方で，計算力は急激に増加し続けるからです
それゆえ，これらの機能拡張は帯域幅削減と実装コストの間の良いバランスを提供します。