こんちわ。Pocolです。
今日は,
[Lin 2022] Daqi Lin, Markus Kettunen, Benedikt Bitterli, Jacopo Pantaleoni, Cem Yuksel, Chirs Wyman, “Generalized Resampled Importance Sampling: Foundations of ReSTIR”, SIGGRAPH 2022.
を読んでみようと思います。
いつもながら誤字・誤訳があるかと思いますので,ご指摘いただける場合は正しい翻訳例とともに指摘していただけるとありがたいです。
シーンがより複雑になり、リアルタイムアプリケーションにレイトレーシングが採用されるようになると、少ないサンプル数で最大の品質を実現するパスサンプリング・アルゴリズムが不可欠になります。Talbotら[2005]のResampled Importance Sampling(RIS)を基にした最近のリサンプリングアルゴリズムは,パスを時空間的に再利用し,ピクセルあたり数サンプルで驚くほど複雑な光輸送をレンダリングします。これらのレゼバーベースの時空間重点サンプラー(ReSTIR)とその基礎となるRIS理論は、サンプルの独立性を含む様々な仮定を置いています。しかし、サンプルの再利用は相関をもたらすので、ReSTIRスタイルの反復再利用はRISの理論が提供する収束保証のほとんどを失います。
我々はGeneralized Resampled Importance Sampling(GRIS)を導入し、理論を拡張し、未知のPDFを持ち、様々な領域から採取された相関のあるサンプルに対するRISを可能にします。これにより、理論的な基礎が固まり、ReSTIRに基づくサンプラーにおける分散境界と収束条件を導出することが可能になります。また、実用的なアルゴリズム設計の指針となり、複雑なシフトマッピングによるピクセル間の高度な経路再利用を可能にします。
複雑なシーンでインタラクティブに動作するpath-traced resampler(ReSTIR PT)を紹介し、ピクセルごとに1つのパスをシェーディングしながら、多数のバウンスの拡散照明と鏡面照明をキャプチャします。我々の新しい理論的基礎により、オフラインレンダリングのための収束を保証するためにアルゴリズムを修正することもできます。
1 INTRODUCTION
モンテカルロ法は、現代のレンダリングの核となるアルゴリズムです。元々はオフラインレンダリングでのみ実現可能でしたが、レイトレーシングのハードウェア[Kilgariff et al. 2018]によって、このようなアルゴリズムはリアルタイムシステムでも実用化されるようになりました。しかし,ゲームにおける厳格なリアルタイム制約は,実現可能なフレームごとのレイカウントを制限し[Halen et al. 2021],多くの現代のリアルタイムパストレーサーにピクセルあたり最大1つのパスのバジェットを与えています。
重点サンプリングは、標本分布を改善することにより、低い標本数での分散を低減します。しかし、図1のような複雑なグローバル照明では、最適な分布からのサンプリングが不可能であり、困難です。パスガイディングは複雑な分布をオンラインで学習することを目的としていますが,複雑なデータ構造[Vorba et al. 2019]やニューラルモデル[Muller et al. 2019]を更新する必要があります。
その代わりに,リサンプルドインポータンスサンプリング(RIS)[Talbot 2005] に基づくアルゴリズムの新しい群は,フレーム内およびフレームをまたがるサンプルの再利用によって,サンプルの母集団を最適分布に向けて継続的に進化させます。理想的には、十分な再利用があれば、各サンプルはその「完璧な」重要度分布に収束します。このようなレゼバーベースドスパシオテンポラルリサンプリング(ReSTIR)アルゴリズムは、直接照明[Bitterliら、2020]、グローバル照明[Ouyangら、2021]、およびボリューム散乱[Linら、2021]で動作します。ReSTIRはストリーミングアルゴリズムによってGPU並列性を活用し,再利用しない等時間レンダリングと比較して最大100倍まで誤差を低減することができます。
しかし、これらのランダムな分布の収束はあまり研究されていません。Nabataら[2020]はTalbot RISの収束を上界で近似していますが,ピクセル間のサンプル再利用がない場合のみです。Bitterliら[2020]は,これらの分布が不偏であることを示しましたが,すべての状況で収束することを証明したわけではありません。
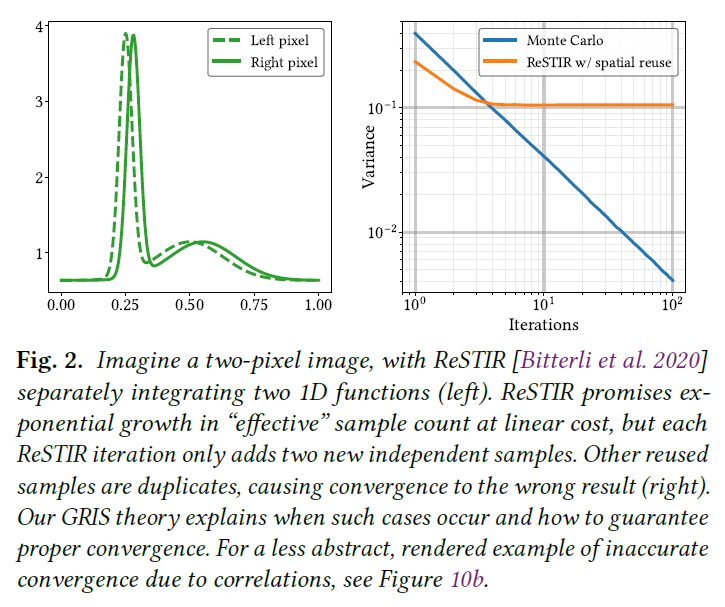
実際、図2には、不偏であるにもかかわらず、サンプルの再利用が誤った結果に収束してしまう些細な例を示しています。
結局のところ、ReSTIRは重要な問題を無視しています。RISは独立同分布(i.i.d.)サンプル、しばしば単一のソース分布からのサンプルを仮定しています。再利用はこの独立性に違反し、この仮定を無視することは収束を示し、あるいは発散を引き起こします。先行研究では、経験的に十分に小さい相関は収束を妨げないことが示唆されています[Bitterli et al. 2020; Lin et al. 2021; Ouyang et al. 2021; Wyman and Panteleev 2021]。しかし、その相関最小化の努力(例えば、再利用される空間的な近傍のランダム化)が収束を保証するかどうか、また、いつ保証するかは不明なままです。より複雑な照明のためにリサンプリングする場合、十分な非相関性を維持することは、より深い理論的理解なしには不可能であるかもしれません。
一般化リサンプルドインポータンスサンプリング(GRIS)を紹介します。これは、i.i.dの仮定を解除し、ReSTIRのような複雑なサンプラーの理解、設計、収束の議論に役立つ新しい理論フレームワークです。GRISでは、潜在的に異なる領域から抽出され、単一の積分を推定するためにマッピングされた、相関のある候補サンプルを組み合わせるためにリサンプリングを適用できます(セクション4参照)。
Talbot [2005]とBitterliら[2020]の多くの導出は我々の理論の特殊例です。我々はReSTIRが不偏かつ一貫している条件を証明しながら先行研究を一般化します。
我々の貢献は以下を含ます:
- シフトマッピングにより、他のピクセルからの経路を持つRISを導出する。
- 不偏性と収束の条件を与える。
- 収束制約を満たすMIS重みを導出し、分散の最小化を支援する(セクション4.4)
- ReSTIRの設計上の決定事項、例えばM-cappingが収束を確実にするためにどのように不可欠であるかを説明する(セクション6.4)
- BSDFローブ固有の接続により、性能と品質を向上させた適切なシフトマッピングを表示する(セクション7.5と7.6)。
- GRISの理論を応用し、ガラス越しなどの経路を再利用できるReSTIR PTを導き出す。
具体的には、関数\(f\)を積分するときに収束を保証する(セクション5参照)ためには、次のようにします:
- サンプルの再利用時には正しいMISウエイトを使用する。
- \(f/{\hat p}\)が恣意的に大きくならないように、ターゲット関数\({\hat p}\)を選択する。
- \({\rm Var}[\sum w_i] \rightarrow 0\)なので,サンプルのリサンプリング重み\(w_i\)を制御する。
- \(f\)の領域全体で十分なサンプル数を確保する。特に、十分な「正準」サンプル数を確保する(セクション5.5を参照)。
- テンポラルにリサンプリングする場合は、フレーム間の相関を制限するために適度な\(M\)-capを使用します。
新しい理論とシフトマップにより、サンプルをより効率的に再利用し、非常に複雑な照明シナリオにも対応できる堅牢で不偏な光輸送アルゴリズムが得られるとともに、効率的なGPU並列化と実時間利用にも十分に適応できます(図1参照)。また、テンポラルリサンプリングを行わない場合、ReSTIRはオフラインレンダラーを大幅に高速化するために使用できることも示しています。本論文にはソースコードが含まれており、読者が実験できるようになっています。
多くの証明と導出は補足資料に譲りますが、セクション4と5は数学的に密な内容となっています。また、重要な結果を囲み、理論にあまり興味のない読者が読み飛ばせる部分には星印をつけています(★)。エンジニア向けには、セクション4.1を読み、セクション7まで読み飛ばすことをお勧めします。
1.1 Paper Roadmap
セクション 2 では、GRIS が基づいている主要な背景について、密接に関連するリサンプリングおよびサンプラー再利用アルゴ リズムの概要を含め、説明します。
セクション3では、リサンプルドインポータンスサンプリング理論の最先端を簡単にレビューし、その拡張の必要性を動機づけます。
セクション4では、勾配領域レンダリングに類似したシフトマップ\(T_i: \Omega_i \rightarrow \Omega\)を用いて、複数の入力領域\(\Omega_i\)から目標領域\(\Omega\)にリサンプリングするためのRISの新しい一般化を紹介します。GRISが\(\Omega\)上で定義された任意の関数\(f\)を不偏に積分する条件と、出力サンプル分布が指定されたターゲットリサンプリングPDF \({\hat p}\)に収束する条件を確立します。
セクション5では、積分誤差がRIS正規化係数の分散に直接関係することを示します。この分散がなくなると、GRISはゼロ分散の積分器となります。これは、現在の正準的なピクセルから(遠い隣接ピクセルからだけでなく)追加のサンプルを取り,堅牢なリサンプリングMISウェイトを使用することで実現できます。
GRIS収束制約に従うようにReSTIRを設定することで、セクション6で非マルコフ連鎖になり、1ピクセルあたり1サンプラーで永遠に経路空間を探索することが確認します。静止シーンでは、フレームを平均化することで収束し、リアルタイムでの使用では、各フレームで連鎖の単一状態を得ることができます。フレーム間の相関はオフラインレンダリングの収束を妨げますが、空間的な再利用は依然として有益です。
セクション7では、ピクセル間パス再利用のためのシフトマッピングを設計し、効率を向上させるいくつかの新しいシフト修正を紹介します。セクション8では、ReSTIR PTの実装について述べ、セクション9では、結果と実験的検証を示します。
補足資料のセクションSには、数学的な証明と導出、追加の解析、そして我々の実装に関する詳細が含まれています。また、結果のビューアと動画も提供します。
2 BACKGROUND
サンプリング、重点サンプリング、サンプラー再利用は、現代のレンダラーにとって重要であり、グラフィックスにおける重要な研究分野を形成しています。RISとReSTIRを一般化することで、我々はリサンプリングとサンプラー再利用の手法に密接に関連付けます。サンプリングの大きな文脈を簡単にまとめた後、これらの技術に議論を集中します。
我々の研究は、パスの再利用[Bauszat et al. 2017; Bekaert et al. 2002]、パスガイド[Müller et al. 2017; Vorba et al. 2014]、パスの摂動と変異[Kelemen et al. 2002; Veach and Guibas 1997]、next-event estimation[Donikian et al. 2006; Vévoda et al. 2018]、比率推定[Heitz et al. 2018; Stachowiask 2015]、双方向パス接続[Chaitanya et al. 2018; Lafortune and Willems 1993; Popov et al. 2015; Tokuyoshi and Harada 2019]、ライト重点サンプリング[Peters 2021; Shirley et al. 1996]、サンプル検索を高速化する機構[Jensen 2001; Moreau et al. 2019l Walter et al. 2005]、低ディスクレパンシーサンプリング[Heitz and Belcour 2019]、オンライン学習ベースサンプリング[Müller et al. 2019l; Pantaleoni 2020; Vorba et al. 2014; Zhu et al. 2021]の豊かな歴史に適合します。
リアルタイムをターゲットとする場合、ハードウェア・レイトレーシングを用いても、パフォーマンスの追求での品質向上は不十分であり、低いサンプルバジェットを持つ結果にはデノイズが必要です[Chaitanya et al. 2017; Hasselgren et al. 2020]。広く使われていデノイザー[Schied et al. 2018]は、ポストプロセスとして働き、中間的なレンダリングデータを破棄します。最近のデノイザーには、レンダラーからのサンプルを直接処理するものがあり[Gharbi et al. 2019]、リサンプリング[Talbot 2005]や逐次モンテカルロ法[Ghosh et al. 2006]は、確率分布のフィルタリングとみなすことができ、フィルタリングした領域のサンプル品質を向上させることができます。また,勾配領域レンダリング(Gradient-domain rendering)[Hua et al. 2019; Kettunen et al. 2015; Lehtinen et al. 2013]は,パス空間のノイズをキャンセルするために相関のあるサンプルを使用するとみなすことができます[Kettunen 2020].パス空間フィルタリング[Binder et al. 2019; Pantaleoni 2020]は時空間近傍のパスの寄与を平均化し、分散とバイアスをトレードします。
2.1 Resampling Algorithms
我々の研究は、サンプリングインポータンスサンプリング(SIR) [Rubin 1987] に基づく最近のリサンプリング手法を一般化したものです。SIRは,i.i.d.標本\((X_i)^M_{i=1}\)の集合をリサンプリングウェイト\(w_i = {\hat p}(X_i)/p(X_i)\)に比例してサブサンプリングすることにより,より良い分布の標本\((Y_i)^N_{i=1}=(Y_1, \cdots, Y_N)\)を得るもので,\({\hat p}(x)\)は望ましい(正規化されていない)目標分布を表しています。\(M\)が大きくなるにつれて、サンプル\(Y_i\)の分布は\({\bar p}={\hat p}(x)/ ||{\hat p}||\)に収束します。SIRの詳細な概要についてはGuets [2012]を参照してください。関連する手法として、Population Monte Carlo (PMC) [Cappé et al. 2004; Lai et al. 2007]があります。これは、リサンプリング、変形、再生成を組み合わせて、サンプル母集団を複数の反復で目標分布に向かって発展させるものです。
Resampled Importance Sampling.
Talbot [2005]はRISを導入し,モンテカルロ積分においてSIRで選択されたサンプルに適切な正規化を提供します。RISはSIRを拡張し、単一領域内の異なる確率分布から\((X_i)^M_{i=1}\)を調達できるようにし、目標分布への収束を保証する多重点サンプリング(MIS)ウェイトを提供します。
Reservoir Sampling.
Chao [1982] は,入力集合\((X_i)^M_{i=1}\)からランダムなサンプルをシングルパスでストリーミング選択するレゼバーサンプリングアルゴリズムを紹介しています。レゼバーには、選択されたサンプル、現在のストリームの長さ\(M\)、重み\(w_i(i \leq M)\)の合計が格納され、各新しいストリーム要素\(X_i\)は、選択されたサンプルを確率\(w_i /\sum_{j \leq i}w_j\)で置き換えます。レゼバーサンプリングはリサンプリングと自然に組み合わされ、これらを組み合わせることで、一定のメモリフットプリントでストリーミング方式でRISを実行します。
Reservoir-based spatiotemporal RIS.
ReSTIR [Bitterli et al. 2020]は連鎖したレゼバーリサンプリングを用いて、ピクセルやフレーム間でサンプルを共有します。これは、各レゼバー(例えばピクセルごと)に対して新しい独立したサンプルを生成し、類似したレゼバー(すなわち領域)間でサンプルを再利用することを交互に行います。積分領域間で十分に分散されたサンプルを共有することで、サンプル分布が改善され、最初のサンプル生成にかかるコストが償却されます。ReSTIRは、積分領域とピクセル(すなわち、すべての照明の表面)間で固定されている画面空間での再利用と直接照明に最初に適用されました。最近の研究では、ReSTIRをワールド空間のサンプル再利用[Boissé 2021; Boksansky et al. 2021]とグローバル照明の長いパス[Lin et al. 2021; Ouyang et al. 2021]に拡張し、積分領域と正しさの推論がより複雑になっています。
Shift mappings.
パス再利用アルゴリズムでは、ピクセル間のパスサンプルを再利用することでピクセルの色を評価します。ReSTIRやRISと同様に、Bekaertら[2002]の定式化はパスサンプルが共有領域から来ることを要求していますが、より最近の研究[Bauszatら2017]は異なる積分領域を許容し、それらの間のパスをマッピングするシフトマッピングを明示的に定義しています。これは、ガラスや鏡からのスペキュラリティを含む複雑な光輸送パスをより良く再利用します。一般的なシフトマッピングを利用するためにRISとReSTIRを拡張することによって、我々はOuyangら[2021]よりもこれらの複雑さをよりよく扱うことができます。
シフトマッピングはもともと,勾配領域のレンダリング [Kettunen et al. 2015; Lehtinen et al. 2013] で生まれたもので,画像は隣接するピクセルにシフトされたパスのコピーから寄与分を差し引くことで評価される離散画像勾配で再構築されます。
多くのシフトマッピングが提案されています:最初の荒い頂点への再接続[Lehtinen et al. 2013]、マニホールド探索シフト[Lehtinen et al. 2013]とスペキュラ輸送のためのハーフベクトルコピー[Kettunen et al. 2015]、乱数リプレイ[Hua et al. 2019; Kettunen et al. 2015; Manziet al. 2016]、そして多数の拡張,例えば双方向パストレーシング[Manzi et al. 2015]、フォトンマッピング[Gruson et al. 2018l Hua et al. 2017]、関与媒質[Gruson et al. 2018]、vertex connection and merging[Sun et al. 2017]、スペクトル・レンダリングへ[Petitjean et al. 2018]等です。Huaらの2019年の最新サーベイでは,シフトマッピングと勾配領域レンダリングについてより深い見解が示されています。経路摂動とシフトマッピングは、メトロポリス光輸送[Van de Woestijne et al. 2017; Veach and Guibas 1997]とローカルQMC探索[Tessari et al. 2017]でも発生します。
3 RESAMPLED IMPORTANCE SAMPLING REVIEW
セクション4でGRISを紹介する前に、まず、我々の一般化理論の表記法と用語を用いて、リサンプル重点サンプリング(RIS)について概説します。図3はTalbot [2005]などの既存の理論と我々の新しい一般化理論の相違点を示しています。
3.1 Identically Distributed Samples
基本的なRISは、ある領域\(\Omega\)において、既知のPDF \(p\)で分布する独立かつ同一に分布する(i.i.d)ランダムサンプル\((X_i)^M_{i=1}\)のシーケンスを入力として取ります。目標は、そのPDF、\(p_Y\)が\(\Omega\)上の関数\(f\)の積分に対してより良い重点サンプラーを構成するようにシーケンスからランダムに\(Y\)を選択することです。
より正確には、非負の目標関数\({\hat p}\)を定義し、入力サンプル数\(M\)が大きくなるにつれて、実現されたPDF \(p_Y\)が正規化\({\hat p}\)にますますよく近似する(すなわち、\(p_Y\)が\({\bar p}(x) = {\hat p}(x) / ||{\hat p}||\)に近似する)ように\(Y\)をランダムに選択します。
アルゴリズム的には、入力\(X_i\)から、リサンプリングウェイト\(w_i\)を用いて、確率\(P_r[s=1] = w_i / \sum_{j=1}^M w_j\)で、\(Y=X_s\)を一つ選択します。先行研究では\(w_i\)を\({\hat p}(X_i)/p(X_i)\)と定義しています(例えば、Bitterliら[2020]の式5)。重みは相対的であるため、選択確率は乗法定数に対して不変であり、表記上の一貫性を保つために以下のように定義します。
\begin{eqnarray}
w_i = \frac{1}{M} {\hat p}(X_i) W_i \quad {\rm and} \quad W_i = \frac{1}{p(X_i)} \tag{1}
\end{eqnarray}
選択されたサンプル\(Y\)のPDFは解決困難ですが、その不偏の寄与ウェイト
\begin{eqnarray}
W_Y = \frac{1}{{\hat p}(Y)} \sum_{i=1}^M w_i \tag{2}
\end{eqnarray}
は\(1/p_y(Y)\)の代わりに使用することができます(例. Bitterliら[2020], 式12)。想定しているのは\(p_Y \gt 0\)で,ここで\(f \gt 0\)、すなわち\({\rm supp} f \subset {\rm supp} Y\)とすると、次のようになります。
\begin{eqnarray}
\int_{\Omega} f(x) dy = {\mathbb E}[f(Y) W_Y] \tag{3}
\end{eqnarray}
適切な制約があれば、\(p_Y\)は\({\bar p}\)に収束し、モンテカルロ分散\({\rm Var}[f(Y)W_Y]\)は\(Y\)のPDFが正確に\({\bar p}\)であった場合に期待される分散に漸近的に近づきます。\(f(Y)W_Y\)に比例する\({\hat p}\)を選択すると、推定\(f\)が漸近的にゼロ分散となることが保証されます。
3.2 Differently Distributed Samples
サンプル\(X_i\)が異なるPDF \(p_i\)を持つ場合、状況はより複雑になります。これは、\(m_i \geq 0\)の場合,重み\(m_i\)を持つ単位元のパーティションをリサンプリングMISと呼び,\({\hat p}\)の台上のすべての\(x\)について
\begin{eqnarray}
\sum_{i=1}^M m_i(x) = 1 \tag{4}
\end{eqnarray}
です。Talbot [2005]は、Veach [1998]のバランスヒューリスティックに類似した重みを提案しています。
\begin{eqnarray}
m_i(x) = \frac{p_i(x)}{\sum_{j=1}^M p_j(x)} \tag{5}
\end{eqnarray}
アルゴリズムの重要な変更点は、\(w_i\)(式1)の\(1/M\)の項をこのMISの重みに置き換えることです(図3、青列参照)。すなわち,
\begin{eqnarray}
w_i = m_i(X_i){\hat p}(X_i) W_i \quad {\rm and} \quad W_i = \frac{1}{p_i(X_i)} \tag{6}
\end{eqnarray}
少なくとも1つのPDF \(p_i\)が各\(x \in {\rm supp}{\hat p}\)をカバーしていると仮定すると、式3は、これらの更新された\(w_i\)を用いて式2の\(W_Y\)で成り立ちます。収束にはセクション3.1よりも多くの仮定が必要ですが、達成可能です(例えば、セクション5.7)。
3.3 Why Generalize Resampling?
RISの初期の適用例であるBSDF重点サンプリングでは、\(f\)を安価に近似する\({\hat p}\)を選択し、安価に生成された複数の候補からリサンプリングすることで収束を早めることを目的としています。
しかし、ReSTIRでは、複数の積分を同時に推定するために、ピクセル間でサンプルを再利用し、コストを償却しています。この目的のため、過去のサンプルの再利用が新しいサンプルの生成より安価であれば、\({\hat p}\) は \(f\) よりも単純である必要はありません。また,再利用されるサンプルのPDFが目的の積分値をよりよく近似する場合,ReSTIRは効率を上げることができます。RISの使用を繰り返すような場合、特に複雑な経路の場合、\({\hat p}=f\)を使用することが合理的かもしれません(例えば、Lin et al.[2021])。
TalbotのRIS理論では、独立なサンプル\(X_i\)が共有領域\(\Omega\)にあることを仮定しています。ReSTIRはこの仮定を拡張しているので、理論的な収束保証が保たれていない可能性があります。実際、一見無害に見えるアルゴリズムの修正で、相関のある再利用が誤った結果に収束することがあります。
4 GENERALIZED RIS
我々の一般化リサンプルドインポータンスサンプリング(GRIS)は,領域間のサンプルのマッピングを可能にし、これが不偏で収束する制約を特定します。
ある領域の独立したサンプルから選択する従来のRISとは異なり、異なる領域\(\Omega_i\)からの潜在的に相関のある入力\((X_i)_{i=1}^M\)を許容します。一般化RISはサンプル\(X_s\)をランダムに選択し、シフトマッピング \(Y=T_s(X_s)\)を介して\(f\)の領域\(\Omega\)にマッピングし、\(Y\)のPDFが目標\({\bar p}\)(すなわち、正規化された\({\hat p}\))に近づくようにします。
4.1 Overview
我々の一般化のための理論的詳細を掘り下げる前に、我々のアプローチを簡単に概観し、従来のRISと関連付けます。
入力サンプル\(X_i\)は、おそらく様々な領域\(\Omega_i\)からのもので、独立である必要はなく、積分のために\(1/p_i(X_i)\)を置き換えることができる不偏の寄与ウェイト\(W_i \in {\mathbb R}\)と対になっていると仮定します。これは、事前のリサンプル入力を明示的に許可しています。リサンプル入力\(X_i\)は難解なPDF \(p_i\)を持ちますが、その重み\(W_i\)は扱いやすいです(すなわち、式2)。我々は、セクション4.2で不偏の寄与ウェイトを定式化します。
\(f\)を\(\Omega\)上で積分するためにサンプルを再利用するには、ランダムサンプル\(X_s \in \Omega_s\)をシフトマッピング\(T_s: \Omega_s \rightarrow \Omega\)で\(\Omega\)にマッピングする必要があります。このシフトはPDF変換法則によってPDFを修正し、シフトマップのヤコビアン行列式\(|\partial T_i/\partial x|\)を必要とします。セクション4.3で我々はシフトマッピングを定式化します。
アルゴリズム的には、RISの様々な側面が変化します(図3、緑の欄参照)。サンプルを共通の領域\(\Omega\)に変換しなければならないので、リサンプリングウェイトにはシフトマップ\(T_i\)とその行列式が含まれます。
\begin{eqnarray}
w_i = m_i (T_i(X_i)) {\hat p}(T_i(X_i)) W_i \cdot | \partial T_i / \partial X_i | \tag{7}
\end{eqnarray}
扱いやすい\(p_i\)は必要としません。\(W_i = 1/p_i(X_i)\)を使用してもよいですが、例えば、事前のRISパス(式2)からの数値的な寄与ウェイト\(W_i\)を使用してもよいです。選択されたサンプルを積分(またはさらなるリサンプリング)に使用する前に、それを適切な領域にシフトする必要があります、つまり、出力サンプルは\(Y = T_s(X_s)\)です。
出力\(Y\)に対する不偏の寄与ウェイト\(W_Y\)は、再び式2で与えられます。以下で導出する制約により、\(p_Y\)は、\({\rm Var}[f(Y)W_Y]\)が\({\rm Var}[f(Y)/{\bar p}(Y)]\)に近づくことが保証されるような\({\bar p}\)に収束します。これは、\({\hat p} \propto f\)の場合、単一の\(Y\)で漸近的なゼロ分散積分を達成します。
4.2 Unbiased Integration with Generalized RIS
ここでも、任意のソース領域\(\Omega_i\)を持つ潜在的に相関のある入力サンプル\((X_i \in \Omega_i)^M_{i=1}\)を想定しています。さらに、サンプル\(X_i\)は不偏の寄与ウェイト\(W_i\)と対になっていなければならず、潜在的に難解な逆数のPDFs \(1/p_i(X_i)\)の置き換えとして作用します。
まず、領域\(\Omega\)上の関数\(f\)について、ほぼ任意のリサンプリングウェイト\(w_i\)を仮定し、不偏の積分器を導出します。セクション4.4では、これらの任意の\(w_i\)を、ターゲットPDF \({\bar p}\)への漸近的収束をもたらす重みに置き換えます。
不偏の寄与ウェイト\(W_i\)を以下のように正式に定義します:
定義 4.1. 確率変数\(X \in \Omega\)に対する不偏の寄与ウェイト\(W \in {\mathbb R}\)は、以下のような任意の実数値の確率変数\(W\)は,任意の積分可能関数\(f : \Omega \rightarrow {\mathbb R}\)について
\begin{eqnarray}
{\mathbb E}[f(X)W] = \int_{{\rm supp}(X)} f(x)dx \tag{8}
\end{eqnarray}
である。
\(f(X)W\)という式は、モンテカルロ積分における比率\(f(X)/p(X)\)を一般化したものです:もし\(p\)が扱いやすいなら、\(W=1/p(X)\)を使うことができます。そうでない場合、RISで\(X\)を選ぶときのように、これらの重みで不偏積分を行うことができます。積分は当然、\(p \gt 0\)、すなわち\({\rm supp}(X)\)に限定されます。同様の定義は、コンピュータグラフィックス以外でも用いられており、例えば、Liu and Liu [2001]やLiang and Cheon [2009]があります。RISにおける逆数の確率密度関数の推定とは別に、連続多重点サンプリングのフレームワーク[West et al. 2020]における条件付き確率密度関数も不偏の寄与ウェイトの例です。
不偏の寄与ウェイトは、当然、周辺確率密度関数の逆数に置き換えられ、実際、不偏に推定されます。
\begin{eqnarray}
{\mathbb E}[W \, | \, X] = \frac{1}{p_X(X)} \tag{9}
\end{eqnarray}
これは偶然ではなく、同値です。逆数の周辺確率密度関数(式9)に対する任意の不偏推定量は不偏寄与ウェイト(式8)であり、その逆もまた同様です(定理A.1)。
RISでは、\(X_i\)を\(w_i\)に比例してリサンプルします。これを行うには、まず、各サンプル\(X_i\)に、インデックス\(s=i\)を選択した場合に評価される寄与関数\(g_i: \Omega_i \rightarrow {\mathbb R}\)を対応させます。
次に、\(g_s(X_s)W_s\)の期待値をインデックス\(s\)のRIS選択確率で割ったものを参照し、選択インデックス\(p_s(i) = w_i/\sum_{j=1}^M w_j\)のPMFとなり、多少の注意は必要ですが、次のようになります。
\begin{eqnarray}
{\mathbb E} \left[ \frac{g_s(X_s)W_s}{p_s(s)} \right] &=& {\mathbb E} \left[ \sum_{i=1}^M g_i(X_i) \frac{\cancel{p_s(i)}}{\cancel{p_s(i)}} W_i \right] \\
&=& \sum_{i=1}^M \int_{{\rm supp}(X_i)} g_i(x_i) dx_i \tag{10}
\end{eqnarray}
最初のステップでは、期待値を可能なケースについての和として展開し、2番目のステップでは、不偏の寄与ウェイトの定義を利用して期待値の和を積分値の和に変換します。RISは、確率変数がゼロのPDFを持つ領域のサンプリングを自然にスキップし、積分を\(X_i\)の台に限定します。この結果、未知数\(g_i\)を慎重に選択することにより、残りの積分和を\(f\)の積分に変換することができます。
右辺が\(f\)の積分となるように\(g_i\)を選ぶと、選択された標本\(Y=X_s\)の不偏の寄与が得られます。\(X_i\)がすべて同じ領域\(\Omega\)と台\(S\)からで、すべての\(w_i\)が\(S\)において正であるという特別な場合、すべての\(i\)について\(g_i = \frac{1}{M}f\)を選ぶことによって基本RISをリカバーすることができ、以下のようになります。
\begin{eqnarray}
{\mathbb E} \left[ \frac{1}{M} f(Y) \frac{\sum_{j=1}^M w_j}{w_s} W_s \right] = \int_{{\rm supp}(Y)} f(x) dx \tag{11}
\end{eqnarray}
式8と比較すると、この限定されたケースでは、期待値は、\(W_Y\)を持つ\({\mathbb E}[f(Y)W_Y]\)の形式であり,
\begin{eqnarray}
W_Y = \frac{1}{M} \frac{\sum_{j=1}^M w_j}{w_s} W_s \tag{12}
\end{eqnarray}
\(W_Y\)を\(Y\)に対する不偏の寄与ウェイトとすること、すなわち、\({\mathbb E}[f(Y)W_Y]\)は台\(Y\)上で任意の関数\(f\)を積分します。セクション4.3では、この結果を複数の領域\(\Omega_i\)から来るサンプル\(X_i\)に拡張します。
Degenerate case.
すべての \(w_i\) が 0 の場合、サンプルは選択されず、寄与は 0 となります。直感的には、サンプリング領域と積分領域の外(すなわち、\({\hat p}(Y_{\emptyset})=f(Y_{\emptyset}) = 0\))に、寄与度ゼロのヌルサンプル\(Y_{\emptyset}\)を返すと考えることができます。その場合、\(W_{Y_{\emptyset}}\) の値は無関係であり、ゼロに設定することができます。
4.3 Shift Mapping
GRISでは、サンプル\(X_i\)は任意の領域\(\Omega_i\)から由来する可能性があります。\(f: \Omega \rightarrow {\mathbb R}\) をサンプル \(X_i\) で積分するには、式 10 の右辺を \(f\) の積分に変換する必要があります。そのためには、\(X_i \in \Omega_i\) を \(\Omega_i\) から \(\Omega\) に写像する \(g_i\) を選び、その結果で \(f\) を評価します。
\(\Omega_i\)から\(\Omega\)への写像は、積分の変数を変えるので、全単射でなければなりません。複雑な領域間の写像を構成することは自明ではないので、\(\Omega_i\)の部分集合から\(\Omega\)におけるそのイメージへの全単射に確定します。先行研究(例えば、Manziら[2014])と同様に、このような全単射をシフト写像、\(T_i\)と呼び、各領域\(\Omega_i\)に1つを関連付けます。
定義 4.2. \(\Omega_i\)から\(\Omega\)へのシフト写像\(T_i\)は、部分集合\({\mathcal D}(T_i) \subset \Omega_i\)からその画像\({\mathcal I}(T_i) \subset \Omega\)への全単射関数である。
直観的には、寄与関数
\begin{eqnarray}
g_i(x) = c_i(y_i) f(y_i) \left| \frac{\partial T_i}{\partial x} \right| \tag{13}
\end{eqnarray}
を選択すべきで,ここで\(y_i\)は\(T_i\)について簡潔にした表記で,寄与MISウェイト\(c_i : \Omega \rightarrow {\mathbf R}\)は,\(y \in \Omega\)についての単位元\(\sum_{i=1}^M c_i(y) = 1\)の任意の部分で,\( | \frac{\partial T_i}{\partial x} |\)は\(x \rightarrow y_i\)のヤコビアン行列式です。原則的に、この実装は
\begin{eqnarray}
\sum_{i=1}^M \int_{\Omega_i} g_i(x) dx = \int_{\Omega} f(x) dx \tag{14}
\end{eqnarray}
ですが,細部には注意が必要です; 例えば,式13は \(x \notin {\mathcal D}(T_i)\)については定義されません。\(x \notin {\mathcal D}(T_i)\)に対して\(g_i(x) = 0\)を定義し、寄与MISウェイト\(c_i\)を更新して補正することで、これを修正しました。
重み\(w_i\)はターゲット関数\({\hat p}\)に関係する任意の非負の確率変数で、次のように仮定します:\(X_i \in {\mathcal D}(T_i)\)の場合に限り,\(w_i \gt 0\)が成立し,\({\hat p}(Y_i) \gt 0\)です。 基本的には\(Y_i=T_i(X_i)\)のときに\(w_i \gt 0\)が存在し、\({\hat p}\)の台にあるときは\(w_i \gt 0\)、そうでないときは\(w_i=0\)で\(X_i\)を選択しないようにします。後で、この制約を少し緩和します。
これらの仮定の下で、各可能な\(Y\)は\({\rm supp} \, {\hat p}\)にあり、正のPDFを持つ1つ以上の\(X_i\)によって\(Y = T_i(X_i)\)としてサンプル可能でなければならず(すなわち、\(X_i \in {\rm supp} \, X_i\)),その逆もまた同様です。数学的には,次のようになります。
\begin{eqnarray}
{\rm supp} \, Y = {\rm supp} \, {\hat p} \cap \cup_{i=1}^M T_i ({\rm supp} \, X_i) \tag{15}
\end{eqnarray}
これは\({\rm supp}\, Y \subset {\rm supp}\, {\hat p}\)を意味します。その後、\({\rm supp}\, {\hat p} \subset {\rm supp}\, Y\)を仮定すると、\({\rm supp} \, Y = {\rm supp} \, {\hat p}\)も含意されます。
上記の\(g_i\)を、\(x \in {\mathcal D}(T_i)\)なら\(g_i(x)=0\)として、式10の左辺に注意深く入すると、次のような等式が得られます。
\begin{eqnarray}
{\mathbb E} \left[ c_s(Y)f(Y) \left| \frac{\partial T_s}{\partial X_s} \right| \frac{\sum_{j=1}^M w_j}{w_s} W_s \right] = \int_{{\rm supp}(Y)} f(x) dx \tag{16}
\end{eqnarray}
ここで、\(W_s\)は\(X_s\)の不偏の寄与ウェイトです。
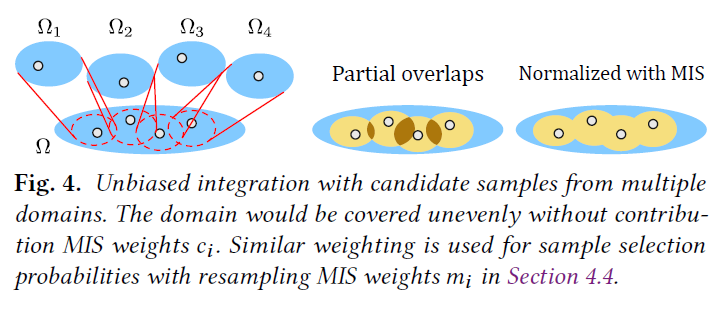
これが成立するために寄与MISウェイト\(c_i\)が満たすべき制約は、すべての\(y \in {\rm supp}Y\)について、以下の通りです。
\begin{eqnarray}
\underset{y \in T_i({\rm supp} X_i)}{\sum_{i=1}^M} c_i(y) = 1 \tag{17}
\end{eqnarray}
これは、「複数の\(\Omega_i\)の中から実現可能なすべての\(y\)を、合計で正確に1回カバーする必要がある」と解釈してください(図4参照)。和は、\(y\)が非ゼロPDFで\(y=T_i(x_i)\)として実現できる領域\(\Omega_i\)のみを考慮します。原理的には、\(c_i\)は負の値でも機能しますが、後に、\(c_i \geq 0\)のみがGRISの複数のパスを連鎖させることを可能にすることがわかります。
ここでも、式16の期待値は、\(\Omega\)における任意の被積分関数\(f\)に対して\({\mathbb E}[f(Y)W_Y]\)という形式をとり、右辺は式8の不偏の寄与ウェイトの定義に従って、\(Y\)の台の上で\(f\)を積分します。これは、次のようなことを意味します。
\begin{eqnarray}
W_Y = c_s(Y) \left( W_s \left| \frac{\partial T_s}{\partial X_s} \right| \right) \left[ \frac{\sum_{j=1}^M w_j}{w_s} \right] \tag{18}
\end{eqnarray}
\(f(Y)W_Y\)は\(Y\)の台に対する\(f\)の積分を不偏に推定し、\(W_Y\)は\(1/P_Y(Y)\)の不偏な推定値です。
これは、あるサンプリング領域、例えば\(\Omega_1\)を\(f\)の領域として選び、\(\Omega_1\)上で恒等シフト\(T_1(x) = x\)を使い、被積分関数\(f\)のために設計された重点サンプラーで\(X_1\)を生成します。つまり、\(f(x_1) \gt 0\)であるときは必ず\(p(x_1) \gt 0\)となるようにすれば自動的に実現されます;このようなサンプルを後に正準なサンプルと呼ぶことにします。\(p_{X_1}\)は既知なので、不偏の寄与ウェイト\(W_1 = 1/p_{X_1}(X_1)\)を使うことができます。
後述するように、ReSTIRサンプラーはこれらの観測結果をもとに事後的に構築することができますが、まずセクション4.4では、式19で\(w_i\)を設定することにより、目標密度\({\bar p}\)への収束を実現する方法を説明します。そして、対応する\(W_Y\)は、式22で与えられます。
制約の緩和★.
\(Y_i=T_i(X_i)\)の場合、\({\hat p}(Y_i) \gt 0\)のときに\(w_i \gt 0\)という条件は、\(c_i(Y_i)=0\)または\(W_i=0\)、すなわち期待値が変化しないときにも\(w_i =0\)を割り当てることで緩和することができます。式15を成立させるためには、台\({\hat p} \cap \bigcup_i T_i({\rm supp}X_i\)で式17の妥当性を明示的に保証する必要があります。これらの制約と推定量の不偏性をセクションS.7.1で導出します。次セクションの\(w_i\)を用いることで、これらの制約の必要性はなくなります。
4.4 Asymptotically Perfect Importance Sampling★
上記では、RISを複数領域に一般化し、任意に近い重みで不偏な積分を実現しました。TalbotのRISと同様に、GRISの目標は、望ましい分布に従ってサンプルを生成することです。出力サンプル\(Y\)の周辺確率密度\(p_Y\)は、入力サンプル数が無限大に近づくと\({\bar p}\)に収束するようにします。
この現象は、以下のリサンプリングウェイトで起こることを示します:
\begin{eqnarray}
w_i = \begin{cases} m_i(T_i(X_i)) \, {\hat p}(T_i(X_i)) W_i \cdot | \frac{\partial T_i}{\partial X_i} |, & {\rm if} \quad X_i \in {\mathcal D}(T_i) \\
0, & {\rm otherwise} \end{cases} \tag{19}
\end{eqnarray}
リサンプリングMISウェイト\(m_i\)と不偏の寄与ウェイト\(W_i\)が与えられます。\(w_i\)を正規化するとリサンプリング確率が得られるので、\(w_i\)は非負でなければなりません。このことから,\(m_i\)と\(W_i\)も非負でなければないため(証明はセクションS.7.2),以下ではこれを仮定します。
重み\(w_i\)は、\({\hat p}=0\)として、\({\rm supp} {\hat p}\)の外ではゼロとなります。\(m_i\)の要件は\(c_i\)の要件と同様です。\({\rm supp} Y\)のすべての\(y\)について、
\begin{eqnarray}
\underset{y \in T_i({\rm supp} X_i)}{\sum_{i=1}^M} m_i(y) = 1 \tag{20}
\end{eqnarray}
ただし、\(m_i \geq 0\) も必要です。総和は、正のPDFで\(y\)を生成できるインデックスのみを含みます。不偏な積分はまた、\(c_i(y) \neq 0\)であればいつでも\(m_i(y) \gt 0\)を必要とするので、\(m_i\)は\(c_i\)によって形成される単位元のパーティションを無効にしません(セクションS.7.3.で証明します)。
式19の\(w_i\)を式18に直接代入すると、新しいサンプル\(Y\)の不偏の寄与ウェイトが得られます
\begin{eqnarray}
W_Y = \left[ \frac{c_s(Y)}{m_s(Y)} \right] \frac{1}{{\hat p}(Y)} \sum_{j=1}^M w_j \tag{21}
\end{eqnarray}
\(c_i(y) \neq 0\)のとき\(m_i(y) \gt 0\)という条件は、これでゼロによる除算を自然に避けることができます。次に、\(m_i = c_i\)を選ぶことが理想的であり、自然にこの条件を満たすことを示します。
式21の\(W_Y\)には複数の分散要因があります。総和\(\sum_{j=1}^M w_j\)は入力\(X_j\)によって変化し、比\(c_s(Y) / m_s(Y)\)はインデックス\(s\)によって変化します。漸近的に目的の標本密度\({\bar p}\)に近づくには、総和分散\({\rm Var}[\sum_{j=1}^M w_j]\)がゼロに近づくことが必要です。この合計を定数として固定しても、比率\(c_s(Y)/m_s(Y)\)は大きな変動を加えることができます。これは\(c_i(y) = m_i(y)\)を選択することで解消されます。
GRISのための改良された、よりシンプルな不偏の寄与ウェイトは次のようになります。
\begin{eqnarray}
W_Y = \frac{1}{{\hat p}(Y)} \sum_{j=1}^M w_j \tag{22}
\end{eqnarray}
これは、従来のRISの再定式化(式2)に使用し、今回の一般化のために準備しました。以下、\(W_Y\)についてこの式を使用します。
これにより、リサンプリングされた\(Y\)のPDFである\(p_Y\)の\({\bar p}\)への漸近的収束を保証する付録Aの定理A.2が導かれます:\(M\)の増加に伴うリサンプリング結果\(Y_M\)(\({\rm supp}{\hat p} \subset {\rm supp}Y_M\)付き)のシーケンスの挙動を考えてみます。リサンプリング重みの総和の分散が0になる場合、
\begin{eqnarray}
{\rm Var}\left[ \sum_{i=1}^M w_{M, i} \right] \overset{M \rightarrow \infty} \longrightarrow 0 \tag{23}
\end{eqnarray}
このとき、\({\bar p}(Y)/p_Y(Y)\)は平均二乗の意味で1に収束します。この和は\({\hat p}\)の積分を近似しています:
\begin{eqnarray}
{\mathbb E}\left[ \sum_{i=1}^M w_i \right] = {\mathbb E}\left[{\hat p}(Y)W_Y \right] = \int_{{\rm supp}Y} {\hat p}(y)dy = || {\hat p} || \tag{24}
\end{eqnarray}
入力サンプル数\(M\)を増やすと、総和の項数が増えるので、各\(w_i\)は小さくなる傾向があります。\(p_Y\)の\({\bar p}\)への収束は、\(\sum_{i=1}^M w_i\)が\({\rm Var}[\sum_{i=1}^M w_i] \rightarrow 0\)のように\(|| {\hat p} ||\)に近づくこと、すなわち
W_Y = \frac{1}{{\hat p}(Y)} \sum_{j=1}^M w_j \approx \frac{|| {\hat p}||}{{\hat p}(Y)} = \frac{1}{{\bar p}(Y)} \quad {\rm for} \, {\rm large} \, M
\end{eqnarray}
式23からの保証はかなり強いです。\({\bar p}\)の\(p_Y\)の収束は点別でないかもしれませんが(新しいサンプルは一時的な変動をもたらすかもしれない)、任意のサイズのエラーの確率はゼロに近づき、\(\Omega\)の各サブセットは漸近的に、サンプルの正しい比率を受け取ることになります。
さらに,セクション5.2で示したように,積分分散も(\({\hat p} \approx f\)の場合)ゼロになり,すなわち,極限では,\(Y\)が目標PDF\({\bar p}\)で正確に分布する場合に期待される分散を得ることができます。
5 CONVERGENCE AND VARIANCE ANALYSIS★
上記では、新しいGRISの理論と目標分布への漸近収束の条件を示しましたが、積分推定量としての漸近挙動、特にモンテカルロサンプリングに対する漸近挙動についてはまだ議論されていません。サンプル数を無限に増やすことは現実的ではないので、有限個のサンプルを使用した場合の分散についても解析したい。
5.1 Reasonable Distributions★
分散を研究する前に、まず、合理的な重点サンプリング分布を正式に定義することから始めます:
定義 5.1(適正分布). 以下のような境界\(C_f\)が存在する場合、PDF \(p\)は非負関数\(f\)の妥当な重点サンプリング分布である(または\(p\)は[積分]\(f\)の妥当な分布である)と言う。
\begin{eqnarray}
f(x) \leq C_f p(x) \quad {\rm for} \, {\rm all} x \tag{26}
\end{eqnarray}
また、不偏の寄与ウェイト\(W_X\)を持つ確率変数\(X\)が\(f\)に対して合理的に分布していると言うのは、境界\(C_f\)が存在する場合である。
\begin{eqnarray}
f(X) W_X \leq C_f \quad {\rm with} \, {\rm probability} \, 1 \tag{27}
\end{eqnarray}
基本的に、適正分布は、有界モンテカルロ寄与を保証する。標準的なモンテカルロでは\(f(X)/p(X) \leq C_f\)、不偏の寄与ウェイトでは\(f(X) W_X \leq C_f\)である。
5.2 Asymptotic Variance of Integral Estimation★
分布\(p_Y\)の漸近収束は、当然、積分分散に反映されます。\({\bar p}\)が関数\(f\)の適正分布であると仮定すると、不偏積分推定値\(f(Y)W_Y\)は漸近的に\({\bar p}\)と\(f\)の不一致による分散のみを持つことになります。\({\hat p}\)が\(f\)に比例して選ばれるなら、\({\bar p} \propto f\)と推定値\(f(Y)W_Y\)は漸近的にゼロ分散になります。
定理A.3ではこれを公式化します。\(p_Y\)の\({\bar p}\)への収束は定理A.2によって提供され、もし,ある\(C_f \gt 0\)に対して\(0 \leq f \leq C_f {\hat p}\)であれば,このとき
\begin{eqnarray}
{\rm Var}[ f(Y) W_Y] \overset{M \rightarrow \infty}{\longrightarrow} {\rm Var} \left[ \frac{f(X)}{{\bar p}(X)} \right] \tag{28}
\end{eqnarray}
ここで、\(X\)は密度\({\bar p}\)を持ちます。\(f(x) / {\bar p}(x)\)が一定であれば、ゼロ分散の結果が自然に導かれます。
5.3 Variance in the Finite Case★
上記では、サンプル数が無限に増加した場合のGRISの漸近的な挙動を調べました。実際には、有限の\(M\)に制限されるので、ある計算バジェットで分散を最小化することを目指します。幸いなことに、積分推定値に対して明示的な分散境界を与えることができます:
定理1. 定理A.3の仮定で
\begin{eqnarray}
{\rm Var}[ f(Y) W_Y] \leq {\rm Var} \left[ \frac{f(X)}{{\bar p}(X)} \right] + b, \tag{29}
\end{eqnarray}
ここで,\(X\)は密度\({\bar p}\)を持つ分布で,そして
\begin{eqnarray}
b = {C_f}^2 \sqrt{ {\rm Var}\left[ \sum_{i=1}^M w_i \right] } \left( ||{\hat p}|| + 2 \sqrt{ {\rm Var}\left[ \sum_{i=1}^M w_i \right] } \right) \tag{30}
\end{eqnarray}
証明. セクション S.5.4. □
ここで、\(C_f\)は\(f\)の適正分布\({\hat p}\)の境界定数です。定理1は、リサンプリングは\({\rm Var}[ \sum_{i=1}^M w_i]\)を減少させることで\({\bar p}\)に収束するとし、これは現在の収束状態の具体的な代理として機能します。\({\rm Var}[\sum_{i=1}^M w_i]\)がゼロに近づくと、残りの分散は\({\hat p}\)と\(f\)の間の潜在的なミスマッチに起因します。
総分散の法則は分散の別の分解を提供し、\(f(Y)W_Y\)に適用すると、次のようになります。
\begin{eqnarray}
{\rm Var}[f(Y) W_Y] = {\rm Var} \left[ \frac{f(Y)}{p_Y(Y)} \right] + {\mathbb E}[ f(Y)^2 {\rm Var}[W_Y | Y] ], \tag{31}
\end{eqnarray}
これは、分散には、\(f\)と周辺密度\(p_Y\)のミスマッチと、\(W_Y\)の条件付き期待値\(1/{\bar p}(Y)\)からの平均二乗偏差\({\rm Var}[W_Y | Y]\)の2つの原因があるとするものです。直感的には、\({\rm Var}[W_Y | Y]\)がゼロになるように\(W_Y\)が\(1/{\bar p}(Y)\)に近づけば、当然、\({\rm Var}[f(Y) W_Y]\)も\({\rm Var}[f(Y) / {\bar p}(Y)]\)に近づきます。
等式\(f(x)=C_f{\hat p}(x)\)の特殊な場合、正確な分散を導き出すことができます(式22を使用)
\begin{eqnarray}
{\rm Var}[f(Y)W_Y] = {\rm Var} \left[ \frac{f(Y)}{{\hat p}(Y)} \sum_{i=1}^M w_i \right] = {C_f}^2 {\rm Var} \left[ \sum_{i=1}^M w_i \right]. \tag{32}
\end{eqnarray}
5.4 Avoiding Singularities★
一般化されたRISは、モンテカルロ積分から自動的に特異点を取り除くことはできません。通常通り、大きな外れ値を回避するためには、追加の保証が必要です。より具体的には、\(\sum_{i=1}^M w_i\)が非有界である場合、その寄与は次のようになります。
\begin{eqnarray}
f(Y) W_Y = \frac{f(Y)}{{\hat p}(Y)} \sum_{i=1}^M w_i \tag{33}
\end{eqnarray}
上記は非有界も可能です。
明らかに、非常に大きな\(w_i\)は、\({\rm Var}[\sum_{i=1}^M w_i]\)をゼロにするという我々の目標に弊害をもたらします。我々は、重みの総和を作ることを目指します
\begin{eqnarray}
\sum_{i=1}^M w_i = \underset{X_i \in {\mathcal D}(T_i)}{\sum_{i=1}^M} m_i(T_i(X_i)) \cdot {\hat p}(T_i(X_i)) W_i \cdot \left| \frac{\partial T_i}{\partial X_i} \right| \tag{34}
\end{eqnarray}
を可能な限り単位化しています。項を見ながら、統一性を保つための潜在的な課題を整理していきます:
(1) あるサンプル\(y\)は、極限状態でも有限個の\(T_i\)を経由して到達可能であるかもしれません。
(2) リサンプリングMISの重み\(m_i\)は\(1/M\)を大きく超える可能性があります。
(3) 積の\({\hat p}(T_i(X_i))W_i\)は、非有界が可能です。
(4) ヤコビアンは非有界が可能です。
これらは、例えば、(1)\(M\)を増やすときにすべてのソース領域からサンプルを追加する、(4)シフトマップの領域を修正して極端なヤコビアンをカットする(双射性を維持しながら)など、一つ一つ対処することができます。
その代わりに、適切なサンプリング方式と2つのロバストなMISウェイト族を設計することで、4つの問題を同時に解決します。これにより、寄与の有界化、\({\hat p}\)への漸近的収束が保証され、複数領域からのサンプルによる漸近的なゼロ分散積分が実現します。
5.5 Canonical Samples★
複数のストラテジーを持つサンプルのMISウェイトを設計するには、通常、すべてのストラテジーを持つサンプルのPDFを知る必要があります。リサンプリングは、そのようなPDFへのアクセスを提供します。その代わりに、我々は、サンプル\(X_i\)が\({\hat p}\)のように、\(p_{X_i}\)の代理として機能する非負の非正規化ターゲット分布\({\hat p}_i\)に関連していると仮定することによって、ロバストなMISウェイトを設計します。
RISやその一般化では、目的の分布\({\bar p}\)に漸近的に収束するためには、概念的に無限のランダムサンプルの流れが必要です。もし、\({\rm supp}{\hat p}\)の部分集合がこのストリームによって有限回しか巡回されない場合、\(p_Y\)はこの部分集合において一般に\({\bar p}\)に収束することができません。
光輸送のように、他の領域\(\Omega_i\)からのサンプル\(X_i\)で\({\hat p}\)の台をカバーすることが難しい場合もあります。\({\hat p}\)を直接対象とする重点サンプラーからサンプルを取ることで、収束に必要な回数だけ\({\rm supp}{\hat p}\)をカバーすることができます。我々は、Bitterli [2021]を動機として、\(\Omega\)の\({\hat p}\)を直接対象とするサンプル\(X_i\)を、恒等シフトマップと\({\hat p}_i={\hat p}\)で正準と定義し、以下の数学的定義を提示します:
定義 5.2(正準なサンプル). 入力サンプル\(X_i \in \Omega_i\)は、その領域が\(\Omega\)で、IDシフトマップ\(T_i(x)=x\)を使用し、\({\hat p}_i={\hat p}\)を用いて、\({\rm supp}{\hat p}\)(すなわち\({\rm supp}{\hat p} \subset {\rm supp}X_i\))をカバーする場合、正準です。
5.6 Designing Robust MIS Weights★
セクション5.4で動機づけられたように,入力サンプル\(X_i\)がターゲット関数\({\hat p}_i\)に対して適正分布していると仮定して,選択されたサンプル\(Y\)の寄与が有限になるようにリサンプリングMISウェイトを設計します。導出を簡単にするために、新しい記号 “\({hat p}\) from \(i\) “を定義します
\begin{eqnarray}
{\hat p}_{\leftarrow i}(y) = \begin{cases} {\hat p}_i({T_i}^{-1}(y)) | \partial {T_i}^{-1}/ \partial Y_i|, & {\rm if} \, y \in T_i ({\rm supp} X_i) \\
0 & {\rm otherwise}
\end{cases} \tag{35}
\end{eqnarray}
すなわち、サンプル\(y\)について、元の領域\(\Omega_i\)のサンプル位置\(x\)におけるそのプロキシPDF\({\hat p}_i\)を評価し、シフトのヤコビアン行列式を乗じます。
我々は、リサンプリングウェイト\(w_i\)を束縛することを目指し、これを保証するMISウェイトの2つの族を構築します。そして、その上界を導出しますが、この上界は正準サンプルが増えるにつれて減少します。その後、これらの境界を利用して、\(p_Y\)の\({\bar p}\)への収束を保証します。
Generalized Talbot MIS.
セクションS.1で導出する最初の族は、Talbot [2005]の重みを以下に一般化したものです:
\begin{eqnarray}
m_i(y) = \frac{{\hat p}_{\leftarrow i}(y) }{ \sum_{j=1}^M {\hat p}_{\leftarrow j}(y)} \tag{36}
\end{eqnarray}
Talbotの[2005]形式は、1つの領域(\(\Omega_i=\Omega\), \(T_i(x)=x\))上の独立したサンプルを仮定し、\({\hat p}_{\leftarrow k}\)の代わりに正確なPDF \(p_k\)を使用することによって得られます。このMIS族は、サンプル\(Y\)の可能なソース間のバランスヒューリスティック[Veach 1998]に類似しています。
Generalized pairwise MIS.
セクションS.1で導出されたMIS重みの二つ目の族は,Bitterli [2021]のペアワイズMISを一般化したもので,本来は単一の正準サンプルと領域(\(|R|=1\), \(\Omega_i=\Omega\), \(T_i(x)=x\))について,以下の守備的な確率変数のために与えられたものです.ペアワイズMISの重要な利点は、\(O(M^2)\)から\(O(M|R|)\)への大幅なコスト削減です。これは、MISの適用をターゲット関数の個々のペアに制限し、それぞれがターゲット\({\hat p}\)とソース\({\hat p}_{\leftarrow i}\)のみを含み、\(i\)が正準サンプルでない場合は、ペア\(({\hat p}, {\hat p}_{\leftarrow j})\)間のMISの平均をそれ以外の場合に適用することによります。一般化されたペアワイズMISファミリーについてはセクションS.1で詳しく説明しますが、ここでは、すべての入力がサンプル\({\hat p}_{(\leftarrow)}\)値を持つ場合に等しい重みを与える、均一な確率変数を示します。
\begin{eqnarray}
m_i(y) = \begin{cases}
\frac{1}{M – |R|} \sum_{j \notin R} \frac{{\hat p}(y)}{|R|{\hat p}(y) + (M – |R|){\hat p}_{\leftarrow j}(y) }, & {\rm if} \, i \in R \\
\frac{{\hat p}_{\leftarrow i}(y)}{|R| {\hat p}(y) + (M – |R|){\hat p}_{\leftarrow i}(y) }, & {\rm if} i \notin R
\end{cases} \tag{37}
\end{eqnarray}
と、若干効率は悪いですが、しばしばより堅牢な防御的な確率変数は、正準サンプルに非正準サンプルより高いMISウェイトを常に与えます。
\begin{eqnarray}
m_i(y) = \begin{cases}
\frac{1}{M} + \frac{1}{M} \sum_{j \notin R} \frac{ {\hat p}(y) }{ |R|{\hat p}(y) + (M-|R|) {\hat p}_{\leftarrow j}(y) }, & {\rm if} \, i \in R \\
\frac{M – |R|}{M} \frac{ {\hat p}_{\leftarrow}(y) }{ |R| {\hat p}(y) + (M – |R|){\hat p}_{\leftarrow i}(y) }, & {\rm if} \, in \notin R
\end{cases} \tag{38}
\end{eqnarray}
Resampling weight bounds.
これらの定義により,リサンプリングウェイト\(w_i\)が有界であることが保証されます(定理A.4):\(m_i\)が式36、37、38で与えられ、サンプル\(X_i\)が\({\hat p}_i\)を積分するために適正分布している場合、すなわち、ある\(C_i\)に対して\({\hat p}_i(X_i) W_i \leq C_i\)である場合、\(X_i\)のリサンプリングウェイトは次のように有界です。
\begin{eqnarray}
w_i \leq \frac{C_i}{|R|} \tag{39}
\end{eqnarray}
\({\hat p}_i(X_i)W_i\)が有界であるという条件は、\(W_i\)の理想値\(1/{\bar p}_i(X_i)\)からの相対誤差が有界であることと等価です。独立したサンプルから始めると、帰納的にこれを保証することができます:
Bounded variance.
ターゲット関数\({\hat p}_i\)(すなわち\({\hat p}_i(X_i) \leq C_i p_i (X_i)\))に対して合理的な重点サンプリング戦略で\(X_i\)を独立にサンプリングすれば、\({\hat p}_i(X_i)W_i = {\hat p}_i(X_i) / p_i(X_i) \leq C_i\)となり、式39が\(X_i\)に適用されます。
すべての入力サンプル\(X_i\)が定数\(C_i\)に対して\({\hat p}_i(X_i) W_i \leq C_i\)を満たす場合、以下のようになります。
\begin{eqnarray}
{\hat p}(Y) W_Y = \sum_{i=1}^M W_i \leq \sum_{i=1}^M \frac{C_i}{|R|} \tag{40}
\end{eqnarray}
となり、\({\hat p}(Y)W_Y\)が有界であるため、式39が\(Y\)に適用されます。
誘導的に、独立したサンプルから始めるGRISの連鎖は、\(f/{\hat p}\)が有界であると仮定して、有限のワーストケースのリサンプリングウェイト和と有限のワーストケースの寄与\(f(Y)W_Y\)を保持します。
\(f(Y)W_Y\)のような有界の確率変数は、有限分散を特徴とします。また、このような変数を平均化すると期待値に収束します。この重要な特性は、以前のReSTIRの研究で暗黙のうちに使用されたリサンプリングMISウェイトによって自動的に保証されるものではなく、\(m_i=1/M\)はしばしば単一性を適切に分割できず、さらに式33の特異点を説明できない場合があります。
Constant resampling weights.
定数リサンプリングMISのウェイト\(m_i(y)=1/M\)は非常に安価に評価できます。しかし、そのようなMISウェイトは、時々しか\(m_i\)(式20)の制約を満たしません。すなわち、任意の実現可能なサンプル\(X_i\)が正のPDFで他のすべての領域\(\Omega_j\)からサンプリングされていたときです。これは一般に真実ではありませんが、重要な例外は、すべての入力サンプルが正準である場合です。これは、例えば、毎回少なくとも1つの正準サンプルを使用するGRISで入力サンプルを生成し、上記のリサンプリングMISスキームの1つを使用することで達成できます。一般的なケースで定数ウェイトを使用する場合、\({\bar p}\)への収束は、収束と分散の結果とともに失われます。Bitterliら[2020]が提案したような適切な寄与MISを用いることで、バイアスを除去することは可能です。
Tractable PDFs.
すべての入力サンプルが既知の扱いやすいPDFを持つ場合(例えば、\(X_i\)は既知のPDF \(p_i\)を持つ重点サンプラー由来)、一般化ペアワイズおよびTalbot MISウェイトは、\({\hat p}_i\)の代わりに\(p_i\)を使用し、\({\hat p}\)のインスタンスは固定正準サンプル\(X_c\)のPDF \(p_c\)と置き換えられるように修正できます。正準サンプルは、\({\hat p}\)を積分するのに妥当なPDFを持たなければなりません。詳細については、セクションS.1.4を参照してください。
5.7 Guaranteeing Convergence★
これまで、GRISは\({\rm Var}[\sum_{i=1}^M w_i] \rightarrow 0\)を要求するだけで\(p_Y\)の\({\bar p}\)への漸近収束を達成することを示しました。本セクションでは、一般化RIS理論の直接応用として、収束を保証する方法を示します。セクション6では、この解析をストリーミング方式で収束を保証するマルチパスアルゴリズムに拡張し、有限のメモリのみを必要とし、複数の積分間の計算を償却します。
Independent samples.
ロバストなリサンプリングMISウェイトを持つ複数領域の場合(セクション5.6)を想定し、定理A.4を適用してリサンプリングウェイトの有界\(w_i \leq C_i/|R|\)を求めます。また、ペア\((X_i, W_i)\)が独立であると仮定すると、\(w_i\)は独立であり、\({\rm Var}[\sum_{i=1}^M w_i = \sum_{i=1}^M {\rm Var}[w_i]\)としてPopoviciuの不等式により分散を拘束します。
\begin{eqnarray}
\sum_{i=1}^M {\rm Var}[w_i] \leq \sum_{i=1}^M \frac{1}{4} \frac{{C_i}^2}{|R|^2} \tag{41}
\end{eqnarray}
これは、\(|R|\)が\(M\)と\(C_i\)に比べて十分に速く成長する場合、ゼロに収束します。実用的な制約は、追加サンプルの重点サンプリング品質が際限なく悪化しないこと、すなわち、すべての\(i\)について\(C_i \leq C\)となるような上界\(C\)が存在することを主張します。そして、\(|R|\)が\(\sqrt{M}\)となるような\(|R|/\sqrt{M} \rightarrow \infty\)よりも速く成長する場合にゼロへの収束を保証する、\({\rm Var}[\sum_{i=1}^M w_i] \leq C^2 \frac{M}{4|R|^2}\)を得ます。例えば、ある\(c \gt 0\)の\(|R| \approx c M^{0.5001}\)は、極限で(ゆっくり)収束します。しかし、より現実的には、正準サンプルの比率\(|R|/M\)が、十分に大きな\(M\)に対して、ある定数\(\gamma \gt 0\)を下回らないことを保証することができます。これは、分散の観点から、最悪の場合、\(O(1/M)\)の収束率を保証します。
Dependent samples.
我々のGRIS理論は、サンプルの独立性を仮定していません。収束と分散の結果は、\({\rm Var}[\sum_{i=1}^M w_i] \rightarrow 0\)が真であることを仮定しているだけです。独立したサンプルの場合、この制約を証明するのは簡単です。依存するサンプルでは、この制約が真であるとは限りません。簡単な反例として、重複したサンプル\(X_i\)を使用します。サンプル数が増えても分散の減少は起こりません。
サンプルの相関が十分弱ければ収束します。\(|R|/M \geq \gamma\)、\(w_i \leq C/|R|\)が全ての\(i\)の場合を想定します(例えば、\(m_i=1/M\)のシングル領域、あるいは我々の新規\(m_i\)を持つ複数領域)。これは一般的には収束しないかもしれませんが、リサンプリングウェイト\(w_i\)と\(w_{i+k}\)の間の相関が\(k \rightarrow \infty\)としてゼロになる傾向があると仮定することで収束を保証することができます。より正確には、\(i\)に関係なく、相関\(\rho_{i, i+k} \leq b_k\)と\(b_k \rightarrow 0\)が成り立つような非負の数列\(b_k\)が存在するものとする。このとき,次を操作することができます。
\begin{eqnarray}
{\rm Var} \left[ \sum_{i=1}^M w_i \right] = \sum_{i=1}^M {\rm Var}[w_i] + 2 \sum_{i=1}^M \sum_{k=1}^{M-i} {\rm Cov}(w_i, w_{i+k}) \tag{42}
\end{eqnarray}
ここで、第1項は式41に続く議論によってゼロに収束し、第2項についてはセクションS.2で導出されます。
\begin{eqnarray}
\sum_{i=1}^M \sum_{k=1}^{M-i} {\rm Cov}(w_i, w_{i+k}) \leq \frac{C^2}{4 \gamma^2} \left( \frac{1}{M} \sum_{k=1}^M b_k \right) \overset{M \rightarrow \infty}{\longrightarrow} 0 \tag{43}
\end{eqnarray}
ここで、\(\gamma\)は\(|R|/M\)の最小比率、\(C\)はすべての\(C_i\)の上界です。\(b_k\)の平均は0に収束するので、従属サンプルで収束が得られます。
また、セクションS.2には、最大相関\(b_k\)が補償するのに十分な速さで低下する場合、\(M\)が大きくなるにつれて比率\(|R|/M\)が減少することを可能にする一般化した結果が含まれています。例えば、\(\sum_{k=1}^{\infty} b_k \lt \infty\)の場合、ある\(c \gt 0\)について\(|R| \geq c \cdot M^{0.5001}\)との収束を保証することができます。
6 AMORTIZATION OVER AN IMAGE WITH RESTIR
ここでは、一般化されたRISの上に2つのReSTIRのバリエーションを再定義します:新しいプログレッシブオフラインレンダラーとGRISを用いたBitterliら[2020]の再定義です。また、ReSTIRを不偏の探索的な非マルコフ連鎖として再解釈し、それを用いて生成された画像を平均化すると、いつグランドトゥルースに収束するのか説明します。
光輸送では、各ピクセルの色\(I_i\)が積分によって決定される画像を作ることを目指します。
\begin{eqnarray}
I_i = \int_{\Omega} h_i({\bar {\mathbf x}}) f({\bar {\mathbf x}}) d{\bar {\mathbf x}} \tag{44}
\end{eqnarray}
ピクセルインデックス\(i\)、センサから光への経路\(\Omega\)、画像フィルタ\(h_i\)、経路寄与関数\(f\)です。経路\({\bar {\mathbf x}}\)はフィルタ\(h_i\)により一般に数ピクセルに寄与しています。
一般的なフィルタリング方法では、各ピクセルのパスをサンプリングし、カーネル\(h_j\)で画像に寄与\(f(X)/P_X(X)\)をスプラットします。これにより、一般性を損なうことなく、ピクセル\(i\)に直接寄与する経路\(\Omega_i\)のみを積分することができます。これは\(h_i\)にボックスフィルタを使うことに相当しますが、より複雑なフィルタに一般化するのは簡単です。
各ピクセルの\(I_i\)をその領域\(\Omega_i\)にのみ積分することで、以下のようになります。
\begin{eqnarray}
I_i = \int_{\Omega_i} f({\bar {\mathbf x}}) d{\bar {\mathbf x}} \tag{45}
\end{eqnarray}
であり、領域\(\Omega_i\)と\(\Omega_j\)の間でパスを共有することは、パスを変更しない限り不可能です。我々は、シフトマッピングをリサンプリングに組み込むことで、より効率的に積分間のパスを共有することを目指します。
6.1 Formulation
ピクセル\(i\)をパス空間領域\(\Omega_i\)、被積分関数\(f_i\)(すなわち、\(\Omega_i\)に限定された\(f\))、およびターゲット関数\({\hat p}_i\)に関連付けますが、これは例えば、グレースケールのパス寄与関数\(|f_i|\)または、有界相対誤差を持つ安い近似値であるかもしれません。
各ピクセル\(i\)は、\({\hat p}_i\)を積分するのに妥当な正準パス\(X_i\)のサンプラーを備えていると仮定します。サンプルは、例えば、\({\hat p}_i\)に対して直接重点サンプリングされるか、または、適正に重点サンプリングされた複数の初期候補からRISを用いてリサンプリングされます。
6.2. Reservoirs and Weighted GRIS
セクション2のレゼバーに関する議論を少し拡張して、レゼバーのマージを複数の入力領域に一般化します。リザーバ\(r\)は、入力のストリームから\(X_r\)をサンプリングするための従来のリザーバの使い方と同様に、パス\(X_r\)、その重み\(W_r\)、サンプル数\(M_r\)を格納します。この文脈では、\(M_r\)は現在の\(X_r\)がリサンプリングされるサンプル数であり、\(X_r\)は新しい入力サンプルに出会うたびに、適切な確率でランダムに保持または置換されるため、\(M_r\)は1ずつ増加します。レゼバー\(r_1\)と\(r_2\)のレゼバー・マージは新しいレゼバー\(r_m\)を構築し、\(X_{r_m}\)は\(X_{r_1}\)と\(X_{r_2}\)からリサンプリングされ、あたかも入力サンプルまたは\(r_1\)と\(r_2\)の連結からリサンプリングされたかのようになり、\(M_{r_m}\)は単純に\(M_{r_1} + M_{r_2}\)となります。
\(M_r\)をサンプル数として解釈することは、ReSTIRには厳しすぎます。レゼバー・マージは、単純に\(X_{r_m}\)を正準サンプル\(X_{r_1}\)と\(X_{r_2}\)からRISでリサンプリングし、MISウェイト\(m_{r_i}(y) = M_{r_i}/(M_{r_1} + M_{r_2})\)をリサンプリングします。この文脈での\(M_r\)の意味は、対応するサンプルの相対重みです。我々は積分を推定するために\(X_r\)を使用し、\(M_r\)はこれらのサンプルの相対重みを定義するので、我々は\(M_r\)をコンフィデンスウェイトと呼びます。実際、ReSTIRは\(M_r\)を定数\(M_c\)にキャップし、古いサンプルの信頼度を制限し、サンプル数としての古い解釈を無効にしています。
リザーバのマージは、適切なMISウェイト(セクション5.6)を持つ重み付きGRISに一般化され、MIS式の\({\hat p}\)と\({\hat p}_{\leftarrow}\)に対応するリザーバの\(M_r\)を乗算するだけです。リサンプリング結果は\(X_{r_m}\)と\(M_{r_m} = {\rm min}(M_c, \sum_j M_{r_j})\)に格納されます。このレゼバー・マージの一般化された形式は次のセクションで使用されます。
6.3 ReSTIR as Chained GRIS
我々は、ReSTIRアルゴリズム、すなわちBitterliら[2020, Algorithm 5]のキーとなる観点を、GRISリサンプリングステップのシーケンスとして書き直します:
\(Y_i^{t-1}\)を、フレーム\(t-1\)上のピクセル\(i\)のリサンプリング(またはサンプリング)パスとし、後に再利用するために、その不偏の寄与ウェイト\(W_{Y_i^{t-1}}\)とともに保存します。
(1) (Initial candidates) 各ピクセル\(i\)について独立サンプル\(X_i^t\)を生成し、その寄与ウェイト\(W_{X_i^t}\)を評価します。
(2) (Temporal reuse) GRISを使用して、最後のフレームのサンプル\(Y_i^{t-1}\)と新しいサンプル\(X_i^t\)の間でリサンプリングを行い、\(Z_i\)を選択します。ピクセルの対応は、モーションベクトルを介して識別することができます。
(3) (Spatial reuse) 各ピクセルは、多数のランダムな空間的近傍\(j\)を選択し、GRISを介して\(Z_i\)と近傍サンプル\(Z_j\)との間のリサンプリングによって\(Y_i^t\)を選択します。このステップは、割り当て\(Z_i := Y_i^t\)で複数回実行することができます。
(4) ピクセル積分\(I_i^t \approx f_i (Y_i^t)W_{Y_i^t}\)を推定します。
新しいサンプル\(X_i^t\)は、\(M_r=1\)のレゼバーとして扱われ、コンフィデンスウェイトを考慮して、\(Y_i^{t-1}\)を格納するレゼバーとマージされます。空間リサンプリングは確率的畳み込みのように動作し、ランダムな近傍ピクセルからのレゼバーをマージします。最後のサンプル\(Y_i^t\)はそのピクセルのレゼバーに格納され、空間的リサンプリングからの信頼度重みは次のフレームのテンポラルリサンプリングステップで使用されます。
付録Bでは、パフォーマンスと正しさに関連するその他の詳細について説明します。
6.4 Path Space Exploration via M-capping
\(M_r\)を一定の\(M_c\)(セクション6.2)にキャップすることが重要です。\(M_r\)を制限しないと、新しいサンプルの相対的な重みが指数関数的にゼロに近づき、図2のように間違った結果に収束してしまいます。
\(M\)-cappingでは、時間的に再利用されるサンプルの相対的な重みは最大でも\(M_c/(M_c+1)\)に制限され、これは直感的にセクション5.7の収束制約を満たすはずです。上記の制約は入力サンプルの要件であり、制約が満たされたとしても、空間入力サンプルの数が増加しないため(\(M \cancel{\rightarrow} \infty\))、ReSTIRの結果自体はまだ収束しません。代わりに、ReSTIRは、静止シーンにおいてフレーム間の平均が収束するように経路空間を探索します: 仮に、ピクセル\(i\)について、\({\hat p}= f_i\)で、過去のフレームの一つからパスを再サンプルすると仮定します。すなわち\(Y=Y_i^s\)で、\(s\)はランダムです。そのPDFは\(f_i / ||f_i||\)に近づき、その寄与の分散はゼロに収束し、その寄与はReSTIRフレームの平均\(f_i(Y)W_Y = \cancel{ \frac{f_i(Y)}{{\hat p}(Y)} } \sum_{t=1}^T \frac{1}{T} \cdot f_i (Y_i^t) W_{Y_i^t}\)となります。
6.5 ReSTIR for Offline Rendering
テンポラルパスの再利用は現在のフレームの分散を減らしますが、サンプルを時間的に相関させます。このため、プログレッシブ・レンダラーで時間的に累積すると、収束が遅くなります(図9b)。代わりに、空間のみのGRISで独立したフレームをレンダリングすることを提案します。これにより、収束が速くなり、既存のシステムへの組み込みが容易になるはずです。
このオフラインアルゴリズムは単純な2パス法です。1回の繰り返しで、最初のパスはGRISで1回または複数回のピクセル間再利用を行い、他のピクセルから正準サンプルをリサンプルします。2回目のパスでは、生成された画像を単純に平均化します。
空間的な再利用パスに相関があるにもかかわらず、平均の収束を証明するのは簡単になりました: 適切なMISウェイトを持つGRISは、相関関係にもかかわらず不偏のままであり、式40により、空間再利用パスの固定数を持つGRISの寄与は、有界のままです。したがって、独立にサンプリングされたフレームの平均化は収束します。
厳密に言えば、上記の収束はスカラー関数\(f_i\)にのみ当てはまります。実際には、\(f_i\)はベクトル値であり、例えばグレースケール\({\hat p}_i = |f_i|\)を使用し、ランダムフレーム\(s\)からサンプリングされたパス\(Y = Y_i^s\)の明るさ\(|f_i|\)への収束を保証します。文字通り、不偏の寄与を評価すると、次のようになります。
\begin{eqnarray}
f_i(Y) W_Y = \frac{f_i(Y)}{|f_i(Y)|} \cdot \sum_{t=1}^T \frac{1}{T} | f_i(Y_i^t)| W_{Y_i^t}, \tag{46}
\end{eqnarray}
これはカラーノイズを含むことがあります。しかし、オフラインのコンテキストでは、複数サンプルの予算を想定しているため、明示的な平均式を推奨します。
\begin{eqnarray}
{\tilde I}_i = \frac{1}{T} \sum_{t=1}^T f_i(Y_i^t) W_{Y_i^t} \tag{47}
\end{eqnarray}
上記はカラーノイズを除去したものです。
例えば、\(Y_i^t\)のランダムなサブセットを再サンプリングして各ピクセルに保存し、次のアニメーションフレームのレンダリングをブートストラップしたり、マテリアルの変更後に再レンダリングしたりすることができます。
7 DESIGNING SHIFT MAPPINGS
パスを操作して再利用するこれまでの光輸送技法(勾配領域レンダリングなど)は、ピクセル間のパスをマッピングするためにさまざまなシフトマッピングを導入しています。一般に、単一のシフトマップが最適であることはなく、最適なシフトマップは、異なるハードウェア上での計算効率だけでなく、シーン特性の両方に依存します。このセクションでは、効果的なシフトマップの主要な特性について説明し、実用的なシフトマッピングの一般的な構成要素を紹介します。
また、サンプリングされたBSDFローブに基づく新しい設計原理戦略と、ノイズを回避するための新しいヒューリスティックについても述べます。
7.1 Shift Mapping
シフト・マップ\(T\)は、ピクセル\(k\)のパス\({\bar {\mathbf x}}\)を取り、ピクセル\(j\)の別のパス\({\bar {\mathbf y}}\)にマップします。元のパス\({\bar {\mathbf x}}\)をベース・パス、シフトされた\({\bar {\mathbf y}}\)をオフセット・パスと呼びます。Veachの[1998]頂点パラメタリゼーションを用いて、\(\Omega_k\)から\(\Omega_j\)への一般的なシフトマップ\(T\)を次のように定義します。
\begin{eqnarray}
T([{\mathbf x}_0, {\mathbf x}_1, {\mathbf x}_2, {\mathbf x}_3, \cdots ]) = [{\mathbf y}_0, {\mathbf y}_1, {\mathbf y}_2, {\mathbf y}_3, \cdots ] \tag{48}
\end{eqnarray}
頂点\({\mathbf y}_0\)は通常センサー上で指定され、\({\mathbf y}_1\)は被写界深度パラメータを考慮したピクセル\(j\)を通してトレースされたものです。
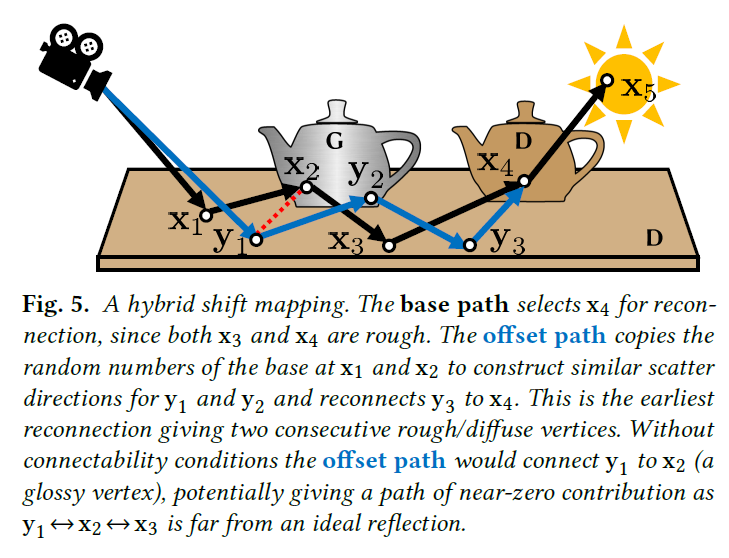
シフトマップを設計する際、主な自由度(そして課題)は、頂点\({\mathbf y}_2\)以降のヒューリスティックを設計し、シフトがパス寄与、\(f_k(T_k({\bar {\mathbf x}}) \approx f_j({\bar {\mathbf x}})\)と\(|\partial T_k / \partial {\bar {\mathbf x}}| \approx 1\)をほぼ保持するようにすることです。パスの寄与の類似性を最大化することは、近接するピクセルに対して(ほぼ)同じパスを再利用することにほぼ等しく、一般的な設計ヒューリスティックです。図5は、ランダム・リプレイとリコネクションのハイブリッド・シフト・マッピングを例として示しています。
Local decisions.
オフセット・パス\({\bar {\mathbf y}}\)を見つける一般的な方法は、\({\mathbf y}_1\)から始めて、ローカルのベースとオフセット・パスのジオメトリを分析しながら、頂点ごとに順次オフセット・パスを構築します。各\(i\)について、次のオフセット頂点\({\mathbf y}_{i+1}\)は、ベースパス頂点\({\mathbf x}_{i-1}\)、\({\mathbf x}_i\)、\({\mathbf x}_{i+1}\)とオフセット頂点\({\mathbf y}_{i-1}\)、\({\mathbf y}_i\)に基づいて決定されます。例えば、頂点\({\mathbf x}_i\)、\({\mathbf x}_{i+1}\)、\({\mathbf y}_i\)がラフマテリアルを持つ場合、\({\mathbf y}_{i+1} = {\mathbf x}_{i+1}\)を選択することで、ベースパスとオフセットパスを接続するのが一般的な戦略です。以前の頂点\({\mathbf x}_{i-1}\)と\({\mathbf y}_{i-1}\)もハーフベクトルコピーを実行するために使用できます[Keuttunen et al. 2015]。
Ensuring bijectivity.
オフセットパスの逐次的な構築は、突然停止することがあります:例えば、ハーフベクトルコピーでは、局所的な決定が屈折を全反射にマッピングすることはできますが、その逆は決して起こらないため、両対称性が破れます。両対称性はパス空間全体で達成できるとは限りませんが、それは大きな問題ではありません:すべてのパスがシフトマッピング領域に属する必要はないからです。シフトは、パスをシフトしようとした後、単に「未定義」を返すかもしれません。これは、そのパスがシフトの領域に属さないことを示します。
\({\bar {\mathbf x}}\)が\({\bar {\mathbf y}}\)にシフトする場合、\({\bar {\mathbf y}}\)を\({\bar {\mathbf x}}\)に戻す逆シフトが存在しなければなりません。しばしば、\(T_{k \rightarrow j}({\bar {\mathbf x}})= {\bar {\mathbf y}}\)の場合、\(T_{j \rightarrow k}({\bar {\mathbf y}})= {\bar {\mathbf x}}\)となるような対称シフトマッピングを設計することで、若干多くのことが保証されます。写像の領域からパスを削除することはノイズの原因となり、計算の無駄となりますが、双射性を無視することは重大なバイアスをもたらします。
7.2 Common Building Blocks
オフセット・パスを構築するためのローカルな決定は、ベース・パスの何らかの特性を固定することに起因することが多いです。このような不変量はパス間で情報を共有し、シフトの逆転を可能にします。ここでは、シフトマッピングの一般的な戦略について簡単に説明します。
Vertex copy (reconnection).
オフセットパスとベースパスをできるだけ早く再接続するのが一般的ですが、これは頂点の共有が安価で、パスの寄与を似たような状態に保てることが多いからです。\({\mathbf x}_i\)、\({\mathbf x}_{i+1}\)、および\({\mathbf y}_i\)がすべてラフマテリアル上にある場合、Lehtinenら[2013]は\({\mathbf y}_{i+1} = {\mathbf x}_{i+1}\)と設定することでオフセットパスをベースパスにリコネクションします。\({\bar {\mathbf x}}\)の後続の頂点も通常コピーされます。この戦略はディフューズとラフマテリアルに適しています。
Half-vector copy.
リコネクションはスペキュラーに近い頂点のパスの類似性を壊します。Kettunenら[2015]はベースパスのハーフベクトルをローカルタンジェント空間に変換し、オフセットパスにコピーし、頂点\({\mathbf y}_{i+1}\)を反射(または屈折)方向に再トレースしました。
Direction copy.
方向コピーは、ベース・パスの頂点からの退出方向をグローバル座標でオフセット・パスにコピーし、次の頂点\({\mathbf y}_{i+1}\)を見つけるために再トレースします。方向コピーは環境マッピングでよく使われます。
Random replay.
ランダム・リプレイは、ベース・パスの乱数をコピーして、ベース・パスで使用された方法で\({\mathbf y}_{i+1}\)を再トレースします。ランダム・リプレイは、多くの場合、ハーフ・ベクトルや方向をコピーしたり、next-event-estimationの場合にエリア・ライトに再接続したりするのとほぼ同様の判断を行います。
Manifold exploration.
スペキュラリティのためにリコネクションが不可能な場合、Lehtinenら[2013]は次の接続可能な頂点を見つけ、それをコピーし、中間の(スペキュラリティに近い)頂点に対してマニフォールド探索[Jakob and Marschner 2012]を適用しました。この戦略は、比較的高コストではありますが、高品質のオフセットパスを反復的に構築します。
素早く再接続することは良い戦略であることが多いですが、落とし穴もあります。パスシフトの課題としては、光沢のあるサーフェイスでの理想的な反射を忠実に再現できないこと、オクルージョンを通過してリコネクションしようとすること、リコネクションセグメントの長さを大幅に変更すること、異なる物体やマテリアルの間でシフトすること、(反射や屈折などにより)単純に発散しすぎることなどがあります。
7.3 A Full Shift Mapping
フルシフトマッピングはこれらの構成要素を組み合わせたもので、多くの場合、単純なヒューリスティックに基づいています。例えば、Kettunenら[2015]は、頂点\({\mathbf x}_i\), \({\mathbf x}_{i+1}\), \({\mathbf y}_i\)が全て「十分に」ラフでなければならないという単純な条件を用いて、ベースパスとオフセットパスを順次解析し、適切な再接続を見つけます。このテストに合格した場合、ベースパスとオフセットパスはリコネクションされ、そうでない場合はハーフベクトルコピーが使用され、次の頂点に対してテストが繰り返されます。Huaら[2019]は、ハーフベクトルコピーをランダムリプレイに置き換えることで同等の結果を示しています。我々は、HuaらのアプローチがGPU上でより効率的であり、若干一般的であることを発見したので、いくつかの改良を加えて採用しました。
7.4 Shift Mappings Optimized for Real-Time Rendering
2つの異なるシフトマッピングを研究し、リアルタイムレンダリングをターゲットとするGPU実装に適したものにするために、必要に応じて修正します:
- リコネクションシフト[Lehtinen et al 2013]は、\({\mathbf y}_2 = {\mathbf x}_2\)を常に最初の間接頂点で接続するように設定します。これはほとんどの拡散シーンでうまく機能します。ReSTIR GI [Ouyang et al. 2021]は、暗黙的にこの選択を使用しますが、性能と正確性をトレードします。
- ランダムリプレイとリコネクションのハイブリッド[Hua et al. 2019]は、特定の接続可能性条件が満たされない場合、ランダムリプレイを使ってリコネクションを先送りします。我々はこのシフトマッピングの改良型を提示します。
リコネクションシフトを効率的に実装するのは簡単で、再接続頂点を保存し、パスの寄与を再評価するだけでよいです。ハイブリッド・シフトを効率的に実装することは自明ではありません。ランダムリプレイはリコネクションなしでは効率的ではありませんが、リコネクションの先送りの可能性があるため、すべてのベースパスの頂点をリコネクションの候補として保存する必要があります。GPUレイトレーシングはしばしばメモリに縛られるため、これは理想的ではありません。
ベースパスに1つの再接続可能な頂点を選択させることで、メモリ使用量を最小化します;\({\mathbf x}_i\)と\({\mathbf x}_{i+1}\)の接続可能条件を満たす最初のベースパス頂点\({\mathbf x}_i\)を事前に計算します。リコネクションはこの頂点で起こるか、起こらないかのどちらかです。これは、全パスの代わりに頂点\({\mathbf x}_{i+1}\)を保存するだけでよいです。
この制約は合理的です。パスの再利用に役立てるためには、ベースパスとオフセットパスは比較的類似している必要があります。さらに、我々の両対称性要件はこの保証を強制します。\({\mathbf y}\)を構築するとき、もしそれが最も早く可能な再接続頂点で不一致であることが分かれば、シフトは逆転できないので「未定義」を返さなければなりません。
7.5 Connectability Conditions
我々は、接続可能性条件について、従来の研究と比較して2つの新しい改善策を提案し、これらの改善策により、我々の手法で頻繁にノイズとアーチファクトが大幅に減少することを発見しました。
Distance condition.
レンダリング方程式のエリア定式化には、コーナーなどの短いパスセグメントで特異となるジオメトリ項が含まれます。単方向パスのトレースでは、この特異点はnext-event-estimationに起因しますが、標準的なMISでは除去されます。近接する頂点をリコネクションする際にも同様の特異点が現れ、ジオメトリのエッジ付近でノイズが増加します。
我々は、短いセグメントを導入するリコネクションをスキップすることで、この問題を軽減することを提案します。これはManziら[2014]の距離テストに似ていますが、マニフォールドウォークを発生させる代わりに、ランダムリプレイを行うことでリコネクションを先送りします。より具体的には、\(||{\mathbf x}_{i+1} – {\mathbf x}_i || \geq d_{\rm max}\)の場合にのみ\({\mathbf x}_{i+1}\)へのリコネクションを許可します。対称性により、セクション7.4で説明するように、\({\mathbf y}_{i+1}\)が\({\mathbf x}_{i+1}\)になるためにはオフセットパスが\(||{\mathbf x}_{i+1} – {\mathbf y}_i|| \geq d_{\rm max}\)を満たす必要があります。
Lobe-specific connectability.
Kettunenら[2015]は、\({\mathbf x}_i\), \({\mathbf x}_{i+1}\), \({\mathbf y}_i\)のラフネスの値が全て所定の閾値を超えることを保証することにより、リコネクションの実現可能性をテストしています。しかし、BSDFはしばしば複数の別々のローブを合計するため、このようなテストは曖昧です。このようなマテリアルに適したシフトマップを選択することは、長年の問題です [Kettunen 2020]。単一の戦略では、少なくとも1つの層が誤って扱われる可能性が高いです。
単方向パスのトレーサーは、頂点ごとに1つのBSDFローブだけを分解して評価することで、サンプリングを最適化することが多いです[Szésci et al 2003]。我々は、シフトマッピングについても同じことを提案します:選択したローブだけのラフネスを調べ、それ以外はセクション7.4で説明したように進めます。セクション7.6で、ローブ固有の接続可能性に必要な、ローブインデックスを用いたパスの拡張について詳しく述べます。
7.6 Extending Paths with Lobe Indices
各経路の長さ\(d\)に対して異なる手法で\(N\)個の経路を生成するパストレーサーの場合、標準的な経路積分は次のように書くことができます。
\begin{eqnarray}
I = \sum_{d=1}^{\infty} \sum_{n=1}^N \int_{\Omega_d} \omega_n ({\bar {\mathbf x}})f({\bar {\mathbf x}}) d{\bar {\mathbf x}} \tag{49}
\end{eqnarray}
ここで、\(\omega_n\)はパス戦略\(n\)のMISウェイトです。簡単のため、\(N=2\)と仮定すると、\(n=1\)は最後の頂点をサンプリングするためにnext-event-estimationを使用し、\(n=2\)はBSDFサンプリングを使用します。バランスヒューリスティックMISウェイトは\(\omega_n({\bar {\mathbf x}}) = \frac{ p_n({\bar {\mathbf x}}) }{ p_1({\bar {\mathbf x}}) + p_2({\bar {\mathbf x}}) }\)で与えられ、ここで\(p_1\)と\(p_2\)はパスのNEEとBSDFサンプリングPDFであり、すべてのBSDFローブに渡って合計します。
セクション7.4で改良したシフト戦略では、BSDFをローブに分割する必要があります。我々は式49をローブ拡張されたパス空間を使用するように変換し、発見的な議論を必要とせず、単純な置換によってReSTIRを実装することを可能にします。
パス\({\bar {\mathbf x}} = ({\mathbf x}_0, \cdots, {\mathbf x}_d)\)とローブ・インデックス\({\bar \ell}= (\ell_1, \cdots, \ell_{d-1})\)のシーケンスを組み合わせて、\(({\bar {\mathbf x}}, {\bar \ell})\)の組で表される長さ\(d\)のパス\(\Omega_d\)の拡張パス空間にします。各\(\ell_j\)は正の整数\(1 \leq \ell_j \leq N_{\rm lobe}\)(BRDFモデルのローブ数)、またはパスがnext-event estimationで終わる場合は特別なシンボル\(\ell_{d-1} = {\mathcal N}\)となります。
\(f\)は通常のパス寄与関数を表し、部分寄与関数\(f_{\bar \ell}\)を次のように定義します:完全にBSDFサンプリングされたパスの場合、各頂点\({\mathbf x}_j\)でローブ\(\ell_j\)のみを評価します。最後の頂点\({\mathbf x}_d\)がNEEサンプリングされた場合、すなわち、\(\ell_{d-1}={\mathcal N}\)の場合、\({\mathbf x}_{d-1}\)におけるBSDFはすべてのローブで評価されます。
ローブ・インデックス配列の集合を\(L_d\)とすると、式49は次のように書き換えられます。
\begin{eqnarray}
I = \sum_{d1}^{\infty} \sum_{ {\bar \ell} \in L_d} \int_{\Omega_d} \omega_{n({\bar \ell})} ({\bar {\mathbf x}}) f_{\bar \ell}({\bar {\mathbf x}}) d{\bar {\mathbf x}} \tag{50}
\end{eqnarray}
最後の頂点が NEE サンプリングか BSDF サンプリングかに基づいて \(n(\ell) \in \{1, 2\}\)を指定します。最後に、Veach [1998]に似た積分に合計を結合します。これは、すべての長さ\(d\)のペア\({\tilde {\mathbf x}} = ({\bar {\mathbf x}}, {\bar \ell})\)について、拡張パス空間\({\tilde {\mathbf x}} \in {\tilde \Omega}\)にわたって積分します:
\begin{eqnarray}
I = \int_{\tilde \Omega} \omega_{n({\bar \ell})} ({\bar {\mathbf x}}) f_{\bar \ell} ({\bar {\mathbf x}}) d{\bar {\mathbf x}} \tag{51}
\end{eqnarray}
この定式化により、頂点ベースのパス空間では不可能な、BSDFローブを推論するシフト・マッピングの使用が可能になります。
パスをシフトするには、頂点\({\mathbf x}_{j+1}\)をサンプリングするために選択されたローブ\(\ell_j\)のラフネスを調べることによって、頂点\({\mathbf x}_j\)が十分に粗いかどうかをテストします。NEEでサンプリングされた頂点は、そのBRDFローブの少なくとも1つが十分に粗い場合、粗いものとして扱います。すべてのライト頂点はラフとして扱われます。3つの再接続頂点\(({\mathbf x}_j, {\mathbf x}_{j+1}, {\mathbf y}_j)\)全てがラフネスと距離の条件(セクション7.5)をパスした場合、リコネクションを実行します。そうでなければランダムリプレイで\({\mathbf y}_{j+1}\)をサンプリングします。
ランダムリプレイを使用する場合、ベースパスとオフセットパスは通常同じBRDFローブを選択します。リコネクションシフトはベースパスの頂点からローブインデックスをコピーします。どちらの場合も、パスの寄与は保持されます。BRDFローブを頻繁に分離することで、ハイブリッドシフトの効率が大幅に向上します(図12参照)。
8 IMPLEMENTATION
我々は、ReSTIRパストレーシング(ReSTIR PT)と呼ぶ概念実証のパストレーシング・アルゴリズムにGRIS理論を適用します。我々は、Falcor GPUレンダリングフレームワーク[Kallweit et al. 2021]をベースとし、セクション6.3に従って、連鎖したGRISパスとしてReSTIR PTを実装します。
ReSTIR PTは、ピクセル間のパスを再利用するためにどのようなシフトマップを使用することもできますが、我々は、前節で述べた2つのシフトを実装します。すなわち、ランダムリプレイとリコネクションを組み合わせたハイブリッドシフトと、我々のローブ固有の改良を加えたもの、そして、常に最初のインダイレクト頂点にリコネクションする、より単純なリコネクションシフトです。
多くのパストレースと同様に、BSDFサンプリングされた頂点に対してはサンプリングされたBSDFローブのみを評価し、NEEサンプリングされた頂点に対してはすべてのローブを評価します。我々は、セクション7.6で説明するように、ローブの選択を追加のパスパラメータとして扱い、サンプリングされたローブのラフネスを用いて、リコネクションとランダムリプレイのどちらかを選択します。
我々のReSTIR PTの実装は、サーフェイスからサーフェイスへの完全な光輸送を扱います。Linら[2021]は暗黙のうちに1つの可能性を定義し,Grusonら[2018]は別の可能性を提案しているが,リサンプリングのための高速なボリューメトリックシフトを見つけることは興味深い将来の課題です。
我々は2つのプロトタイプを持っており、不偏的なリアルタイムとオフラインの光輸送をターゲットにしているが、どちらも性能は最適化されていません。これはOuyangら[2021]とは対照的で、バイアスドですが最適化された先駆者です。我々の一般化された理論に基づき、ReSTIR PTは、任意のシフトマップをサポートすることで、スペキュラー光輸送をよりよく扱う、アンバイアスドなグローバルイルミネーション手法です。
私たちのGRIS理論から直接照明の利点を期待しているが、私たちの実装は主に間接照明に対処している。直接照明にはReSTIR DI [Bitterli et al. 20202]を使用します。
以下では、設計の選択と実装の詳細について説明します。
8.1 Jacobian Determinants
まず、リコネクションとランダム・リプレイ・シフトに対するヤコビアン行列式を与えます。頂点\(i\)までのベースパスとオフセットパスは固定であると仮定します。以下の確率密度は、それ以前のパス状態に対する条件付きとして理解してください。
\({\mathbf x}_i\)から\({\mathbf x}_{i+1}\)までのベクトルを\(\omega_i^x\)とし、頂点\({\mathbf x}_i\)から\({\mathbf x}_{i+1}\)までの対応する乱数を\({\bar {\mathbf u}}_i^x\)とします。オフセット・パスも\(y\)と同様の表記です。
Solid angle. 一般的な立体角パラメータ化を使用する場合、リコネクションシフトのヤコビアンは次のようになります(例えば、Kettunen et al [2015])。
\begin{eqnarray}
\left| \frac{ \partial \omega_i^y }{ \partial \omega_i^x } \right| = \left| \frac{ \cos\theta_2^y}{ \cos \theta_2^x} \right| \frac{ || {\mathbf x}_{i+1} – {\mathbf x}_i ||^2 }{ || {\mathbf x}_{i+1} – {\mathbf y}_i ||^2 } \tag{52}
\end{eqnarray}
\(\theta_2^{\bullet}\) は、\(\omega_i^{\bullet}\) と \({\mathbf x}_{i+1} = {\mathbf y}_{i+1}\) でのジオメトリックサーフェイスの法線との間の角度です。ランダム・リプレイによって\({\mathbf y}_{i+1}\)を決定するためのヤコビアンは次のようになります。
\begin{eqnarray}
\left| \frac{\partial \omega_i^y }{ \partial \omega_i^2 } \right| = \left| \frac{\partial \omega_i^y}{ \partial {\bar {\mathbf u}}_i^y } \right| \left| \frac{ \partial {\bar {\mathbf u}}_i^y }{ \partial {\bar {\mathbf x}}_i^x } \right| \left| \frac{ \partial {\bar {\mathbf u}}_i^x }{ \partial \omega_i^x} \right| = \frac{p_{\omega_i^x}({\mathbf x}_{i+1}) }{ p_{\omega_i^y}({\mathbf y}_{i+1}) } \tag{53}
\end{eqnarray}
すなわち、頂点\(i\)までのパスが与えられたときの、次の頂点の立体角サンプリング確率の比となります。
局所的なシフト決定を使用するため、全経路シフトのヤコビアンは各頂点からのヤコビアンの積となります。
Primary-sample space(PSS).
パストレーサーは、乱数列\({\bar {\mathbf u}} = (u_1, u_2, \cdots, )\)に基づいてパス\({\bar {\mathbf x}}\)を構築し、一次サンプル空間\({\mathscr U}\)を定義します。実際には、\(\int_{\Omega} f({\bar {\mathbf x}}) d{\bar {\mathbf x}}\)の形の積分は\(\int_{\mathscr U} \frac{f(x({\bar {\mathbf u}}))}{p_X(x({\bar {\mathbf u}}))} d{\bar {\mathbf u}}\)で評価され、\(x\)は乱数を用いてパスを構築します。
我々のプロトタイプは、実装を容易にするために一次サンプル空間を使用しています。結果は同じですが、解釈は変わります:積分は領域\({\mathscr U}\)上の\(f(x({\bar {\mathbf u}})) / p_X(x({\bar {\mathbf u}}))\)であり、一次サンプルのPDFは\(p_U=1\)です。セクションS.3では、経路積分のPSS定式化を簡単に紹介します。
PSSパラメタリゼーションにおけるランダムリプレイのヤコビアンは常に1であり、立体角のヤコビアンは式53の右辺で割ることによって一次サンプル空間に変換することができます。パスの頂点から頂点への構成により、次のようになります。
\begin{eqnarray}
\left| \frac{ \partial {\bar {\mathbf u}}_i^y }{ \partial {\bar {\mathbf u}}_i^x } \right| = \left| \frac{ \partial {\bar {\mathbf u}}_i^y }{ \partial \omega_i^y } \right| \left| \frac{\partial \omega_i^y}{ \partial \omega_i^x} \right| \left| \frac{ \partial \omega_i^x }{ \partial {\bar {\mathbf u}}_x } \right| = \frac{ p_{\omega_i^y}({\mathbf y}_{i+1}) }{ p_{\omega_i^x}({\mathbf x}_{i+1}) } \left| \frac{ \partial \omega_i^y }{ \partial \omega_i^x } \right| \tag{54}
\end{eqnarray}
Mixing PSS and path space shifts.★
ランダムリプレイとパススペースシフトを混在させることは、概念的な課題をもたらします。パスサンプラーは多くの場合、パスの次元よりも多くの乱数を消費します。この次元の不一致は、パス空間と一次サンプル空間の間のヤコビアンが存在しないことを意味します。Bitterliら[2017]は、余分な未使用次元でパスをパディングすることで、パスとその乱数の間を双対的にマッピングします。この理論的な双射が存在すると仮定すると、多くの場合、パス空間のシフトとランダム・リプレイを混在させることができます。
8.2 Reservoir Storage
我々のレゼバー(セクション6.3)は、ハイブリッドシフトをサポートしながら、パスあたり88バイトを消費します。寄与ウェイト\(W_r\)とコンフィデンスウェイト\(M_r\)(セクション6)を保存するだけでなく、シフトマップに必要な情報、つまりパスの選択された再接続頂点とランダムリプレイの情報を保存します。詳細はセクションS.4を参照してください。
8.3 Parameters
以下では、セクション6.3で説明したReSTIRアルゴリズムのステップを参照します。
Offline.
オフラインレンダリングでは、パストレーシングによって各ピクセルに対して32個の初期パスツリーをサンプリングし、(Linら[2021]と同様に)RISで1つのパスをリサンプルします。選択されたパスは空間再利用の3回のイテレーションで再利用されます。すべての再利用パスは、現在のピクセルと、低ディスクレパンシーを介して半径10ピクセルから選択された6つの近傍からリサンプルされます。これは、オフラインレンダリングにほぼ最適な構成であることがわかりました。セクションS.6には、パラメータアブレーションが含まれています。
Real-time.
リアルタイムレンダリングでは、パストレースでサンプリングされた1つのパスツリーのみからパスをリサンプルします。1回の空間的再利用パスで、半径20ピクセル内の3つのランダムな近傍を選択します。これにより、空間的再利用コストは低く抑えられ、テンポラルリユースにより依存して分布が改善されます。\(M_c=20\)で\(M\)の上限を設定します。つまり、事前フレーム信頼度は新しいサンプルの最大20倍です。
Connectability thresholds.
距離とラフネスの閾値が良い値であることは重要ですが、比較的安定しています。シーンのスケールは距離の閾値に影響するため、異なるテストシーンで1%~5%のシーンサイズを使用しました。関心領域までのカメラ距離とマテリアルのグロシネスが最適なパラメータに影響します。理想的なパラメータを自動的に設定することは今後の研究に委ねます。
Resampling MIS.
空間的再利用には、ペアワイズMISの守勢的変形(式38)を用います。リアルタイムの変種は、さらにテンポラルリユースのために一般化されたTalbot MIS(式36)を使用します。両者とも\(|R|=1\)であり、収束はオフラインの場合、複数の独立したフレームをレンダリングすることで実現されます。
9 RESULT AND DISCUSSION
以下では、まずReSTIR PTの収束がセクション5の保証と一致することを検証します。セクション9.2では、セクション7から我々のシフトマップの品質を定量化し、セクション9.3では、ReSTIR PTと最近のグローバルイルミネーションアルゴリズムを比較します。リアルタイムとオフラインの結果を別々に示します。すべての性能数値は\(1920 \times 1080\)でGeForce RTX 3090で測定されました。
9.1 Convergence Results
我々は、ラフネス0.5のランバーシアンとGGXマイクロファセットBSDF[Walter et al.2007]を混合した変更されたマテリアルを用いて、コーネルボックスのシーンにおける収束を研究しました(図6a)。
我々は3バウンド間接照明の収束挙動を評価し、簡単のためにリコネクションシフトを使用します。収束結果をGRISにマッピングするために、グレースケール画像で誤差を計算します。
Asymptotic convergence with fixed reuse window.
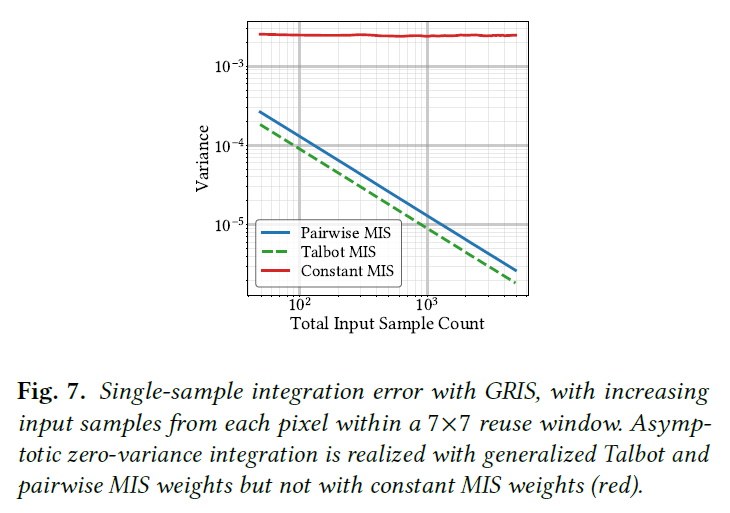
セクション5.6と5.7は、ある相関と重点サンプリング基準の下で、漸近的に単一標本のゼロ分散積分を実現するロバストなTalbotとペアワイズリサンプリングMISウェイトを与えます。図7では、空間のみの再利用の固定ウィンドウについて独立入力サンプル数を増やすと、比\(|R|/M\)を固定します。
我々の一般化されたペアワイズMISウェイトとTalbot MISウェイトはともに、漸近的なゼロ分散積分を示す直線曲線を実現しますが、定数MISウェイトはそうではありません。Talbotウェイトはサンプルあたりの誤差が小さいですが、ペアワイズMISのアルゴリズムの複雑さが小さいため、同様の分散を6~7倍安く達成できます。
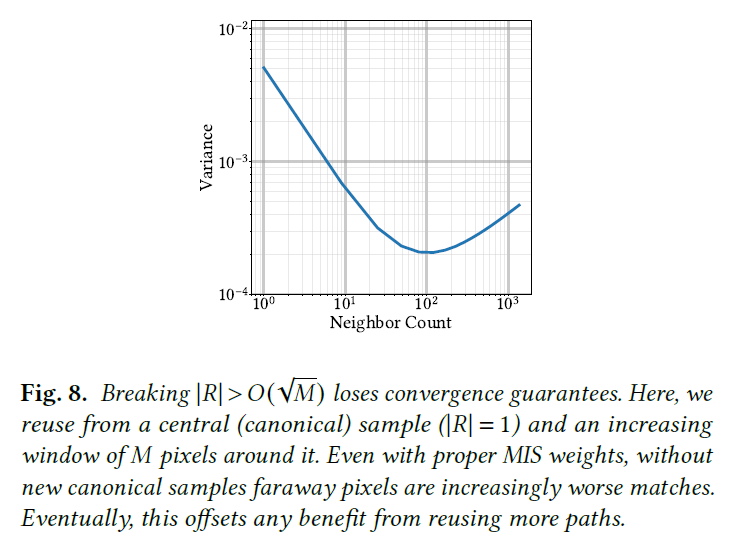
Non-convergence with increasing reuse windows.
\(|R| > O(\sqrt{M})\)の場合のみに収束を保証します。この基準を破る1つのケースは、増加するウィンドウにわたって各ピクセルからのサンプルを再利用する、つまり\(|R|=1\)ですが\(M\)は増加する場合です。パス空間の一部が正準(中央)サンプルによってのみカバーされる場合、これは収束しない可能性があります。より多くの非正準サンプルを追加することは、中央のものを選択する機会を減少させるので、十分にカバーされていない領域は徐々にサンプリングが悪くなります。図8は、より大きなウィンドウでの再利用は、最初は分散を下げますが、ある点を超えると分散が増加することを示しています。
Temporal history and M-cap.
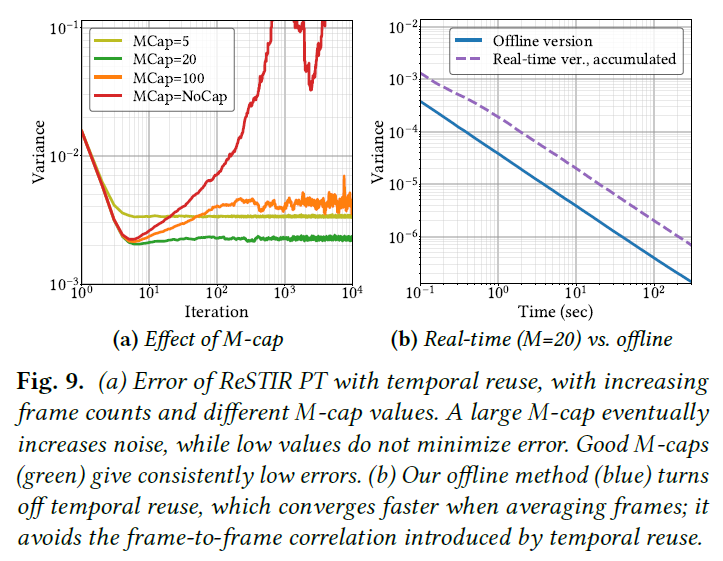
セクション6.3では、ReSTIRレゼバーにおけるテンポラルコンフィデンスウェイト\(M_r\)の上限について議論します。キャップ\(M_c\)が増加すると、セクション5.7で\(b_k\)は1に近づきます。\(M_c=\infty\)の使用は\(b_k=1\)に対応し、全ての保証を失います。図2はこの失敗の簡単な例を示しており、静的で間違った結果に収束します。
図9aに、テンポラルリユースとフレーム数の増加によるReSTIR PTの統合誤差を示します。色は異なる\(M\)-cap値に対応します。アニメーションによる誤差を避けるため、シーンは静的です。
ピクセルは各反復で新しい独立したサンプルを計算し、それは前のフレームからのテンポラルリザルトでリサンプリングされる。古いサンプルの相対的な重みは\(M_r/(M_r+1)\)であり、このサンプルは非常に有利に働きます。これは指数移動平均に似ています。
事前にフレームサンプルを再利用することで、モンテカルロ分散が改善されます。しかし、\(M_r\)が上限に達するまで、新しいサンプルの相対的な重みは減少し、フレーム間の相関が増加します。これは、SIRで一般的なサンプルの改善と類似しており、この相関の蓄積を止めない限り、ユニークなサンプルは少なくなっていきます。
最終的には、\(M\)-capに達するまで、相関の増大が再利用(赤、オレンジ)の利点を覆い、分散の増大をもたらします。テンポラルリユース(緑)の利点を最大化するために\(M\)に上限を設定することが、ReSTIRによるリアルタイムレンダリングの鍵です。図10は、\(M\)キャッピングが視覚的に与える影響を示しています。
図9bでは、私たちのリアルタイムReSTIR PTの連続フレームを有限の\(M\)-cap(紫色)で平均化したときの収束挙動を示しています。\(M\)-capは時間的に離れたフレームを非相関化するため、つまり時間的相関を忘れるため、経験的に収束することがわかります。
Offline rendering.
オフラインレンダリングの目標は少し異なります。各フレームの個々の品質を最大化するのではなく、より長いレンダリング時間にわたって最良の画像を生成したいです。この目的のためには、テンポラルリユースによる相関関係は役に立つというよりもむしろ害になることがわかり、オフラインレンダリングではテンポラルリユースをオフにすることを提案します。追加のレンダリング時間により、わずかに異なるレンダリングパラメータを使用することができ(セクション8.3)、両方の改善により、結果として得られるアルゴリズムはしばしば著しく速く収束します(図9b、青)。
9.2 Shift Mapping Result
コーネル・ボックスのシーンで、リコネクションとハイブリッド・シフトを持つReSTIR PTを研究します。ラフネスの変形(GGXラフネス0.5、図6a)とグロッシーな箱(ラフネス0.15、図6b)の結果を分析します。
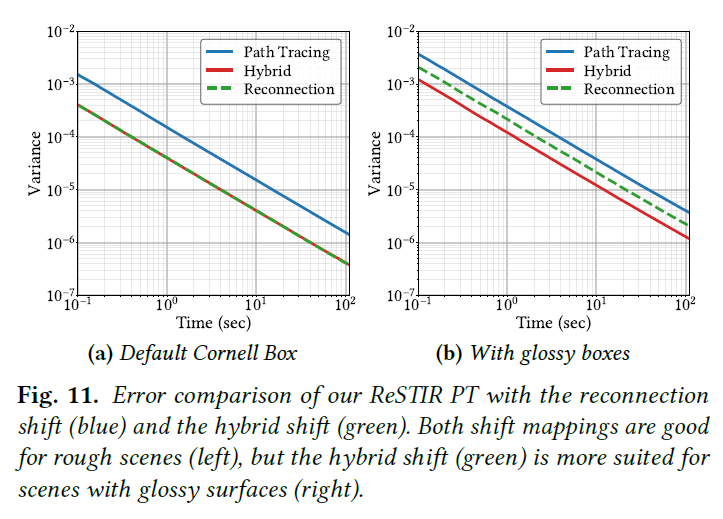
Reconnection is good for rough.
図11に、パストレーシングのベースラインによる収束をプロットします。勾配領域のレンダリング(例えばKettunenら[2015])から知られているように、リコネクションシフトはラフサーフェイス(図11a、緑)に対して効率的であり、間接光からの安価なパスの再利用を可能にします。リコネクションシフト(緑)は、BSDFに関係なく、一次ヒットの後に常に再接続するため、光沢のある相互作用を含むパスを効率的に再利用できません(図11b、緑)。
Hybrid is more robust.
ランダム・リプレイはグロッシーなサーフェイスによりよく対応します。私たちのハイブリッド・シフトはこの特性を受け継ぎながら(図11b、赤)、ラフサーフェイスにも有効です(図11a、赤)。
Visual comparison.
図6は、さまざまな種類のマテリアルにおけるシフトマップの挙動を示しています。光沢のあるコーネルボックスでは、ReSTIR PT(図6c)を使って、時空間再利用でピクセルごとに1つのパスをレンダリングします。ラフサーフェイスでは、我々のハイブリッド・シフト(図6c、下)はリコネクション・シフト(図6c、上)に似た振る舞いをしますが、我々のハイブリッドの距離基準はボックスのエッジでのノイズを減らすのに役立ちます。
我々のハイブリッド・シフトは、ランダムリプレイを挿入することで、光沢のあるマテリアルでの再接続を延期する。これにより、しばしば後の再接続が改善され、光沢のあるサーフェイスでのノイズが減少します(図6c、光沢のある箱の側面)。
リコネクションシフトの質の低さは、そのコストの低さによっていくらか相殺されます。等時間比較は、アルゴリズムの複数の独立した反復を平均化することを可能にします(例えば、図15のように)。
Separate handling of lobes.
多くのレンダラーは、BSDF評価ごとに1つのランダムローブしか評価しません。ローブごとに選択するシフトマップを変えると、ノイズが大幅に減少し、パフォーマンスが向上します(図12参照)。リコネクションはラフなBSDFに有効であり、ランダムリプレイはグロッシーなBSDFに有効です。いずれのシフトもマルチローブマテリアルには理想的ではありませんが、ローブを別々にシフトすることで問題は解決します。
Caustics.
コースティックスパス(すなわち、Heckbert [1990]による{LS+DE})は、鏡面性の高いシーンで重要です。興味深いことに、我々の2つのシフトマップは、ReSTIR PTで異なるタイプのコースティクスに対してうまく機能することがわかります。
我々のハイブリッド・シフトは、コンタクト・コースティックス、つまり近くのサーフェイスに光が集中する場合のパスを効果的に再利用します(図13、上参照)。バニーを通るオフセットパスをトレースするとき、ランダムリプレイはベースパスに似たパスを生成します。このパスが同じ光源に当たる場合、ランダムリプレイはパスをうまく再利用します。しかし、リコネクションシフトは、ニアデルタBRDFではリコネクションに失敗することが多いです。
例えば、図13(下)のランプの反射のように、遠くのハイライトからのコースティクスは、ハイブリッドシフトではうまくいきません。ランダムリプレイによって生成されたオフセットパスは、小さなハイライトを見逃すほど簡単に発散し、ノイズを増加させます。逆に、リコネクションでは、遠くのウィンドウにリコネクションするときに入射方向がわずかに変わるだけなので、パスの発散が最小限に抑えられ、パスの寄与が増加します。
マニフォールド探索シフト[Lehtinen et al. 2013]が両方のケースを改善すると期待されます。すべてのパスに適用するとコストがかかりますが、ReSTIR PTはパスツリーからリサンプリングされた単一パスで動作するため、そのようなシフト実可能です。これは興味深い将来の研究です。
9.3 Rendering Results
このセクションでは、3つのコンテキストで我々の結果を比較します:Bekaertら[2002]のパス再利用に対する明示的な比較、他のリアルタイム手法との一般的な品質比較、そしてオフラインコンテキストでの比較です。
平均的な光量はシーンによって大きく異なるため、視覚的な提示のためにトーンマップします。しかし、HDRの結果については、MAPE(平均絶対)パーセントエラーで誤差を報告しています。このL1指標は、サンプル再利用アルゴリズムで時折発生するファイアフライに対してより耐性があります。
比較のために、Falcor[Kallweit et al. 2021]の組み込みのユニディレクショナルパストレーサーを使用し、ReSTIR PT、Bekaert-style path reuse (BPR) [Bekaert et al. 2002]、ReSTIR GI [Ouyang et al. 2021]、ReSTIR DI [Bitterli et al. 2020]をこのフレームワークを使用して実装しました。
Versus Path Reuse.
図14では、ReSTIR PTとリコネクションシフト、パストレーシング、BPRを比較しています。Bekaertら[2002]に従ってBPRを再実装し、各ピクセルのパスツリーをサンプリングし、画像を\(N\)-rooksタイルに分割し、リコネクションシフトを使用してタイル内のすべてのパスにピクセルを接続します。ここでは16ピクセルのタイルを使用します。
しかし、タイル上でのパスの再利用は、特にサンプル数が少ない場合、明らかなタイルの境界が生じます。ReSTIRスタイルの再利用は、再利用半径がピクセルごとに個別に選択されるため、アーティファクトエッジは発生しません。タイルのアーティファクトのため、Bekaertとのリアルタイム比較は省略します。
Real-Time Rendering.
リアルタイムの比較では、特に言及しない限り、すべてのアルゴリズムがReSTIR DI[Bitterli et al. 2020]を介して直接照明を計算します。したがって、画像の違いは、さまざまなアルゴリズムが間接照明をどのように計算するかに依存します。図15の2列目と3列目はReSTIR DIを切り替えます。これは直接光における分散を大幅に低減しますが、間接光におけるノイズは他の方法を必要とします。
等時間比較のために、ハイブリッドシフトを使用したReSTIR PTでレンダリングし、(ほぼ)等時間になるように他の方法でサンプル数を増やします。リコネクションシフトを用いたReSTIR PTでは、このコストに合わせるために、複数の独立したReSTIRチェーンを同時に実行します。図12から図15は、ReSTIR PTが視覚的品質のためにテンポラルリユースに過度に依存するのを防ぐために、カメラが動いている間にキャプチャされました。アンチエイリアシングやノイズ除去は行っていません。
図15では、我々のハイブリッド・シフトまたはリコネクション・シフトを用いたReSTIR PTが最も低い誤差を達成しています。我々のハイブリッド・シフトは、光沢のあるサーフェイスや屈折するサーフェイス(例えば、屈折するワイングラス、SanMiguelの鏡、金属製のVeachJar、ZerodayとVeachAjarシーンのマルチレイヤーサーフェイス)の品質を大幅に向上させます。
我々のハイブリッドシフトは、幾何学的なエッジ付近(例えば、最初のキッチンの挿入図)のノイズも低減します。しかし,リコネクションシフトは,例えば十分にラフなサーフェイス(2番目のKitchenの挿入図)やカラーノイズを減らすのに役立つ場合(2番目のZerodayの挿入図)など,より多く,より安価なサンプルの方が良い場合に優れた性能を発揮します。
数値的には、ReSTIR PTはパストレーシングと比較して24%~75%低いMAPEを達成しますが(どちらもReSTIR DIを使用)、主観的な視覚的改善ははるかに大きいです。補足資料には、視覚的な検査用の結果のビューアが含まれています。
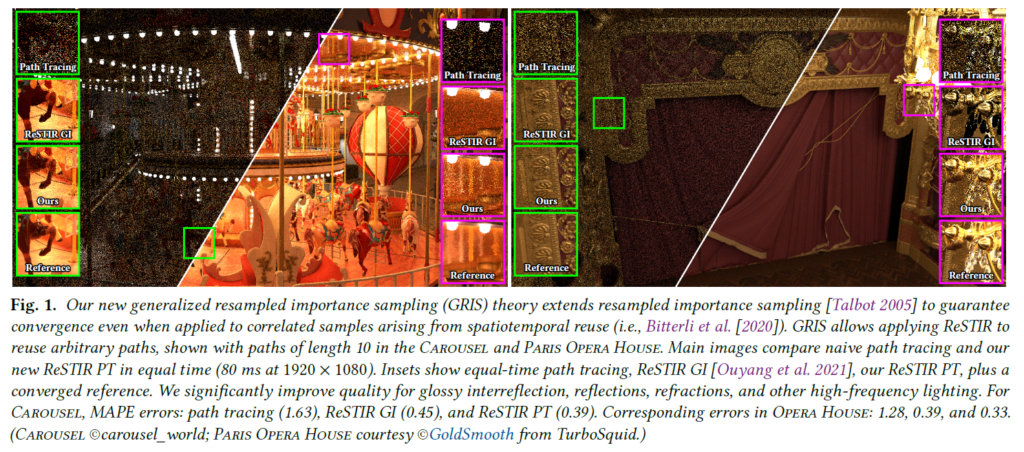
図1は2つの複雑なシーンでReSTIR PTを比較したもので、MAPEはReSTIR GIより16%低いです。ReSTIR GIは拡散面をよく処理するが、光沢面と屈折はうまく処理できず、バイアスが生じます。図15の全ての手法はアンバイアスです。
Offline Rendering.
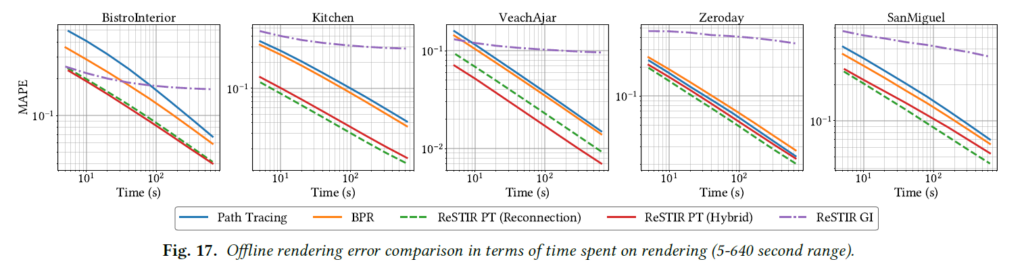
オフラインでの比較のために、代表的なシーンの5秒間の等時間レンダリングを示します(図16参照)。図17では、すべてのシーンの収束プロット(最大640秒)を示す。これらの図は、間接光についてのみ結果を示し、誤差を測定しています。
ハイブリッドシフトまたはリコネクションシフトを用いた我々のReSTIR PTは、短時間と長時間のレンダリング時間の両方で、パストレーシングとBPRを凌駕しています。BPRは、Zerodayを除いてパストレーシングを上回りました、BPRのリコネクションシフトは、光沢のあるマルチレイヤーサーフェイスとの相互作用が弱かったです。リコネクションシフトを用いたReSTIR PTは、GRISを用いた場合にサンプルコストの償却から恩恵を受け、BPRよりもはるかに速く収束します。
我々のシーン全体では、BPRはパストレーシングよりも最大2.8倍速く同じMAPEに到達し、リコネクションシフトを用いたReSTIR PTは最大14.4倍速く、ハイブリッドシフトを用いたReSTIR PTは最大10倍速く収束します。ReSTIR GIは拡散面において良質なサンプリングを行いますが、バイアスを加えます。光沢反射は多くのフレームを蓄積しても低品質になることがあります。
興味深いことに、我々のハイブリッド・シフトの実時間レンダリングにおける優位性は、オフラインでは完全には発揮されません。唯一の例外はVeachAjarで、光沢のあるティーポットは、等時間比較においてハイブリッド・シフト・マッピングの恩恵を大きく受けています。
我々は次のような説明を仮定しています。より良いシフトマップは空間的再利用を向上させますが、テンポラルリユースも向上させます(これは将来の空間的再利用につながります)。したがって、時間的再利用の向上は非常に有益な投資です。オフラインレンダリングでは、テンポラルリユースを無効にし、(我々のハイブリッドシフトのように)改善されたテンポラルシフトマップによるこの余分な利点を失います。
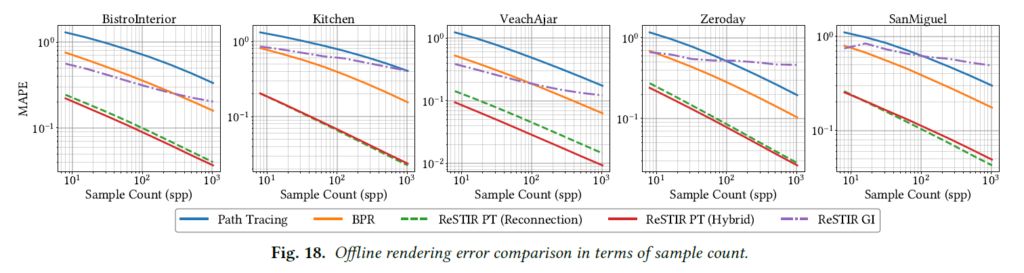
スレッドはしばしば異なる長さのパスをトレースするため、等時間比較はGPUスレッドの発散によって影響を受けます。等時間ではなく等サンプル数での収束を比較すると(図18)、図13(下)の苛性経路を除いて、我々のハイブリッドシフトはリコネクションシフトよりも一般的に優れています。これは、ランタイムコストがハイブリッドシフトの利点を打ち消していることを示唆しています。ダイバージェンス、より良いワークロードバランシングや他の最適化によって改善することができ、ハイブリッドシフトをより一般的に魅力的なものにすることができます。
10 CONCLUSION
我々は一般化されたRIS理論を導入し、リサンプルドインポータンスサンプリング[Talbot 2005]を拡張して、コンテキストを考慮したシフトマッピングを用いて、複数の領域(ピクセル)から取得した相関パスを再利用できるようにします。リサンプリングは、ユーザが指定したターゲット関数\({\hat p}\)に従って、漸近的に完全な重点サンプリングを与えます; \({\hat p}=f\)を選択すると、漸近的にゼロ分散積分が得られます。RISに対するアルゴリズムの主な違いの要約は図3を参照してください。
この理論に基づき、我々はReSTIRの時空間再利用を再定式化し、長いパスや複雑な鏡面輸送であっても一貫性とアンバイアスドを維持します。Bitterliら[2021]と同様に、我々のストリーミングアルゴリズムは、多くのピクセルにわたってパス生成を償却し、GPU並列性とテンポラルパスヒストリーを活用して、インタラクティブフレームレートでの分散を劇的に減らします。
一貫性のあるアンバイスドなアルゴリズムによるロバスト性の向上だけでなく、ReSTIR GI [Ouyang et al.2021]を、ノイズを低減する新しいハイブリッドシフトマップでさらに改善します。これは、サンプリングされたBSDFローブを考慮し、メモリトラフィックを制限するために接続頂点を事前選択することにより、シフトマップのための一般的に使用されるビルディングブロックのツールボックスを拡張します。少し驚くことに、ReSTIR PTは多くの場合、単純なコースティックパスを再利用することさえできます。
我々の理論は、これらの改善を保証する条件を与えます。ユーザは適切なMISウェイトで領域の変化を考慮し、無制限の\(f/{\hat p}\)比を避け、リサンプリングの重み分散\({\rm Var}[\sum w_i]\)を制御し、領域の一部のアンダーサンプリングを避けるために十分な数の正準パスを確保し、フレームを蓄積する場合は、時間的相関を制限するために妥当な\(M\)-capを使用しなければなりません。
これらの制約に基づき、インタラクティブなReSTIR PTを紹介し、一貫性のあるオフラインレンダリングのためにパスを適切に再利用する方法を示しました。これらの再設計されたアルゴリズムは、例えば図2のような、ピクセルの収束が遅い場合など、不愉快な不意打ちを避けることができます。
10.1 Future work
我々のGRIS理論は、リサンプリングと経路再利用アルゴリズムに関する将来の様々な研究を推進するのに役立つと信じています。
Shift mapping and gradient-domain rendering.
我々が拡張したローブパス空間は、より効率的なマニフォールド探索[Lehtinen et al 2013]を含め、勾配領域の問題におけるシフトマッピングに役立つ可能性があります。また、マニフォールド探索は、局所的なシフト決定がハイブリッドシフトの制限となる場合にも役立ちます(例えば、図13、下)。
Color noise.
ReSTIRはグレースケールターゲット関数\(|f|\)を用いてパスをリサンプリングしますが、これはピクセルの輝度を重点サンプルしますが、彩度\(f/|f|\)はしません。修正は、おそらく波長間でリサンプリングするか、カラーノイズを助けるために代表波長を使用することができます。
MIS between shift mappings.
GRISは相関サンプルをサポートしているため、複数のシフトマップを自然にMISすることができます。例えば、複数のシフトマップを適用した1つのサンプルをリサンプルし、より効果的なシフトにより高い選択確率を自動的に与えることができます。
Undersampling.
GRIS、ReSTIR、およびサンプルの再利用は、依然としてアンダーサンプリングに悩まされる可能性があります。我々のようなスクリーン空間の実装では、小さなジオメトリや非常に高い周波数の光、例えばシャープなコースティクスなどのアンダーサンプリングによって再利用が制限されることがあります。これはノイズ、ストリーク、スプロッチの原因となる可能性があり、さらなる調査が必要です。
ACKNOWLEDGMENTS
ユタ大学へのNVIDIAプロフェッサー・パートナーシップによる資金提供を含め、この研究に関する議論と支援をしてくれたAaron Lefohnに感謝します。さらに、ReSTIR GIについて議論してくれたYaobin Ouyang、初期の論文草稿に貴重なフィードバックをくれたMatt Pharr、Macro Salvi、Pete Shirleyにも感謝します。
REFERENCES
A THREOREMS
この付録では、一般化RISに関する最も重要な数学的定理を示します。証明は補足資料のセクションS.5にあります。従属標本による収束はセクションS.2で証明されています。
A.1 Unbiased Contribution Weights, Section 4.2
定理A.1. \(X\)と実数値\(W\)を\(\Omega\)の確率変数とします。 以下は等価です:
(1)積分可能なすべての\(f: \Omega \rightarrow {\mathbb R}\)について,
\begin{eqnarray}
{\mathbb E}[f(X)W] = \sum_{{\rm supp}(X)} f(x)dx, \tag{55}
\end{eqnarray}
(2)\(W\)は\(X\)の周辺密度の逆数に対する不偏推定量です。
\begin{eqnarray}
{\mathbb E}[W | X] = \frac{1}{p_X(X)} \tag{56}
\end{eqnarray}
証明. セクション S.5.1 □
A.2 Asymptotic Sample Distribution, Section 4.4
定理A.2 (漸近的サンプル分布). 各\(M\)について(別々に、ある\(M_0\)から始めて)サンプル\((X_i \in \Omega_i)_{i=1}^M\)のシーケンス(簡潔にするためにインデックス\(M\)を省略します)を仮定し、式19で与えられる重み\(w_{M, i}\)に比例して\(Y_M(=T_{sM}(X_{sM}))\)をリサンプルします。また,生成されたサンプルは \({\hat p}\) のサポートをカバーすると仮定します.
\begin{eqnarray}
{\rm supp}\, {\hat p} \subset {\rm supp}\, Y_M \quad when M \geq M_0 \tag{57}
\end{eqnarray}
ウェイトの合計の分散がゼロになる傾向がある場合、すなわち
\begin{eqnarray}
{\rm Var}\left[ \sum_{i=1}^M w_{M, i} \right] \overset{M \rightarrow \infty}{\longrightarrow} 0 \tag{58}
\end{eqnarray}
このとき,
(1) \(p_Y\)は確率的に\({\bar p}\)に収束します。すなわち,任意の\(\epsilon \gt 0\)について
\begin{eqnarray}
{\rm Pr}[|p_Y(Y) – {\bar p}(Y)| \gt \epsilon] \overset{M \rightarrow \infty}{\longrightarrow} 0 \tag{59}
\end{eqnarray}
(2) 密度比\({\bar p}(Y)/ p_Y(Y)\)は平均二乗で1に近づきます。すなわち,
\begin{eqnarray}
{\mathbb E} \left[ \left| \frac{{\bar p}(Y)}{p_Y(Y)} – 1 \right|^2 \right] \overset{M \rightarrow 0}{\longrightarrow} 0 \tag{60}
\end{eqnarray}
(3) \(p_Y\)の\({\bar p}\)からの絶対誤差の積分は0に近づきます。すなわち、
\begin{eqnarray}
\int_{\Omega} |p_Y(y) – {\bar p}(y)| dy \overset{M \rightarrow \infty}{\longrightarrow} 0 \tag{61}
\end{eqnarray}
(4) \(p_Y(y)\)が収束する集合において、それは\({\bar p}(y)\)に収束します(ゼロ測度の集合の可能性を除いて)
証明. セクション S.5.2. □
A.3 Asymptotic Variance, Section 5.2
定理 A.3(漸近分散). 定理A.2の仮定に加え、\(f \geq 0\)かつ
\begin{eqnarray}
f \leq C_f {\hat p} \quad for \, some \, C_f \gt 0 \tag{62}
\end{eqnarray}
そして、生成されたサンプル\(Y\)は\({\hat p}\)と\(f\)の台をカバーします。そして
(1) \(f(Y)W_Y\)は平均、二乗平均、確率において\(f(Y)/{\bar p}(Y)\)に近づきます。すなわち,
\begin{eqnarray}
{\mathbb E}\left[ \left| f(Y)W_Y – \frac{f(Y)}{{\bar p}(Y)} \right|^p \right] \overset{M \rightarrow \infty}{\longrightarrow} for \, p = 1, 2, \quad and \tag{63} \\
{\rm Pr}\left[ \left| f(Y)W_Y – \frac{f(Y)}{{\bar p}(Y)} \right| \gt \epsilon \right] \overset{M \rightarrow}{\longrightarrow} for \, all \, \epsilon \lt 0. \tag{64}
\end{eqnarray}
(2) \(f(Y)W_Y\)は漸近的に\(f(X)/{\bar p}(X)\)の分散を持ち、\(X\)は密度\({\bar p}(X)\)を持ちます。
\begin{eqnarray}
{\rm Var}[f(Y) W_Y] \overset{M \rightarrow}{\longrightarrow} {\rm Var}\left[ \frac{f(X)}{{\bar p}(X)} \right] \tag{65}
\end{eqnarray}
(3) \({\hat p}(x) \propto f(x)\)の場合,次のようになります。
\begin{eqnarray}
{\rm Var}[f(Y)W_Y] \overset{M \rightarrow}{\longrightarrow} 0 \tag{66}
\end{eqnarray}
証明. セクション S.5.3. □
A.4 Resampling Weight Bounds, Section 5.6
定理 A.4(リサンプリングウェイトの境界). 入力サンプル\(X_i\)のリサンプリング重み\(w_i\)を式19で与え、すべてのソース領域\(\Omega_i\)をターゲット分布\({\hat p}_i\)に関連付けます。正準サンプルのインデックスを\(R\)とし,\(|R| \leq 1\)と仮定します。
\(m_i\)が式36、37、または38で定義されたMIS重みスキームの1つによって与えられ、サンプル\(X_i\)が\({\hat p}_i\)を積分するために適正分布している場合(すなわち、ある\(C_i\)に対して\({\hat p}_i(X_i) W_i \leq C_i\))、\(X_i\)のリサンプリングウェイトは次のように境界付けられます。
\begin{eqnarray}
w_i \leq \frac{C_i}{|R|} \tag{67}
\end{eqnarray}
証明. セクション S.1.3. □
B CORRECTNESS NOTES
このセクションでは、性能と正しさに影響を及ぼす可能性のあるReSTIRのいくつかの側面について説明します。
On Visibility.
セクション6.1の議論に関連して、ReSTIR DI [Bitterli et al. 2020]は、可視性の項\(V({\mathbf x}_1 \leftrightarrow {\mathbf x}_2))\)を含まないターゲット\{\hat p}_i\)を使用しました。我々のReSTIR PTは常に頂点間の可視性を考慮します。実際、視認性を無視すると、オクルージョンのために\(X_i\)としてサンプリングされることのない正の\({\hat p}_i\)を持つパスが生成されるため、収束保証を維持するのが難しくなります。これは\({\rm supp}\, {\hat p}_i \not \subset {\rm supp} \, X_i\)を意味し、\(X_i\)を非正準にします。
追加の保証がなければ、\(X_i\)からリサンプリングされた\(Y\)はもはや\({\hat p}_i\)をカバーせず、式23の\({\hat p} \subset {\rm supp}\, Y_M\)の仮定を破り、\(p_Y\)の\({\bar p}\)への収束を妨げます。
ReSTIR DIは、アルゴリズムの各段階を通じて再利用を綿密に追跡することで、これを回避しています。テンポラルリユースのための\({\hat p}_i\)が可視性をチェックする一方で、空間的再利用はコストを削減するために除外されていないターゲット\({\hat p}_i^{-V}\)を使用します。\({\hat p}_i^{-V}\)の領域を完全にカバーしなければ、中間分布は収束しません。この設計は、\(f_i\)の領域のカバレッジを保証し、最終的な推定値が不偏性を保つことを可能にします。直接照明の場合,\({\hat p}_i\)への早期収束は理論的な興味だけかもしれず,Bitterliら[2020]の選択は可視性コストからのボトルネックを回避しています。典型的なパスサンプラーは\(V({\mathbf x}_i \leftrightarrow {\mathbf x}_{i+1})=0\)でオクルードパスを選択しないためです。
Temporal Reuse.
テンポラルサンプラーの再利用は、適切なMIS重み、例えば我々の一般化されたTalbotやペアワイズMISでは不偏ですが、GRISのMISウェイトを評価するには、前フレームと現フレーム間のパスを両対称的にシフトする必要があるため、テンポラルシフトマッピングが必要です。場合によっては、例えば相反するモーションベクトルでは、両対称性を保持するために慎重なマップ定義が必要となります。
この制約は、完全に不偏のテンポラルリユースは、現在のフレームと前のフレームの両方でパスを評価しなければならないことを意味し、動的な環境では面倒です。例えば、視認性を無視する[Ouyang et al.2021]など、テンポラルMISのバイアス近似を使用することができます。Linら[2021]は時間的変化を明示的に考慮し、動的な照明に対する応答時間を短縮することを報告しています。