わふー。Pocolです。
twitterみてたら,
Physically-Based Real-Time Lens Flare Renderingの特許が切れていると話題を見て,
https://patents.google.com/patent/US20140210844A1/enを見てみたら,確かに
Abandonedとなっていたので,ちょっと実装する気が湧いてきたので,まずは論文を読むことにしました。
[Hullin 2011] Matthias Hullin, Elmar Eisemann, Hans-Peter Seidel, Sungkil Lee, “Physically-Based Real-Time Lens Flare Redering”, SIGGPRAH 2011, No.108, pp.1-10.
いつもながら、誤字・誤訳があるかと思いますので,ご指摘頂ける場合は正しい翻訳例と共に指摘して頂けるとありがたいです。
Abstract
レンズフレアは、光がフォトグラフィックレンズシステムを意図しない形で通過することで発生します。レンズフレアは、写真を劣化させるものと考えられがちですが、現実的な画像には欠かせない要素であり、明るさを感じさせる芸術的な手段でもあります。これまでのところ、複雑な光の相互作用を説得力のある形でシミュレーションできるのは、コストのかかるオフラインプロセスだけでした。本論文では、フォトグラフィックなレンズのための新しい手法を紹介します。ベースとなるモデルは、欠陥、色収差、幾何学的収差、反射防止レンズコーティングなど、リアリズムに重要な多くのコンポーネントをカバーしています。様々なアクセラレーション手法により、性能と品質のトレードオフを実現し、この手法をリアルタイムアプリケーションと高品質なプロダクションレンダリングの両方に適用することができます。さらに、我々のシステムのアーティスティックな拡張についても説明します。
1 Introduction
レンズフレアとは、光が写真レンズを設計上の意図とは異なる方法で通過することによって生じる効果のことで、最も重要なのは光学素子間の相互反射(ゴースト)によるものです。フレアは、シーン内に少数の非常に明るい光が存在する場合に最も顕著になります。慣例的に写真や映画では、レンズフレアは画質を低下させるものであり、好ましくないものと考えられています。光学系の迷光を低減するための対策としては、鏡筒設計の最適化、反射防止膜、レンズフードなどがあります。
一方で、フレアのような効果は、非常に明るい光源の存在を示唆するために意図的に使用されることが多く、それによって現実感を高めることができます。実際、最近では、画像や映像の編集だけでなく、ゲームでもレンズフレアを使うことが多くなっています。コンピュータで生成された映画を制作するために,映画用レンズの物理的な欠陥や制限をすべてモデル化するために多大な努力が払われています [Pixar 2008].
レンズフレアのレンダリング問題は、2つの方向からアプローチされています。非常にシンプルで効率的ですが、正確さに欠ける手法として、光源の位置に応じて動く静的なテクスチャ(星型、円、リング)を使用し、ベース画像に加算して合成する方法があります。テクスチャビルボードから生成されたフレアは、多くの状況で説得力を持って見えますが、実際のレンズフレアの複雑なダイナミクスとバリエーションを捉えることはできません。
その一方で、すべての光学要素を持つ仮想のレンズを使って光線やパスを追跡する高度な技術も実証されています。結果はほぼ正確ですが、計算コストは非常に高く、現在のデスクトップコンピュータでは1フレームあたり数時間のレンダリング時間がかかるのが一般的です。さらに、多くのサンプルがレンズシステム内でブロックされてしまうため、計算時間が無駄になり、収束が遅くなってしまいます。また、この解法は幾何光学の制限内でしか成立しません。しかし、実際のレンズフレアでは、波動光学効果による現象も見られます。これらを光線光学の枠組みに統合することは決して容易ではなく,計算コストもさらに増大します。
疎なレイトレーシングとラスタライズを組み合わせることで、我々のレンダリング技法は複雑なレンズデザインのレンズフレアをシミュレートし、インタラクティブなフレームレートで高い臨場感を実現することが可能です。色収差や幾何学的なレンズ収差も自然に再現され、さらに高度なエフェクトで拡張することも可能です。
具体的には、以下のような貢献をしています:
- 現実的なレンズフレアのモデル
- 品質と効率のトレードオフを微調整することができる効率的なアルゴリズム
- 扱いにくい不完全さを、もっともらしい近似値で表現
また、後者は様式化の手段でもあります。我々は、表現力豊かなレンズフレアが、私たちの研究の自然な延長線上にあることを示します。
2 Previous Work
コンピュータグラフィックスの研究では、仮想環境内での光のやり取りやインタラクションのシミュレーションに注目が集まります。このような計算では、物理的に忠実な画像を得ることができますが、簡略化されたカメラモデルが実際のものに比べて不十分であるという、ある種のリアリズムの欠如があります。多くの効果(被写界深度やモーションブラーなど)は,リアルな画像合成に欠かせない要素であり,多くの研究者がカメラの特性にもっと焦点を当てる必要性を強調しています[Kolb et al.1995; Lee at al.2010; Steinert et al.2011].
また、カメラやレンズシステムのシミュレーションをより忠実に行うことで、迷光もカバーすることができ、レンダリングに大きなリアリティを与えることができます。迷光は、レンズシステムの埃や欠陥が原因となる場合もありますが、レンズフレアのより顕著な特徴は、内部反射(ゴースト)に由来します[Kingslake 1992]。
レンズフレアのシミュレーションが魅力的なのは、人間がフレアやベール状のグレアの存在を極端な明るさを示すものと解釈するように訓練されているからです。この知覚効果は,ディスプレイデバイスの物理的な限界を超えているように見せるために使用することができ[Ritschel et al.2009],映画[Pixar 2008]や最近のゲーム[Wenzel 2005]などでよく使用されています。
これまでのインタラクティブ技術は、かなりの近似値に頼っていました。Kilgard[2000]は,フレームバッファにブレンドされたテクスチャースプライトを,アドホックな変位関数に従って画面中心を通る線上に配置することを提案しました。King[2001]は、光源とカメラの間の角度に応じて、スプライトのサイズと不透明度を変化させました。Maughan[2001]は、エリアライトの可視ピクセル数に応じて制御することもできる明るさの変化を追加しました[Sekulic 2004]。Oat[2004]は、操縦可能なフィルタを用いて追加される光の筋に集力しています。[Alspach 2009]は,レンズフレアを,ユーザが指定した統計に基づいて生成される,「ハロ」,「レイ」,「リング」などの一連のベクトル形状として説明しています。これらのケースでは、基礎となるカメラやレンズのモデルは考慮されていません。
また、仮想的なコンテンツと現実的なコンテンツを合成する場合や、レンズシステムを設計する場合、レンズシステムを通したシーンの見え方を予測する場合など、より正確なシミュレーションが必要な場合もあります。これまでの高品質な近似法[Chaumond 2007; Keshmirian 2008]は,パストレーシングやフォトンマッピングに依存していました。このようなアプローチは、理論的には高品質を実現しますが、スペクトル(色収差やレンズコーティングなど)、回折効果、開口部の形状などのいくつかの側面は、通常は無視されます。さらに、短い計算時間では視覚的な品質が不十分で、ズームなどのインタラクションができないこともあります。
波動光学効果(特に回折や干渉)のシミュレーションは、通常、グラフィックス用途では手の届かないものと考えられています。ZEMAXやCodeVのようなハイエンドの光学設計ツールでは、点広がり関数の計算や、回折効果を含む迷光の粗い予測も可能です[Tocci 2007; Perrin 2004]。これらのツールは物理的な精度は高いものの、非常に一般的なソリューションを提供しているため、高品質で効率的なフレアのレンダリングには最適化されていません。純粋なレイベースのフレームワークでは、[Oh et al.2010]が、ライトフィールド変換が解析的に表現できる単純な規則的構造に対して、回折のような効果をどのようにエミュレートできるかを示しました。本研究では,一般的なアパーチャ形状に対して,フーリエ変換を用いて,前処理として同様の効果を近似します。
我々のレンダリング方式は、物理的な動機付けがなされているにもかかわらず、インタラクティブからリアルタイムのパフォーマンスで動作します。レイトレーシング手法に基づいて、個々の光線を考慮するだけでなく、光束内の光線の強い相関関係を利用しています。放射束は、ビームトレーシングやペンシルトレーシングに似た方法で扱われますが(包括的な文献の概要については、例えば[Ernst et al.2005]を参照)、適応的な精密化の必要はありません。
さらに、私たちのソリューションは、物理的なコンポーネントを誇張したり置き換えたりすることができます。また、初期の段階で忠実に再現されているため、アーティスティックな調整を行っても、結果として説得力のある、もっともらしい外観を保つことができます。
3 Model of the Optical System
このセクションでは、光学系の様々な側面について説明し、それらをどのように数学的に表現するかを説明します。アプリケーションの要求に応じて,モデルを単純化して性能を向上させるために,いくつかの効果を省略することができます。以下のものは、必要に応じて正確にモデル化したり、誇張したり、アート的に必要な方法で変更したりすることができる積み木と考えてください。図2は、本システムの構成要素を示しており、光学系のモデル、光の輸送、および実装(セクション4)の概要を示しています。
Geometry
光の伝播は、一連のレンズ面と特性面(入射面、絞り面、センサー面)での光の透過と反射によって支配されます。ここでは,写真用レンズの定義として[Smith 2005]を,また,手元にあるレンズの特許として[Ogawa 1996]を参考にしています。幾何学的モデルは,代数的に定義された曲面,すなわち球と平面の集合として実現される.なお、この手法では、特定の形状やレンズ材料を強制するものではありません。また,魅力的なフレアを得るためには,光学設計上のルールが必ずしも必要ではありません。
Iris Aperture
絞り(ダイアフラム、アイリス、ストップとも呼ばれる)は、機械的な羽根で構成されており、回転することで瞳孔の大きさを制御します。絞り開放時には鏡筒の中に隠れてしまうため、断面は円形になります。絞りを絞ると、羽根の数、形状、位置によって多角形の輪郭になります。この仕組みを再現し(図3)、得られたマスクをテクスチャとして保存します。
Optical Media and Dispersion
光学媒体としては、実数の屈折率を持つ完全な誘電体に限定されます。すべての光学ガラスは分散媒質です。すなわち、屈折率\(n\)は光の波長\(\lambda\)の関数です。ここではSellmeierの経験的な近似式[Sellmeier 1871]に従って光学ガラスの分散を記述する。
\begin{eqnarray}
n^2(\lambda) = 1 + \frac{B_1 \lambda^2}{\lambda^2 – C_1} + \frac{B_2 \lambda^2}{\lambda^2 – C_2} + \frac{B_3 \lambda^3}{\lambda^2 – C_3} \tag{1}
\end{eqnarray}
ここで,\(B_{\{1, 2, 3\}}\)および\(C_{\{1, 2, 3\}}\)は,製造データベース[Schott AG 2011]やその他の情報源[Polyanskiy 2010]から得られる材質定数です。
3.1 Reflection and Transmission: Fresnel Equations
光線が2つの媒体の界面に当たるたびに、その一部が反射し、残りが透過します。この反射した部分がゴーストとなり、それをシミュレートしたいのです。滑らかな表面では,相対的な量はフレネルの方程式に従っており,結果として生じる光線の方向は,それぞれ反射の法則とスネルの法則に従っています[Hecht 2001]。
フレネル方程式では、偏光状態によって異なる透過係数と反射係数が得られます。偏光していない光が媒質1から媒質2に伝搬する場合(屈折率\(n_i\)と法線に対する角度\(\theta_i\)を持つ)、表面の全体的な反射率\(R\)と透過率\(T\)は次のように表すことができます。
\begin{eqnarray}
R &=& \frac{1}{2} \left( \frac{n_1 \cos \theta_1 – n_2 \cos \theta_2}{n_1 \cos \theta_1 + n_2 \cos \theta_2} \right)^2 + \frac{1}{2} \left( \frac{n_1 \cos \theta_2 – n_2 \cos \theta_1}{n_1 \cos \theta_2 + n_2 \cos \theta_1} \right)^2 \\
{\rm and} \quad T &=& 1 – R
\end{eqnarray}
偏光の扱いは、後述する反射防止膜の内部構造にとって重要です。フレネル反射や透過は部分的に偏光しているので、光と表面の相互作用のシーケンスは、光線の偏光状態を追跡するのが理想的です。しかし、限界利益は出費を正当に説明できないため、現在のレイトレーサーの実装では、光学系全体に偏光を伝播させないようにしています。各光学面において、入射光はS偏光とP偏光(定義は[Hecht 2001]を参照)が等分に存在すると仮定します。
Anti-Reflection Coating
反射を最小限に抑えるために、光学表面には反射防止膜が施されていることが多いです。反射防止膜は、異なる界面を持つ透明な素材を重ね合わせて、相互に干渉させたものです。特に、位相が逆で振幅が同じ2つの反射があると、お互いに打ち消し合って表面の正味の反射率が下がります。高級レンズに使用される多層膜のパラメータは、企業秘密になっています。
どんなに優れたコーティング剤でも、完璧ではありません。残留反射率は、波長と角度の関数である\(R(\lambda, \theta)\)で表されます。実際のレンズを見てみると、界面によって白色光の反射色が異なることから、それぞれに異なるコーティングが施されていると考えられます(図4)。
そのためには、「1/4波長」と呼ばれるコーティングを採用しました。これは薄い1枚の層で構成されています。このようなコーティングでは、中心波長\(\lambda_0\)、入射角\(\theta_0\)の場合、表面の反射率を最小にすることができます。このためには、非常に低い屈折率の固体材料が必要です。実際には、\({\rm MgF_2}\)が最適です。層の厚さは、\(\pi/2\)の位相シフトになるように選択されます(これが名前の由来です)。
ほとんどの場合、\(R(\lambda, \theta)\)の解析的な式を導き出すことができますが、単純な1/4波長のコーティングでさえ、フレネル方程式の複数のインスタンスが含まれるため、式は比較的複雑になります。図4に1/4波長コーティングのプロット例を示します。このような関数を近似する1つの方法は、事前に計算された2Dテクスチャに保存することで、任意の利用可能なコーティング関数を記録または使用することができます。しかし、実際には、GPUの演算能力は、関数を直接評価するのに十分なほど高いのが普通です。シェーダで使用している\(R(\lambda, \theta)\)の計算スキームを補足資料として掲載しています。
3.2 Absorptance
すべての光学ガラスは、通過する光を部分的に吸収します。しかし、これは弱い効果であり(典型的な光の損失はレンズシステム全体で数パーセント),周波数も低いです(グローバル減衰)。そのため、今回のモデルにはこの効果を含めないことにしました。
3.3 Diffraction
光は、システムのアイリスアパーチャのような小さな形状や、指紋、埃、傷などの小さな欠陥を通過すると、幾何学的な影の部分に回折されます。これを物理的に説明すると、「波面上のすべての点は、球状の波の放射体と考えることができる」というホイヘンスの原理になります。結果として得られるパターンは,これらの基本的な波の重畳によって定義されます[Hecht 2001; Goodman 2005]。
このシステムでは、回折の典型的な現象として、光源のイメージを中心としたスターバースト形状と、各反射ゴーストの境界にある微妙なリンギングパターンの2つが発生します。波動光学の枠組みでは、センサー上のすべての点について、いわゆる回折積分を評価することで、両方とも正確に計算することができます。しかし、これは非常にコストがかかり、リアルタイムでは不可能です。その代わりに、計算量の少ない近似法に興味があります。結果的には,一般的なフラウンホーファー近似とフレネル近似をそれぞれ用いて小さなテクスチャセットを事前に計算することで,上記の効果を説得力のある形で再現することができました。
Starburst pattern – Fraunhofer approximation
透過型のアパーチャを通過し、さらに自由空間を伝搬する光は、特徴的なファーフィールドパターンに回折されます。平行な(視準が合った)光(波長\(\lambda\))が一様に入射し、実数値の振幅透過関数\(T(x, y)\)があると仮定すると、開口部から距離\(z_0\)の観測面におけるフラウンホーファーパターン\(T'(x’, y’)\)は、\(T\)のフーリエパワースペクトル(すなわち、二乗マグニチュードのフーリエスペクトル)で与えられます[Hecht 2001]。画像座標\((x’, y’)\)とフーリエ周波数\((u, v)\)の関係は次のように与えられます。
\begin{eqnarray}
(x’, y’) = (u, v) \cdot \lambda \cdot z_0 \tag{2}
\end{eqnarray}
したがって、ある開口部の形状に対しては、1つのフーリエ・スペクトルを計算し、それを波長に応じて線形にスケーリングすれば十分です。ここでは,単位サイズのポリゴン透過関数から始めて,任意にノイズを加えます(図14,右)。[Ritschel 2009]と同様に、アパーチャのパワースペクトルの複数のスケーリングされたコピーを重ね合わせて、3チャンネルのスターバーストテクスチャ\(V_{\rm {RGB}}(s, t)\)を計算します。個々のスペクトル項に存在する放射状のリンギングをぼかすためには、5nmの波長ステップが十分に細かいことがわかりました。最終的に得られたテクスチャ(例として図5を参照)は,カラーチャンネルごとの単位放射束で正規化されています。実行時には,光源の投影されたセンサー位置を中心にして,サイズ\((w,h)\)と強度\(I\)を次のようにスケーリングします。
ここで,\(\#\)はF値で(“\(f/\#\)”のように),\(I_{\rm {RGB}}\)は\({\rm RGB}\)ベクトルとして表現されるレンズに入射する放射束です。光学系に特有の正確なスケーリング定数\(w_0\)(「大きさ」)と\(I_0\)(「強さ」)を簡単に得る方法を私たちは知りません。そのため、ユーザーは、与えられた光学系の外観を再現したり、スターバーストを思い通りに増幅したり、サイズを変更したりすることができます。
Ringing pattern – Fresnel approximation
光学系は通常、レンズ系の後段で開口面がセンサー面にフーリエ変換されるようにレイアウトされています。相互反射がある場合には、絞りそのものの像からそのフーリエ変換まで、任意の変換が可能ですが、特に空間領域とフーリエ領域の両方の特徴を持つ中間パターンが存在します。
数学的には、空間領域とフーリエ領域の間の連続性は、フーリエ演算子の分数乗で表すことができます。波動光学の研究では,この分数次フーリエ変換(FrFT)と,近接場回折のいわゆるフレネル近似との間に密接な関係があることが示されています[Ozaktas et al.2001]。フーリエ光学を深く理解しなくても、[Ozaktas et al. 2001]のFrFTコードを使えば、与えられたアパーチャ関数をもっともらしいリンギングパターンで装飾することができます(図6)。与えられたフレアパターンを再現するために、唯一のパラメータである分数次数\(\alpha\)の適切な値を見つけるのに、それほど手間はかかりません。発見的には、次のようにするとうまくいくことがわかりました(波長が長く、口径が小さいとリンギングが強くなります):
\begin{eqnarray}
\alpha = 0.15 \cdot (\lambda / 400 {\rm nm}) \cdot (\#/18) \tag{5}
\end{eqnarray}
次のセクションで説明しますが、これらの事前に計算されたテクスチャは、ラスタライズの段階で使用することができ、標準的なレイトレーシングで得られるシャープな開口画像を置き換えることができます。
4 Rendering System
前節では、レンズフレア効果の重要な側面をどのようにモデル化するかを分析しました。ここでは,実際の光の伝搬をシミュレートするためのレンダリング技術を紹介します。この手法は,光学系からフィルム面(センサー)までの光線追跡に基づいています。高価なオフラインアプローチ[Keshmirian 2008; Steinert et al. 2011]とは対照的に,我々はスパースな光線セットのみをトレースします。各光線は,レンズシステムの走査に関する値を記録します。センサーに到達した光線は、暗黙のうちに光線グリッドを定義し、そのグリッドを横切って記録された値を画像空間に補間します。これにより、実際には撮影されなかった光線の結果を近似することができ、近似的なビームトレーシングが可能になります。レンダリングパイプラインの概要を図7に示します。以下では、パイプラインの各ステージについて詳しく説明します。
Assumption
ここでは、太陽光、街灯、自動車のヘッドランプなど、ほとんどのフレアの原因となる指向性のある、つまり遠方の光源を想定します。この仮定は、本アルゴリズムに必要な条件ではありませんが、高速化には有効です。
4.1 Rendering Scheme
Ghost Enumeration
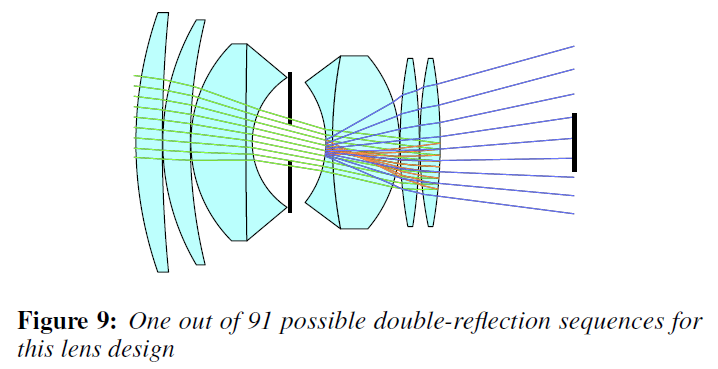
レンズ系を通過した光線は、レンズで反射したり屈折したりする。相互反射により発生するフレア成分(以下、ゴースト)は、この透過と反射の特定の順序に対応しています。偶数回の反射を伴うシーケンスのみがセンサーに入射します。反射回数が2回以上のものは、通常、無視することができます。光のごく一部しか反射しないため、通常、最終的な画像への影響は桁違いに弱くなります(図8)。ここでは、光がレンズ鏡筒に入り、センサーに向かって伝搬し、光学面で反射し、戻ってきて再び反射し、最終的にセンサーに到達するという2回反射のシーケンスをすべて列挙します(図9)。1つの光学系に\(n\)個のフレネルインターフェースがある場合、このようなシーケンスは\(N = n(n – 1)/2\)個存在し、それぞれ独立して処理され、一度に1つのゴーストをレンダリングします。
Bundle Tracing
あるゴースト指数と入射光の方向に対して、平行な光線の束がレンズ鏡筒の入射口にかかります。次に,レンズ系を介して追跡する光線のスパースな一様セットを選択します。各ゴーストの正確な交差シーケンスがわかっているので,古典的なレイトレーシングとは異なり,再帰的なスキームや精巧な交差テスト,空間加速構造を用いて各光線を追跡する必要はありません。我々は、代数的に定義されたレンズ表面に対する交差テストの決定論的な順序にシーケンスを解析します。これにより、この手法はGPUでの実行に特に適しています。
それぞれの交差点で、光線のヒットポイントとそれぞれの表面の直径を比較し、システムを通過する途中で光軸からの正規化された最大距離を記録します。
\begin{eqnarray}
r_{\rm {rel}}^{({\rm new})} = {\rm {max}}(r_{\rm {rel}}^{({\rm {old}})}, r / r_{\rm {surface}})
\end{eqnarray}
ここで、\(r\)はヒットポイントの光軸までの距離、\(r_{\rm {surface}}\)は光学素子の半径を表しています。また、光線が開口面を通過する際には、交点座標のペア\((u_a, v_a)\)が格納されます。なお、システムから脱出した光線(\(r_{\rm {rel}} \gt 1\))は破棄しないことに注意してください。なぜなら、これらの光線でさえ、光線グリッドでの補間に価値があるからです(以下を参照)。さらに、各光学面の機能は、その定義された代数関数を頼りに、公称レンズ径を超えて仮想的に外挿します。この拡張機能を実現するために、一般的な最近接面チェックを厳密に整理された交差に置き換え、結果として得られるレイパラメータが負になることを許容します(図10)。これにより,数学的に連続した方法でより多くの光線がシステムを通過できるため,小さな光線密度に対するシミュレーションの数値的安定性が向上します.なお、これらの非物理的な光線は最終的なレンダリングには使用されず、補間用のデータポイントとしてのみ使用されます。実際に描画される補間された光線については、次のサーフェスも最も近いものになります。
光線が次の面とまったく交わらなくなったとき、あるいは全内部反射を起こしたときに初めて剪定されます。これにより、レイグリッドに穴ができる可能性がありますが、洗練された戦略の必要性は感じませんでした。というのも、光線の輸送エネルギーは、全内部反射の近傍でゼロに近づき、最終的なレンダリングでは、光線グリッド上の隣り合った領域が黒く表示されるからです。
Rasterization and Shading
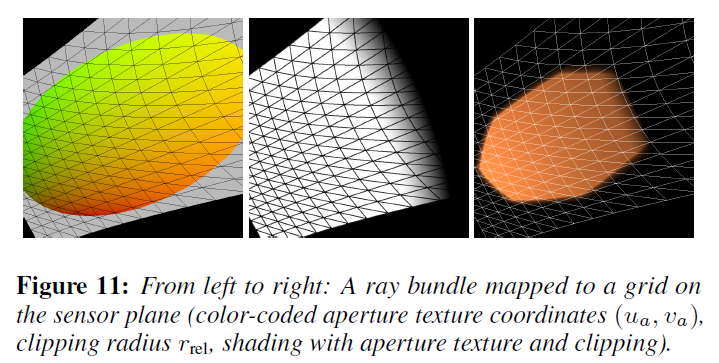
光線がシステムを介してトレースされると、センサー面上に光線のグリッドが形成されます(図11)。光線のセットはまばらで、それぞれの光線を単体で捉えた場合、十分な品質が得られません。私たちの目的は、隣接する光線の情報を補間して、光線全体の挙動を推定することです。この目的のために、ランダムな疎な光線セットを使用せず、最初のレンズ要素に配置された一様なグリッドとして光線セットを初期化します。入射面上の各グリッドセルは,同じ光線の間にあるセンサ上のグリッドセルと一致させることができます。従来のビームトレーシングと同様に、各ビームを介して輸送される全放射パワーは、対応する四角形の領域に均等に分配されるようになり、レンズフレアの強度変化につながります。さらにシェーディング項(特にランベルシアンコサイン項)が考慮されます。
なお、ここまでは、レンズ系や絞りで遮られた光線はカットせずに、それぞれの面の半径に対して、絞りを通過した位置\((u_a, v_a)\)と、その光軸までの最大距離\(r_{\rm {rel}}\)を記録しています。ビームを扱う際には、これらの座標を対応する四角形の上に補間することができるようになりました。これにより、補間された光線のより正確な内側/外側のチェックが可能になります。補間された半径が限界距離を超えた場合、フラグメント単位でクリッピングを適用します。最後に、開口部上の位置は、アパーチャ・テクスチャのルックアップによってゴーストの形状を決定するために使用されます。リンギングパターンが事前に計算され、アパーチャテクスチャに保存されているため、この時に「フレネル的」回折が発生します(3.3項)。
4.2 Accelerations
前述のアルゴリズムは、単純なレンズシステムでは納得のいく結果が得られます。ここでは、品質と速度の点で基本的なソリューションを改善するためのいくつかの戦略を紹介します。
Ray Bounding
ある方向からレンズに入ってくる光線のうち、実際にセンサーに届くのはごく一部の光線です。多くの光線は障害物に遮られ、特にアイリスアパチャーを小径に設定した場合は遮られます。そこで、計算資源を節約するために、センサーまで到達する可能性のあるすべての光線を囲むように選ばれた、光線のスパースセットを入口絞り上の長方形の領域に制限します。
この境界領域の位置と寸法は、光の方向、絞りの大きさ、場合によっては他のパラメータ(ズームやフォーカス)に自明ではない形で依存するため、ランタイムでのパラメータ検索は困難です。そこで、各ゴーストに最適な境界領域を推定する前処理を提案します。与えられた設定に対して、実際にセンサーに到達したすべての光線を回復するために、低解像度グリッドを用いた以前の基本アルゴリズムを採用します。このグリッドに基づいて,入口開口部の境界矩形を決定します。この境界は,現在のパラメータ設定と隣接するパラメータ設定のすべての有効な光線を含むのに十分な幅であることがわかりました。細分化されたスキームは,この境界処理を高速化するのに役立ちます。
Adaptive Resolution
レンズフレアは、複雑な光学系のコースティクスの集合体であり、非常に高い周波数が発生することも意味しています。レイバウンディングは、パフォーマンスと品質を大幅に向上させますが、微妙な変化を見逃すこともあります。我々のアルゴリズムでは、入射光線の規則的なグリッドが、センサー上の多かれ少なかれ均質なグリッドにマッピングされます。ほとんどの場合、グリッドは単純なスケーリングとトランスレーションを行い、粗いテッセレーションであっても十分な精度でキャプチャされます(図11)。しかし、いくつかの構成では、非線形効果の蓄積により、深刻な変形が起こり、グリッドが折り重なったり、トポロジーが変化したりすることがあります(図12)。このようなゴーストは、より高いグリッド解像度が必要となります。
各ゴーストのグリッド解像度を調整するために、ヒューリスティックなアプローチを採用しています。指標としては、グリッドセルの大きさを用います。グリッド間のばらつきが大きいと、不均一な変形が起きていることになり、より高い精度が必要となります。そこで、計算前にこのばらつきを評価し、各ゴーストに固定の詳細レベルのうちの1つを割り当て、1つのバンドルあたりの解像度を\(16 \times 16\)から\(512 \times 512\)光線としました。このようにして、困難なゴーストを早期に発見することで、より高度な細分化技術の使用を避けることができます。
Intensity LOD
もう一つの情報は、結果として得られるゴーストのおおよその強度です。この情報があれば,ユーザは実行時に,評価する最も明るいゴーストの数を固定することで,予算をコントロールすることができます。
Aperture Culling
虹彩の開口部が小さい場合、光線が遮られることなく何度も開口部を通過することはほとんどありません。その結果,対応する2回反射のシーケンス(3回の開口部通過)は,通常,強いアーチファクトを引き起こすことなく無視することができます。これにより、列挙されるシーケンスの数は\(N = (f(f-1) + b(b-1))/ 2\)まで大幅に減少します。ここで、\(f\)および\(b\)はそれぞれ、絞りの前または後ろのレンズ面の数です。
Symmetries
光学系の対称性は、計算の複雑さを軽減するのに役立ちます。写真用レンズの多くは設計上、軸対称になっていますが、映画業界ではアナモフィックレンズ(光軸に沿って交差する2つの直交する対称面を持つレンズ)が一般的です。アナモルフィックレンズは、現在のところ本システムではサポートされていませんが、球形のレンズ表面をより一般的な楕円形に置き換えることで、追加することができます。
軸対称の場合、必要な事前計算の量を大幅に減らすことができます。光線追跡までのすべての計算は、一定の方位角の入射に対して行われ、それを所定の位置に回転させることになります。さらに,フレアの配置が鏡面対称であることを利用して,入射面上の半分の光線だけを考慮することで,疎な光線セットを減らすことができます.センサー上のグリッドは、対称軸に沿ってミラーリングすることができます。光線を直接ブロックせず、絞りの座標と交点の距離を記録するという我々の選択により、システム全体を対称と見なすことができることに注意してください。
Spectral Rendering
反射防止膜やレンズの色収差を処理するには、波長に応じた評価が必要です。全力で評価すると、ほとんどのゴーストは3つの波長(RGB)だけで十分に表現できますが、少数のゴースト(通常、140個のゴーストのうち3個)では、スムーズな結果を得るために60個の波長が必要になることがあります。LOD(Level of Detail)のアプローチも考えられますが、ここでは計算コストを抑えて3波長(標準品質/RGB)または最大7波長(高品質)でレンダリングし、補間戦略を採用しています。各波長帯の結果を画像空間でフィルタリングして、トランジションを作ります。必要な1次元ブラーカーネルの方向と寸法は、事前計算の段階で、隣接する波長帯間の空間的変化から導き出されています。フィルタのサイズは、バンド間のギャップを埋めるように選択されます。フィルタリングされた表現は、RGBAフレームバッファ内でブレンドされ、滑らかな結果をもたらします。
4.3 GPU Implementation
Basic Algorithm
レイトレーシングはバーテックスシェーダで行います。全反射に対応するために、カリングされた光線はテクスチャ座標を介してフラグが立てられます。ジオメトリシェーダでは、グリッド内のビームクワッドからトライアングルストリップを生成します。ここでは、各グリッドセルの面積も計算され、放射照度の計算に使用されます。レイセットの半分だけがトレースされる対称的なシステムの場合、ジオメトリシェーダはフレア配置の対称軸に沿って各トライアングルをミラーリングします。このトライアングルの2倍化は、イメージベースのミラーリングよりも効率的です。センサー上の結果の四角形は、フラグメントシェーダでラスタライズされます。フラグメントシェーダは、ブロックされた光線(\(r_{\rm {rel}} \gt 1\)、セクション4.1参照)に対応する場合、フラグメントを破棄することができます。頂点ごとの放射照度の値が四角形の上に補間され、アパーチャー座標に基づいてテクスチャのルックアップが行われ、レンダリングが完了します。最後に、すべてのゴーストが加算合成されます。
Smooth shading
クワッドシェーディングではなく、頂点をシェーディングして補間することで、品質を向上させることができます(グーローシェーディング)。各頂点には、その周囲の近傍領域の平均値を格納します。光線の規則的なグリッドと、最近のグラフィックスハードウェアのトランスフォームフィードバック(またはストリームアウト)メカニズムを組み合わせることで、隣接する四角形の値のルックアップが非常に簡単になります。
5 Artistic Control
他のレンズ効果[Lee et al. 2010]と同様に,フレアは,合成画像や写真の魅力を高める創造的なツールとなり得ます。我々のアルゴリズムは,物理的な限界を超えて現実的な外観を維持するために,基本的なパイプラインと相互作用する多くの可能性を提供します.すべての相互反射を列挙するというアプローチにより、特定の、おそらく最も美しいゴーストのみをレンダリングに選択することができます。さらに、不完全な部分は非常に近似した方法でうまく表現することができます。
Create Use of Optical Elements
一般的なレンズは正多角形の開口部を持っていますが、2次元の任意の形状を使用することができます。例として、SIGGRAPHのロゴを使用したところ、珍しいスターバーストパターン(図14)と、画像全体にロゴのゴーストが変形しています(図16)。
Adding Realism through Imperfections
現実の世界では、レンズは埃や表面の欠陥によって劣化し、回折パターンに影響を与えることがよくあります。フーリエスペクトルを求める前に、絞りに埃や傷のテクスチャを加えることで、この影響をコントロールしています。汚れのテクスチャを描画することも可能ですが、ユーザーが定義した統計情報(密度、方向、長さ、サイズ)に基づいて、傷や埃をプロシージャルに生成することもできます。キズはレンズフレアに新たな筋を加えるのに対し、ホコリは虹色の斑点を加える傾向があります。さらに、[Ritschel et al. 2009]のように、テクスチャをアニメーション化してダイナミックな効果を得ることもできます。
Imperfect Symmetries
実際のレンズシステムは完全な対称性を持たないため、レンズフレアはミラー軸上に完全に並ぶことはありません。この不完全さをモデル化するために、各ゴーストを像面内でわずかに平行移動させる分散を加えます。この修正は、レンズシステムの変更に対応するよりも、より直感的な制御を可能にします。
Anti-Reflective Coating
それぞれのゴーストの色は、主に原因となるレンズ表面の反射防止膜によって決定されます。この効果は、各ゴーストのカラーランプやグローバルな色の変化をユーザーに提供させることで、簡単に抽象化することができます。
6 Results
このソリューションは、Intel Core 2 Quad 2.83 GHzにNVIDIA GTX 285カードを搭載して実装しました。光学系の複雑さやシミュレーションの精度にもよりますが,我々の手法はインタラクティブからリアルタイムまでのフレームレートを達成しています.図15に示すように,この手法は,要求の厳しいリアルタイムアプリケーションだけでなく,高品質なシミュレーションにも有効です。図19に示すように、解像度を大幅に下げても、本技術を用いて算出したゴーストは、レイトレースされたリファレンスに近い値を示しています。性能面では、特に美しいゴーストだけをピックアップすることも可能で、アーティスティックな表現を維持しつつ、大幅なスピードアップを図ることができます。実際には、20%の弱いゴーストをカリングすることで、目に見えるアーティファクトを発生させることなく、20%のスピードアップを実現しています。インタラクティブなアプリケーションでは、40%でもまだ許容範囲内です(約50%のスピードアップ)。図15では、異なる品質設定に対するパフォーマンス評価を示しています。また,使用した設定を横に並べて比較した結果を図17に示します。我々のソリューションの最もコストのかかる効果は、高度に異方的なゴーストにおけるコースティクス(例えば、図18)であり、ここでは光線束がスペクトルと空間の変化に最も敏感であるためです。
このソリューションでは、光線の疎なセットを拘束するために、適度に迅速な前計算を行う必要があります。ブレンデルのプライムレンズ(9個のゴースト)のような単純なレンズでは、この事前計算は0.1秒以下ですが、ニコンのズームレンズ(142個のゴースト)では5分、キヤノンのズームレンズ(312個のゴースト)では、すべてのゴースト\( \times 90\)個の光の方向\(\times 64^2\)個の光線\(\times 20\)個のズームファクター×8個の絞りを繰り返し計算するのに20分かかります。後者の2つは、カメラの設定をその場で自由に変更することができます。
このアルゴリズムは、物理的にリアルなレンズフレアのレンダリングを行います(図1)。ほとんどの重要な効果が説得力を持ってシミュレートされており、実際の映像と見分けがつかないほどの画像になっています。
主な違いは、レンズシステムの不完全さに加えて、回折効果を近似的に処理していることにあります。さらに、レンズのコーティングが不明であるため、推定値にならざるを得ません。
このアルゴリズムでは、複雑な変形やコースティクスを自然に扱うことができます(図18)。これまでのリアルタイム手法では、システムを通過する光の経路をシミュレートしないとこの効果を再現できないため、同様の結果を得ることができませんでした。このモデルでは、従来の手法では無視されていた多くの側面が考慮されています(例えば、波長と角度の関数としてのレンズコーティングの反射率など)。このような改良を加え、最高の空間およびスペクトル解像度で、最も複雑な光学設計でもフレアのレンダリングに数秒もかからないようにしました。これは,今日のデスクトップコンピュータでは収束までに数日どころか数時間もかかる典型的な経路追跡ソリューションよりもはるかに高速です[Steinert et al.2011]。
このアルゴリズムのメモリ消費量は、主に、アパーチャとそのフーリエ変換を含むテクスチャ(16ビットの浮動小数点データで24MB相当)と、3つのレンダリングバッファ(さらに24MB)によって定義されています。
7 Discussion and Limitations
7.1 Applications
我々のアルゴリズムは、メモリオーバーヘッドが少なく、計算効率が良い。このアルゴリズムは、様々なアプリケーション・シナリオに利用できます。
CG Movie Production
我々のレンダリングスキームは、これまでの多くのオフライン技術を上回る品質を実現しており、プレビューとしてはもちろん、最終的なレンダリングソリューションとしても興味深いものです。また、アーティスティックなコントロールにより、ユーザーはリアルな外観を維持しながら、効果を微調整したりカスタマイズしたりすることができます。
Computer Games
コストのかかる計算を無効にすることで、全体のパフォーマンスが向上し、ゲームに役立つソリューションとなっています。さらに、2回の反射を仮定することで、ユーザーが重要と考える特定のゴーストを選択することができます。よく整備されたフレアでは、非常に少量の光線(例えば\(4 \times 4\))でも、補間ステップのおかげで高品質が得られます。
Image and Video Processing
現在のレンズフレアフィルターは、ゴーストの変形が無視されるなど、静的な表現にとどまっているため、説得力がありません。我々の手法は時間的にコヒーレントなので、映画の映像にも適しています。画像内の光源を検出し、追従します(強度閾値を使用)。シーンの要素を強調したり、観察者を誘導するために、光を手動でアニメーションさせることもできます。このような場合、我々の即時フィードバックは非常に役立ちます。
Lens-System Design
実写の映画撮影でも、レンズフレアは望ましい効果とされることがあります[Woerner 2009]。レンズベイビーのようなある種のレンズシステムは、収差やその他の光学的効果を創造的に利用するために設計されています。このアルゴリズムは,従来のレンズ設計ツールと組み合わせることで,レンズ設計者が光学設計のフレア特性をプレビューし,最適化するのに役立つでしょう。
Deflaring
また、実際の写真からフレアのパターンを予測して除去するというのも面白いかもしれません。しかし、そのためには、無数のパラメータや未知の要素を含む光学系を完全に記述する必要があり、現状では手の届かないものとなっています。
7.2 Limitations
Light Sources
現在のレンダリングメカニズムは、単一の可視点/指向性光源を持つことに最適化されています。エリアライトは、点光源とその見え方に比例したエネルギー放射で近似することができますが、そのような解決策は近似的なものにとどまります。より正確に表現するには、追加コストをかけて光源をサンプリングする必要があります。
Precomputing Resolution
レイバウンディングの事前計算では、様々なライトの位置に対してシステム内の光線をトレースしますが、これらの低解像度の画像をレンダリングに使用できると結論づけるべきではありません。当初、画像のワーピング戦略を試してみましたが、微妙な変化(変位や変形など)にうまく対応できず、無駄に終わってしまいました。また、このようなソリューションはメモリを大量に消費しますが、我々のソリューションでは、境界線となる長方形の小さなルックアップテーブルを保存するだけです。
Aliasing
三角形が1ピクセルよりも小さくなると、ラスタライズエイリアシングという問題が発生します。この状況では、非常に高い強度が得られますが、エラーが発生しやすいラスタライズになる可能性があります。実際には、この問題は非常に異方的なゴースト(min/max ratio > 1000)に対してのみ発生し、その数は非常に少ない(ニコンのレンズの場合、142のうち3)。必要であれば、これらのフレアを選択し、高解像度のフレームバッファで処理し、最終的に標準フレームバッファに追加することができます。また、これらの小さな三角形のラスタライズをポイントレンダリング技術で置き換えることもできます。
8 Conclusion
複雑なレンズシステムのレンズフレアをシミュレートするインタラクティブなレンダリングアルゴリズムを発表しました。これまでのインタラクティブなソリューション、さらにはオフラインでの提案に比べて、優れた結果を示しました。また,スタイライゼーションの目的で,物理的な限界を超えてレンダリングをアーティスティックに修正・強化するための様々な手段を紹介しました.我々のアルゴリズムは、ユーザーがアプリケーションのコンテキストで最も重要なシミュレーションされた効果を選択できるようにすることで、精度と性能の間の微妙なトレードオフを可能にするという意味で、柔軟性があります。これにより、我々の手法は、高品質および中品質のリアルタイム目的に対応することができます。
将来的には、この高速アルゴリズムが、未知の光学系のパラメータを回復するためのツールとなることを期待しています。フレアパターンがわずかなパラメータの変化に非常に敏感であるという事実を考慮すると、Analysis-by-Synthesisスキームは非破壊的なレンズ特性評価を可能にするでしょう。このようにして校正されたフレアを合成すれば、そのシステムで撮影されたHDR画像を「デフレア」にすることができるかもしれません。アーチファクトのないHDRデータを撮影することは未解決の問題です。
また、匿名の査読者の方々には、貴重なご意見やご提案をいただきました。本研究の一部は、ザールランド大学のインテル・ビジュアル・コンピューティング・インスティテュートから資金提供を受けています。Sungkil Leeは,教育・科学・技術省の韓国国立研究財団による基礎科学研究プログラム(2-11-0014015)の支援を受けていることを感謝します。