こんらみ。Pocolです。
今日は,
[d’Eon 2021] Eugene d’Eon, “An analytic BRDF for materials with spherical Lambertian scatters”, Eurographics Symposium on Rendering 2021.
を読んでみようと思います。
いつもながら,誤字・誤訳があるかと思いますので,ご指摘頂ける場合は正しい翻訳と共に指摘して頂けると有難いです。
Abstract
球状ランバート散乱で構成される多孔質材質の新しい解析的BRDFを提案します。BRDFのパラメータは1です:ランバートパーティクルのアルベドです。結果として得られる外観は、Oren-Nayarのようなハイトフィールドに基づくモデルでは再現できない強いバックスキャッタリングとと飽和効果を示しています。
1. Introduction
双方向反射率分布関数(BRDF)は、コンピュータグラフィックスなどの分野で基本的な構成要素となっています。BRDFの測定により、実世界のマテリアルが幅広い反射率挙動を示すことが示されています[MPBM03, DJ18]。測定されたデータは直接利用することができますが、かさばるのと、編集が困難です。一方,パラメトリックBRDFはコンパクトであり,アーティストによる制御が可能ですが,現実世界の外観の全範囲に渡るパラメトリックBRDFは一つもありません。そのため、様々なマテリアルをカバーする柔軟な解析的パラメトリックBRDFの小さなセットを定義することが重要です。
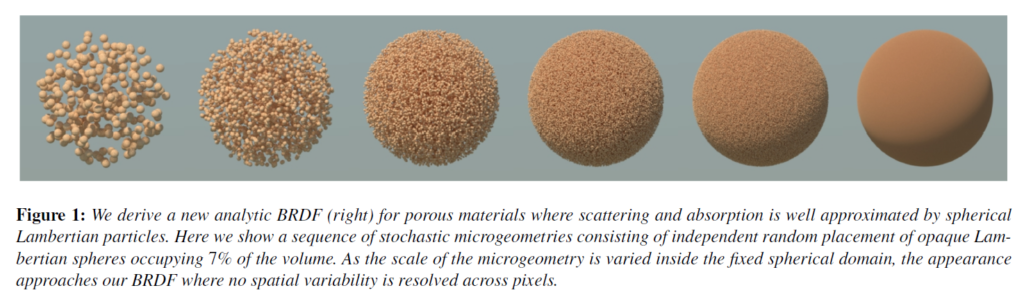
最も一般的なパラメトリックBRDFは、Smith [Sim64] のランダムなハイトフィールドの幾何学的・統計的処理 [CT82, Bli82, vGSK98, Sta01, WMLT07, Hei14] に由来するものです。これらのモデルは,様々なサーフェイス統計量 [RBMS17],異方性 [Hei14],重点サンプリング [Hd14] およびスペキュラー,ディフューズまたは混合マイクロファセットによる多重散乱 [HD15, HHdD16, MBT*17] をサポートしています。これらのBRDFは非常に成功しており、広範囲のマテリアルをカバーしていますが、ハイトフィールドの仮定は必ずしも有効ではありません[DHd16]:これらのBRDFは、図1に示す合成例やカーボン煤のような材質のサーフェイスプロファイルのような多孔質/粒状/容積/粒子状マイクロジオメトリをモデル化することはできません[SOPB08]。
ディフューズハイトフィールドの制限を超える広範囲の拡散挙動をシミュレートするために、平面平行な仮定の下でスラブ内のスカラー放射伝達を考慮することによってボリュームメトリックな BRDF を導き出すことができます [vdH80, Yan97, KP03].これは、体積中にランダムに分布する吸収・散乱粒子の配列として微細構造をモデル化するものです。複数の体積スラブをランダムなハイトフィールドの間でインターリーブし、完全に一般的な層スタックを形成することができます[Sta01]。これは”位置が自由”な方法で確率的に評価でき[GHZ18]、加算/倍算や関連する方法を用いて数値的に事前テーブル化できます[Sta01、 JdJM14、 ZJ18、 Bel18]。これらの方法を用いると、非常に多様なパラメトリックな層状マテリアルを評価することができますが、より単純な解析的BRDFの複雑さ、コスト、メモリ要件を大きく上回る可能性があります。より効率的なレイヤリングは可能ですが[WW07]、その代償として互恵性と正確さが失われます。一つの例外は、半解析的なBRDF(ChandrasekharのBRDF) [Cha60, KC17]が知られている、等方性散乱を持つ半空間です。
ChandrasekharのBRDFは、他の解析的なハイトフィールドBRDFと同様に、効率的かつ広範囲に適用できるユニークな厳密体積BRDFです。これは月のレゴリスのBRDFにインスピレーションを受け[Hap81]、境界でのフレネル反射をサポートするために拡張されました[WNO98, Wil06]。ChandrasekharのBRDFと一致する確率的幾何学(幾何光学のもと)は、純粋に吸収性のマトリックス中のミラー球状パーティクルのまばらな懸濁液である。この論文では、散乱体を白色Lambertian球とすることで、このBRDFのOren-Nayar [ON94] 相当となるものを導出しました。古典的放射伝達の等価原理 [vdH80] により、これは吸収ランバート球状パーティクルを持つvoidマトリックスと等価です。この結果は、Oren-NayarのハイトフィールドBRDFや、ChandrasekharやDisneyの拡散BRDF [Bur12]のような方位角対称の拡散BRDFとは異なる外観を提供する、塵や多孔質マテリアルの新しい近似解析的BRDF(図1)です。
まず、第2節で述べるLambertian sphereのファーフィールド位相関数を思い出すことから始めます。この位相関数の重点サンプリングと加倍積分を導出し、それが3項のLegendre展開でよく近似されることに注目します。このことは、3項半空間の正確なBRDFに関する既知の結果を適用することを可能にし、これを用いて、第3節では、方位対称多重散乱を仮定した従来の一般的な近似法[Hap81, Hap02]よりも正確な解析的近似法を導出します。セクション4では、新しいBRDFの外観をこれまでの解析的な拡散BRDFと比較し、また、ポジションフリーとダブルリングの両方のアプローチを用いたレイヤードマテリアル構成におけるパフォーマンスを比較します。
2. Lambertian sphere phase function
白色で滑らかなLambertian sphere(LS)のファーフィールド幾何光学位相関数は、[Bli82]のようになります。
\begin{eqnarray}
p(\mu) = \frac{ 2(\sqrt{1 -\mu^2} – \mu \cos^{-1}(\mu)) }{ 2\pi^2} = \frac{2(\sin(\theta) – \theta \cos(\theta)}{3\pi^2} \tag{1}
\end{eqnarray}
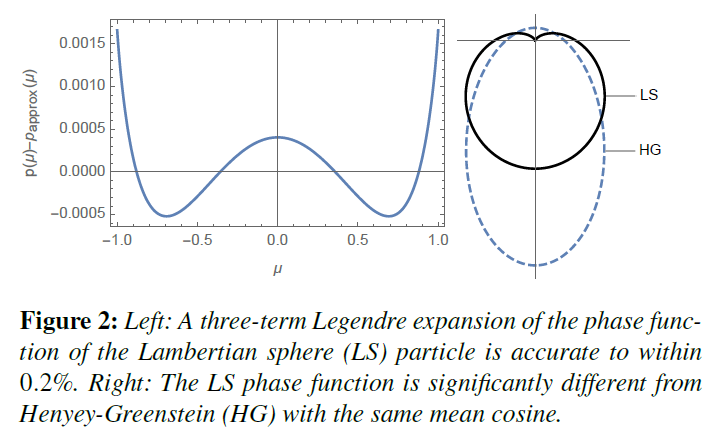
ここで,\(\mu = \cos \theta\)です。この位相関数は、1760年にランバート自身が正確な数表を添えて初めて導き出したものです [Lam60, p.471]。LS位相関数の平均余弦は\(g = -4/9 \approx -0.444444\)であり、多くのパラメトリックモデルとは異なり、光を直接前方に散乱させない、\(p(1)=0\)です。この位相関数の全体的な振る舞いは、Henyey-Greenstein (HG) [Bli82] などの他の一般的なパラメトリックモデルとは十分に異なっており、独自の調査が必要です(HGとの比較は図2 [右] を参照してください)。
LS位相関数のLegendre展開について
\begin{eqnarray}
p(\mu) = \frac{1}{4\pi} \sum_{k=0}^{\infty} A_k P_k (\mu) \tag{2}
\end{eqnarray}
ここで、展開係数は次のように定義されます。
\begin{eqnarray}
A_k = 2\pi(2k+1) \int_{-1}^{1} p(\mu) P_k(\mu) d\mu \tag{3}
\end{eqnarray}
最初の数個の展開係数を求めます。
\begin{eqnarray}
A_0 = 1, \quad A_1 =-\frac{4}{3}, \quad A_2 = \frac{5}{16}, \quad A_3 = 0, \quad A_4=\frac{1}{64}, \quad A_5 = 0 \tag{4}
\end{eqnarray}
位相関数の大部分は展開図の最初の3つの項で表現されていることから(図2)、この最初の3つの項のみを用いて位相関数を近似すると、次のようになります。
\begin{eqnarray}
p(\mu) \approx \frac{1}{4\pi}\left( \frac{27}{32} – \frac{4\pi}{3} + \frac{15\mu^2}{32} \right) \tag{5}
\end{eqnarray}
これにより、半空間BRDFに対する厳密な導出法[HC61]を適用することができ、これを用いて実用的な完全解析的近似値を導出します。
2.1. Importance Sampling
近似モデルのグランドトゥルースの検証のために、LS位相関数を用いた均質な半空間における粒子輸送のモンテカルロ・シミュレーションを行いました。我々の知る限り、この位相関数を重点サンプリングする手順は公表されておらず、ここではその手順を2つ提案します。厳密な結果としては、(Lambertian BRDFサンプリングといくつかの単純化とともに球への均一なディスク投影を考慮することにより)偏差の余弦は、次のようにランダムにサンプリングできることに注目します。
\begin{eqnarray}
\mu(\xi_1, \xi_2, \xi_3) = \sqrt{(1 – \xi_1)(1 – \xi_2)} \sin (2\pi \xi_3) – \sqrt{\xi_1\xi_2} \tag{6}
\end{eqnarray}
ここで、\(\xi_1\), \(\xi_2\), \(\xi_3\) は \([0, 1)\) から一様に引いた3つの独立な乱数です。あるいは、1つの一様な乱数実数\(\xi\)で、逆CDFの近似を使用して\(\mu\)をサンプリングすることができます。
\begin{eqnarray}
\mu(\xi) \approx 1 – 2 \left( 1 – \xi^{0.0401885 \xi + 1.01938} \right)^{0.397225} \tag{7}
\end{eqnarray}
これは,最大絶対誤差は \(|\mu – \mu_{exact} | \lt 0.0005\) となります。後者の方がより効率的と思われるので、不一致の少ない乱数列を使用する場合はこのサンプリングを推奨します。
2.2. Fourier Integrals
加算/倍算[vdH80, JdJM14]などのフーリエの枠組みで位相関数を使うには、フーリエ積分が必要です:
\begin{eqnarray}
p_l(\mu_i, \mu_o) = \frac{2 – \delta_{0l}}{\pi} \int_{0}^{\pi} p(\mu_i, \mu_o, \phi) \cos(l\phi) d\phi \tag{8}
\end{eqnarray}
Lambertian sphere位相関数の3項Legendre近似(式8の\(p\)を式5に置き換える)を用い、コサインで位相関数\(p(\mu)\)を評価します。
\begin{eqnarray}
\mu = \mu_i \mu_o + \sqrt{1 – \mu_i^2} \sqrt{1 – \mu_o^2} \cos(\phi) \tag{9}
\end{eqnarray}
次が求まります。
\begin{eqnarray}
p_0(\mu_i, \mu_o) &=& \frac{ 45\mu_i^2 (3\mu_o^2 – 1) -256\mu_i \mu_o – 45\mu_o^2 + 207 }{ 768 \pi } \tag{10} \\
p_1(\mu_i, \mu_o) &=& \frac{ (45\mu_i\mu_o -64) \sqrt{(\mu_i^2 – 1)(\mu_o-2 -1)} }{ 192 \pi } \tag{11} \\
p_2(\mu_i, \mu_o) &=& \frac{ 15(\mu_i^2 -1)(\mu_o^2 -1) }{ 256 \pi } \tag{12}
\end{eqnarray}
ただし,\(k \gt 2\)について,\(p_k= 0\)です。
3. BRDF derivation
Horak and Chandrasekhar [HC61]は、一般的な3項位相関数を持つ半空間の正確なBRDFを導きました。
\begin{eqnarray}
cp(\cos\theta) = {\bar \omega}_o + {\bar \omega}_1 P_1(\cos\theta) + {\bar \omega}_2 P_2 (\cos\theta) \tag{14}
\end{eqnarray}
ここで、\(P_1\) と \(P_2\) は Legendre 多項式です。彼らの結果は、先に与えられた非吸収半空間の特別な場合 [Cha60, p.158] を一般化したものです (非吸収の場合については [Aue61] の6ページ、4項の位相関数については [Smo76] 、一般の問題については [CLCC63, Sob68, VdH70] も参照してください)。彼らの表記法では、単一散乱アルベド\(c\)(ここでは球状パーティクルの拡散アルベド)は位相関数に折り込まれるため、式4の係数で与えられる3項の打ち切りの場合、次のようになります。
\begin{eqnarray}
{\bar \omega}_0 = c, \quad {\bar \omega}_1 = \frac{-4c}{3}, \quad {\bar \omega}_2 = \frac{5c}{16}. \tag{15}
\end{eqnarray}
3項半空間のBRDFは、3つのフーリエモードの総和として正確に与えられます。
\begin{eqnarray}
f_r({\vec \omega}_i, {\vec \omega}_o) = f^{(0)}(\mu_i, \mu_o) + f^{(1)}(\mu_i, \mu_o) \cos(\phi) + f^{(2)}(\mu_i, \mu_o) \cos(2\phi) \tag{16}
\end{eqnarray}
関数\(f^{(i)}(\mu_i, \mu_o)\)は錐体間伝達関数であり、加算/倍算や関連する数値計算法に用いられる伝達行列と密接な関係があります [vdH80, JdJM14]。コサイン \(\mu_i\)を持つ方向から到来する光に対して、コサイン \(\mu_o\)を持つ円錐に沿って物質を離れる平均放射輝度は\(f^{(0)}(\mu_i, \mu_o)\)であり、高次の項は、相対方位\(\phi\)によってパラメータ化される円錐内の出射放射輝度の変動を決定する離散コサイン列を与えます。
関数\(f^{(i)}(\mu_i, \mu_o)\)はすべての次数の散乱を含み、3項位相関数の場合は複素数式となります。BRDFの単一散乱成分については、既知の簡単な解析式を利用します [Cha60, HK93] 。
\begin{eqnarray}
f_1({\vec \omega}_i, {\vec \omega}_o) = c \frac{ p(-{\vec \omega}_i \cdot {\vec \omega}_o) }{ \mu_i + \mu_o } \tag{17}
\end{eqnarray}
この結果を利用し、さらに単一散乱を正確に表現するために、最終的なBRDFを単一散乱と多重散乱の項の合計として表現することにします。
\begin{eqnarray}
f_r({\vec \omega}_i, {\vec \omega}_o) = f_1({\vec \omega}_i, {\vec \omega}_o) + f_m({\vec \omega}_i, {\vec \omega}_o) \tag{18}
\end{eqnarray}
ここで、単一散乱の部分は式17を用いて計算します。したがって、位相関数の3項展開は多重散乱成分の解法にのみ使用することにします。
\begin{eqnarray}
f_m({\vec \omega}_i, {\vec \omega}_o) = f_m^{(0)} (\mu_i, \mu_o) + f_m^{(1)}(\mu_i, \mu_o) \cos (\phi) + f_m^{(2)} (\mu_i, \mu_o) \cos(2\phi).
\end{eqnarray}
これらの関数は、対応する\(H\)関数と定数を解けば、一般的な導出法[HC61]から決定することができます。
3.1. The \(H\) functions
Horak と Chandrasekhar [HC61]は、不変性原理を用いて、3項の位相関数を持つ半空間のBRDFを導出しました。彼らの導出は、対応する3つの\(H\)関数を持つ3つの擬似問題 [Cha60, p.351] を導き出します。これらの概念はコンピュータグラフィックスにとって新しいものであるため、ここではその背景を簡単に説明します。等方散乱のある均質な半空間での平面平行輸送の場合、衝突密度\(C(x)\)について輸送の積分方程式は第二種のFredholm積分方程式となります。
\begin{eqnarray}
C(x) = C_0(x) + c \int_0^{\infty} C(x’) K_C(x – x’) dx’ \tag{19}
\end{eqnarray}
この方程式の解(特に解のラプラス変換)は、Chandrasekharが\(H\)関数と呼ぶ、関連する非線形積分方程式の解と関連しています。
\begin{eqnarray}
\frac{1}{H(\mu)} = 1 – \mu \int_0^1 \frac{ H(x) + \Psi(x) }{\mu + x} dx \tag{20}
\end{eqnarray}
\(H\)関数が見つかれば、半空間のBRDFは完全に決定され、むしろ単純に次のようになります[Cha60]。
\begin{eqnarray}
f_r(\mu_i, \mu_o) = \frac{c}{4\pi} \frac{ H(\mu_i) H(\mu_o) }{ \mu_i + \mu_o } \tag{21}
\end{eqnarray}
しかし、散乱が非等方的になると、BRDFは複数の\(H\)関数を含むようになります。これらの\(H\)関数(位相関数のLegendre展開における非ゼロ次数ごとに1つ)はそれぞれ式20を満たしますが、異なる特性\(\Psi(\mu)\)を持ちます。これらの\(H\)関数は、それぞれ本来の等方性輸送問題に似ていますが、それ単体ではいかなる物理問題にも対応しないため、Chandrasekharはこれを擬似問題と呼びました。以下では、擬似問題の解法について既知の結果を適用し、より詳細については関連する研究を参照することにします。Ivanovの素晴らしいまとめが出発点として強く推奨されます[Iva94]。
3項半空間BRDFの特性関数\(\Psi^{(i)}(\mu)\)は、式15を一般解 [HC61, p.5] に挿入することで得られます。
\begin{eqnarray}
\Psi^{(0)}(\mu) &=& \frac{1}{384} c (-15(c-1)(4c + 9)\mu^4 + (c(20c+281) – 346)\mu^2 + 207), \\
\Psi^{(1)}(\mu) &=& -\frac{1}{192} c(\mu^2 – 1)(5(4c + 9)\mu^2 -64), \\
\Psi^{(2)}(\mu) &=& \frac{15}{256} c(\mu^2 -1)^2
\end{eqnarray}
次に、Fok/Chandrasekhar方程式[Foc44, Kre62]を用いて、\(H\)関数を数値的に評価することができます。
\begin{eqnarray}
H^{(i)} (\mu) = {\rm exp} \left(- \frac{\mu}{\pi} \int_0^{\infty} \frac{1}{1 + \mu^2 t^2} \log K^{(i)} (t) dt \right) \tag{22}
\end{eqnarray}
ここで,関数\(K^{(i)}(t)\)は[Kre62]によって与えられます。
\begin{eqnarray}
K^{(i)}(t) = 1 – \int_1^{\infty} \left( \frac{1}{s – it} + \frac{1}{s + it} \right) \frac{\Psi^{(i)} (\frac{1}{s})}{s} ds \tag{23}
\end{eqnarray}
これらを計算すると、次のようになります。
\begin{eqnarray}
K^{(0)}(t) &=& 1 – \frac{ c((256c – 301)t^3 + ((346 – c(20c + 281))t^2 – 15(c-1)(4c+9)+207t^4) \tan^{-1}(t) + 15(c-1)(4c+9)t ) }{ 192t^5 }, \tag{24} \\
K^{(1)}(t) &=& 1 – \frac{ c((40c +282)t^3 -3(t^2+1)(20c+64t^2+45) \tan^{-1}(t) + 15(4c+9)t ) }{ 288t^5}, \tag{25} \\
K^{(2)}(t) &=& 1 – \frac{ 5c(3(t^2+1)^2 \tan^{-1}(t) – t(5t^2+3)) }{ 128t^5} \tag{26}
\end{eqnarray}
これらを式22と組み合わせて\(H\)関数を数値的に評価し、レンダリングに直接利用できるより効率的な解析的近似式を作成する予定です。また,求積法 [Cha60, HC61] を用いて \(H\) 関数を評価することも可能です。
3.2. Second-order Fourier mode
完全なBRDFの2次フーリエモード\(f^{(2)}(\mu_i, \mu_o)\)(式16)について、MCリファレンスを用いて観察すると(図3)、多重散乱成分\(f_m^{(2)}(\mu_i, \mu_o)\)はBRDFの全エネルギー(さらには多重散乱エネルギーだけ)と比べて非常に弱いことがわかります。これは、すでに低周波の位相関数が、2回以上の衝突の後に、ほぼ線形-コサイン形状に畳み込まれるために起こります。このことを適切に利用し、単純に\(f_m^{(2)}(\mu_i, \mu_o) \approx 0\)とすることで解析的なBRDFを単純化します。したがって、我々の近似では、オーダーの\(\cos(2\phi)\)のすべての方位角変動は、単一散乱項(式17)に暗黙的に含まれることになります。
3.3. First-order Fourier mode
図3では、多重散乱の1次フーリエモード\(f_m^{(1)}\)が無視できない値になっていることがわかります。このことは、\(f_m\)がある関数 \(f\) に対して \(f(\mu_i, \mu_o) \cos(\phi)\) の形の項を持つことを要求しています。この項は厳密解から近似しており、\(f_m^{(1)}=0\)を仮定した従来の近似解との大きな違いの一つです[Hap81, Hap02]。
BRDFの正確な一次モードは [HC61, Eq.(43)]
\begin{eqnarray}
f^{(1)}(\mu_i, \mu_o) = \frac{cH^{(1)}(\mu_i) H^{(1)}(\mu_o) }{ 6 \pi (\mu_i + \mu_o)} \sqrt{ (1 -\mu_i^2)(1-\mu_o^2)} \times \left( 1 + \left( l^2 + \frac{45m}{64} \right) \mu_i \mu_o + l(\mu_i + \mu_o) \right) \tag{27}
\end{eqnarray}
という2つの定数\(\{l, m\}\)と関数\(H\)を決定する必要があります。我々は、式22と式25を用いて、\(H^{(1)}(\mu)\)の近似値をフィッティングしました。その結果、分離可能な近似値は次であることが分かりました。
\begin{eqnarray}
H^{(1)}(\mu) \approx H^{(1)}H_{c=1}^{(1)}(\mu) \tag{28}
\end{eqnarray}
ここで,
\begin{eqnarray}
H_{c=1}^{(1)}(\mu) \approx e^{-0.0894878 \mu^{-1.12831\mu^3 + 1.85728 \mu^2 – 1.07879\mu + 0.459442}} \tag{29}
\end{eqnarray}
そして,
\begin{eqnarray}
H^{(1)}(1) \approx e^{0.242851c^2 -0.144839c} \tag{30}
\end{eqnarray}
は,\(0.5%\)以内の精度(相対誤差)です。
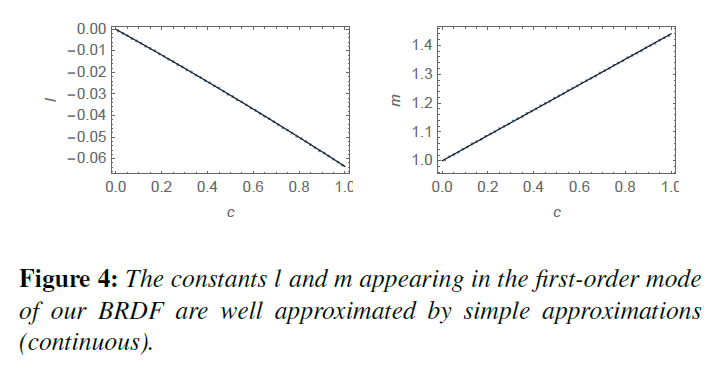
1次モードでは 2つの定数 \(\{l, m\}\) が現れますが, これらは関数\(H\)のモーメントから導かれます [HC61, p.56]。 関数\(H\)のモーメントの数値評価を用いて、我々は以下の近似が非常に正確であることを見出しました(図4)。
\begin{eqnarray}
l &\approx& -0.00473696c^2 -0.0589037c, \tag{31} \\
m &\approx& 0.44038c + 1. \tag{31}
\end{eqnarray}
式28は、すべてのオーダーの散乱を含んでいます。単散乱の結果を正確に利用するためには、3項位相関数近似を用いて\(f^{(1)}(\mu_i, \mu_o)\)から近似的に単散乱を差し引く必要があります。BRDF表記ではベクトルが表面から離れる方向に向くため、負の余弦で評価した近似位相関数(式9)を用いて単一散乱成分を評価します。
\begin{eqnarray}
f^{(1)}_1 (\mu_i, \mu_o) &=& \frac{1}{\pi} \int_{-\pi}^{\pi} \frac{c}{\mu_i + \mu_o} p(-\mu) \cos \phi d \phi \tag{33} \\
&=& \frac{ c(45\mu_i \mu_o + 64) \sqrt{({\mu_i}^2 – 1)({\mu_o}^2 – 1)} }{384\pi(\mu_i+\mu_o)} \tag{34}
\end{eqnarray}
であり、最終的な多重散乱項は
\begin{eqnarray}
{f_m}^{(1)}(\mu_i, \mu_o) = f^{(1)}(\mu_i, \mu_o) – {f_1}^{(1)}(\mu_i, \mu_o) \tag{35}
\end{eqnarray}
です。
3.4. Zeroth-order Fourier mode
0次モードに関しては, 厳密解 [HC61, 式(57)] を用いて \(f^{(0)}(\mu_i, \mu_o)\) を次のように書きます。
\begin{eqnarray}
f^{(0)}(\mu_i, \mu_o) = \frac{1}{2\pi} \frac{H^{(0)}(\mu_i) H^{(0)}(\mu_o) }{ \mu_i + \mu_o } \times \left( A + B(\mu_i + \mu_o) + C \mu_i \mu_o + D\mu_i \mu_o(\mu_i + \mu_o) + E{\mu_i}^2 {\mu_o}^2 + F({\mu_i}^2 + {\mu_o}^2) \right) \tag{36}
\end{eqnarray}
\(f^{(0)}(\mu_i, \mu_o)\)の評価には、式22と式24を用いて\(H\)を数値積分する必要があります。このコストを回避するために、等方散乱を用いた2つのストリーム近似から生じる単純な形式にヒントを得て、近似式を導出しました[Hap81]。
\begin{eqnarray}
H^{(0)} (\mu) \approx \frac{1 + a\mu^d}{1 + \frac{a\mu^d}{H^{(0)}(\infty) } } \tag{37}
\end{eqnarray}
ここで,無限における値は[Iva94],
\begin{eqnarray}
H^{(0)}(\infty) = \frac{1}{\sqrt{K^{(0)} (0)} } = \frac{12}{ \sqrt{(c-16)(c-1)(4c+9)} }
\end{eqnarray}
定数\(a\)と\(d\)を解くために、数値フィッティング法を用いました。
\begin{eqnarray}
a = \frac{ 1.50112s^{6.05435} + 8.21644 }{ 4.17593 – 1.21222s }, \quad d = \frac{ 7.7731 – 0.565811s^{0.961546} }{ 8.65912 – 0.159974s^7}
\end{eqnarray}
ここで,\(s = \sqrt{1-c}\)です。その結果、\(\{\mu, c\} \in [0, 1]\)の範囲で相対誤差が1%未満であることを確認しました。
式36を評価するためには、定数\(A\)、\(B\)、\(C\)、\(D\)、\(E\)、\(F\)が必要ですが、このうち2つは簡単な関係から導かれます[HC61、式(63)]。
\begin{eqnarray}
A = \frac{69c}{128}, \quad E = \frac{15}{128}(1-c)c \left( \frac{4c}{3} + 3 \right) \tag{38}
\end{eqnarray}
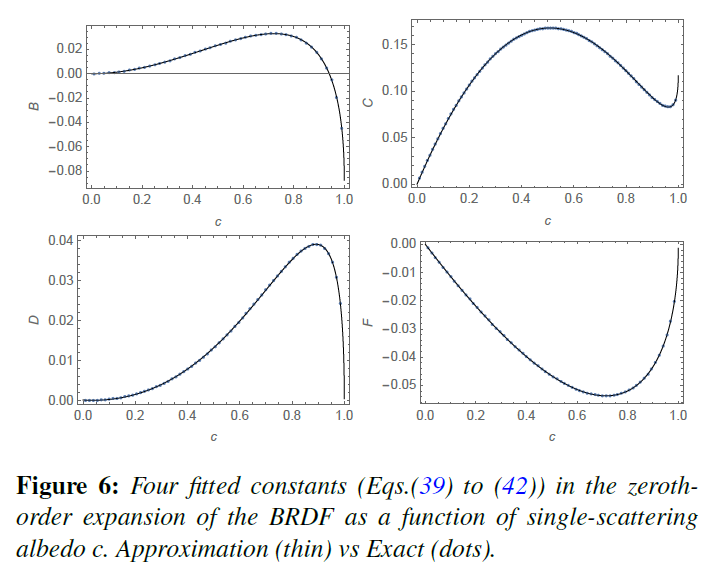
他の4つの定数は関数\(H\)のモーメントに関わるものであり、関係式であるため、以下の近似値を当てはめます。
\begin{eqnarray}
B &=& \frac{ 0.346689(1-c)^{3/2} -0.777574(1-c) + 0.515357 \sqrt{1-c} 0.084463 }{ 0.182602(1-c) – 0.665502 \sqrt{1-c} + 0.964893 } \tag{39} \\
C &=& \frac{ -5602.45(1-c)^{3/2} + 7487.99(1-c) -24567.74 \sqrt{1-c} + 682.848 }{ 1480.025(1-c) -4008.33 \sqrt{1-c} + 5850.6 } \tag{40} \\
D &=& \frac{ 166.883(1-c)^{3/2} – 327.48(1-c) + 160.397 \sqrt{1-c} + 0.285529 }{ 596.423(1-c) -412.984 \sqrt{1-c} + 674.191 } \tag{41} \\
F &=& \frac{ 266.063(1-c)^{3/2} -21.9141(1-c) -242.16 \sqrt{1-c} -1.9209 }{ 215.773(1-c) + 457.42 \sqrt{1-c} + 1499.9 } \tag{42}
\end{eqnarray}
これらの近似の精度を図6に示します。HC61]の55ページの最後の式の最後の項(\(t\)の場合)は\(+[\xi {a_1}^{(0)} – {a_3}^{(0)}] F\)と読むべきであり、マイナス記号を修正したことに注意してください。
式36は、すべてのオーダーの散乱を含んでいます。単散乱の結果を正確に利用するためには、3項位相関数近似を用いて\(f^{(0)}(\mu_i, \mu_o)\)から近似的に単散乱を減算する必要があります。一次の場合と同様、次のように計算します。
\begin{eqnarray}
{f_1}^{(0)}(\mu_i, \mu_o) &=& \frac{1}{2\pi} \int_{-\pi}^{\pi} \frac{c}{\mu_i + \mu_o} p(-\mu) d\phi \tag{43} \\
&=& \frac{ c(207 + 135{\mu_i}^2 {\mu_o}^2 – 45({\mu_i}^2 + {\mu_o}^2) + 256 \mu_i \mu_o ) }{ 768 \pi (\mu_i + \mu_o) } \tag{44}
\end{eqnarray}
となり、最終的な多重散乱項は
\begin{eqnarray}
{f_m}^{(0)} (\mu_i, \mu_o) = f^{(0)}(\mu_i, \mu_o) – {f_1}^{(0)}(\mu_i, \mu_o) \tag{45}
\end{eqnarray}
これで、LS半空間の近似的なBRDFの導出が完了しました。我々の解析的近似は、逆数的かつエネルギー保存的な厳密な結果から導かれたものです。構成上(そして検査によって簡単に検証できる)、我々のBRDFは相反となります。非吸収の場合(\(c=1\))、我々の近似はグレージング角度で少量の(<1%)エネルギーを失います。
3.5. Albedo Mapping
マテリアル中のパーティクルの単一散乱アルベド\(c\)とマテリアルの球面/結合アルベドである\(k_d\)の間のマッピングには、以下の適合近似式を用います(アーティストコントロールには拡散色\(k_d\)がより直感的です)。
\begin{eqnarray}
c &=& \frac{1 – (1-k_d)^{2.73556}}{ 1- 0.184096(1-k_d)^{2.48423}} \tag{46} \\
k_d &=& \frac{ 1 – 0.453029 (1-c) -0.544162 \sqrt{1-c} }{ 1.42931 \sqrt{1-c} +1 } \tag{47}
\end{eqnarray}
これらは,近似BRDFを数値的に積分することによって生成された境界アルベドのテーブルを入力とし,Mathematica でフィッティング最適化を行うことによって導き出されました。
3.6 Fast Variant
前節の解析的フィッティングは、他の解析的BRDFと比較して、まだかなりの計算コストがかかるBRDFであり、リアルタイムのアプリケーションにはコストがかかりすぎる可能性があります。より効率的にするために(精度は落ちますが)、記号回帰ソフトウェアTuringBotを使った以下の近似も見つけました。
\begin{eqnarray}
f_r({\vec \omega_i}, {\vec \omega_o}) = {\rm max} \left( 0, f_1({\vec \omega_i}, {\vec \omega_o}) + 0.234459 k_d^{1.85432} + \frac{0.0151829(c – 0.249978)(|\phi|+ \sqrt{\mu_i \mu_o}) }{ \frac{\cos^{-1}(S) }{S} + 0.113706 } \right) \tag{48}
\end{eqnarray}
ここで,\(S = \sqrt{1 – {\mu_i}^2} \sqrt{1 – {\mu_o}^2} \). 図7は、この近似の精度を前節のものと比較したものです。また、Hapkeの一般的な位相関数に対する近似 [Hap81]とも比較しました。この近似は、単一散乱成分を正確に含むが、等方散乱の半空間に対する関数\(H\)に基づく方位不変の多重散乱成分を仮定したものです。この論文における他のすべての結果は、完全な導出を用いています。
4. Results
LS BRDFはMitsuba [Jak10]で実装し、拡散色\(k_d\)でパラメータ化し、式46でパーティクルアルベドに変換しました。BRDFは、式18(および関連する式)とユーザーによるランバート重点サンプリングを用いて実装されました。我々は,より単純なLambertianおよびOren-Nayar [ON94]のBRDFと比較して,レンダリング時間が最大30%増加する一般的な傾向に注目しました。いくつかの正確なタイミングは、以下の結果で提供されています。我々はまた、確率的レイヤー評価[GHZ18]をテストするための位相関数そのものと、Mitsuba 2[ZJ18]で構築されたレイヤーラボ加算/ダビングフレームワークのフーリエ実装を実施しました。ソースコードは公開予定です。
我々のLS BRDFは、Lambertian、Oren-Nayar [ON94]、Chandrasekharの鏡面パーティクルに対するBRDFなどの標準的な拡散BRDFと外観が大きく異なります(図8, 図9, 図10)。他のモデルと比較して、バックライトのバックスキャッタ―と飽和色が増加することに注意してください。我々のBRDFは他のボリュームBRDF(Chandrasekharのもの)に最も似ていますが、Chandrasekharのものの明るいシルエットは我々の新しいBRDFで回避されています(図9、図10)。
私たちのボリュームネトリックなBRDFは、まばらな拡散性粒状物質の外観を正確にモデル化することができます。図1は、我々のモデルが、まばらなランバート球の粒状ミクロジオメトリと密接に一致している様子を示しています。ここでは、確率的に独立した球の構成が、一定の体積率を維持しながら右に向かって密度を増しています(数は300から120万)。古典的な放射伝達の仮定(散乱は空間的に独立である)に反する様々な球体のパッキングと比較するために、図12では、すべてのケースでランバートアルベドを固定したまま、パッキングの密な配列を考えてみます。我々は、ハイトフィールドモデルが、ラフネス\(\alpha=2.4\)程度まで、このような球体クラスター形状を近似する際に妥当な仕事をすることを観察しましたが、これは完全なBRDFを表すために必要な散乱の多くのオーダーを説明するために、かなりの確率的評価が必要です。(Oren Nayarモデルは2つのバウンスしか考慮せず、そのようなラフネスの範囲には及ばず、過度に明るく表示されます)。この点で、ハイトフィールドの仮定は矛盾しており、球状のNDFがより適切です[DHd16]。このラフネスのレベルを超えると、ラフディフューズ Beckman BRDF [HD15]は暗いアーティファクトを示すようになりますが、これはラフネスの仮定が、プロファイルが不当にとがったものになるまでハイトフィールドをスケールするためです [DHd16]。
この実装を検証するために、加算/倍算を使ってレンダリングした結果(図11)と比較します[JdJM14]。拡散アルベド\(k_d = (0.18, 0.05, 0.6)\)を持つスカラーRGB実装と,シルエットでの差異を避けるための\(\mu\)での\(n=60\)展開順序の場合,フーリエBRDF表現は3チャンネルで152KiBのストレージを必要とします。解析結果は、より単純なランバート重点サンプリングスキームを使用するにもかかわらず、同様のノイズレベルでより速くレンダリングされました。対応するg-matched HGレンダーも含まれており、より平坦な見た目を示しています。
球体を吊り下げるものが必要なため、疎であるという仮定は、単独でのBRDFの物理的な動機付けに挑戦しています。 薄い結合構造か、空気の指数に近いランバーシアン粒子をサスペンドする誘電性の非関与媒質マトリックスのどちらかです。より妥当なシナリオは、一般的な指数\(\eta \gt 1\)の誘電体マトリックスに埋め込まれた粒子のケースで、これは倍増法または位置フリー確率的アプローチのいずれかを使ってシミュレーションすることができます。図 13 では、Beckmanラフネス \(\alpha=0.05\) の粗い誘電体界面の下に BRDF を重ね、このような誘電体コーティングを比較しています。2倍のBRDF計算では、3チャンネルで2MiBのデータが生成されました。ポジションフリー評価(b)は、倍加法(c)の外観と一致していますが、倍加法はBRDF全体を単一のよくサンプリングされた結果に合成するため、レンダリング時間が著しく長く、ノイズも大きくなっています。しかし、確率的なアプローチは、非粗いコーティングを許可することができ、事前計算されたデータを必要としません。このポジションフリー評価では,LS位相関数をボリュームレイヤーで評価するのとは対照的に,解析的なBRDFをサーフェイスとして使用します(レンダリング速度が130倍遅く,ノイズが大幅に増加します)。これは、高散乱、高アルベド、厚い体積に対するポジションフリーアプローチの明確な限界を示すとともに、このような複雑さを単一の結果でカプセル化するよりも解析的な結果の利点を示しています。ランバーシアン(a)とHG(d)ベースも示していますが、両者の違いはコーティングされた状況ではあまり明らかではありませんが、コーティングされていないケースで観察された全体的な傾向はそのまま残っています。
5. Conclusion
我々は、従来のモデルに欠けていたバックスキャッタリングと飽和効果を示す、埃っぽい/多孔質表面のための新しい実用的な解析的BRDFを発表しました。我々の導出は、van de Hulst [VdH70]によって「アルファベットの文字では足りない方程式のセット」として美しく要約された、重要ではありますが、それでも非実用的な厳密半解析ベンチマーク解 [HC61] から直接導かれるものです。我々の導出は、擬似問題と関連する近似技術をグラフィックスに導入し、他の低次位相関数に対する同様の実用的な近似を触発する可能性があります。その結果得られたBRDFは、アーティストや測定データのフィッティングに新しい直感的な外観動作を提供します。また、Lambertian-sphere位相関数をサンプリングし、それをdoublingフレームワークに含めるための新しい結果も含まれています。
今後の課題としては、この挙動が現実のマテリアルでも見られるかどうか、実測データを調査することです。また、球状ガウスNDFとそのような媒体を扱うためのSmithのモデルの新しい形式[d’E16]を使用してモデル化した図12に示されているような微細形状のシーケンスを考慮することによって、Lambertianからハイトフィールドモデルを経て我々の新しいBRDFにブレンドする単一の解析的BRDFを導出したいとも考えています。このような定式化において、我々の新しいLS BRDFは、その導出の主な動機であるラフ拡散マテリアルの新しい表現ファミリーの無限ラフネスの終点となります。
6. Acknowledgements
アルベドマッピングの改善に関する提案など、有益なフィードバックをいただいた査読者の方々に感謝します。また、初期のドラフトをレビューしてくれたM.M.R. WilliamsとJakub Boksanskyに感謝します。Williams と Jakub Boksansky には初期のドラフトをレビューしてもらい、Lionel Simonot には Lambertian-sphere phase function を Lambert の本で探し出してもらいました。 Matt Pharrには、彼の英訳本へのアクセスを提供していただきました。