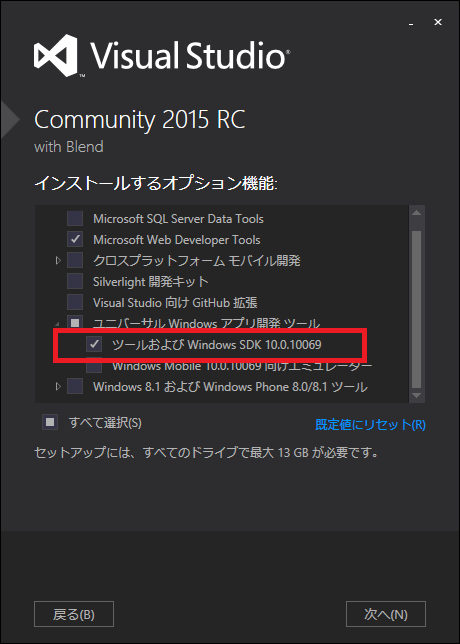
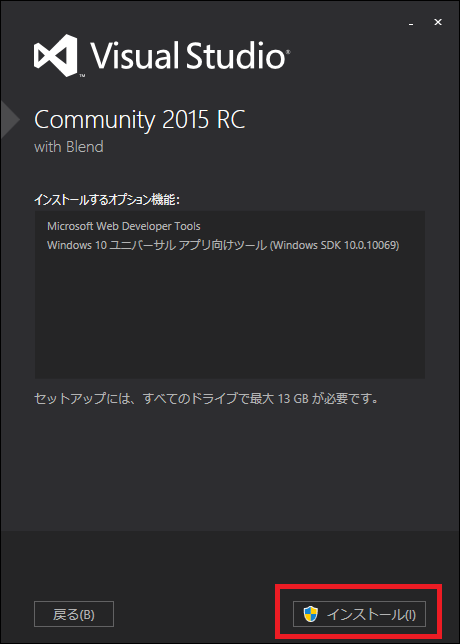
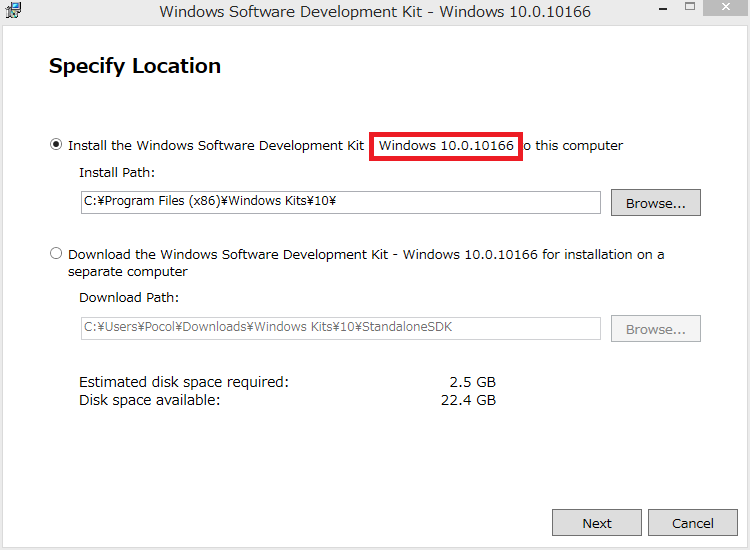
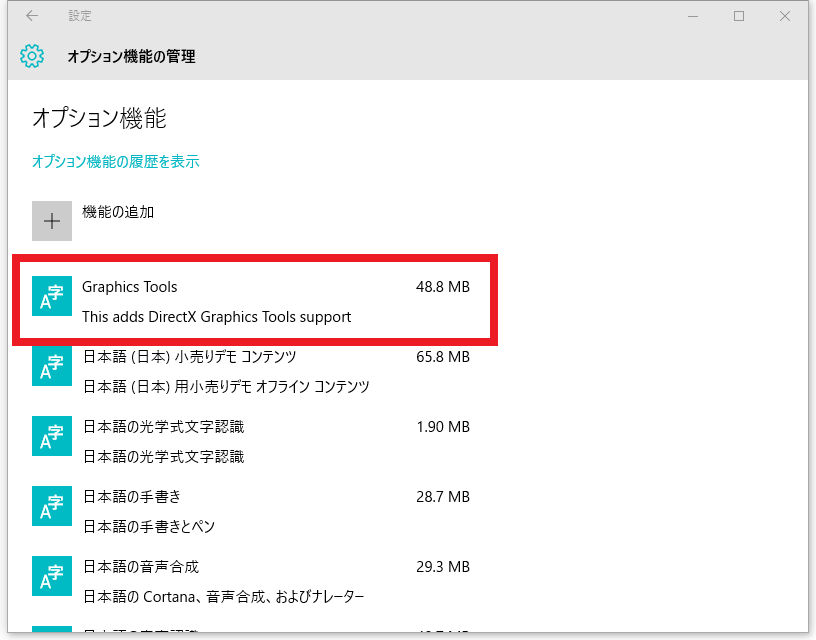
※2015/10/04 やっぱりHLSLのコードが間違えていたようで修正しました。
LogPSMで出てきたエイリアシング誤差の可視化を実装してみました。
実装に当たっては,”Robust Hard Shadows”のAppendix A.3 Sampling rateと,博士論文でない方のLograthimic Perspective Shadowの論文中の式84, 式85を参考にしました。
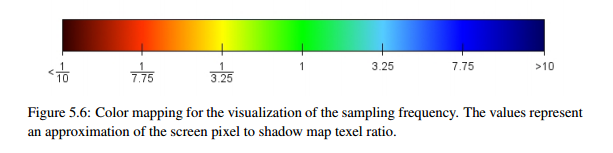
※図はMartin Stingl, 2011, Robust Hard Shadows. p.58より引用。
論文中で使われている下の画像ようなものを表示するためのものです。
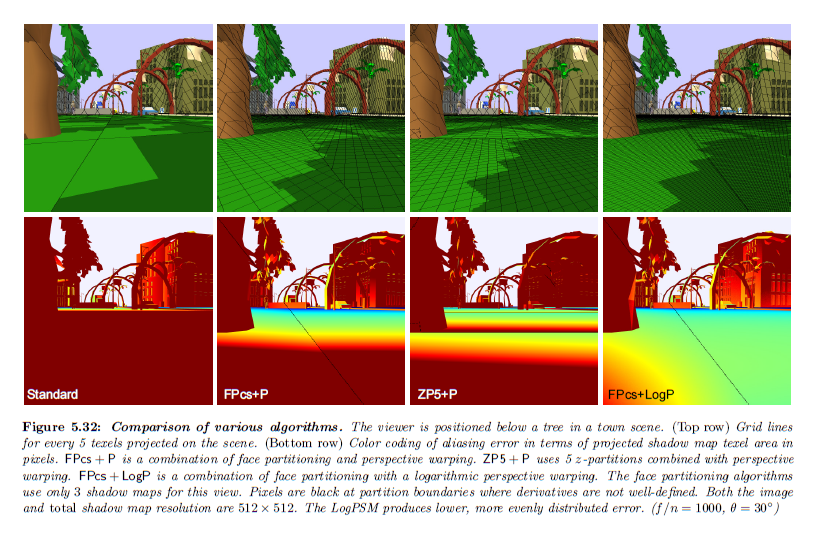
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.116 より引用。
float3 VisualizeError( float2 shadowCoord, float2 shadowMapSize )
{
const float3 values[] = {
float3( 0.0f, 1.0/7.75, 1.0f/7.75f ),
float3( 1.0f/7.75f, 1.0f/3.25f, 1.0f/3.25f - 1.0f/7.75f ),
float3( 1.0f/3.25f, 1.0f, 1.0f - 1.0f/3.25f ),
float3( 1.0f, 3.25f, 2.25f ),
float3( 3.25f, 7.75f, 4.5f ),
float3( 7.75f, 10.0f, 7.75f ),
};
const float3 colors[] = {
float3( 0.2f, 0.0f, 0.0f ),
float3( 1.0f, 0.2f, 0.0f ),
float3( 1.0f, 1.0f, 0.0f ),
float3( 0.0f, 1.0f, 0.0f ),
float3( 0.3f, 0.8f, 1.0f ),
float3( 0.0f, 0.0f, 1.0f ),
float3( 0.0f, 0.0f, 0.2f )
};
float2 ds = shadowMapSize.x * ddx( shadowCoord );
float2 dt = shadowMapSize.y * ddy( shadowCoord );
float error = max( length( ds + dt ), length( ds - dt ) );
float3 result = (float3)1.0f;
[unroll]
for( int i=0; i<6; ++i )
{
if ( error >= values[i].x && error < values[i].y )
{
result = lerp( colors[i], colors[i+1], (error - values[i].x) / values[i].z );
break;
}
else
{
result = colors[6];
}
}
return result;
}
Uniform Shadow Mapに適用すると下記のようになります。

うちのサンプルで公開しているものは,それなりによさげに見えます。
Prallel-Split Shadow Mapの方にも適用してみました。

PSSM適用するまでもないシーンなのですが,一応緑色が占める割合が多いので,適切にシャドウマップが適用されていることが分かりますね。
奥の方はこんだけちっこいシーンなので当たり前ですがオーバーサンプリング気味になっているので,カスケードの枚数を減らしても大丈夫そうな気がします。
再びUSMで2048×2048だったシャドウマップのサイズを256×256に落とすと下記のようになります。
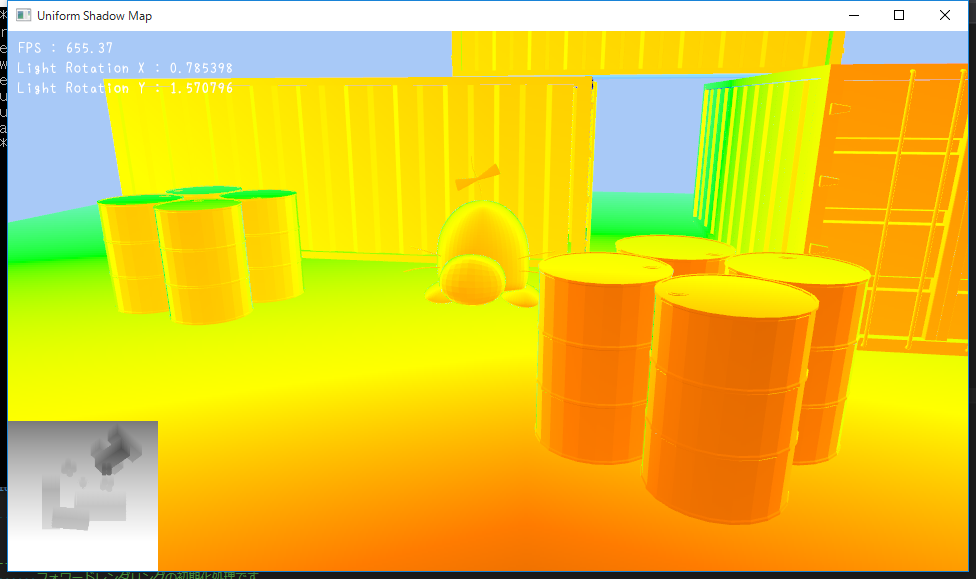
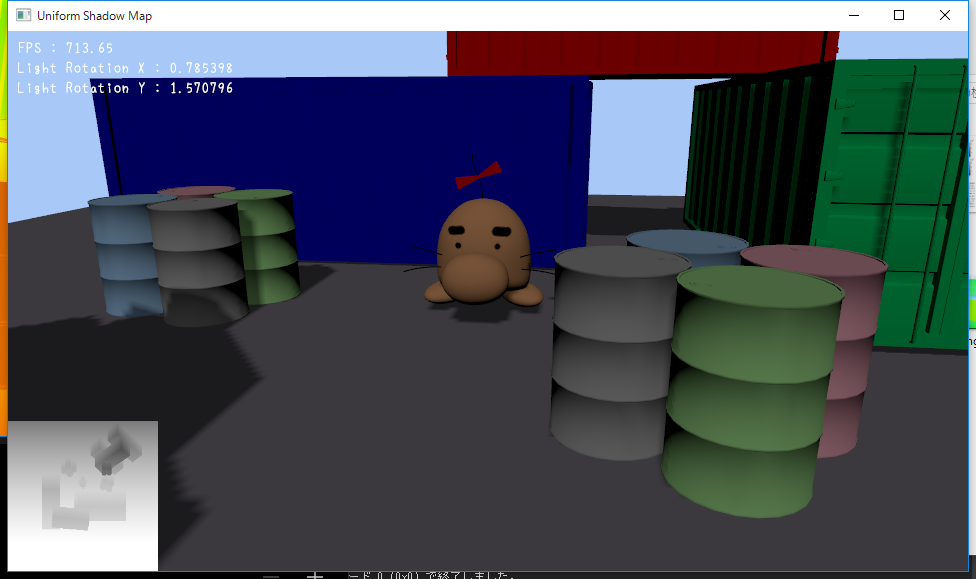
奥の方は緑色になっているので確かにシャドウが適切に表示されていますね。
手前部分は赤から黄色に近い色になっているので,確かにちょっと汚いのが見て取れます。
こういう感じでデバッグに結構役立ちそうです。
もし実装間違え等があれば,正しい実装と一緒に指摘していただけると幸いです。