明けまして、おめでとうございます。
今年もProject ASURAをどうぞよろしくお願い致します!!
去年は、ツラい思い出しかなかったので今年は楽しんで過ごしたいです。
明けまして、おめでとうございます。
今年もProject ASURAをどうぞよろしくお願い致します!!
去年は、ツラい思い出しかなかったので今年は楽しんで過ごしたいです。
こんばんわ。Pocolです。
本年度、最後の更新です。今年一年を振り返ろうと思います。
まずは,自分がシステム構築など行ったゲームが無事に世に出て良かったです。
ほとんどやったのはシステム構築だけで最後まで関われなかったので,
製品まできちんと出来たのは自分以外の人の努力の結晶だと思います。
間接的ながら,少しだけ仕事に関わることが出来て良かったと思います。
また,ミリオンも達成できて良かったと非常に思います。
いつも,エンジンやらライブラリやらしか作っていないので,
製品のスタッフロールに載ることは殆ど無いのですが…
(XXX Team やら XXX 株式会社なりでまとめられてしまうので,名前が載ることはないのです)
今回はスタッフロールに載せて頂けたので,非常に良い経験となりました。
10月には,皆様に大変お待たせしましたが,ようやく執筆していた本を発売することができました。
レビューアの皆様ならび,編集担当の落合様には大変互助力をしていただきました。
この場で,再度お礼を申し上げます。ありがとうございました。
来年には,皆で打ち上げやりましょう!
後は最近うちのホームページなんか見ている人これっぽっちもいないだろうと思っていて,そろそろpublicなホームページは辞めたいなって思っています。
privateなページにして,のほほんとやっていきたい。自由に書きたい。
Githubに人知れずこっそりと記事をあげたりとか,今あんまり使っていないSlackとかで投稿するのも良いかもしれないなぁって感じています。
…ということで,そのうちページ閉じるかもという予告でした。
来年はどんな一年になるんでしょうか?
楽しい1年にしたいな。
それでは,皆様良いお年を!
大変申し訳ございません。
下記の通り、誤記がありましたので謹んでお詫びして訂正いたします。
P.245 中央部の数式
【誤】
\begin{eqnarray}
x &=& r \sin \theta \cos \theta \\
y &=& r \cos \theta \\
z &=& r \sin \theta \sin \theta
\end{eqnarray}
【正】
\begin{eqnarray}
x &=& r \sin \theta \sin \phi \\
y &=& r \cos \theta \\
z &=& r \sin \theta \cos \phi
\end{eqnarray}
P.245 6行目
【誤】
また,立体角は平面角2つを用いて表すことも可能です。球の半径を\(r\),天頂角を\(\theta\),方位角\(\phi\)とした場合,3次元空間上の任意の点は球面座標を使って次のように表せます。
円弧の長さは半径\(r\)と平面角の積で求められるので,方位角方向の弧の長さは \(r \sin \theta d\phi\)で表されます。同様にして,天頂角方向の弧の長さを求めると\(r d\theta\)となります。
方位角方向と天頂方向の円弧によって形成される面積\(dA\)を考えると,次のようになります。
【正】
また,立体角は平面角2つを用いて表すことも可能です。球の半径を\(r\),仰角を\(\theta\),方位角\(\phi\)とした場合,3次元空間上の任意の点は球面座標を使って次のように表せます。
円弧の長さは半径\(r\)と平面角の積で求められるので,方位角方向の弧の長さは \(r \sin \theta d\phi\)で表されます。同様にして,仰角方向の弧の長さを求めると\(r d\theta\)となります。
方位角方向と仰角方向の円弧によって形成される面積\(dA\)を考えると,次のようになります。
P.341 リスト10.16
【誤】
auto invW = 1.0f / float(w - 1); auto invH = 1.0f / float(h - 1);
【正】
auto invW = 1.0f / float(w); auto invH = 1.0f / float(h);
サンプルプログラム Chapter.10 IESProfile.cpp
【誤】
auto idx = (w - 1) * y + x;
【正】
auto idx = w * y + x;
P.245 6行目
【誤】
また,立体角は平面角2つを用いて表すことも可能です。球の半径を\(r\),天頂角を\(\theta\),方位角\(\phi\)とした場合,3次元空間上の任意の点は球面座標を使って次のように表せます。
円弧の長さは半径\(r\)と平面角の積で求められるので,方位角方向の弧の長さは \(r \sin \theta d\phi\)で表されます。同様にして,天頂角方向の弧の長さを求めると\(r d\theta\)となります。
方位角方向と天頂方向の円弧によって形成される面積\(dA\)を考えると,次のようになります。
【正】
また,立体角は平面角2つを用いて表すことも可能です。球の半径を\(r\),仰角を\(\theta\),方位角\(\phi\)とした場合,3次元空間上の任意の点は球面座標を使って次のように表せます。
円弧の長さは半径\(r\)と平面角の積で求められるので,方位角方向の弧の長さは \(r \sin \theta d\phi\)で表されます。同様にして,仰角方向の弧の長さを求めると\(r d\theta\)となります。
方位角方向と仰角方向の円弧によって形成される面積\(dA\)を考えると,次のようになります。
こんにちわ。Pocolです。
「お、遅かったじゃないか…。」
そう言われても仕方ありませんね。
Direct3D 12 ゲームグラフィックス実践ガイドの正式な発売が決定しました!
10月15日発売です!
三宅さんのAI本の一日後なので,三宅さんの本を買う人は一日遅らせて一緒に買いましょう。
本日より,先行販売している書店さんもあるようです。一日でも早く手に入れたいという方は,先行販売している書店さんに行ってみると良いかもしれません。
10/6先行販売『Direct3D12 ゲームグラフィックス実践ガイド』#技術評論社 (978-4-297-12365-9)Pocol 著◆「#3DCG 」棚にて展開中!入門書レベルを卒業し脱初心者を目指している読者に有益な情報を提供する書籍。#Direct3D12 pic.twitter.com/8ZrNrw9lqq
— 書泉ブックタワーコンピュータ書【営業時間11:00~20:00】 (@shosen_bt_pc) October 6, 2021
10/6先行販売:ISBN978-4-297-12365-9 技術評論社『Direct3D12 ゲームグラフィックス実践ガイド』Pocol著 10冊入荷 pic.twitter.com/EviyAGZ4Wb
— ジュンク堂書店池袋本店 PC書担当 (@junkudo_ike_pc) October 7, 2021
また,本日の先行販売に合わせて,書籍のサンプルプログラムのダウンロードページが公開されました。
下記ページの「本書のサポートページ」にアクセスするとzipファイルでサンプルプログラムがダウンロードできる状態になっています。
書籍のページ上の都合で,本にはプログラムコードがフルで書かれていませんので,こちらのサンプルを見ながら,本と照らし合わせて見て頂けると良いかと思います!
あと,ページレイアウト決まった後で,サンプルプログラムで未使用変数があるというビルド警告が出る箇所を見つけてしまったのですが,プログラムが実行できないなどの致命的な問題ではないのと,諸所の事情で修正できませんでした。
該当の箇所は,
Chapter9/Tonemap/Sample/res/TonemapPS.hlsl 107行目のL0 108行目のL1
です。
こちらはプログラム上で使っておりませんので,削除あるいはコメントアウトして頂けるとビルド警告が表示されなくなりますので,お手数ですが各自で修正をお願い致します。
…というわけで,来週発売になりますのでよろしくお願い致します!
A Fast and Stable Feature-Aware Motion Blur Filterの疑似コード。
float cone(float dist, float r) {
return saturate(1.0f - abs(dist) / r);
}
float cylinder(float dist, float r) {
return sign(r - abs(dist)) * 0.5f + 0.5f;
}
// linear depth.
float zCompare(float za, float zb) {
const float SOFT_Z_EXTENT = 0.1f;
return saturate(1.0 - (za - ab) / SOFT_Z_EXTENT);
}
float3 MotionBlur(float2 p)
{
// parameter setting (see. 5. Implementation and Results).
const auto N = 35; // sample count.
const auto eta = 0.95; // a larger maximum jitter value (in pixel units). (see p.6)
const auto phi = 27; // user-determined constant which affects the "baseline2 jitter level. (see p.6)
const auto kappa = 40; // use-parameter to bais its importance. (see p.6)
const auto r = 40; // a maximum image-space blur radius. (see p.2)
const auto gamma = 1.5; // minimum user threshold (see p.4)
auto j = Halton(-1, 1);
// sOffset jitters a tile lookup (but never into a diagonal tile).
auto vmax = FetchNeighborMax(p/r + sOffset(p, j));
auto mag_vmax = length(vmax);
if (mag_vmax <= 0.5f)
{
return FetchColor(p);
}
auto wn = vmax / mag_vmax;
auto vc = FetchVelocity(p);
auto wp = (-wn.y, wn.x); // vmax⊥.
if (dot(wp, vc) < 0.0)
{
wp = -wp;
}
auto mag_vc = length(vc);
auto wc = normalize(lerp(normalize(vc), wp, (mag_vc - 0.5) / gamma); // Eq. (1).
// First integration samples: p with center weight
auto totalWeight = N / (kappa * mag_vc);
auto result = FetchColor(p) * totalWeight;
auto j_dash = j * eta * phi / N;
auto z_p = FetchDepth(p);
for(int i=0; i<N; ++i)
{
auto t = lerp(-1.0, 1.0, (i+j_dash + 1)/(N+1)); // jitter sampler
// Compute point S; split samples between {vmax, vc}
auto d = (i & 0x1) ? vc : vmax; // iが奇数なら vc, iが偶数なら vmax.
auto T = t * mag_vmax;
auto S = int2(t * d) + p;
// Compute S's velocity and color
auto vs = FetchVelocity(S);
auto colorSmaple = FetchColor(S);
auto z_S = FetchDepth(S);
// Fore-vs. background classification Y w.r.t p
auto f = zCompare(z_p, z_S);
auto b = zCompare(z_S, z_p);
// Sample weight and velocity-aware factors (Sec.4.1)
// The length of v_s is clamped to 0.5 minimum during normalization
auto weight = 0;
auto wA = dot(wc, d);
auto wB = dot(normalize(vs), d);
auto mag_vs = length(vs);
// 3 phenomenological cases (Sec. 3, 4.1): Object
// moving over p, p's blurred motion, & their blending.
weight += dot(f, cone(T, 1 / mag_vs)) * wB;
weight += dot(b, cone(T, 1 / mag_vc)) * wA;
weight += cylinder(T, min(mag_vs, mag_vc)) * max(wA, wB) * 2;
totalWeight += weight; // For normalization
result += colorSample * weight;
}
return result / totalWeight;
}
McGuireのG3Dエンジンでは論文実装よりも変更がある。以下のように内積計算部分がガッツリなくなっている。
https://sourceforge.net/p/g3d/code/HEAD/tree/G3D10/data-files/shader/MotionBlur/MotionBlur_gather.pix
auto f = zCompare(z_p, z_S); auto b = zCompare(z_S, z_p); auto weight = 0.0f; weight += b * cone(T, 1 / mag_vs); weight += f * cone(T, 1 / mag_vc); weight += cylinder(T, min(mag_vs, mag_vc)) * 2.0f; totalWeight += weight; result += colorSample * weight;
こんばんわ。Pocolです。
もうすぐSIGGRAPHですね。SIGGRAPHのコースで「なねぃと」についての話があるそうで,そのコースを受ける前にある程度は調査しておこうと思いました。Sさん、問題あればご連絡を。
今回の調査では下記のようなことを知りたいなと思ったので,調査してみました。
なねぃとは仮想化マイクロポリゴンジオメトリシステムです。いわゆるVirtual Textureみたいなテクスチャストリーミングのメッシュ版という感じのやつです。細かいポリゴンを扱えるのが売りになっていて,ものすごくいい感じのディテールが表現できます。
なねぃとを実現するためのキーだと思っているものは次の通りです。
まずGPU駆動描画はその名の通り,GPU上で描画するかどうかを判定を行い,その結果で描画が駆動する手法のことを言ったりします。これはカプコンさんだったり,アサクリだったり,Trialsだったりと色々な会社さんがすでに取り組まれています。内容について知らない方がいたら下記の資料などを読むと良いと思います。
UE5はバウンディングのスケールに応じてソフトウェアラスタライズとハードウェアラスタライズの分岐がコンピュートシェーダ上で決定されます。
小さな三角形はコンピュートシェーダを用いたソフトウェアラスタライズが実行され,大きな三角形に対してハードウェアラスタライザが実行されます。
ソフトウェアラスタライザですが,小さな三角形に対しては平均で3倍高速化したと「Nanite | Inside Unreal」の動画でKarisが言っていました。恐るべき速度ですね。
あとは,この高速なソフトウェアラスタライズを支える技術として,Deferred Materialを使用しています。いわゆるVisibility Bufferというやつです。
これの何が良いかというと,深度とマテリアルインデックスをバッファに出力してしまい,マテリアル評価を遅延実行できるというメリットがあります。つまり,いちいちシェーダの切り替えをしなくて良いということです。これによりUE5は不透明物体の描画を1ドローで実現しています。
さらにNaniteを見ていてがんばっているなーと思うのがデータの圧縮です。1トライアングルにつき平均14.4Byteだそうです。一応自分でもソースコードを追ってみて,確かにそうだなということを確認しました。
まずは,レンダラーの流れをつかみ大雑把にどんなことをやっているのかを把握してみました。
レンダラーの実装は,Engine/Source/Runtime/Renderer/Private/DeferredShadingRenderer.cppにあります。これがディファードレンダリングの実装になっており,Render()メソッドに実装があるので,これを地味に読み解いていきました。なんとこの関数1600行ほどあります。
この関数をところどころを端折った疑似コードが下記のような感じになります。
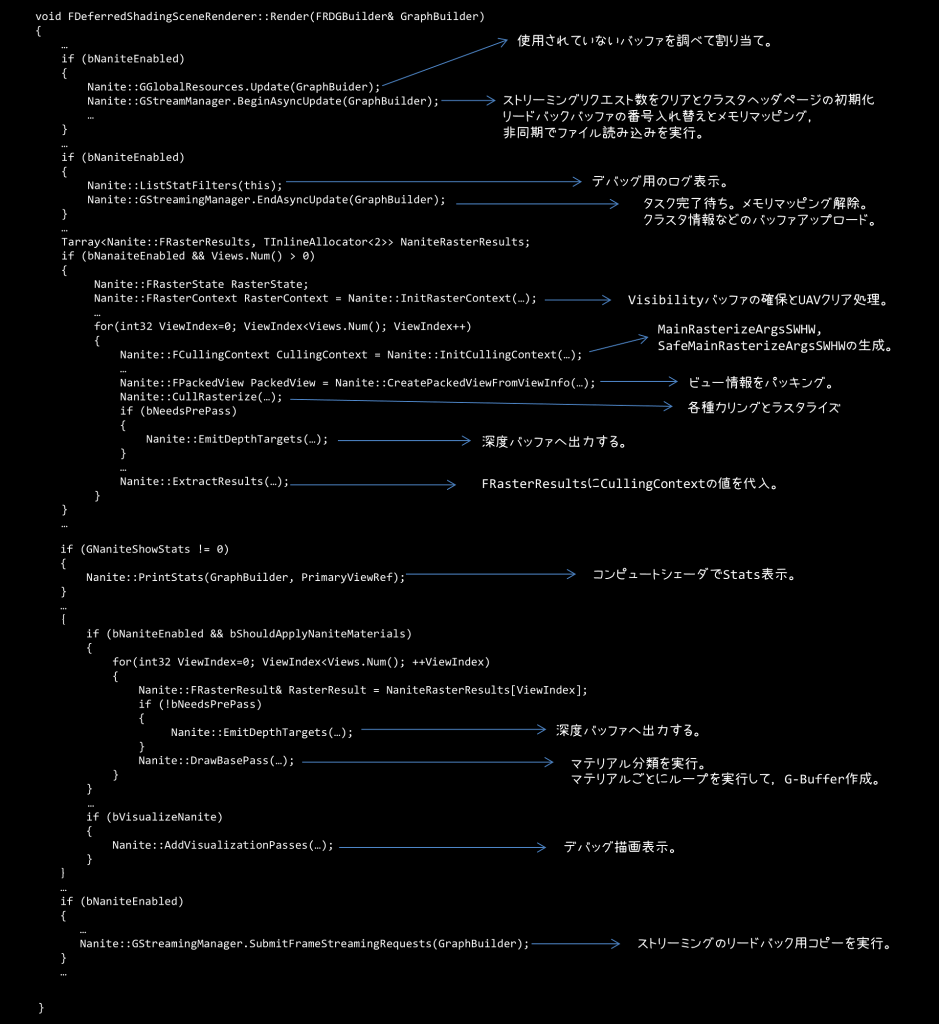
ざっくりですが,処理をまとめておくと
…という感じです。
下記のシェーダが実行されるようです。
左側は実行される関数で,右側はその関数が実装されているファイルパスを表します。
PersistentCull()がおそらく一番巨大なシェーダコードになると思うのですが,クラスタ階層のトラバーサルとかカリング,あとはソフトウェアラスタライズかハードウェアラスタライズかどうかの切り分けなんかも行っています。
MicroPolyRasterize()がソフトウェアラスタライズを行っているのですが,R32G32のバッファに書き込みをします。Rチャンネルの25bit分がVisibleIndexで,残りの7bitがTriangleIDになっています。GチャンネルはDepthに割り当てられているようです。
下記のシェーダが実行されるようです。
名前通りの処理っぽいです。
下記のシェーダが実行されるようです。
ClassifyMaterials()の中では,VisibleなMaterialとMaterial Rangeを決定するようです。Material Rangeにはマテリアルのマスクビットが格納されています。
大雑把な理解として,描画対象となるマテリアルの矩形範囲を決めているようです。
FullScreenVS()では,決定したマテリアルの矩形範囲にあるタイルで,本当にそのマテリアルの描画必要かどうかを判定して,要らないところはNaNを頂点シェーダで設定して,タイルをカリングするという処理を行うようです。タイルカリングには5つのモードがあるようです。
ストリーミングの管理はFStreamingManagerというクラスで管理されているようです。
Engine/Source/Runtime/Engine/Public/Rendering/NaniteStreamingManager.hにクラスの宣言があります。
・クラスタページデータ
・クラスタページヘッダ
・クラスタ修正更新バッファ
・ストリーミングリクエストバッファ
・ストリーミングリクエストリードバックバッファ
・ペンディングページ
・リクエストハッシュテーブル
などを保持しているようですが,まだ理解しきれていないので,理解できるようになったら別の記事として書くことにします。
ページリクエストは,PersistentClusterCull()というシェーダが実行されてRequestPageRange()という関数内でリクエストが書き込まれるようです。
このシェーダで書き込んだページリクエストの取得はディファードレンダラー内のAsyncUpdate()内でバッファをmapすることでCPU側で取得されるようです。
リクエストハッシュテーブルにGPUから取得したものを登録して,被るものがあるかどうかをチェック。チェックにヒットしたらストリーミングするページとしてプッシュし,優先度でソートして,LRUを更新しています。
一方,検索にヒットしない場合は,優先度付きリクエストヒープにいったんプッシュするようです。その後、このヒープからポップしてストリーミングするページを選択しています。
ストリーミングするものは読み込みされている状態なので,送ればいいのですが,これから読み込みしないといけないペンディング状態のものについては,ペンディング状態のページを収集し,ランタイムリソースIDがコンピュートシェーダで書き込まれるので,これを利用してFbyteBulkDataを取得するようです。取得したデータをFIORequestTaskに登録し,ParallelFor文を用いて,ファイルの非同期読み込みが実行さるようです。
ストリーミングマネージャのEndAsyncUpdate()という関数で,読み込み完了待ちをしてからResourceUplodTo()関数を使ってGPUに転送しているみたいです。
FStaticMeshBuilder::Build()経由でBuildNaniteFromHiResourceModel()が呼び出されて,データが作成されるようです。
BuildDAG(), ReduceDAG(), FindDAGCut()などの内部の処理がまだ全然理解できていないので,鋭意調査中です。
ジオメトリデータはEncodeGeometryData()という関数でエンコードされるようです。
Positionデータは63bitに。
法線ベクトルはOctrahedronで表現し,XYで18bitに。
テクスチャ座標はXYで32bitに。
ここまで合計14byteになるので,確かにKarisが言っていた平均14.4Bという数字は納得できます。
ちなみに頂点カラーやUV数を増やす場合はさらにデータ容量が増えていく感じです。
今回は,えらくざっくりですが,どんな感じで動くのかについて調査しました。
レンダリングフローについては理解できたのですが,実際のストリーミングの詳しい処理内容や,階層LODの作成方法など,まだまだわからない箇所もあるので次回調査してみたいと思います。
こんばんわ、Pocolです。
アレですが,順調に進んでおります。機が熟したら書きますので、もう少しお待ちください。
実装用の資料として,THE LAST OF US PARTⅡのスクショを張っておきます。動画も上げようと思ったのですが,サイズが大きくて上げられませんでした。
























こんにちわ、Pocolです。
執筆している本ですが…,順調に進んでいます。
企画から5年。そして無名ということで企画が通るまでの,半年近くはほぼ何もできず。
担当さんの地道な根回しがあって,ようやく執筆までたどり着いた本です。
折角企画も通り,発売に向けて動き出したので…
発売後にマサカリ投げられるのは,嫌なので説明部分に関してはあらかじめ豪華メンバーに査読していただきました。
説明については丁寧にレビューしていただきました。
本当にこの場を借りて,感謝を述べさせていただきたいと思います。
「本業がありタイトル開発などお忙しい中,レビューアーの皆様本当にありがとうございました!」
実をいうと,レビューで心が折れました。
やっぱり,色々と見てもらうと自分がいかに愚か者であるかということをヒシヒシと感じますね。
説明の仕方もそうですが,言葉の選び方や言い回しなんかもそうです。
独りよがりはやっぱりいかんなと改めて思いました。
また、レビューしていただいて本当によかったなと心の底から感じています(本当最初の状態は酷かった)。
レビュー無しで,国会図書館なんかに寄贈されて,ダメダメな説明とかが自分が死んだ後も一生記録されてしまうと思うと,ゾッとしますね。
レビューが無かったら,そうした恥をさらしながら生きていかなければならないのですが,レビューをしてもらうことで,少しでも回避することができて本当によかったなと思います。
やはり,レビューをしてもらって感じたのですが,きちんとした議論があってこそ,良いものが生まれてくるんだろうなと… そう感じました。
自分が見ていて「これは良いな!」と思う書籍は共著だったり,きちんと監修が付いていたりしますしね。
自分は筆不精でして,期待されて待っている方には本当に申し訳ないのですが,
実はとある競合書籍が発売されていなければ,今頃は既に発売済みだったんですね。
何もせずに,当初通りそのまま発売というのもありだったのですが,単なる2番煎じになるもの,流石にどうかなと思いまして…。
(まぁ、だったら先越される前に早く書けよっていうのはごもっともです。)
やはり,先手を打ち出されてしまうと,後手側は何かしらの対策を練らねければなりません。
何も対策を練らないというのは愚の骨頂ではないかと思いましたし,何かしら付加価値を付けて提供したいと思いました。
また,何もせずにそのまま発売にもっていってしまうのは,色々な方の力を借りている分,自分として申し訳なかったですし,待っている方にも申し訳が立たないです。
担当さんは,「こちらのほうが先にやっているのに…後からを先越されて…」と,がっくし来ていたみたいです。
自分もさらに,その本の内容を見てガックシきました。ちなみに,その本の内容は,細かい所は違えど目指す方向性としては,自分が一番最初に出版社に企画を出してボツになった内容ほぼそのものでした。こっちの出版社だったら,すんなり受け入れられていたかもしれないな…って。
まぁ、いずれこういう先に越されることは目に見えていたので,筆不精な自分が悪い以外のなにものでもないんですけどもね。
ただ,今書いている内容はボツになったものとは方向性が違います。
…というか,出版社側のダメ出しだったり,他社に先越されるのとか想定して,じゃぁちょっと変えましょうと,企画段階で変更したんですよね。
だから,そのまま予定に沿って発売に向けて動いても問題はなかったのですが,何か悔しいなと思って…。
何かしら手は打たねばならないと思いました。
そこで,1章分を新たに追加執筆し,さらに開発に役立つと思われる付録もちょっとしょぼい内容ですが一応付けました。
具体的な内容については,もう少し言える状況になったらお伝えしたいと思います。
(内容を書いて競合他社にパクられて,差別化をするためにまた発売を延期するのは流石に勘弁したいので…)
皆さん,完成まで着々と進んでいます。もうしばらくお待ちください!!