こんにちわ,Pocolです。
今日はGPU最適化のための自分用のメモを書いておこうと思います。
自分がある程度理解できればいいことを前提に書いているので,「そもそも間違っている」とか「全然正しくない」とか「こうした方がもっといい」とかあれば,ご指摘ください。
P3 Method
基本的には,Louis Bavoil氏が書いている「The Peak-Performance-Percentage Analysis Method for Optimizing Any GPU Workload」に従ってボトルネックを探し,改善を行っていきます。GDCでも講演があるので,興味がある方はそちらの動画を見ると良いと思います。
この手法は次のステップで最適化を行います。
(1) “Top SOL%”の値をチェックする。
– (A) 80%より大きいの場合: SOLユニットから処理を取り除くことを試みる。
– (B) 60%より小さいの場合: top SOL%の値が増加するように試みる。
– 上記以外の場合: (A)と(B)の両方を行う。
(2) Top SOLユニットがSMの場合(あるいは,SOL%の項目が近い場合)
“SM Throughput for Active Cycles”の値をチェックする。
– (C) 80%より大きい場合: 命令群を適宜スキップしてみたり、特定の計算をルックアップテーブルに移行することを検討してみる。
– (D) 60%より小さい場合: SM占有率(実行中のアクティブワープ数)の増加を試みる & SM発行ストールサイクルの数を減らすことを試みる
– 上記以外の場合: (C)と(D)の両方を行う
(3) その他がTop SOLユニットの場合、そのユニットに送られる作業量を減らすことを試みる。
ここまで出てきた用語は次の意味です。
- SOL:Speed Of Light。最大スループットを意味する。
- SM:Streaming Multiprocessor。共有メモリやコンスタンスとキャッシュ,テクスチャキャッシュ,複数のスカラープロセッサなどから構成されるもの。ものすごく雑に言えばUnified Shaderのこと。
- Throughput。ハードウェアが単位時間あたりに処理できるデータ量のこと。あるいは,その数値を使ってデータ処理能力やデータ転送速度を表す。
さて,最適化する上で肝心なのは「Top SOLをどうやって調べるか?」ということになります。これはNVIDIA Nsight Graphicsを使って調べることができます。
まず,Nsightを立ち上げる前にパフォーマンスカウンターなどを取得できるように設定を変更しておきます。NVIDIAコントロールパネルを開きます。Windowsのタスクバー右下にある^をクリックして,NVIDIA設定を右クリックし,NIVIDIAコントロールパネルを選択します。選択してもコントロールパネルが開かない場合は,何らかの異常が発生している恐れがあるのでグラフィックスドライバーを再インストールして改善するか試してみてください。コントロールパネルを開いたら,メニューの「デスクトップ」から「開発者設定を有効にする」にチェックを入れておきます。これでカウンター等の値がとれるようになるはずです。
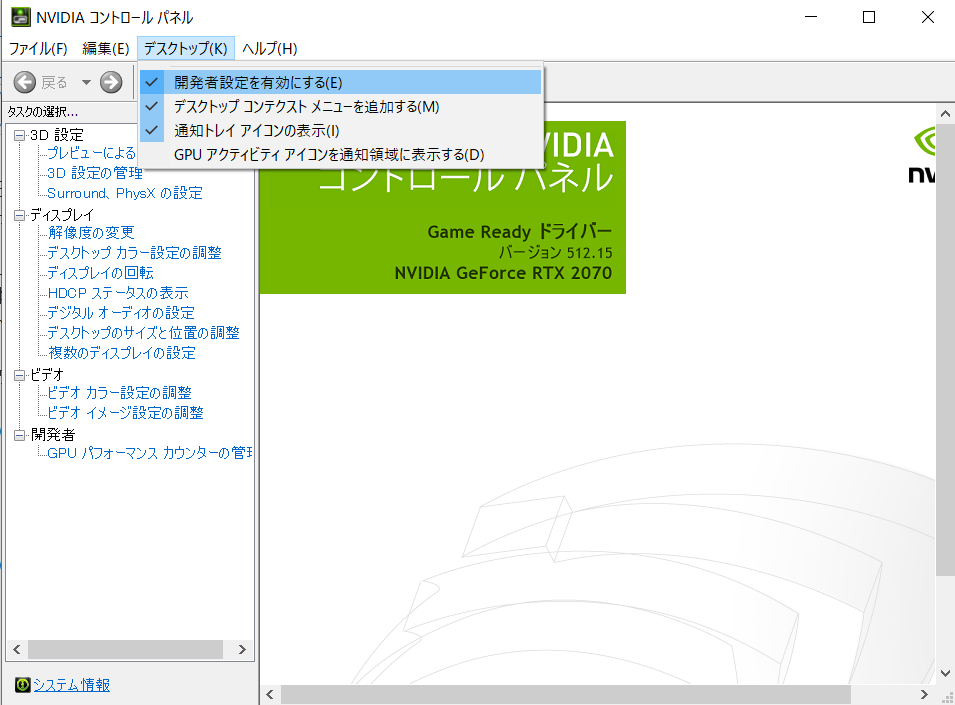
図1.NVIDIAコントールパネルでの設定
続いて計測を行います。Nsight Graphicsを立ち上げFrame Profilerとしてアプリケーションを立ち上げます。立ち上げ方はConnect to processのウィンドウで,Activityの項目をFrame Profilerに設定して,Application Executableにアプリケーション実行パスを指定,Working Directoryに作業ディレクトリを設定してください。自動的にアタッチする場合はAutomatically ConnectにYesを,Steamなどのようにいったん別exeをかましてから立ち上げる場合はNoに設定しておき,Target PlatformでAttachタブを選択してから,プロセスにアタッチするという方法を取ります。
アプリケーションが立ち上がったら,左上にオーバーレイが表示されるので,F11を押して測定したいフレームをキャプチャーします。

図2.オーバーレイの表示
キャプチャーすると,画面右上にRange Profilerというものが表示されるので,調べたいドローコール部分をRange Profilerでクリックします。クリックすると,少し時間をおいてから次のようにRange InfoやPipeline Overviewなどが表示されます。
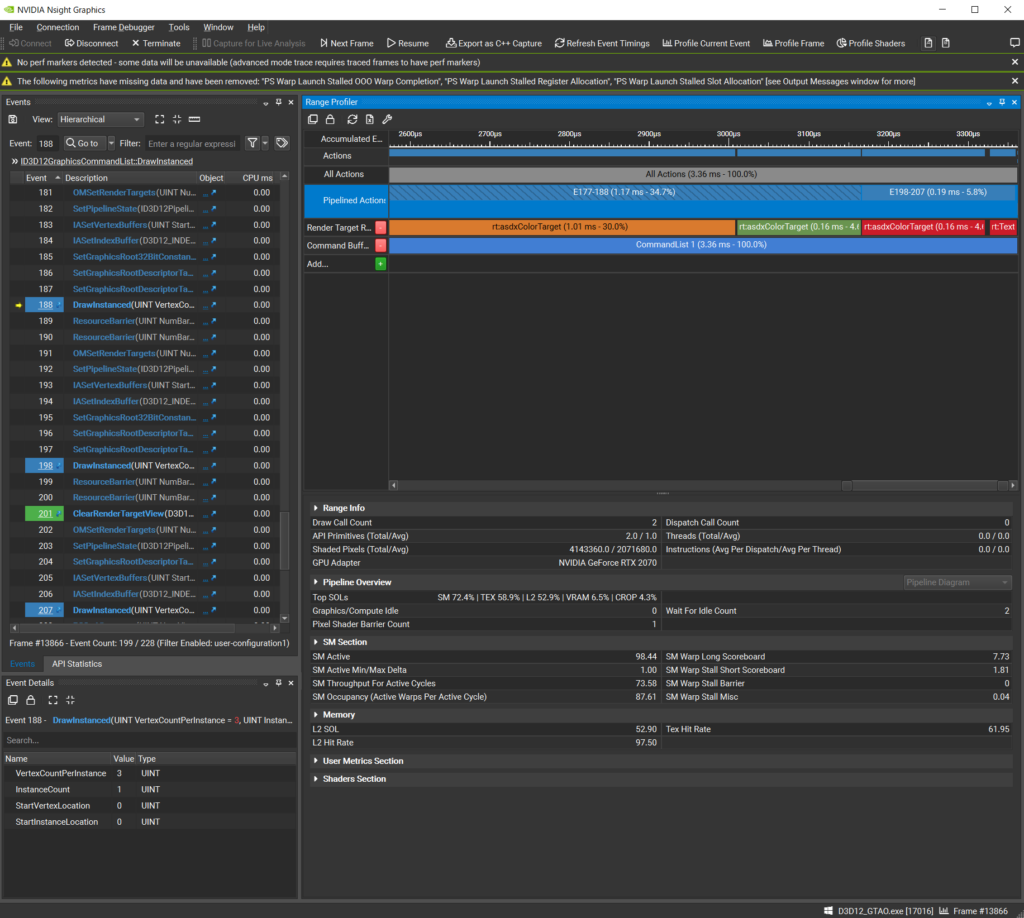
図3.フレームキャプチャー
あとは,Pipeline Overviewに表示されるSM / L2 / VRAM / CROP / RAS の値を見て上記のステップに沿って改善を行います。

図4.Pipeline Overview
(A) Top SOL% > 80% の場合
GPU上で非常に効率的に動作していることが分かります。高速化するためには,このTop SOLユニットを処理から削除し,他のユニットのボトルネックを探していきます。例えば SM が Top SOL ユニットの場合は,命令群をスキップしてみたりなど。もう一つの例としては構造化バッファのロードを定数バッファに移して高速化するなどです。
(B) Top SOL% < 60% の場合
トップ SOL%の値が60%未満場合、トップ SOL ユニットと SOL% が低い他のすべての GPU ユニットは、使用率が低い(アイドルサイクル)、非効率的に動作している(ストールサイクル)、または与えられた作業負荷の仕様により高速パスに当たらないということを意味します。このような状況の例としては、以下のようなものがあります。
- アプリケーションが一部CPUに制限される
- Wait For IdleコマンドやGraphic←→ComputeスイッチでGPUパイプラインを何度も消耗している
- テクスチャオブジェクトからのTEXフェッチは、フォーマット、次元、またはフィルタモードによって、設計上、スループットが低下して実行されます(GTX 1080のこれらの合成ベンチマークを参照)。例えば、3Dテクスチャをトライリニアフィルタリングでサンプリングする場合、50%のTEX SOL%が期待されます。
- TEXやL2ユニットのキャッシュヒット率が低い、VRAMアクセスがまばらでVRAM SOL%が低い、GPU VRAMではなくシステムメモリからVB/IB/CB/TEXをフェッチするなど、メモリサブシステムの非効率性。
- 入力アセンブリの32ビットインデックスバッファのフェッチ(16ビットインデックスに比べ半減)
この場合、トップSOL%の値を使用して、非効率な処理を削減することによってこの処理負荷で達成できる最大利得の上限を導き出すことができます。
(C) SM Throughput For Active Cycles > 80% の場合
SM がトップ SOL ユニットで、「SM Throughput For Active Cycles」が 80%より大きい場合、現在の処理負荷は主に SM スケジューラの発行率によって制限されているため、SM の占有率を上げてもパフォーマンスは大きく向上しません(少なくとも、処理負荷は 5%以上増加しない)。
この場合,次のステップは、SMスケジューラの帯域幅を飽和させているのはどのような命令かを把握することです。典型的なのは算術命令(FP32や整数演算)ですが、テクスチャフェッチや共有メモリアクセスなどのメモリ命令もあり得えます。また、SMがトップSOLユニットで、SM Throughput for Active Cyclesが80%以上のワークロードでは、TEXユニットもSMのSOL%に近い値でなければ、TEX命令(SRVおよびUAVアクセス)が性能を制限している可能性はないでしょう。
(D) SM Throughput For Active Cycles < 60% の場合
このGTC 2013の14分の講演のスライド15にあるように、あるワープ命令が発行できない場合(オペランドの準備ができていない、あるいは実行に必要なパイプラインサブユニットの準備ができていないため、これをワープストールと呼びます)、SM命令スケジューラは、別のアクティブワープに切り替えてレイテンシーを隠蔽しようとします。そこで、SMスケジューラがSMアクティブサイクルあたりにより多くの命令を発行できるようにするには、2つの方法があります。
(1)SMの占有率(スケジューラが切り替え可能なアクティブなワープの数)を上げる
(2)SM発行ストール待ち時間を短縮する(ワープがより少ないサイクルでストール状態に留まるようにする)。
アプローチ1:SM占有率を増加する
SMがトップSOLユニット(またはそれに近い)、「アクティブサイクルのSMスループット」60%未満であれば、SMの占有率を上げるとパフォーマンスが向上するはずですが、まず何が制限になっているかを把握する必要があります。
ピクセルシェーダとコンピュートシェーダで最も一般的な SM 占有率のリミッタは、シェーダが使用するスレッドごとの ハードウェアレジスタの数です。
ハードウェアのレジスタ数が最大理論占有率(アクティブサイクルあたりのアクティブワープ数)に与える影響は、CUDA Occupancy Calculatorで確認できます。
Maxwell、Pascal、Volta GPU では、レジスタの他に、以下のリソースでも SM 占有率を制限することができます。
グラフィックスシェーダについて:
- 頂点シェーダー出力アトリビュートの合計サイズ。
- ピクセルシェーダーの入力アトリビュートの合計サイズ
- HS、DSまたはGSの入力および出力アトリビュートの合計サイズ。
- ピクセルシェーダの場合、ピクセルワープのアウトオブオーダー完了(通常、動的ループや早期終了ブランチなどの動的制御フローに起因する)。CS のスレッドグループは任意の順序で完了できるため、CS にはこの問題があまりないことに注意してください。Gareth Thomas & Alex Dunnによる「Practical DirectX 12」についてのGDC 2016講演のスライド39をご覧ください。
コンピュートシェーダについて:
- スレッドグループのワープがSM上でall-or-none方式で起動するため、スレッドグループのサイズはSMの占有率に直接影響します(つまり、スレッドグループのすべてのワープが必要なリソースを利用でき、一緒に起動するか、または何も起動しないかです)。スレッドグループのサイズが大きくなると、共有メモリやレジスタファイルなどのリソースの量子化が粗くなります。アルゴリズムによっては純粋に大きなスレッドグループを必要とする場合もありますが、それ以外の場合は、開発者はできるだけスレッドグループのサイズを64スレッドまたは32スレッドに制限するようにすべきです。これは、64 または 32 スレッドサイズのスレッドグループが、シェーダプログラムに最適なレジスタターゲットを選択する際に、シェーダコンパイラに最も柔軟性を与えるからです。
- さらに、レジスタ使用量が多く (>= 64)、SM (HLSL の GroupMemoryBarrierWithGroupSync()) におけるスレッドグループバリアのストール時間が長いシェーダでは、スレッドグループのサイズを 32 に下げれば、64 と比較してスピードアップする可能性もあります。64 レジスタのガイダンスにより、SM あたり最大 32 スレッドグループの制限(CUDA Occupancy Calculator のアーキテクチャ依存の「Thread Blocks / Multiprocessor」制限)が、SM 占有率の主要制限要因にならないようにします。
- CUDA Occupancy Calculatorに様々な数値を入力することで、スレッドグループごとに割り当てられる共有メモリの総バイト数もSMの占有率に直接影響を与えることが分かります。
- 最後に、短いシェーダ(例えば、TEX命令と2つの算術命令)を持つDispatchコールのシーケンスでは、SMの占有率は、上流ユニットのスレッドグループの起動率によって制限される場合があります。この場合、連続したDispatchコールをマージすることが有効な場合があります。
CUDA Nsightのドキュメントページ「Achieved Occupancy」には、Compute ShadersのSM占有率制限の候補がいくつか挙げられています。
- スレッドグループ内の処理負荷が偏っている。
- 起動したスレッドグループが少なすぎる。これは、GPU Wait For Idles の間に SM を完全に占有するのに十分なワープを起動しないグラフィックシェーダの問題にもなりえます。
注:スレッドグループのサイズを小さくするには、実際には2つのアプローチがあります。
- アプローチ1:スレッドグループのサイズをN倍に下げ、同時にグリッドの起動次元をN倍にする。
- アプローチ2:N>=2個のスレッドの作業を1個のスレッドに統合する。これにより、マージされたN個のスレッド間でレジスタを介して共通データを共有したり、アトミック演算(HLSLのInterlockedMinなど)を用いて共有メモリではなくレジスタで削減を実行したりすることができます。さらに、このアプローチには、N個のマージされたスレッド間でスレッドグループの統一操作を自動的に償却する利点もあります。しかし、この方法によるレジスタの肥大化の可能性には注意する必要があります。
注:もし、あるワークロードの SM 占有率が、主にフルスクリーン・ピクセルシェーダとコンピュー トシェーダのどちらでレジスタカウントが制限されているかを知りたい場合は、次のようにしてください。
- スクラバーで追加し… “Program Ranges” を実行し、調査したいシェーダプログラムの範囲を見つけます。Program Range を右クリックし、Range Profiler を起動し、Pipeline Overview Summary の “SM Occupancy” 値を確認します。
- スクラバーの「Time(ms)」行をクリックして、Range内のいくつかのレンダーコールを選択します。タブを API Inspector に切り替え、ワークロードのサイクルのほとんどを占めるシェーダステージ(PS または CS)を選択し、シェーダ名の横にある「Stats」リンクをクリックします。
- 「Shaders」Nsightウィンドウが表示され(下図14参照)、「Regs」列にシェーダのハードウェアレジスタ数が表示されます。シェーダの統計情報が入力されるまで数秒待つ必要があることに注意してください。
- CUDA Occupancy Calculator グラフを使用して、このレジスタカウントに関連する Max Theoretical Occupancy を調べ、このシェーダの Range Profiler が報告する実際の 「SM Occupancy」 と比較します。
- もし、達成した占有率が最大占有率よりずっと低ければ、SMの占有率はスレッドごとのレジスタの量だけでなく、他の何かによって制限されていることが分かります。
あるシェーダに割り当てられるレジスタの総数を減らすには、DX シェーダのアセンブリを見て、シェーダの各ブランチで使用されるレジスタの数を調べればよいです。ハードウェアは、最もレジスタを必要とするブランチに対してレジスタを割り当てる必要があり、そのブランチをスキップするワープは、最適ではない SM 占有率で実行されます。
フルスクリーンパス(ピクセルまたはコンピュートシェーダ)の場合、この問題に対処する典型的な方法は、ピクセルを異なる領域に分類するプリパスを実行し、各領域に対して異なるシェーダの並べ替えを実行することです。
- コンピュートシェーダについては、このSIGGRAPH 2016のプレゼンテーションでは、シェーダの順列ごとにスレッドブロックの数を変えながら、画面上の異なるタイルに特殊なコンピュートシェーダを適用するためにDispatchIndirectコールを使用したソリューションが説明されています。
“Deferred Lighting in Uncharted 4” – Ramy El Garawany (Naughty Dog).
- ピクセルシェーダについては、異なる特殊化アプローチを使用することができます。フルスクリーンのステンシルバッファをプリパスで満たし、ピクセルを分類することができます。それから、ピクセルシェーダ実行の前に起こるステンシルテストに依存し(これは我々のドライバによって自動的に行われるべきです)、現在のシェーダの順列が触れていないピクセルを破棄するステンシルテストを使用することによって、複数の描画コールを効率的に実行することができます。このGDC 2013のプレゼンテーションでは、このアプローチでMSAA遅延レンダリングを最適化します。”The Rendering Technologies of Crysis 3″ – Tiago Sousa, Carsten Wenzel, Chris Raine (Crytek).
最後に、あるコンピュートシェーダのSM占有率制限をよりよく理解するために、我々のCUDA Occupancy Calculatorスプレッドシートを利用することができます。使用するには、GPU の CUDA Compute Capability とシェーダのリソース使用量(スレッドグループサイズ、Shader View からのレジスタ数、共有メモリサイズ(バイト))を記入するだけです。
アプローチ2:SM発行ストール待ち時間を減らす
SM占有率を上げる以外の方法でSM Throughput For Active Cyclesを上げるには、SM issue-stall cyclesの回数を減らすことです。これは、命令発行サイクル間のSMアクティブサイクルで、オペランドの1つがレディでない、または命令を実行する必要があるデータパス上のリソース競合が原因で、ワープ命令がストールしている間です。
PerfWorksのメトリクスsmsp__warp_cycles_per_issue_stall_{reason}は、ワープが{reason}で停止した命令イシュー間の平均サイクルを示しています。PerfWorksメトリックsmsp__warp_stall_{reason}_pctは、サイクルごとにその理由で停止したアクティブなワープの%です。これらのメトリックは、Range ProfilerのUser Metricsセクション、およびSM Overview Summaryセクションで、降順にソートされて公開されています。ワープが停止する理由としては、以下のようなものが考えられます。
- “smsp__warp_stall_long_scoreboard_pct” PerfWorks メトリクスは、L1TEX (local, global, surface, tex) オペレーションのスコアボード依存を待つためにストールしたアクティブワープのパーセンテージを示します。
- “smsp__warp_stall_barrier_pct” PerfWorks指標は、スレッドグループのバリアで兄弟ワープを待つためにストールしたアクティブワープのパーセンテージを示します。この場合、スレッドグループのサイズを下げるとパフォーマンスが向上する場合があります。これは、各スレッドが複数の入力要素を処理するようにすることで実現できる場合があります。
“sm__issue_active_per_active_cycle_sol_pct” が 80% より低く、 “smsp__warp_stall_long_scoreboard_pct” がワープストールの理由のトップなら、そのシェーダは TEX-latency limited であることが分かっているはずです。これは、失速サイクルのほとんどが、テクスチャフェッチ結果との依存関係 から来ていることを意味します。この場合は…
- シェーダのコンパイル時に反復回数がわかるループがある場合(ループ回数ごとに異なるシェーダの並べ替えを使用する場合もある)、HLSL の [unroll] ループ属性を使用して FXC にループを完全に展開させるようにしてみてください。
- シェーダが完全にアンロールできない動的ループ(たとえば、レイマーチ ングループ)を実行している場合は、テクスチャフェッチ命令をバッチして、TEX 依存のストールの数を減らしてください(HLSL レベルで、 独立したテクスチャフェッチを 2~4 のback-to-back命令のバッチに まとめることによって)。
- シェーダが与えられたテクスチャのピクセルごとにすべての MSAA サブサンプルを反復している場合、そのテクスチャの TEX 命令の 1 バッチで、すべてのサブサンプルを一緒にフェッチします。MSAA サブサンプルは VRAM 内で隣り合わせに保存されるため、一緒にフェッチすれば TEX ヒット率は最大になります。
- テクスチャの負荷が、ほとんどの場合、真になると予想される条件に基づいている場合(例えば、if (idx < maxidx) loadData(idx))、負荷を強制して座標をクランプすることを検討する(loadData(min(idx,maxidx-1)))。
- TEXキャッシュとL2キャッシュのヒット率を向上させることで、TEXレイテンシーを減少させてみてください。TEX および L2 ヒット率は、サンプリングパターンを微調整して隣接ピクセル/スレッドがより多くの隣接テクセルをフェッチするようにし、該当する場合はミップマップを使用し、さらにテクスチャのサイズを小さくしてよりコンパクトなテクスチャフォーマットを使用することによって向上させることが可能です。
- 実行されるTEX命令の数を減らしてみてください(おそらく、TEX命令述語としてコンパイルされる、テクスチャ命令ごとのブランチを使用します、例としてFXAA 3.11 HLSLを参照してください、例.”if(!doneN) lumaEndN = FxaaLuma(…);”).
トップSOLユニットがSMではない場合
どのユニットかを確認して,下記に従って対処を行います。
(1)トップSOLユニットが,TEX, L2, あるいは VRAMの場合
トップ SOL ユニットが SM ではなく、メモリサブシステム ユニット(TEX-L1、L2、および VRAM)の 1 つである場合、性能低下の根本原因は、GPUフレンドリーではないアクセスパターン(通常、ワープ内の隣接スレッドが遠く離れたメモリにアクセスする)により発生した TEX または L2 キャッシュのスラッシングである可能性があります。この場合、最上位制限ユニットは TEX または L2 であるかもしれませんが、根本的な原因は SM によって実行されるシェーダにある可能性があるため、最上位 SOL ユニットが SM の場合を使用して SM のパフォーマンスをトリアージ方法で決定する価値があります。
トップ SOL ユニットが VRAM であり、その SOL% 値が悪くない(60% 以上)場合、このワークロードは VRAM スループットが制限されており、別のパスでマージすることでフレームが高速化されるはずです。典型的な例は、ガンマ補正パスと他のポストプロセッシングパスをマージすることです。
(2)トップSOLユニットがCROPあるいはZROPの場合
CROP がトップ SOL ユニットである場合、より小さいレンダーターゲット形式(例:RGBA16F の代わりに R11G11B10F)を使用してみたり、Multiple Render Targets を使用している場合、レンダーターゲットの数を減らしてみたりすることができます。また、ピクセルシェーダでより積極的にピクセルをキルすることは価値があるかもしれません(たとえば、特定の透明効果では、不透明度が1%未満のピクセルを破棄する)。透明レンダリングを最適化するための可能な戦略については、「透明(または半透明)レンダリング」を参照してください。
ZROP が Top SOL ユニットである場合、より小さい深度フォーマット(例:シャドウマップ の D24X8 の代わりに D16、または D32S8 の代わりに D24S8)を使用し、さらに不透明オブジェクトを前から後ろへの順番に描いて、ZCULL(粗視化深度テスト)が ZROP とピクセルシェーダを起動する前に多くのピクセルが廃棄できるようにするとよいでしょう。
(3)トップSOLユニットがPDの場合
前述したように、PDは入力された頂点のインデックスを収集するために、インデックスバッファのロードを行います。PDがトップSOLユニットである場合、32ビットではなく16ビットのインデックスバッファを使用してみることができます。それでも PD の SOL%が増加しない場合は、頂点の再利用とローカリティのためにジオメトリを最適化することを試してみることができます。
(4)トップSOLユニットがVAFの場合
この場合、頂点シェーダーの入力アトリビュートの数を減らすと効果的です。
また、位置ストリームを他のアトリビュートから分離することは、z-only またはシャドウマップレンダリングに有効な場合があります。
頂点アトリビュートを減らす
前述した,P3 Methodでも出てきますが,頂点アトリビュートを減らすと高速になるケースがあります。プラットフォームによってはドキュメントに「XXX以下にすると速くなります」みたいな記述が載っていたり,実際にどのぐらい数でどういう結果が得られたのかをグラフ化してくれていたりします。
ここで重要なのは,なるべくパッキングして数を減らすということです。例えば,下記のようにします。
//変更前
struct VSOutput
{
float4 Position : SV_POSITION;
float2 TexCoord0 : TEXCOORD0;
float2 TexCoord1 : TEXCOORD1;
float2 TexCoord2 : TEXCOORD2;
float2 TexCoord3 : TEXCOORD3;
};
// 変更後
struct VSOutput
{
float4 Position : SV_POSITION;
float4 TexCoord01 : TEXCOORD01; // TEXCOORD0 and TEXCOORD1
float4 TexCoord23 : TEXCOORD23; // TEXCOORD2 and TEXCOORD3
};
データ容量は変わっていないですが,これだけで高速化します。過去の経験ではモデル描画のシェーダに対して適用したところ全体で1[ms]程度の高速化が出来た記憶があります。とにかくピクセルシェーダで使っていないアトリビュートがあったら,削る。削れないときはまとめることによって数を減らすということを考えると良いです。
サイズを減らす
計算等に利用するテクスチャサイズを減らすことによってテクスチャキャッシュに載りやすくし,高速化するテクニックがあります。例えば,Deinterleaved RenderingやCheckerboard Renderingといったものがこれに当たります。特に縮小バッファにして描画品質があまりにも落ちすぎるのを避けたい場合などに使うと良いです。
テクスチャフェッチをバッチする
NVIDIAのBlog記事にもありますが,レイマーチループのような動的ループ内でテクスチャフェッチをバッチかすることによってTEXのレイテンシーを隠すことができます。
典型的なSSRレイマーチングループのHLSLは次のような感じです。
float MinHitT = 1.0;
float RayT = Jitter * Step + Step;
[loop] for ( int i = 0; i < NumSteps; i++ )
{
float3 RayUVZ = RayStartUVZ + RaySpanUVZ * RayT;
float SampleDepth = Texture.SampleLevel( Sampler, RayUVZ.xy, GetMipLevel(i) ).r;
float HitT = GetRayHitT(RayT, RayUVZ, SampleDepth, Tolerance);
[branch] if (HitT < 1.0)
{
MinHitT = HitT;
break;
}
RayT += Step;
}
ループ内で,隣り合わせで2回テクスチャフェッチするように処理を置き換えます。
float MinHitT = 1.0;
float RayT = Jitter * Step + Step;
[loop] for ( int i = 0; i < NumSteps; i += 2 )
{
float RayT_0 = RayT;
float RayT_1 = RayT + Step;
float3 RayUVZ_0 = RayStartUVZ + RaySpanUVZ * RayT_0;
float3 RayUVZ_1 = RayStartUVZ + RaySpanUVZ * RayT_1;
// batch texture instructions to better hide their latencies
float SampleDepth_0 = Texture.SampleLevel( Sampler, RayUVZ_0.xy, GetMipLevel(i+0) ).r;
float SampleDepth_1 = Texture.SampleLevel( Sampler, RayUVZ_1.xy, GetMipLevel(i+1) ).r;
float HitT_0 = GetRayHitT(RayT_0, RayUVZ_0, SampleDepth_0, Tolerance);
float HitT_1 = GetRayHitT(RayT_1, RayUVZ_1, SampleDepth_1, Tolerance);
[branch] if (HitT_0 < 1.0 || HitT_1 < 1.0)
{
MinHitT = min(HitT_0, HitT_1);
break;
}
RayT += Step * 2.0;
}
ブログ記事では,GTX1080で0.54[ms]だったものが0.42[ms]に高速化したと記載されています。また2回ではなく4回にすることで0.54[ms]から0.33[ms]になるという記述もあります。レイマーチ処理は基本的に重くなりやすいので,アルゴリズム的に最適化出来ない場合は,こうしたバッチ化により高速化するとよさそうです。