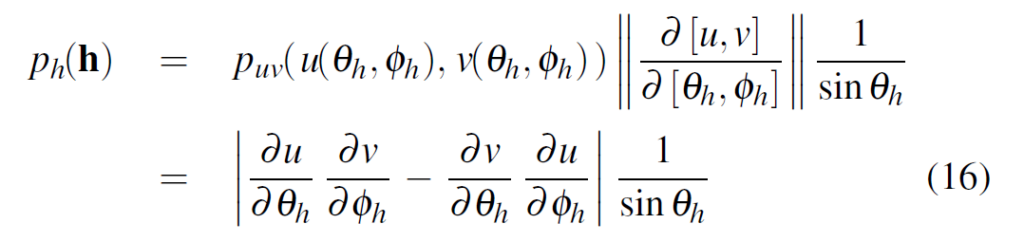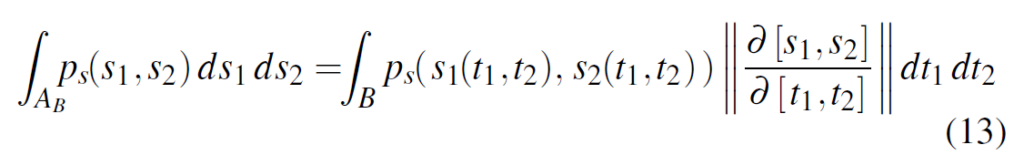こんねねー。Pocolです。
ハーフベクトルのヤコビアンが良く分かりません。
shikihuikuさんの記事を見れば済むことなんですが，せっかくなのでメモっておこうと思います。

2変数関数のヤコビアン

ヤコビアンは，大学の教養の数学（解析学）で勉強するかと思います。用途としては変数変換に用います。
もし勉強したことが無い人がいたら，第11回プログラマの為の数学勉強会@ワークスアプリケーションズを参照してください。
半球状のライティングをこれから考えていくため，角度\(\theta\)と角度\(\phi\)の2変数によって反射方向を表現することを考えます。

積分変数の変換は次のような内容でした。

2変数関数のヤコビアンは上記のように表現できました。

確率密度関数がハーフベクトルの場合について

最近の物理ベースレンダリングで使用するGGXあるいは古典的なシェーディング用いられることがPhongなどのBRDFはハーフベクトルを用いて定義されます。そこで，BRDFと比例関係であることが望ましい確率密度関数(PDF)もハーフベクトルの関数として表すことができれば，BRDFに近いPDFを作ることができるのではないでしょうか？
そこで，ハーフベクトルを用いてPDFを表現することを考えます。これには変数変換が必要です。つまり，変換するためにヤコビアンが出てきます。
正規化Lambertでも記述しているように，変換を行うとsin項が出てきます。ここで，[Walter 2005]のSection 3.2に書いてある通りに議論を進めます。sin項が出てくるので，計算結果が1になるようにするため，これをキャンセルするように追加で(1/sin項)を加えます。すると次のようになります。

反射ベクトルとハーフベクトルの関係は極座標系を用いることで表すことができます。ここで，この座標を区別するために\(\star\)を付けて表すことにします。つまり\({\theta_o}^{\star} = 2{\theta_h}^{\star}\)と，\({\phi_o}^{\star} = {\phi_h}^{\star}\)とします。
これを，[Walter 2005]の式(15)に代入して整理すると次のようになります。

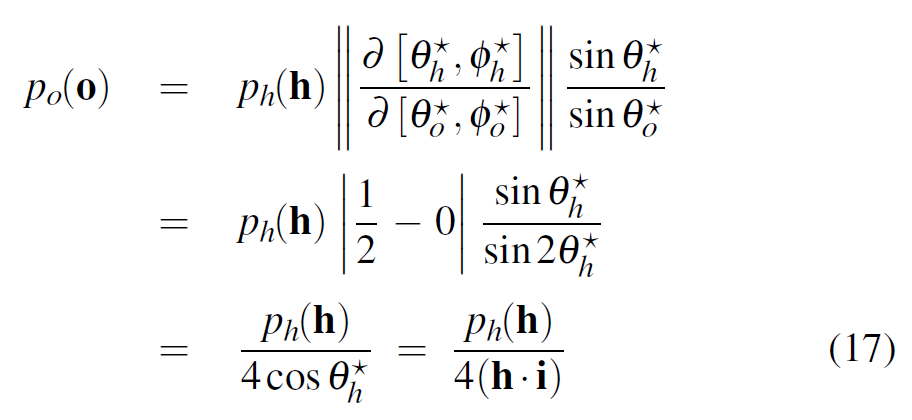
上式は\(\star\)が無くなった式で表されています。
ここで，[Walter 2005]の式(13)と見比べてみます。

ヤコビアンに対応する部分が，
\begin{eqnarray}
\frac{1}{4({\mathbf h} \cdot {\mathbf i})}
\end{eqnarray}
となることが分かります。

よって，Frostbite[Lagarde ]の資料にもあるように，ヤコビアンが 1/(4 * dot(V, H)) で求められることに一致します。

…というわけで，ハーフベクトルのヤコビアンの話でした。

参考資料

• [Walter 2005] Bruce Walter, “Notes on the Ward BRDF”, Technical Report PCG-05-06, 2005.
• [Lagarde 2014]Sebastien Lagarde, Charles de Rousiers, “Moving Frostbite to Physically Based Rendering 3.0”, SIGGRAPH 2014.