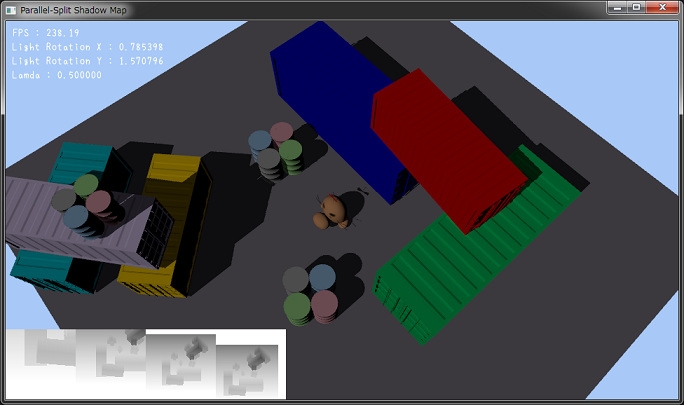
平行分割シャドウマップ
★ 1.はじめに…
カスケード系は何一つ実装したことがなかったので,平行分割シャドウマップ(Parallel Split Shadow Map)を実装してみました。
カスケードシャドウマップはマニュアルで分割距離を調整するものもあったりするのですが,
マニュアル調整だとめんどっちいので,平行分割シャドウマップを取り上げてみます。


★ 2.カスケードシャドウマップについて
大規模なシーンでシャドウマップを適用したことがある方なら,わかると思うのですが1枚のシャドウマップだとかなりジャギジャギになって絵的に厳しい状況になります。
そこで近年よく使われているのは,カスケードシャドウマップと呼ばれる下記のように錐台を複数個に分割して,分割した各錐台に対してシャドウマップを適用してシーンの影を描画する方法です。最近発売されているゲームであれば大体実装されてるかと思います
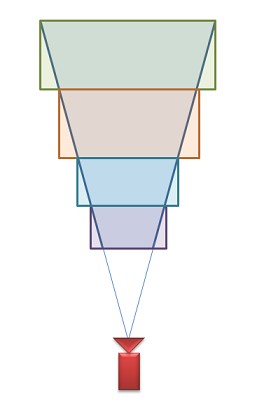
カスケードシャドウマップでは,各錐台の大きさによってシャドウマップの品質が変わってくるので大事になってくるのは,錐台の分割方法です。今回取り上げる,平行分割シャドウマップは錐台の分割位置を実用的分割スキーム(Practical Split-Scheme)という方法によって求めます。
そこで近年よく使われているのは,カスケードシャドウマップと呼ばれる下記のように錐台を複数個に分割して,分割した各錐台に対してシャドウマップを適用してシーンの影を描画する方法です。最近発売されているゲームであれば大体実装されてるかと思います

カスケードシャドウマップでは,各錐台の大きさによってシャドウマップの品質が変わってくるので大事になってくるのは,錐台の分割方法です。今回取り上げる,平行分割シャドウマップは錐台の分割位置を実用的分割スキーム(Practical Split-Scheme)という方法によって求めます。
★ 3.シャドウマップのエイリアシング
平行分割シャドウマップの説明に入る前に,シャドウマップのエイリアス問題について触れておきます。
シャドウマップのエイリアシングエラーは下記の式で定義されます。

一応式の導出についても説明しておきます。
シャドウマップのエイリアシングエラーですが直観的には,シャドウマップの1ピクセルと対応するカメラから見たときの1ピクセルの大きさが,カメラのピクセルよりも小さければエラーは発生せず,カメラのピクセルに収まらず大きくなった場合にエラーが出そうな気がしますので,今知りたいのは,カメラから見たときのピクセルとシャドウマップのピクセルの関係がわかれば良いです。
そこで,カメラから見たときのピクセルとシャドウマップのピクセルの比率に着目して式を立ててみます。
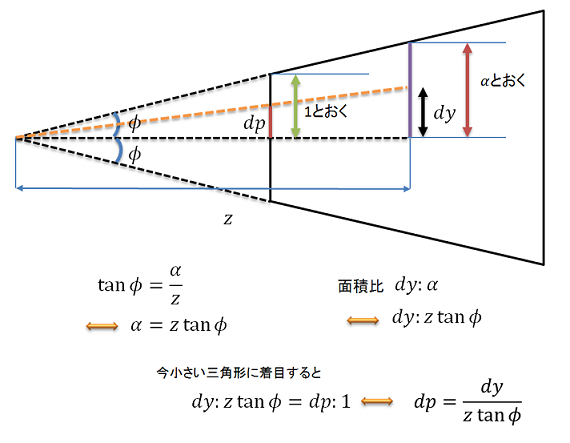
上図のように三角形の相似に着目して\(dp\)の大きさを求めると\(dp = \frac{dy}{ztan{\phi}}\)となります。
\(dp\)が\(dy\)を使って表すことができます。 次に,\(dy\)と\(dz\)の関係について考えて式を立てます。

上記の計算で\(dy\)が求まったので,\(dp\)の式に代入して式を解いてみます。
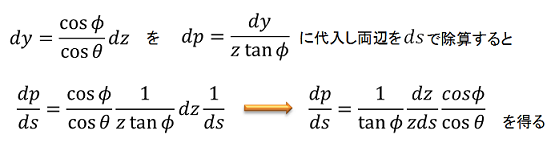
上記のように計算していくことで,シャドウマップのエイリアシングエラーの式が求まります。
このエイリアシングエラーの式ですが,透視エイリアシング\(\frac{dp}{ds}\)と射影エイリアシング\(\frac{cos{\phi}}{cos{\theta}}\)に2つの分解して考えます。
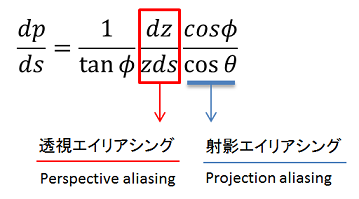
射影エイリアシングは,局所的なジオメトリの詳細に依存するので解析が難しいです。
そのため平行分割シャドウマップでは透視エイリアシングのエラーを低減のみに焦点を当てているようです。
理論的に最適な透視エイリアシングの分配は,深度範囲全体で\(\frac{dz}{zds}\)の値が一定であること…とGPU Gems3に書いてあります。この一文自分にはよくわからないですが,シャドウマップを使う側からしたら,各ピクセルごとに式が違うと面倒なのでシャドウマップ全体に対して一定な値の方がコーディングするときには楽そうな気がします。そんなわけで,\(\frac{dz}{zds}\)の値が一定であることが理論的に最適な透視エリアシングであるということにしておきましょう。\(\frac{dz}{zds}\)が一定であることを式に表して解いてみます。定数を\(\rho\)として式を立てると…
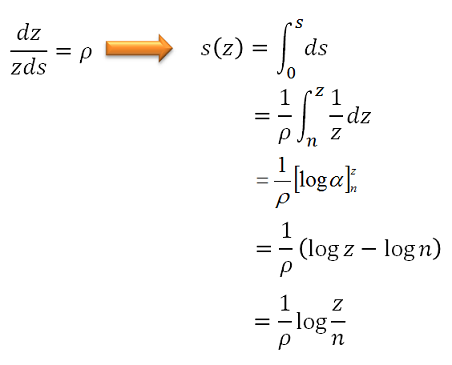
計算で解くことができました。理論的に最適な値は\(\frac{1}{ρ}log\frac{z}{n}\)だそうです。
シャドウマップのエイリアシングエラーは下記の式で定義されます。

一応式の導出についても説明しておきます。
シャドウマップのエイリアシングエラーですが直観的には,シャドウマップの1ピクセルと対応するカメラから見たときの1ピクセルの大きさが,カメラのピクセルよりも小さければエラーは発生せず,カメラのピクセルに収まらず大きくなった場合にエラーが出そうな気がしますので,今知りたいのは,カメラから見たときのピクセルとシャドウマップのピクセルの関係がわかれば良いです。
そこで,カメラから見たときのピクセルとシャドウマップのピクセルの比率に着目して式を立ててみます。

上図のように三角形の相似に着目して\(dp\)の大きさを求めると\(dp = \frac{dy}{ztan{\phi}}\)となります。
\(dp\)が\(dy\)を使って表すことができます。 次に,\(dy\)と\(dz\)の関係について考えて式を立てます。

上記の計算で\(dy\)が求まったので,\(dp\)の式に代入して式を解いてみます。
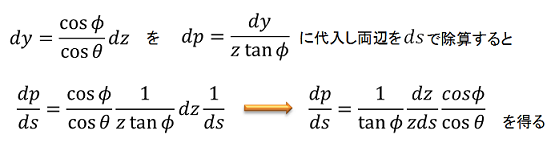
上記のように計算していくことで,シャドウマップのエイリアシングエラーの式が求まります。
このエイリアシングエラーの式ですが,透視エイリアシング\(\frac{dp}{ds}\)と射影エイリアシング\(\frac{cos{\phi}}{cos{\theta}}\)に2つの分解して考えます。

射影エイリアシングは,局所的なジオメトリの詳細に依存するので解析が難しいです。
そのため平行分割シャドウマップでは透視エイリアシングのエラーを低減のみに焦点を当てているようです。
理論的に最適な透視エイリアシングの分配は,深度範囲全体で\(\frac{dz}{zds}\)の値が一定であること…とGPU Gems3に書いてあります。この一文自分にはよくわからないですが,シャドウマップを使う側からしたら,各ピクセルごとに式が違うと面倒なのでシャドウマップ全体に対して一定な値の方がコーディングするときには楽そうな気がします。そんなわけで,\(\frac{dz}{zds}\)の値が一定であることが理論的に最適な透視エリアシングであるということにしておきましょう。\(\frac{dz}{zds}\)が一定であることを式に表して解いてみます。定数を\(\rho\)として式を立てると…
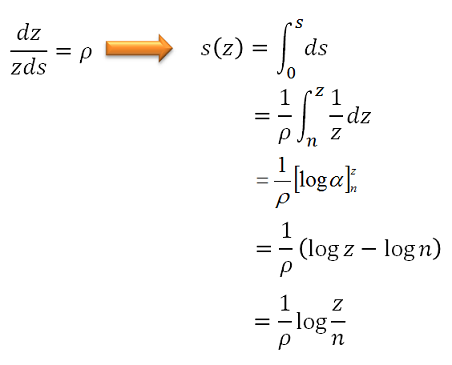
計算で解くことができました。理論的に最適な値は\(\frac{1}{ρ}log\frac{z}{n}\)だそうです。
★ 4.平行分割シャドウマップ
さて,ようやく平行分割シャドウマップの説明に入ります。
平行分割シャドウマップでは,下記で与えられる実用的分割スキームによる方程式で分割位置を決定します。
\[ C_i = {\lambda}C^{log}_i+(1-{\lambda})C^{uni}_o \hspace{1.5cm}(0<{\lambda}<1) \] 上記の式に沿って分割位置をコーディングしてみます。
さて,このままでも問題なのですが,この分割に用いているのはlamdaとnearClipとfarClipです。GPU Gems3によると
あとは上記の実用分割スキームによって決定された距離を用いて,各錐台を構築します。この処理は,ComputeShadowMatrixPSSM()メソッド内の下記処理で行っています。
まず,AdjustClipPlanes()メソッドですが,これはシャドウマップ上に無駄な空間ができないように,ニア平面までの距離とファー平面までの距離をタイトになるように設定しています。具体的な処理はソースコードを参照してください。つづいてカスケード処理に入るのですが,今回は4段のカスケードになっています。今回の実装では,まず通常のシャドウマップ行列を求めておき,この結果を各錐台で部分クリッピングするような行列を求めて,乗算することで各錐台ごとのシャドウマップ行列を求めています。
あとはこうして求まった平行分割シャドウマップ行列を用いて,シャドウマップの描画を行っていきます。
今回のサンプルではテクスチャ配列を用いずに真面目に4回Drawするという方法をとりました。…というのも,ジオメトリシェーダを使って実装もしてみたのですが,ジオメトリシェーダ使うと遅いということが色々と試してみて分かったので,ジオメトリシェーダは使わないことにしました。そのため,シャドウマップを描画するシェーダは下記のようにものすごく単純になります。
頂点シェーダのコードは下記のような感じになります。
平行分割シャドウマップでは,下記で与えられる実用的分割スキームによる方程式で分割位置を決定します。
\[ C_i = {\lambda}C^{log}_i+(1-{\lambda})C^{uni}_o \hspace{1.5cm}(0<{\lambda}<1) \] 上記の式に沿って分割位置をコーディングしてみます。
01098: void SampleApp::ComputeSplitPositions
01099: (
01100: s32 splitCount,
01101: f32 lamda,
01102: f32 nearClip,
01103: f32 farClip,
01104: f32* positions
01105: )
01106: {
01107: // 分割数が1の場合は,普通のシャドウマップと同じ.
01108: if ( splitCount == 1 )
01109: {
01110: positions[0] = nearClip;
01111: positions[1] = farClip;
01112: return;
01113: }
01114:
01115: f32 inv_m = 1.0f / f32( splitCount ); // splitCountがゼロでないことは保証済み.
01116:
01117: // ゼロ除算対策.
01118: assert( nearClip != 0.0f );
01119:
01120: // (f/n)を計算.
01121: f32 f_div_n = farClip / nearClip;
01122:
01123: // (f-n)を計算.
01124: f32 f_sub_n = farClip - nearClip;
01125:
01126: // 実用分割スキームを適用.
01127: // ※ GPU Gems 3, Chapter 10. Parallel-Split Shadow Maps on Programmable GPUs.
01128: // http://http.developer.nvidia.com/GPUGems3/gpugems3_ch10.html を参照.
01129: for( s32 i=1; i<splitCount + 1; ++i )
01130: {
01131: // 対数分割スキームで計算.
01132: f32 Ci_log = nearClip * powf( f_div_n, inv_m * i );
01133:
01134: // 一様分割スキームで計算.
01135: f32 Ci_uni = nearClip + f_sub_n * i * inv_m;
01136:
01137: // 上記の2つの演算結果を線形補間する.
01138: positions[i] = lamda * Ci_log + Ci_uni * ( 1.0f - lamda );
01139: }
01140:
01141: // 最初は, ニア平面までの距離を設定.
01142: positions[ 0 ] = nearClip;
01143:
01144: // 最後は, ファー平面までの距離を設定.
01145: positions[ splitCount ] = farClip;
01146: }
そのまま式を打ち込んだだけなので問題ないでしょう。さて,このままでも問題なのですが,この分割に用いているのはlamdaとnearClipとfarClipです。GPU Gems3によると
he weight λ adjusts the split positions according to practical requirements of the application. λ = 0.5 is the default setting in our current implementation.とあり,\(\lambda\)は0.5使ったぜ!というような記述があります。実際に色々と試した結果,ライトと視線ベクトルが平行に近づくような状況がない場合は対数分割スキームよりで値を設定すると綺麗にでます。経験則だと70%~80%ぐらいです。しかし,ライトとカメラが平行に近づくような場合だと対数分割よりに設定しておくと結構汚くなるケースがあります。その場合は大人しくGPU Gems3に書いてあるように\({\lambda}=0.5\)ぐらいに設定しておくと綺麗に出るようです。各自が実装されているゲームやアプリケーションによってカメラの挙動は異なると思うので,実装されているものに合わせて\({\lambda}\)の値を設定した方がよいと思います。
あとは上記の実用分割スキームによって決定された距離を用いて,各錐台を構築します。この処理は,ComputeShadowMatrixPSSM()メソッド内の下記処理で行っています。
00950: // カメラ位置を算出.
00951: asdx::Vector3 pos = m_Camera.GetCamera().GetPosition();
00952:
00953: // カメラの方向ベクトルを算出.
00954: asdx::Vector3 dir = m_Camera.GetCamera().GetTarget() - pos;
00955: dir.Normalize();
00956:
00957: // クリップ平面の距離を調整.
00958: AdjustClipPlanes( casterBox, pos, dir, nearClip, farClip );
00959:
00960: // 平行分割処理.
00961: f32 splitPositions[ MAX_CASCADE + 1 ];
00962: ComputeSplitPositions( 4, m_Lamda, nearClip, farClip, splitPositions );
00963:
00964: // カスケード処理.
00965: for( u32 i=0; i<MAX_CASCADE; ++i )
00966: {
00967: // ライトのビュー射影行列.
00968: m_ShadowMatrix[i] = m_LightView * m_LightProj;
00969:
00970: // 分割した視錘台の8角をもとめて,ライトのビュー射影空間でAABBを求める.
00971: asdx::BoundingBox box = CalculateFrustum(
00972: splitPositions[ i + 0 ],
00973: splitPositions[ i + 1 ],
00974: m_ShadowMatrix[ i ] );
00975:
00976: // クロップ行列を求める.
00977: asdx::Matrix crop = CreateCropMatrix( box );
00978:
00979: // シャドウマップ行列と分割位置を設定.
00980: m_ShadowMatrix[i] = m_ShadowMatrix[i] * crop;
00981: m_SplitPos[i] = splitPositions[ i + 1 ];
00982: }
上記の処理を少し補足していきます。まず,AdjustClipPlanes()メソッドですが,これはシャドウマップ上に無駄な空間ができないように,ニア平面までの距離とファー平面までの距離をタイトになるように設定しています。具体的な処理はソースコードを参照してください。つづいてカスケード処理に入るのですが,今回は4段のカスケードになっています。今回の実装では,まず通常のシャドウマップ行列を求めておき,この結果を各錐台で部分クリッピングするような行列を求めて,乗算することで各錐台ごとのシャドウマップ行列を求めています。
あとはこうして求まった平行分割シャドウマップ行列を用いて,シャドウマップの描画を行っていきます。
今回のサンプルではテクスチャ配列を用いずに真面目に4回Drawするという方法をとりました。…というのも,ジオメトリシェーダを使って実装もしてみたのですが,ジオメトリシェーダ使うと遅いということが色々と試してみて分かったので,ジオメトリシェーダは使わないことにしました。そのため,シャドウマップを描画するシェーダは下記のようにものすごく単純になります。
00007: ///////////////////////////////////////////////////////////////////////////////////////////
00008: // VSInput structure
00009: ///////////////////////////////////////////////////////////////////////////////////////////
00010: struct VSInput
00011: {
00012: float3 Position : POSITION; //!< 位置座標です(ローカル座標系).
00013: float3 Normal : NORMAL; //!< 法線ベクトルです(ローカル座標系).
00014: float3 Tangent : TANGENT; //!< 接ベクトルです(ローカル座標系).
00015: float2 TexCoord : TEXCOORD; //!< テクスチャ座標です.
00016: };
00017:
00018: ///////////////////////////////////////////////////////////////////////////////////////////
00019: // VSOutput structure
00020: ///////////////////////////////////////////////////////////////////////////////////////////
00021: struct VSOutput
00022: {
00023: float4 Position : SV_POSITION; //!< 位置座標です(ビュー射影空間).
00024: };
00025:
00026: ///////////////////////////////////////////////////////////////////////////////////////////
00027: // CBMatrix buffer
00028: ///////////////////////////////////////////////////////////////////////////////////////////
00029: cbuffer CBMatrix : register( b1 )
00030: {
00031: float4x4 World : packoffset( c0 ); //!< ワールド行列です.
00032: float4x4 ViewProj : packoffset( c4 ); //!< ビュー射影行列です.
00033: };
00034:
00035:
00036: //-----------------------------------------------------------------------------------------
00037: //! @brief 頂点シェーダメインエントリーポイントです.
00038: //-----------------------------------------------------------------------------------------
00039: VSOutput VSFunc( VSInput input )
00040: {
00041: VSOutput output = (VSOutput)0;
00042:
00043: float4 localPos = float4( input.Position, 1.0f );
00044: float4 worldPos = mul( World, localPos );
00045: float4 viewProjPos = mul( ViewProj, worldPos );
00046:
00047: output.Position = viewProjPos;
00048:
00049: return output;
00050: }
00051:
00052: /* この頂点シェーダに対応するピクセルシェーダはありません./*
シャドウを描画する際は,実用分割スキームで求めた分割距離の範囲内に,描画するオブジェクトが入っているかどうかを判定して,適切な平行分割シャドウマップ行列を用いて描画すれば良いです。頂点シェーダのコードは下記のような感じになります。
00007: ///////////////////////////////////////////////////////////////////////////////////////////
00008: // VSInput structure
00009: ///////////////////////////////////////////////////////////////////////////////////////////
00010: struct VSInput
00011: {
00012: float3 Position : POSITION; //!< 位置座標です(ローカル座標系).
00013: float3 Normal : NORMAL; //!< 法線ベクトルです(ローカル座標系).
00014: float3 Tangent : TANGENT; //!< 接ベクトルです(ローカル座標系).
00015: float2 TexCoord : TEXCOORD; //!< テクスチャ座標です.
00016: };
00017:
00018: ///////////////////////////////////////////////////////////////////////////////////////////
00019: // VSOutput structure
00020: ///////////////////////////////////////////////////////////////////////////////////////////
00021: struct VSOutput
00022: {
00023: float4 Position : SV_POSITION; //!< ビュー射影空間の位置座標です.
00024: float4 WorldPos : WORLD_POSITION; //!< ワールド空間の位置座標です.
00025: float3 Normal : NORMAL; //!< 法線ベクトルです.
00026: float2 TexCoord : TEXCOORD0; //!< テクスチャ座標です.
00027: float3 LightDir : LIGHT_DIRECTION; //!< ライトの方向ベクトルです.
00028: float3 CameraPos : CAMERA_POSITION; //!< カメラ位置です.
00029: float4 SplitPos : SPLIT_POSITION; //!< 分割距離です.
00030: float4 SdwCoord[4] : SHADOW_COORD; //!< シャドウ座標です.
00031: };
00032:
00033: ///////////////////////////////////////////////////////////////////////////////////////////
00034: // CBMatrix buffer
00035: ///////////////////////////////////////////////////////////////////////////////////////////
00036: cbuffer CBMatrix : register( b1 )
00037: {
00038: float4x4 World : packoffset( c0 ); //!< ワールド行列です.
00039: float4x4 View : packoffset( c4 ); //!< ビュー行列です.
00040: float4x4 Proj : packoffset( c8 ); //!< 射影行列です.
00041: float4 CameraPos : packoffset( c12 ); //!< カメラ位置です.
00042: float4 LightDir : packoffset( c13 ); //!< ライト位置です.
00043: float4 SplitPos : packoffset( c14 ); //!< 分割距離です.
00044: float4x4 Shadow0 : packoffset( c15 ); //!< シャドウマップ行列0.
00045: float4x4 Shadow1 : packoffset( c19 ); //!< シャドウマップ行列1.
00046: float4x4 Shadow2 : packoffset( c23 ); //!< シャドウマップ行列2.
00047: float4x4 Shadow3 : packoffset( c27 ); //!< シャドウマップ行列3.
00048: };
00049:
00050:
00051: //-----------------------------------------------------------------------------------------
00052: //! @brief 頂点シェーダメインエントリーポイント.
00053: //-----------------------------------------------------------------------------------------
00054: VSOutput VSFunc( VSInput input )
00055: {
00056: VSOutput output = (VSOutput)0;
00057:
00058: float4 localPos = float4( input.Position, 1.0f );
00059: float4 worldPos = mul( World, localPos );
00060: float4 viewPos = mul( View, worldPos );
00061: float4 projPos = mul( Proj, viewPos );
00062:
00063: output.Position = projPos;
00064: output.WorldPos = worldPos;
00065: output.LightDir = -LightDir.xyz;
00066:
00067: output.Normal = input.Normal;
00068: output.TexCoord = input.TexCoord;
00069:
00070: output.CameraPos = CameraPos.xyz;
00071:
00072: // カスケードシャドウマップ用.
00073: output.SplitPos = SplitPos;
00074: output.SdwCoord[0] = mul( Shadow0, worldPos );
00075: output.SdwCoord[1] = mul( Shadow1, worldPos );
00076: output.SdwCoord[2] = mul( Shadow2, worldPos );
00077: output.SdwCoord[3] = mul( Shadow3, worldPos );
00078:
00079: return output;
00080: }
ピクセルシェーダの処理は下記のようになります。
00099: //------------------------------------------------------------------------------------------------
00100: //! @brief ピクセルシェーダのエントリーポイントです.
00101: //------------------------------------------------------------------------------------------------
00102: PSOutput PSFunc( VSOutput input )
00103: {
00104: PSOutput output = (PSOutput)0;
00105:
00106: // ディフューズマップをフェッチ.
00107: float4 mapKd = DiffuseMap.Sample( DiffuseSmp, input.TexCoord );
00108:
00109: // アルファテスト.
00110: clip( ( mapKd.a < 0.125f ) ? -1.0f : 1.0f );
00111:
00112: // スペキュラーマップをフェッチ.
00113: float4 mapKs = SpecularMap.Sample( SpecularSmp, input.TexCoord );
00114:
00115: float sdwThreshold = 1.0f; // シャドウにするかどうかの閾値です.
00116: float sdwBias = 0.01f; // シャドウバイアスです.
00117: float sdwColor = 0.1f; // シャドウのカラーです.
00118:
00119: // 各ピクセル位置までの距離.
00120: float dist = input.Position.w; // ビュー空間でのZ座標.
00121:
00122: //int index = 0;
00123: if ( dist < input.SplitPos.x )
00124: {
00125: //index = 0;
00126: float2 coord = input.SdwCoord[0].xy / input.SdwCoord[0].w;
00127: float depth = input.SdwCoord[0].z / input.SdwCoord[0].w;
00128: sdwThreshold = ShadowMap0.SampleCmpLevelZero( ShadowSmp, coord, depth - sdwBias );
00129: sdwThreshold = saturate( sdwThreshold + sdwColor );
00130: }
00131: else if ( dist < input.SplitPos.y )
00132: {
00133: //index = 1;
00134: float2 coord = input.SdwCoord[1].xy / input.SdwCoord[1].w;
00135: float depth = input.SdwCoord[1].z / input.SdwCoord[1].w;
00136: sdwThreshold = ShadowMap1.SampleCmpLevelZero( ShadowSmp, coord, depth - sdwBias );
00137: sdwThreshold = saturate( sdwThreshold + sdwColor );
00138: }
00139: else if ( dist < input.SplitPos.z )
00140: {
00141: //index = 2;
00142: float2 coord = input.SdwCoord[2].xy / input.SdwCoord[2].w;
00143: float depth = input.SdwCoord[2].z / input.SdwCoord[2].w;
00144: sdwThreshold = ShadowMap2.SampleCmpLevelZero( ShadowSmp, coord, depth - sdwBias );
00145: sdwThreshold = saturate( sdwThreshold + sdwColor );
00146: }
00147: else
00148: {
00149: //index = 3;
00150: float2 coord = input.SdwCoord[3].xy / input.SdwCoord[3].w;
00151: float depth = input.SdwCoord[3].z / input.SdwCoord[3].w;
00152: sdwThreshold = ShadowMap3.SampleCmpLevelZero( ShadowSmp, coord, depth - sdwBias );
00153: sdwThreshold = saturate( sdwThreshold + sdwColor );
00154: }
00155:
00156: // スペキュラーマップをフェッチ.
00157: float4 spe = SpecularMap.Sample( SpecularSmp, input.TexCoord );
00158: {
00159: float3 N = normalize( input.Normal );
00160: float3 V = normalize( input.WorldPos.xyz - input.CameraPos );
00161: float3 L = normalize( input.LightDir );
00162:
00163: float3 diffuse = NormalizedLambert( Diffuse * mapKd.rgb, L, N );
00164: float3 specular = NormalizedPhong( Specular * mapKs.rgb, Power, V, N, L );
00166: output.Color.rgb = ( diffuse.rgb + specular.rgb ) * sdwThreshold;
00179: output.Color.a = Alpha;
00180: }
00181:
00182: return output;
00183: }
★ 5.おわりに
結構実装的に怪しい箇所も多々ありますが,一応平行分割シャドウマップをやってみました。
ライト空間透視シャドウマップ等のシャドウマップ技法と組み合わせて使うこともできるので,ガッツがある方は実装してみてください。
ライト空間透視シャドウマップ等のシャドウマップ技法と組み合わせて使うこともできるので,ガッツがある方は実装してみてください。
★ Download
本ソースコードおよびプログラムはMIT Licenseに準じます。
プログラムの作成にはMicrosoft Visual Studio 2012 Express Editionを用いています。
プログラムの作成にはMicrosoft Visual Studio 2012 Express Editionを用いています。
