
正規化Phong
★ 1.はじめに…
今回は,Phongを正規化してみます。


★ 2.Phongのおさらい
Phongモデルは,光沢のあるプラスティックなどの鏡面反射の計算によく使われるそうです。

フォンさんは何をやったかというと,視線が物体で跳ね返ったときの反射ベクトルRを求めて,反射ベクトルとライトベクトルLと近ければ強い光に,RとLが離れていれば弱い光になるように定式化したそうです。
Phongモデルの鏡面反射のBRDFは以下のようになります。
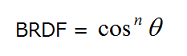

フォンさんは何をやったかというと,視線が物体で跳ね返ったときの反射ベクトルRを求めて,反射ベクトルとライトベクトルLと近ければ強い光に,RとLが離れていれば弱い光になるように定式化したそうです。
Phongモデルの鏡面反射のBRDFは以下のようになります。
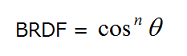
★ 3. 正規化Phong
Phongモデルも物理的な法則に従ったライティングモデルではないのですが,Half-Lambertの時と同様に一応エネルギー保存を考えていきます。
まず,積分式を計算していきます。普通は0~2πと0~πで積分するのですが,今回のPhongのBRDFは(cosθ)のn乗で,cosθのθの値は(π/2)を超えると,マイナスの値になってしまうので,ライティングには影響がありません。
そこで,積分の区間を0~(π/2)に替えて積分計算を行っていきます。
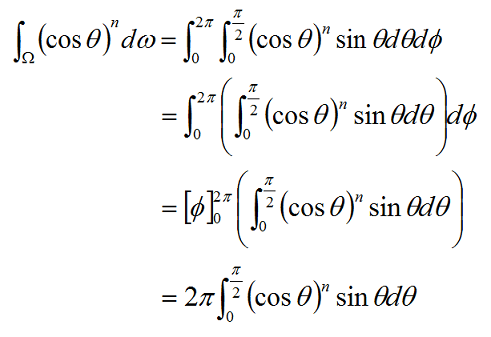
ここで,積分計算に詰まりました。
この式の変形結果を見るとcosθとsinθで対称性があり,これ以上式変形ができないという状況なので,部分積分法を適用します。
この辺りがわからない人は高校数学の数Ⅲあたりを復習してください(数Ⅱ・Bまでしか習ったことねぇよ!…という人は知らないっすw)。
さてさて,部分積分法を適用すると下記のようになります。

上記を見るとわかるのですが,部分積分を解くと途中で同じ式がまた出てきてしまうので,漸化式を解いています。
この漸化式が割と単純な式となり解くことができます。正規化係数は解いた結果の逆数ですから,(n+1)/2πが正規化係数となります。
まず,積分式を計算していきます。普通は0~2πと0~πで積分するのですが,今回のPhongのBRDFは(cosθ)のn乗で,cosθのθの値は(π/2)を超えると,マイナスの値になってしまうので,ライティングには影響がありません。
そこで,積分の区間を0~(π/2)に替えて積分計算を行っていきます。
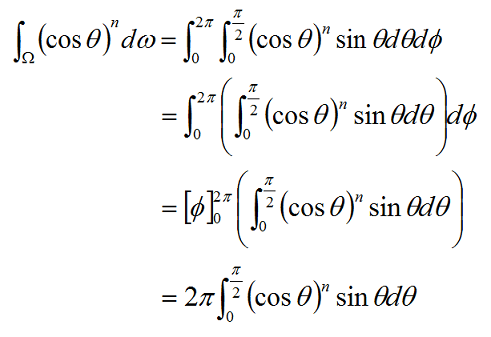
ここで,積分計算に詰まりました。
この式の変形結果を見るとcosθとsinθで対称性があり,これ以上式変形ができないという状況なので,部分積分法を適用します。
この辺りがわからない人は高校数学の数Ⅲあたりを復習してください(数Ⅱ・Bまでしか習ったことねぇよ!…という人は知らないっすw)。
さてさて,部分積分法を適用すると下記のようになります。

上記を見るとわかるのですが,部分積分を解くと途中で同じ式がまた出てきてしまうので,漸化式を解いています。
この漸化式が割と単純な式となり解くことができます。正規化係数は解いた結果の逆数ですから,(n+1)/2πが正規化係数となります。
★ 4. 実装
上述の式から,正規化係数が(n+1)/2πと求まりましたので,この値を使ってPhongシェーディングを正規化します。
実際に実装すると下記のようになります。
実際に実装すると下記のようになります。
00026: //---------------------------------------------------------------------------------------
00027: //! @brief 正規化フォンライティングを行います.
00028: //!
00029: //! @param [in] specular 鏡面反射色.
00030: //! @param [in] power 鏡面反射強度.
00031: //! @param [in] viewDir 視線ベクトル.
00032: //! @param [in] normal 法線ベクトル.
00033: //! @parma [in] lightDir ライトベクトル.
00034: //! @return フォンライティングの結果を返却します.
00035: //---------------------------------------------------------------------------------------
00036: float3 NormalizedPhong( float3 specular, float power, float3 viewDir, float3 normal, float3 lightDir )
00037: {
00038: float3 R = -viewDir + ( 2.0f * dot( normal, viewDir ) * normal );
00039:
00040: return specular * pow( max ( dot( lightDir, R ), 0.0f ), power ) * ( ( power + 1.0f )/ ( 2.0 * PI ) );
00041: }
★ Download
本ソースコードおよびプログラムはMIT Licenseに準じます。
プログラムの作成にはMicrosoft Visual Studio 2012 Express Editionを用いています。
プログラムの作成にはMicrosoft Visual Studio 2012 Express Editionを用いています。
