
正規化Lambert
★ 1.はじめに…
物理ベースレンダリングを少し勉強してみます。まずはLambertからです。


★ 2.Lambertのおさらい
ランバート照明は視線方向に依存しない光源の入射方向と面の法線だけで算出される陰影処理技法です。
この技法ではランバートの余弦則(Lambert's cosine law)が定義されています。この法則が意味しているのは「物体の表面で反射する光の輝度は,光の入射ベクトルLと表面に対する法線ベクトルNとが成す角度の余弦に比例する」ということです。
ランバートの余弦則を数式で表すと次のようになります。
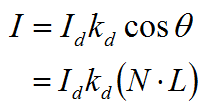
ただし,Idは光の強さ,θは入射角,kdは物体の反射係数,Nは法線ベクトル,Lは物体から光源へと向かうライトベクトルを示します。
また,cosθの値が負の場合(法線がライトと反対の方向を向いてしまっている場合)には値は0にします。
ランバートの余弦則にのっとった入射した光の強さが見る色に比例するような光を拡散反射光(Diffuse reflection light)と言うそうです。
この技法ではランバートの余弦則(Lambert's cosine law)が定義されています。この法則が意味しているのは「物体の表面で反射する光の輝度は,光の入射ベクトルLと表面に対する法線ベクトルNとが成す角度の余弦に比例する」ということです。
ランバートの余弦則を数式で表すと次のようになります。
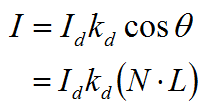
ただし,Idは光の強さ,θは入射角,kdは物体の反射係数,Nは法線ベクトル,Lは物体から光源へと向かうライトベクトルを示します。
また,cosθの値が負の場合(法線がライトと反対の方向を向いてしまっている場合)には値は0にします。
ランバートの余弦則にのっとった入射した光の強さが見る色に比例するような光を拡散反射光(Diffuse reflection light)と言うそうです。
★ 3.正規化Lambert
Lambertライティングですが,ライティングというだけに扱っているのは光になります。高校物理で習うとおもうのですが,光もエネルギーを持っています。エネルギー保存則が適用されるわけです。
物理的に考えるのであれば,今考えているLambertも光を扱っているのでエネルギー保存則が成立しなければいけません。ここでのエネルギー保存則は,反射されたエネルギーが入射したエネルギーより大きなってはいけないということになります。
要するに「入射光 >= 放射光」ということです。
では,まず放射光の総量を求めてみましょう。放射光は,法線となす角度θで,その強度はcosθに比例するということは,ランバートの余弦則で示されました。今は,ある平面に反射したときに放射される光の総量を求めようとしていますから,反射するのは半球上ということになります。従って,cosθを半球積分すれば,放射する光の総量がわかりそうです。そんなわけで,積分計算してみます。
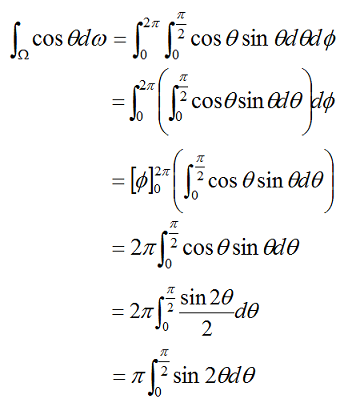
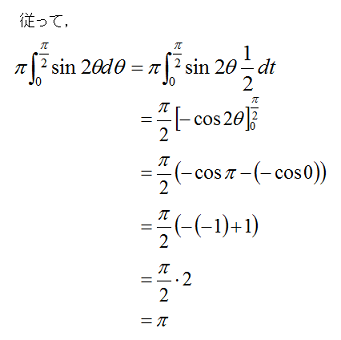
上記の結果から,放射する光の総量がπであることがわかりました。
つまり,入射光を1とした場合に,放射光はπ倍されて出てしまうということになります。これだとエネルギー保存則に反してしまい物理的には正しくないです。そこで,放射する光の総量であるπで割って正規化を行います。正規化を行うことによって,エネルギーが保存され物理的に正しい結果となります。
物理的に考えるのであれば,今考えているLambertも光を扱っているのでエネルギー保存則が成立しなければいけません。ここでのエネルギー保存則は,反射されたエネルギーが入射したエネルギーより大きなってはいけないということになります。
要するに「入射光 >= 放射光」ということです。
では,まず放射光の総量を求めてみましょう。放射光は,法線となす角度θで,その強度はcosθに比例するということは,ランバートの余弦則で示されました。今は,ある平面に反射したときに放射される光の総量を求めようとしていますから,反射するのは半球上ということになります。従って,cosθを半球積分すれば,放射する光の総量がわかりそうです。そんなわけで,積分計算してみます。
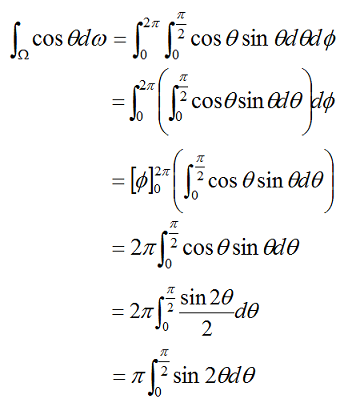
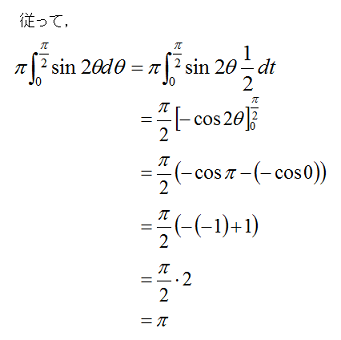
上記の結果から,放射する光の総量がπであることがわかりました。
つまり,入射光を1とした場合に,放射光はπ倍されて出てしまうということになります。これだとエネルギー保存則に反してしまい物理的には正しくないです。そこで,放射する光の総量であるπで割って正規化を行います。正規化を行うことによって,エネルギーが保存され物理的に正しい結果となります。
★ 4.実装
では,実際に実装してみます。
…といっても大したことはなくて,リニア空間でLambertライティングしてやって,結果をπで割ってから出力すればいいだけです。
…といっても大したことはなくて,リニア空間でLambertライティングしてやって,結果をπで割ってから出力すればいいだけです。
00013: //---------------------------------------------------------------------------------------
00014: //! @brief 正規化ランバートライティングを行います.
00015: //!
00016: //! @param [in] diffuse 拡散反射色.
00017: //! @param [in] lightDir ライトベクトル.
00018: //! @param [in] normal 法線ベクトル.
00019: //! @return ランバートライティングした結果を返却します.
00020: //---------------------------------------------------------------------------------------
00021: float3 NormalizedLambert( float3 diffuse, float3 lightDir, float3 normal )
00022: {
00023: return diffuse * max( dot( normal, lightDir ), 0.0f ) * ( 1.0f / PI );
00024: }
00025:
00026:
00027: //----------------------------------------------------------------------------------------
00028: //! @brief ピクセルシェーダのメインエントリーポイントです.
00029: //!
00030: //! @param [in] input 頂点シェーダからの出力値です.
00031: //! @return 各レンダーターゲットへの出力値を返却します.
00032: //----------------------------------------------------------------------------------------
00033: PSOutput PSFunc( VSOutput input )
00034: {
00035: // ゼロクリア.
00036: PSOutput output = (PSOutput)0;
00037:
00038: // ディフューズアルベドマップをフェッチ.
00039: float4 diffuseMapColor = DiffuseMap.Sample( DiffuseSmp, input.TexCoord );
00040:
00041: // アルファテスト.
00042: clip( ( diffuseMapColor.a < 0.125f ) ? -1.0f : 1.0f );
00043:
00044: // 法線ベクトル計算.
00045: float3 N = normalize( input.Normal );
00046:
00047: // ライトベクトル計算.
00048: float3 L = normalize( input.LightDir );
00049:
00050: // ディフューズカラー計算.
00051: float3 diffuse = NormalizedLambert( Diffuse * diffuseMapColor.rgb, L, N );
00052:
00053: // 出力値設定.
00054: output.Color0.xyz = diffuse;
00055: output.Color0.a = Alpha;
00056:
00057: return output;
00058:
00059: }
★ Download
瀬戸フォントミニ-Pは,瀬戸のぞみさんの著作物です。
詳細は,http://nonty.net/item/font/をご覧下さい。
本ソースコードおよびプログラムはMIT Licenseに準じます。
プログラムの作成にはMicrosoft Visual Studio 2012 Express Editionを用いています。
詳細は,http://nonty.net/item/font/をご覧下さい。
本ソースコードおよびプログラムはMIT Licenseに準じます。
プログラムの作成にはMicrosoft Visual Studio 2012 Express Editionを用いています。
