今回は8章の”Instancing”を読んでみることにします(5章, 6章, 7章は飛ばします)。
インスタンシングとは,変換行列を別に持って置き,あるオブジェクトのローカル座標を変換行列で変換して,それぞれ異なる位置に配置することを指します。
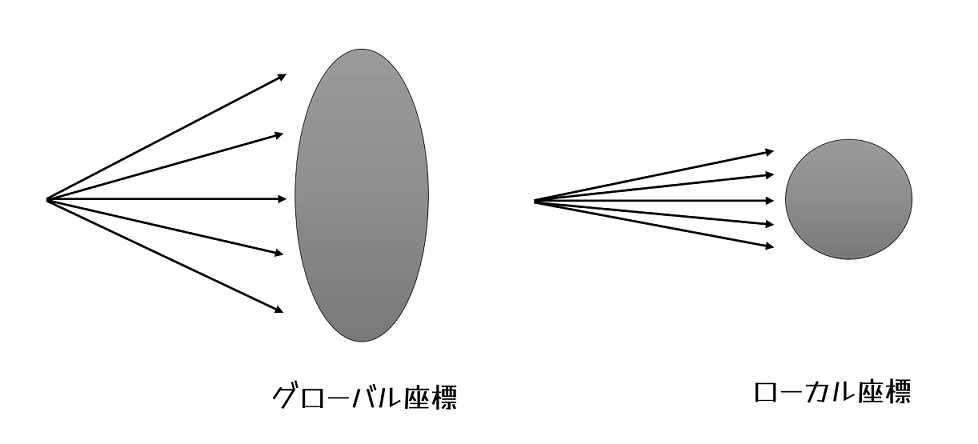
Zバッファを用いるグラフィックスシステムでは,オブジェクトの各頂点は描画される前に行列によって変換されます。例えば,Z成分に対して0.5倍のスケール値が適用されると,オブジェクトはその方向に対して縮められます。レイトレーシングでは,インスタンシングは管理が簡単ですが,変換を行う方法は少し難しいです。レイトレーシングについてのインスタンシングの基本的な考え方を図 1に示します。

インスタンシングの良い所は,異なる変換行列を持つ,異なるインスタンスを同じオブジェクトに関連付けることができる点です。
さて,インスタンシングを実装するためには変換行列について理解しておく必要があります。復習しておきましょう。
4×4の変換行列クラスを実装する必要があり,行列は次の値を持ちます。
\begin{eqnarray} \mathbf{M} = \begin{bmatrix} m_{00} & m_{01} & m_{01} & m_{03} \\ m_{10} & m_{11} & m_{12} & m_{13} \\ m_{20} & m_{21} & m_{22} & m_{23} \\ 0 & 0 & 0 & 1 \end{bmatrix} \end{eqnarray}
行列の表記は,列優先表現になっている点に注意してください。
ある行列\({\mathbf M}\)とある点\({\mathbf p}\)が与えれたとき,変換のルールは次のようになります。
\begin{eqnarray} {\mathbf M}{\mathbf p} = \begin{bmatrix} m_{00} & m_{01} & m_{02} & m_{03} \\ m_{10} & m_{11} & m_{12} & m_{13} \\ m_{20} & m_{21} & m_{22} & m_{23} \\ m_{30} & m_{31} & m_{32} & m_{33} \end{bmatrix} \begin{bmatrix} p_x \\ p_y \\ p_z \\ 1 \end{bmatrix} = \begin{bmatrix} m_{00} p_x + m_{01} p_y + m_{02} p_z + m_{03} \\ m_{10} p_x + m_{11} p_y + m_{12} p_z + m_{13} \\ m_{20} p_x + m_{21} p_y + m_{22} p_z + m_{23} \\ m_{30} p_x + m_{31} p_y + m_{32} p_z + m_{33} \end{bmatrix} \end{eqnarray}
実用上は行列の一番下の行列の要素は\( (0, 0, 0, 1 )\)になることが多いので,\(m_{30}, m_{31}, m_{32}, m_{33}\)に当てはめると,最後の要素は1になります。
方向を示すベクトル\({\mathbf v}\)を変換する場合は平行移動成分は変化しないので次のような式になります。
\begin{eqnarray} {\mathbf M}{\mathbf v} = \begin{bmatrix} m_{00} & m_{01} & m_{02} & m_{03} \\ m_{10} & m_{11} & m_{12} & m_{13} \\ m_{20} & m_{21} & m_{22} & m_{23} \\ m_{30} & m_{31} & m_{32} & m_{33} \end{bmatrix} \begin{bmatrix} v_x \\ v_y \\ v_z \\ 0 \end{bmatrix} = \begin{bmatrix} m_{00} p_x + m_{01} v_y + m_{02} v_z \\ m_{10} p_x + m_{11} v_y + m_{12} v_z \\ m_{20} p_x + m_{21} v_y + m_{22} v_z \\ m_{30} p_x + m_{31} v_y + m_{32} v_z \end{bmatrix} \end{eqnarray}
サーフェイスの法線ベクトルは慣習上のベクトルとは異なる方法で変換します。これは図を見るとわかるように,方向ベクトルは変換後も変わりませんが,法線ベクトルは変換によって変化するためです。\({\mathbf M}{\mathbf n}\)の代わりに, \(({\mathbf M^{-1}}) {}^{\top} {\mathbf n}\)を用いて変換を行います。ここで\(\top\)は転置を表します。\({\mathbf N} = {\mathbf M}^{-1}\)とすると,これは次のように書けます。
\begin{eqnarray} ({\mathbf M^{-1}}) {}^{\top} {\mathbf n} = {\mathbf N}^{\top} {\mathbf n} = \begin{bmatrix} n_{00} & n_{10} & n_{20} & n_{30} \\ n_{01} & n_{11} & n_{21} & n_{31} \\ n_{02} & n_{12} & n_{22} & n_{32} \\ n_{03} & n_{13} & n_{23} & n_{33} \end{bmatrix} \begin{bmatrix} v_x \\ v_y \\ v_z \\ 0 \end{bmatrix} = \begin{bmatrix} n_{00} v_x + n_{10} v_y + n_{20} v_z \\ n_{01} v_x + n_{11} v_y + n_{21} v_z \\ n_{02} v_x + n_{12} v_y + n_{22} v_z \\ n_{03} v_x + n_{13} v_y + n_{23} v_z \end{bmatrix} \end{eqnarray}
ただし、\(n_{ij}\)は\({\mathbf M}^{-1}\)の要素とします。
我々は,レイ\({p}(t) = {o} + t {v} \)を変換したいので,\({o}\)と\({v}\)を変換する必要があります。コード上ではこれらを別々の関数”transformAsLocation”, “transformAsOffset”, “transformAsNormal”とすることにします。最初の演算は位置\({\mathbf o}\)を別の位置\({\mathbf o}’\)へと移動させるtransform-locationなので,
\begin{eqnarray} \begin{bmatrix} o_x’ \\ o_y’ \\ o_z’ \\ 1 \end{bmatrix} = \begin{bmatrix} m_{00} & m_{01} & m_{02} & m_{03} \\ m_{10} & m_{11} & m_{12} & m_{13} \\ m_{20} & m_{21} & m_{22} & m_{23} \\ 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} o_x \\ o_y \\ o_z \\ 1 \end{bmatrix} = \begin{bmatrix} m_{00} o_x + m_{01} o_y + m_{02} o_z + m_{03} \\ m_{10} o_x + m_{11} o_y + m_{12} o_z + m_{13} \\ m_{20} o_x + m_{21} o_y + m_{22} o_z + m_{23} \\ 1 \end{bmatrix} \end{eqnarray}
次は行列\({\mathbf M}\)を用いてベクトル\({\mathbf v}\)を変換するので,
\begin{eqnarray} \begin{bmatrix} v_x’ \\ v_y’ \\ v_z’ \\ 0 \end{bmatrix} = \begin{bmatrix} m_{00} & m_{01} & m_{02} & m_{03} \\ m_{10} & m_{11} & m_{12} & m_{13} \\ m_{20} & m_{21} & m_{22} & m_{23} \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} v_x \\ v_y \\ v_z \\ 0 \end{bmatrix} = \begin{bmatrix} m_{00} v_x + m_{01} v_y + m_{02} v_z \\ m_{10} v_x + m_{11} v_y + m_{12} v_z \\ m_{20} v_x + m_{21} v_y + m_{22} v_z \\ 0 \end{bmatrix} \end{eqnarray}
となります。
変換済みオブジェクトとの交差判定の基本的な考え方は次の図のようになります。
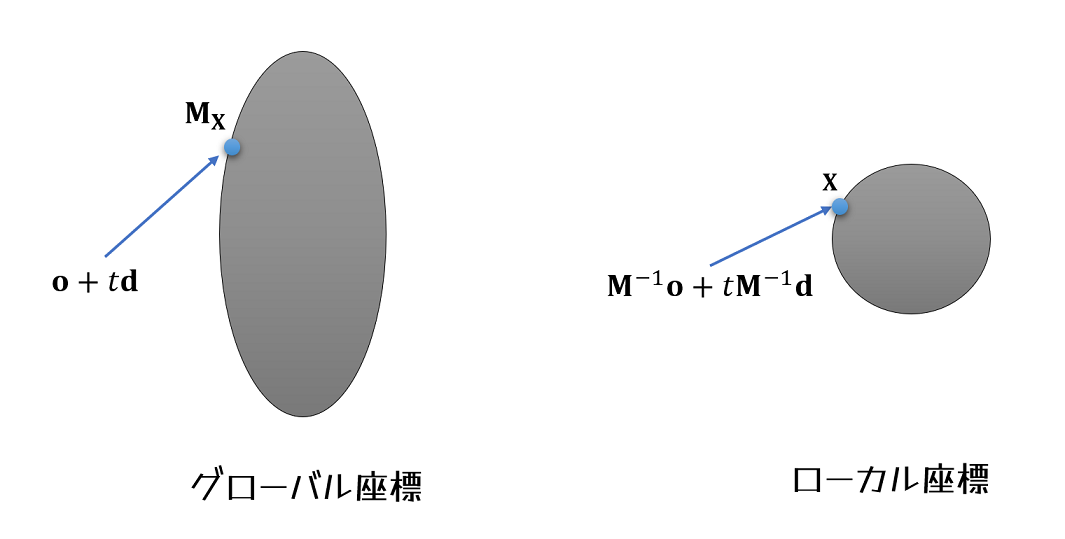
少し複雑なのはオブジェクト上の点を変換するよりも,レイを変換する方が良いということです。これはレイをローカル座標へ変換することを意味します。このローカル座標に変換されたレイ\({\mathbf M}^{-1} {\mathbf o} + t {\mathbf M}^{-1} {\mathbf d} \)はローカル座標系でオブジェクトと交差し,その交差点は\({\mathbf x}\)となります。
この交差点はワールド座標では\({\mathbf M}{\mathbf x}\)となります。ローカルの法線ベクトルが\({\mathbf n}\)のとき,ライティング計算のために使用される変換された法線は\(({\mathbf M^{-1}}) {}^{\top} {\mathbf n}\)となります。
インスタンシングで予期されることの一つとして,レイのベクトルの長さが厳密に1にならない可能性があります。\({\mathbf d}\)の長さが1の場合,ローカル座標系におけるスケールされたバージョンの\({\mathbf d}\)は任意の長さになる可能性があるということに注意してください。
行列\({\mathbf M}\)によって変換されたサーフェイスsurfとの交差についての疑似コードは以下のようになります。

今回はインスタンシングについて理解を深めました。