わふー。Pocolです。
今日は,[Yan 2015] Ling-Qi Yan, Chi-Wei Tseng, Henrik Wann Jensen, Ravi Ramamoorithi, “Physically-Accurate Fur Reflectance: Modeling, Measurement and Rendering”, ACM Transaction on Graphics, Vol.34, Issue 6, November 2015.
を読んでみることにします。
いつもながら,誤字・誤訳があるかと思いますので,ご指摘頂ける場合は正しい翻訳例と共に指摘して頂けるとありがたいです。
Abstract
動物の毛皮をフォトリアリスティックに表現することは、コンピュートグラフィックスの長年の課題でした。毛皮の幾何学的な複雑さをモデル化することにはかなりの努力が払われていますが、繊維の反射率についてはよくわかっていません。毛皮は、MarschnerのヘアモデルやKajiya-Kayのモデルでは捉えられない、独特の拡散性と飽和性のある外観を持っています。本論文では、毛皮繊維の物理的に正確な反射率モデルを開発しました。解剖学的な文献や測定結果に基づいて、生物学的に観察される複数のキューティクル層に覆われたコルテックスを二重円筒で、散乱する内部構造を髄質として内円筒で表現しています。我々の重要な貢献は、髄質の散乱を正確にモデル化したことです。一方、人間の髪の毛の場合、髄質の幅は最小限であり、したがって反射率への影響は無視できます。髄質の散乱は、拡散性の反射ローブだけでなく、追加の反射および透過経路をもたらします。我々の物理モデルを実際の毛皮繊維の測定で検証し、9つの毛皮サンプルの反射率プロファイルをコンピュータグラフィックスで表現した最初のデータベースを紹介します。その結果、我々のモデルは、Marschnerの毛髪反射率モデルよりも、測定データへの適合性が大幅に向上したことを示しました。また,効率的なレンダリングのために,2次元の毛皮の散乱プロファイルを事前に計算し,因数分解されたローブで反射率モデルを解析的に近似する手法を開発しました。この手法の精度は、我々のレンダリングモデルとフル3D光輸送シミュレーションを比較することで検証されます。我々のモデルは豊富なコントロールセットを提供しており、我々がフィットさせたパラメータを直接使用してリアルなファーをレンダリングしたり、アーティストが希望する外観のためにパラメータを手動で調整するための出発点とすることができます。
1 Introduction
コンピュータグラフィックスでは、動物の毛並みをリアルに表現するために、物理的な根拠に基づいた正確な毛並み表現が求められることがあります。この問題は長年の課題であり[Kajiya と Kay 1989],毛皮の幾何学的な複雑さを解決するために多くのアプローチが提案されています。しかし,現在の毛皮の反射率モデルは,経験的に導き出されたものや,Kajiya-Kay [1989]やMarschnerモデル [2003]のような人間の髪の毛の反射率モデルを用いたものがほとんどです。図1に示すように,毛皮には独特の拡散性と飽和性がありますが,これらのモデルは鏡面反射と屈折に主眼が置かれているため,完全には捉えられていません。また,様々な種類の毛皮の測定を行い,これまでの毛髪反射モデルでは毛皮繊維の反射プロファイルに適合しないことを確認しました(図8,11,12参照)。
これらの観察結果は、毛髪と毛皮の違いに関する文献[Carrlee と Horelick 2011; Deedrick と Koch 2004a; Deedrick と Kock 2004b]を調べるきっかけとなりました(4章)。簡単に言うと、単一の毛皮繊維は、毛髪モデルのように単純な誘電体の円柱としてモデル化することはできません。毛皮繊維の内部には、多くの場合、髄質と呼ばれる無視できない散乱構造が含まれており(図3)、これが毛皮繊維の外観に大きな影響を与えています。一方,人間の髪の毛の場合,髄質は通常,繊維直径の3分の1以下しか占めておらず,無視することができます。この論文の重要な洞察は,物理的に正確な毛皮の反射率モデルを構築するために,髄質の散乱を考慮することです。我々の主な貢献は以下の通りです。
Double Cylinder Fur Fiber Model: 5章では、毛皮繊維の物理的な二重円筒モデルを開発します。このモデルは、図5に示すように、解剖学的にキューティクル、コルテックス、髄質の3つの要素から構成されています。外側の円柱の表面はキューティクル、内側の円柱は散乱する髄質、そしてその間にあるのがコルテックスです。また,反射効果をより適切に表現するために,多層のキューティクルモデルを導入しています(図.4)。
Measurement and Database of Fur Reflectance: この物理モデルを検証するために,ガントリーを用いて,9種類の動物の毛皮の単一繊維の2次元反射率プロファイルを測定しました。我々の物理モデルを測定データに当てはめたところ,2次元反射率プロファイルの空間において定量的な一致が見られました(図8)。また、Kajiya-KayやMarschnerのような既存の毛髪反射率モデルは、外観の主要な特徴に適合しないことを示しています(図11、12)。これらの結果は、キューティクルの反射と髄質の散乱を正確にモデル化することが、毛皮のレンダリングに不可欠であることを明確に示しています。
9種類の動物の毛皮の反射率測定値とフィットパラメータをコンピュータグラフィックスで初めてデータベース化しました。これらのパラメータは、我々のレンダリングモデルに直接プラグインすることができます。また、アーティストが異なるタイプの外観を得るためにパラメータをわずかに変化させるためのベースラインにもなります。表2に適合パラメータを示します。
Rendering Model for Animan Fur: 7章では,近距離散乱を考慮した,単一毛髪繊維の効率的で正確な反射率モデルを開発しました[Zinke と Weber 2007]。概念的には,(キューティクルのスケールから得られる)ラフネスを蓄積し,(髄質から得られる)散乱効果を追跡しながら,二重円筒内の主鏡面光線を追跡します。露骨なボリュームシミュレーションを避けるために,髄質の散乱を事前に計算します。以前のヘアモデルとの一貫性を保つために,因数分解されたローブ(Marschner et al.2003; d’Eon et al.2011)をさらに近似し,縦方向と横方向の2D反射率プロファイルを別々に表現しました。これらの近似により,トレースステップの解析的解法が可能になり,髄質散乱の評価がテーブルルックアップに簡略化されます。図8では,我々のレンダリングモデルが,フルボリュームシミュレーションに匹敵する精度であることを検証しています。この毛皮繊維の反射モデルは,どのようなグローバルイルミネーションレンダラーでも,また,複数の種類の動物の毛皮にも使用することができます(図1および8章)。
2 Related Work
Physically-based hair reflectance models: Marschnerら[2003]は、物理ベースの髪の毛の反射率モデルを提案しました。毛髪繊維を粗い誘電体の円柱とみなし,一次光と二次光に寄与する3つの散乱経路をモデル化しています。\(R\),\(TT\),\(TRT\)です。各経路からの反射ローブは,緯度方向と方位角方向の散乱プロファイルの積に分離されます。Zinkeら[2007]は、BCSDF(Bidirectional Curve Scattering Distribution Functions)という概念を導入することで、毛髪の反射率モデルを公式化しました。d’Eonら[2011]は、\(TRRT\)のような高次の散乱ローブをモデル化し,グレージング角におけるエネルギー保存の問題を解決することで、エネルギー保存の観点からMarschnerのモデルを拡張しました。最近では、d’Eonら[2014]が、緯度方向の寄与を相対的な方位角方向と関連付けることで、緯度方向と方位角方向に因数分解された表現を維持しつつ、「分離しない」反射ローブ表現を提案しています。これらの方法は、毛髪に対しては優れた結果が得られますが、毛皮に対しては適していません(図1、11参照)。毛皮繊維に顕著な髄質からの散乱が除外されているからです。同時進行の研究[Khungurn と Marschner 2015]では、楕円形の毛髪繊維に明示的に焦点を当て、円形断面と比較して異なる光学特性を明らかにしています。
Non physically-based hair/fur reflectance models: Kajiya と Kay [1989] は,毛皮を 3D テクスチャで表現する方法と,経験的な毛皮のシェーディングモデルを紹介しました。このモデルでは,毛皮の繊維を不透明な円柱として近似しています。Phongモデルを拡張することで、繊維の接線を中心としたディフューズローブとスペキュラーローブを生成しています。Goldmanら[1997]は、Kajiya-Kayモデルを経験的に改良し、異なる視野角に対して異なる不透明度の値を与えることで、このモデルを実現しました。Zinkeら[2009]は,測定された人間の毛髪繊維からの散乱をMarschnerのモデルに適合させることができないことに気づき,測定データで観察された拡散性の毛髪反射を捉えるために,Marschnerのモデルにディフューズローブをブレンドすることで,アドホックな方法を提案しました。これらの方法では、もっともらしいレンダリング結果を得ることができますが、物理的な根拠がなく、エネルギーの保存もされません。さらに、これらの手法は、物理ベースのモデルほど、毛皮繊維の反射率プロファイルの観測値に正確に適合しません。
Multiple scattering inside hair volumes: 毛髪には多くの繊維が含まれているため、多重散乱を計算することは困難です。二重散乱近似法[Zinke ら 2008]は,髪の毛の繊維が局所的に似ていると仮定し,解析的な多重散乱モデルを導き出します。シャドウマップ関連の手法[Lokovic と Veach 2000; Yuksel と Keyser 2008; Sintorn と Assarsson 2009]では,[Kajiya と Kay 1989]で不足していた光の透過率を補うために透明度を用いています。Moonら[2006]は、フォトンマッピングを髪の毛のボリュームに適用し、ノイズをオーバーブラーやバイアスと置き換えています。この論文では、単一の毛皮繊維からの光学的特性に焦点を当て、標準的な多重散乱レンダラー[Jakob 2010]を使用してグローバルな効果を得ています。
Importance sampling for hair: 反射率モデルを効率的に使うには、グローバルイルミネーションレンダラーでの重点サンプリング手法が必要です。Hery と Ramamoorthi [2012] は,Marschner モデルの反射ローブに対する重点サンプリング方式を提案しました。d’Eon ら[2013]は,d’Eon ら2011の拡張モデルに基づいて,まず各散乱タイプのエネルギーに基づいてローブ選択を行い,次に緯度方向と方位方向の散乱プロファイルをそれぞれ重点サンプリングすることで,効率的な手法を提案しました。また,[d’Eonら 2013]を参考にして,毛皮の反射率モデルに対して効果的な重点サンプリング手法を開発した。
Near field scattering and far field approximation: ファーフィールド近似法[Kajiya と Kay 1989; Marschnerら 2003; d’Eon ら 2011]は,単一の毛髪繊維を細い曲線と見なし,繊維の幅方向に平行な入射光を想定しています。この近似法により、近距離で見ると毛髪繊維は平らに見えます。Zinke ら [2007] は,近距離で見た繊維を表現するための解析的なニアフィールド解法を提案しました。我々の手法はニアフィールドの散乱に基づいており,ファーフィールドの近似が必要な場合は[d’Eon et al 2011]の同じ積分手法を参照しています。
Precomputation and empirical models: [Sloan ら 2002; Wang ら 2005; Nguyen と Donnelly 2005; Ogaki ら 2010; Ren ら 2013]のような事前計算ベースのレンダリング手法は、問題のサブセットを事前に解決することで機能します。これらの方法は通常、非常に効率的です。しかし,事前に計算されたデータは大量のストレージを必要とするため,限られた入力セットの下でしか実用的ではありません。[Stam 1995; Peers ら 2006; Donner ら 2009]のような経験的モデルでは,反射率や散乱プロファイルを得るために,近似法や数値計算法が用いられます。これらのモデルは,パラメータ空間全体をカバーする測定やシミュレーションを必要とすることが多いです。我々のモデルでは、低次元の3Dパラメータ空間で髄質の散乱を考慮した事前計算ステップを行い、これらのパラメータの組み合わせごとに1Dプロファイルを保存します。事前に計算されたプロファイルは20MBに圧縮されます。
3 Background
毛髪反射モデルでは、毛髪繊維を円柱として、BCSDF(Directional Curve Scattering Distribution Function)を用いて繊維の反射特性を表現しています。
\begin{eqnarray}
L_r(\omega_r) = \int L_i (\omega_i) S(\omega_i, \omega_r) \cos\theta_i d \omega_i \tag{1}
\end{eqnarray}
ここで、\(L_i\)と\(L_r\)は、それぞれ\(\omega_i\)方向からの入射放射輝度と\(\omega_r\)方向への出射放射輝度であり、\(S\)は、BCSDFです。
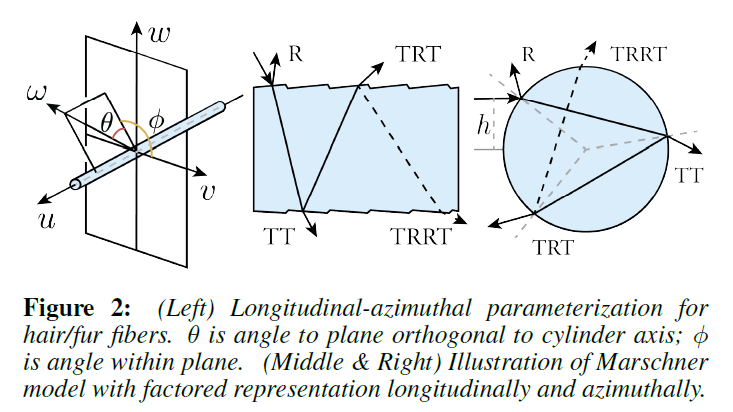
図2に示すように、[Marschner ら 2003]の緯度-方位角\((\theta, \phi)\)のパラメータ化に従っています。
\begin{eqnarray}
L_r(\theta_r, \phi_r) = \int_{-\pi}^{\pi} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} L_i(\theta_i, \phi_i) S(\theta_i, \theta_r, \phi_i, \phi_r) \cos^2 \theta_i d \theta_i d \phi_i \tag{2}
\end{eqnarray}
ここで、1つの余弦項が2乗になるのは、このパラメータ化では立体角が\(d\omega_i = \cos \theta_i d \theta_i d \phi_i\)になるからです。
Kajiya-Kayモデルでは、毛髪繊維を不透明な固体の円柱とみなします。反射率は、拡散成分と鏡面成分に分けられます。[Zinke と Weber 2007]に従い,BCSDFは
\begin{eqnarray}
S(\theta_i, \theta_r, \phi_i, \phi_r) = k_d + k_s \frac{\cos^n(\theta_r + \theta_i)}{\cos \theta_i} \tag{3}
\end{eqnarray}
ここで、\(k_d\)と\(k_s\)はそれぞれ拡散係数と鏡面係数です。なお、Kajiya-Kayモデルは方位に依存しません。
Marschner model: Marschnerら[2003]が提案したBCSDFでは,毛髪繊維をガラスのような誘電体の円筒とみなしています。図2に示すように,このBCSDFでは,異なる鏡面反射経路\(p \in R, TT, TRT\)を考慮しています。\(R\)は反射,\(T\)は透過を表します。\(p\)の寄与は、緯度方向と方位角方向のイベントを表す\(M\)と\(N\)のプロファイルの積に因数分解されます。
\begin{eqnarray}
S(\theta_i, \theta_r, \phi_i, \phi_r) &=& \sum_{p} S_p (\theta_i, \theta_r, \phi_i \phi_r) / \cos^2 \theta_d \tag{4} \\
&=& \sum_{p} M_p (\theta_h) \cdot N_p (\phi; \eta’) / \cos^2 \theta_d.
\end{eqnarray}
ここで、\(\theta_h = (\theta_r + \theta_i) / 2\)と\(\theta_d = (\theta_r – \theta_i) / 2\)はそれぞれ縦半分の角度と差の角度、\(\phi = \phi_r – \phi_i\)は相対的な出射方位、\(\eta’ = \sqrt{\eta^2 – \sin^2 \theta_d} / \cos \theta_d\)は皮質の仮想屈折率で、傾いた緯度方向の入射方向を考慮しています。その後,d’Eonら[2011]によって,\(TRRT\)などの複数の内部反射イベントを扱えるように鏡面反射パスの種類が拡張されました。また,オリジナルのMarschnerモデル[2003]は,d’Eonら[2011]によって解決されたエネルギー保存の問題を抱えているため,本稿では,レンダリングと比較のすべてにおいて,[d’Eonら2011]をMarschnerモデルの正しい実装とみなし,Marschnerモデルという名称を維持しています。
Near/far field scattering models: ニアフィールド散乱では、入射位置として方位角方向に実際のオフセット\(h\)を指定します(図2)。ファーフィールド近似では、繊維の幅を覆う平行光を想定しています。したがって、ファーフィールド近似では、すべての可能なオフセット\(h \in [-1, 1]\)に対して積分することで、方位角方向の散乱関数\(N_p\)が得られます。
\begin{eqnarray}
N_p(\phi) = \frac{1}{2} \int_{-1}^{1} N_p (h, \phi; \eta’) d h \tag{5}
\end{eqnarray}
ファーフィールド近似のための積分は、解析的に解くこともできますが[Marschner ら 2003]、単純なタイプのパスの場合に限られます。
4 Differences between hair and fur fibers
ここでは、髪の毛と毛皮の繊維の主な違いについて説明します。コンピュータグラフィックスではあまり注目されていませんが、他の分野の文献[Carrlee と Horelick 2011; Deedrick と Koch 2004a; Deedrick と Koch 2004b; Stamm ら 1977]では、微細な違いについて議論されているので、ここではそれをまとめます。
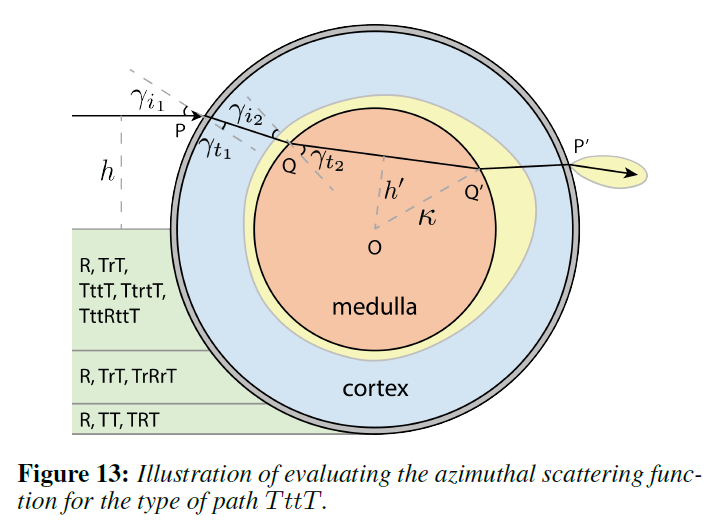
毛髪と毛皮の繊維には共通の構造があります。それらは、ある程度の偏心を持った円筒形であることが多いです。図3に示すように、1本の繊維は外側から内側に向かって、繊維の表面を鱗状に覆っているキューティクル、繊維内のほぼすべての着色色素を含むコルテックス、繊維の中心部に位置し、透過した光を散乱させる複雑な内部構造を持つメデュラの3層に分かれています。
このように共通の構造を持つ毛髪と毛皮の繊維ですが、構造的にはいくつかの違いがあります。ここでは、明らかに異なる光学特性をもたらす、このモデルにとって最も重要な特徴のみを紹介します。包括的で詳細な研究のためには、このセクションの冒頭で述べた文献を参照してください。
Medulla: 最も明らかな違いは、動物の毛皮の繊維は通常、内部に大きな髄質があることです。人間の髪の毛の場合、髄質は非常に小さく、おろそかになりがちです。しかし、動物の毛皮繊維には、円筒の大きさに匹敵するほどの髄質があります(図3)。
髄質ボリューム内の構造は複雑なものが多く、一方でホッキョクグマのように毛皮の中に中空の髄質がある動物もいます。いずれにしても、髄質は内部散乱構造として働き、毛皮に全体的な拡散性を与えています。髄質の中には固体の透明物質が入っていることもあれば、単に空気が入っていることもあり、髄質が皮質とは異なる屈折率を持っている可能性もあります。通常、髄質の内部には色素は存在しません。
Cutile: 人間の髪の毛のキューティクルは、屋根板のような形をしていますが、毛皮のキューティクルは複雑な形をしています(図3)。ここでは[d’Eon ら 2011]に倣い,毛皮繊維の緯度方向と方位角方向の両方のラフネスを考慮しています。
また、図4に示すように、キューティクル層はコルテックスの上に透明な被膜を形成しており、その中には複数のキューティクル・スケールが積み重なって層状構造を形成しています。これらの特性により、キューティクルの反射率は、誘電体界面からのフレネル反射に比べて高くなります。我々のモデルでは、キューティクルを、各層の両側に空気が存在する複数の層の誘電体スラブとみなしています。各層の無偏光反射率は、[Stokes 1860]によって次のように与えられます。
\begin{eqnarray}
F(\theta_i, 1) = \frac{1}{2} \left \lbrace F_s(\theta_i) + \frac{[1 – F_s(\theta_i) ]^2 F_s(\theta_i)}{1 – {F_s}^2(\theta_i)} \right \rbrace + \frac{1}{2} \left \lbrace F_p(\theta_i) + \frac{[1 – F_p(\theta_i) ]^2 F_p(\theta_i)}{1 – {F_p}^2(\theta_i)} \right \rbrace \tag{6}
\end{eqnarray}
ここで,\(F_s\)と\(F_p\)は\(s\)極に分解されたフレネル反射率と\(p\)極に分解されたフレネル反射率をそれぞれ表します。\(l\)層を合わせて考えると、反射率は[Stokes 1960]で次のように与えられます。
\begin{eqnarray}
F(\theta_i, l) = \frac{l \cdot F(\theta_i, 1)}{1 + (l – 1) \cdot F(\theta_i, 1)} \tag{7}
\end{eqnarray}
[Stamm ら 1977]や[Hashimoto 1988]で指摘されているように,キューティクル層の内部組成によって,コルテックスとは異なる屈折率が生じることがあります。さらに、層間の空気界面が存在しない可能性もあります。ここでは,キューティクルとコルテックスの屈折率を同じにして,\(l\)を実数に拡張することで,これらの特性を単純化しています。\(l\)は通常(0.5, 1.4)の範囲内にありますが、単一の誘電体界面の場合、\(F(\theta_i, 1)\)は両面スラブのため、\(l \approx 0.5\)の値になります。
5 Double cylinder fur fiber model
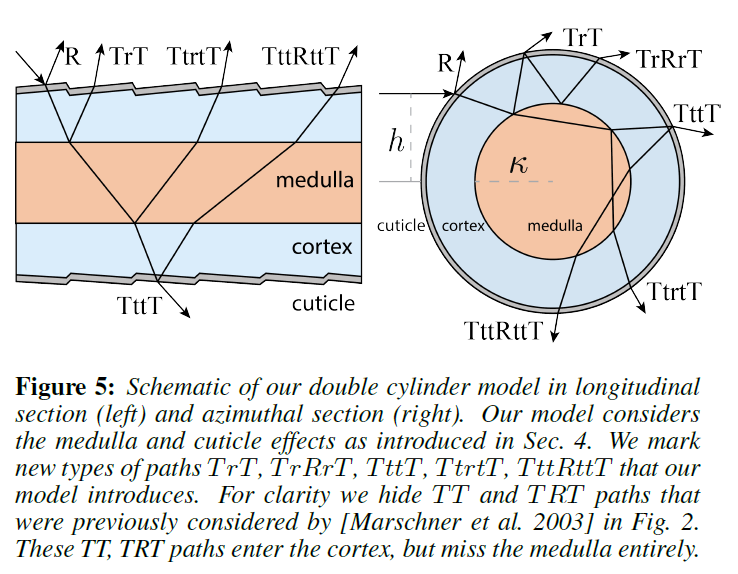
ここでは、上記の観察結果に基づいて、単一の毛髪繊維に対する物理的な二重円筒モデルを開発します。このモデルは、キューティクル、コルテックス、髄質という3つの構造要素で構成されており、それぞれが物理的に基づいた光学特性を持っています。図5に示すように、外筒の表面は(多層の)クチクラ、内筒は髄質、そして皮質はその間に位置しています。2つの円柱は同軸上にあり、外円柱の相対半径は1、内円柱の相対半径は\(\kappa\)で,これは髄指数と呼ばれ、髄質の半径と毛皮繊維の半径との比です。
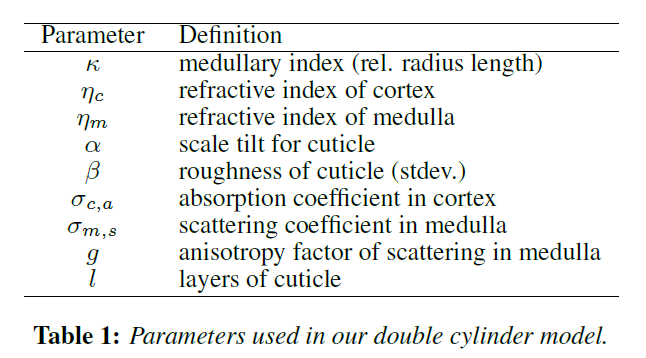
表1は、本モデルで使用したすべてのパラメータの一覧です。これらのパラメータは、主に[Marschner ら 2003]のものを使用しています。屈折率\(\eta\)とラフネス\(\beta\)、スケールチルト\(\alpha\)、外筒(コルテックス)の吸収係数\(\sigma_{c, a}\)などです。さらに、皮質と髄質の(おそらく異なる)屈折率についても考慮する必要があります。さらに、髄質が散乱媒体であることから、その散乱係数\(\sigma_{m, s}\)と異方性\(g\)を持つ位相関数を含める必要があります。なお、コルテックスには散乱構造がなく、また、第4章で述べたように、色素は髄質にはほとんど見られません。したがって、我々のモデルでは、コルテックスの散乱と髄質の吸収は必要ありません。我々は偏心パラメータを明示的に使用していないが、[Marschner ら 2003]のように屈折率に考慮されている。
二重円筒モデルでは、一本のファイバーを通る経路の種類が格段に増えます。従来のヘアモデルで考えられていた経路以外にも、図5に示すように、\(TrT\)、\(TrRrT\)、\(TttT\)、\(TtrtT\)、\(TttRttT\)など、従来の手法では捉えられなかった新たな経路の種類が導入されています。大文字は我々の円筒のインターフェースとの相互作用、小文字は内円筒のインターフェースとの相互作用を示す。光が内筒の界面を透過すると、体積散乱現象が起こります。
メデュラが1本の繊維の光学特性に大きく貢献していることは、髄質をコルテックスと同様の屈折率を持つ媒体で満たした場合に観察される。これにより、髄質はより均質になり、散乱が大幅に減少する。図6に示すように,逆光になると,マウント媒体で満たされた髄質はほとんど見えなくなる。しかし、空気で満たされている場合は、内部反射と散乱のために暗くなります。このモデルでは、\(\sigma_{m, s}\)と\(\eta_m\)を適宜調整することで、同様の結果が得られます。この現象は、我々の知る限り、他の毛髪・毛皮の反射モデルでは再現できません。
6 Database: measurements and validation
この二重円筒モデルを正当化し、キューティクルと髄質の影響を実験的に観察するために、毛皮繊維の2次元遠方反射率を完全に測定しました。9種類の動物の毛皮を使った反射率プロファイルのデータベースを作成しました(人間の毛もあります)。また,各データセットから,二重円筒モデルのパラメータセットをフィッティングしました。生の反射率データとフィットパラメータは、次のサイトで入手できます。http://viscomp.ucsd.edu/projects/fur。
Measurement Setup: 測定にはUCSD社製の球形ガントリーを使用しています(図7)。ガントリーには2本のロボットアームがあり、その上に光源とセンサーがそれぞれ試料から約2フィートと3フィートの距離に取り付けられています。光源には、150ワットのDCレギュレーター付き石英ハロゲン電球、35mmレンズ付きデジタルカメラ、12ビットの1/1.8インチCCDセンサーを使用しています。試料板の上に毛皮の繊維をまっすぐに置き,光の入射方向を繊維上の一点に固定して,出射球全体の離散的な方向への放射輝度を記録します。詳細は[Tseng 2015]に記載されています。
光源を\((\theta_i, \phi_i) = (-40^{\circ} , 0^{\circ})\)に固定し、カメラで\(\phi_r \in [-20^{\circ}, 200^{\circ}]\)を5°ステップ、\(\theta_r \in [10^{\circ}, 50^{\circ}]\)を2°ステップで掃引して撮影します。簡略化のため、\(r\)の添え字を省略し、\((\theta, \phi)\)で2次元の反射率プロファイルを表現しています。掃引範囲は、従来の人間の髪の毛の反射率モデルで導入されていた鏡面反射と拡散反射のすべてのローブをカバーしていますが、効率性を考慮して1/4球の範囲にとどめています。言い換えれば,毛髪繊維が入射面に対して対称であることを暗黙のうちに仮定しています。この仮定の妥当性を確認するために,2D測定を行う前に,定性的に対称な1D法線面反射率プロファイルが得られるまで,毛皮繊維をその接線に沿って回転させます。もし、このような対称性のある反射パターンが観察されない場合は、そのサンプルを単に廃棄します。非対称性のために廃棄されるサンプルの割合は約10%です。
各方向とも、シャッタースピード5段分の画像を5枚撮影します(合計25枚)。それぞれの画像は、まず繊維を含む25×25ピクセルのパッチに切り取られます。次に,時間的なノイズを除去するために,各シャッタースピードで撮影した5つのパッチを平均します。最後に,異なるシャッタースピードで平均化された5つのパッチを利用して,HDRの輝度信号を再構成します。このプロセスでは,カメラの絞りをf/8に固定し,HDR輝度値を構築するためのシャッタースピードを12.5,25,50,100,200msの5段階に設定しています。25×25ピクセルの各画像パッチでは、サンプル繊維が約100~200ピクセルを占めており,実際の幅に応じて異なります。なお、測定とその後のフィッティングでは、データをグレースケール画像とみなしています。
Database: データベースに登録されている動物は、ヤマネコ、ネコ、シカ、イヌ、ネズミ、ウサギ、タヌキ、キツネ、スプリングボックの9種類です。毛皮の繊維は剥製屋から寄贈されています。また、先行研究との比較検証のために、人間の髪の毛の反射率プロファイルを測定しています。毛皮繊維の反射率パターンの範囲を調べることが目的です。分類学上の詳細にはこだわらず、9種の名前は参考程度にとどめています。記録されたプロファイルは,人間の毛髪繊維を含む10個のサンプルがBCSDF領域において質的に大きな空間を占めていることを示しており,最も重要な反射現象を含んでいると考えられます。
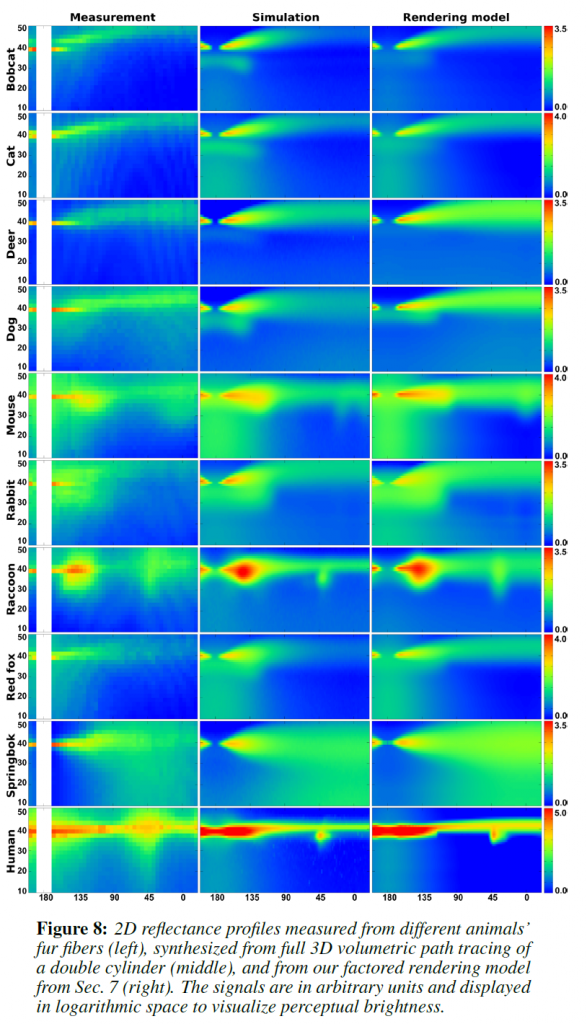
図8の左欄には、データベース全体が表示されています。なお,\(\phi = 180^{\circ}\)周辺の2次元プロファイルのうち,カメラが直接光源を向いている小さな領域は,正確に測定できませんでした。また、多くのプロファイルでは、明るいストライプと暗いストライプの微妙なパターンが解消されていることにも注目してください。この縞模様は、キューティクル層の表側と裏側で反射した光が薄膜状に干渉して生じたものだと考えられます。この干渉パターンを二重円筒モデルでモデル化することは、本稿では不可能です。
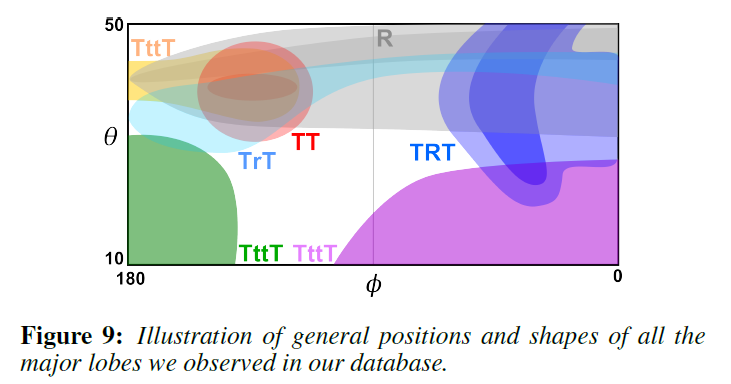
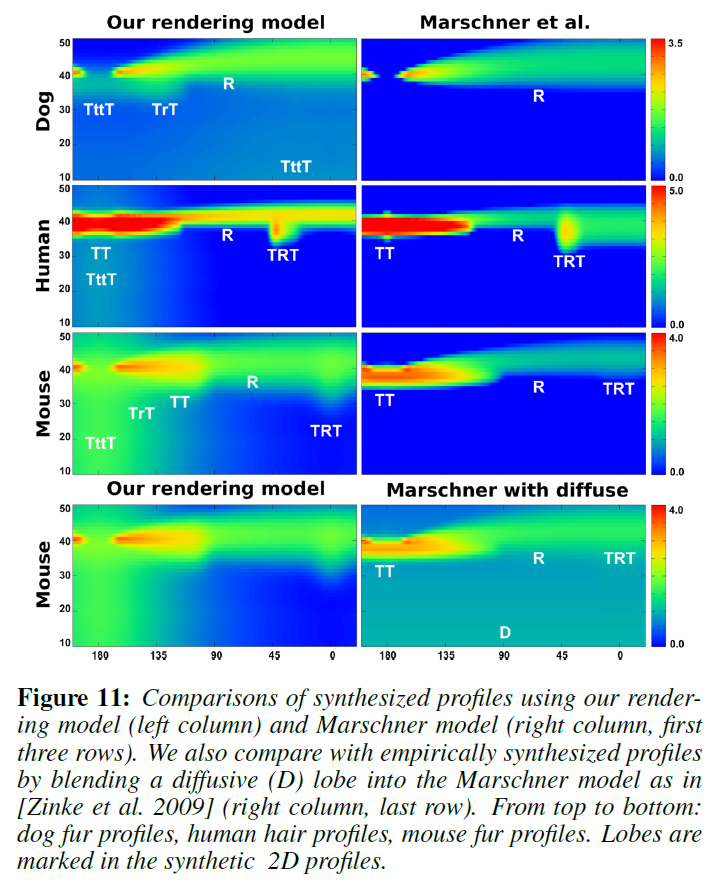
これらの測定で観測されたキーローブの模式図を図9に、いくつかの例を図11の左列に示します。各ローブの名前は、その寄与経路に対応しており、その割り当ては、3D二重円筒モデルの体積光輸送シミュレーションを用いた仮想実験によって検証されています。Marschnerモデルは、\(R\)、\(TT\)、\(TRT\)ローブしかサポートしていないため、図11の右欄に示すように、毛皮繊維の反射率プロファイルに満足のいくフィットを得ることができませんでした。さらに、この3つのローブであっても、Marschnerモデルの予測と反射率プロファイルの観察との間には大きな矛盾があります。主な特徴は以下の通りです。
- 毛皮の繊維からの反射率は、\(\phi = 180^{\circ}\)付近の\(TT\)成分がぼやけて一部が見えなくなっていたり(マウス、ラクーン)、\(TT\)成分がない場合もあります(ネコ)。特にアライグマでは、\(TT\)成分が消失した\(\phi \approx 150^{\circ}\)の部分で急激な変化が見られます。さらに、\(TRT\)成分が薄くなったり(マウス)、無くなったり(ネコ)することもあります。これらの現象は、光が髄質によって本来の\(TT\)と\(TRT\)の経路から離れて散乱されることによるものです。
- 毛皮繊維の反射率プロファイルの\(R\)成分は、通常、非常に明るく、ぼやけていて、フレネル反射だけでは説明できません(犬、ネズミ、アライグマ、スプリングボック)。この現象はキューティクルによるもので、キューティクルの表裏面からの反射によって反射率が高められています。
- 多くのプロファイルでは、前方または後方に拡散するローブが現れます。ローブの中心は、ほとんどの場合、\(\theta \approx 0^{\circ}\)のある法線面の周辺に位置しています(ネコ、アカギツネ、スプリングボック)。これらのローブは、ランダムに配置された誘電体界面で満たされた体積を持ち、多重散乱が起こりやすい髄質に起因する可能性が高いです。さらに、髄質を通った散乱の少ない光は、場合によっては\((\theta, \phi) = (40^{\circ}, 180^{\circ})\)付近でグローとして観察されることもあります(マウス、レッドフォックス)。
これらの現象はすべて、前節で提案した二重円筒モデル(図8の中段)でよくモデル化できます。
Parameters and Fitting: 次に、測定された2次元反射率プロファイルから、二重円筒モデルのパラメータ値(表1)をフィッティングした。次に,これらのパラメータを使用して,明示的な二重円筒の形状を定義し,3次元の体積光輸送シミュレーションを実行することができます。シミュレーションされた反射率プロファイルを測定値と比較してみます(図8の2列目)。また,7章で紹介した因数分解されたレンダリングモデルで同じパラメータセットを用いて生成された反射率(3列目)とも比較しました。
私たちのモデルはこれまでのヘアモデルよりもパラメータが多いため,[Marschner ら 2003; Sadeghi ら 2013]のように,測定された反射率プロファイルの1次元スライス上でパラメータをフィッティングすると,オーバーフィッティングになってしまいます。そこで,測定された2次元プロファイルに直接フィッティングしました。
各ファーサンプルについて、パラメータの最初の推定値を手動で初期化します。次に,二重円筒上でフル3Dの体積光輸送シミュレーションを行い,合成2次元反射率プロファイルを生成します。そして,期待値最大化アルゴリズムを用いて,2次元反射率の実測値とシミュレーション値との二乗誤差が最も小さくなるように,最適化されたパラメータを繰り返し求めました。シミュレーションは,シミュレーションされた反射率プロファイルを生成するために最適化の内部ループで使用する必要があり,滑らかなエネルギー景観を提供するためにはノイズが無い必要があるため,この最適化は非常にコストがかかります(ただし,オフラインで一度だけ実行する必要があります)。しかし,我々が測定した反射率プロファイルの解像度(\(45 \times 21\))で,1ピクセルあたり512サンプルを使用した場合,最適化手順は数時間以内に許容できる最小値に収束させることができます。比較のために必要な場合は、MarschnerモデルとKajiya-Kayモデルのパラメータをフィットさせるために同様の最適化を行います。唯一の違いは、モンテカルロ・シミュレーションを使用する代わりに、これらのモデルの解析形式を直接使用して2Dプロファイルを生成することです。
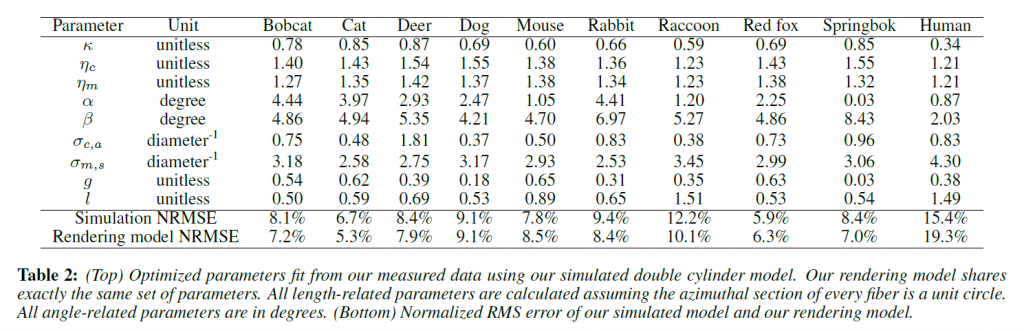
表2は,各毛皮サンプルに対して最適化された二重円筒モデルのパラメータの一覧である。また,7章で紹介する実用的なレンダリングモデルを用いて,図10の各素材の毛玉をレンダリングしました。なお,測定値はグレースケールであるため,レンダリングに色を導入するためには,皮質吸収のRGB値を手動で設定する必要があります。すべての毛玉に対して、元のフィットパラメータ \(\sigma_{c, a}= 0.2, 0.4, 0.6\)を置き換えて\(\sigma_{c, a}\)を設定しました。
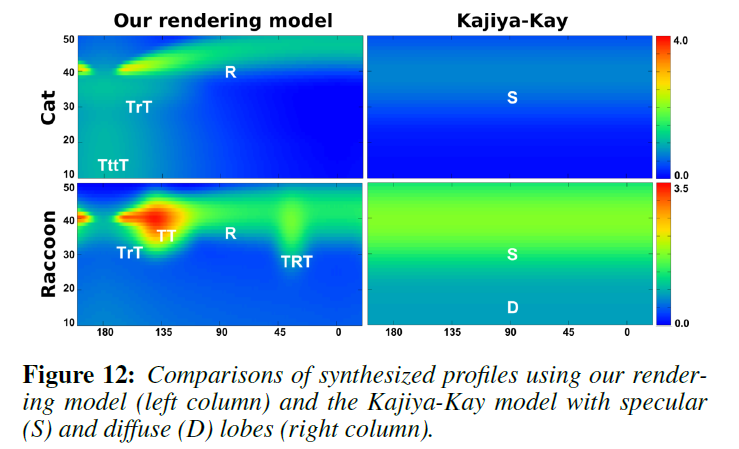
図10からいくつかの観察結果が得られました。まず、どのレンダリングも大きな黒い領域を表示していません。これは、Marschnerモデルのローブがすべて純粋なスペキュラであるため、再現するのが難しいということです。図18は、Marschnerモデルがエリア照明の下で大きな黒い領域を生成することを示しており、この観察をさらに検証しています。次に、前方/後方に散乱したローブが外観に大きく影響します。強い前方散乱(マウス、アカギツネ)は、これらの毛玉の中央にある領域をぼかします。通常、後ろにはより多くの毛繊維があるため、前方散乱エネルギーが浸透してさらに散乱します。後方散乱(スプリングボックス)は、通常、毛皮の層が薄く、垂直に見られない上部と下部の領域をぼかし、反射ローブを視覚的に強調しています。これらの効果は、図12の比較で示されているように、散乱ローブは厳密には方位角方向に一様であるため、Kajiya-Kayモデルでは表現が不十分であることを示しています。第三に、同じようなラフネスとコルテックスの屈折率を持つ反射ローブでは、クチクラの層数が多い方が常に強い反射ローブになります(ネコはヤマネコよりやや明るく、シカはイヌよりかなり明るいです)。このように、我々の髄質モデルとキューティクルモデルは、従来の手法では捉えられなかった毛皮の見た目の質的な違いを生み出しています。
Validation: 図8に示すように,実測した2次元プロファイルと,実際の二重円筒をパストレーシングしてシミュレーションしたプロファイル,そして7章で紹介するレンダリングモデルを用いて生成したプロファイルとの間に,定量的な類似性があることを示しています。RMSエラーを表2に示しますが,シミュレーションとレンダリングモデルはほぼすべてのケースで10%以下と同程度です。
図11では、Marschnerモデルと視覚的に比較しています。Marschnerモデルは純粋な鏡面反射であるため、人間の髪の毛の場合を除いて、測定されたすべてのプロファイルで同様の結果を得ることができません。また,[Zinke ら 2009]で提案されているように,拡散ローブをブレンドした場合でも,測定された反射率と一致しませんでした。これは、ブレンドされた拡散ローブが\(\theta = 0^{\circ}\)で常に緯度方向に対称であり、前方散乱効果と後方散乱効果を区別していないためです。また、Kajiya-Kayモデルを用いて生成した2Dプロファイルの比較も示します。Kajiya-Kayモデルは方位に依存せず、形状もゆっくりと変化するため、図12では代表的な2本の毛髪繊維のみを比較しています。Kajiya-Kayモデルでは、拡散ローブとスペキュラコーンのみが生成され、他の興味深いローブはすべて排除されています。
7 A Practical Rendering Model
物理的な二重円筒モデルを用いることで、光学的に忠実に表現されたファーファイバー上で光輸送シミュレーションを行うことができます。しかし,複数の体積散乱イベントの積分を評価するにはコストがかかるため,このモデルはレンダリングには適していません。このセクションでは、グローバルイルミネーションレンダラーに組み込むことができる、実用的なレンダリングモデルを開発します。
7.1 Overview
毛髪の反射率モデルは,遠方界近似のもとでは,ほとんどの場合,繊維のコンパクトなBCSDFを得ることができます。しかし,第2章で紹介したように,近距離での毛皮のより洗練された外観をモデル化するためには,近距離場の効果を含めることが不可欠であり,必要であれば,これらを統合して遠距離場近似を得ることもできます。そこで,二重円筒に入射する光線の,入射位置と方向に応じた潜在的な散乱経路を解析します。
このアプローチを実用化するために、いくつかの重要な近似を行います。まず,我々のニアフィールドモデルは,ファーフィールドのヘアモデルと同様に,レンダリングのための因数分解近似を取り入れています[Marshner ら 2003; d’Eon ら 2011]。しかし,これらのモデルでは,ファイバーの幅方向に平行になったらすべての入射光線によって緯度方向と方位角方向の反射率プロファイルが集合的に生成されると考えられているのに対し,我々は,繊維内をトレースする各光線によって方位角方向と緯度方向の分布が生成されると考えています。このアプローチは,図5の\(h\)の上でBCSDFを変化させることと同じで,我々のモデルを遠方界のBCSDFフレームワークと互換性のあるものにしながら,近方界の効果を可能にしています。[Zinke と Weber 2007]では,我々が使用しているアプローチは,一定の入射照明を用いた近距離場の散乱モデルに分類されています。したがって、以前の研究を活用して、\(R\)、\(TT\)、および\(TRT\)項を同一に保ちつつ、図5および13に示すように、\(TrT\)、\(TttT\)、\(TtrtT\)、\(TrRrT\)、および\(TttRttT\)経路のローブを追加することができます。このフレームワークは、一般的な高次の散乱を扱うこともできますが、我々の実験では、これらのパスからの寄与は重要ではありませんでした。
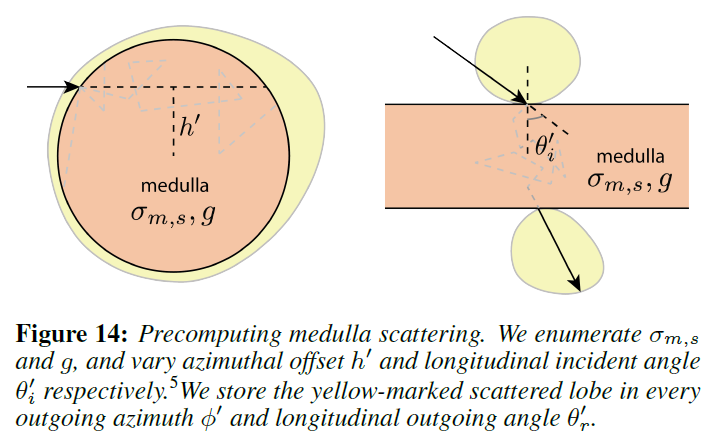
あとは、各ローブの方位角と緯度方向の散乱関数の形を見つけるだけです。概念的には,繊維に入射する光線の入射位置と方向が与えられれば,繊維の2次元の方位角および緯度方向の断面上で,その主鏡光線をレイトレースします [d’Eon ら 2011; Zinke ら 2008]。 主鏡光線がファイバーから出ていく方向をリフレタンス・ローブの中心と考え,減衰係数と鏡面経路に沿った方位角および緯度方向のラフネスをガウス型のアウトゴーイング・ローブの形で蓄積していきます。これは、図13の方位角セクションの\(TttT\)パス\(PQQ’P\)に示されています。実際には、閉形式の解析式を使って光線をトレースします。緯度方向の分布は、以前の研究に準拠してさらに単純化され、効果的なクチクラの傾き/ラフネスのためのオフセット/幅を持つガウスに縮小されます。最後に、髄質に入り、それによって散乱されるパスについては、散乱ローブも含めなければなりません(図13の\(Q’\)にある幅広い黄色のローブを参照)。[Donner ら 2009]に基づいて、2Dの方位/緯度方向のプロファイルに対して髄質の散乱を別々に事前計算し(図14)、散乱をテーブルルックアップに減らしました。
形式的には、各光線のニアフィールド散乱分布は
\begin{eqnarray}
S(\theta_i, \theta_r, \phi_i, \phi_r, h) = \frac{\sum_p M_p^u (\theta_i, \theta_r)N_p^u(h, \phi)}{\cos^2 \theta_i} + M^s (\theta_i, \theta_r, \phi) \frac{\sum_p N_p^s(h, \phi)}{\cos^2 \theta_i} \tag{8} \\
p \in \{ R, TT, TRT, TrT, TttT, TtrtT, TrRrT, TttRttT \}
\end{eqnarray}
ここで、\(\phi = \phi_r – \phi_i\)であり、\(M_p\)、\(N_p\)はそれぞれ緯度方向と方位角方向の散乱プロファイルで、表1のファーパラメータに依存します。式4をいくつかの点で一般化します。近接場散乱の場合は、\(h\)パラメータ(図5、13)に注意してください。上付きの\(s\)と\(u\)は、それぞれ髄膜で散乱された経路と、散乱されていない経路を表す。(単一の緯度方向の\(M^s\)がすべての散乱経路\(p\)に対して適切であることがわかります)。パス\(p\)には、これまでの毛髪モデルの\(R\)、\(TT\)、\(TRT\)に加え、毛皮に特有の新しい項も含まれています。\(R\)、\(TT\)、\(TRT\)、\(TrT\)、\(TrRrT\)のうち、髄質に伝わらないパスには、散乱していないローブだけが存在し、\(TttT\)、\(TtrtT\)、\(TttRttT\)には、散乱したローブと散乱していないローブの両方が存在することに注意してください。最後に、d’Eonら[2011]が分析したように、相互性を失う代償としてグレージング角でのエネルギー保存の問題を軽減するために、\(1/\cos^2 \theta_d\)項を\(1/\cos^2\theta_i\)に置き換えることを選択しました[Hery と Ramamoorthi 2012]。この置換により,式2で余弦項が完全に相殺されるため,レンダリングモデルも単純化されます。
Simple Lobes: 髄質に全く入らない光線を考えます(\(p \in \{R, TT, TRT, TrT, TrRrT\}\))。この場合、髄質からの散乱はないので、上付き文字を削除することができます。方位角方向のプロファイルは単純に
\begin{eqnarray}
N_p (h, \phi) = A_p(h) \cdot D_p(h, \phi) \tag{9}
\end{eqnarray}
ここで、\(A_p\)は経路\(p\)に沿った減衰で、キューティクル上のフレネル項と内部経路での吸収を考慮しています。\(D_p\) は,散乱エネルギーの方位角分布で,光線が相互作用したすべての表面からのラフネスを考慮して決定される幅を持つガウス分布です。\(A_p\)と\(D_p\)は、式12と式13の中で、非散乱ローブと同じ表現をしています。光線の緯度方向のプロファイルについては,[Marschner ら 2003; d’Eon ら 2011]に従い,ガウス分布で近似します。
\begin{eqnarray}
M_p(\theta_i, \theta_r) = G(\theta_r; – \theta_i + \alpha_p, \beta_p) \tag{10}
\end{eqnarray}
ここで,\(\alpha_p\)はキューティクルのスケールとの相互作用による経路\(p\)上の主鏡面線の累積角度傾斜であり,\(\beta_p\)は経路\(p\)のラフネスであり,これは経験的にキューティクルのラフネスの累積によって与えられます。これらの式は、毛髪モデルのローブ\(R\)、\(TT\)、\(TRT\)に関するこれまでの研究に還元されます。次に、髄質と相互作用する経路の一般的な定式化を行います。
7.2 Unscattered Lobes
まず、\(M_p^u\)と\(N_p^u\)の表現を用いて、髄質によって散乱されていないローブについて説明します。図13の方位角方向のプロファイルを考えます。概念的には、\(P\)に入射する主鏡面光線を2次元の方位角断面で光線追跡し、経路に沿って減衰とサーフェイスのラフネスを蓄積して、\(P’\)を中心とする出射ガウスローブの強度と幅を与えるだけです。実際には、光線追跡を単純な解析式で置き換えることができます。
興味深いのは、ある種のパスがオフセット時間内に特定の領域でのみ発生するということです(図13参照)。例えば、髄質の大きさに応じて、従来のヘアモデルのパス\(T\)、\(TT\)、\(TRT\)は\(h\)が大きい場合にのみ可能であり、そうでない場合は髄質に入らなければなりません。実際には、\(r_{i2} = 90^{\circ}\) および \(r_{t2} = 90^{\circ}\) に対応するこれらの領域の境界を幾何学的に解き、各領域内の関連するパスのみを考慮します。
Azimuthal Scattering Profile: 方位角プロファイルは式9で与えられますが、髄質に当たって入ってくる主鏡面反射については追加の処理が必要です(\(p \in \{TttT, TtrtT, TttRttT\}\))。この寄与を2つの項に分けます:1つは、事前に計算された髄質散乱に基づいて次のサブセクションで\(M^s\)と\(N^s\)を計算する多重散乱光、もう1つは、髄質を通過する際に単純に減衰する、ここで考慮する非散乱光です。例えば、図13に示すような\(TttT\)経路では
\begin{eqnarray}
N_p^u(h, \phi) = A_{Tt}(h) \cdot A_{tt}(h) \cdot A_{tT}(h) \cdot D_p^u(h, \phi) \tag{11}
\end{eqnarray}
ここで、\(A_{tt}\)は、髄質を透過する主鏡光線の減衰係数です(図13の\(QQ’\))。
このような背景から、一般的な高次パスの簡単な表現を書くことができ、これは出射\(TTRT\)と\(TTRT\)ローブにも使用することができます。\(p\)を長さ\(n\)の文字列と見なし、\(p_i(i = 1 \cdots n)\)が\(p\)の各頂点を表すとすると、次のように書けます。
\begin{eqnarray}
A_p(h) = \prod_{i=1}^{n} F(p_i) \cdot \prod_{i=2}^{n} \exp (-\sigma_t(p_{i-1} p_i) \cdot | p_{i-1} p_i | ) \tag{12}
\end{eqnarray}
ここで、\(F\)は(拡張)フレネル項、\(|p_{i-1} p_i|\)はセグメント\(p_{i-1}p_i\)の長さ、\(\sigma_t(p_{i-1}p_i)\)はセグメントの消衰係数として、コルテックスの\(\sigma_{c, a}\)または髄質の\(\sigma_{m, s}\)のいずれかに等しいです。
同様に、すべての交差点で、\(p\)の方向は角度\(\Gamma(p_i)\)だけ変化します。したがって、これらの偏差角を\(\Phi_p(h) = \pi + \sum_{i=1}^n \Gamma(p_i)\)として累積することで、出射方位角を算出することができ,ここで\(\pi\)は入射方位の反転を考慮しています。分布項\(D\)については、[d’Eon ら 2011; Zinke ら 2008]と同様に、経路\(p\)に沿った各交点\(p_i\)における粗さ、すなわち\(\beta^2\)を累積する。出射分布は\(\Phi_p(h)\)を中心としたガウスローブ\(G\)なので、解析的な形を導き出すことができます。
\begin{eqnarray}
D_p^u(h) = G \left ( \Phi_p(h), \sqrt{ \sum_{i=1}^n \beta^2(p_i)} \right) \tag{13}
\end{eqnarray}
ここで、交点\(p_i\)がキューティクル上にない場合、\(\beta(p_i)=0\)となる。明示的には、幅は大文字(コルテックス)の文字数で与えられ、\(p \in \{R\}\)については\(\beta\)、\(p \in \{TT, TrT, TttT, TtrtT\}\)については\(\sqrt{2}\beta\)、\(p \in \{TRT, TrRrT, TttRttR\}\)については\(\sqrt{3}\beta\)となります。
Longitudinal Scattering Profile: 散乱していない縦方向のプロファイルは、式10で与えられます。あとは、非散乱ローブの中心\(\alpha_p\)と幅\(\beta_p\)を決定するだけです。ここでは、\(R\)ローブと\(TT\)ローブのこれまでの研究に倣い、キューティクルの傾きと粗さに対応するRについては、\((\alpha_R、\beta_R) = (\alpha, \beta)\)とし、\((\alpha_{TT}, \beta_{TT}) = (-\alpha/2, -\beta/2)\)。その他のローブについては,近似的に
\begin{eqnarray}
\alpha_p &=& \alpha_{TT} – n_R \alpha \\
\beta_p &=& \beta_{TT} + n_R \beta + ( n {\rm mod} 2)(\beta / 2) \tag{14}
\end{eqnarray}
ここで,\(n\)は\(p\)の長さ,\(n_R\)は\(p\)に現れる\(R_s\)の数である。一般的な考え方は,キューティクルが反射するたびにその傾斜角が減少し,ラフネスが増加するというものである。最後の\(\beta/2\)は、後方に抜けるローブは通常前方のローブよりも広いため、これを補正する[d’Eon et al.] したがって、\(\alpha_p = \alpha\)は\(p \in R\)、\(\alpha_p = – \alpha/2\)は\(p \in \{TT, TrT, TttT, TtrtT\}\)、\(\alpha_p = -3 \alpha/2\)は\(p \in \{TT, TttT\}\)、\(\beta_p = \beta\)は\(p \in \{R, TrT, TtrtT\}\)、\(\beta_p = 2 \beta\)は\(p \in \{TRT, TrRrT, TttRttR\}\)を表します。我々の知る限り、緯度方向のローブのパラメータはほとんどの先行研究で経験的に与えられていました。式14は、先行研究を髄質に入る可能性のある一般的な経路に拡張するための合理的な近似式です。
7.3 Scattered Lobes
経路\(p \in \{TttT, TtrtT, TttRttR\}\)が内筒を通るときには散乱現象が起こり、この髄膜の散乱を考慮する必要があります(図13の\(Q’\)からの広い黄色のローブ)。実用的なレンダリングモデルを実現するために、我々は事前計算に頼り、完全な体積多重散乱計算に対していくつかの重要な近似を行っています。
Precomputation of Medulla Scattering: 我々の事前計算アプローチは、Donnerら[2009]による経験的なBSSRDFモデルと精神的に似ています。しかし,因数分解されたローブを使用しているため,図14に示すように,散乱パラメータのすべての可能な組み合わせについて,方位角成分と緯度方向成分を別々に2Dボリュームメトリックパストレーシングによって散乱プロファイルを事前に計算します。ここでは、髄質の表面効果(反射、屈折、フレネルなど)は考慮せず、代わりに評価ステップでこれらの効果を計算します。実際には、方位方向に\(C^N(\phi’, h’, \sigma{m, s}, g)\) ,緯度方向に\(C^M(\theta_r’, \theta_i’, \sigma_{m, s}, g)\)という4次元テーブルを事前に計算しています(3次元のパラメータセットに対する1次元のプロファイル)。表記と主要なパラメータを区別するために、素数を使用しています。この事前計算はシーンに依存せず、一度だけ行う必要があります。また、\(C^N\)と\(C^M\)をオンラインで公開し、他の研究者が直接使用できるようにしています。これらのテーブルは、圧縮後、約20MBしかありません。詳細は付録に記載されています。
Azimuthal Scattering Profile: 散乱ローブは通常、大きくて拡散性があるため、サーフェイスラフネスの小さな影響には大きく影響されません。また,コルテックスと空気の界面による屈折を無視し,髄質から出る光はコルテックスの厚さに対応する一定の係数で減衰すると仮定しています。さらに,事前に計算された髄質からの散乱ローブは,外部に透過した後も形状が変化しないと仮定しています。最後に,コルテックスで反射されない散乱ローブは1つだけであると仮定しています。
式11との類似性から、TttTパスからの方位角方向の散乱プロファイルは
\begin{eqnarray}
N_p^s(h, \phi) = A_{Tt}(h) \cdot {A’}_{tT}(h) \cdot D_p^s(h, \phi) \tag{15}
\end{eqnarray}
となります。なお、分布\(D^s\)は正規化されておらず、すでに検討した非散乱ローブによるエネルギー\(1-A_{tt}(h)\)の減少を考慮しています。最終的な減衰量\({A’}_{tT}\)は、コルテックスの厚さに対応する\(exp[-\sigma_{c, a} \cdot(1 – \kappa)]\)として単純に近似されます。ここで、単純に\(TtrtT\)の減衰項を1つ追加するだけです。
\begin{eqnarray}
N_p^s(h, \phi) = A_{Tt}(h) \cdot A_{tr}(h) \cdot {A’}_{tT}(h) \cdot D_p^s(h, \phi) \tag{15}
\end{eqnarray}
散乱したローブは最後の\(rt\)セグメントのみで発生し、それ以前のセグメントでの散乱は\(TttT\)の一部とみなされることに注意してください。\(TttRttT\)ローブについても同様の表現を用いることができます。より一般的には、散乱ローブの減衰は2つの部分から構成されます。まず、エネルギーが髄質に到達します。第二に、散乱されたエネルギーはさらに吸収され、コルテックスを通過します。
散乱ローブの分布項\(D\)は、事前に計算された方位角散乱プロファイル\(C^N(\phi’; h’, \sigma_{m, s}, g)\)への問い合わせに過ぎません。髄質を単位円として事前に計算しているので、\(h’\)と\(\sigma_{m, s}\)は半径\(\kappa\)で正規化する必要があり、次のようになります。
\begin{eqnarray}
D_p^s(h, \phi) = C^N(\phi – \Phi_p(h); h’/\kappa, \sigma_{m, s}/ \kappa, g) \tag{17}
\end{eqnarray}
ここで、\(\Phi_p\)は光線が髄質に入る角度です。
Longitudinal Scattering Profile: 緯度方向の散乱ローブ\(M^s\)は、どの種類のパス\(p\)も同じ\(\theta_i\)と\(\theta_r\)を持っているので、\(p\)-非依存である。しかし、それは\(\phi\)-依存です。Fig.14に示すように、事前に計算した緯度方向のプロファイルは、\(\phi=0\)(上側のローブ)と\(\phi=\pm 180^{\circ}\)(下側のローブ)の場合です。両方の方位で\(M^s\)を計算し、任意の\(\phi\)に対して結果を線形補間します。したがって,以下では簡単のために\(\phi\) を省略し,説明のために \(\phi=0\) とします。
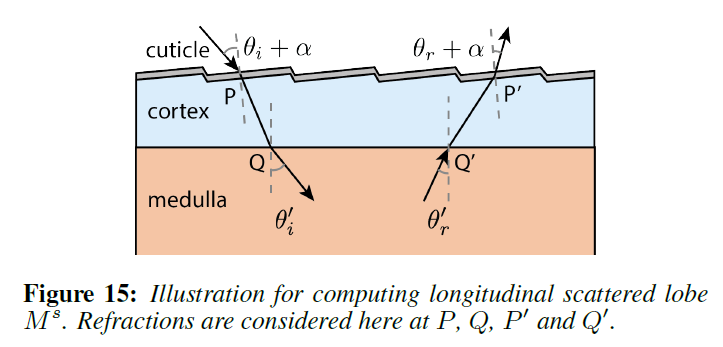
キューティクルとコルテックスを介した屈折を考慮して、あらかじめ計算された髄質\(C^M\)の緯度向の分布を照会しました。図15が示すように、\({\theta’}_i\)と\({\theta’}_r\)は幾何学的に解くことができました。方位角方向の場合と同様に、\({\theta’}_r\)で事前に計算された分布を問い合わせます。
\begin{eqnarray}
M^s(\theta_i, \theta_r) = \mu \cdot F_t \cdot C^M({\theta’}_r; {\theta’}_i, \sigma_{m, s} / \kappa, g) \tag{18}
\end{eqnarray}
ここで\(F_t = (1 – F(\theta_r + \alpha, l)) \cdot (1 – F({\theta’}_r))\)は(拡張)フレネル反射率の積であり,\(\mu\)は正規化項で詳細は付録に記載されています。
7.4 Implementation Details and Validation
Importance Sampling: 重点サンプリングの方法は[d’Eon ら 2013]と同様で,まずローブの選択を行い,次にこのローブを方位と緯度方向にサンプリングします。ここでは,散乱したローブをすべて一緒に扱います。散乱されていないローブ\(p\)が選ばれた場合、その方位角方向の出射中心\(\Phi_p(h)\)と対数方向の出射中心\(-\theta_i + \alpha_p\)の周りにガウスをサンプリングします。これにより、ほぼ完璧な重点サンプリング方式になります。散乱ローブを選択した場合、散乱ローブが滑らかであることを利用して、緯度方向には余弦加重サンプリングを、方位角方向には一様サンプリングを行います。与えられた出射方向のPDFを問い合わせる多重点サンプリングでは,まず同様にローブ選択を行い,次に散乱ローブと散乱上ローブのどちらを選択するかに応じて,出射方向の対応するPDF値を計算します。
Non-separable lobes: [d’Eon ら 2014]では,髪の毛の繊維を通る光の散乱を正確に捉えるために,分離不可能なローブ表現が導入されました。この表現では、緯度方向のローブの中心と幅は、さらに相対的な方位\(\phi\)に依存します。実際,原著論文のレンダリング結果と比較して,品質の向上が見られます。しかし、主な違いは、\(R\)ローブの形状であり、このローブだけが方位角の広い範囲に渡っていることがわかります。そこで、我々の二重円筒モデルに適用する際には、\(R\)ローブは単純に分離できないものとして表現し、他のローブは従来の表現のままにしています。
Validation: レンダリングモデルを用いて生成した2Dプロファイルを、実測データやシミュレーションと比較したのが図8です。我々のレンダリングモデルは,測定された反射率プロファイルとほぼ一致し,フルシミュレーションと同等の誤差(表2)を示し,場合によっては測定値に近い値を示すこともあります。これは、物理的な二重円筒モデルがまったく同じであるため、驚くことではありません。わずかな違いは,緯度方向および方位角方向の散乱プロファイルの因数分解,経験的な緯度方向ローブの中心と幅,髄質の散乱の近似値などの近似値に起因します。
8 Results
このセクションでは、我々のレンダリングモデルを使用して生成された結果と、従来の手法との視覚的な比較を示します。すべての結果は,我々のレンダリングモデルをMitsuba [Jakob 2010]のシェーダーとして使用しており,CPUはIntel 6コア3.6GHz i7 4960Xで,12スレッドにハイパースレッド化されています。ストランド数,サンプル数,タイミングなど,各シーンの統計データを表3に示します。時間はグローバルイルミネーションを含めたウォールクロックの実行時間であり,我々のモデルの評価コストは,ほぼ同じタイムが得られるMarschnerモデルの評価コストと同等です。すべてのシーンにおいて,異なる色を考慮した吸収項\(\sigma_{c, a}\)を除き,すべてのパラメータは表2のデータベースから直接得られたものです。また、\(\sigma_{c, a}\)に髄質指数 \(\kappa\) を乗じることで、髄質が光を吸収しないことを考慮しています。なお,オオカミとシマリスについては,対応する毛皮のサンプルがないため,データベースにあるイヌとネズミのパラメータを参考にしています。
比較の際には、[d’Eon ら 2011]をMarschnerモデルの正しい実装とみなし、生成された暗い外観は、エネルギー保存の問題ではなく、モデル自体の鏡面性に起因するものとしています。また,Marschnerモデルについては,方位角のラフネスを大きくするなどの産業界の場当たり的な設定ではなく,図11から得られた最適化されたフィッティングパラメータを用いています。Kajiya-Kayモデルでは、モデル自体がエネルギー保存するものではないため、式3を正規化してグローバルイルミネーションを有効にしています。
Wolf: 図1は、ウルフモデルのレンダリング結果を、Marschnerモデルと並べて比較したものです。ウルフモデルはターンテーブルの上に置かれており、ビデオの中で回転させることで、我々のレンダリングモデルの一貫性を示しています。レンダリングの前に環境照明を手動でぼかしている。MarschnerモデルとKajiya-Kayモデルとの比較のために、挿入図を掲載しています。すべてのレンダリングは,解像度\(1920 \times 1080\),ピクセルあたり\(1600\)サンプル(spp)を用いてパストレース(繊維と環境間のグローバルイルミネーション)されています。我々の二重円筒モデルは、拡散して飽和した外観になっていますが、Marschnerモデルは、高い鏡面性と暗さを表現しています。なお、Marschnerモデルよりも我々のモデルの方が、局所的なコントラストが低いため、視覚的には明らかではありません。Kajiya-Kayモデルは、グローバルイルミネーションでも硬くて固い印象を与えます。直感的には、我々のモデルと比較して、BRDF対BSDRDF(BCSDF)の比較に視覚的に似ています。
Cat: 図16では、環境照明の下で被写界深度効果を用いて猫の頭部をクローズアップし、毛皮の繊維一本一本のディテールを表現しています。データベースに登録されている猫の毛皮の最適化されたフィットパラメータを使用しています。すべてのレンダリングは、\(2500\) sppのサンプリングレートと\(1024 \times 1024\)の解像度を使用しています。このレンダリングでは、配置や向きの違いにより、ぼやけた部分(目の左上)とはっきりとした外観(ヒゲの周り)の両方が生じていることがわかります。
また、アーティストがモデルの主要なパラメータを手動で変更して、さまざまな外観を得る方法も紹介します。図16は、散乱係数\(\sigma_{m, s}\)と髄質の大きさ\(\kappa\)を変化させた場合のレンダリング結果です。芸術的には、\(\sigma_{m, s}\)は彩度を密接にコントロールし、\(\kappa\)は「鏡面性」、つまり髪の毛と毛皮の類似性の度合いを決定することがわかります。動画では、環境照明を回転させて、異なる照明条件の下で猫の毛が金色から濃いオレンジ色へと色が変化する様子を示しています。
Chipmunk: 図17は、シャープで強いエリアライトと、比較的薄暗い環境光で撮影しています。シマリスの皮膚は濃い色をしている。Marschnerモデルでは、光が繊維を透過して皮膚に当たるため、ここでも非現実的な鏡面性と暗さが表現されます。しかし、Marschnerモデルでは、一次色(無色)と二次色(有色)のハイライトが見えています。どちらのモデルも \(1600\) spp、解像度 \(1920 \times 1080\) でレンダリングされています。動画では、エリアライトを回転させて動くハイライトを確認していますが、他の部分はモデルが完全に暗くなることはありません。
Fur pelt: 図18は、\(1024 \times 1024\)の解像度で\(1024\)sppを使ってレンダリングされたチェッカーボードの上に置かれた毛皮の毛束です。大きなエリアライトが左上から毛皮を照らしています。我々のモデルは拡散して飽和したようなリアルな表現になっているのに対し、Kajiya-Kayモデルは硬くてしっかりした表現になっています。Marchnerモデルでは、古典的な一次および二次ハイライトが得られますが、その他の領域は黒くなります。[Zinke ら 2009]の提案(業界で広く採用されているソリューション)のように、Marchnerモデルに拡散ローブをブレンドすることで、拡散的な外観を作り出すことができます。しかし、このブレンド技術は、特に反射ローブ\(R\)について、Marschnerモデルの元のローブの強度を下げてしまうため、フラットな外観になってしまいます。また、この手法は経験的なものであり、拡散ローブの存在を物理的に説明することはできません。
9 Discussion and Limitations
More complex animal fur: 現実の動物の毛皮は、このモデルでは表現できないほど複雑になっています。私たちの観察は、光学特性に影響を与える構造的特徴の一部にのみ焦点を当てています。これまでの研究では省略されてきた毛皮繊維の最も重要な光学特性を捉えていますが、それ以外の側面は無視しています。例えば、現在、私たちは対称的な繊維にのみ注目しており、反射パターンに対称性がない測定サンプルは破棄しています。しかし,私たちのモデルは,不規則な形状の方位角の断面など,他の興味深い特徴をさらに考慮するための良い出発点になると考えています。動物の毛皮に関するより詳細な観察結果については,[Deedrick と Koch 2004a; Deedrick と Koch 2004b]を参照してください。
Medulla scattering approximations: レンダリングモデルの重要な点は、従来の研究では必要とされていなかった、髄質の散乱を効率的に事前計算することです。我々は因数分解化されたローブ近似を求めているので,方位角方向と緯度方向のプロファイルについて別々のシミュレーションを行いました。この因数分解化された事前計算では正確な結果が得られますが,直交する方位角/緯度方向の平面における2次元散乱の近似が必要となるため,さらなる評価が必要です。今後の研究では、この近似の限界や、より一般的な散乱ローブについて調査する予定です。
Application to human hair/ これまでのヘアモデルは、我々の研究から恩恵を受けることができます。最も重要な理由は、人間の髪の毛の繊維の中に目に見える髄質が存在する可能性があるからです[Deedrick と Koch 2004a]。さらに、アーティストは髪の毛がより拡散して飽和した外観を示すことを望むかもしれませんが、これは従来のモデルでは、特にヘアスタンドの数が限られている場合、簡単には扱えません。
10 Conclusions and Future Work
動物の毛皮の繊維の外観を正確に捉えるために、物理的に正確な毛皮の反射率モデルを提示しました。このモデルは、毛皮繊維を二重円筒として扱い、内部に髄質散乱が存在することを考慮したニアフィールドベースのモデルです。また、事前に計算された経験的な髄質の散乱プロファイルに基づいて、レンダリングのための高速評価アルゴリズムを導き出します。このレンダリングモデルは,フルボリュームシミュレーションと同等の誤差で,測定データによく適合することを実証しました。また、多くの動物の毛皮繊維の反射率の測定結果をコンピュータグラフィックスで初めてデータベース化し、生の2次元散乱プロファイルとフィットパラメータの両方を提供しています。我々のモデルは、様々なリアルな動物の毛皮の外観を生成することができ、従来の手法よりも大幅にリアルな結果が得られることを示しています。
将来的には、このモデルを前処理のない完全な解析モデルにする可能性を探りたいと思います。また、不規則な繊維断面、複雑なクチクラのスケール配置、不連続な図室など、より多くの特徴を扱えるように拡張することも興味深いです。また、芸術的な観点からの再解釈が生まれれば、産業界にもメリットがあるかもしれません。最後に,コーン・トレーシング[Qin et al. 2014]のような手法を用いてレンダリングを高速化する可能性が考えられます。我々のモデルを使って近似多重散乱を行う高速で正確な方法は、リアルタイムファーレンダリングアプリケーションに大きく貢献するでしょう。
11 Acnowledgements
和訳省略。
Appendix
Precomputation and Compression: 散乱係数\(\sigma_{m, s} \in [0, 20]\)と異方性\(g \in [0.0, 0.8]\)を列挙し、異なる入射方向を指定する追加のパラメータを変化させます。方位角プロファイルでは,すべてのサブパスが水平に髄質に入ると仮定して,オフセット\(h’ \in [-1, 1]\)とします(図14)。縦方向のプロファイルでは、入射角\({\theta’}_i \in [-\pi/2, pi/2]\)です。\(g\)の範囲を16ステップに離散化し、他のパラメータについては64ステップとしました。
入射パスが単位エネルギーを運ぶと仮定して,2Dの体積パストレーシングを用いて,髄質の方位角と緯度方向の散乱プロファイルを別々にシミュレーションしました。方位角方向には滑らかな単位円を、緯度方向には距離2のダブルスラブをトレースします。すべての散乱現象に対して,平面的なHenyey-Greenstein位相関数[Davis 2006]を使用しています。
\begin{eqnarray}
\rho(\theta, g) = \left (\frac{1}{2\pi} \right ) \frac{1-g^2}{1 + g^2 – 2 g \cos \theta} \tag{19}
\end{eqnarray}
異方性を考慮するために、\(\theta\)は各散乱イベントが以前の経路から逸脱する角度である。
事前に計算された各出射プロファイルは、全方向をカバーする720個のビンを使って格納され、出射エネルギーが記録されます。縦方向の散乱については,上部ローブと下部ローブをそれぞれさらに正規化し,両者をPDF化します。そして,次のステップでの便宜のために,それらのCDFを蓄積します。これらのプロファイルは一般的に滑らかであるため、各プロファイルを4つのセグメントに分割してさらに圧縮し、各セグメントを二次関数でフィットさせます。
Refining azimuthal scattered lobes: フレネル効果により、散乱したローブは髄質やキューティクルの表面で反射され、さらに散乱してより滑らかになります。この割合を\(\lambda = 1 – (1 – F(\pi/2))(1 – F(\pi/2, l))\)と近似します。これは、多重内部反射を無視して、2つの界面を垂直に透過した後の残りのエネルギーです。そのため、方位角方向の散乱ローブは次のように拡張できます。
\begin{eqnarray}
N_p^s(h, \phi) = A_p^s(h) \cdot [D_p^s(h, \phi) \cdot(1 – \lambda) + I_j^s \cdot \lambda] \tag{20}
\end{eqnarray}
ここで,より多くの散乱現象が起こった後,反射された後方散乱ローブが等方的になるという仮定の下で,\(I_j^s = [1 – {\rm exp}(- \sigma_{m, s} \cdot |p_j p_{j+1}|] / 2\pi\)は散乱したエネルギーの一様分布です。\(j\)はパスが髄質に入って散乱する頂点の位置で,\(A^s\)は散乱ローブの有効減衰量です。
Normalizing longitudinal scattered lobes: 最終的な緯度方向の散乱ローブ\(M^s\)は正規化されているので、\(\int M^s d\theta_r = 1\)となります。式18によれば\(\int F_t \cdot C^M d\theta_r = 1 /\mu\)となります。このとき,およそ\(\int F_t d \theta_r \cdot \int F_t \cdot C^M d \theta_r = 1 /\mu\)となります。この2つの独立した積分を\(U\)と\(V\)とすると、\(U\)はある種の毛皮が読み込まれたときに数値的に計算でき、オンザフライでレンダリングしてもオーバーヘッドが発生しないことがわかりました。\(V\)については、まず積分領域を\({\theta’}_r\)に変換し、\(P’\)と\(Q’\)におけるスネルの法則の式を微分して\(\frac{d{\theta’}_r}{d\theta_r} \approx \frac{\cos\theta_r}{\eta_c \cos {\theta’}_r}\)を使用します。そうすれば、\(C^M\)が積分されるべき\({\theta’}_r\)の範囲がわかります。事前に計算された\(C^M\)は正規化されたPDFであるため、積分はそのCDFに対する問い合わせであり、これは単に事前計算ステップで蓄積されたものです。そのため、正規化係数として\(\mu = (UV)^{-1}\)を使用します。