わふー。Pocolです。
今日は，Weta Digitalによる
[d’Eon 2011] Eugene d’Eon, Guillaume Francois, Martin Hill, Joe Letteri, Jean-Marie Aubry, “An Energy-Conserving Hair Reflectance Model”, Eurographics Symposium on Rendering 2011, Vol.30, No.4, 2011.
を読んでみることにします。
いつもながら、誤字・誤訳があるかと思いますので，ご指摘頂ける場合は正しい翻訳例と共に指摘して頂けると幸いです。

Abstract

人毛繊維のような粗い表面を持つ誘電体円柱の反射率モデルを紹介します。このモデルはエネルギー保存し、任意の数の内部反射を評価することができます。スペキュラコーンの圧縮と収縮を考慮することで、非ガウス型でオフスペキュラピークを含む新しい緯度散乱関数が得られます。方位角方向のラフネスを考慮すると、ヘアファイバー全体での積分となり、ガウス求積法を用いて効率的に評価することができます。三次方程式を解く必要がなく，コースティクスも一貫した方法でモデルに含まれ，多くの内部経路を考慮することで，より正確な色を予測することができます。

1. Introduction

髪の毛や毛皮の反射率を正確に計算することは、映画やゲームのキャラクターをリアルに表現するために非常に重要です。この目標を達成するための最初のステップは、個々の髪の毛からの反射率の正確なモデルを所有することです。Marschnerら[MJC*03]によるこの課題に関する代表的な研究は、内部屈折経路分析に基づく解析的な因数分解モデルを提示しています。このモデルは広く普及していますが、いくつかの単純化された仮定に基づいているため、吸収率の低い髪（明るい金髪や白髪など）、グレージング角度の照明、高いサーフェイスラフネスの場合には精度が制限されます。約10年前には、実測データと一致する最も効率的なモデルを得るために、近似値が選択されていました。今日では、Marschnerらのモデルを粗いサーフェイスに適用することを再検討し、いくつかの望ましい特性を持つより複雑な散乱関数を導き出すことが実用的であると考えています。

2. Related work

この論文では、物理ベースの解析的なファイバー反射率モデルにのみ焦点を当てます。Kajiya と Kay [KK89] はそのようなモデルを初めて発表しました。このモデルは Marschner ら [MJC*03] によって，方位角方向の反射率の変化を考慮し，内部吸収とコースティクスを考慮することで大幅に改良されました。Marschnerら[MJC*03]の方法は、いくつかの論文で拡張されています。ZinkeとWeber[ZW07]は，毛髪繊維の近距離のレンダリングやグローバルイルミネーションに重要な，BCSDF（双方向曲線散乱分布関数）とニアフィールドモデルの形式を導入しました。彼らはまた、我々の新しいモデルの方位角成分と非常によく似たファーフィールドモデルを発表しましたが、方位角方向のラフネスの扱いが異なっていました。

Zinkeら[ZRL*09]は，非物理的な拡散項と主反射項をスケーリングするパラメータを追加することで，Marschnerら[MJC*03]のモデルを実測データにフィッティングする際の精度が向上することを見出しました。Sadeghiら[SPJT10]は、Marschnerモデルの使用を簡略化したアーティストフレンドリーなモデルを発表しました。これらの修正は実際には有用ですが、本稿の目的であるグローバルにエネルギーを保存するモデルを提供するものではありません。

Ogakiら[OTS10]は，ユーザがモデル化した半透明の毛髪繊維の微細形状を介したフォトン・トレーシングに基づいて，毛髪の反射率関数を生成するシミュレーション主導のアプローチを提案しています。結果として得られた反射率データは、Nguyen と Donnelly [ND05]が提案したようなテーブルに格納され、リアルタイムのヘアレンダリングに利用されます。この方法では、エネルギーを保存したモデルを作成することができますが、解析的なパラメトリックモデルの制御ができないため、ユーザーが希望する髪型のマイクロジオメトリを測定し、モデル化する必要があります。

私たちのモデルは、ヘアボリューム内の多重散乱を計算する従来の方法に効率的に組み込みすることができます[LV00, MM06, ZYWK08, SSD*10]。ヘアシェーディング、アニメーション、モデリング技術の広範な批評については、Wardらによる調査を参照してください[WBK*07]。

3. Factored Hair Reflectance Models

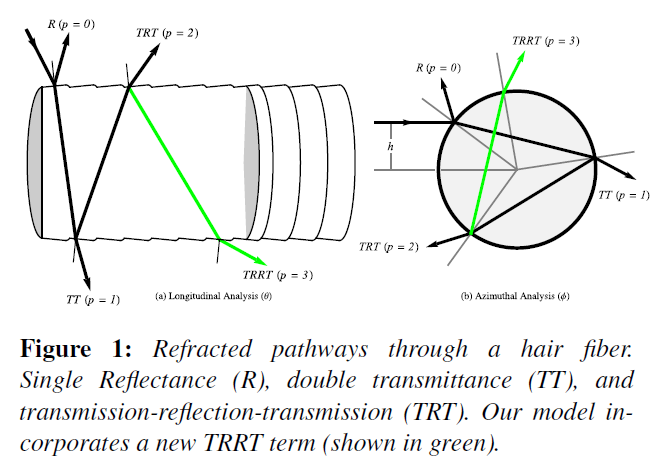
Marschnerら[MJC*03]の解析モデルでは，反射率を別々の伝搬モデルに分解することで，豊富な現象を予測しています。彼らは、最初の3つのモード(直接反射(R)、2回透過(TT)、正確に1回の内部反射を伴う経路のセット(TRT))に対するソリューションを提示しています(図1)。我々の新しいモデルの基礎となる、Marschnerらによる滑らかな髪の毛の繊維に対する因数分解された経路分析をレビューし、続いて表面の粗さを処理する方法を検討します。

※図は[d’Eon 2011]より引用。

　ここでは，Marschnerら[MJC*03]の表記法を採用し，入射方向と反射方向の関数として記述されたパラメトリックな毛髪反射率モデルを，それぞれ\({\vec {\omega}_i}\)と\({\vec {\omega}_r}\)と表記しています。毛髪のローカル座標系{\({\vec u}\), \({\vec v}\), \({\vec w}\)}は、毛髪の成長方向に\({\vec u}\)が接しており、{\({\vec v}\), \({\vec w}\)}で囲まれた平面を法線平面と呼びます。対称性があるため、法線面に対する緯度の傾き\(\theta_i\)と\(\theta_r\)、および相対的な方位\(\phi=\phi_r – \phi_i\)でパラメータ化することができます。経度方向の差角\(\theta_d = (\theta_r – \theta_i) / 2\)と半角\(\theta_h = (\theta_r + \theta_i) / 2\)を参照することで表記を簡略化しています。髪の毛の屈折率\(\eta\)は、通常1.55に固定されています。毛髪内部の吸収は、主にユーメラニンとフェオメラニンの2つの色素によるもので、それぞれの濃度は\(\rho_e\)と\(\rho_p\)です。各波長の光に対するユーメラニン\(\sigma_{a,e}\)とフェオメラニン\(\sigma_{a,p}\)の吸収断面積（6.1項参照）を考えると、分光吸収係数は\(\mu_a = \rho_e \sigma_{a, e} + \rho_p \sigma_{a, p}\)となります。

因数分解化された反射率モデル\(S(\theta_i, \theta_r, \phi)\)は，理想化された滑らかな円形の毛髪繊維のBravais特性を利用したものです。全反射率は，毛髪の内部にある\(p \in \{R = 0, TT = 1, TRT= 2, TRRT=3, \cdots \}\)の毛髪から出る前のパスセグメント\(p\)の数によってインデックスされた寄与の合計に分解されます(図1参照)。全反射関数\(S\)は、そのような構成要素の散乱関数\(S_p\)の総和です。

\begin{eqnarray}
S(\theta_i, \theta_r, \phi) = \sum_{p=0}^{\infty} S_p(\theta_i, \theta_r, \phi) \tag{1}
\end{eqnarray}

それぞれが緯度散乱関数\(M_p\)(図1a)と方位角散乱関数\(N_p\)(図1b)に因数分解されます。

\begin{eqnarray}
S_p(\theta_i, \theta_r, \phi) = M_p(\theta_i, \theta_r) N_p(\theta_i, \theta_r, \phi) \tag{2}
\end{eqnarray}

表面が滑らかな円形のファイバーでは、最初の4つの散乱関数\(S_p\)を正確に解くことができます。楕円形の毛髪繊維、表面の粗さ、傾いたキューティクルのスケールによる影響は、理想化されたモデルを適切な方法で修正することにより、近似的に導入されます。

4. Longitudinal Scattering

ここでは、均一な白色環境下で、非吸収の毛髪繊維を観察するという思考実験を考えます。\(1/{\eta}^2\)の立体角の圧縮と収縮が相殺され、すべての経路が白につながるため、髪の毛は白い背景と区別がつきません。この問題（具体的には、等価逆問題）の解析により、Marschnerら[MJC*03]の粗い毛への過去の拡張は、すべてのラフネスと照明/視野の角度に対してエネルギー保存的ではないことを示しています。我々は同じ分析を用いて、我々の新しい提案する散乱関数のエネルギー保存性を示します。

4.1. The Gaussian \(M_p\) Longitudinal Scattering Function

Marschnerら[MJC*03]は，表面が粗い毛髪繊維からの反射率をシミュレートするための効率的な方法を提案しています。滑らかな円形の毛髪という理想的なケースでは、単一の入射傾斜\(\theta_i\)に沿って到達した光は、スペキュラーコーン\(\theta_r = -\theta_i\)に限定された反射光を生成します（図2左）。これにより、すべての\(p\)に対して緯度散乱関数\(M_p\)が得られ、エネルギーが保存されます。髪の毛の表面のラフネスによる完全な鏡面円錐からの反射方向のずれをシミュレートするために、Marschnerら[MJC*03]は、半角のガウス関数を使うことを提案しています。

\begin{eqnarray}
M_p = g(\beta_p; \theta_h – \alpha_p) \tag{3}
\end{eqnarray}

ただし，

\begin{eqnarray}
g(\beta; \theta) = \frac{e^{-\theta^2 / (2\beta^2)}}{\sqrt{2\pi} \beta} \tag{4}
\end{eqnarray}

は緯度の傾き\(\theta\)の正規化されたガウシアンで、\(\beta\)はラフネスの項（具体的にはスペキュラーコーンからの緯度の偏向の標準偏差），\(\alpha_p\)はキューティクルスケールの傾斜の単純な関数です(図1)。式(3)の放射輝度の角度再配分は、いくつかの理由で非保存的です。

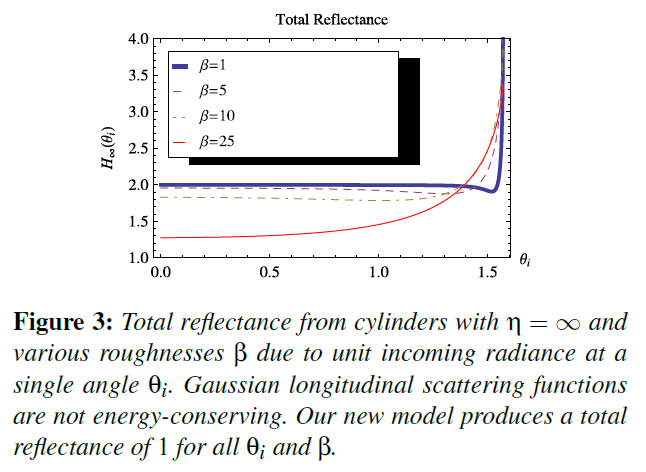
• 式(4)のガウスは\(\theta \in \{-\infty, \infty\}\)に対して正規化されていますが、\(\theta_h \in \{-\pi/2, \pi/2\}\)で評価されています。また、\(\theta\)の代わりに\(\theta_h\)を使うと、反射エネルギーが平均して2倍になります(図3)。
• あるスペキュラーコーン\(-\theta_i\)から別のスペキュラーコーン\(-\theta_r\)への光の偏向は、\(\theta_i \neq – \theta_r\)のときにコーンの圧縮または収縮を伴う（図2参照)。これはMarschnerら[MJC*03]の\(1/\cos^2 \theta_d\)項でおおよそ説明できる程度です。
• グレージング照明角付近での偏向は、かなりのエネルギーを範囲\(\theta \in \{-\pi/2, \pi/2\}\)の外の角度（絶対に受け取れない角度）に移動させ、エネルギーを失わせます。

※図は[d’Eon 2011]より引用。

この非保存的な散乱の特徴は、単位単方向の照明の下で、吸収のない(\(\mu_a = 0)\)ヘアファイバーの全反射を考えることで見ることができます。分析を簡単にするために、\(\rm R\)にすべてのエネルギーを反射させる（屈折率を\(\infty\)にする）ことによってのみ、\(M_{\rm R}\)の挙動を観察します。このとき、全反射エネルギーは次のようになります。

\begin{eqnarray}
H_{\infty} (\theta_i) = \int_{-\pi}^{\pi} \lbrack \int_{-\pi/2}^{\pi/2} N_R(\phi) \frac{M_R(\beta_R, \theta_h)}{\cos^2 \theta_d} \cos^2 \theta_r d \theta_r \rbrack d \phi \tag{5}
\end{eqnarray}

ここで，

\begin{eqnarray}
N_R(\phi) = (1/4) | \cos(\phi/2) | \tag{6}
\end{eqnarray}

は，\(R\)についての方位角の散乱関数で\(M_R = g(\beta_R; \theta_h)\)[MJC*03]です。様々なレベルのサーフェイスラフネスに対する全反射率のプロットを図3に示します。ガウス型の\(M_p\)関数は、グレージング角に対して余分なエネルギーを生み出します。小さなラフネスの場合、ほとんどの\(\theta_i\)の値で全エネルギーは2に近くなります（\(\theta\)で正規化された分布関数で\(\theta_h\)を使用しているため）。このエネルギーの倍増は、\(M_R = g(\beta_R; 2 \theta_h)\)[ZW07, ZYWK08]に変更することで解消されました。しかし、ガウシアンでは、グレージング角では余分なエネルギーが発生し、高いラフネスではエネルギーが失われます。TTやTRTなどの他の項でも同じような挙動が見られます。実際、式(5)は、\(\mu_a = 0\)、\(\alpha_p\)と\(\beta_p\)が全ての\(p\)に対して一定であるとすると、屈折率\(\eta = 1.55\)の髪の全反射を考えることと同等です（緯度関数\(M_p\)はその後全て等しくなり、因数分解され、単位積分の方位分布関数\(\sum_{p=0}^{\infty} N_p(\phi)\)が\(N_R(\phi)\)の代わりとなります）。

※図は[d’Eon 2011]より引用。

4.2. An Energy-Conserving Longitudinal Scattering Function \(M_p\)

我々は、反射された放射輝度を球体上の方向に保存的に再分配する新しい緯度散乱関数を導き出しました。これは、球面ガウスの畳み込みを採用することで実現しています。因数分解された反射率モデルで使用するために、方位角方向の挙動を平均化することで、純粋な緯度関数を導き出します。ここでは，球の表面上のディラック円の球面ガウス畳み込みを考えます。得られた分布の緯度のプロファイルが、新しい散乱関数です。完全な導出については、付録Aを参照してください。結果として得られる関数は以下の通りです。

\begin{eqnarray}
M_p (v, \theta_i, \theta_r) = \frac{{\rm csch}(1/v)}{2v} e^{\frac{\sin(-\theta_i) \sin\theta_r}{v}} I_o \lbrack \frac{\cos(-\theta_i)\cos\theta_r}{v} \rbrack \tag{7}
\end{eqnarray}

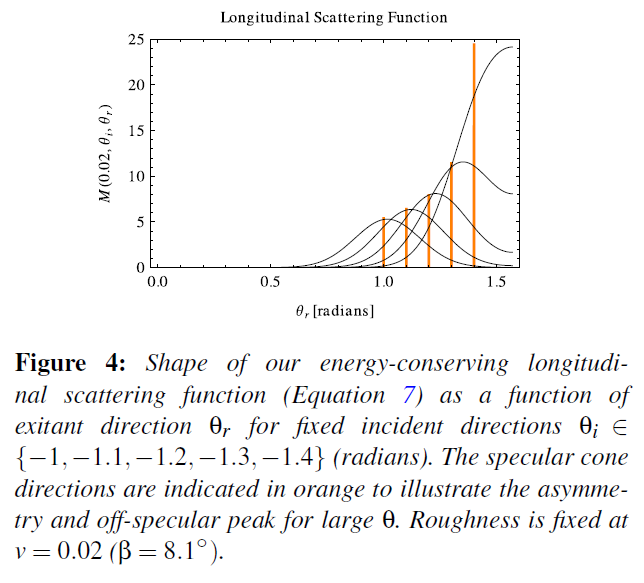
ここで，\(v = \beta^2\)はラフネス分散で\(I_o(x)\)は第1種変形ベッセル関数です。新しい緯度散乱関数の形状を、さまざまな入射角について図4に示します。これはスペキュラーコーンの角度に対して非対称で、平面BRDFに似たオフスペキュラーピークを示しており、すべての粗さに対してエネルギー保存性があります：

\begin{eqnarray}
H_{\infty} = \int_{-\pi}^{\pi} \lbrack \int_{-\pi/2}^{\pi/2} N_R(\phi) M_p(v, \theta_i, \theta_r) \cos\theta_i d\theta_i \rbrack d\phi = 1
\end{eqnarray}

なお、すべての入射角と出射角は1つの逆数関数(式7)に含まれています。これはラスタライズの枠組みでは便利なことで、あるピクセルに対するあるファイバーの寄与は、そのピクセルのカバー率\(C\)と、最終的な散乱関数\(S\)(式(1))，そして\(CS(\theta_i, \theta_r, \phi)\)に比例します。従来のモデルで必要とされていた、ピクセル内の髪の毛の長さ、髪の毛の幅、\(\cos \theta_i\)、\(\frac{1}{\cos^2\theta_d}\)の要素がありません。BCSDFへの変換は簡単に行えます。

※図は[d’Eon 2011]より引用。

5. Azimuthal Scattering

Marschnerら[MJC*03]は，平滑な円柱のBravais特性を利用して，ファイバー内部の方位角方向の散乱挙動を，緯度方向の挙動とは別に解析しています。修正された屈折率\(\eta’ = \frac{\sqrt{\eta^2 – \sin^2 \theta_d}}{\cos \theta_d}\)を用いることで、一般的な解析を法線面のみでの同等の解析に制限することができます。方位角方向の正味の変化\(\Phi\)は，毛髪繊維からのオフセット\(h \in \{-1, 1\}\)(図1b)と，考慮される反射のモードである\(p\)に，次のように関係します。

\begin{eqnarray}
\Phi (p, h) = 2 p \gamma_t – 2\gamma_i + p \pi \tag{8}
\end{eqnarray}

ここで，\(\gamma_i = {\rm argcsin}(h)\)で\(\gamma_t = {\rm arcsin}(\frac{h}{\eta’})\)です。
　式(8)が与えられたとき、Marschnerら[MJC*03]は、光が髪の毛からカメラに向かって出るようなすべての値\(h\)を解く（\(\Phi(p, h) = \phi\)となるような\(h\)を見つける）ことになります。吸収、フレネル、および式(8)の微分により、この離散的な経路セットに沿って出射する放射輝度が生成されます。\(R\)反射モードの場合、最終的な\(N\)関数は単純にコサインとなります(式(6))。高次の項になると急激に複雑になります。TTの場合、単一の正確な\(h\)の解は

\begin{eqnarray}
h_{TT} = \frac{{\rm sign}(\phi) \cos(\phi/2)}{\sqrt{1 + a^2 – 2a {\rm sign}(\phi) \sin(\phi/2)}}
\end{eqnarray}

ここで，\(a = 1/\eta’\)です。TRTパスでは、与えられた\(\phi\)に対して1つまたは3つの\(h\)の値が存在し、具体的には次のような解となります。

\begin{eqnarray}
\sin(\phi/2) = -h + 2a^2 h^3 + 2 a h \sqrt{1 – h^2} \sqrt{1 – a^2 h^2} \tag{9}
\end{eqnarray}

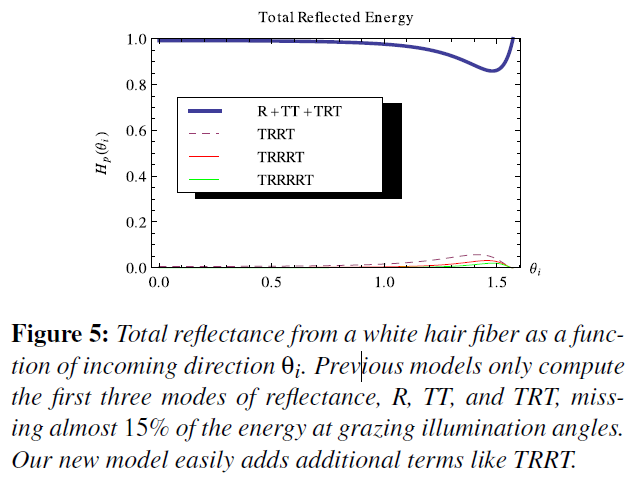
上記は、閉形式で存在しますが、実装するにはかなり複雑で不便です。TRRTには閉形式の解が存在しますが、TRRRTには存在しません。吸収が大きい場合、高次項\(p \gt 2\)は無視できる程度ですが、吸収が非常に小さい毛（白髪など）では、入射角が大きい場合、反射エネルギーの15%近くがTRRTと高次項によるものになります(図5)。

※図は[d’Eon 2011]より引用。

Marschnerら[MJC*03]は、\(h\)を解く際に式(8)の3次近似を用いて、高次の項の複雑さを軽減し、任意の望ましい反射モード\(p\)に対する近似的な解法を提供しています。しかし、この近似の精度は、\(p\)が大きい場合や、相対屈折率が低い場合(水中の髪の毛に生じる)には検証されていません。

ルートソルバーを必要とする複雑さに加えて、\(h\)を解くというアプローチは、コースティクスによる特異点によってさらに制限され、それを制御するためのアドホックなユーザー定義のパラメータが必要となります。さらに、ラフネスに依存しない離散的な方位角の経路を考慮すると、ラフネスの増加に伴って発生する出射方向の広がりやカラーシフトを説明できません。本研究では、高次の散乱項まで容易に拡張でき、コースティクスを一貫して安定的に含み、ラフネスに依存したカラーシフトを示す代替の方位角散乱関数を提示します。

5.1. Roughened Azimuthal Scattering Functions \(N_p\)

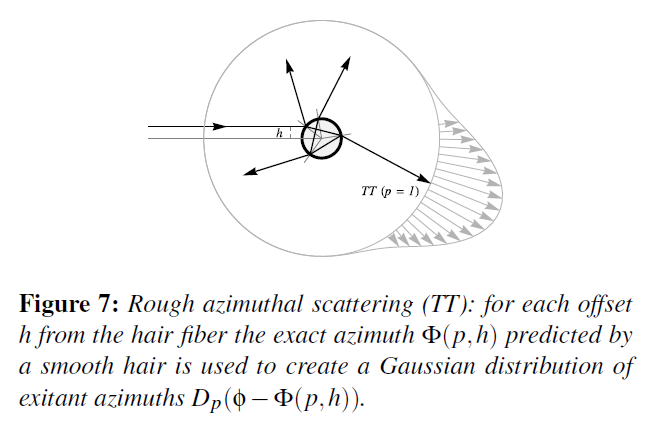
法線面での偏差のガウス分布を仮定することによって、表面の粗さの影響をシミュレーションしました。ファイバーの各オフセット\(h\)は，出射方位\(D_p(\phi – \Phi(p, h))\)の連続的な分布を生み出します。これらの分布は\(\phi\)状でガウス型で、滑らかな髪の毛で予測される離散的な方位\(\Phi(p, h)\)を中心にしています(図7)。全出射量は，ファイバー全体で積分することで求められます。

\begin{eqnarray}
N_p(\phi) = \frac{1}{2} \int_{-1}^{1} A(p, h) D_p(\phi – \Phi(p, h)) dh \tag{10}
\end{eqnarray}

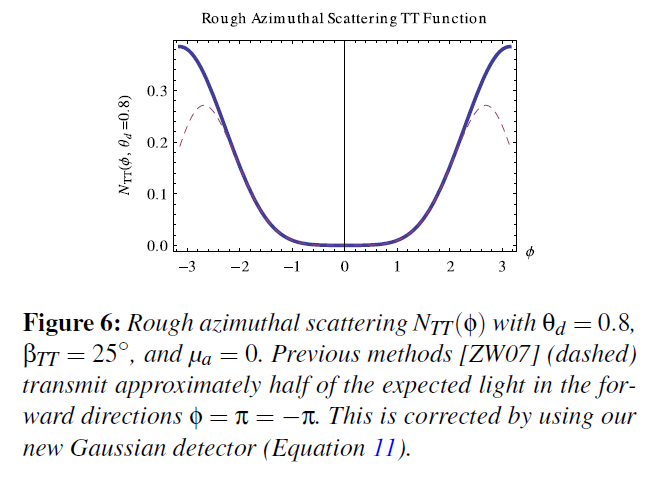
ここで、\(A(p, h)\)は吸収とフレネル[MJC*03]による各経路での減衰量です。我々は、\(2\pi\)という全ての倍数の等価性を持つ特殊な正規化ガウス関数\(D_p\)を採用しています。\(2\pi\)の倍数での検出は、すべての出射光を考慮するために重要です。出射光は、\(p \gt 1\)の場合、毛髪内部で完全な方位角の回転を数回繰り返すことがあります。Zinke と Weber [ZW07]の処理では、この効果が完全には解消されていないことがわかりました（例えば、\(\pi – \epsilon\)と\(-\pi + \epsilon\)といった値の近接性は処理されていませんでした。図6参照）。この新しい分布関数をGaussian detectorと呼ぶことにします。

\begin{eqnarray}
D_p(\phi) = \sum_{k=-\infty}^{\infty} g(\beta_p; \phi – 2 \pi k) \tag{11}
\end{eqnarray}

法線面の粗さは、緯度方向の機能で使用したのと同じ標準偏差\(\beta_p\)を使用したり、異方性のある粗さを生成するために別のパラメータを使用することができます。ラフネス\(\beta\)が0に近づくと、Gaussian detectorはディラックのデルタ関数に近づき、Marschnerら[MJC*03]の散乱関数が式(10)から再構成されます。新しい方位角散乱関数を使用すると、光の広がりに加えて、ラフネスに依存したカラーシフトが見られます(図8)。

※図は[d’Eon 2011]より引用。

※図は[d’Eon 2011]より引用。

※図は[d’Eon 2011]より引用。

6. Final Model and Implementation

完全を期すために、モデルの残りの部分を提供します（Marschnerら[MJC*03]とはいくつかの点で異なっています）。\(\rm R\)の減衰項は特殊なケースです。

\begin{eqnarray}
A(0, h) = F(\eta, \frac{1}{2} {\rm arccos}(\omega_i \cdot \omega_r)) \tag{12}
\end{eqnarray}

ここで、\(F(\eta, \theta\)\)はフレネル反射率で、物理的な整合性を保つために半値角を用いて評価しています。なお、Marschnerら [MJC*03]が提案したBravais Fresnelの項は不要であり、他のすべての項は以下のものを使用することができます。

\begin{eqnarray}
f = F(\eta, {\rm arccos}(\cos(\theta_d) \cos({\arcsin}(h))) \tag{14}
\end{eqnarray}

吸収項\(T (\mu_a, h) = {\rm exp}(- 2\mu_a(1 + \cos(2\gamma_t)))\)には、減少した吸収係数\(m_a’ = \mu_a /\cos(\theta_t))\)を使用しています。キューティクルスケールの傾きの影響は、緯度散乱関数を\(M_p(v_p, \theta_i, \theta_r – \alpha_p)\)で評価することで加えることができます。これは近似でしかないことに注意してください。スケールが傾いていることによる連続した内部バウンスの長さの変化（図1aに示す）は考慮されていません。Gaussian detecor（式11）は、3番目の楕円テータ関数で閉形式表現されています。実際には、高次の項は合理的なラフネスレベル((\beta \lt 80^{\circ}\))では無視できるので、有限の範囲の\(k\)で実装するのが最も簡単となります。\(I_0\)を評価するために以下の級数展開を使用します。

\begin{eqnarray}
I_0(x) \approx \sum_{i=0}^{10} \frac{x^{2i}}{e^i(i!)^2} \tag{15}
\end{eqnarray}

式(10)をガウス型求積法を用いて評価します。その結果，非常に滑らかな毛を除いては(\(\beta \lt 2^{\circ}\))，35次の求積法で十分であることがわかりました。\(N_p\)関数は、\(\mu_a\)と\(\beta_p\)の所望の組み合わせごとに、2Dテーブルで事前に計算することができます[ND05]。さらに，対称性を利用して，\(h\)で積分し，\(\phi\)と\(-\phi\)の両方で検出できるようにGaussian detectorを拡張することで，コストを削減することができます。非ガウス的なラフネスは、一般的な偏向分布関数をガウスの和として近似することでシミュレートできます。

6.1 RGB Melanin Absorption Cross-Sections

Donner と Jensen [DJ06]によって与えられたメラニン吸収断面積の解析的な近似値をもとに，40のスペクトルバンドを用いて吸収色を計算し，D65の光源に基づいてsRGBにマッピングしました。その結果，RGBの断面積は，スペクトルモデルで予測される色と完全には一致しないものの，ほぼ一致することがわかりました。その値は、\(\sigma_{a,e}=\{0.419, 0.697, 1.37\}\)と\(\sigma_{a,p} = \{0.187, 0.4, 1.05\}\)（単位は\({\rm R}^2\)濃度に比例し、\(1/R^3\)付近では黒髪になります。\(R\)は髪の毛の半径）です。その結果、図9のような色になりました。図の上下にある横棒は、分光吸収の計算値とRGBの近似値を比較したものです。両者は非常によく一致しており、両者の間の水平方向のエッジは目立ちにくいです。

※図は[d’Eon 2011]より引用。

7. Results

このセクションでは、我々のモデルをPixarのフォトリアリティスティックなRendermanで実装して得られた画像を紹介します。我々のモデルがシームレスに統合されているDual Scattering法[ZYWK08]を用いて多重散乱を計算します。図11は，ガウス緯度関数（エネルギーの倍増を避けるため，\(M_R = g(\beta_R; 2\theta_h)\)）と我々の球面ガウス畳み込み緯度関数の両方を使用した光の髪の二重散乱シミュレーションを比較したものです。Dual Scatteringは、複数の散乱現象を大きな有効粗さを持つ1つの計算として近似しているため、新しい散乱関数を使用すると、光はより暗い領域に広がっていきます。このような大きなラフネスは、ガウス型緯度関数が大きなエネルギーを失う場所です（図3に見られるように、ほとんどの角度で）。

※図は[d’Eon 2011]より引用。

私たちは、図10に示すように、スペクトル的に一致したメラニン濃度から得られるあらゆる種類の髪の色を示しています。図12は、物理的に自然な色の例で、スムージング制御を必要としない、エネルギー保存したグリントを示しています。グリントは、Marschner[MJC*03]と同様に、回転や偏心などの毛髪繊維の物理的特性を変更することで容易に調整することができます。

※図は[d’Eon 2011]より引用。

※図は[d’Eon 2011]より引用。

8. Conclusions and Future Work

私たちは、人毛繊維の新しい因数分解反射率モデルを発表しました。このパラメトリックモデルは，すべてのラフネスとと吸収レベル，およびすべての照明角度に対してエネルギーを保存することができます。このモデルの実装は簡単で、ルートソルバーを必要とせず、すべてのオーダーの内部反射に簡単に拡張できます。私たちは、このモデルで現実的な結果を示し、リアルタイムおよびプロダクションパイプラインに実装しました。今後の課題としては，この新しいモデルの現象論的な比較と，非吸収性の髄質を含むような不均一な発色団分布への容易な拡張が挙げられます。このアイデアを用いた予備実験では、色の微妙な変化が見られたため、実際に検証するための測定が必要となりました。TRRTおよび高次項のエネルギー解析により、これらが、以前に提案されたような、毛髪で観察される拡散色反射の原因ではないことが示唆されました。この現象は、一次項を脱色させる内殻散乱によって生じるに違いないと考えています。羽毛への拡張も期待できそうです(図13)。

※図は[d’Eon 2011]より引用。

9. Acknowledgements

和訳省略。

Appendix A: Derivation of the \(M_p\) function

\(P \in S^2\)を中心とした分散\(v\)の正規化球面ガウスを関数\(x \mapsto g(x, P) = \frac{{\rm csch}(1/v)}{2v}e^{\frac{P \cdot x}{v}}\)とし、緯度\(\theta_r \in (-\frac{\pi}{2}, \frac{\pi}{2})\)の円に沿って平均化すると、次のようになります。

\begin{eqnarray}
G(x) := \frac{1}{2\pi} \int_{0}^{2\pi} g(x, P) d \theta_r
\end{eqnarray}

ここで，\(P = P(\theta_r, \phi_r)\)は球面座標上です。\(x = x(\theta_i, \phi_i)\)の場合

\begin{eqnarray}
x \cdot P = \cos(\theta_i) \cos(\theta_r) \cos(\phi_i – \phi_r) + \sin(\theta_i) \sin(\theta_r)
\end{eqnarray}

従って

\begin{eqnarray}
G(v) &=& \frac{{\rm csch}(1/v)}{2v} \frac{e^{\frac{\sin(\theta_i)\sin(\theta_r)}{v}}}{2\pi} \int_{0}^{2\pi} e^{\frac{cos(\theta_i) \cos(\theta_r) \cos(\phi_r – \phi_i)}{v}} d\phi_r \\
&=& \frac{{\rm csch}(1/v)}{2v} \frac{e^{\frac{sin(\theta_i)\sin(\theta_r)}{v}}}{2\pi} \int_{0}^{2\pi} e^{\frac{\cos(\theta_i) \cos(\theta_r) \cos(\phi_r)}{v}} d\phi_r \\
&=& \frac{{\rm csch}(1/v)}{2v} e^{\frac{\sin(\theta_i)\sin(\theta_r)}{v}} I_0 \lbrack \frac{\cos(\theta_i)\cos(\theta_r)}{v} \rbrack
\end{eqnarray}

角度\(\theta_i\)で入射すると、\(-\theta_i\)にスペキュラコーンができます(したがって、式(7)の否定となります)。