こんるる~。Pocolです。
今日は,[Francois 2009] Guillaume Francois, Pascal Gautron, Gaspard Breton, Kadi Bouatouch, “Image-Based Modeling of the Human Eye”, IEEE Transactions on Visual and Compute Graphics, Vol.15, No.5, 2009.
を読んでみることにします。
いつもながら、誤字・誤訳があるかと思いますので、ご指摘頂ける場合は正しい翻訳例と共に指摘して頂けると幸いです。
Abstract
リアルな有機物のレンダリングは難しい問題です。人間の目は非言語的コミュニケーションの重要な要素であり、バーチャルキャラクターのリアリズムを高めるためには、特定のモデリングおよびレンダリング技術が必要となります。私たちは、仮想の目の説得力のある画像を生成するために、虹彩の形態と散乱の特徴の両方を推定する画像ベースの方法を提案します。そこで本研究では、虹彩の写真を屈折させない技術を開発しました。人間の虹彩の形態を、不規則な多層構造の組織としてモデル化します。そして、撮影された虹彩の散乱の特徴を近似します。最後に、サブサーフェステクスチャマッピング表現に基づいたリアルタイムレンダリング技術を提案し、事前に計算された屈折関数と、角膜界面での光の相互作用を考慮したコースティック関数を導入します。
1 Introduction
人間の顔のレンダリングに関する研究は、主に皮膚のモデリングとレンダリングに焦点を当てています。しかし、バーチャルキャラクターのリアリティを高めるためには、非言語コミュニケーションの重要な要素である人間の目を注意深くモデリングし、レンダリングする必要があります。近年のグラフィックスハードウェアの向上により、複雑な有機物をリアルタイムに描画できるようになりました。しかし、有機物質の形態的特性や光学的挙動を復元したり近似したりすることは、依然として困難な課題です。私たちの目的は、画像ベースの手法を用いて人間の目の外観を模倣することであり、実物に近い仮想の目を素早く生成することです。映画制作では、美しい映像を提供するためにアーティスティックななデザインが重視されます。しかし、物理的・解剖学的研究の利点を生かすことで、モデリングやレンダリングの手法をより一般的で使いやすいものにすることができます。この論文では、それを目指しています。
私たちは、眼科分野の領域知識を活用して、虹彩の解剖学的特性を推論することを提案します。ほとんどの有機物と同様に、虹彩は半透明で、いくつかの層から構成されています。虹彩の全体的な色は特定の色素濃度によるものですが、その色合いの局所的な変化は、その組織の不均一な厚さに支配されていることがほとんどです。本研究では、生体内の眼球写真に基づいて、虹彩の構造と散乱の特徴を近似し、レンダリングされた虹彩が実際の虹彩を忠実に再現できるようにするパイプラインを提案します。私たちは、虹彩写真を屈折させない技術を開発しました。これにより、虹彩のレリーフを取得することができます(第4章)。第2段階では、眼球写真から、撮影された虹彩の散乱特性を推定します(5章)。最後に,虹彩の構造をサブサーフェイステクスチャ[1]として表現し,屈折関数とコースティクス関数を導入することで,リアルタイム眼球描画アルゴリズムを提案します(第6章)。7章で我々の結果を提示し考察します。
2 Background
2.1 Related Work
人間の目のモデリングとレンダリングに関するこれまでの研究の多くは、目の解剖学的構造に部分的にしか依存していません。さらに、人間の虹彩の視覚的に心地よいモデルを生成するという問題に取り組んでいる論文はわずかしかありません。従来の手法では、色の変化を表すテクスチャを用いて目の特徴をモデル化していました。この方法では、虹彩の色の変化は、虹彩の色素の密度の変化によるものだと仮定し、虹彩の組織内での光の散乱を無視しています。
Sagarら[2]は,シンプルなGouraudシェーディングモデルとテクスチャを用いて,外科手術の練習用に人間の目を表現し,レンダリングしています.
Lefohnら[3]は、眼科学者の研究に基づいた方法を紹介しています。彼らは、人間の虹彩のクローンを作成するために、手作業でデザインされた複数の色の層を重ねて、説得力のある虹彩を作成するという、美的感覚に基づいた方法を導入しています。しかし、半透明のレイヤーをたくさん塗るのは面倒な作業です。そこで我々は、虹彩写真に含まれるRGBとスケールの情報を利用した別のアプローチを提案します。
ZuoとSchmid[4]は,合成繊維を用いて虹彩を生成し,虹彩層の繊維状の性質を模倣しました。しかし,この方法は,虹彩認識アルゴリズムの評価のために開発されたものであり,与えられた虹彩を模倣してレンダリングするという問題には対処していません。
Lam and Baranoski [5]は,虹彩内の光散乱を正確にシミュレートするために,モンテカルロベースのレンダリング手法を提案しています。この手法、すなわちILITは、人間の虹彩の層の解剖学的および生物物理学的特性を用いて、虹彩の正確なモデリングとレンダリングを可能にします。BaranoskiとLam[6]は,このレンダリング手法を用いて,医療目的に有用な虹彩のメラニン分布など,人間の虹彩の物理的・化学的情報を正確に推測できることを示しています。ただし、これはオフラインのレンダリング手法であり、人間の眼球のクローン化の問題には対応していません。そこで私たちは、写真をもとに、眼科の文献からヒントを得て、半自動の手法を開発しました。虹彩写真とレンダリングされた仮想虹彩を比較することで、虹彩層の不規則な構造とそれぞれの散乱特性にアプローチしています。[5]で提案されたILITモデルよりも精度は劣るものの、数回のユーザーインタラクションで済む、高速でシンプルな人間の目のモデリングが可能です。また、角膜と光の相互作用を高速かつ正確に推定するために、屈折関数とコースティクス関数を導入することで、リアルタイムレンダリング手法を提案しています。このレンダリング技術は、虹彩の厚さや散乱パラメータをリアルタイムに変更することを可能にし、かつ信憑性の高い結果を得ることができます。この機能は、人間の目に関する生物物理学的な知識が不足しているグラフィックデザイナーにとって、特に有用なものです。
2.2 Anatomy of Human Eye
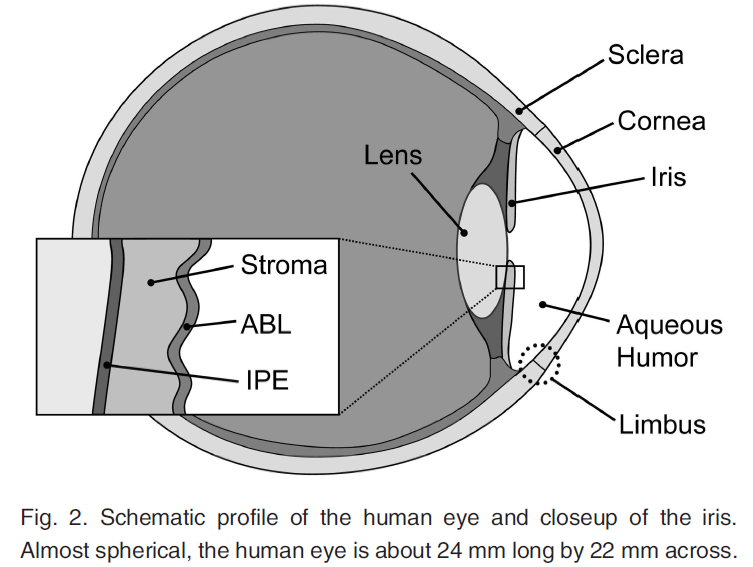
人間の目は何十年も前から研究されています。目は複雑な器官であり、視覚を適応させ、対象物に焦点を合わせるための適切なメカニズムを含んでいます。ここでは、指紋のように一人一人に固有のものである虹彩など、目に見える眼球組織(図2)について説明します。虹彩は、指紋のように人それぞれに固有のものであり、リアルな眼球を表現する上で非常に重要です。
2.2.1 The Sclera
強膜とは、眼球の形を作る白い外被のことです。強靭な繊維質の組織で、コラーゲンの束が高度に圧縮された平らな帯状になっており、光を散乱させます。この特性により、強膜は非常に透明性の高い組織となっています。その散乱特性は[7]に記載されています。強膜の上には、血管を持つ繊維組織である上強膜が重なっており、強膜と角膜の境界部分、すなわち辺縁部で血管を示し、角膜を洗浄しています。さらに、上強膜は涙の膜で覆われており、その表面は高い反射性を持っています。
2.2.2 The Cornea and Anterior Chamber
角膜は目の前にあり、虹彩の上に位置しています。角膜は脱水して血管がなくなった透明な組織で、人間の目のレンズシステムの最初で最も強い凸状の要素として切断されます。そのため、光の屈折のほとんどは空気と角膜の境界面で起こり、水晶体は焦点を「調整」するだけです。人間の角膜の平均直径は11mm,平均屈折率は1.376です[8]。角膜の外側には角膜前涙膜があり、角膜表面には独特の薄膜反射が見られます。後方の角膜表面には特徴的な薄膜反射が見られます。角膜後面には屈折率1.336の房水が付着しています。しかし、角膜と房水の屈折率が似ているため、光の屈折のほとんどは角膜外層の界面で起こることに注意してください[9]。
2.2.3 The Iris
角膜と房水に挟まれた虹彩は、目に入る光の量を調節するための開口部として機能する色のついた隔膜です。円筋と橈骨筋で構成された虹彩の直径は平均11.6mmで、明るいところでは約2mm、暗いところでは約8mmの範囲で瞳孔を広げたり縮めたりすることができます。
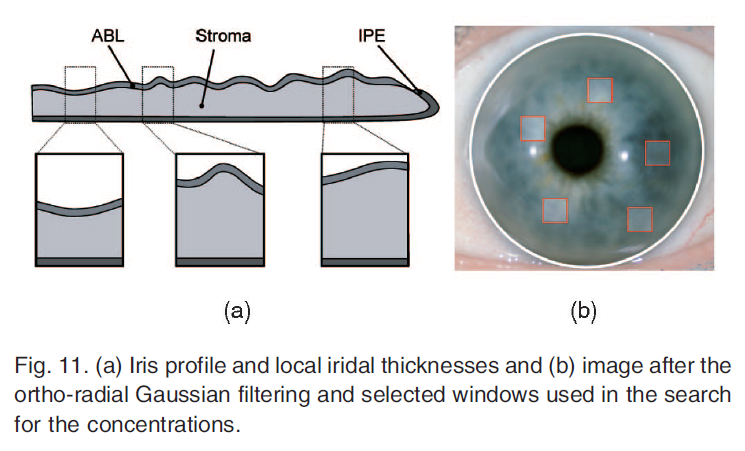
虹彩は、半透明の層状の組織です(図2)。虹彩の一番外側の層である前境界層(ABL)は、コラーゲンでできた間質を覆っており、虹彩の最も厚い層です。最も内側にある「虹彩上皮」(IPE)は、光が目に入るのを防ぐ不透明な組織です。
虹彩の色は、グレー、ブルー、グリーン、ヘーゼル、ブラウンなど、複数の色素で構成されています。しかし、虹彩細胞にはヘモグロビンやカロテノイド色素が含まれているにもかかわらず、虹彩の色調特性に質的・量的に最も大きく寄与しているのはメラニンです[10]。人間の皮膚や髪の毛と同様に、虹彩にも茶褐色のユーメラニンと赤黄色のフェオメラニンの2種類のメラニンが存在します[11]。IPEは、すべての虹彩に最大限の色素を与え、入ってくる光をすべて吸収します。そして、虹彩の色は、そのABLとストロマの色素によって決定されると考えることができます[12]。青色や色素の薄い虹彩では、ABLや間質のメラニン濃度が低いため、コラーゲンのレイリー散乱により、ほとんどの青色の波長が観測者に戻ってきます。暗い色の虹彩は一般的に厚く、色素が濃いです[12]。
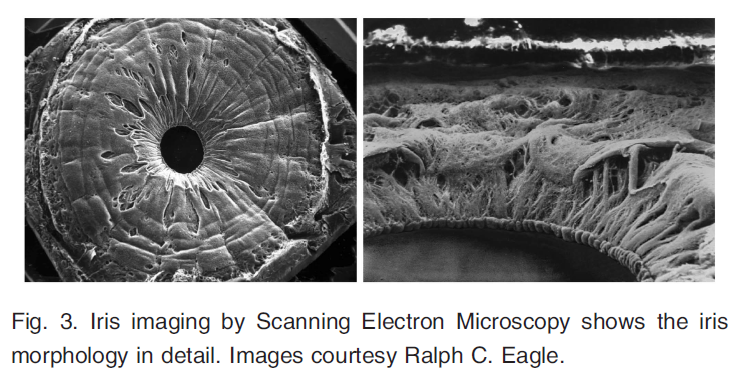
ヒトの虹彩は、その表現型によって、さまざまな複雑な形態を示します。虹彩組織の不規則性は、虹彩の外観に重要な影響を与えます。私たちは、図3に見られる構造的特徴を写真で復元することに興味を持っています。それは、コラレットの両側にある一連の開口部であるフックスのクリプト、瞳孔縁の小さな隆起である瞳孔隆起、コラレットと虹彩の起点のほぼ中間にあるひだである円形収縮溝です。
3 Overview of the method
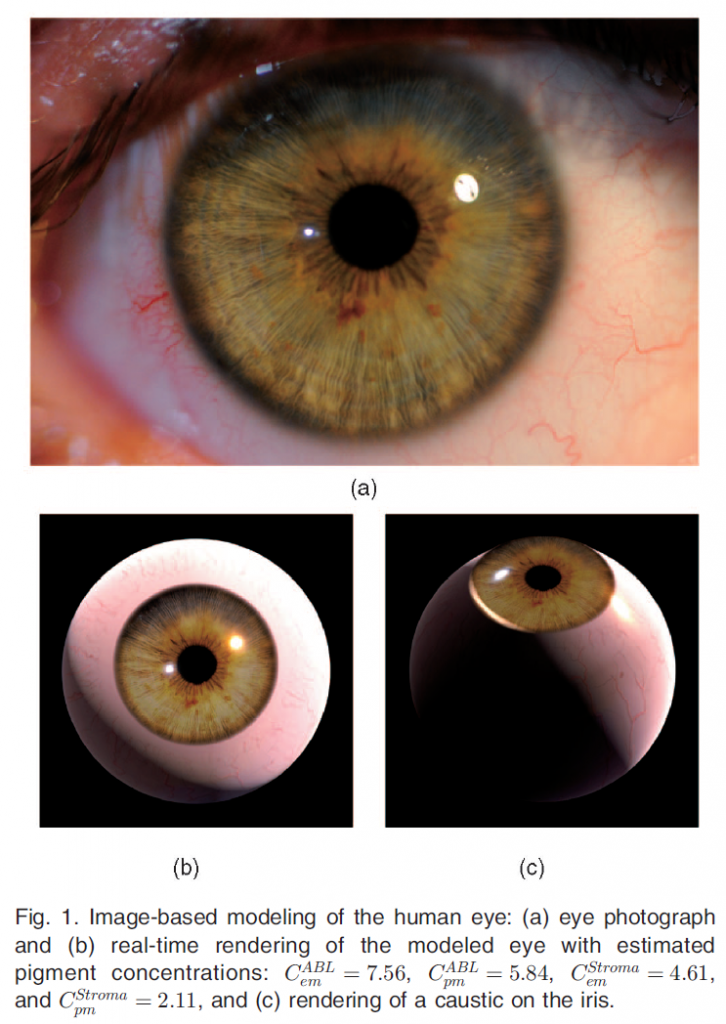
このセクションでは、人間の目の外観を模倣するための全体的な方法について説明します。虹彩のモデリングとレンダリングのアルゴリズムは、虹彩の層の構造を表す虹彩形態パラメータ\(T\)、虹彩色素濃度\(C\)、環境照明またはライトプローブ\(L_i\)の3つの主な未知のパラメータグループに依存します。
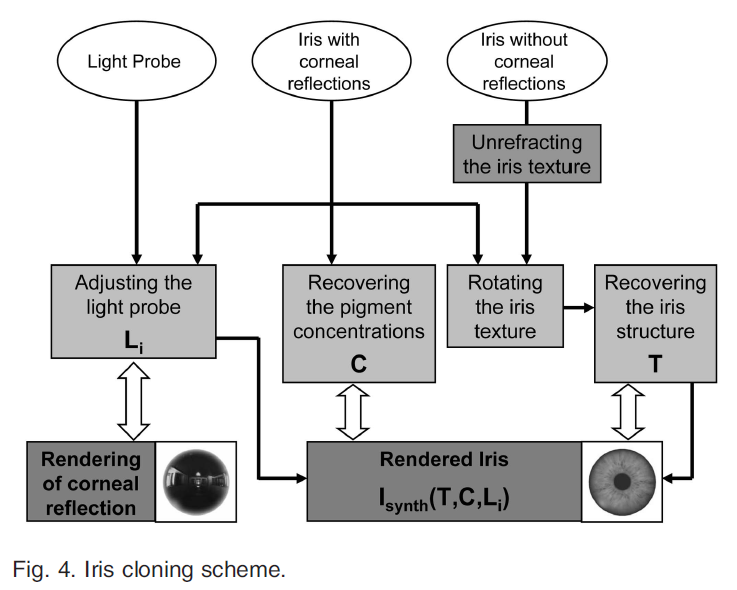
本稿では、レンダリングされた虹彩画像を\(I_{synth}(T, C, L_i)\)と表記します。この画像は表示用に使われているだけではありません。\(I_{synth}\)は、画像の比較から、我々の復元アルゴリズムにも必要とされています(図4)。
虹彩のレンダリング画像が実際の虹彩に近いものになるように、シンプルで高速な画像ベースの技術を用いて、これらの虹彩パラメータを推論するために、さまざまなソリューションや仮定を採用しています。この論文では、虹彩の構造と散乱の特徴を評価するために、リアルタイムレンダリング技術を使用しています。このレンダリングプロセスについては,6章で説明します。しかし、これから紹介するクローニング方式は、ユーザーが特定のレンダリング技術を使用することを制約するものではありません。本手法では、評価に使用されたレンダリング手法に適応した、解剖学的にインスパイアされたクローンを生成し、レンダリングされた虹彩と実際の虹彩の最適なマッチングを実現します。
私たちのクローニング方法は以下のように構成されています。偏光フィルターを用いて、角膜が反射している虹彩写真と、反射していない虹彩写真を撮影します。また、複数の露出を連結することで、環境の高ダイナミックレンジ(HDR)写真を取得しています[13]。なお、このステップでは、カメラのキャリブレーションも行うことができます。
まず、撮影された環境\(L_i\)の中で、その角膜反射が、角膜反射のある写真で見える反射と同様になるように、仮想の目の位置を決めて登録します。調整が完了したら、レンダラーで\(L_i\)を使用して仮想の目を照明します(鼻やまぶたからの間接照明は無視できると仮定しています)。なお、Nishinoら[14]は、角膜の反射光から環境照明を自動的に復元しています。しかし、この方法では、虹彩の反射と角膜の反射を区別することができないため、ダークブラウンの虹彩にしか使用できません。私たちは、彼らの発見を利用して、目の写真に含まれる情報だけでカメラの位置を推定しています(4.1節)。
照明環境を整えた後、無反射写真に含まれる情報を用いて虹彩構造\(T\)を近似します。この写真を使うことで、角膜の反射が虹彩テクスチャをマスクしないようにしています。この画像をまず屈折させずに、反射を伴う虹彩写真に合わせて向きを変えます。この最後のステップでは、再構成された虹彩のレンダリングと、反射を伴う虹彩写真を比較することができます。我々のレンダラーで使用した場合、屈折していない画像の詳細は、光の散乱のために実際の虹彩の形態とは直接一致しません。そこで,虹彩のテクスチャをデコンボリューションして,実際の虹彩構造を模倣することで,この問題に対処しています(4章)。
虹彩の形態が推定されると、レンダリングされた虹彩と、反射を伴う虹彩写真を比較することで、虹彩の色素濃度\(C\)を自動的に評価します(5章)。
図5は、図4で説明したステップをまとめたもので、本論文に沿って提案されます。各ステップは、以下のセクションで説明され、各セクションの最後に短いアルゴリズムとして提示されます。
4 Capturing and reconstructing the eye morphology
眼科医は、バイオマイクロスコープあるいはスリットランプを使って、眼のさまざまな部分を詳細に観察します。
私たちは、シンプルなデジタルカメラとマクロレンズを使って、視覚的に重要な虹彩の特徴を撮影することを提案します。角膜で反射した光は、偏光フィルターを使って避けています。照明装置とカメラのレンズの両方に直交する偏光フィルターを装着し、角膜で反射した光(極性を保つ光)が撮影画像に写らないようにしています。Wangら[15]は,フィルタを使用せずに角膜反射を除去する計算手法を提案しています。しかし,この方法では,角膜反射によって頻繁に焼けてしまう虹彩部分を正確に復元することはできませんし,撮影装置の制限もあります。
4.1 Unrefracting an Iris Photograph
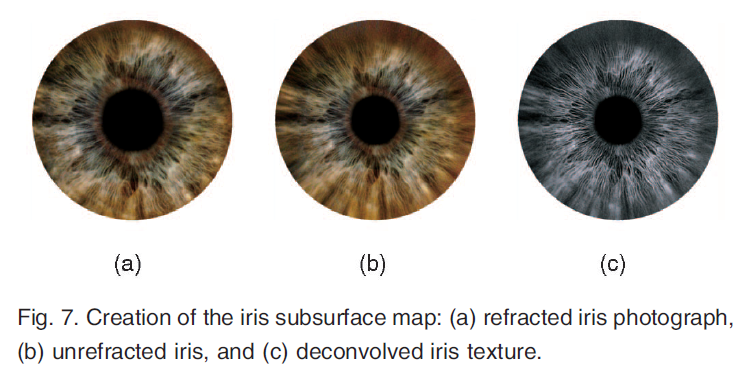
虹彩の上には、角膜と房水という屈折率の高い要素が重なっています。そのため、眼球写真では、屈折していないはずの虹彩が歪んで写ってしまいます(図7a)。
4.1.1 Recovering the Camera Parameters
まず、虹彩とカメラの間の未知の相対的な距離と方向を決定します。写真では、強膜と角膜の境目である辺縁部が楕円形に見えます。目の縦軸とカメラ方向の間の極角\(\theta\)は、以下のように推定できます:
\begin{eqnarray}
\theta = {\rm arccos} \left( \frac{r_{min}}{r_{max}} \right) \tag{1}
\end{eqnarray}
長軸と短軸の\(r_{max}\)と\(r_{min}\)は,[14]と同様に,検出された辺縁部から推定される。画像中の楕円の長軸が実際の辺縁部の直径に相当することから,虹彩の中心からカメラ位置までの距離Dは
\begin{eqnarray}
D = r_{limbus} \frac{f}{r_{max}} \tag{2}
\end{eqnarray}
ここで、\(r_{limbus}=5.5\)mmは肢体の半径、\(f\)はをピクセル単位での焦点距離を表しています。カメラの向きと距離がわかれば、虹彩写真の屈折を解除することができます。なお、これらのカメラパラメータは、比較可能な画像を生成するためにレンダラーでも使用されます。
4.1.2 Unrefraction Algorithm
虹彩写真の屈折補正は、各画素と実際の虹彩面上の対応する点との関係を見つけることです。この段階では、前房の大きさに比べて虹彩の厚さの変化が小さいため、平面的な虹彩を想定しています。ここでは、[16]で得られた一般的な角膜プロファイルを使用します:
\begin{eqnarray}
pz^2 – 2Rz + x^2 + y^2 = 0 \tag{3}
\end{eqnarray}
ここで,\(p = 0.75\)で,\(R = -0.78\)です。
涙液の屈折率は角膜の屈折率と非常によく似ているため、全体の屈折率に与える影響を無視しています。角膜と房水の屈折率が異なっていても,主な光の屈折は空気と角膜の界面で起こります[9]。そこで、角膜上層部の界面での屈折のみを考慮して、これらの屈折を近似しています。
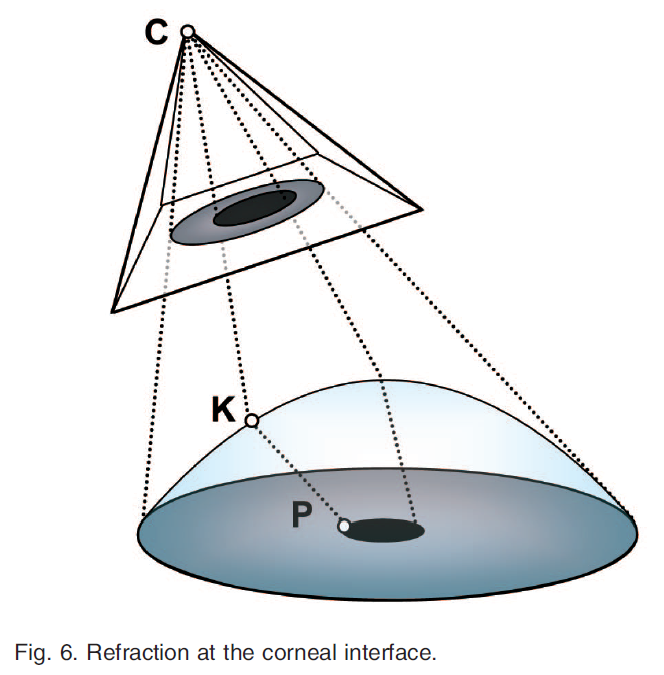
これらの仮定のもと、虹彩面上の各点\(P\)からカメラ\(C\)までの実際の光路を推定します(図6)。フェルマーの原理に従って、光路\(L(K)\)が最小になるように角膜上の点\(K\)を探します:
\begin{eqnarray}
argmin_{K \in cornea} L(K) \\
L(K) = n_{air} || CK || + n_{cornea} ||KP|| \tag{4}
\end{eqnarray}
この最小化問題は、古典的なNewton-Raphsonアルゴリズムを用いて光路微分のルートを数値的に求めることで解決し、信頼性の高い点\(K\)の推定値を得ることができます。図7では、撮影された虹彩画像とオリジナルの虹彩形態が大きく異なっていることがわかります。
4.2 Recovering the Iris Morphology
私たちは、虹彩の3次元形状の信頼できる推定値を得るために、屈折していない画像\(I(x, y)\)のピクセル値を操作することに興味があります。
反射のある虹彩画像を使って画像比較を行う段階では、まず、屈折していない虹彩のテクスチャと虹彩写真を登録します。なお、人間の目の反射瞳孔の適応により、撮影された虹彩の形態は2枚の写真で異なる場合があります。しかし,この2つの写真は同じ環境で撮影されているため,瞳孔の大きさのわずかな変化が虹彩の構造を大きく変えることはありません。
1枚の画像から深度マップを計算することは、典型的なシェーディングからの形状問題です。残念ながら、虹彩は多層の半透明な組織であるため、この問題には大きな制約があります。写真から虹彩の構造を推論することを提案しているので、虹彩の層の構造の近似値を導入する必要があります。まず、間質の膠原線維は一様に分布していると考えます。これは、その複雑な分布の正確な測定は、走査型電子顕微鏡を用いた体外でしか行えないからです。第二に、前縁層は一定の厚さ\(T_{ABL} = 0.05675\)mm [17]を持ち、均一な色素を持つと考えます。
前に、間質はコラーゲン構造をしているため、散乱性の高い組織であると述べました。さらに、超音波バイオマイクロスコピーで厚さを測定した色素上皮(IPE)に到達すると、光が吸収されてしまいます:\(T_{IPE} = 0.07\) mm。
その結果、ABLは一定の厚さと均一な色素濃度を持っていると考えられるため、虹彩の間質が厚い領域では光の散乱が大きく、薄い領域では光の散乱が小さいと仮定しています。その結果、虹彩写真の明るい部分は間質の厚い部分に、暗い部分は薄い部分に対応しています。7章の結果では、この仮定によって、元の目に視覚的に近い仮想の目が得られることを示しています。
これらの仮定を用いて虹彩の厚さを近似する際には、そばかすやコラレット部分の高いメラニン色素など、虹彩の一般的な欠点を考慮する必要があります。これらの病変は、虹彩上に暗褐色の斑点として現れるが、間質の薄い部分に対応するものではなく、ABLにおけるメラニン色素の高密度化によるものです[12]。
まず、屈折していない虹彩写真の中から、色の範囲でこれらの特殊性を見つけ出します。そして、写真からそれらを取り除き、隣接する虹彩の色で穴を埋めます。ここでは手作業でそばかすを抽出していますが,最近ではユーザの作業を支援する高度な技術も登場しています[18]。5章で紹介した色素濃度の評価は、これらの領域では行われていないことに注意してください、そばかすは我々のレンダラー(6.4節)で特別に処理されます。
4.2.1 Stromal Thickness Estimation
虹彩はそれぞれ固有の形態をしています。我々は、間質の厚さを、虹彩の一般的な厚さを表すものと、個々の虹彩の特異性を表すものとの2つの要素に分けています。
人間の虹彩の一般的な厚さは、その半径\(r\)に沿ってゆっくりと変化します。我々は、超音波生体顕微鏡[19]を用いて得られた正確な測定値の平均を用いて、それらの測定値に二次多項式をフィッティングすることにより、一般的な虹彩プロファイル\(IT(r)\)を生成します(図8)。ABLとIPEの厚さは一定と考えられるので、半径\(r\)にのみ依存する一般的な間質の厚さの式を導き出します: \({\bar T}_{stroma}(r) = IT(r) – T_{IPE} – T_{ABL}\)。
次に、虹彩の個別性を考慮して、一般的なプロファイルの周りの局所的な厚さの変化を検討します。屈折していない虹彩画像から、それらのバリエーションを導出します。任意の偏光照明環境を使用することにしたので、まずピクセル強度を正規化します:
\begin{eqnarray}
I_{norm} (x, y) = I(x, y) – {\bar I}(x, y) \tag{5}
\end{eqnarray}
ここで、ある画素\((x, y)\)について、\(I(x, y)\)は屈折していない虹彩画像の画素強度、X\({\bar I}(x, y)\)は隣接する画素の画素強度の平均値です。
光の散乱により、写真では虹彩が「ぼやけて」見え、実際よりも大きく見えることを考慮しなければなりません。D’Eonら[20]は,入射放射輝度をガウスフィルタの和で畳み込むことで,層状物質内の光散乱を推定しています。不均一な層構造を持つ組織を考慮しているにもかかわらず、屈折していない虹彩画像にガウスデコンボリューションを適用すると、潜在的な間質の厚さの変化\(I_{deconv}\)を合理的に正確に推定できることがわかりました(図7c)。我々はRichardson-Lucyデコンボリューション法を用いています:任意のガウスフィルタ\(G(\sigma, \mu)\)が与えられた場合、デコンボリューション画像は次のようになります。
\begin{eqnarray}
I_{deconv} = Deconv( I_{norm}, G(\sigma, \mu)) \tag{6}
\end{eqnarray}
このとき、一般的な間質の厚さと、デコンボリューションされた虹彩画像のピクセル強度の加重和として、間質の厚さ\(T_{stroma}\)が推定されます:
\begin{eqnarray}
T_{stroma}(x, y) = {\bar T}_{stroma}(r) + \alpha I_{deconv}(x, y) \tag{7}
\end{eqnarray}
ここで\(\alpha\)は、間質の局所的な個別特徴の重要性を制御するスカラー値です。我々のレンダリング技術を用いても納得のいく結果が得られる\(\alpha = 350 \mu {\rm m}\)に設定しました。
デコンボリューションのパラメータである\(\sigma\)と\(\mu\)は、虹彩写真と高品質なレンダリング画像を比較することで推測することができます。レンダリング画像の虹彩の詳細が写真の詳細と一致するまで、ガウスデコンボリューションのパラメータ\(\sigma\)を調整します。図9は、デコンボリューションがレンダリングされた虹彩に与える影響を示しています。実験の結果、デコンボリューションに分散\(\sigma=0.5\) mmを使用すると、元の写真と比較して説得力のある結果が得られることがわかりました(7章参照)。パラメータ\(\mu\)はゼロになるように選択されています。なお、デコンボリューションでは、リンギング・アーチファクトが発生することがあります。しかし、フィルターカーネルのサイズは虹彩の特徴のサイズに比べて非常に小さいため、後者はほとんど見えません。
本節で紹介する虹彩再構築の手順を図10にまとめました。まず,[5]で提案されているような一般的な顔料濃度を用いた虹彩レンダリングと虹彩写真を比較して,粗い厚み\({\tilde T}\)を推定します。これにより、個々の虹彩の散乱パラメータを推定するための合成画像を作成することができます。虹彩の散乱特性が推定されたら、フィルターの分散\(\sigma\)を再調整することで、より正確なデコンボリューションを行い、間質の厚さの変化をより正確に推定します。
5 Recovering the iris scattering parameters
層状組織の波長依存性散乱パラメータを直接再変換することは困難な作業です。我々は、これらの後者および小規模な組織がABLおよび間質に一様に分布していると仮定して、色素濃度の評価からこれらのパラメータを近似することを提案します。
5.1 Light Scattering within the Iris Layers
虹彩の見た目は、複数の色素が関わっています。しかし、虹彩のメラニン色素は発色団であり、虹彩の色に最も影響を与えています。そこで、LamとBaranoski[5]に倣って、虹彩標本ごとにヘモグロビンとカロテノイドの濃度を一定にして考えます。
この引用論文では、オキシヘモグロビンとデオキシヘモグロビン、\(\sigma_a^{ox}\)と{\sigma_a^{deox}\)、およびルテイン\(\sigma_a^{lut}\)とゼアキサンチン\(\sigma_a^{zea}\)の吸収係数を、医学文献に掲載されているスペクトルモル吸光曲線と濃度\(C_{ox}\), \(C_{deox}\), \(C_{lut}\), \(C_{zea}\)から推定しています(表1参照)。なお、すべての分光吸収曲線は、CIE RGB Matching Functionsを用いてRGB空間に投影されています。
虹彩色のメラニン色素は、人間の髪の毛や皮膚に含まれるメラニンとはほんの少ししか違いません。ユーメラニンとフェオメラニンの分光吸収は、それぞれべき乗則でよく近似できます:
\begin{eqnarray}
\sigma_a^{em}(\lambda) &=& 6.6 \times 10^{10} \times \lambda^{-3.33} {\rm mm}^{-1} \tag{8} \\
\sigma_a^{pm}(\lambda) &=& 2.9 \times 10^{14} \times \lambda^{-4.75} {\rm mm}^{-1} \tag{9}
\end{eqnarray}
ここで、\(\lambda\)は光の波長(ナノメートル)、\(\sigma_a^{em}\)はエヌメラニンの分光吸収係数、\(\sigma_a^{pm}\)はフェオメラニンの分光吸収係数です。式(8)は[21]のデータにフィットし、(9)はDonnerら[22]が提案したデータにフィットしています。
間質の純分光吸収率は、色素の分光吸収率をそれぞれの体積分率で加重したものの合計として計算されます:
\begin{eqnarray}
\sigma_a(\lambda) = C_{em} \sigma_a^{em}(\lambda) + C_{pm} \sigma_a^{pm}(\lambda) + C_{ox} \sigma_a^{ox}(\lambda) + C_{deox} \sigma_a^{deox}(\lambda) + C_{lut} \sigma_a^{lut}(\lambda) + C_{zea} \sigma_a^{zea} (\lambda) \tag{10}
\end{eqnarray}
ベースラインの吸収は、メラニンの吸収に比べて非常に小さいため、無視しています。ABLのスペクトル吸収は同じ式に従いますが、この層にはヘモグロビンとカロテノイドがないと仮定しました。
光の散乱は、コラーゲンからなる間質でのみ起こり、レイリー理論に従うと考えます。半径\(r_c=30 {\rm nm}\)の球状コラーゲン線維を考慮して、散乱密度を推定しました:
\begin{eqnarray}
N = \left( \frac{4}{3} {r_c}^3 \pi \right)^{-1} f_{collagen} \tag{11}
\end{eqnarray}
ここで,\(f_{collagen} = \pi / (4 \sin (\pi / 3)) \)は,組織内のコラーゲン線維が占める間質の体積分率です[5]。散乱係数は,次のように導かれます。
\begin{eqnarray}
\sigma_s(\lambda) = \frac{8 \pi^3}{3N} \left( (\frac{n_c}{n_b})^2 – 1 \right)^2 \lambda^{-4} \tag{12}
\end{eqnarray}
ここで、\(n_c\)と\(n_b\)はそれぞれ、コラーゲン線維と間質の基線の屈折率で、0.47と1.5に等しいです[7], [24]。
(10)に続き、次項で説明するメラニン濃度\(C_{em}\)と\(C_{pm}\)の評価を用いて、ABLとストローマの吸収係数を評価します。
5.2 Comparing Iris Photographs and Renderings
虹彩の形態\(T\)が復元されると、画像比較に基づく反復法を用いて虹彩の散乱パラメータを推定します。上述したように、虹彩の色調は、主にユーメラニン色素とフェオメラニン色素の濃度に依存します。
そばかすやコラレットなどの色素沈着を除けば、虹彩写真の輝度値は間質層の厚さと関係があることを述べました。しかし、虹彩の色そのものは、ABLと間質の両方で同時に行われる光の相互作用に依存しています。前節で述べたように、ヘモグロビンとカロテノイドの濃度は一定であり、どのタイプの虹彩でも同様であると仮定します。このような仮定のもとでは、第3節で導入した濃度パラメータCはメラニン濃度にのみ依存します。そのため、濃度の四則演算(\(C_{em}^{ABL}, C_{pm}^{ABL}, C_{em}^{stroma}, C_{pm}^{stroma}\))を推定する必要があります。
LamとBaranoski[5]がILITのシミュレーションで使用したメラニン濃度\(\beta_m\)を考えると、フェオメラニンとユーメラニンの比率はほぼ一定です:\(\beta_m \approx 0.226\)。そこで、まず、フェオメラニン濃度を\(0.226C_{em}\)の値に制限します。
虹彩写真とそれに対応するレンダリングされた虹彩の違いを最小にするABLとストロマのユーメラニンの濃度\(C_{em}\)を探します。
画像から得られる平均虹彩色を比較すると、制約の少ない問題となり、複数の濃度設定で同じような平均虹彩色になることから、複数の解が得られます。我々は、虹彩の形態学的特性、すなわち、間質の厚さの変化を利用しています。図11aは、同じ虹彩の複数の異なるローカルプロファイルを示しています。厚みの異なる領域の画像差を同時に最小化する解を見つけることで、最適な濃度設定の数を減らすことができます。
差分のイメージは以下のように定義されます。
\begin{eqnarray}
I_{diff} = | I_{photo} – I_{synth}({\tilde T}, C, L_i ) | \tag{13}
\end{eqnarray}
ここで\(C\)は、\({\tilde T}\)と\(L_i\)をすでに推定しているので、唯一の変動パラメータです。
しかし、レンダリングされた虹彩は、虹彩構造\({\tilde T}\)の粗い事前推定(4.2節)を行っているため、虹彩写真と直接比較することはできません。
2.2節で紹介したように、虹彩の特徴は、ほとんどが瞳孔から眼窩までの放射状の溝で、直角放射状の特徴はあまり見られません。直角方向のガウスフィルタリングを行うことで、間質の厚さを推定する際に生じる誤差を無視することができます。ortho-radialガウシアンフィルタ\(g(\sigma_r, \sigma_{\theta}, \mu_r, \mu_{\theta})\)は,虹彩の全体的なカラーバリエーションを変更することなく,虹彩の詳細を平滑化します。ガウスフィルタの分散\(\sigma_r\), \(\sigma_{\theta}\)と平均値\(\mu_r\), \(\mu_{\theta}\)は、画像\(I_{diff}\)を適度にぼかすために任意に選択されています(フィルタパラメータの値は7章に記載されています)。
このフィルタリングステップには他にもいくつかの利点があります:まず、ピクセル単位では一致しない写真とレンダリング画像の比較を行うことができます。さらに、このフィルタを適用することで、虹彩写真とレンダリング画像の両方に存在するノイズを最小限に抑えることができます。このノイズは、キャプターの感度に起因するものと、ILIT [5]のようなモンテカルロレンダリング法を用いて合成画像を生成した場合に現れるものがあります。また、マクロ写真でよく見られる被写界深度の減少による写真のボケを無視することができます。
画像がフィルタリングされると、画像\(I_{diff}’\)の各ピクセルのRGB値を最小化する濃度(\(C_{em}^{ABL}\), \(C_{em}^{stroma}\))が検索されます:
\begin{eqnarray}
I_{diff}'(x, y) = g(\sigma_r, \sigma_{\theta}, \mu_r, \mu_{\theta}) \ast I_{diff} (x, y) \tag{14}
\end{eqnarray}
合成画像の計算と探索の収束を高速化するために,図11bに示すように,比較対象を画像\(I_{photo}\)の選択されたウィンドウのセットに限定しました。
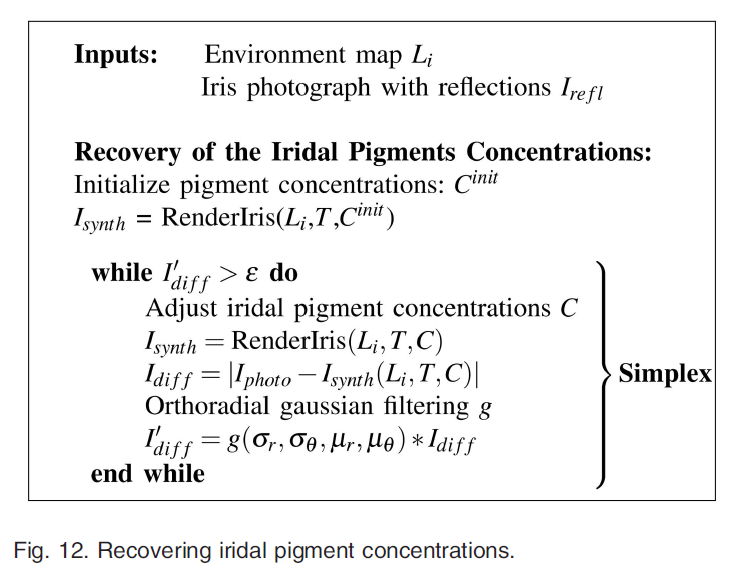
この最小化問題をSimplexアルゴリズム[25]を用いて解き、虹彩色に対する量的・質的な影響など、濃度変化に関する追加の仮定は考慮しませんでした。エヌメラニン濃度を評価した後、最後に、同じ方法でエヌメラニンとフェオメラニンの比率、\(\beta^{ABL}\)、\(\beta^{stroma}\)を修正することで、間質とABLのフェオメラニン濃度をより正確に推定します。
図12は、虹彩色の色素濃度を探索するステップをまとめたものです。なお、この方法の収束は保証されていない。しかし、我々の実験では、この方法が有効であり、視覚的に美しい虹彩モデルが得られることがわかりました(7章参照)。
6 Iris rendering
私たちは、虹彩の厚さと色素濃度を迅速に評価するためのリアルタイムレンダリング技術を開発しました。しかし、この論文で紹介されている推定を行うためには、どのような虹彩レンダリング手法でも使用することができます。[5]で紹介されているようなモンテカルロ法は、速度は遅いものの、虹彩組織内の光散乱をより正確に推定することができます。この光の伝播は、Radiative Transport Equation(放射輸送方程式)[26]によって支配されます。リアルタイムのフレームレートのために,我々は表面下散乱推定を単一の散乱項に限定し,多重散乱の寄与を無視しています。
6.1 Iridal Subsurface Map
人間の虹彩の層構造は,サブサーフェステクスチャマッピング技術を用いてモデル化され,レンダリングされます[1]。
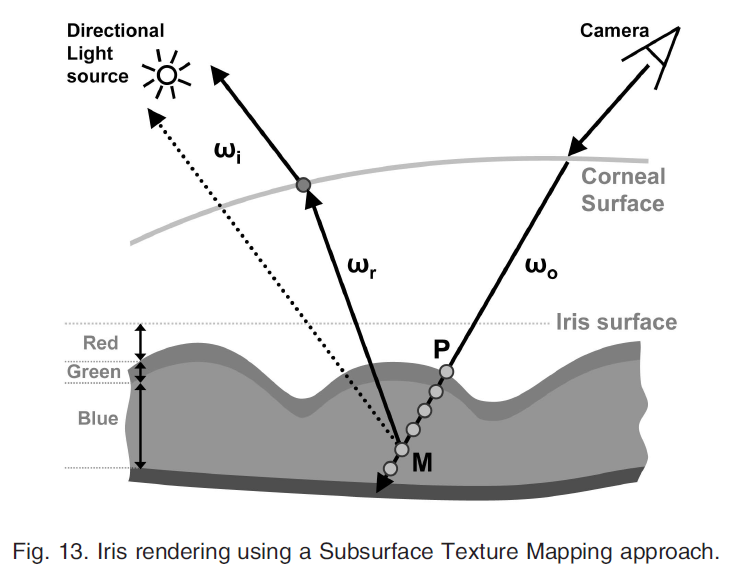
サブサーフェイスマップは、2次元テクスチャの\(RGB\alpha\)の4チャンネルを使って4つの層の厚さを符号化したもので、非常に少ないメモリと計算コストで高精細な虹彩を表現することができます。Policarpoら[27]によって提案されたレリーフマッピング技術と同様に,図13に示すように,赤チャンネル内の虹彩表面上のプランとABLの表面との間の距離を符号化します。そして、ABL自体の厚さはグリーンチャンネルで、ブラーチャンネルは間質層の厚さの変化をエンコードします。IPEの厚さは、結果として得られる虹彩色への寄与が無視されるため、マップにはエンコードされません。我々のレンダリング手法であるSubsurface Texture Mappingアルゴリズムは、グラフィックス・ハードウェア上に実装されており、図13に示すように、レイ・マーチング・アルゴリズムを用いて眼球組織内の単一散乱を推定します。
カメラの光線は、角膜を通過する際にそれぞれ屈折します。その後,光線は第1虹彩層に到達した時点でサンプリングされます(到達点Pは虹彩サブサーフェスマップとして取得されます)。各サンプルポイントMにおいて、我々のアルゴリズムは、虹彩の色素濃度(5.1節)から得られた散乱係数と吸収係数を用いて、単一の散乱寄与を推定します。
単一の散乱評価では、点\(M\)に到達する入射光の推定も必要です。Subsurface Texture Mappingのレンダリング手法では、光が多層材料に入射する際の減衰のみを考慮していますが、私たちは角膜の界面での光の屈折も考慮しています。そのために、虹彩の大きさが小さいために、どんな点光源も合理的に指向性光源として近似できるという観察に基づいて、事前に計算された屈折関数を導入し、リアルタイム性能を実現しています。
グレージングされた照明条件では、虹彩にコースティクスがよく現れます。そこで、この現象をリアルタイムレンダラで処理するために、コースティクス関数も定義しています。
6.2 Refraction Function
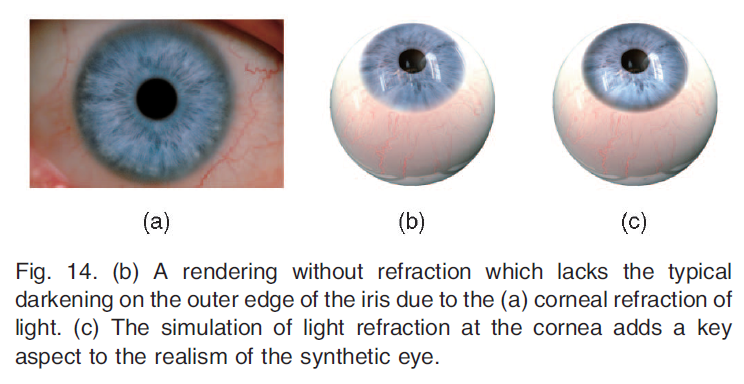
虹彩の見え方は、角膜への入射光の屈折率に大きく依存します(図14)。角膜を通る2つの定点間の最小光路を計算するのは時間がかかるため、あらかじめ計算された屈折関数\(f_r(P, \omega_i)\)を定義しています。
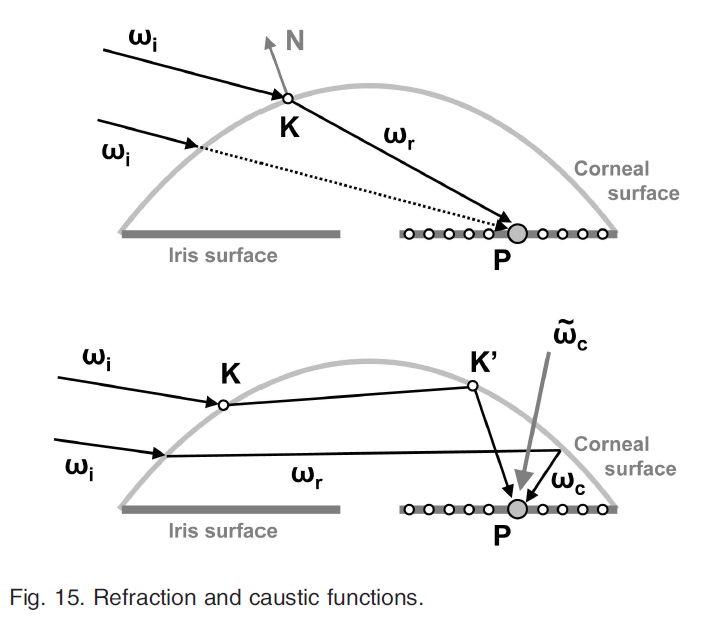
この関数は,虹彩上の任意の点\(P\)と任意の入射光方向\(\omega_i\)に対して,光路が最小となるような屈折光線\(\omega_r\)の方向を返します(図15):
\begin{eqnarray}
f_r(P, \omega_i) = T_c (1 – F_i) e^{-\sigma_t^{ah} ||KP|| } \omega_r \tag{15}
\end{eqnarray}
\(f_r(P, \omega_i)\)のノルムは、屈折した光線によって運ばれる光の強さの量を示しており、\(F_i = F(\omega_i \cdot N, \eta)\)は角膜界面のフレネル係数、\(N\)は光の入射点の法線、\(\eta\)は空気と角膜の屈折率の比です。\(e^{- \sigma_t^{ah}||KP||}\)は前眼部での光の吸収を表し,\(\sigma_t^{ah}\)は純水に近いとされる房水の吸収係数です([28]参照)。\(T_c\)は角膜の透過率です:
\begin{eqnarray}
\log (T_c) = -0.016 – c \lambda^{-4} \tag{16}
\end{eqnarray}
ここで,\(c\)は入射光の角度に依存します[29]。
4.1節で紹介した方法と同様の方法で、方向\(\omega_i\)と虹彩上の点\(P\)のセットに対するこの関数の値を事前に計算します。方向\(\omega_r\)から点\(P\)に入射する放射輝度は、方向\(\omega_i\)から見た光源の放射輝度を\(I_s\)とすると、\(f_r(P, \omega_i)I_s\)に等しいです。
角膜は、縦軸を中心に左右対称になっています。虹彩の厚さの変化は、眼球の前房を通る光路の長さに比べて小さいので、虹彩表面の方程式は\(IT(r)\)に等しいと考えます。これは、\(P\)に対して垂直軸の周りに対称な虹彩を考えることを意味します。このとき、屈折関数もz軸の周りに対称であるため、虹彩の1つの半径上のいくつかの点\(N_P\)について評価します。各サンプル点Pに対して、周囲の半球上の\(N_{\omega_i}\)方向を一様にサンプリングして、屈折関数を計算します。ランタイムでは、\(P\)と\(\omega_i\)の中間の値に対して、それらの値が線形補間されます。(3)に示すように、角膜の輪郭は滑らかで連続しています。そのため、少数のサンプル点と方向で、屈折関数を正確に表現することができます。
我々は、\(P\)と\(\omega_i\)の非補間値に対して、光の入射点\(K\)の回復における屈折関数をテストしました。虹彩上の100のサンプルポイントと2,500のサンプル方向で、補間誤差は0.08mm以下を維持し、生のストレージコストはわずか300KBです。
6.3 Caustic Function
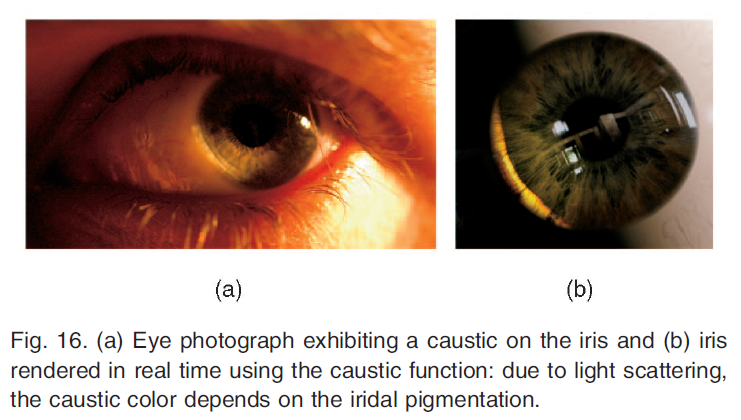
グレージング照明の角度の場合、光は眼球の前房に入り、角膜の内面で反射して虹彩にコースティクスを生成します(図16)。屈折関数と同様に、上半球の各サンプル方向\(\omega_i\)の虹彩のサンプル半径で計算されるコースティック関数\(f_c(P, \omega_i)\)を開発しました。
虹彩上の任意の点\(P\)と、方向\(\omega_i\)に平行な光線のセットに対して,角膜による屈折と角膜の内面で反射のため,この関数は\(P\)における入射レイの加重平均を返します。
コースティクス関数は射影性があります(図15)。この問題に対処するために、\(f_c(P, \omega_i)\)は、入射する放射の結果として考えられる単一の方向\({\bar w}_c\)を、コースティックレイ\(\omega_c\)の加重和として返します:
\begin{eqnarray}
f_c(P, \omega_i) &=& \sum T_c (1 – F_i) F_r e^{-\sigma_t^{ah}( || KK’|| + ||K’P||)} \omega_c \\
&=& \kappa {\bar \omega}_c \tag{17}
\end{eqnarray}
\(f_c(P, \omega_i)\)のノルム,\(\kappa\),は点\(P\)に対する累積屈折/反射係数で,入射方向は\(\omega_i\)です。コースティクスレイによって運ばれてくる入射光は、フレネル項の積によって減衰します:入射レイの屈折に関して\(F_i = F(\omega_i \cdot N, \eta)\)で,内部反射に対して\(F_r = (\omega_r \cdot N’, \frac{1}{\eta})\)です。\(T_c\)は角膜の透過率を表し、\(e^{-\sigma_t^{ah}(||KK’|| + ||K’P||)}\)は房水の光の吸収を表します。
このとき、\(\omega_c\)方向から点\(P\)に入射する全放射輝度は\(\kappa I_s\)となり、\(\omega_i\)方向から見た光源の放射輝度を\(I_s\)とします。
周囲の半球上の2,500個の入射方向\(\omega_i\)と、虹彩の半径上の100個の点\(P\)に対して、方向\(\omega_i\)に平行な光線を角膜表面に向けて40万本照射することで、各\(f_c(P, \omega_i)\)を推定します。これにより、コースティック関数の信頼性の高い推定値が得られ、事前に計算された値を補間することで、虹彩コースティックのリアルタイムレンダリングが可能になります。
6.4 Freckles and Collarette Hyperpigmentation
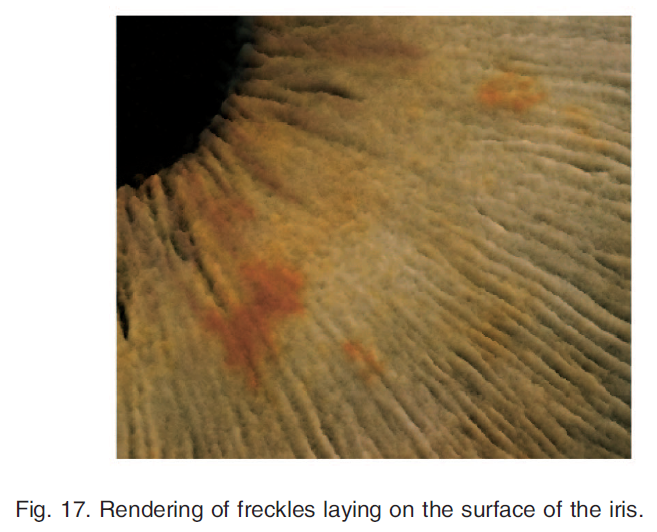
黄褐色から濃い褐色までの小さな色素の斑点が、成人の約半数の人の前頭部に観察されます[30]。虹彩斑は、ABLの表面に存在する比較的バラバラな細胞のコロニーとして現れます(図17)。
4.2項で説明したように、これらの虹彩の欠点を見つけ出し、斑のテクスチャを作成します。斑の色に応じて、ユーメラニンまたはフェオメラニンのABL濃度を局所的に増加させることで、これらの斑を虹彩モデルに含めています。襟足の部分に色素沈着が見られるヘーゼルの虹彩も、同様のテクスチャリング方法でモデル化しています。
6.5 Volumetric Veins in Episclera
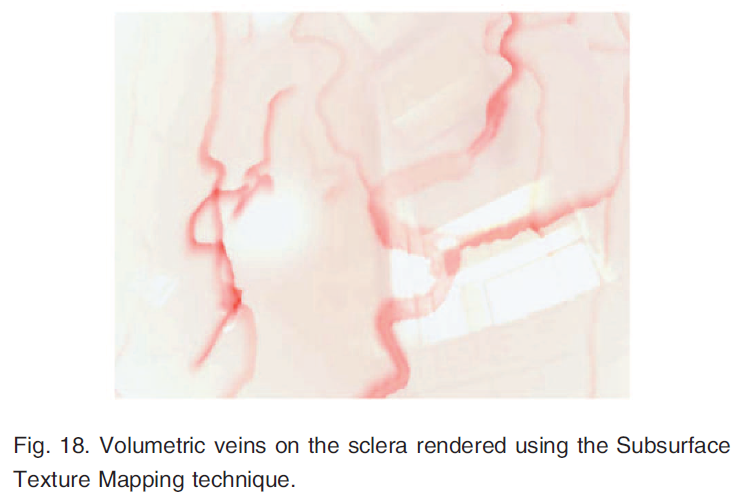
目の外側の白い膜である強膜の上に、上強膜が重なっています。ここでは,上強膜の静脈をボリュームレンダリングできるように,この2つの組織をサブサーフェスのテクスチャマップ[1]としてモデル化しました(図18)。強膜の散乱係数は[7]で発表されたデータから導き出され,上腕静脈はオキシヘモグロビンの最大濃度を考慮してモデル化されています。最後に,強膜と角膜の境目である辺縁部のレンダリングは,古典的なブレンディングを用いて行われています。
7 Result and validation
虹彩画像は、12.3メガピクセルのNikon D300に105mmのマクロレンズと36mmのエクステンションチューブを装着して撮影しました。なお,評価に使用した合成虹彩はすべて,推定されたカメラの位置と焦点距離を用いてレンダリングされています。偏光していない間接照明を最小限に抑えるため、すべての標本は2つのコリメートされた偏光スポットライトで照らされた暗室で撮影されました。また,我々の屈折防止アルゴリズムは任意のカメラ位置に対応していますが,虹彩テクスチャの解像度とシャープネスを最大化するために,すべての眼を正面から撮影することにしました。クローニング処理は、我々のリアルタイム・レンダリング手法を用いて行われました。
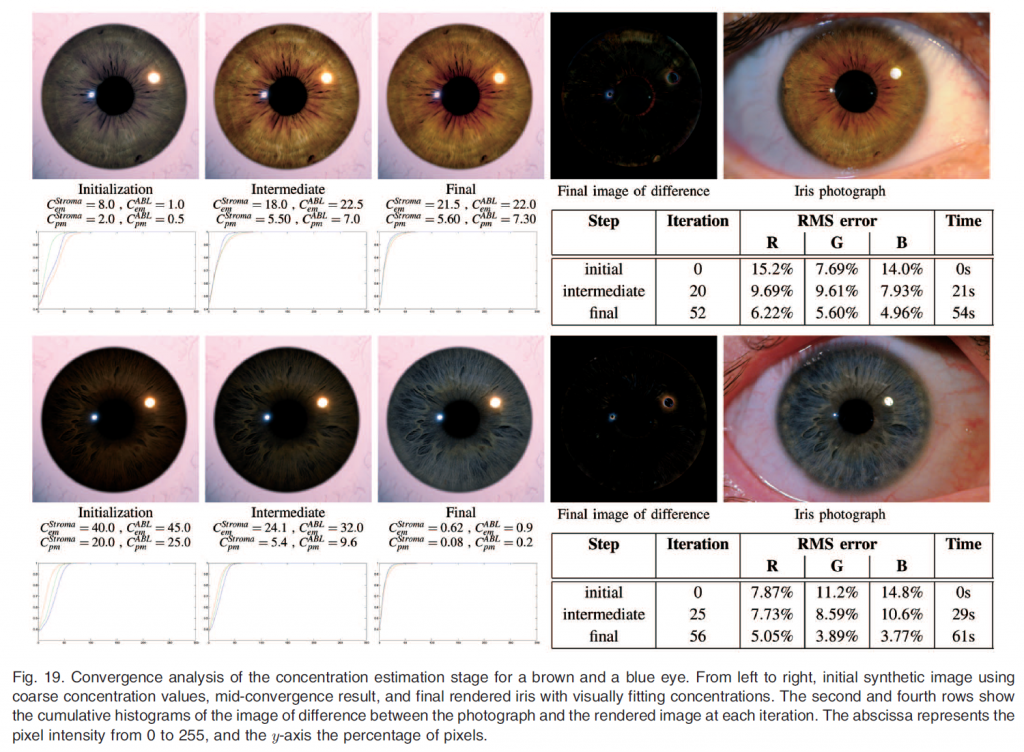
図19のクローン虹彩は、環境照明に近似した25個の点光源を用いてレンダリングしたものです。虹彩の色素濃度を推定するために使用したSimplexアルゴリズムは,約50回の繰り返しで視覚的に満足のいく結果を得ることができました.濃度探索のステップ数を増やしても、虹彩の見え方に大きな変化はありませんでした。
写真とCGを比較することは、ピクセル単位では一致しないため、複雑な問題です。私たちは、検索アルゴリズムのベースとして、単純かつ高速な二乗平均平方根(RMS)距離を選びました。しかし、画像の違いを慎重に解釈する必要があります。図19は、虹彩の異なる濃度を決定することを目的とした反復プロセスを示しており、色素濃度検索アルゴリズムの初期化、中間ステップ、最終ステップのそれぞれにおいて、差のある画像の累積ヒストグラムを提供しています。
なお、反復プロセスのロバスト性を示すために、顔料濃度の初期推定値には非常に粗い値を選びました。図19の表は,反復探索の各ステップにおける各チャネルのRMSエラーを示しています。最終的な誤差の平均値は約5%で、目立たない程度です。アルゴリズムが収束すればするほど、RGBヒストグラムは\(y\)軸に近づき、画像の差が徐々に一様に減少していくことがわかります。さらに、RGBヒストグラムの曲線が互いに近づいていることもわかります。これは、各チャンネルで同じ量の誤差が発生していることを意味しており、実際の虹彩のクロミナンスを復元していることになります。
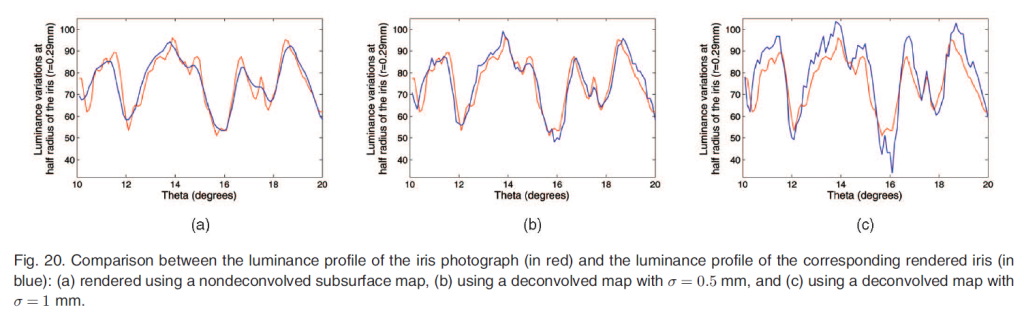
図20は,実際の虹彩の半径方向の輝度プロファイルと,虹彩の形態の異なる推定値を用いてレンダリングされた虹彩の輝度プロファイルを比較したものです。放射状の輝度プロファイルは、この虹彩上の円弧上にある点の輝度を示していることに注意してください。屈折していない非解像テクスチャで間質の厚さを表現した場合、レンダリングされた虹彩の輝度は「平滑化」されたように見え(Fig.20a)、実際の虹彩の形態とは一致しません。デコンボリューションされたテクスチャを使って虹彩をレンダリングすると、よりシャープな結果が得られます。しかし、図20cに示すように、\(\sigma=1\)mmのデコンボリューションを使用すると、間質の厚さの変化を過大評価する傾向があります。で、\(\sigma=0.5\)mmを用いて虹彩テクスチャをデコンボリューションすることにしました(図20b)。これにより、オリジナルの虹彩の輝度変化と完全に一致しないまでも、視覚的にオリジナルに近い仮想の虹彩が得られます。
我々のレンダリングアルゴリズムは、Pentium4 2.6GHzとGeforce 8800GTXでテストされており、2つの点光源、\(800 \times 600\)の解像度で約35fpsのフレームレートを実現しています。私たちが開発したリアルタイムレンダリング手法では、ユーザーがインタラクティブにストローマの厚さや色素濃度を変更しながら、視覚的に納得のいく虹彩の画像を生成することができます。また、図19の表に示されているように、色素濃度を約1分で高速検索することも可能です。
この手法は近似値を使用するため、いくつかの制限があります。実際、斑を除去するステップは、虹色の斑点が見逃された場合、濃度回復のエラーの原因となる可能性があります。これにより、虹彩の厚さと色素濃度の推定値が一致しなくなる可能性があります。しかし、5章で紹介する、差のある画像に適用された直交ラジアルガウスフィルタ(\(\sigma_r = 1\)mm, \(\sigma_{\theta} = 7\)mm, \(\mu_r = \mu_{\theta} = 0\))を使用することで、よりロバストな復元が可能になります。ユーザーが選択しなければならないパラメータはわずかであるにもかかわらず、これがアーティファクトの原因となっている可能性があります。しかし、本稿で提示したパラメータ\(\sigma\)と\(\alpha\)を用いることで、実物に近い虹彩が得られると考えています。
物理的に正確ではありませんが、私たちの技術は眼科の文献と一致しています。私たちは、ABL内のメラニンがストロマ内のメラニンよりも虹彩色に影響を与えることを発見しました。これは[6]の記述と一致しています。また、図1のような緑の虹彩は、青や茶の瞳よりも比率\(\beta_m\)が高い傾向にあることもわかりました。このように緑の試料ではフェオメラニンの比率が高いことは、[31]で注目され、測定されています。ABLの厚さが一定で、間質の厚さだけが変化する場合、虹彩の全体的な色の変化を復元するための信頼性は高いと考えられます。しかし、個々の虹彩の非常に局所的な特殊性を扱うために、斑のテクスチャを追加しています。最後に、環境照明を推定するために点光源の数を増やしてクローニングアルゴリズムを実行しましたが、ABLや虹彩間質内のメラニン濃度に大きな変化は見られませんでした。
8 Conclusion
生体内での解剖学的特徴の評価は複雑な問題であり、単純な解決策はありません。私たちは、シンプルなデジタルカメラと古典的なマクロレンズを使用して、人間の目を模倣するためのユーザーフレンドリーで手頃なプロセスを提案しました。また、角膜での光の反射を避けるために、偏光フィルターを利用しました。人間の虹彩は、その解剖学的特徴に基づいてモデル化しました。虹彩の中で光が散乱することで、色のバリエーションが生まれます。これは、色素濃度の違いだけではありません:虹彩の反射率は、その層の厚さの変化にも依存します。そこで、一般的な虹彩の眼科的知識と、屈折していない虹彩の写真、およびデコンボリューションした虹彩の写真を用いて、虹彩の層の厚さを近似しました。
皮膚のような層状物質の散乱特徴の推定には問題がありますが、虹彩の形態にはより良い解決策があります:私たちは、虹彩の厚さの変化を利用して、ABLとストローマのメラニン濃度を近似する方法を提案しました。
グラフィックスハードウェアを活用し、事前に計算された屈折関数とコースティクス関数を導入することで、合成眼球のリアルタイムレンダリングを実現しました。このような関数を使用することで、対称性のある屈折物体のレンダリングを高速化できると考えています。今後の課題は、医療目的のために虹彩の形態と散乱パラメータの推定を改善することです。また、厚さが不均一な層状物質の多重散乱をリアルタイムで推定することや、他の有機組織のクローニングを検討し、この手法を人間以外の眼にも拡張したいと考えています。
Acknowlegements
和訳省略。