こんにちわ、Pocolです。
今日は2003年に発表された…
[Marschner 2003] Stephen R. Marschner, Henrik Wann Jensen, Mike Cammarano, Steve Worley, Pat Hanraha, “Light Scattering from Human Hair Fibers”, SIGGRAPH 2003
を読んでみることにします。
Abstract
髪の毛からの光の散乱は、Kajiya と Kayの古典的な現象論的モデルを用いてコンピュータグラフィックスで通常はシミュレーションされます。私たちは、個々の髪の毛からの散乱を新たに測定したところ、KajiyaとKayのモデルでは予測できない視覚的に重要な効果が見られました。我々の測定は、面外散乱を調べることで、これまでの毛髪測定を超えたものであり、この先行研究と合わせて、複数のスペキュラーハイライトと、繊維軸を中心とした回転に伴う散乱の変化を示しています。これらの効果原因を、毛髪繊維を、内部が吸収体で、表面が傾いた鱗片で覆われた透明な楕円柱と見立てて説明します。また,円柱の解析的な散乱関数に基づいて,測定で示された散乱挙動と定性的に一致する実用的な毛髪のシェーディングモデルを提案します。また,実写とレンダリング画像を比較することで,新しいモデルが実際の髪の毛の外観と一致することを実証します。
1 Introduction
人や動物を表現する上で、髪の毛をリアルに表現することは不可欠ですが、リアルに表現するためには、髪の毛の構造や挙動に起因する多くの課題に直面します。数千から数百万本の繊維の形状を決定し、繊維からの光の散乱をシミュレートし、その結果として生じる画像の細い曲線をエイリアシングが発生しないようにサンプリングする必要があります。髪の毛に関する研究のほとんどは、繊維の集合体のジオメトリのモデリングとアニメーション化[Sourinら 1996; Chenら 1999; HadapとMagnenant-Thalmann 2000; KimとNeumann 2000; KimとNeumann 2002; Changら 2002; Magnenat-Thalmannら 2002]、スキャンラインレンダリングのための効率的なアンチエイリアシングと曲線描画のアルゴリズム[WatanabeとSuenaga 1992; KongとKakajima 2000]、そして髪の毛内の影の近似化[LokovicとVeach 2000; KimとNeumann 2001]などに費やされてきました。しかし、繊維の特定の集合体の外観を決定する散乱モデルについては、あまり注目されていません。溝のある表面からの反射モデル[Kajiya 1985; Poulin と Fournier 1990]が櫛状の繊維からの散乱を計算するために使われることもありますが,ほとんどのヘアレンダリングでは,Kajiya and Kay [1989]の古典的な現象論的モデルが使われています。
KajiyaとKayのモデルは、繊維からの散乱の最も明白な特徴、すなわち、繊維の方向に垂直な画像に線状のハイライトが現れることを捉えるように設計されています。このモデルは、円柱の表面からの平行光の反射が、髪の毛の軸を中心とした円錐形になるという観察に基づいています。このモデルでは、その円錐を中心に一定の強度のハイライトを配置します。他のすべての散乱は,入射角の余弦に比例した輝度を生成する拡散項によって説明されます。しかし、このモデルは長年の実績がありますが、いくつかの点で問題があります。ひとつは、物理ベースのレンダリングに重要なエネルギー保存性がないことです。
しかし、物理的な正しさを必要としない場合でも、Kajiya-Kayモデルは、観察される視覚効果のいくつかを予測できません。繊維を不透明な円柱としてモデル化しているため、透過や内部反射を考慮していないからです。髪の毛は誘電体であり、金髪、茶髪、赤髪などの明るい色の髪の毛は非常に透き通っています。Goldmanは,前方への透過と後方への反射の相対的な量を制御する指向性パラメータを追加することで,半透明性をシミュレートしました[Goldman 1997]。Kimはこのモデルを拡張し、2項の位相関数を提案している[Kim 2002]。第1項は,光線密度の独立変数に基づいて,カーディオイドとしての表面反射をモデル化しています.私たちのR成分も同様ですが,フレネル係数を考慮し,斜入射を扱います。2番目の項は、透過を前方散乱コサインローブとしてモデル化しており、透明な円柱からの法線入射散乱のモンテカルロ計算によって裏付けられています。我々はKimのモデルを拡張し、フレネル係数と体積吸収を考慮して、内部反射も含めた解析モデルを構築し、異なる反射モードによるハイライトの分離をモデル化し、偏心の影響を近似しました。
化粧品業界の2つの研究グループは、髪を美しく健康的に見せる要因を解明するために、毛髪繊維の散乱特性を測定しました。Stammら[1977]は,個々の繊維のラックからの相対的な散乱を,繊維軸と同一平面上の方向(すなわち入射面)に対する照明および視野角の関数として測定しました。彼らは2つの期待される動作からの逸脱を発見しました。1つ目は、鏡面方向から数度離れた場所に主要なスペキュラーピークが発生すること。この角度のずれは、毛髪繊維のキューティクルを形成する鱗片の傾きによるものと推測されました。2つ目は、鏡面方向の反対側に発生する2次ローブです。BustardとSmith[1991]は,第1のピークは偏光を維持しているのに対し,第2のピークは脱偏光していることを観察しています。また、両グループは、黒髪には第2のハイライトが存在しないことも観察しています。また、BustardとSmithは、繊維細胞に垂直な面内での方位角散乱を予備的に観測し、内部反射コースティクスと思われる強いピークを観測したことを報告しています。これらの実験は、副次的なピークが繊維細胞の背面からの内部反射によるものであるという仮説を支持するものです。
我々は、人間の髪の毛の個々の繊維からの光の散乱を実験的・理論的に研究し、コンピュータ・グラフィックスに使用できる簡単な実用モデルを開発しました。具体的には
- StammらやBustard Smithによる入射面での測定に加えて、我々は繊維細胞に垂直な面での散乱も測定しています。また、完全な3次元半球状散乱の測定も初めて報告しています。この3Dデータでは、いくつかの新しい出現現象が見られます。まず、一次光のハイライトは髪の毛の周りにずっと続いていますが、二次光のハイライトは光源に向かって髪の毛の側に限定されています。次に、一対の大きな面外のピーク(輝き)が存在し、入射角が大きくなるにつれて、ピークは入射面に近づき、最終的には合体して消えていきます。
- 散乱分布、特に二次的なハイライトは、毛髪繊維の軸を中心とした回転角度に依存します。これは、毛髪繊維の断面が一般的に円形ではないことから予想されることです[Robbins 1994]。
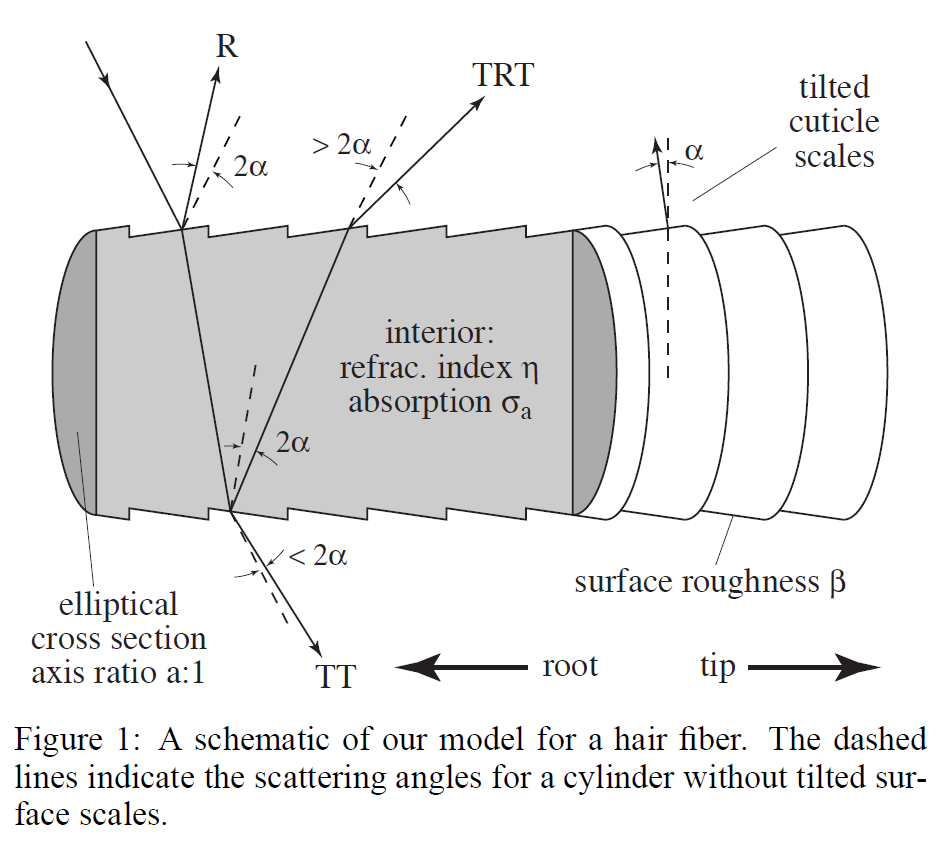
- 我々の観察結果を説明するために、我々は毛髪繊維の構造と組成に基づいた単純なモデルを提案します(図1)。髪の毛は、内部が着色された透明な円柱で、表面は荒く傾いた鱗片で構成されていると近似しています。
- この理論に基づいて、人間の髪の毛のシェーディングモデルを提案します。茶色の髪の毛のレンダリング例をいくつか作成することで、その使用方法を説明します。このシェーディングモデルはシンプルで、標準的なレンダリングアルゴリズムに簡単に組み込むことができます。最後に、このモデルを実験データと比較して検証し、質的によく一致することを示します。
2 Fibers
まず、人間の毛髪繊維の背景を紹介します。また,本稿で使用する表記法を紹介し,繊維の光散乱関数を定義します。
2.1 Hair fibers and fiber scattering
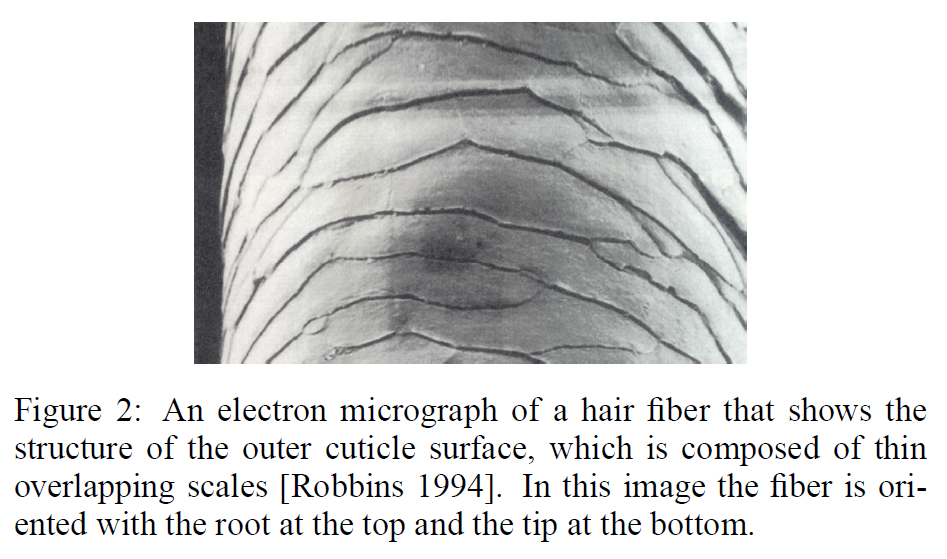
人間の頭皮の髪の毛は、大きく分けて2つの部分から構成されています:キューティクルとコルテックスです。キューティクルとは、内側のコルテックスを囲む外側の薄い保護膜のことです。キューティクルは、繊維と空気の界面を形成するため、光の散乱において特に重要となります。扁平な細胞が屋根板のように重なり合って構成されており(図2)、繊維が入れ子状になったコーンのように見えます。重ねて配置されているため、鱗片の表面は繊維の表面全体の法線からわずかに、しかし体系的にずれており、その表面は繊維の根元側に約\(3^{\circ}\)傾いています[Bustard と Smith 1991; Robbins 1994]。
コルテックスは繊維の大部分を形成しています。中心部には色素のついた芯、髄質があります。皮質と髄質の色素によって髪の色が決まります。この論文では,繊維内部の光学的性質を,約1.55の屈折率\(\eta\)[Stammら1977]と,繊維全体で一様であると仮定した吸収断面積\(\sigma_a\)の2つの量で近似されます。
後述するように、毛髪繊維の形態から、散乱関数の主な特徴を説明することができます。毛髪繊維は、傾いた鱗片で覆われ、内部が色素で覆われた誘電体の円柱としてモデル化されています(図1)。円柱からの指向性ビームを反射すると、反射光のいくつかの異なる成分が生成され、すべてが出射方向の円錐形に向けられます。表面からの反射により、円錐の周りにかなり均一に広がった成分が得られます。髪の毛を透過すると、非常に明るい成分が髪の毛の反対側の方向に向かって集中している。毛髪表面の内側で反射した光は、後方散乱成分となります。この成分はより複雑で、シリンダーの形状と入射角に応じて、エネルギーを円錐形全体に広げたり、1つまたは複数のコースティクスに集中させたりします。TとRを円柱界面での透過と反射に見立てて、これら3つの反射モードをR、TT、TRTと表記します。
図1に示すように、キューティクル・スケールの傾きによって、R成分とTRT成分の錐体が理想的なスペキュラ錐体からわずかにずれます。さらに重要なのは、この2つの成分が逆方向に移動することで、視覚的に区別できる2つのハイライトに分かれてしまうことです。R成分のハイライトは表面反射なので白く、TRT成分のハイライトは繊維の内部を通過した光で形成されるので色がついています。
2.2 Scattering
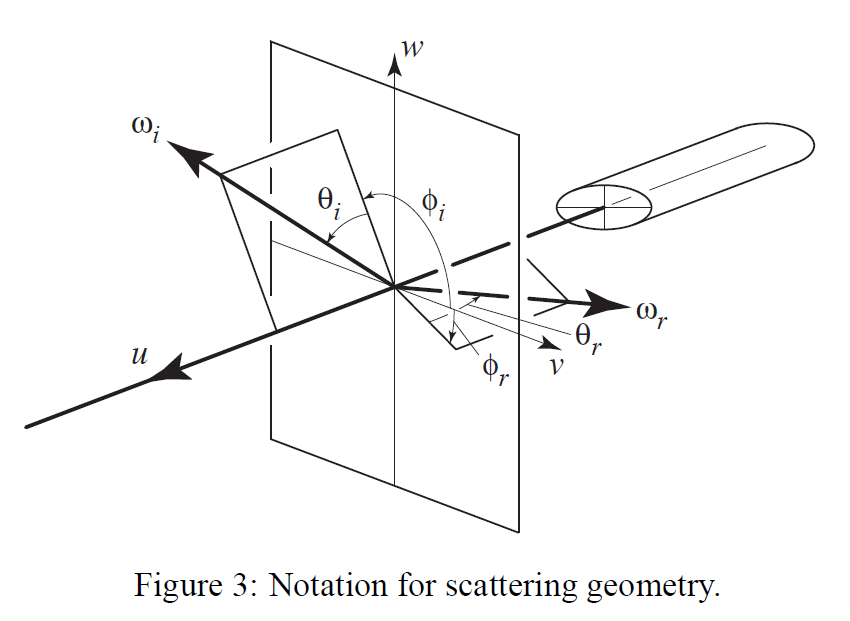
詳細を説明する前に、本稿で使用する散乱ジオメトリ(図3)の表記法を確立しておきましょう。髪の毛の接線を\(u\)とし、根元から先端に向かう方向を指します;ベクトル\(v\)と\(w\)は右手系の正規基底を完成させ、断面が楕円の場合は\(v\)が長軸、\(w\)が短軸となります。ここでは、\(v-w\)面を法線平面と呼びます。照明の方向を\(\omega_i\)、散乱光の計算または測定を行う方向を\(\omega_r\)とします; 双方の方向が中心から離れています。\(\omega_i\)と\(\omega_r\)を球面座標で表します。また、法線平面に対する傾きを\(\theta_i\)、\(\theta_r\)とします(\(0^{\circ}\)が髪に垂直、\(90^{\circ}\)が\(u\)、\(-90^{\circ}\)が\(-u\)となるように測定)。髪の毛を中心とした方位を\(\phi_i\)、\(\phi_r\)(\(v\)が\(0^{\circ}\)、\(w\)が\(+90^{\circ}\)になるように測定)と表記します。
また、いくつかの導出した角度を使用しています。差分角\((\theta_r – \theta_i)/2\)を\(\theta_d\)と表記します。相対方位\(\phi_r – \phi_i\)を単に\(\phi\)と表記します。平均値\(\theta_h = (\theta_i + \theta_r) /2\)と\(\phi_h = (\phi_i + \phi_r) / 2\)を半角と呼びます。
繊維についての双方向散乱関数\(S\)は,サーフェイスの双方向反射分布関数\(f_r\)と物理単位は同じですが,異なります。入射光と反射光には、それぞれ曲線放射照度\({\bar E}\)(単位長さ当たりのパワー)と曲線強度\({\bar L}\)(単位長さ当たりの強度)を使用します。これらの単位は、サーフェイス上の放射照度(単位面積当たりの仕事率)と放射輝度(単位面積当たりの強度)に類似しています。
\begin{eqnarray}
S(\omega_i, \omega_r) = \frac{d {\bar L}_r(\omega_r)}{dE_i(\omega_i)}
\end{eqnarray}
ここで、\({\bar L}_r\)は繊維の無限長から散乱される曲線強度、\({\bar E}_i\)は繊維のその部分の曲線放射照度です。この放射照度は入射放射照度に比例します:
\begin{eqnarray}
d{\bar E}_i (\omega_i) = DL_i (\omega_i) \cos \theta_i d \omega_i
\end{eqnarray}
ここで、\(D\)は繊維の直径です(楕円形遷移の場合は\(\phi_i\)に依存します)。なお,放射照度を測定する領域は\(Ddl\)であり,\(dl\)は繊維に沿った無限大の弧長です。
この定義があれば、散乱積分は次のように書かれます。
\begin{eqnarray}
{\bar L}_r(\omega_r) = D \int S(\omega_i, \omega_r) L_i(\omega_i) \cos \theta_i d \omega_i \tag{1}
\end{eqnarray}
なお、積分が上半球に及ぶ曲面とは異なり、この積分は球体全体に及びます。この式に\(D\)があるということは、太い繊維は細い繊維に比べてより多くの光を遮断するため、遠くからでも明るく見えることを示しています。
3 Scattering measurements
私たちが行った毛髪の実験は、毛髪の散乱モデルで説明する必要のある現象を、定性的かつ定量的に理解することを目的としています。この論文では,これらの測定の概要を簡単に説明します。私たちの実験の詳細な説明は,今後の論文で行う予定です。
実験では、毛髪1本1本に細いビームを照射し、光源とCCDカメラを試料から任意の方向に配置した4軸ゴニオメーターを用いて、さまざまな方向の散乱光を測定しました。私たちは、1〜2cm程度のわずかな長さの髪の毛だけに集光ビームを照射し、この照射された部分が測定する髪の毛の長さとなります。これにより、髪の毛の長さによる特性の変化の影響を抑えることができました。
3.1 Incidence plane
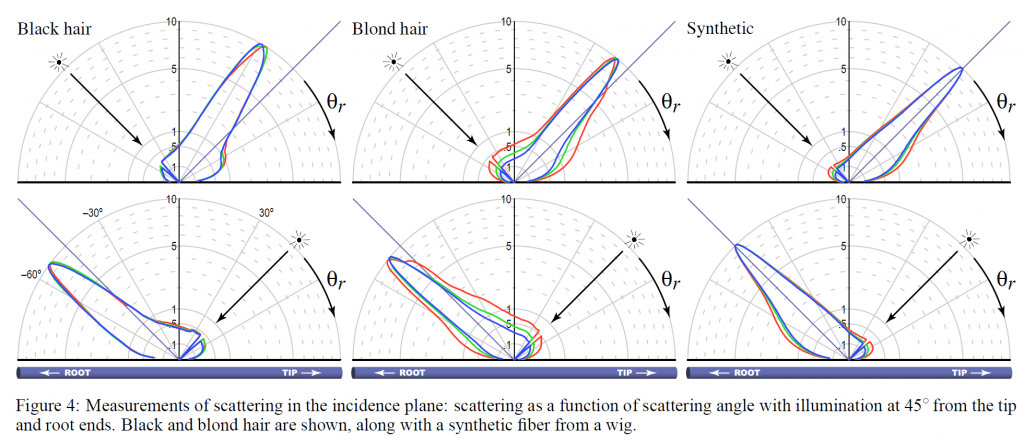
StammらやBustardとSmithの測定は、入射面での測定であり、光源と検出器が繊維と同一平面上にある場合の散乱関数の2次元スライスのみを観測したことになります。これらの初期の結果を検証するために、数種類の髪の毛のサンプルと、かつらの合成繊維で同じような測定を行いました(図4)。
それぞれのサンプルについて、入射角を\(45^{\circ}\)に設定し、出射角を変化させて散乱を測定しました。この実験は,根元の方向から照明した場合(\(\theta_i = -45^{\circ}\))と,先端の方向から照明した場合(\(\theta_i = 45^{\circ}\))の2回行いました。それぞれの測定は、可視波長域の3つのカラーバンドで行われました。なお、各プロットの入射角付近にある小さな隙間は、カメラが光源を遮っているためです。
散乱関数で最も顕著な特徴は、\(\theta_r = – \theta_i\)の時にほぼ発生するスペキュラーハイライトです。合成毛髪では鏡面方向にちょうどハイライトが発生しますが、実毛ではどの方向から照射しても根元に向かって6〜10度の範囲でハイライトが発生します。さらに、黒髪ではなく金髪では、色に依存したローブの非対称性が見られ、サイドローブがプライマリーハイライトよりもスペキュラー方向に近い位置に現れています。拡散反射の背景が存在し、それは金髪の方がより大きく、より多くの色を持っています。このタイプの他の測定では、2次ハイライトは常に観察されますが(黒髪を除く)、その強さと幅はかなり異なります。
入射面での散乱関数に対する\(\theta_i\)と\(\theta_r\)の両方の影響を調べるために,1本のブロンドファイバーについて2回目の測定を行いました。この測定は,\(\theta_h\)と\(\theta_d\)の項でパラメータ化しました。それぞれのスイープは,光源と検出器を固定して\(\theta_d\)を固定し,毛髪を回転させて\(\theta_h\)を変化させながら行いました。
この全入射面測定の結果の一部を図5に示します。これらのプロットでは、鏡面方向に対応するゼロの両側に、プライマリハイライトとセカンダリハイライトの両方が見えています。この構成の髪には、非常に強いセカンダリーハイライトがあり、ほとんどの角度で実際にプライマリーハイライトよりも強くなっています。 散乱角が大きくなると、セカンダリーハイライトはフェードアウトし、プライマリーハイライトはより一定の広さを保ちます。どちらのピークもほぼ一定の幅を保っています。高角度では、一次ハイライトは鏡面方向に非常に近いところに現れる鋭いピークに変わります。この現象は、Stammらが「等角度ピーク」と名付けたものと同じであると考えられます。
3.2 Normal plane
散乱関数の3次元的な複雑さ、特に2次的なハイライトを理解するために、別の平面2次元測定を行いましたが、光源と検出器の平面が繊維に対してほぼ垂直になるように、つまり法線方向に配置しました。この平面内で,方位\(\phi_i\)と\(\phi_r\)をそれぞれ独立して変化させました。より正確に言うと、入射方向は法線面上にありますが、散乱方向は\(\theta_r = 10^{\\circ}\)の円錐上にあります。これは、我々が観察した、クチクラの鱗片の傾きによるハイライトのずれが、法線方向に正確に測定した場合、第2のハイライトを観察することができないためです。今回の測定では、赤の波長帯のみを表示しているが、これは2次的なハイライトが最も顕著に現れる場所だからです。
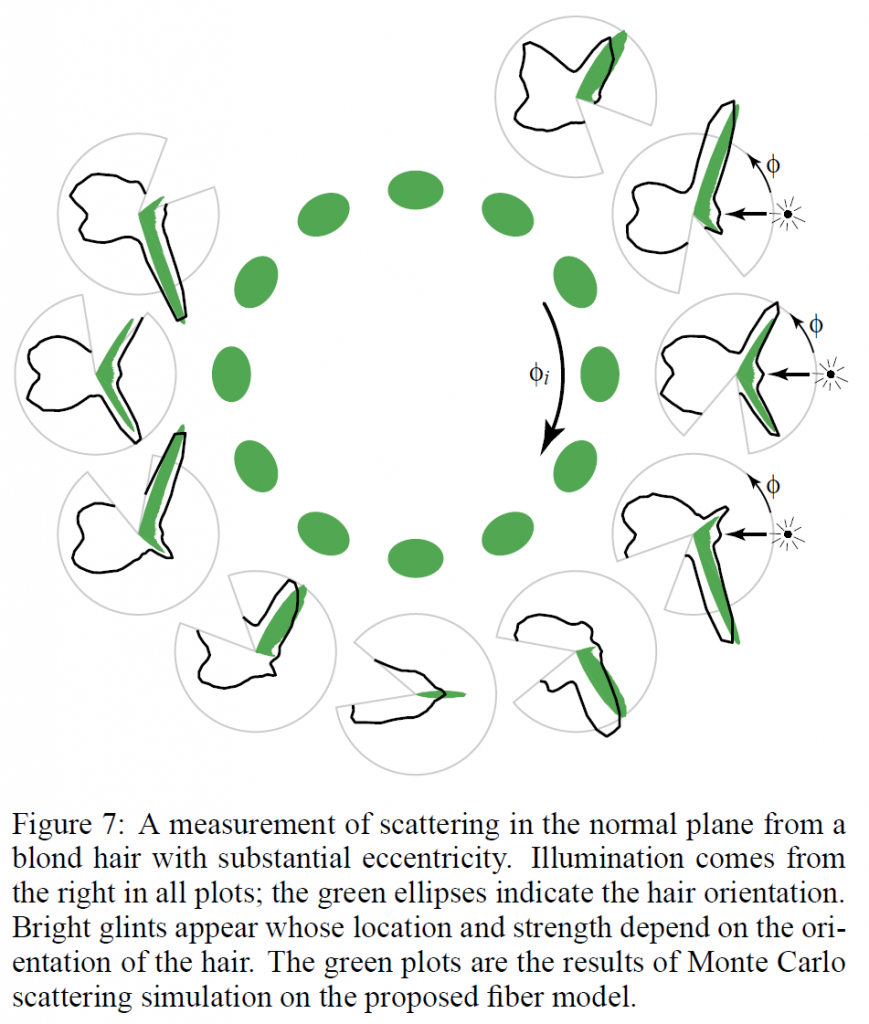
その結果を図7に実線で示します。私たちはデータを\(\phi_i\)と相対的な方位\(\phi\)で整理したので、各極の散乱図は光源を固定したカメラのスイープに対応し、図から図への移動は光源の角度を変えること(等価的には毛髪をその軸の周りで回転させること)に対応します。データが欠けているのは、ゴニオメーターの機械的な制約によるものです。
この測定では、2つの明るい面外のピークがあることがわかります。ピークの強さや\(\phi\)の位置は髪の毛ごとに異なります。このピークがもたらす視覚的効果を、私たちは「グリント」と呼んでいます。
さらに、\(\phi_i\)の関数として、グリントの明るさや位置が大きく変化していることから、髪が回転対称ではないことがわかります。しかし、この図では2つの対称性が明らかになっています。1つは\(\phi_i\)の\(180^{\circ}\)回転対称性(正反対のプロットが似ている),もう1つは\(\phi_i\)と\(\phi\)の両方を無効化することによる対称性(図全体の垂直方向の両方向の対称性)です。これらの対称性から、髪の毛は\(180^{\circ}\)回転対称であり、断面は左右対称であることがわかります。
グリントのパターンが入射面に対して対称(\(\phi_i=0\))の場合、断面が円形の球や円柱での屈折によるコースティクスの形成によく似ています。より一般的には、繊維の回転に伴うピークの変化は、6.1項で述べたように、透明な楕円柱からの内部反射に似ています。同じ個体から採取した別の繊維を顕微鏡で観察したところ、偏心率は0.7:1でした。
3.3 3D hemispherical measurements
3.3.1 Changes in glints with angle of incidence
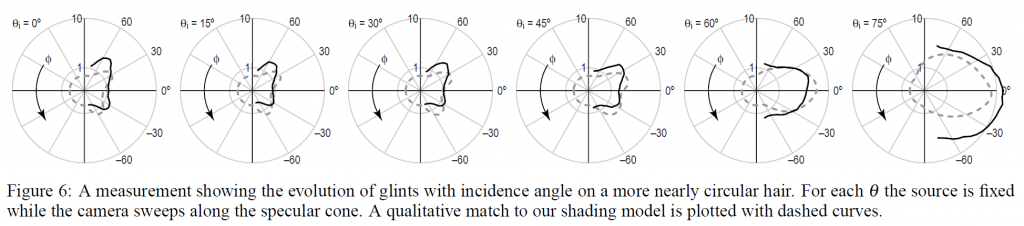
入射角を変化させながら、2次的なハイライトを\(\phi\)の関数として調べることは有益です。これは、光源に対する髪の傾きが変化したときに、このハイライトがどのように変化するかを示すものです。この測定は、光源とカメラを法線面の反対側にほぼ等しい入射角\(\theta\)で配置し、光源を固定したままカメラを円錐形に沿ってスイープすることで、\(\phi\)の依存性を測定しています。その結果を図6に実線で示します。
先ほどの測定と同様に、最大のグリント強度を観測するためには、カメラを光源よりも先端に少し近づける必要があるため、\(\theta_i\)を変化させながら、\(\theta_i + \theta_r = 10^{\circ}\)という条件を維持しています。
この測定で示された現象は、グリントが発生する方位が入射角の関数として変化することであり、入射角が垂直からグレージング角に向かうにつれて、グリントは入射面に向かって移動します。そして、\(\theta = 60^{\circ}\)のあたりでマージしているように見えます。この挙動は、構造を知るためのもう一つの手がかりとなります。このようなマージングトランジションは、円柱の内部反射によって形成されるコースティクスに特徴的です[Mountら1998]。この繊維の偏心率の測定値は約0.8:1です。
3.3.2 Hemispherical scattering
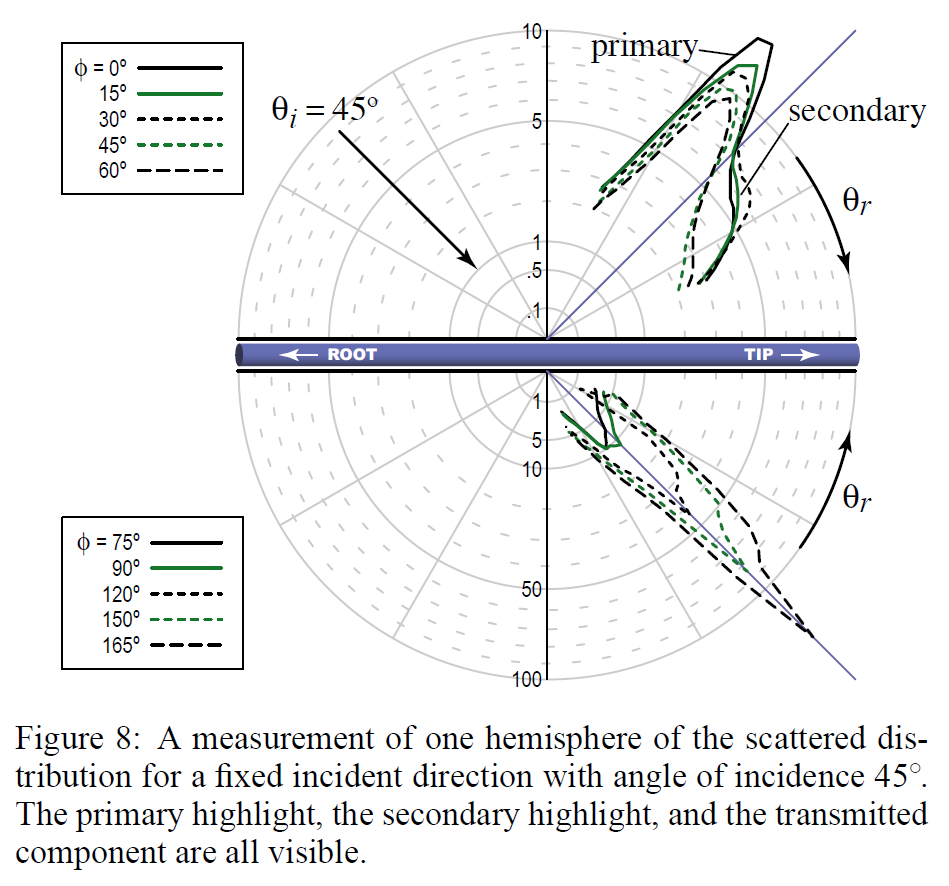
この測定では、1次元入射面の測定を拡張し、\(\theta_r\)だけでなく\(\phi_r\)も変化させることで、散乱方向が半球全体で変化するようにしました。入射方向が固定されている場合、これは散乱関数の完全な測定となります(またはその半分で十分ですが、これは両側対称性(\(\phi_i\)を変化させない場合、正確ではないものの妥当な仮定)を考慮したものです)。
その結果を図8に示します。このプロットでは、\(\theta_r\)に対して、\(\phi\)の固定値に対するいくつかのカーブが一緒にプロットされています。\(\theta_r = 40^{\circ}\)で一次的なハイライトが現れ、\(50^{\circ}-80^{\circ}\)付近で二次的なハイライトが広く現れます。カーブからカーブへと移動する際、プライマリーハイライトはスペキュラーコーンからの広さとシフトをほぼ一定に保っています(プロットでは青線で示されています)。セカンダリーハイライトが強くなり、\(\phi=30^{\circ}\)付近でピークを迎え、その後消えていきます。散乱関数の前方散乱の半分は、下の軸に大きなスケールで示されており、スペキュラーコーンから大きくシフトしていない強い前方散乱成分によって支配されています。
3.4 Summary
以上、毛髪繊維の光の散乱を測定した結果、以下のような現象が確認されました。ここでは,これらの現象を誘電体円柱の散乱モードの観点から分類します(2節)。
- R:プライマリー・スペキュラー・ピークのルート側へのシフト。このずれは、毛髪繊維上の鱗片が傾いているためと考えられます。
- TT:明るい色の髪から強い前方散乱成分。このため、後ろから光を当てると、金髪、茶髪、グレー、白髪が非常に明るく見えます。
- TRT:
- 白いプライマリスペキュラーピークから先端に向かって移動した色付きのセカンダリスペキュラーピーク。髪の毛の場合、プライマリーのすぐ上にセカンダリーハイライトが見えますが、これは独立した特徴というよりも、プライマリーのカラーフリンジのように見えることがあります。
- セカンダリーハイライトは,\(\phi\)の関数として変化します。一般的には、2つのピーク、つまりグリントを含んでいます。ピークの位置は入射角に依存し、\(\theta\)が大きくなるにつれて入射面に収束していきます。さらに、断面が円形でない毛髪の場合、グリントの強さと位置は、毛髪の軸周りの回転角に強く依存します。これにより、毛髪繊維は独特のきらめきを持つようになります。
- セカンダリーハイライトのエネルギーのほとんどは、この2つのグリントの間に含まれています。
4 Theory of scattering from fibers
このセクションでは、平滑な円柱からの散乱に適用される背景理論を紹介します。円柱は対称性があるため、4次元の散乱関数は2つの2次元項の積に因数分解できることを示します。1つの項(\(M\)と呼ばれる)は\(\theta\)依存性を、もう1つの項(\(N\)と呼ばれる)は\(\phi\)依存性を表しています。また、円柱の場合の\(N\)も導き出しました。この2つのパートは、次のセクションで展開される完全な実用的モデルの基礎となるものです。このセクションでは、\(M\)の表現、\(N\)を楕円柱に拡張するための近似、\(N\)を効率的に近似するための手順を紹介します。
4.1 Scattering from cylinders
固定された断面を単一の軸に沿って移動させることで形成された繊維では、4次元の散乱関数を2次元の項の積に分離することができます。ここでは、繊維からの散乱に関する過去の研究で使用された特性を利用しています[Marcuse 1974; Adler et al 1998; Mount et al. 1998]:
- 誘電体円柱に軸に対して特定の傾きで入射した光線は、屈折や反射の順序にかかわらず、常に同じ傾きで出てきます。
つまり、\(\omega_i\)方向からの平行な入射光線の束は、繊維軸を中心とし、\(-\omega_i\)を含む円錐上に方向がある散乱光線の集合体を生成することになる(付録A)。髪の毛の内部で屈折した光線の方向も円錐上にあります。散乱は\(\theta_r = -\theta_i\)のときにしか起こらないので、これにより、散乱関数は4次元から3次元になります。もちろん、この等式が成り立つのは、表面が粗い場合に限られますし、円柱内部に体積散乱がないという仮定にも依存します。 - 散乱分布の\(\phi_r\)依存性は、毛髪に垂直な平面への投影のみを検査することで解析できます。
入射ベクトルと反射ベクトルは、3Dの場合と同様に、投影された表面の法線を挟んで対称に配置されているので、3Dの円柱からの鏡面反射は、投影された場合も鏡面反射のままであることがわかります。
誘電体界面での入射ベクトルと透過ベクトルを表面法線を含む平面に投影すると、投影されたベクトルは依然としてスネルの法則に従いますが、屈折率の\(\eta\)を\(\eta'(\eta, \theta) \gt \eta\)に置き換えたものになる、というBravaisの法則(付録Bで導出)により、屈折した光線についても同様のことが言えます。なお、\(\eta’\)は投影面からの入射光線の傾き(\theta\)にのみ依存し、投影面内の角度には依存しないものです。このように、特定の入射方向から発生するすべての光線は、法線面に対して同じ傾きを維持することがわかっているので、任意の屈折率に対して法線面で機能する2D解析で3D散乱関数を記述することができます。
この2つの事実から、任意の断面を持つ平滑な円柱の散乱関数を次のように書くことができます:
\begin{eqnarray}
S(\phi_i, \theta_i; \phi_r, \theta_r) = \delta(\theta_r + \theta_i)N(\eta'(\theta); \phi_i, \phi_r)/ \cos^2 \theta
\end{eqnarray}
第1の因子は、散乱がスペキュラーコーン内でのみ起こることを示し、第2の因子Nは、方位角方向の散乱関数を表し、\(\cos^2\theta\)はスペキュラーコーンの投影立体角を表します。\(\theta_i = \theta_r\)であることを強調するために、単に\(\theta\)と書きます。\(\theta\)は\(\eta’\)を通じて間接的に\(N\)に影響を与えるだけなので、2D解析を用いて\(N\)を独立して導き出すことができます。次のセクションでは、この式を次のように一般化します。
\begin{eqnarray}
S(\phi_i, \theta_i; \phi_r, \theta_r) = M(\theta_i, \theta_r) N(\eta'(\theta_d); \phi_i, \phi_r) / \cos^2 \theta_d; \tag{2}
\end{eqnarray}
つまり、より複雑な\(\theta\)の依存性を認めることになります。ここでは、\(M\)を縦方向の散乱関数と呼ぶことにします。
4.2 Scattering from a circular cross section
ここでは、円形の断面を想定して\(N\)を導出します。円対称の場合、\(N\)は\(\phi_i\)と\(\phi_r\)の差である\(\phi\)にのみ依存するため、2次元の方位角散乱関数はさらに1次元に縮小され、この文脈では\(N\)を単一の角度引数で表記します。誘電体円からの散乱はよく研究されており、Descartesが雨の中の虹の形成を説明するために最初に分析しました(詳しい議論については、例えばHumphreys[1964]を参照)。なお、有効屈折率\(\eta’\)は、この後の議論全体に関わるパラメータであるため、分かりやすくするために、議論していないときは暗黙のパラメータとして残してあります。
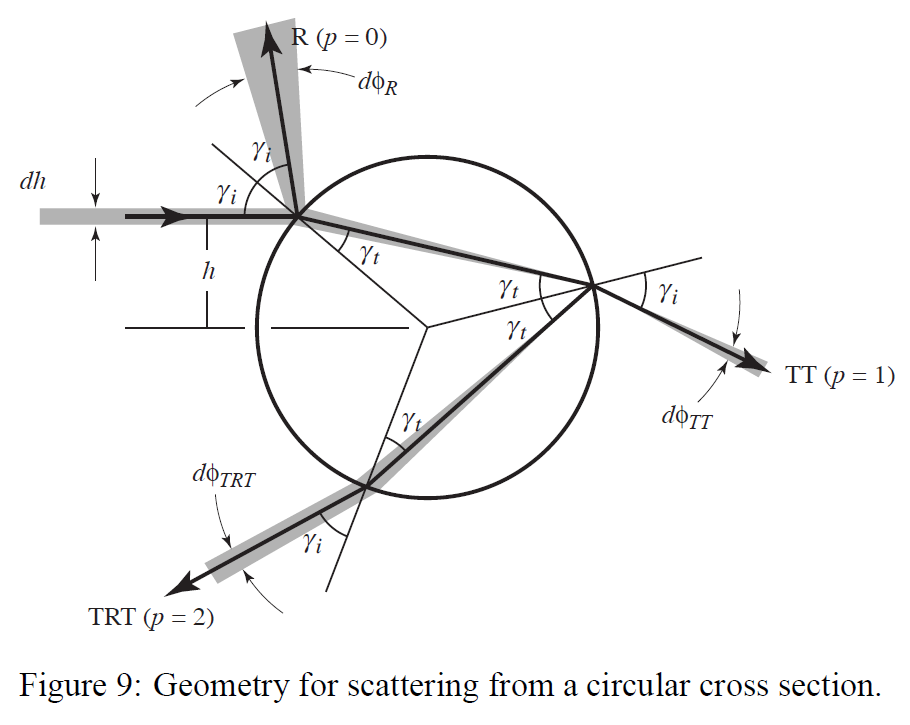
円の中で屈折する光線を追跡することで、遠方界の強度を求めることができます。単位円の中心から\(-1 \lt h \lt 1\)の位置に入射する光線を考えます(図9参照)。角度\(\sin \gamma_i = h\)は入射角、\(\eta’ \sin \gamma_t = h\)は屈折した光線の角度です。円に入った光線が屈折したり反射したりするのを追いかけることで、出射角\(\phi(h)\)を計算することができます。
図9から、入射光線は、円に入るときに\(\gamma_t – \gamma_i\)、内部反射のたびに\(\pi + 2 \gamma_t\)、円から出るときに再び\(\gamma_t – \gamma_i\)、合計で
\begin{eqnarray}
\phi(p, h) = 2 p \gamma_t – 2 \gamma_i + p \pi \tag{3}
\end{eqnarray}
です。ここで,\(p\)は内部パスセグメントの数です。この式は、\(p\)の値が異なる場合、興味のある3つの散乱モード(表面反射R\((p=0\))、屈折透過TT\((p=1)\)、内部反射TRT\((p=2)\))をすべて包含している。この分析の残りの部分では、\(p \gt 2\)の項は無視します。
上記のレイトレーシング計算では、パスを\(h\)でパラメータ化しています。しかし、散乱計算では、与えられた方向\(\phi\)で散乱に寄与するすべてのパスを見つける必要があることがよくあります。これらのパスの\(h\)値は、関数\(phi(p, h) – \phi) = 0\)の根を解くことで求められます。これらの根を関数\(h(p, r, \phi)\)で表し、\(r\)の値が異なると異なる根で表します。\(p=0\)と\(p=1\)の場合、根は1つであり、したがってパスも1つである。しかし、\(p = 2\)の場合は、1つまたは3つの根があり、したがって1つまたは3つのパスがあります。
関数\(\phi\)は滑らかなので、1本の出射光線から3本の出射光線への移行は、\(\phi(2, h)\)の折り返しを表し、この折り返しは\(\frac{d\phi}{dh} = 0\)のときに発生します:
\begin{eqnarray}
h^2 = (4 – (\eta’)^2)/3 \tag{4}
\end{eqnarray}
この式は対称的であり、2つの対称的な極大値が存在することを予測します。[Humphreys 1964].
\(\phi\)と\(h\)を関係づける式(3)ができたので、エネルギー保存の原理を使って、散乱光の強度を計算することができます。繊維に曲線放射照度\(\bar E\)が照射されると,その幅方向の断面に均一な放射照度\(E(h) = {\bar E}/2\)が落とされます。このとき、減衰はさておき、入射ビームの小さな間隔\(dh\)からのパワーは、出射ビームの強度分布の角度間隔\(d\phi\)に散乱されます(図9)。
\begin{eqnarray}
{\bar L}(\phi(h)) d\phi = E(h) dh = ({\bar E}/2) dh \tag{5}
\end{eqnarray}
あるいは
\begin{eqnarray}
{\bar L}(\phi(h)) = \left| 2 \frac{d\phi}{dh} \right|^{-1} {\bar E} \tag{6}
\end{eqnarray}
この式は、関数\(\phi\)の折り返し点で強度が無限大になることを意味しています。この強度の特異点をコースティックと呼びます。
円柱の場合は、一対のコースティクスが光りの原因となります。円柱の中では、Bravais指数\(\eta’\)が\(\theta\)とともに大きくなるので、入射光が髪に対して斜めになるにつれて、2つのコースティクスは平面に近づくことになります。\(\eta’\)が2になると、コースティックは形成されなくなります。このコースティックのマージの移行は、図6にプロットされた測定値で見ることができます。
4.3 Attenuation by absorption and reflection
この節では、繊維内部での体積吸収と、界面でのフレネル反射の項を追加しています。
吸収のために、繊維内の経路長を知る必要があります。図9の三角形に余弦の法則を適用すると、内部の各パスセグメントの長さは、髪の毛の半径の\(2 + 2 \cos (2 \gamma_t)\)倍となります。単位長さあたりの体積吸収量を\(\sigma_a\)とし、単位長さを髪の毛の半径と定義します。そして、髪の毛の内部にある\(p\)個のセグメントは、それぞれ\(T(\sigma_a, h) = \exp(-2 \sigma_a(1 + \cos(2 \gamma_t))) \)倍の吸収率を持っています。
ここでは、経路がもたらす強度の前に、減衰係数を導入することができます。
\begin{eqnarray}
{\bar L}(\phi) = A(p, h) \left| 2 \frac{d\phi}{dh} \right|^{-1} {\bar E} \tag{7}
\end{eqnarray}
ここで,
\begin{eqnarray}
A(0, h) &=& F(\eta, \gamma_i) \\
A(p, h) &=& (1 – F(\eta, \gamma_i))^2 F(1/\eta, \gamma_t)^{p-1} T(\sigma_a, h)^{p}
\end{eqnarray}
Bravaisの法則では、正射影の幾何学的要素が斜入射でも機能するように、パラメータを変更するだけで\(A\)を斜入射に一般化することができます。付録Bでは、通常のフレネル公式と2つの仮想屈折率\(\eta'(\theta)\)および\(\eta^{\prime\prime}(\theta)\)を用いて、正しいフレネル係数を計算できることを示しています。同様に、すべての内部経路セグメントは、軸に対する傾き\(\theta_t\)が同じであるため、\(1 / \cos \theta_t\)倍の長さになり、\({\sigma}_a’ = \sigma/ \cos \theta_t\)を\(\sigma_a\)に置き換えることで、3Dへの一般化が完了します:
\begin{eqnarray}
A(0, h) &=& F(\eta’, \eta^{\prime\prime}, \gamma_i) \\
A(p, h) &=& (1 – F(\eta’, \eta^{\prime\prime}, \gamma_i))^2 F \left( \frac{1}{\eta’}, \frac{1}{\eta^{\prime\prime}}, \gamma_t \right)^{p-1} T(\sigma_a’, h)^{p}
\end{eqnarray}
完全な法線平面の散乱関数は次のようになります。
\begin{eqnarray}
N(\phi) &=& \sum_{p} N_p(p, \phi) \\
N_p(p, \phi) &=& \sum_r A(p, h(p, r, \phi)) \left| 2 \frac{d\phi}{dh}(p, h(p, r, \phi)) \right|^{-1} \tag{8}
\end{eqnarray}
ここでは、複数の根を持つパス(\(r\))を含む、異なるタイプのパス(\(p)\)の合計を表しています。
4.4 Summary
このセクションで開発された理論では、指向性ビームからの光は完全な円錐形に散乱され、円錐形の周りの分布は3つの異なる散乱モードの合計であると予測しています。これにより、新しい散乱モデルは次のような形になります:
\begin{eqnarray}
S(\phi_i, \theta_i; \phi_r, \theta_r) = \\
& & M_{R}(\theta_h) N_{R}(\eta'(\eta, \theta_d); \phi)/ \cos^2 \theta_d + \\
& & M_{TT}(\theta_h) N_{TT}(\eta'(\eta, \theta_d); \phi) / \cos^2 \theta_d + \tag{9} \\
& & M_{TRT}(\theta_h)N_{TRT}(\eta’, (\eta^{\ast}(\phi_h), \theta_d); \phi) / \cos^2 \theta_d
\end{eqnarray}
この式は式2から派生したものですが、次のセクションでいくつかの有用な近似式を紹介するための一般化が含まれています。\(M_{R}\),\(M_{TT}\),\(M_{TRT}\)の3つの項は、3つの別々の縦方向の散乱関数です。これらにより、3つのモードで異なるキューティクルのスケールの影響をシミュレートすることができます。\(N_{R}\), \(N_{TT}\), \(N_{TRT}\)の3つの項は、方位方向の散乱関数の3つのモードです。このうち最初の2つは,
\begin{eqnarray}
N_{R}(\phi) &=& N_p(0, \phi) \\
N_{TT}(\phi) &=& N_p(1, \phi)
\end{eqnarray}
は式8から直接定義されますが、\(N_{TRT}\)の計算についてはセクション5.2.2で詳しく説明します。\(\eta^{*}\)という関数は、\(N_{TRT}\)の有効屈折率を\(\phi_h\)に依存させるもので、5.2.3項で紹介した楕円形の断面に対する近似が可能になります。
なお、式9の右辺に現れるのは、角度\(\theta_d\)、\(\phi\)、\(\theta_h\)、\(\phi_h\)のみです。このように\(M_S\)と\(N_S\)を和と差で書くことで、\(S\)の自然な対称性が強調され、モデルが相互に影響し合っていることが容易にわかるでしょう。
5 A practical shading model for human hair
このセクションでは、前のセクションの結果を、レンダラーに組み込むのに適した完全で実用的なモデルに拡張します。そのために、滑らかな円柱の理論では予測できない縦方向の散乱関数(\(M_R\)など)の経験的な関数を導入します。また、サーフェイスラフネスがある場合の\(N_{TRT}\)の計算方法や、\(N_R\)、\(N_{TT}\)、\(N_{TRT}\)の計算に使用する\(h(p, r, \phi)\)の近似値についても説明します。最後に,このモデルを制御するための便利なパラメータを紹介します。
ここでのモデルの目的は、レンダリングで重要な現象を捉えることだと認識することが重要です。モデルの形状や基本的なエネルギー分布は、前節で紹介した理論に基づいていますが、細部については単純な解析ができない部分も多く、経験的に補っています。
5.1 The longitudinal scattering function \(M\)
滑らかな円柱の解析では、反射光はスペキュラーコーンの中に正確に留まると予測されます。私たちのヘアモデルには、この挙動から逸脱する原因となる2つの特徴があります。まず、界面が粗いこと。光線が円柱の中を伝搬するとき、その粗さのために、光線の方向がモデルで予測された方向からランダムにずれてしまいます。全体的な効果は、散乱分布をぼかすことであり、異なる散乱モードは異なる程度にぼかされます。次に、キューティクルのスケールによって、理想的な円柱に対するサーフェイスの法線が傾き、散乱ローブがスペキュラーコーンの中央に位置しなくなります。
図1は、ローブの位置がどのように変化するかを示したもので、Rモードは毛根方向に\(2\alpha\)ずれています; TRTモードはそれ以上先端に向かって変位し、TTモードは先端に向かって変位しています。\(M\)の平均値を各ローブごとにずらすことで、スケールの影響を近似的に表現しています。
\begin{eqnarray}
M_{R}(\theta_h) &=& g(\beta_{R}; \theta_h – \alpha_{R}) \\
M_{TT}(\theta_h) &=& g(\beta_{TT}; \theta_h – \alpha_{TT}) \\
M_{TRT}(\theta_h) &=& g(\beta_{TRT}; \theta_h – \alpha_{TRT})
\end{eqnarray}
ここで、\(g\)は幅\(\beta\)の単位積分、ゼロ平均のローブ関数です。今回の実装では,標準偏差\(\beta\)の正規化ガウス関数を用いました。
5.2 The azimuthal scattering function \(N\)
このセクションでは、方位角散乱関数の3つの近似式を紹介します。1つ目はパスを解くための効率的な方法、2つ目は2次的なハイライトの現象論的モデル、3つ目はグリントの簡単なモデルです。
5.2.1 Solving for paths
円を通る道を見つけるためには、式3を解いて、散乱角\(\phi\)をもたらす\(h(p, r, \phi)\)の値を求めなければなりません。\(\phi\)の公式にはスネルの法則、つまりアークサインが含まれるため、\(h\)を正確に解くには計算量が多くなります。
角度依存性を単純化するために、スネルの法則を、\(\pm90^{\circ}\)での正確な式の値と微分に一致する3次多項式で近似します:
\begin{eqnarray}
\gamma_t = \frac{3c}{\pi} \gamma_i – \frac{4c}{\pi^3} {\gamma_i}^3
\end{eqnarray}
ここで、\(c = \sin^{-1}(1 /\eta’)\)です(この表現では、角度\(\gamma\)はラジアンで測定されます)。最大近似誤差は\(\eta \lt 1.5\)について\(0.75^{\circ}\)未満です。
この近似を用いて, \(\phi\)は\(\gamma_i\)の3次式となります:
\begin{eqnarray}
{\hat \phi}(p, \gamma_i) = \left( \frac{6pc}{\pi} – 2 \right) \gamma_i – \frac{8pc}{\pi^3}{\gamma_i}^3 + p \pi \tag{10}
\end{eqnarray}
この式の根元には\(\gamma_i\)があり、そこから\(h\)を簡単に求めることができます。RとTTの場合は常に正確に1つの根がありますが、TRTの場合は1つまたは3つの根があります。
5.2.2 Approximation for TRT
我々の理論は滑らかな表面に基づいており、TRT成分のコースティクスが\(S\)に無限の強度を持つ特異点を作り出すことを予測しています。これは非現実的であり、特にサーフェイスラフネスがある場合には、\(N_{TRT}\)からコースティックを取り除き、コースティックの位置を中心とした滑らかなローブに置き換えます。このローブの幅は、ラフネスによるコースティックのぼかしをシミュレートしています。
コースティックが現れる角度\(\phi_c\)は、それが定義されている場合にはDescartesの式(式4)から計算できますが、コースティックのマージ点を過ぎた入射角では定義されません。連続性を保つために、\(\phi_c=0\)でコースティックを挿入し続け、マージを過ぎた短い入射角の範囲で滑らかにフェードアウトさせています。この成分を正確に説明するには、その計算方法を示すのが最も簡単です:
この手順では、\(\phi_c\)の\(w_c\)以内にマッピングされる\(h\)の区間のサイズ\(\Delta h\)を\(d^2 \phi / dh^2\)を使って推定することで、強度分布から除去されるパワーを大まかに推定します。コースティクスマージでは\(d^2\phi / dh^2\)がゼロになるため、\(\Delta h_M\)という制限が必要です。関数\({\rm smoothstep}(a, b, x)\)は、\(x \gt a\)で1、\(x \gt b\)で0、その間は滑らかです。
この関数についてユーザーが調整可能なパラメータはコースティクスについてブラー幅\(w_c\),グリントの強さを調整する係数\(k_G\),マージ後のコースティクスのフェードアウトについての\(\eta’\)の幅\(\Delta \eta’\),そしてコースティクスパワー上の制限\(\Delta h_M\)です。
5.2.3 Approximation for eccentricity
繊維の断面が円形ではなく楕円形の場合、\(N\)の単純な解析解は得られません。しかし,TRT成分の見え方は,軽度の偏心でも大きな影響を受けます:コースティクスが現れる角度\(\phi_c\)は、\(a=0.85\)から\(a=1/0.85\)までの範囲で\(\pm100%\)変化します。この範囲の偏心は非常に一般的であるため、TRT成分に対する偏心の影響を概算することが重要です。これには、式9の関数 \(\eta^{\ast}\)を使用します。
屈折率の変化は、偏心の変化と質的に同じような効果があります。TRT成分でこの関係を簡単に解析できるのは、長軸方向に対称な偏光路の場合です。このような経路では、\(\phi_i = -\phi_r\) となり、長軸上で反射が起こります。\({\gamma_t}’\)を内部反射時の入射角とすると、次のように示すことができます。
\begin{eqnarray}
\frac{d\phi_r}{d{\gamma_t}’} = 2a^2(\eta – 1) – \eta
\end{eqnarray}
この一次近似を用いて、円形モデルの屈折率\(\eta^{\ast} = 2a^2(\eta – 1) – \eta + 2\)を利用することで、円形モデルの挙動を楕円形モデルにほぼ一致させることができます。
これにより、\(\phi_h\)が主軸の1つと一致しているときに、散乱関数のTRT成分が偏心の程度に応じてどのように変化するかの近似値が得られます。この近似値を実用的なモデルに取り入れるためには、単純に正弦波で補間して、\(\phi_h\)のすべての中間値に対して\(\eta^{\ast}\)を定義します:
\begin{eqnarray}
{\eta_1}^{\ast} &=& 2(\eta – 1) a^2 – \eta + 2 \\
{\eta_2}^{\ast} &=& 2(\eta – 1) a^{-1} – \eta + 2 \\
{\eta}^{\ast}(\phi_h) &=& \frac{1}{2} (({\eta_1}^{\ast} + {\eta_2}^{\ast}) + \cos(2\phi_h)({\eta_1}^{\ast} – {\eta_2}^{\ast}) )
\end{eqnarray}
式9に示すように、円形の場合から導き出された式を用いて\(N_{TRT}\)を計算するコードに屈折率\(\eta^{\ast}\)を渡すだけで、偏心をシミュレートすることができます。
5.3 Summary
これで、式9に登場するすべての項を説明することができました。3つの縦方向の散乱関数\(M_R\)、\(M_{TT}\)、\(M_{TRT}\)はガウシアンです。方位角方向の散乱関数\(N_R\)と\(N_{TT}\)は、\(h\)を計算するために式10を使用して、式8から直接評価されます。方位角方向の散乱関数\(N_{TRT}\)は、まず屈折率\(\eta^{\ast}\)で式8と式10を使用して計算され、複数の\(h\)の値の可能性を考慮して合計され、その後、コースティクスを平滑化するためにセクション5.2.2の手順で修正されます。
レンダラーの種類によっては、少量の拡散反射を入れた方が実用的な場合もあります。このモデルでは拡散成分は含まれていませんが,式9に定数項\(M_D\)を導入することで簡単に追加することができます。
すべてのモデルのパラメータは、表1に参考としてまとめられています。
6 Results
6.1 Validation
このセクションでは、髪の毛の構造に関する我々の仮定が有効であり、シェーディングモデルが、測定で見られた動作を定性的に再現できるという証拠を示します。
Validating the hair structure model against measurements.
図7の法線方向の測定結果は、髪の毛を楕円形の円柱と見立てたモデルと完全に一致しており、グリントを最もよく表しています。このことを示すために、モンテカルロ法を用いて、この個人の測定値と同じ偏心率を持つ粗い楕円柱におけるTRTモードによる散乱を計算しました。図は、この数値実験の結果と物理実験の結果をプロットしたものです。ピークの角度と強度の変化が見事に一致しており、内部反射コースティクスとしてのグリントの説明と、髪の毛の断面を楕円としてモデル化したことの両方を明確に証明しています。実際のデータには、もちろん他の散乱モードからの寄与も含まれており、TRTモードが寄与していない前方散乱では顕著です。
Validating the shading model against measurements.
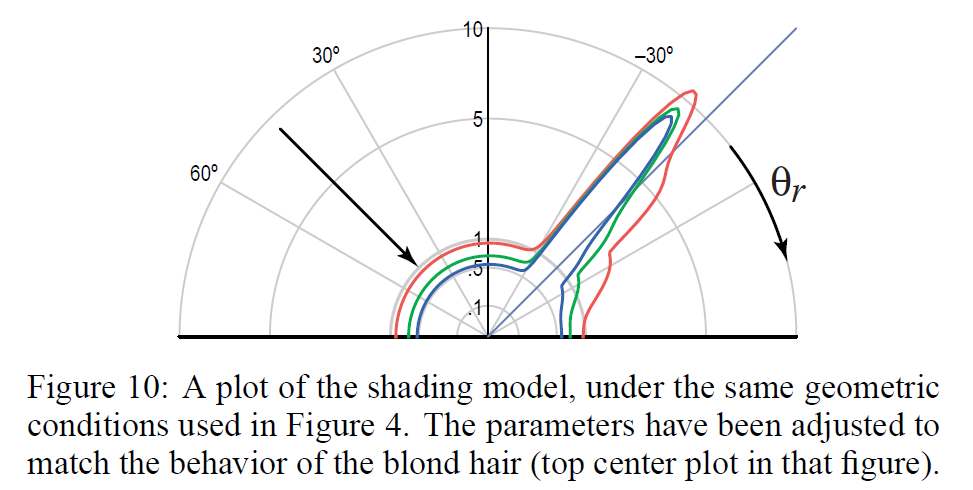
我々のシェーディングモデルが実際の髪の毛の挙動と定性的に一致する能力を実証するために,セクション3の2つの測定値に合うようにパラメータを設定しました。図10は,入射面で測定されたブロンドの髪の毛のように振る舞うように調整したモデルのプロットを示しています(図4,上段中央)。小さなサイドローブと、グレージング方向に広がるローブの両方が予測されていることに注目してください。
図6の測定では、傾斜が変わると苛酷なマージが発生します。シェーディングモデルはデータと一緒に破線でプロットされており、このよりマイルドな偏心ヘアを記述するパラメータのセットを持っています。2つのグリントが合体して消えるという挙動は、定性的には一致しています。
6.2 Renderings
前節で説明したシェーディングモデルを実装し、プロシージャルに生成された髪の毛の繊維の集合体からの光の反射をシミュレートしています。髪の毛のモデル化には,市販のレンダリングソフト「Sasquatch」(Worley Laboratories, http:///www.worley.com)を使用し,各モデルは人間の頭の平均的な髪の毛の数に相当する50,000〜100,00本のスプライン曲線で構成されています.シェーディングのパラメータは繊維ごとに一定でしたが、一部のケース(後述)では、頭皮のノイズ関数を使って、各繊維にランダムな吸収を割り当てました。楕円形の繊維の方位角は、繊維ごとにランダムであるが、各繊維に沿って滑らかです。すべてのレンダリングは、\(\eta=1.55\)、\(\Delta h_M=0.5\)です。パラメータ\(\alpha_{TT}\)と\(\alpha_{TRT}\)は表1からの推奨比率により\(\alpha_R\)から定義されます。
画像のレンダリングにはレイトレーシングを使用し、オクルージョンやシャドウイングは考慮しましたが、毛髪間の多重散乱は考慮しませんでした。髪の毛は,常に光線の方向を向いている平らなリボンとして表現し,その幅は髪の毛の直径と同じにしました。これはシリンダーを使用するよりも効率的であり、我々の散乱関数はストランドのレベル以下のすべての相互作用を抽象化しているので、適切です。
以下の結果では、計算は交差に支配されているため、我々のモデルはKajiyaの非常に単純なモデルよりも計算コストが大幅に高いにもかかわらず、レンダリング時間の増加はわずかなものでした。例えば,新しいモデルに切り替えると,2プロセッサの1GHz Pentium Ⅲシステムでは,図12のレンダリング時間が6分から8分に増加しました。
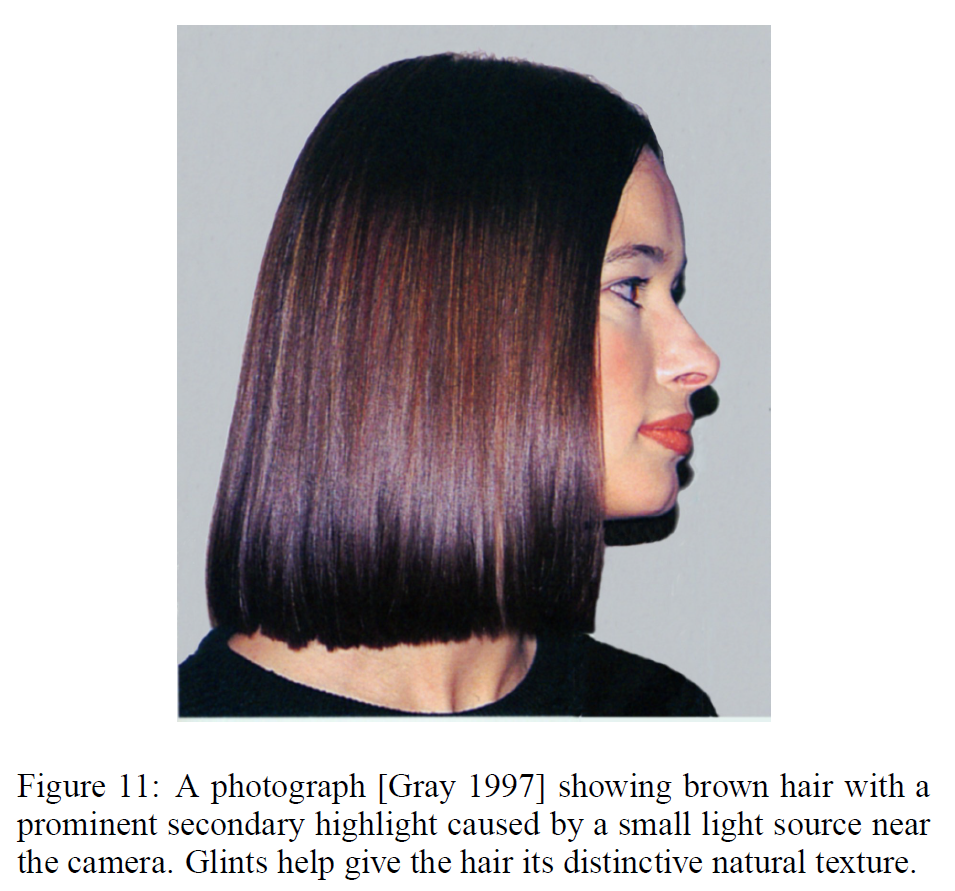
最初のレンダリングは、図11の写真をモチーフにしています。髪の毛がかなり平らに梳かれているため、2次的なハイライトが非常に際立っており、髪の毛の上部と下部が暗く見えることからもわかるように、拡散性の散乱がほとんどありません。
繊維の配置を厳密に再現するのではなく、髪全体の形状とほぼ一致するように、理想的な幾何学的モデルを構築しました。図12は、このモデルを軽度の楕円形のブラウンヘアーに適した設定でレンダリングしたものです。比較のために、同じモデルを同じ照明の下で、Kajiyaのモデルを使ってレンダリングした結果を示します。全体的なブラウンを出すために必要な拡散成分は、ブラウンがセカンダリーハイライトに由来する実際の髪に生じる濃淡の変化を十分に予測できません。両方の画像に同じ手続き上のカラーバリエーションが存在し、提案モデルによる追加のテクスチャは偏心によるものです。この画像に対するパラメータは\(\alpha_R = 3^{\circ}\),\(\beta_R = 14^{\circ}\),\(\beta_{TT} = 8^{\circ}\), \(\beta_{TRT} = 22^{\circ}\),\(\sigma_a = (0.432, 0.612, 0.98) – (0.36, 0.72, 0.94)\),\(k_G = 0.4)\),\(w_c = 1.5^{\circ}\),そして\(a = 0.9\)です。
モデルの構成要素と偏心の影響を説明するために、図14に2つのハイライトを別々に示し、他のすべてのパラメータを一定にした場合の円形と楕円形の髪の比較を示します。これらの画像のパラメータは\(\alpha = 3^{\circ}\),\(\beta_R = 8^{\circ}\),\(\beta_{TT} = 6^{\circ}\),\(\beta_{TRT} = 15^{\circ}\),\(\sigma_a = (0.44, 0.64, 0.9)\),\(k_G = 0.4\),\(w_c = 1.5^{\circ}\),そして\(a = 1\)と\(0.9\)です。
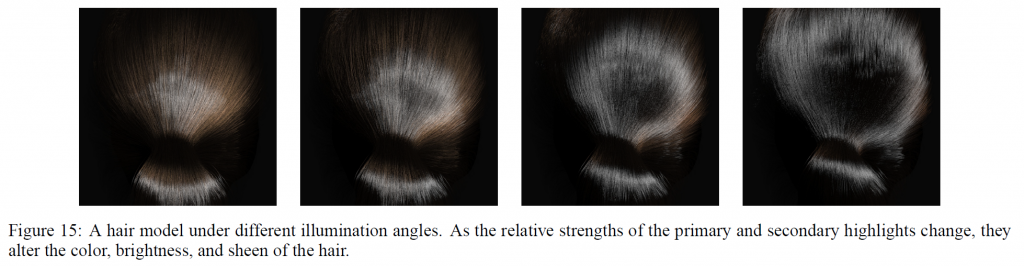
このモデルの性能をさらに示すために,光の方向を変えた場合の結果を図15に,複雑な照明の場合(Agarwalら[2003]の方法を使用)の結果を図13に示します。
7 Conclusion
この論文では、人間の髪の毛からの光の散乱について、現実、理論、そしてレンダリングの実践を見てきました。その結果、個々の毛髪繊維の散乱挙動は、これまでシェーディングモデルで想定されていたものとは大きく異なることがわかりました。誘電体円柱からの散乱の理論により、これらの違いの原因が説明され、偏心によるものを含む関連する視覚効果を、レンダリングに使用するための実用的で調整可能なモデルとして捉えたシェーディングモデルを提示しました。
この研究の最も重要な意味は、リアルな髪の毛のレンダリングには、円柱で発生する複数の散乱モードを考慮する必要があるということです。色は主に拡散散乱に由来するという標準的な仮定は,繊維の場合には証拠によって裏付けられておらず,我々の画像は,この仮定が現在のヘアシェーディングモデルの結果の質を制限していることを示しています。
今回導入したシェーディングモデルは、今後さらに精度を高めていくことが可能です。改善の余地があるのは、偏心と表面の粗さです。より多くの種類の髪を正確にモデル化するためには、円形からのより極端な逸脱を扱うことができると便利です。また、現在のモデルでは、偏心の影響を光線密度係数で近似していますが、フレネル係数では近似していないため、エネルギー分布の定量的な精度に限界があります。私たちのモデルでは、表面の粗さやスケール角の影響を、見た目の現象と一致する最もシンプルな方法で説明しています。これらの表面の特徴の本当の効果は複雑で、散乱形状に依存しています。これらの効果をより正確にモデル化することで、かすみ角に対してより正確な散乱モデルが得られる可能性があります。
私たちの分析は、多くの種類の透明繊維に適用されるので、動物の毛、合成毛、毛皮、そしてあらゆる種類の布のレンダリングに影響を与えます。
Acknowledgements
和訳省略。
A Loci of reflections
この付録では、円筒状の繊維からの反射と屈折の形状を解析しています。円筒繊維の法線ベクトルの集合は、繊維軸に垂直な平面にあり、この平面を法線平面と呼びます。この形状は、単位球を使って最も簡単に視覚化することができ、単位球上の各点は異なる方向を表しています。この球体では、繊維軸は北極にあり、法線ベクトルのセットは赤道に含まれています(図16a参照)。
ある入射方向\(v_i\)に対する反射を解析するために、特定のサーフェイス法線\(n\)とそれに対応する反射ベクトル\(v_r\)を考えます。反射の法則では、\(v_i\), \(n\), \(v_r\)は同一平面上で\(n \cdot v_i = n \cdot v_r\)です。また、類似の三角形を見つけることで、反射則は赤道からの\(v_i\)と\(v_r\)の距離を等しくさせます。この等距離の条件は、どの法線ベクトルにも当てはまるはずです。したがって、ある入射方向に対して形成される反射ベクトルの集合は、赤道から\(v_i\)と同じ距離にある高さ一定の水平な円の上になければなりません。これは、「3次元では、円柱からの反射の集合は円錐を形成する」というよく知られた結果の正式な証明となります。
図16bは、前の図と似ていますが、代わりに屈折した方向を示しています。屈折の法則(スネルの法則)は、反射と似ています。まず、\(v_i\), \(n\), そして\(v_t\)は同一平面上です。次に、スネルの法則で\(\eta \sin \theta_t = \sin \theta_i\)を言っており、相似形の三角形を用いて、この法則は赤道への垂直距離\(h_i\)、\(h_t\)も比\(\eta\)を持つことを意味しています。つまり、透過したベクトルはすべて、\(v_i\)よりも\(\eta\)の倍数だけ赤道に近い円上にあるということになります。
同じ論法で、円柱から出て行く途中で再び屈折する光線は、等距離条件に従います。さらに、内部反射も外部反射と変わりません。結論として、円筒状繊維から出るすべての光線は、反射された光線と同じ円錐形の中になければなりません。
B The Bravais index
断面を軸に沿ってスイーピングすることで、円筒状の繊維が形成されます。Bravaisは、3次元の円筒繊維の光学系を、その断面の光学系の2次元解析に還元できることを示しました。入射方向は、まず断面の平面に投影され、次に2Dで反射と屈折が行われます。しかし,正しい物理現象を2Dでモデル化するには,屈折率を入射角の関数として変更する必要があります.Bravaisの法則は、(氷のハロー[Tricker 1970]のような)結晶を介した屈折の解析によく用いられます。
図16cは、水平面での屈折の様子を示しています。方向\(v_i\)は方向\(v_t\)に屈折している。これを2次元の問題に落とし込むには、ベクトル\(v_i\)と\(v_t\)を、法線を含む垂直面に投影します。投影されたベクトルは、\(v_i’\)と\(v_t’\)とします。目標は、\(v_i’\)を境界で屈折させると\(v_t’\)が得られるような実効屈折率、\(\eta’\)を見つけることです。まず、スネルの法則では、\(\sin \theta_i = \eta \sin \theta_t\)を述べています。 すなわち、\(v_i\)の水平面への投影の長さは、\(v_t\)の投影の長さの\(\eta\)倍であることに注意してください。\(v_i\)と\(v_t\)は平面上にあるので、水平面に描かれた2つの三角形は似ています。左側(入射側)の三角形の各辺の長さは、右側(透過側)の三角形の対応する辺の長さの\(\eta\)倍です。第二に、垂直法線面では等価なスネルの法則が成り立つ。ここで、\(\sin \theta_i’ = \eta’ \sin \theta_t’\)です。しかし\(\sin \theta_i’ = \sin \theta_i \cos \gamma\)であり, ここで、\(\gamma\)は入射ベクトルと法線面への投影の間の角度です。同様に、\(\sin \theta_t’ = \sin \theta_t \cos \delta\)、ここで\(\delta\)は透過方向と法線面への投影の間の角度です。代入すると\(\sin \theta_i \cos \gamma = \eta’ \sin \theta_t \cos \gamma\)が得られ、この式にスネルの法則を代入すると\(\eta \cos \gamma = \eta’ \cos \delta\)が得られます。 等価的には次のようになります。
\begin{eqnarray}
\eta'(\gamma) = \sqrt{\eta^2 – \sin^2 \gamma} / \cos \gamma
\end{eqnarray}
このことから、投影面と角度\(\gamma\)をなす入射光線に対して、通常のスネルの法則を用いて入射方向の投影から屈折方向の投影を計算することができますが、その際、有効屈折率\(\eta’\)を代入しています。
界面でのフレネル減衰も同様の方法で計算することができます。フレネルの公式から、斜入射に対する係数は、反射率の垂直成分に\(eta’\)を用い、第2の指標を用いることで、投影された角度から計算することができることを簡単に確認することができます。
\begin{eqnarray}
\eta^{\prime\prime} (\gamma) = \eta^2 \cos \gamma / \sqrt{\eta^2 – \sin^2 \gamma}
\end{eqnarray}
は平行成分です。この少し一般化したフレネル関数には、\(F(\eta’, \eta^{\prime\prime}, \gamma)\)という表記を使います。