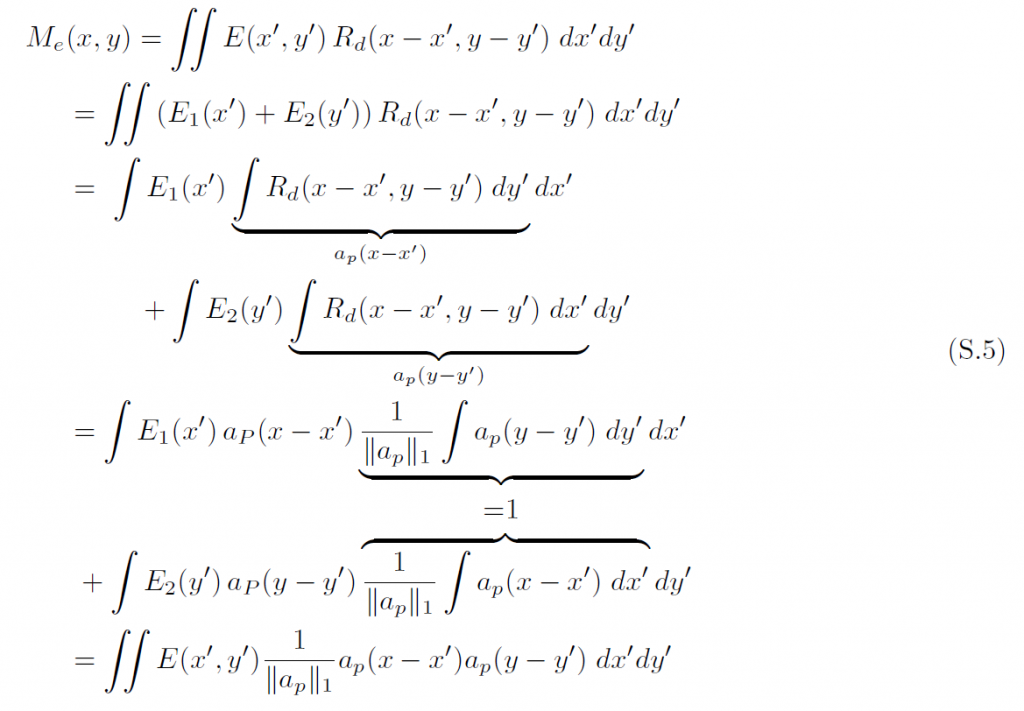こんにちわ。Pocolです。
今日は前に読んだ,Separable Subsurface Scatteringの補足資料を読んでみようと思います。
資料は
[Jimenez 2015] Jorge Jimenez, Karoly Zsolnai, Adrian Jarabo, Christain Freude, Thomas Auzinger, Xian-Chun Wu, Javier von der Pahlen, Michael Wimmer, Diego Gutierrez, “Separable Subsurface Scattering”, Compute Graphics Forum 2015.
のプロジェクトページhttp://www.iryoku.com/separable-sss/にあります。
いつものように誤字・誤訳があるかと思いますので,ご指摘いただける場合は正しい翻訳例と共に指摘していただけると幸いです。
Contents
Separable Subsurface Scatteringという論文の補足資料です。これには、以下の内容が含まれています。
- 現在のドキュメント
- 実際のカーネルと比較した近似カーネルのプロットを含むドキュメント
- メインの補足動画
このドキュメントは以下のセクションが含まれます:
- B 低ランク近似の詳細説明。
- C 事前積分されたカーネルの導出。
- D 誘導最適化のモチベーション
- E シェーダ実装の詳細な説明
- F プロファイルシミュレーションのパラメータ
- G シミュレートされた拡散プロファイルのプロット
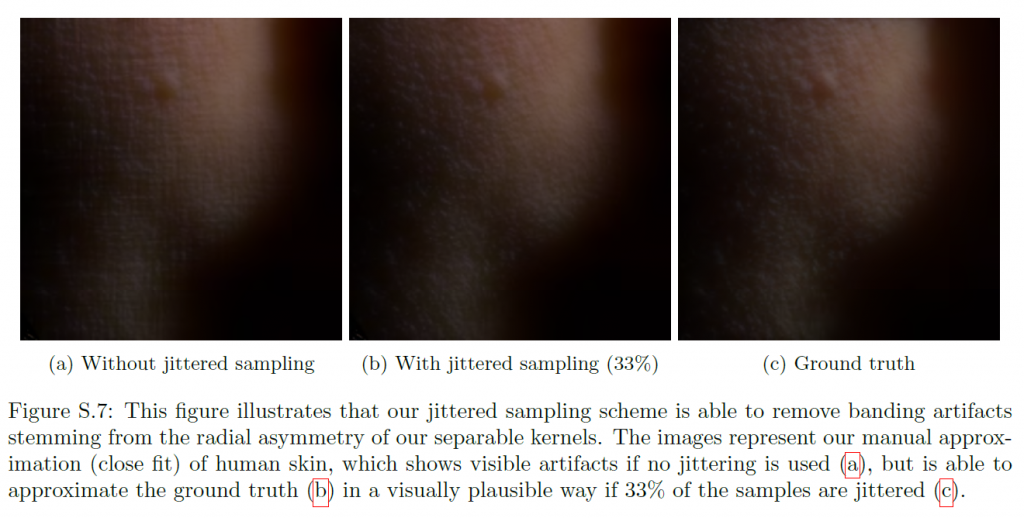
追加レンダリング結果も掲載しています。図S.2とS.5は、それぞれ頭部モデルと人為的な「内積」照明を使用した人間の皮膚のためのカーネル近似のすべての比較を示しています。図S.4には、皿の上の果物のレンダリング例が示されています。複数の距離からレンダリングされた第2の頭部モデルが図S.8に含まれており、図S.6とS.7は、提案されたジッターサンプリングアプローチの利点を説明しています。
B Low-rank approximations
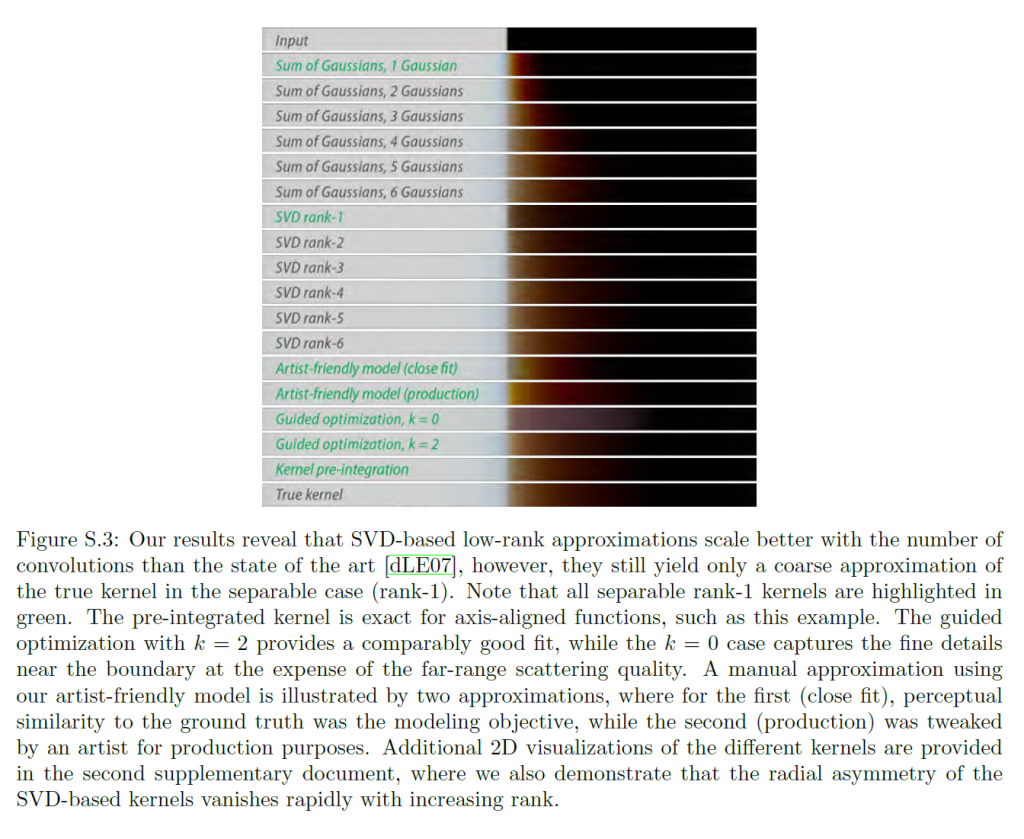
分離可能なカーネル\(A(x,y) = \sum_{i=1}^N a_i(x) a_i(y)\)の和で拡散反射率プロファイル\(R_d(x, y)\)を正確に近似するためには、個々の1次元関数\(a_i\)の適切な選択が必要です。d’Eonら[DLE07]は、ゼロ平均ガウシアン\(G\)がこのタスクに適していることを観察しました。すなわち、
\begin{eqnarray}
R_d(x, y) \approx A_g(x, y) = \sum_{i=1}^N w_i G(x, y; \tau_i) \tag{S.1}
\end{eqnarray}
ここで,\(\tau_i\)はそれぞれのガウシアンの標準偏差を示します。ガウスカーネルの分離性により、\(A_g\)との畳み込みは\(2N\)の1次元畳み込みとして実現できます。d’Eonらは、適切な\(w_i\)と\(\tau_i\)の計算の間に、近似\(A_g\)のエネルギー保存を保証する\(||A_g||_1 = ||R_d||_1\)のような\({\mathcal L}_1\)制約を採用しました。さらに、ガウシアンカーネルは球面対称であるため、\(A_g\)も元のプロファイルのこの特徴を示しています。
しかし、近さの基準を強調し、半径方向の対称性を失わせることで,低い畳み込み、つまりより少ない複雑さで,同等の見た目の品質を生み出す近似をもたらします(図S.5を参照)。リフレレンクタンスデータの低ランク近似のための以前の手法[LRR04, PvBM*06, KM99]に触発されて、我々は離散的な2次元拡散プロファイル\(R_d\)の行列因数分解を採用しています。Eckhart-Youngの定理[EY36]に従って、\(R_d\)の特異値分解(SVD)を切り詰めることで、フロベニウスノルムに関して最もよい低ランク近似が得られます。より詳細には、拡散プロファイルのSVDを与えます:
\begin{eqnarray}
R_d &=& U \sum V^T \\
U &=& (u^{(1)}|u^{(2)}|\dots|u^{(m)}) \\
V &=& (v^{(1)}|v^{(2)}|\dots|v^{(m)}) \tag{S.2} \\
\sum &=& {\rm diag}(\sigma_1, \sigma_2, \dots, \sigma_m)
\end{eqnarray}
近似問題
\begin{eqnarray}
{\rm min}_A || R_d – A ||_F \\
{制約条件} \quad {\rm rank}(A) = N \tag{S.3}
\end{eqnarray}
の厳密解は次のように与えらえます。
\begin{eqnarray}
A_s = U \sum_N V^T \\
{ただし} \quad \sum_N = {\rm diag}(\sigma_1, \dots, \sigma_N, 0, \dots, 0) \tag{S.4}
\end{eqnarray}
フロベニウスノルムは古典的な定義、すなわち\(||A||_F = \sqrt{\sum_{i=1}^m \sum_{j=1}^m a_{ij}^2} = \sqrt{\sum_{i=1}^m {\sigma_i}^2}\)に従い、連続する2次元関数の\({\mathcal L}_2\)ノルムに対応します。\(\sum_N\) は対角行列であり、近似 \(A_s\) は分離可能なカーネルの和、すなわち \(A_S = \sum_{i=1}^N u^{(i)} \sigma_i v^{(i)^T}\) として書くことができることに注意してください。1次元関数\(a_i\)は、\(R_d\)の対称性により、\(u^{(i)} = v^{(i)}\)のため,\(ai_= \sqrt{\sigma_i}u^{(i)}\)で与えられます。
このアプローチは球面対称性とエネルギー保存を保持しませんが、\({\mathcal L}_2\)ノルムの意味での最適な近さを提供します。\(n=3\)から始まる低ランクの近似では、拡散プロファイルがより忠実に再構成され、球面対称性と\({\mathcal L}_1\)ノルムの両方の違反は知覚できません。エネルギー保存は、近似\(A_s\)を\({\tilde A}_s = A_s \frac{||R_d||_1}{||A_s||_1}\)に応じてスケーリングすることによって強制することができます。新しい近似\({\tilde A}_s\)は\({\mathcal L}_2\)の意味では最適ではありませんが、同じ項数のガウス近似\(A_g\)よりも知覚的に良いマッチを提供します。このように、我々のSVDベースの近似スキームは、ガウス近似と比較すると、同じ数の1次元コンボリューションでより良い性能と同等以上の視覚的品質をもたらします(図S.5を参照)。
C Derivation of the pre-integrated approximation
ここでは、主論文の中の式(4)の導出をさらに拡張したものを見ることができます:
D Motivation for the guided rank-1 approximation
事前積分された近似の品質の高さに触発されて、我々は、2-ガウス近似と同様に、実際の拡散プロファイルへの正確なフィットから出発して、単一のパラメータを操作するだけで、ユーザーが近くの散乱または遠くの散乱を強調することができる実用的な最適化フレームワークを実現しようとしました。デフォルトのパラメータでは、解析的に導出された事前積分された近似に近い「ニュートラル」な近似を出力します。
関連する最適化問題を以下のように記述します。
\begin{eqnarray}
a_s = {\rm argmin}_a \int_{{\mathbb R}^2} \Gamma(x, y)(R_d(x, y) – a(x)a(y))^2 dx dy \\
{制約条件} \quad ||R_d||_1 = {||a||_1}^2 \tag{S.6}
\end{eqnarray}
拡散反射率プロファイル\(R_d(x, y)\)に対する分離可能な近似値\(A_s(x, y) = a_s(x) a_s(y)\)を導出します。ガイド関数\(\Gamma(x, y)\)は、所望のアーティスティックな効果を提供するために結果を変更する手段を提供します。任意のガイド関数は膨大な自由度を示すことになるので、我々はその形状を、近・遠方散乱のいずれかを顕著にするという意図された効果に役立つ一次元部分空間に制限することを目指しています。
その出発点として、積分前の近似を再現するガイド関数、すなわち以下のようなガイド関数\(\Gamma_p(x, y)\)を数値計算してみました。
\begin{eqnarray}
a_p = {\rm argmin}_a \int_{{\mathbb R}^2} \Gamma_p (x, y) (R_d(x, y) – a(x)a(y))^2 dx dy \\
{制約条件} \quad || R_d ||_1 = {|| a ||^2}_1 \tag{S.7}
\end{eqnarray}
ここで、\(a_p\)は前節Cの事前積分された近似値です。図S.1aに見られるように、このようなガイド関数は、かなり複雑な構造を示している。関連する複雑さを単一のパラメータに抑えるために, 経験的にパラメータ化されたガイド関数を定義しました。
\begin{eqnarray}
\Gamma(x, y; k) = (x^2 + y^2)^{k/2} (1 – e^{-bx^2})(1 – e^{-by^2}) \tag{S.8}
\end{eqnarray}
指数\(k\)を持つ放射状対称多項式項は、近接または遠方散乱を強調するための外部パラメータとして機能します。この関数の図は、\(k = 1.55\)の場合の図S.1bに示されています。この多項式項は、対角線上での\(\Gamma_p(x, y)\)の振る舞いを再現していることに注意してください(コーナーの小さな正規化依存性の詳細は無視してください)。座標軸に沿った\(\Gamma_p(x, y)\)の形状を再現するために、座標軸の近くでガイド関数が消滅するような「抑制」関数を\(1 – e^{-bx^2}\)と\(1 – e^{-by^2}\)の形で追加しています。我々は\(b = 50\)を選択しました(\(x, y \in [-1, 1]\)を仮定)、フレームワーク全体はこのパラメータの中程度の変化に鈍感です。パラメータ\(k\)を0から4までの範囲で変化させることにより、ユーザは(式S.6の結果として)近接散乱(\(k=0\)に向かって)または遠方散乱(\(k=4\)に向かって)を強調する分離可能な近似を生成することができます。\(k=4\)を超えたところでは、視覚的な効果は観測されないことに注意してください。我々は式S.6を最小化するために逐次二次計画法を使用しました。高次元の最適化問題をすぐに実行しないように、我々は最終カーネルの低解像度バージョンについて式S.6を解いています。その後、各最適化は、次の低分解能版への解の補間で初期化されます。
E Shader Implementation Details
我々の手法はスクリーン空間で動作するため、カーネルのサイズはピクセル内の投影された表面積の関数であり、深度とサーフェイスの向きに依存します。この面積は通常、ピクセルではなくワールドスペースの単位で指定され、アーティストにとってはカーネルサイズの定義がより直感的になります。離散化されたカーネルを使用する場合、アドホック補正係数を使用することにより、サーフェイスの向きの影響を考慮することができる[JSG09]。
対照的に、アーティストフレンドリーな単純化された2ガウスモデル\(A_m\)を使用することで、実世界の距離を扱うことができます。この距離は、その場でプロファイルを適用するために使用され、導関数やアドホックな補正係数を使用するよりも正確な結果が得られます。しかし、このアプローチには2つの問題があります:(1)各サンプルでカバーされている部分を評価してもカーネルの重みを正確にベイクすることはできません(そのため,サンプルの位置でしかカーネルを評価できません), (2)GPU が使用するサンプルあたりのスロット数(DirectX fxc で生成されたもの)は、単純なアドホック補正技術では 16 から 28 に増加し、パフォーマンスがほぼ半減し、プロダクションシナリオでは役に立たなくなります。後者の問題には2つの理由があります。a)深度とピクセル位置から世界空間への変換には、いくつかの追加のALU命令が必要であること、b)2-ガウスRGBプロファイルの評価には6つのexp命令が必要であること、これは最新のGPUでも実行するには非常にコストがかかります。
我々は、Mikkelesen[Mik10]によって提案されたものに類似したアプローチに従うことによってこれらの問題を解決し、3D距離\(d\)上の1Dプロファイルアプリケーションを正確な深度\(d_z\)補正係数を持つ2D距離\(d_xy\)に分離します。これにより、カーネルの評価は次のように変換されます:
\begin{eqnarray}
a_m(\sqrt{{d_xy}^2 + {d_z}^2} &=& w G (\sqrt{{d_{xy}}^2 + {d_z}^2}, \tau_{near}) + (1 – w) G(\sqrt{{d_{xy}}^2 + {d_z}^2}, \tau_{far}) \\
&=& w e^{\frac{-d_z^2}{2 \tau_{near}}} G( d_{xy}, \tau_{near} ) + (1 – w) e ^{\frac{-d_z^2}{2\tau_{far}}} G(d_{xy}, \tau_{far}) \\
& \approx & e^{\frac{-d_z^2}{2 \tau_{max}}} (w G(d_{xy}, \tau_{near}) + (1 – w) G(d_{xy}, \tau_{far}) ) \\
&=& e^{\frac{-d_z^2}{2 \tau_{max}}} {a_m}’ (d_{xy})
\end{eqnarray}
ここで,\(\tau_{max} = max(\tau_{near}, \tau_{far})\)です。我々は、例えば[JSG09]で使用されているアドホックな補正に対して、正確な深度補正へのプロファイルの適用を単純化するガウシアンの最大分散を取るという近似を行っていることに注意してください。これにより、面積積分を用いて\({a_m}'(d_{xy})\)の正確な重みを事前に計算することができ、以下の方法で命令数を16に減らすことができます:a) expの数を6から1つに減らす; b) 深さを直接扱うことによるワールド空間への変換を避ける; c) 典型的な低レベルの最適化を適用する[Per14]。
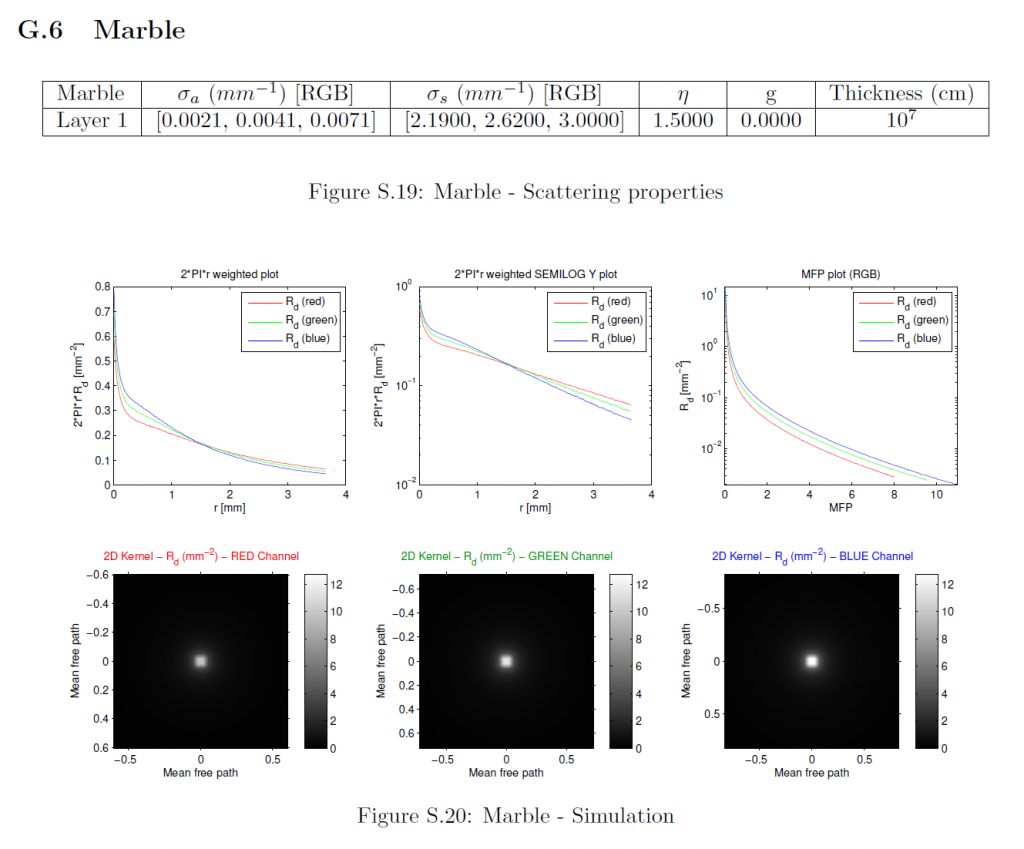
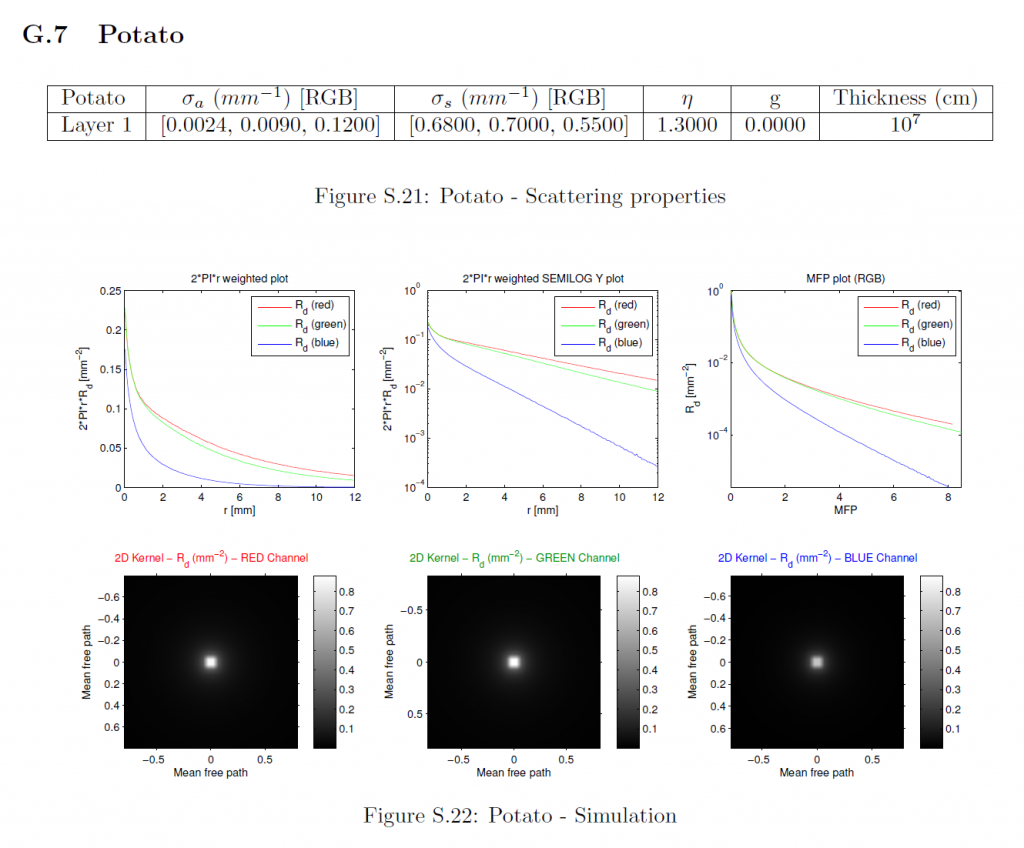
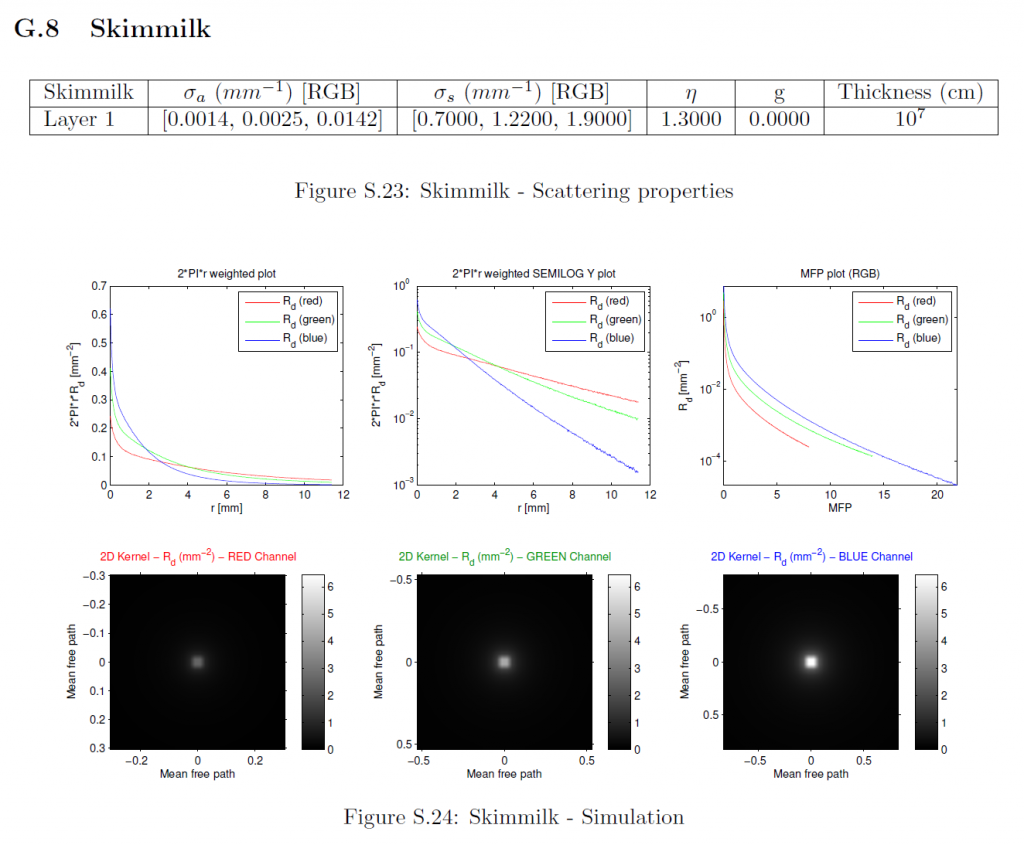
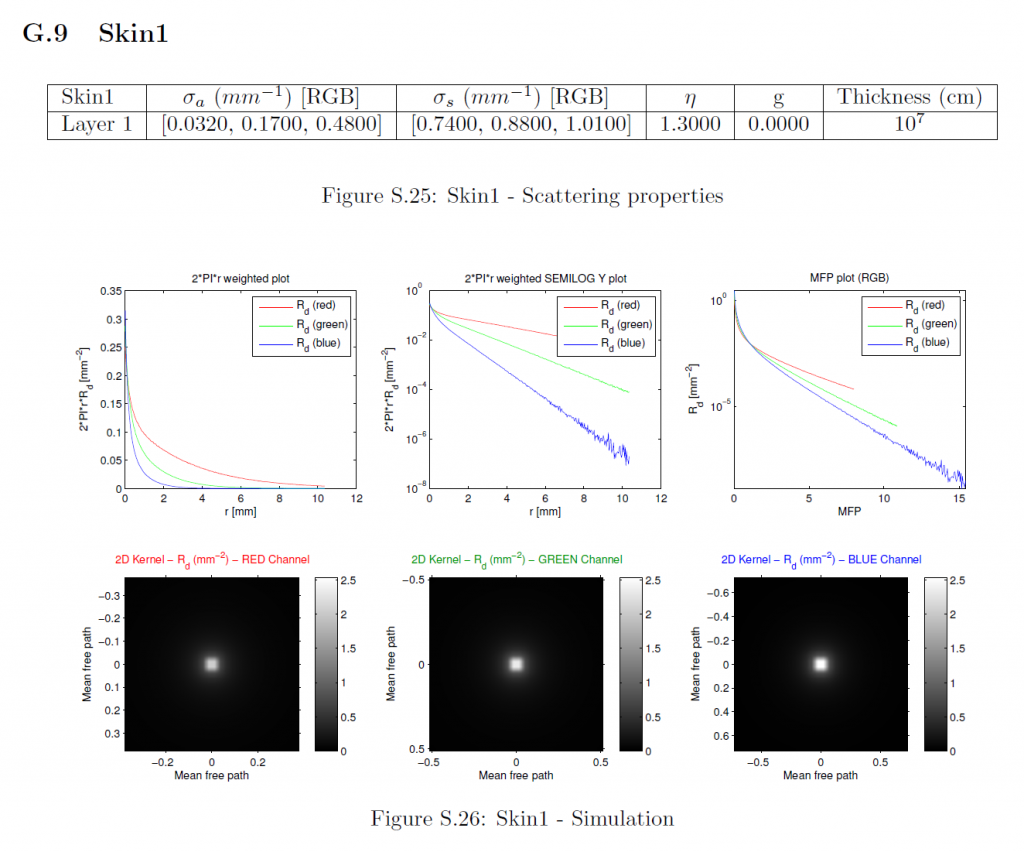
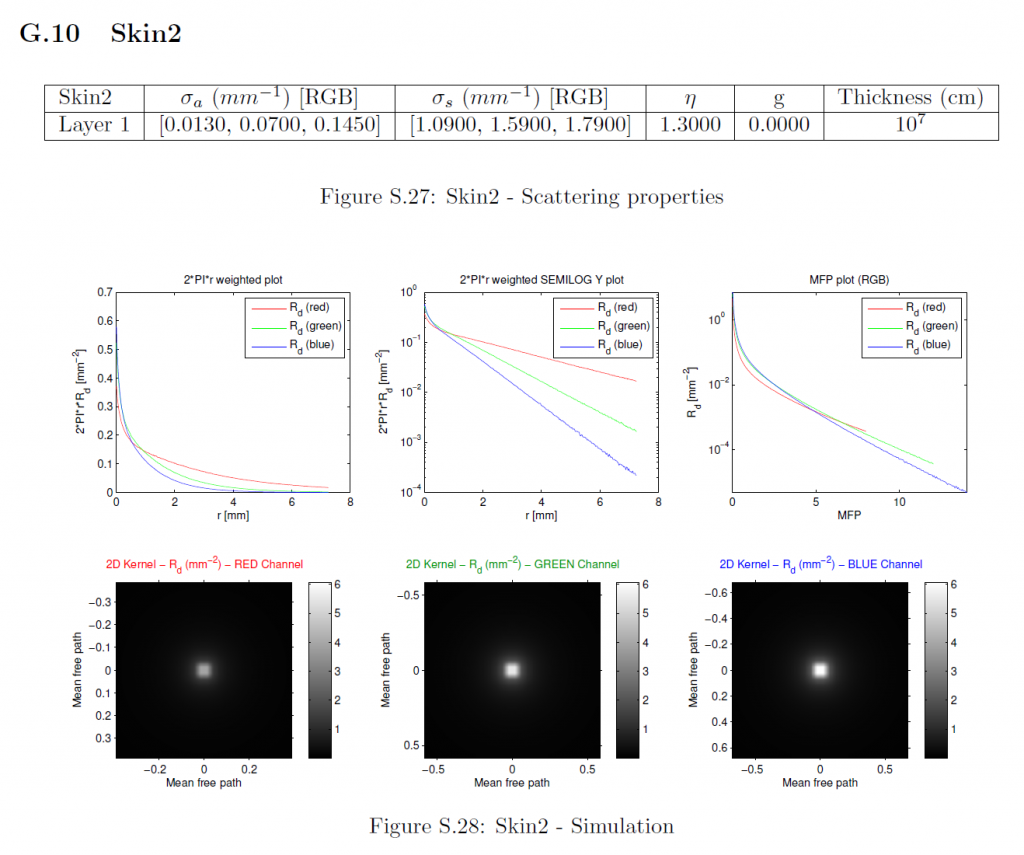
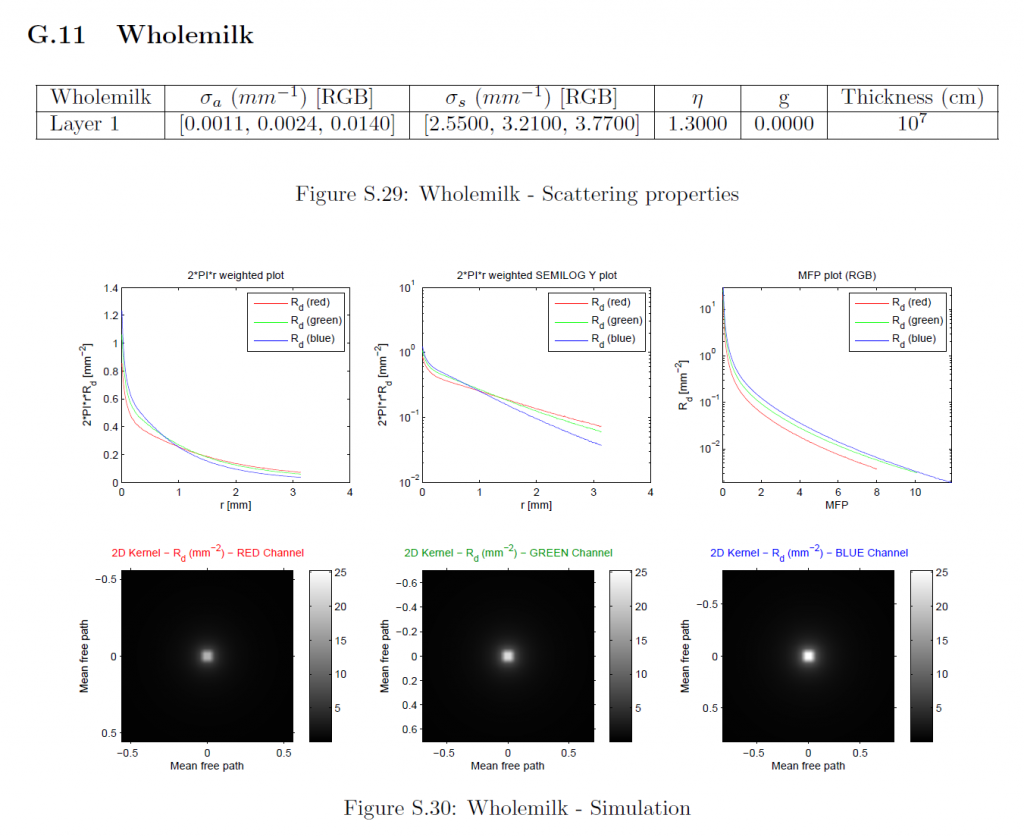
F Profile Simulation (MCML)
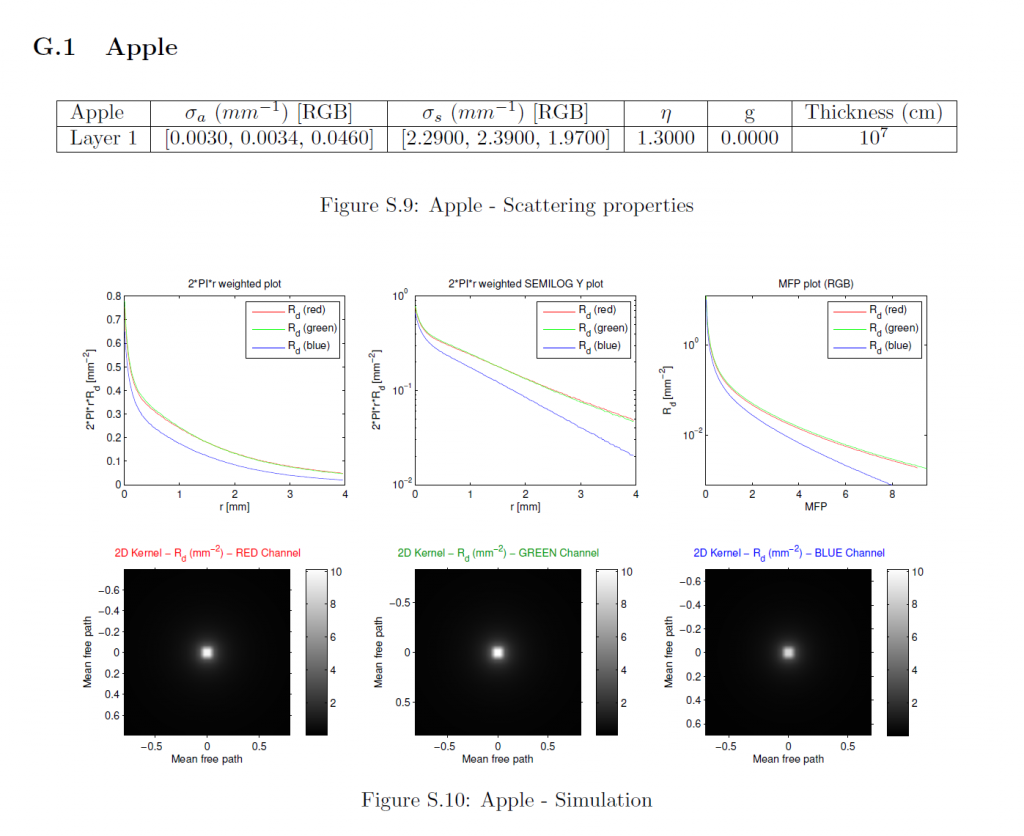
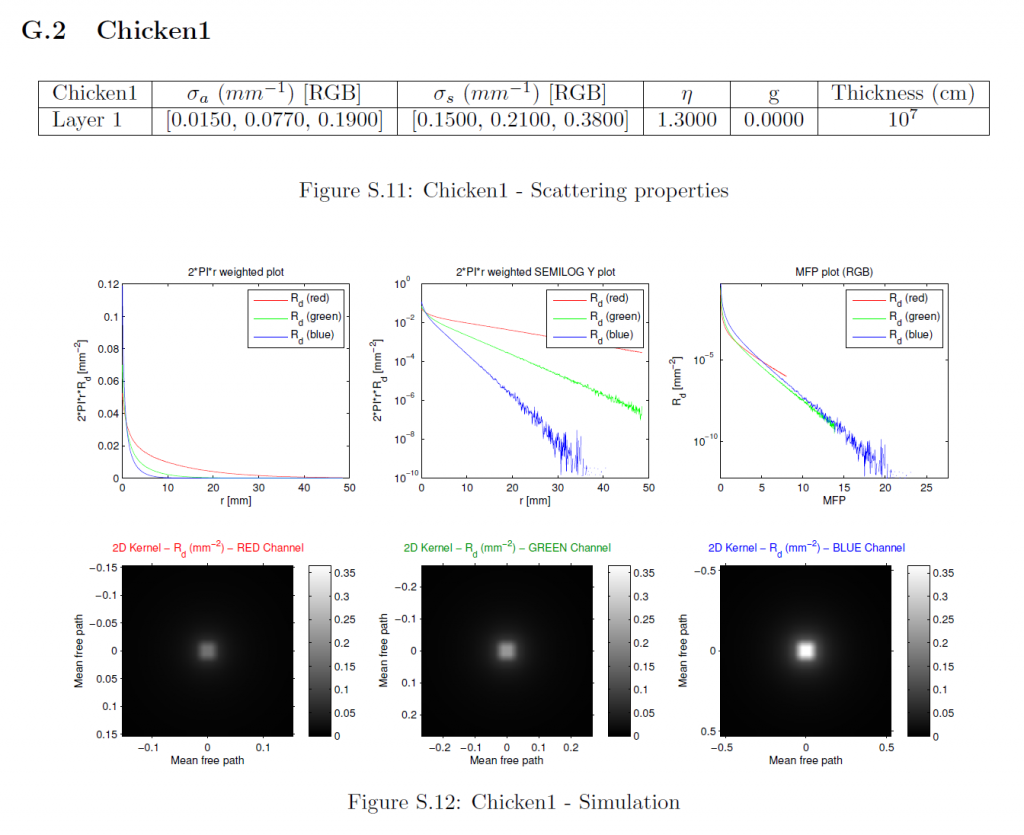
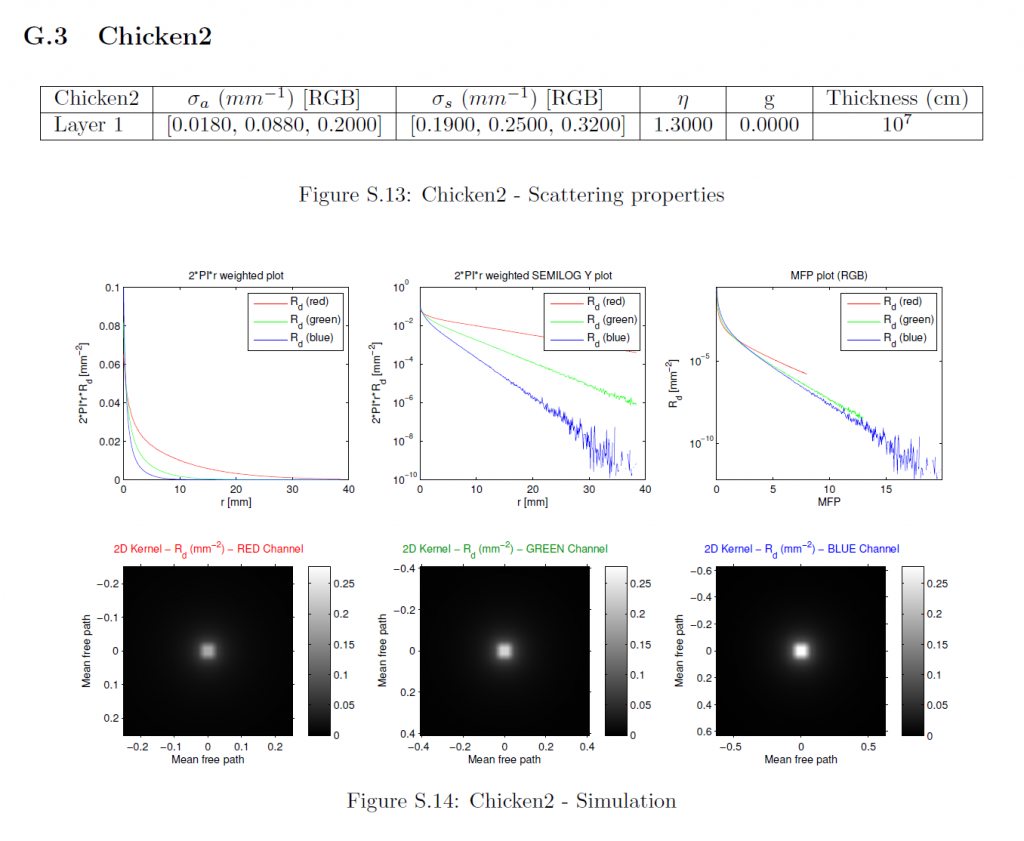
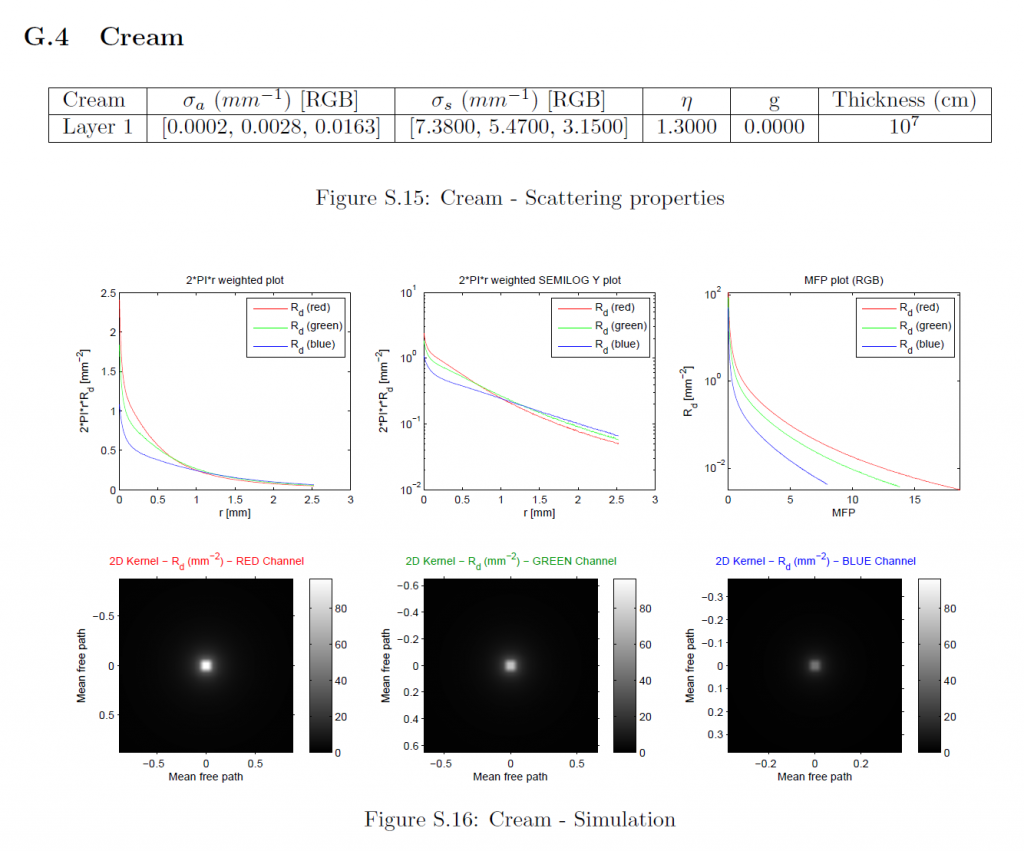
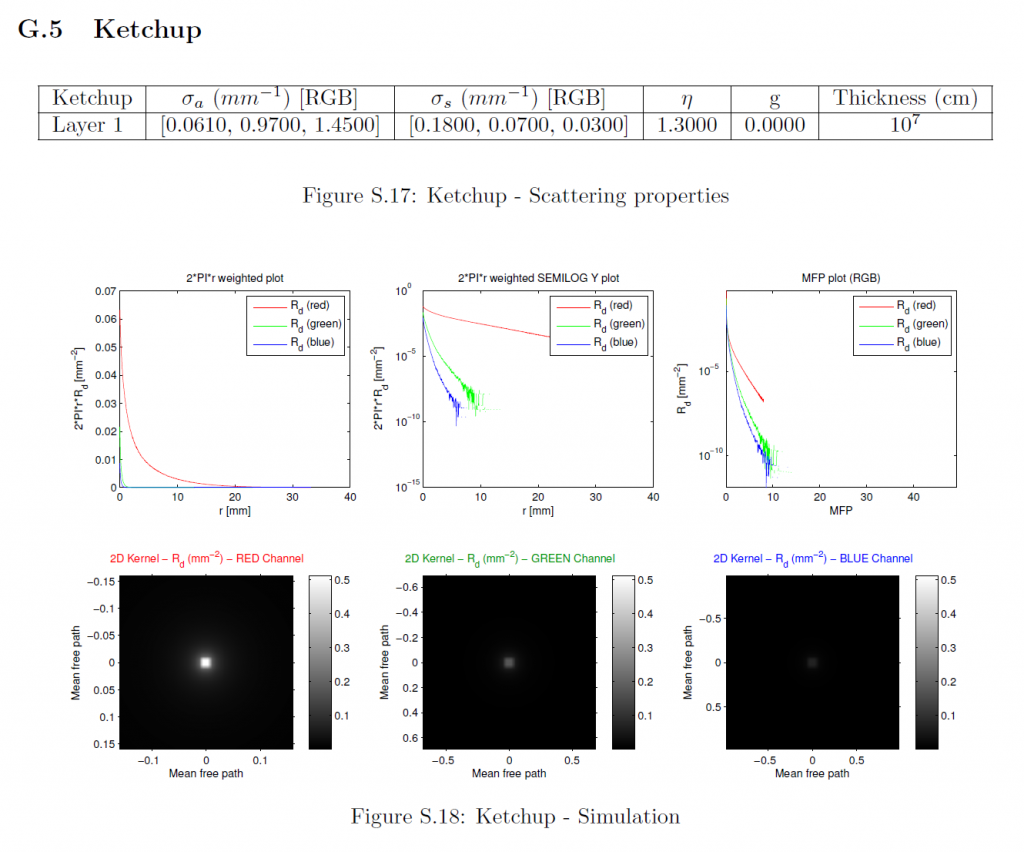
拡散反射率プロファイルはMCML [WJZ95]を用いてシミュレーションしました。シミュレーションに使用したマテリアルパラメータは、以前の研究[JMLH01]から引用したものである。各マテリアルについては、RGBチャンネルを個別にシミュレーションしました。マテリアル特性以外の各チャンネルのパラメータは以下の通りです:
フォトン数:\(10^7\)
グリッド空間:最小平均自由経路を20で割る (\(d_r = \frac{min(MFP_{rgb}}{20}\)).
グリッドの要素数:32倍の最大平均自由経路を\(d_r\)で割る。(\(n_r = \lceil{ \frac{32 * max(MFP_{rgb}}{d_r}) } \rceil\)).
薄さ:\(10^7{\rm cm}\) (ほぼ無限).
平均自由経路は\(\frac{1}{{\sigma_t}’} = \frac{1}{\sigma_a + {\sigma_s}’}\)として計算されます。我々は等方散乱(\(g=0\))をモデルとしているので、減少した散乱係数は自明で、すなわち\({\sigma_s}’ = \sigma_s\)です。MCMLで使用するために、すべてのパラメータはそれぞれ\({\rm cm}\), \({\rm cm}^{-1}\), \({\rm cm}^{-2}\)に変換されています。MCMLは、円筒対称組織モデルをシミュレートし、拡散反射率プロファイルを1次元関数\(R_d(r)\)として出力します。詳細なマテリアルパラメータ、シミュレーションされたプロファイルのプロット、および導出された放射状対称2次元プロファイルは、セクションGに含まれています。
G Simulation Parameters and Results
このセクションでは、測定された各マテリアルの特性、シミュレーションされた1次元プロファイルのプロット、および各被測定物の導出された2次元プロファイルが含まれています。これは、我々の方法への入力の詳細な説明を提供します。これらの入力に対する我々の近似手法の出力は、その大規模なサイズのため、別の補足資料に記載されています。最初の2つのサブプロットに示されている1次元プロファイルは、特定の\(r\)値でのプロファイルの大きさは、放射状に対称な2次元プロファイルの完全な円上の反射率を表しているため、\(2\pi r\)で重み付けされています。3つのチャンネルすべてが同じ最大半径までシミュレーションされたにもかかわらず、1次元プロファイルのプロットがそうでないことを誤って示唆しているかもしれないことは、何の価値もありません。対数スケールのプロットの場合、機械精度に近いすべてのプロファイル値はプロット関数によって省略されます。MFPプロットでは、すべてのチャンネルの半径は、それぞれのMFP値によってスケーリングされており、したがって、各チャンネルは、\(x\)軸上で異なるサポートを持っています。さらに、すべてのMFPプロットは重み付けされていないプロファイルを示し、2Dプロットは最も重要な中心領域のみを可視化します。