わしゃがな!
Pocolです。
今日は,[Jimenez 2020] Jorge Jimenez, XianChun Wu, Angelo Pesece, Adrian Jarabo, “Practical Real-Time Strategies for Accurate Indirection Occlusion”, Technical Memo ATVI-TR-19-01, March 2020.を読んでみようと思います。
PDFはActivision Researchのページからダウンロードできます。
以前に読んだものと比べて疑似コードやグラフなどが追加されているようです。
いつもながら,誤字・誤訳等があるかと思いますので,ご指摘いただける場合は正しい翻訳例と共に指摘していただけるとありがたいです。
Abstract
本研究では、非常に限られた予算の中でリアルタイムにアンビエントオクルージョンを実現するための技術を紹介します。本研究では、スクリーン空間のアンビエントオクルージョンの新しい定式化であるGTAOを提案します。これは、アンビエントオクルージョン方程式をラジオメトリックに正しく定式化し、時空間サンプリングを用いて計算を分散させる効率的な実装を用いることで実現しています。これまでの方法とは対照的に、我々の技術は、効率的で正確な物理ベースのパラメトリック形式を使用して、間接照明のアドホックな近似の使用を避けることによって、相互反射によって失われたエネルギー欠損を含むようにしています。次に、我々はGTAOを方向分解された照明を考慮するために拡張し、可視性と短縮係数の組み合わせを球面調和関数へと高速に投影し、これまでの研究とくまなくに解析します。最後に、可視性とBRDFの組み合わせを考慮した新しいスペキュラーオクルージョン定式化モデルを紹介し、プローブベースの照明から得られるグランドトゥルースの鏡面照明と密接に一致させ、この概念の効率的な実装である集計に基づくGTSOを提案します。我々の技術はリアルタイムで実用的であり、レイトレースされたグランドトゥルースに近い結果を与え、最近のAAAコンソールタイトルに組み込みされています。
1. Introduction
アンビエントオクルージョン(AO)は、限られた予算の中で、近くにある潜在的に小さなオクルーダーによって生成される拡散影をモデル化する、大域的な照明の近似です。これにより、事前ベイクされた照明やライトプローブを介して、低周波の事前計算された間接照明の高周波数の詳細とコントラストを維持することができます。残念ながら、アンビエントオクルージョン積分を解くことは、特定のシナリオ(例:1080pや4Kレンダリング、60fps)では実用的ではないため、過去には目標とする性能予算を達成するための近似値が開発されてきました。
我々は、レイトレースされたグランドトゥルースの解をマッチングさせながら、実用的なリアルタイム性能を目標とした新しいスクリーン空間オクルージョン技術を紹介します。我々は、近距離の間接照明からアンビエントオクルージョンを切り離す新しいアンビエントオクルージョン技術を提案します。これにより、(オブスキュランス推定器を使用する場合に必要な)断片的な積分を回避してアンビエントオクルージョン積分を効率的に解くことができ、同時に、物理ベースの効率的な関数近似を使用して、失われた複数の散乱拡散照明を回復することができます。これにより、グランドトゥルースのオクルージョンだけでなく、照明リファレンスも一致させることができます。次に、我々のアンビエントオクルージョンモデルを遠くのプローブからの方向分解された照明に拡張し、我々の正確なアンビエントオクルージョン項と水平からベント法線計算を用いて、効率的な球面調和関数展開を導出し、アンビエント照明を効率的に積分するために使用することができます。最後に、任意の鏡面物質に対するアンビエントオクルージョンを一般化し、BRDFと可視性を結合する新しい分割積分定式化を用いて定式化します。本論文では、この定式化の効率的な実装を提案する。これは、我々がGTSO(ground truth-based specular occlusion)と呼ぶもので、事前に計算された小さなテーブルにアクセスすることで、実行時に計算を行います。
特に、我々の貢献は次の通りです:
- GTAO: ラジオメトリックに正確なアンビエントオクルージョン積分と一致する効率的なアンビエントオクルージョン技法で、簡単な閉形式の解析式を用いて、近距離間接照明による損失エネルギーを含んでいます。
- Directional GTAO: 方向分解された遠方照明を考慮した拡張で、水平線に基づくベント法線のグランドトゥルースの導出を含みます。
- Specular occlusion (SO): 遠方のプローブからの鏡面反射を効率的に計算するために、可視性と反射率を結合させた任意の鏡面BRDFのための標準的なアンビエントオクルージョン定式を一般化しました。この定式化は、アンビエントオクルージョンと同じ仮定(一様半球とシングルバウンス)の下でグランドトゥルース参照と一致し、本研究の主要な成果の一つです。
- GTSO: マイクロファセットベースのBRDFのためのこのスペキュラー定式化の効率的な実装
図1は、これらの技術の効果を示しており、それらの組み合わせがモンテカルロ・レイトレースされたグランドトゥルースとどのように一致するかを示しています。我々は、これらの技術を効率的に実装し、時間的再投影と空間フィルタリングを活用して、ソニーのプレイステーション4で、1080pで動作するゲーム(標準的な半解像度オクルージョンバッファを使用)のベースラインのアンビエントオクルージョンを1フレームあたりわずか0.5ミリ秒で計算しています。この結果は、現在のハードウェア標準では、性能上の理由から、アドホックなオクルージョン計算を行う必要がなくなったことを強調しています。
2. Related Work
グローバルイルミネーション全般、特にアンビエントオクルージョンについては、これまでに多くの研究が行われてきたことから、ここでは、我々の研究と最も関連のある研究を中心に紹介します。この分野のより広い概観については、Ritschelら[RDGK12]とAalundとBaerentzen[AB12]の調査を引用します。
Screen-Space Ambient Occlusion
アンビエントオクルージョン[ZIK98]は、シーン内の一点からの可視性を積分し、環境照明項を変調します。このため,遮光された点からの可視性の問い合わせを行う必要があります。反射を無視した結果生じる過暗を緩和するために、アドホックなフォールオフ関数を用いて可視性を調整するのが一般的ですが、このような場合、AOをアンビエントオブスキュランスと呼ぶのが一般的です。 Mittring [Mit07]は、カメラから見えるジオメトリのみがオクルーダーとして機能すると仮定して、可視性の問い合わせをスクリーン空間に移動させることを提案しました。彼は、シーンのデプスマップをサンプリングすることでアンビエントオクルージョンを近似し、デプスマップ内のジオメトリに点がオクルージョンしているかどうかを評価し、点のサンプルを使ってボリュームメトリックなオクルージョンを効果的に計算しました。いくつかの研究では、点ではなく線のサンプルを用いて積分を行うことで、サンプリング戦略を改善しています[LS10, SKUT*10, HSEE15]。これらの方法は高品質の結果を得ることができますが、これらの方法は積分関数を単純化してしまい、結果として放射分析的に不正確なアンビエントオクルージョンが生じることになります。Bavoilら[BSD08]は、スクリーン空間レイトレーシングを用いて\(x\)周りのジオメトリの地平角に基づいて線積分を行うことを提案しています。彼らはこの手法をホライゾンベースドAO (HBAO)と呼んでいます。この研究は、水平線がすでにオクルードされている場合、水平線の下にある光線はすべてオクルードされてしまうという点で、ボリュームメトリックラインサンプリングアプローチと似ています。McGuireら[MOBH11, MML12]は後に、正半球上の\(x\)とニアフィールドの位置が相互に見えると仮定することによって、レイトレーシングプロセスを単純化しました。HBAOとその改良は効率的ではありますが、放射分析的には正しくなく、近接場での多重散乱を考慮していません。Timonen [Tim13a, ST15]は、画像全体に沿ってラインスイープを実行し、多数のピクセルにわたってサンプルを償却することにより、一定時間内に所定の方向の最大水平角を求めることにより、HBAOを改善しました。我々のGTAOと密接に関連して、同じ著者[Tim13b]は、ラインスキャンとデプスマップのフィルタリングを行うことで、アンビエントオブスキュランスのための放射分析的に正確な推定器を提案しました。この技術は印象的な結果をもたらしますが、オブスキュランス推定器を使用することで、グランドトゥルースの照度のマッチング(むしろオブスキュランスのマッチング)ができず、ルックアップテーブルを使用して実装されたオクルージョン計算のための部分的な内部積分を使用する必要があります。本研究では、視角に基づいて放射分析的に補正されたアンビエントオクルージョンを効率的に計算することができます。間接照明は物理ベースのパラメータ式で説明されるため、過暗化を避けるためのアドホックなフォールオフ関数を必要としません。これにより、内部積分を解析的に解くことで、AO計算を骨の髄まで減らすことができます。さらに、我々はGTAOを方向性のあるオクルージョンや非Lambertianオクルージョンにも一般化します。
Directional Occlusion
AOが注目されている一方で、プローブなどにエンコードされた環境照明の方向依存性を導入することに焦点を当てた研究は少ないです。事前にフィルタリングされたプローブに頼るのではなく。Ritschelら[REG*09]は、オンザフライでレンダリング方程式を評価することにより、方向性拡散照明を近似しています。近似可視性テストを使用しているにもかかわらず、実用的なリアルタイム環境には遅すぎます。Landis [Lan02]は、アンビエントオクルージョンの方向性の忠実度を高めるために、ベント法線を使ってアンビエントプローブから最も見える方向にフェッチすることを提案しています。それ以来、ベント法線はオフラインでもリアルタイムレンダリングでも広く使われるようになりました。Klehmら[KRES11]はSSAO[Mit07]を拡張し、可視サンプルの方向を平均化してベント法線を扱うようになりました。彼らはまた、水平方向の平均化は3dレイトレースされたベント法線とは一致しませんが、同様の理論的根拠を用いてHBAOのためのバリアントを提案しています。Oat and Sander [oS07]は、アンビエントオクルージョンとベント法線を用いて可視性を事前に計算し、リアルタイムレンダリング中にこの情報を使用して、光源開口部と球面キャップの交点を計算することで、拡散照明に可視性を効果的に適用しました。Ramamoorthi と Hanrahan [RH01]は、ライトプローブを球面調和関数に符号化することを提案しており、リアルタイムで効率的に光を畳み込みすることが可能です。Green [Gre03]は、3重のSH積を用いて可視性を畳み込みました。我々はこれらのアイデアを基にして,より高価で精度の低い3重SH積を避けるために,ランタイムでの可視性と短縮係数の結合を効率的にSHに投影することを提案しています。
Specular Occlusion
過去20年間、アンビエントオクルージョンは大部分が研究されてきましたが、スペキュラーオクルージョンは、物理ベースのシェーディングモデルを採用しているため、同様に重要であるにもかかわらず、あまり注目されていませんでした。Gotanda [Got12]は、アンビエントオクルージョンから経験的にスペキュラーオクルージョンを導き出しました。彼は、アンビエントオクルージョンではBRDFローブの形状を考慮していないため、オクルージョンスケールがミスマッチになることを指摘しています。Lagrade [Ld14]は、同様の経験的アプローチを採用し、GGXベースのマイクロファセットに適用して、サーフェイスの粗さを利用してスペキュラーオクルージョンの形状を決定しました。Jimenezとvon der Pahlen[Jv13]は、アドホックなアプローチを使用する場合でも、フォトリアリスティックなキャラクターをレンダリングするためのスペキュラーオクルージョンの重要性を強調しています。これとは対照的に、我々は、可視性とスペキュラBRDFを結合させた、アンビエントオクルージョンに類似したスペキュラオクルージョン項を正式に導出しました。さらに、このスペキュラーオクルージョン項を用いた効率的なレンダリングモデルを提案します。
3. Background & Overview
法線\(\mathbf n\)を持つ点\(x\)から\(\omega_o\)方向への反射輝度\(L_r(x, \omega_o)\)は、次のようにモデル化することができます。
\begin{eqnarray}
L_r(x, \omega_o) = \int_{{\mathcal H}^2} L(x, \omega_i) f_r (x, \omega_i, \omega_o) \langle {\mathbf n}, \omega_i \rangle^{+} d\omega_i \tag{1}
\end{eqnarray}
ここで、\({\mathcal H}^2\)はその軸として\(\mathbf n\)を持つ\(x\)を中心とした半球であり、\(L(x, \omega_i)\)は\(\omega_i\)方向から\(x\)に入射する放射輝度、\(f_r(,x \omega_i, \omega_o)\)は\(x\)におけるBRDF、\(\langle {\mathbf n}, \omega_i \rangle^{+}\)はモデルを短縮化しています。アンビエントオクルージョン[ZIK98]は、次のような仮定を導入して、式(1)を近似しています:i) \(x\)の周りのすべての表面は純粋に吸収している(すなわち、光を跳ね返さない)、ii) すべての光は、無限の均一な白色環境光(または一般化して、任意の均一な色の)から来ており,\(x\)の周りの幾何学的形状によって閉塞されている可能性がある。そしてiii) \(x\)の表面はLambertianサーフェイスである。これは、式(1)を次のように変換します。
\begin{eqnarray}
L_r(x, \omega_o) &\approx& L_i \frac{\rho(x)}{\pi} \int_{{\mathcal H}^2} V(x, \omega_i) \langle {\mathbf n}, \omega_i \rangle^{+} d\omega_i \\
&=& L_i \frac{\rho(x)}{\pi} {\mathcal A}(x) \tag{2}
\end{eqnarray}
ここで,\({\mathcal A}(x)\)は点\(x\)におけるアンビエントオクルージョン項で,\(\frac{\rho(x)}{\pi}\)はアルベド\(\rho(x)\)を持つディフューズBRDFで,\(V(x, \omega_i)\)は\(x\)における方向\(\omega_i\)での可視項です。これまでの研究[ZIK98, Mit07, BSD08]では、この可視性項\(V(x, \omega_i)\)をオクルーダーまでの距離に対する減衰関数としてモデル化し、\({\mathcal A}(x)\)をオブスキュランスと呼んでいました。この減衰関数は、近接場の相互反射を無視することで生じる典型的な過暗化を回避するためのアドホックな解決策として使用されました。
アンビエントオクルージョンは、均一な照明に対してのみ正確です。しかし、実際には、ライトプローブに格納されている任意の照明に使用されています。このような場合、照明は次のように近似されます。
\begin{eqnarray}
L_r(x, \omega_o) &\approx& \frac{\rho(x)}{\pi} {\mathcal A}(x) \int_{{\mathcal H}^2} L(x, \omega_i) f_r(x, \omega_i, \omega_o) \langle {\mathbf n}, \omega_i \rangle^{+} d \omega_i \\
&=& \frac{\rho(x)}{\pi} {\mathcal A}(x) {\mathcal L}(x, \omega_h) \tag{3}
\end{eqnarray}
ここで,\({\mathcal L}(x, \omega_h)\)はBRDFで事前畳込みされたライトプローブで,\(\omega_h\)はプローブにおいてクエリする方向です。いくつかの研究では、後でアンビエントオクルージョン項\({\mathcal A}(x)\)によって減衰されるプローブをフェッチするためにベント法線\(\omega_h = {\mathbf b}\)に基づいています。これは、入射放射輝度にある程度の指向性を含んでいますが、可視性\(V\)と照明\(L\)の項は、式(3)では分断されたままです。
代替的に一般的なアプローチは、ライトプローブと可視性を\(n\)(次の球面調和関数(SH)展開としてエンコードすることです[RH01]。これにより、SH の二重積として \(L_r(x, \omega_o)\) を効率的に計算することができます。
\begin{eqnarray}
L_r(x, \omega_o) \approx \frac{\rho(x)}{\pi} \sum_{j=0}^n {\hat L}_j, {\hat V}_j \tag{4}
\end{eqnarray}
ここで,\({\hat L}_j\)と\({\hat V}_j\)は\(j\)番目の\(L\)と\(V\)についてそれぞれのSH係数です。残念ながら、短縮系を導入したり、BRDFを追加したりするには、高価なSH3重積が必要であり、このアプローチの適用可能性が制限されることがあります。
Objectives
この研究では、主に2つの目的があります。一方では、要求の厳しいリアルタイムアプリケーションでも十分に効率的に使用できるようにしながら、放射分析的に正確なアンビエントクルージョンの定義に適合する技術を提案します。もう一方では、非均一のドーム照明を含むマテリアルBRDFと入力ライト設定のセットを拡張するためにグランドトゥルースのオクルージョンだけでなくグランドトゥルースの照明にもマッチするために,効率的に近似できるグローバルイルミネーションの量を拡張するしたいと思います。
第一の目標は、入力データ、パス数、命令数の面で厳しい制限を課しています。これらの制限に縛られて、我々は、深度バッファとサーフェイス法線のみを入力として取り、スクリーン空間で動作し、他のグローバルイルミネーション入力(具体的には焼きこみされた放射照度)と共存し、強化することができる技術を第4節で述べます。
第二の目的を達成するために、従来のアンビエントオクルージョンで行われていた仮定をすべて緩和する。具体的には、a)仮定i(4.2節)に対応するために、近接場のオクルーダーのディフューズ相互反射を考慮します。b) 一様ドームの仮定ii(第5節)に対して、高速で正確なLambertianディレクショナルオクルージョンアプローチを導入します。 c) 我々は純粋にLambertianなサーフェイス仮定iiiを緩和するための正式なディレクショナルオクルージョン定式化とスペキュラーオクルージョン定式化を提案します(第6節)。
4. GTAO: Ground Truth-based Ambient Occlusion
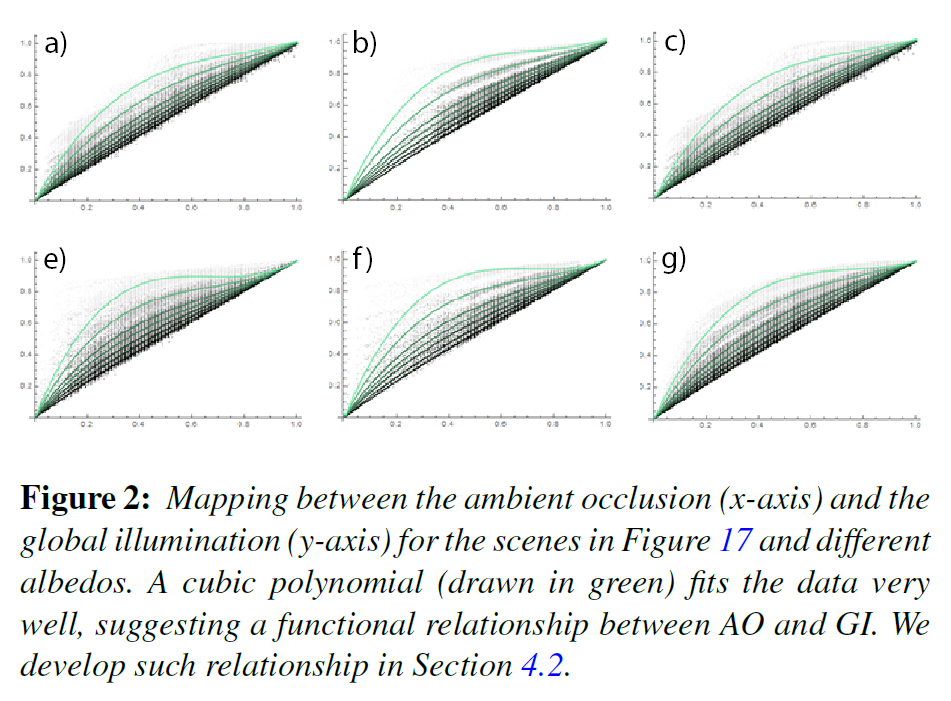
近接場の間接照明を考慮した効率的なモデルを開発するために、図2に示すように、全アンビエントオクルージョン、サーフェイスのアルベド、および\(x\)から反射される間接照明の間に関数的な関係があるという重要な観測を行いました。これにより、GIを意識したアンビエントオクルージョン技術を2つの部分に分けて構築することができます。まず、二値可視性を仮定した場合の放射分析的に正しいアンビエントオクルージョンを計算し(第4.1節)、計算したアンビエントオクルージョンに基づいて失われた間接照明を再導入します(第4.2節)。これには主に2つの利点があります。1) 反射光のモデルを、ヒューリスティックなオブスキュランス項ではなく、物理的に実現可能な近似に基づいてモデル化しています。 2)経験的なオブスキュランス項を排除することで、断片的な内部積分を取り除くことで複雑さを軽減し、その結果、計算は1サンプルにつき1回ではなく、1方向につき1回で済むようになりました。
4.1. Computing ambient occlusion
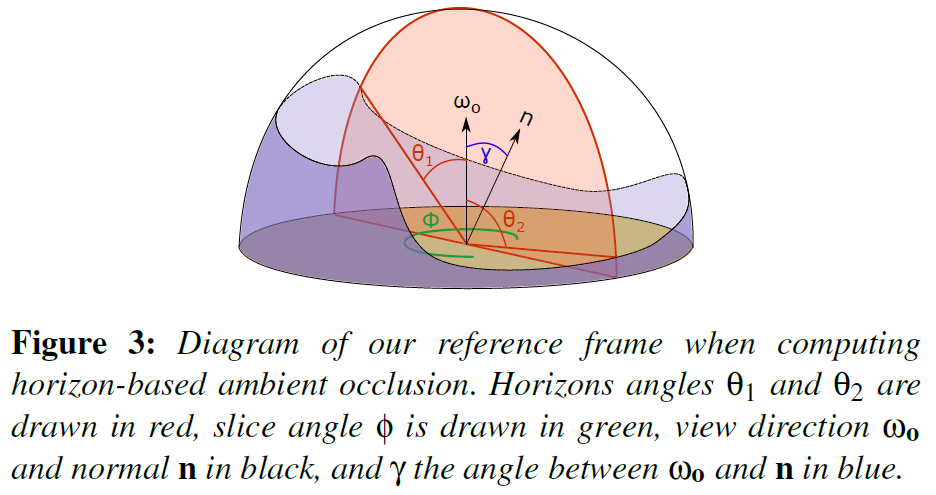
我々のアンビエントオクルージョンの定式化は、水平線に基づくアプローチであるBavoilら[BSD08]に従っており、ハイトフィールドの仮定の下で、式(2)を方位角\(\phi\)に沿った積分として計算します。
\begin{eqnarray}
{\mathcal A}(x) = \frac{1}{\pi} \int_0^{\pi} \int_{-\pi/2}^{\pi/2} V(\phi, \theta) \cos(\theta – \gamma)^{+} | \sin(\theta)| d\theta d\phi \tag{5}
\end{eqnarray}
ここで,\(\theta\)はビューベクトル\(\omega_o\)に沿った極角、\(\gamma\)は法線\(\mathbf n\)とビューベクトル\(\omega_o\)とのなす角度、\(\cos(\theta)^{+} = {\rm max}(\cos(\theta), 0)\)で、\(V(\phi, \theta)\)は可視性減衰関数です。[BSD08]とは異なり, この積分は放射分析的に正しい形で書かれていることに注意してください。 座標系も \((\phi, \theta)\) を接線ベクトルの代わりにビューベクトル \(\omega_o\) を基準にして定義することで変更されています。これは、微小立体角の sin 項を考慮するために abs 値を導入する必要があります。\(\theta\)が水平角\(\theta_1(\phi)\)と\(\theta_2(\phi)\)の上にあるときに1を返し、それらの下にあるときに0を返す2値可視関数\(V(\phi, \theta)\)を仮定すると(参照系については図3を参照)、結果としてサンプルごとの減衰を持たないので、式(5)は次のように変換することができます。
\begin{eqnarray}
{\mathcal A}(x) = \frac{1}{\pi} \int_0^{\pi} \underbrace{\int_{\theta_1(\phi)}^{\theta_2(\phi)} \cos(\theta – \gamma)^{+}|\sin(\theta)| d\theta }_{\hat a} d\phi \tag{6}
\end{eqnarray}
水平角\(\theta_1\) と\(\theta_2\) が与えられると、式(6)の内積分 \(\hat a\) を解析的に解くことができます。
\begin{eqnarray}
{\hat a}(\theta_1, \theta_2, \gamma) = \frac{1}{4}(- \cos(2\theta_1 – \gamma) + \cos(\gamma) + 2 \theta_1 \sin(\gamma)) \\
+ \frac{1}{4} ( – \cos(2 \theta_2 – \gamma) + \cos(\gamma) + 2 \theta_2 \sin(\gamma)) \tag{7}
\end{eqnarray}
この定式化では、法線\(\mathbf n\)が地平線ベクトルで定義された平面\(P\)内にあることが必要であることに注意が必要ですが、これは一般的には保持されません。しかし、次のような同一性が保持されていることを示すことができます[Tim13b]:
\begin{eqnarray}
\int_{- \pi/2}^{\pi/2} \langle {\mathbf n}, \omega_i \rangle^{+} | \sin(\theta)| d\theta = || \bar {\mathbf n} || \int_{-\pi/2}^{\pi/2} \langle \frac{\bar {\mathbf n}}{|| \bar {\mathbf n} ||}, \omega_i \rangle^{+} | \sin(\theta)| d\theta \tag{8}
\end{eqnarray}
ここで,\(\bar {\mathbf n}\)は\(P\)上に投影された法線です。式(6)と結び付け,次を得ます。
\begin{eqnarray}
{\mathcal A}(x) = \frac{1}{\pi} \int_0^{\pi} || \bar {\mathbf n} || {\hat a}(\theta_1 (\phi), \theta_2(\phi), \gamma’) d\phi \tag{9}
\end{eqnarray}
ここで,\(\gamma’ = {\rm arccos}(\langle \frac{\bar {\mathbf n}}{|| \bar {\mathbf n} ||}, \omega_o \rangle)\)です。
この解析積分は、1方向につき1回だけ効率よく実行することができます。さらに、最適化後に必要なのはサンプルごとに2つのcosと1つのsinだけであり、さらに、積分領域を設定するために方向ごとに3つの追加のacos関数が必要であり、これは効率的に近似することができます[Dro14]。
Computing maximum horizon angles
式(9)の解のコアは、画像平面内の方向 \({\hat t}(\phi)\) に対する最大地平角 \(\theta_1(\phi)\) と \(\theta_2(\phi)\) を求めることであり、ここで \(\phi\) は一様に分布する方位角とします。我々は、その結果をレイのパラメタリゼーションを\(r \in [0, 1]\)を持つ\({\hat s}(r) = {\hat x} + {\hat t}(\phi) \cdot r\)を用いて、点\(x\)の投影ピクセル \(\hat x\) からスクリーン空間でレイトレーシングを行い、\(\theta_1(\phi)\) を求めます。各カメラ空間点\(s(r)\)に対して,\(\omega_s(r) = \frac{s(r) – x}{|| s(r) – x ||}\) を計算します。ビューベクトル\(\omega_o\)に対する水平角の最大値は,次のようになります。
\begin{eqnarray}
\theta_1 (\phi) = {\rm arccos}\left( {\rm max}_{r \in [0, 1]} ( \langle \omega_s(r), \omega_o \rangle^{+} \right) \tag{10}
\end{eqnarray}
方向ごとに一定の離散サンプル数を計算します。角度\(\theta_2(\phi)\) は \({\hat s}(r) = {\hat x} – {\hat t}(\phi) \cdot r\) と同様に計算されます。最大スクリーン空間レイトレーシング距離 \(r\) はカメラからの距離に応じてスケーリングされます; これは \({\mathcal A}(x)\) のビューに依存しないようにするために必要です。カメラの近くにあるオブジェクトの大規模な収集領域を避けるために、最大 \(r\) をクランプしていますが、これは GPU キャッシュを無駄にします。アルゴリズム 1 は、GTAO の計算の詳細を示しています。
4.2. Adding indirect illumination
式(9)は、\(x\)の近傍が光を遮るだけであり、したがって相互反射は存在しないと仮定すれば、グランドトゥルースと一致します。この結果、エネルギーが失われ、例えばコーナーでは暗くなりすぎていないことがわかります。言い換えれば、式(9)は式(2)を計算しますが、物理的に正確な式(1)は計算できません。しかし、Nayarら[NIK91]が示すように, \(x\)の近傍\(S(x)\)が一定のアルベド\(\rho(x)\)と拡散反射率を持つと仮定すれば, 式(1)はノイマン級数として次のように表現できます。
\begin{eqnarray}
L_r(x, \omega_o) = L_i \frac{\rho(x)}{\pi} {\mathcal A}(x) + \sum_{m=1}^{\infty} \rho^{m} \int_{S(x)} K_m (x \leftarrow x’) L_i(x’) dx’ \tag{11}
\end{eqnarray}
ここで,\(K_m(x \leftarrow x’)\)は\(x’\)と\(x\)の間の輸送関数です。この式は、\(S(x)\) 上の点で入射する光、\(x\) と点 \(x’\) の間の幾何学的関係 \(K_m (x \leftarrow x’)\)、および \(x\) で反射されたグランドトゥルースの全光を関係付けます。\(S(x)\) における一様な照明 \(L_i\) の仮定を導入し、Stewart and Langer [SL96] に従うと、式(11) の閉形解を次のように求めることができます。
\begin{eqnarray}
L_r(x, \omega_o) &=& L_i \frac{\rho}{\pi} \frac{ \pi^{-1} \int_{{\mathcal H}^2} V(x, \omega_i) \langle {\mathbf n}, \omega_i \rangle^{+} d \omega_i }{1 – \rho( 1 – \pi^{-1} \int_{{\mathcal H}^2} V(x, \omega_i) \langle {\mathbf n}, \omega_i \rangle^{+} d\omega_i )} \\
&=& L_i \frac{\rho}{\pi} \frac{{\mathcal A}(x)}{1 – \rho(1 – {\mathcal A}(x))} \tag{12}
\end{eqnarray}
式(12)は、いくつかの代数演算を行うだけで、\(x\)におけるアンビエントオクルージョンの関数としての間接照明を正確に計算します。これにより、\({\mathcal A}(x)\)を計算する際に、アドホックなオブスキュランス演算を必要としません。
Accuracy analysis
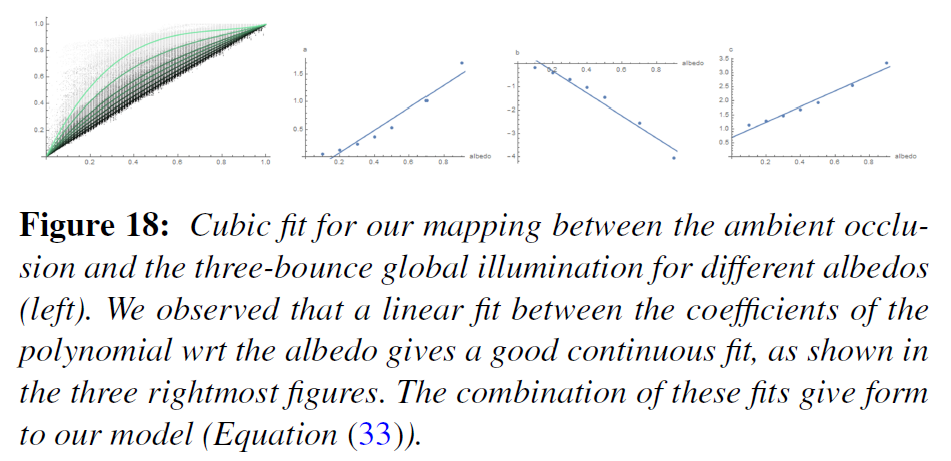
式(12)の精度を、モンテカルロ法を用いた全球照度の測定値と比較して解析します(図2)。このシナリオでの平均反射輝度を解析し、シミュレーション分散の影響を軽減するために、アルベド\(\rho(x)\)、アンビエントオクルージョン項\({\mathcal A}(x)\)、および一様ドームで照らされた全反射輝度に関連する多項式を適合させました。詳細は付録Bに記載されています。図4で観察できるように、式(12)は、サーフェイスのアルベドとサーフェイスアルベドの理想的な範囲の出アンビエントオクルージョンに基づいて、グローバルイルミネーションの非常に正確な近似値を提供します。
4.3. Implementation details
60フレーム/秒で動作するゲームでは、約半ミリ秒が妥当なスクリーンスペースのアンビエントオクルージョンバジェットとなり、最適化が必須となります。同様に、スクリーンスペースでの動作にはいくつかの制限があります。
Spatio-temporal sampling approach
我々は、半解像度でアンビエントオクルージョンを計算し、その後、フル解像度へとバイラテラルアップサンプリングします。さらに、性能を損なうことなくできるだけ多くのサンプルを計算するために、オクルージョン積分を空間と時間の両方に分散させています:我々は、ピクセルごとに1つの方向(方向の両側を含む、合計12ステップ)だけで地平線方向をサンプリングしますが、一様な畳み込み重みを使用して、再構成のためにバイラテラルフィルタを使用して4×4の近傍で収集された情報を使用しています。ピクセルごとの方向性を生成するために、我々は4×4のタイル状の空間一様ノイズを使用しています。さらに、6つの異なる回転を交互に行い、指数関数的な蓄積バッファを使用して結果を再投影することで、時間的なコヒーレンシーを積極的に利用しています。これにより、1ピクセルあたり\(4 \times 4 \times 6 = 96\)の有効サンプリング方向が得られます。図5は、最終的な再構成に対する空間的・時間的ギャザリングの効果を示しています。我々は、ラインスイープ[Tim13a]を使用するのではなく、通常のサンプリングアプローチを選択しました。これは、我々のタイトなバジェットとターゲット品質(1ピクセルあたり12ステップの単一方向)に適合していればより良いからです。ラインスイープアンビエントオクルージョンは非常に高い品質の結果を達成しますが、残念ながら、ピクセルごとに方向をランダムにすることができないため、バンディングを避けるためにはスキャン方向の数を多くする必要があります。Silvennoinenら[ST15]は、Xbox Oneで1280×720画像の場合、1.6msのコストを報告しており、我々のアプローチとは異なるトレードオフを表しています。
Bounding the sampling area
アンビエントオブスキュランス技法とは対照的に、我々の定式化では減衰関数を使用していません。しかし、我々が計算したいのは局所的なアンビエントオクルージョンのみであり、より広い範囲の低周波オクルージョンはベイクド照度やオクルージョンを用いて計算することができます。そこで、我々の定式化を用いてニアフィールドオクルージョンを計算し、その最小値を計算することで、ベイクされた遠方フィールドオクルージョンと組み合わせることで、ニアフィールドオクルージョンを計算します。アーティファクトを最小化するために、保守的な減衰戦略を採用しています。我々は、ニアフィールドオクルージョン領域を超えると、現在のサンプルの水平角コサイン(\(\cos(\theta)\))を-1に向けて線形補間します。つまり、ニアフィールド外のサンプルは徐々に減衰し、他のサンプルは変更されないままになります。
Height-field assumption considerations
スクリーンスペース技法は、深度マップが高さフィールドであることを前提としていますが、これは一般的には保持されません。その結果、深度の不連続性にある薄い特徴は、あまりにも多くのオクルージョンを投げかけてしまいます。これは、例えばデプスピーリングで解決できるかもしれませんが、我々の場合は非現実的です。その代わりに、オブジェクトの厚さがスクリーン空間でのサイズと同じであるという仮定から導き出された保守的なヒューリスティックを導入します。このヒューリスティックな方法は、水平線探索を修正することによって導入します (式(10))。各反復\(i\)について、最大水平角\({\bar {\theta}}^{i}(\phi) = \cos ({\theta}^i (\phi))\)の余弦は、距離\(r_i\)のサンプルを用いて以下のように更新されます。
\begin{eqnarray}
{\bar \theta}^{i}(\phi) \begin{cases}
\langle \omega_s(r_i), \omega_o \rangle^{+} \quad & {\rm if} \langle \omega_s(r_i), \omega_o \rangle^{+} \geq {\bar \theta}^{i-1}(\phi) \\
{\bar \theta}^{i-1} (\phi) – \beta \quad & {\rm if} \langle \omega_s(r_i), \omega_o \rangle^{+} \lt {\bar \theta}^{i-1}(\phi)
\end{cases} \tag{13}
\end{eqnarray}
ここで、\(\beta\)は補正定数であり、\({\bar \theta}^{0} =-1\)です。上付きの表記は、反復処理を地平角の\(\theta_1\)と\(\theta_2\)の表記と区別するために使用され、上線は地平角の余弦を示すためにこの式で使用されていることに注意してください。地平線の後ろにある1つのサンプルでは、計算された地平線が大きく減少することはありませんが、多くのサンプル(例えば、薄い特徴量)では、地平線がかなり減衰してしまいます。これにより、水平角を小さくすることで凸形状のオクルージョンを徐々に減衰させることができますが、室内では単純なコーナーなどの凹みはそのままにしておきます。人間の顔の特徴のような小さな凸状の物体に影響を与えないように補正するには、現在の最大地平線までのサンプル距離が十分で、サンプリング半球のベースから離れすぎていない場合にのみ適用されます。図6は、このヒューリスティックの効果を示しています。
4.4. Results
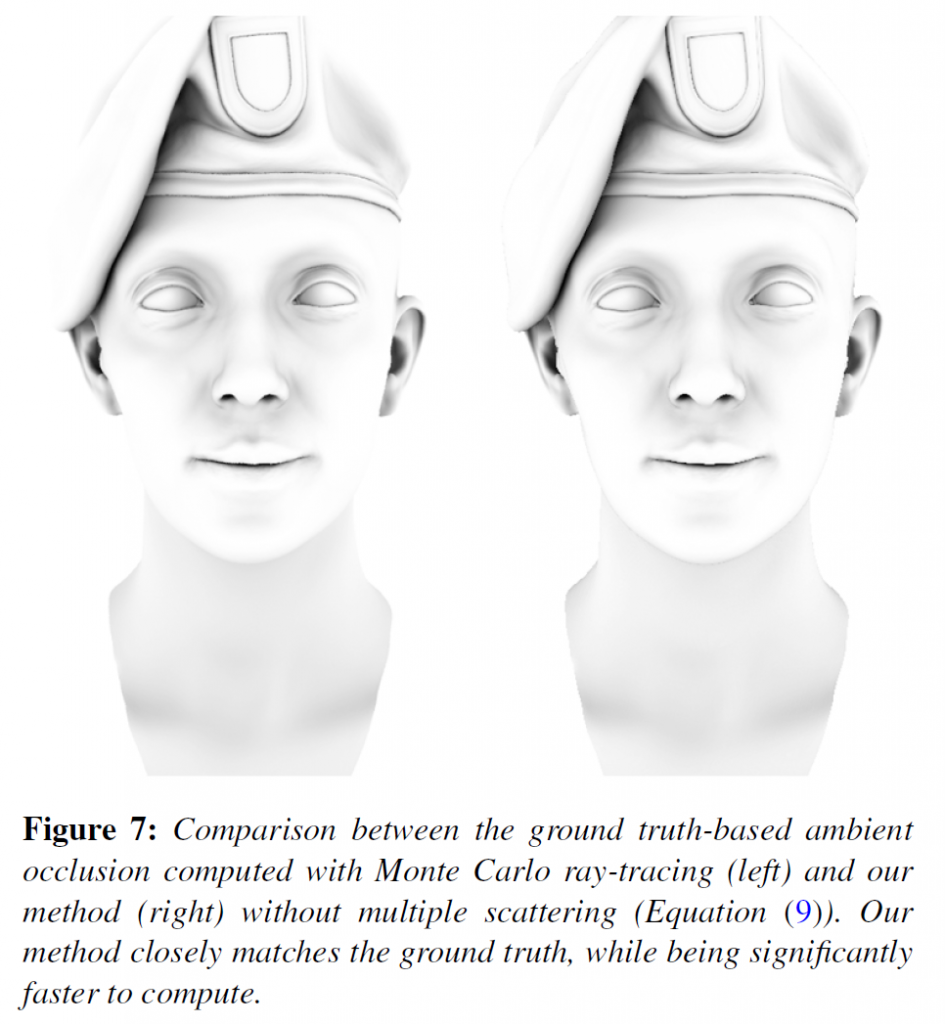
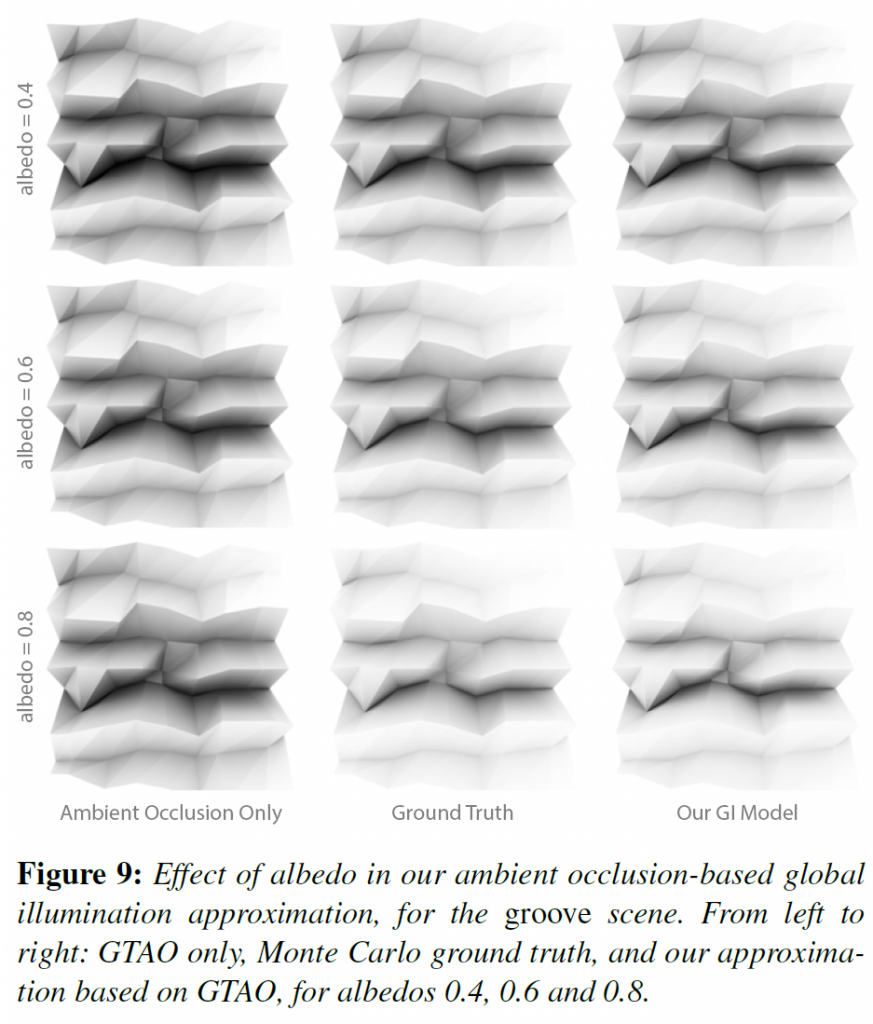
我々はGTAOをDirectXスタンドアロンアプリケーションに実装しています。すべての場合において、モンテカルロ法によるレイトレースされたリファレンスと比較します。図7は、グローバルイルミネーションなし(アンビエントオクルージョンのみ)のGTAOを基準値と比較したものです。同様に、パストレースされたグランドトゥルースに対して、我々の近似グローバル照明をニアフィールドと比較しています。図8は、アンビエントオクルージョンのみでレンダリングされたシーンを示しており、その後、4.2節で提案した解析モデルを用いて、グレーとカラーの両方のアルベドについてグローバルイルミネーションを含めています。図9は、抽象的な溝のような形状で、グレーアルベドの値が増加している場合の同じ比較を示しています。どちらの場合も、均一な遠方照明の場合、我々の技術は、狭い実用的なリアルタイム予算でレンダリングしながらも、グランドトゥルースに近い結果を提供しています。
5. Directional GTAO
これまでは、一様な無限大の光源(つまり色のついたプローブ)を想定していました。残念ながら、このアプローチは実用的な条件ではあまりにも単純化されすぎており、特に環境照明用のライトプローブが広がって使用されます。これを考慮して、リアルタイム性能を維持しつつ、式(1)の光の指向性成分を回復する必要があります。拡散反射率と遠方照明の場合の式(1)を以下のように近似してみましょう。
\begin{eqnarray}
L_r (x, \omega_o) \approx \frac{\rho(x)}{\pi} \int_{{\mathcal H}^2} V(x, \omega_i) L(\omega_i) \langle {\mathbf n}, \omega_i \rangle^{+} d \omega_i \tag{14}
\end{eqnarray}
\(L(\omega_i)\)は無限遠の照明環境(ライトプローブ)から入射する光、\(V(x, \omega_i)\)はその視認性である。式(14)を解くために、積分の項をその球面調和関数展開[RH01]として以下のように投影します。
\begin{eqnarray}
L_r(x, \omega_o) &\approx& \frac{\rho(x)}{\pi} \int_{{\mathcal H}^2} \left( \sum_{j} {\hat L}_j y_j(\omega_i) \right) \left( \sum_{j} {\hat V}’_j y_j(\omega_i) \right) d\omega_i \tag{15} \\
&=& \sum_{j} {\hat L}_j {\hat V}’_j \tag{16}
\end{eqnarray}
ここで、\({\hat L}_j\),\({\hat V}’_j\)はそれぞれ\(L(\omega_i\),\(V'(x, \omega_i)\)のSH展開の\(j\)番目の項であり、\(V'(x, \omega_i)=V(x, \omega_i) \langle {\mathbf n}, \omega_i \rangle^{+}\)であり、\(y_j\)は\(j\)番目の球面調和基底関数です。
可視性\(V(x, \omega_i)\)は、AO項\({\mathcal A}\)の関数として定義された開口角\(\alpha_v\)を持つベント法線\({\mathbf b}\)を中心とした円錐[Lan02]で近似できると仮定すると、可視性と内積の両方を帯域調和関数[Slo08]に投影することができ、実行時に効率よく計算することができます。これにより、式(14)を\(L(\omega_i)\)の展開と\(V'(x, \omega_i)\)の間の単純な内積として計算することができます。
Zonal Harmonics
帯域調和関数 [Slo08] は、軸を中心に回転対称性を持つ関数の球面調和関数への投影です。それらは,展開の中心係数の非ゼロの情報のみを含みます(すなわち,\(m = 0\) の場合の \(y_l^m\))。重要な利点は、実行時に次の新しい方向\(\omega_i\)に効率的に回転させることができることです。
\begin{eqnarray}
f_l^m = \sqrt{ \frac{4\pi}{2l + 1}} z_l y_l^m (\omega_i) \tag{17}
\end{eqnarray}
ここで、\(f_l^m\)は回転した球面調和関数の係数、\(z_l\)はレベル\(l\)の帯域調和関数係数,\(y_l^m(\omega_i)\)は方向\(\omega_i\)の球面調和関数基底です。
Computing the bend normal b
ここでは、コサインで重み付けされたラジオメトリック形式を用いて、次のように\({\mathbf b}\)を計算しています。
\begin{eqnarray}
{\mathbf b} = \int_{{\mathcal H}^2} \omega_i V(x, \omega_i) \langle {\mathbf n}, \omega_i \rangle^{+} d \omega_i \tag{18}
\end{eqnarray}
式(18)は、式(6)と同様のアプローチで、地平線ベースの近似式に従って次のように計算します。
\begin{eqnarray}
{\mathbf b} = \int_{0}^{\pi} \int_{\theta_1(\phi)}^{\theta_2(\phi)} \omega_i (\theta, \phi) \cos(\theta – \gamma)^{+} | \sin(\theta) | d\theta d\phi \tag{19}
\end{eqnarray}
\(\omega_i(\theta, \phi)\)は極座標\((\theta, \phi)\)で定義された方向とします。回転角\(\phi\)で定義された垂直方向のスライスを積分しますが、\(\theta\)に対する内積分は、\(\mathbf b\)の各成分に対して次のように解析的に解くことができます。
\begin{eqnarray}
{\mathbf b}_x &=& \cos(\phi) \int_{\theta_1(\phi)}^{\theta_2(\phi)} \sin(\theta)\cos(\theta – \gamma)^{+} | \sin(\theta) | d\theta = \cos(\phi) {\hat v}_{xy} (\phi) \\
{\mathbf b}_y &=& \sin(\phi) \int_{\theta_1(\phi)}^{\theta_2(\phi)} \sin(\theta)\cos(\theta – \gamma)^{+} | \sin(\theta) | d\theta = \sin(\phi) {\hat v}_{xy} (\phi) \\
{\mathbf b}_z &=& \int_{\theta_1(\phi)}^{\theta_2(\phi)} \cos(\theta) \cos(\theta – \gamma)^{+} | \sin(\theta) | d\theta \\
&=& \frac{1}{12} (- \cos(3 \theta_1(\phi) – \gamma) – \cos(3 \theta_2(\phi) – \gamma) + 8 \cos(\gamma) – 3(\cos(\theta_1(\phi) + \gamma) + \cos(\theta_2 (\phi) + \gamma))) \tag{20} \\
\end{eqnarray}
ここで,\({\hat v}_{xy}(\phi)\)は解析的に解くことができ,次のようになります。
\begin{eqnarray}
{\hat v}_{xy}(\phi) = & \frac{1}{12} & ( 6 \sin(\theta_1(\phi) – \gamma) – \sin(3\theta_1(\phi) – \gamma) \\
&+& 6\sin(\theta_2(\phi) – \gamma) – \sin(3\theta_2(\phi) – \gamma) + 16 \sin(\gamma) \\
&-& 3 (\sin(\theta_1(\phi) + \gamma) + \sin(\theta_2(\phi) + \gamma))) \tag{21}
\end{eqnarray}
なお、\({\mathbf b}\)は計算した後に正規化する必要があります。式(20)は、アンビエントオクルージョン項\({\mathcal A}\)と同時に計算します。これは、セクション4で説明したアプローチと実装、およびアルゴリズム2で詳細に説明しています。
Computing \(V'(x, \omega_i)\)
\(V'(x, \omega_i)\)の球面調和関数展開を効率的に計算するために、帯域調和関数の速度を利用します。このため、\(V(x, \omega_i)\)と\(\langle {\mathbf n}, \omega_i \rangle^+\)は特定の軸に対して半径方向に対称となります。特に、\(V(x, \omega_i)\)を近似する可視円錐は、ベント法線に関して対称であり[Lan02]、内積は\(x\)における法線に関して対称となります。
可視円錐は、ベント法線とアンビエントオクルージョン項を計算することにより、ランタイムで計算します。これらの2つの項により、ベント法線を中心とした視錐台を、視錐台から得られる開口角で計算することができます(詳細は付録Aを参照)。
\begin{eqnarray}
\alpha_v(x) = {\rm arccos}( \sqrt{1 – {\mathcal A}(x)} ) \tag{22}
\end{eqnarray}
そして、効率化のために、幾何学的な法線ではなく、ベント法線を基準にして内積を計算すると、\(V'(x, \omega_i)\)の帯域調和関数展開を次のように計算することができます。
\begin{eqnarray}
z_0 &=& \frac{\sqrt{\pi}}{2} \sin(\alpha_v(x))^2 \\
z_1 &=& \frac{\sqrt{3 \pi}}{3} ( 1 – \cos(\alpha_v(x))^3) \\
z_2 &=& \frac{\sqrt{5 \pi}}{16} \sin(\alpha_v(x))^2 (2 + 6 \cos(\alpha_v(x))^2) \tag{23}
\end{eqnarray}
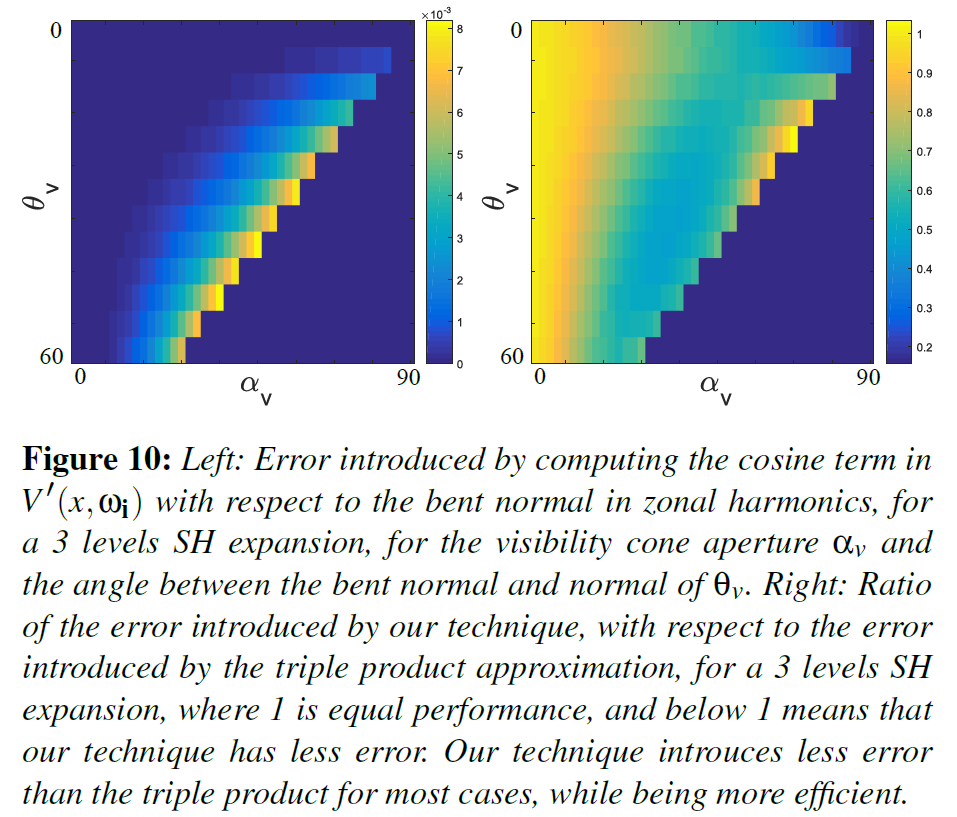
ここでは、最初の3つの係数のみが表示されます。この定式化は、余弦項を計算するのに、\(x\)での法線ではなく、ベント法線を使用するため、誤差が生じます。しかし、両者の間の発散はあまり大きくないことが確認されました(図10、左参照)。さらに、\(V(x, \omega_i)\)のSH投影と余弦項を掛け合わせる代わりに、\(V'(x, \omega_i)\)を計算することで、実用的な低次のSH展開に対して、より正確な近似値が得られます。余弦項はステップ関数\(V(x, \omega_i)\)を平滑化し、SHを用いてよりよく近似することができます(図10右参照)。
5.1. Results
ディレクショナルオクルージョンに対する我々の手法を、標準的な非方向性AO近似、ベント法線近似[Lan02]、および3重積近似[Syn06]と比較します。前者2つは事前にフィルタリングされた環境マップをフェッチすることで計算されますが、3重積と我々のディレクショナルGTAOはプローブの3レベルのSH展開(SH9)を使用します。図11は、異なるプローブについてこのような比較を行った結果を、周波数の増加とともに示したものです。標準的なAO近似はすぐに光の方向性を捉えることができず、安価なベント法線近似は3重積と同様の性能を発揮します。我々のディレクショナルGTAOは、定性的にも定量的にもすべてのシナリオで最高の性能を発揮します(MRSE、図12参照)。
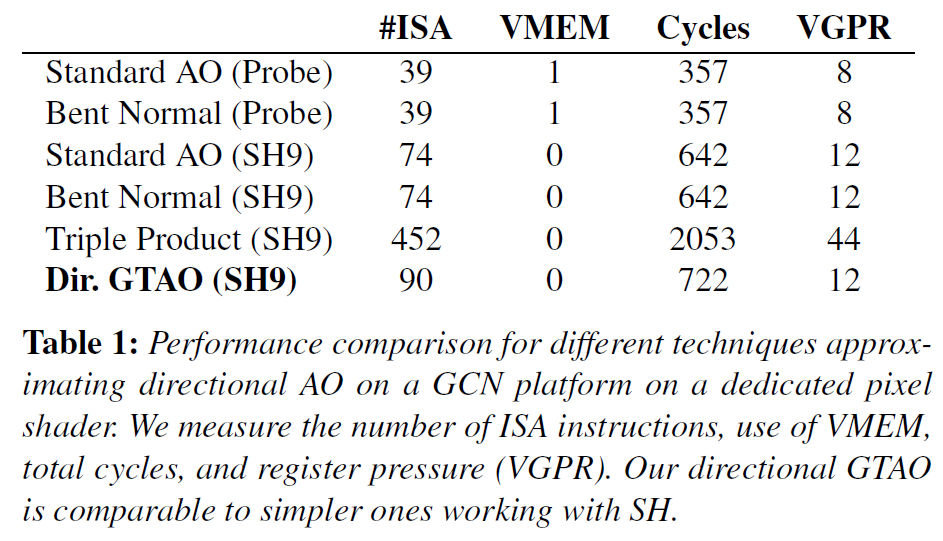
コスト面では、GCNプラットフォーム上で、オクルージョンコードのみを実行する専用ピクセルシェーダの最終的なISA命令を測定することで、性能を評価しました。ベント法線はピクセルシェーダの入力として与えられますが、実際にはGTAOのスクリーン空間でのアプローチ、またはオフラインでのベイクのいずれかから得られます。その結果を表1に示します。意外と知られていないのですが、無指向性AOとプレフィルターされたプローブでのベント法線近似が最も安価なオプションです。SH展開を用いてプローブをモデリングすると、コストはほぼ2倍になります。私たちの手法は、これらのシンプルな手法と同等のコストでありながら、誤差が大幅に少なくなります。なお、これらの手法の実際のコストは、分離時に消費するサイクルに直接比例するわけではなく、どのシェーダ(どこ)に配置されているかにもよりますが、多くの場合、コストは他の演算によって隠されてしまいます。興味深いのは、ベント法線近似が低い誤差をもたらすことです。これは、プレフィルターされた環境マップを使用する場合、この手法が選択される可能性があることを示唆しています。しかし、SH9を使ってライトプローブをエンコードする場合、我々の手法は、より単純な手法に比べて最小限のオーバーヘッドしかもたらさず、一方でエラーを大幅に減少させることができます。
6. Specular Occlusion
ここでは、古典的なLambertianベースのアンビエントオクルージョンを一般化し、スペキュラーベースのアンビエントオクルージョンを提案します。近接場のオクルージョンが遠方の照明を調整する照明モデルを開発し、任意のBRDFモデル(マイクロファセットなど)をサポートします。さらに、一様なドーム照明の場合には、本モデルはグランドトゥルースな結果をもたらします。
ここでは、すべての光が無限に遠い照明環境(ライトプローブ)からの指標であると仮定して、式(1)を次のように表します。
\begin{eqnarray}
L_r(x, \omega_o) = \int_{{\mathcal H}^2} V(x, \omega_i) L(x, \omega_i) f_r(x, \omega_i, \omega_o) \langle {\mathbf n}, \omega_i \rangle^{+} d \omega_i \tag{24}
\end{eqnarray}
この積分を数値積分で計算することは、リアルタイムのアプリケーションではコストがかかりすぎます。式(24)は、式(14)を任意のBRDFに一般化したものであり、セクション5と同様の手順で計算することができます。しかし、全周波数のBRDFに対応するためには、SH展開の係数が多数必要となり、性能が大幅に低下します。現在の最新技術では、一様な完全可視性(\(\forall \omega_i | V(x, \omega_i) = 1\))を仮定し、次のような分割積分近似[Laz13, Kar13]を用いています。
\begin{eqnarray}
L_r(x, \omega_o) \approx {\mathcal L}(x) \cdot {\mathcal F}(x, \omega_o) \\
{\mathcal L}(x) = \frac{1}{C_L} \int_{{\mathcal H}^2} \overbrace{ V(x, \omega_i) }^{=1} L(x, \omega_i) D(x, \omega_h) \langle {\mathbf n}, \omega_i \rangle^{+} d \omega_i \\
{\mathcal F}(x, \omega_o) = \int_{{\mathcal H}^2} f_r(x, \omega_i, \omega_o) \langle {\mathbf n}, \omega_i \rangle^{+} d \omega_i \tag{25}
\end{eqnarray}
ここで,\(D(x, \omega_h\))はサーフェイスの正規分布関数[TS67]で,\(\omega_h\)はハーフベクトル,\(C_L = \int_{{\mathcal H}^2} D(x, \omega_h) \langle {\mathbf n}, \omega_i \rangle^+ d\omega_i\)は\(L(x, \omega_i) = 1\)のときに常に\([0, 1]\)の範囲にあることを保証するために,最初の積分に必要な正規化係数です。直感的に言えば、式(25)の2行目は、均一光の下でのピクセルにおける完全なマイクロファセットBRDFであり、これは事前に計算されたルックアップテーブル(一般的にはenvironment lutと呼ばれる)に保存することができます。一方、最初の積分は、遠方の環境光\(L(x, \omega_i)\)と、マイクロファセットのNDFを近似する円対称のカーネルとの畳み込みです。第一積分は、遠方の照明(キューブマップなど)と異なるサーフェイスラフネスからのローブを畳み込むことで事前に計算することができ、光沢のあるマテリアルのレンダリングに非常に有効です。しかし、ほとんどの近似法はオクルージョンを無視するか、ヒューリスティックに近似しています。
鏡面照明のオクルージョンを考慮するために、式(25)の分割積分近似に似たアプローチを選択します。\(x\)に到達する照明の量を調整するために、可視性の項を第1積分から定数として分離します。これにより、式(25)を3つの積分の積、つまり3分割積分近似に変換することができます:
\begin{eqnarray}
L_r(x, \omega_o) \approx {\mathcal S}(x, \omega_o) \cdot {\mathcal L}(x) \cdot {\mathcal F}(x, \omega_o) \tag{26}
\end{eqnarray}
ここで,\({\mathcal S}\)は可視性をモデル化する我々のスペキュラーオクルージョン項です。これは次のように計算されます
\begin{eqnarray}
{\mathcal S}(x, \omega_o) = \frac{1}{C_V} \int_{{\mathcal H}^2} V(x, \omega_i) f_r(x, \omega_i, \omega_o) \langle {\mathbf n}, \omega_i \rangle^{+} d \omega_i \tag{27}
\end{eqnarray}
正規化項\(C_V = \int_{{\mathcal H}^2} f_r(x, \omega_i, \omega_o) \langle {\mathbf n}, \omega_i \rangle^{+} d\omega_i \)はスペキュラーオクルージョンSが[0, 1]の範囲にあることを保証します。我々のスペキュラーオクルージョンの定義は、BRDFによって重み付けされているため、方向に依存しています。この重みは、一様な照明のグランドトゥルースと一致するように、式(26)で慎重に選択されました。正規化係数\(C_V\)は、後者の積分値\({\mathcal F}\)と同じであるため、式(26)に\({\mathcal S}\)を代入して\(L_r(x, \omega_o)\)を以下のように通分すると相殺されます。
\begin{eqnarray}
L_r(x, \omega_o) \approx {\mathcal L}(x) \cdot \int_{{\mathcal H}^2} V(x, \omega_i) f_r(x, \omega_i, \omega_o) \langle {\mathbf n}, \omega_i \rangle^{+} d \omega_i \tag{28}
\end{eqnarray}
この形式では、一様な遠方照明(\({\mathcal L}(x) = 1\))の場合、式(24)で表されるグランドトゥルースと正確に一致することを観察することができます。
図13は、式(26)における我々の近似値とレイトレースされたグランドトゥルースとの違いを示しています。一定のプローブの場合、我々のスペキュラーオクルージョンの定式化は式(1)を正確にモデル化しますが、環境プローブの場合は、特にスペキュラーマテリアルの場合、レンダリング方程式を忠実に近似する結果となります。次のセクションでは、非常に要求の高いアプリケーションのために式(27)を実用的に解くための手法について説明します。
7. GTSO: Ground Truth-based Specular Occlusion
スペキュラーオクルージョン\({\mathcal S}(x, \omega_o)\)を効率的に計算するための我々の重要なアイデアは、可視性とBRDFローブの両方の近似値をモデル化し、これらの2つの交点をスペキュラーオクルージョンとして計算することです。このように考えると、問題は、いかにして可視性とBRDFの両方をコンパクトに表現するか、そして、いかにして両者の交点を計算するか、という問題に還元されます。
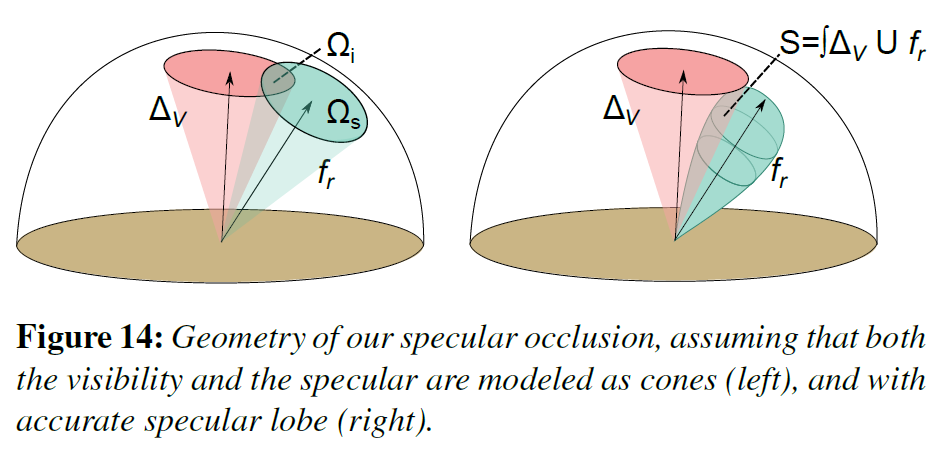
可視性については、第5節と同様の手順で、ベント法線\({\mathbf b}\)を中心とし、式(22)を用いてアンビエントオクルージョン項\({\mathcal A}(x)\)から得られる振幅角を持つ可視円錐を構築します。同様に,スペキュラーローブを反射方向\(\omega_r\)を中心とした円錐形としてモデル化し,\({\mathcal S}(x, \omega_o)\)を可視円錐とBRDF円錐の交点として計算することができます(このアプローチの詳細については,図14(左)および付録Cを参照)。
しかし、残念なことに、タイトにバウンドされているリアルタイムアプリケーションでは、これらの計算はまだ高価です。さらに、スペキュラーローブは、コーンではうまく表現できないことがわかりました。そこで、スペキュラーオクルージョン\({\mathcal S}\)を可視円錐\(\Delta_V\)と実際のBRDF\(F\)の積として事前に計算することで、より正確な近似を行うことにしました(図14右):
\begin{eqnarray}
{\mathcal S}(x, \omega_o) \approx \frac{1}{C_V} \int_{{\mathcal H}^2} \Delta_V (\alpha_v(x), \beta({\mathbf b}(x), \omega_r)) f_r(x, \omega_i, \omega_o) \langle {\mathbf n}, \omega_i \rangle^+ d \omega_i \tag{29}
\end{eqnarray}
\(\beta = {\rm arccos}(\langle {\mathbf b}, \omega_r \rangle)\)はベント法線と反射ベクトル\(\omega_r\)の間の角度、\(\Delta_V(\alpha, \beta)\)は\(\beta \leq \alpha\)場合は\(1\)、それ以外の場合は\(0\)を返すバイナリ関数です。ラフネス\(r\)でパラメータ化されたGGX NDF[WML07]を持つ等方的なマイクロファセットベースのBRDFを仮定し、反射方向\(\omega_o\)を法線\({\mathbf n}\)に対する単一角度\(\theta_o = {\rm arccos}(\langle {\mathbf n}, \omega_r \rangle)\)としてモデル化する。これらの仮定により、明確にするために空間依存性を省略すると、\({\mathcal S}\)を4次元関数として表現することができます。
\begin{eqnarray}
{\mathcal S}(\alpha_v, \beta, r, \theta_o) \approx \frac{1}{C_V} \int_{{\mathcal H}^2} \Delta_V (\alpha_v, \beta) f_r(\omega_i, \theta_o, r) \langle {\mathbf n}, \omega_i \rangle^{+} d \omega_i \tag{30}
\end{eqnarray}
この関数は、4次元の表としてコンパクトにベイクすることができます。法線入射時の反射率を0.04と仮定します。この関数は比較的滑らかであることから、4次元の\(32^4\) BC4の8ビットルックアップテーブルにエンコードすることができ、ランタイムに効率的にアクセスすることができます。今回は検討していませんが、この\({\mathcal S}\)のルックアップテーブルは、\({\mathcal F}(x, \omega_o)\)によく使用されるルックアップテーブルとマージすることができます。
7.1. Results
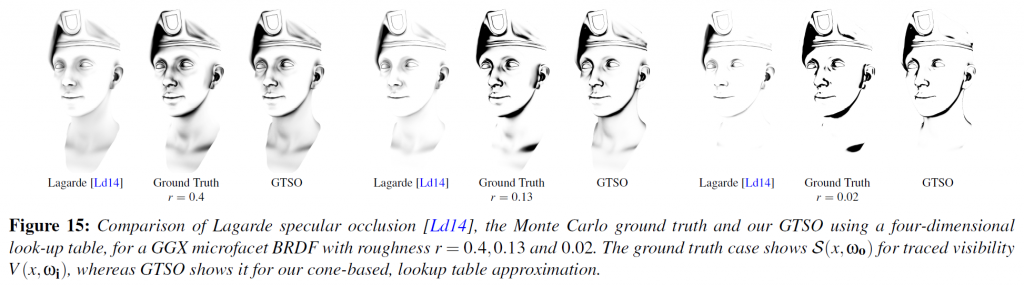
図15は,スペキュラーオクルージョンの計算に4次元ルックアップテーブルを用いたGTSOの実装結果を,グランドトゥルースやLagarde[Ld14]で述べられている経験に基づく手法と比較したものです。マイクロファセットのBRDFのラフネスパラメータがどのようなものであっても,導入された誤差は最小限に抑えられています。
8. Concolusion
本研究では、リアルタイムアンビエントオクルージョンへのいくつかの貢献を紹介しました。まず第一に、GTAOを発表しました。これは、非常に限られた予算内でモンテカルロ法によるグランドトゥルースと一致する、効率的なアンビエントオクルージョンの定式化です。GTAOは、空間的および時間的なコヒーレンスを積極的に利用することで、ピクセルあたり約100個のサンプルを効果的に統合しながら、1フレームあたり1個のサンプルしか計算しないという効率的な手法を実現しています。GTAOは、シェーディングポイントでのアンビエントオクルージョンに基づいてニアフィールドの拡散相互反射をシミュレートするという、シンプルで効果的な手法を備えています。この技術は、これらの相互反射が、局所的なアルベドとアンビエントオクルージョンの関数としてモデル化できるという観察に基づいています。さらに、このGTAOを方向性のある球面調和関数に基づいて一般化し、帯域調和関数を利用して、Lambertianオクルージョンに基づくSHの効率的なオンライン計算を実現しています。最後に、アンビエントオクルージョン演算子をスペキュラーサーフェイスで扱えるように一般化した「Ground-Truth Specular Occlusion」でスペキュラーオクルージョンの近似式を導入し、事前に計算されたルックアップテーブルに基づいて、均一および非均一なプローブベースの照明から鏡面反射を効率的に計算する手法を紹介しました。
図1に示すように、私たちの技術をすべて組み合わせることで、効率的なプローブベースの照明のための完全なソリューションとなり、レイトレースされたグランドトゥルースに一致させることができます。ニアフィールド間接照明、指向性GTAO、GTSOは、アンビエントオクルージョン(GTAO)の効率的な実装で得られた結果に基づいており、ビデオゲームのような非常に厳しいタイムバジェットを対象とした、非常に最適化された技術であり、現行のコンソールプラットフォームにも対応しています(図16)。
Acknowledgemenst
和訳省略。
Appendix A: Aperture Calculation
コーンの可視化方程式は次のように計算できます:
\begin{eqnarray}
{\mathcal A}(x) = \frac{1}{\pi} \int_{0}^{2\pi} \left( \int_{0}^{\alpha_v(x)} \cos(\theta) \sin(\theta) d\theta \right) d\phi = 1 – \cos(\alpha_v(x))^2 \tag{31}
\end{eqnarray}
ここで\(\alpha_v(x)\)を解くと、オクルージョンから開口部角度に変換する式が得られます:
\begin{eqnarray}
\alpha_v(x) = {\rm arccos}( \sqrt{1 – {\mathcal A}(x)} ) \tag{32}
\end{eqnarray}
Appendix B: Polynomial Fitting of Global Illumination
アンビエントオクルージョンとグローバルイルミネーションの間には関係があるという観察結果(図2)に基づき、\(x\)の周りのすべての点\(s\)におけるアルベド\(\rho(s)\)を\(\rho(x) = \rho(x)\)と仮定して、\(x\)におけるアルベドおよびアンビエントオクルージョンと、\(x\)で反射されたグローバルイルミネーションの間のマッピングを設計したいと思います。この機能を構築するために、さまざまな種類のオクルージョン状態を示すシーンの中で、異なるアルベド(\(\rho = [0.1, 0.2, 0.3, 0.4, 0.5, 0.7, 0.9]\))を持つ7つのシミュレーションを計算しました(図17参照)。アンビエントオクルージョンとマルチバウンス間接照明(ここでは、最大3バウンス)の両方を計算します。すべてのポイントの組み合わせを取り、アルベドごとに三次多項式を用いてこのマッピングをフィットさせ(図18(左))、シーンのアルベドごとに多項式係数のセットを生成した。そして、その係数が入力アルベドの関数として線形フィットでよく近似されることを確認しました(図18)。この結果をもとに、アルベド\(rho\)とアンビエントオクルージョン\({\mathcal A}\)の2次元的なマッピングを行うことができました:
\begin{eqnarray}
{\mathcal G}({\mathcal A}, \rho) &=& a(\rho) {\mathcal A}^3 – b(\rho) {\mathcal A}^2 + c(\rho) {\mathcal A} \\
a(\rho) &=& 2.0404 \rho – 0.3324, \\
b(\rho) &=& 4.7951 \rho – 0.6417, \\
c(\rho) &=& 2.7552 \rho + 0.6903 \tag{33}
\end{eqnarray}
Appendix C: Analytical Cone-to-Cone Specular Occlusion
スペキュラオクルージョンは、ビジビリティコーンとスペキュラコーンの交点\(\Omega_i\)と、スペキュラコーン\(\Omega_s\)の比として計算できます(図14左参照):
\begin{eqnarray}
{\mathcal S}(x, \omega_o) = \frac{\Omega_i (x, \omega_o)}{\Omega_s(x, \omega_o)} \tag{34}
\end{eqnarray}
次に、方向と開口部で定義されるビジブルコーンとスペキュラーコーン、およびそれらの交差する立体角\(\Omega_i\)を計算する必要があります。スペキュラーローブからコーンへのマッピングに関するこれまでの研究を活用するため、このセクションで説明する実験では、GGXの代わりにPhongを使用しています。
ビジビリティコーンについては、第6章で説明しました(式(22))。スペキュラコーンの場合、その方向は反射ベクトル\(\omega_r\)で定義されます。一方、開口部\(\alpha_s\)は、ラフネス\(r\)(Phong BRDFの場合はスペキュラー指数\(p\))によって定義されます。これには厳密な解がないため、Uludag[Ulu14]と同様のアプローチを採用し、Walterら[WMLT07]によるPhongインポータンスサンプリングルーチンを使用して、開口部とPhong指数\(p\)を関連付けることにしました:
\begin{eqnarray}
\alpha_s = {\rm arccos}( u^{\frac{1}{p+2}} ) \tag{35}
\end{eqnarray}
ここで、\(u\)は定数です。Uludagとは対照的に、コーンをローブにフィットさせて\(u\)を得るのではなく(\(u = 0.2444\))、得られたGTSOとモンテカルロのグランドトゥルースリファレンスの差を最小化し、\(u = 0.01\)を得ています。
両方のコーンがあれば、その交点の立体角\(\Omega_i\)を計算することができます。この交点は、コーンの開口部と、それぞれの方向(ベント法線\({\mathbf b}\)と反射方向\(\omega_r\))の間の角度の関数として、解析的に解かれます[OS07, Maz12]。