おはござ！Pocolです。

今日は，
[Jimenez 2016] Jorge Jimenez, Xian-Chun Wu, Angel Pescec, Adrian Jarabo，
“Practical Realtime Strategies for Accurate Indirect Occlusion”,
SIGGRAPH 2016 Courses: Physically Based Shading in Theory and Practice, https://blog.selfshadow.com/publications/s2016-shading-course/, 2016.

を読んでみることにします。いつもながら，誤字・誤訳があると思うので、ご指摘いただける場合は正しい翻訳例と共に指摘していただけるとありがたいです。

※図は，[Jimenez 2016]より引用。

Abstract

アンビエントオクルージョンは、ゲームやその他のリアルタイムアプリケーションで、グローバルな照明効果を近似させるためにユビキタスに使用されています。しかし、アンビエントオクルージョンの積分アルゴリズムには解析的な解が存在しないため、実際に使用される近似は、AO積分を正確に解けなくても、経験的に見栄えが良くなるように作られていることが多いです。本研究では、現在のゲーム機のハードウェア上で、0.5ミリ秒でグランドトゥルースの参照と一致するアンビエントオクルージョンの新しい定式化であるGTAOを紹介します。これは、アンビエントオクルージョン方程式の代替定式化と、時空間フィルタリングを用いて計算を分散させる効率的な実装を用いることで実現されています。さらに、アンビエントオクルージョンだけでは失われてしまう近接場のグローバルイルミネーションを考慮した新しい技術でGTAOを拡張しています。最後に、アンビエントオクルージョンと対称なスペキュラーオクルージョン技法GTSOを紹介し、プローブベースの照明から現実的な鏡面反射を計算できるようにします。我々の技法は効率的であり、レイトレースされたグランドトゥルースに近い結果を与え、最近のAAAゲーム機のタイトルに組み込みされています。

1　Introduction

グローバルイルミネーションは、フォトリアリスティックなレンダリングの基本となる重要な視覚的特徴であり、知覚されるシーンの照明の大部分は間接的な反射によるものです。残念ながら、一般的に計算に非常にコストがかかるため、現在のところ簡素な単純化なしにリアルタイムアプリケーションに含めることはできません。これらの近似から、アンビエントオクルージョン（AO）は、物体の形状の知覚（コントラスト）を向上させ、グローバルイルミネーションの最も重要な効果のいくつか、特にオクルーダーに近いソフトシャドウを捉えることができるため、最もポピュラーな手法の一つです。アンビエントオクルージョンは、他のグローバルイルミネーションアルゴリズムとの併用や、事前に計算された（ベイクされた）照度を使用する場合にも有用で、これらの効果を比較的低い空間分解能で計算（またはソート）する必要がある場合が多いため、ピクセル単位でアンビエントオクルージョンを計算することで間接照明の全体的な外観を向上させることができます。残念ながら、アンビエントオクルージョン積分を解くのは、特定のシナリオ（例：1080pのレンダリングを60fpsで行うなど）ではコストがかかるため、過去には十分なパフォーマンスを得るための近似法が開発されてきました。

アンビエントオクルージョンのための新しいスクリーンスペース技法であるGTAO(ground-truth ambient occlusion)を紹介します。この技法の主な目的は、最新のコンソールゲームのような要求の高いアプリケーションにも対応できるように、十分な高速性を実現しながらも、グラウンドトゥルースアンビエントオクルージョンを実現することにあります。我々の技術は、水平線ベースのアプローチをベースにしていますが、問題の別の定式化を使用しています。この定式化により、効果のコストを大幅に削減することができ、シーンがハイトフィールド（デプスバッファ）として表現されていると仮定した場合でも、アンビエントオクルージョン積分を正確に解くことができます。我々は、時間的再投影と空間フィルタリングを使用して、1フレームあたりわずか0.5ミリ秒でノイズのないアンビエントオクルージョン解を計算することにより、技法を効率的に実装しています（ソニー PlayStation 4で、1080pで動作するゲームの場合）。

この定式化に基づいて、アンビエントオクルージョンソリューションを拡張し、アンビエントオクルージョンのみを使用した場合には一般的に無視される照明効果のセットをモデル化しました。一方では、近接場のグローバルな照明を考慮して、非常に高速な補正係数を計算する近似手法を紹介します。この手法は、局所的なサーフェイスアルベドとアンビエントオクルージョンの項と、複数のバウンスを持つ近接場照明との間に関係があるという観測に基づいています。この観測結果を受けて、アンビエントオクルージョンのみで計算した場合に失われる局所的な照明を、効率的でシンプルかつ局所的に補正する手法を開発しました。

最後に、我々は、AOと対称的でありながら、任意のスペキュラーマテリアルに対して一般化された新しい手法、すなわち、グランドトゥルーススペキュラーオクルージョン（GTSO）を紹介します。我々はその定式化を開発し、ある点でのベント法線とアンビエントオクルージョンの関数としての可視性を近似することに基づいて、効率的な計算手法を提示します。GTSOを用いることで、サーフェイスのオクルージョンを考慮したプローブ照明からの鏡面反射を効率的に計算することが可能となります。

2　Background & Related Work

法線\(\mathbf n_{\mathbf x}\)を持つ点\(x\)から\(\omega_{\mathbf o}\)方向への反射放射輝度\(L_r(x, \omega_{\mathbf o})\)は、次のようにモデル化することができます。

\begin{eqnarray}
L_r(x, \omega_{\mathbf o}) = \int_{\mathcal H^2} L_i (x, \omega_{\mathbf i}), f_r(x, \omega_{\mathbf i}, \omega_{\mathbf o}) \langle {\mathbf n_{\mathbf x}}, \omega_{\mathbf i} \rangle^{+} d\omega_{\mathbf i} \tag{1}
\end{eqnarray}

ここで，\(\mathcal H^2\)は\(x\)で中心となる半球で，\(\mathbf n_{\mathbf x}\)をその軸として持ちます。\(L_i(x, \omega_{\mathbf i})\)は\(x\)における方向\(\omega_{\mathbf i}\)からの入射放射輝度で，\(f_r(x, \omega_{\mathbf i}, \omega_{\mathbf o})\)は\(x\)におけるBRDFで，\(\langle {\mathbf n_{\mathbf x}}, \omega_{\mathbf i} \rangle^{+}\)は再帰操作で，すべてのシーンでの反射（および放出）輝度に依存します。多くの研究がこの問題の解決に力を入れてきましたが、ゲームのような要求の高いシナリオでは、まだコストがかかりすぎて解決できません。ここでは、アンビエントオクルージョン技法に焦点を当て、Ritschelらの調査 [RDGK12]を参照して、この分野の概要を詳しく説明します。

アンビエントオクルージョン[ZIK98]は、次のような仮定を導入することによって、式(1)を近似します：
i) すべての光は、\(x\)の周りのジオメトリによって閉塞されている可能性があり，無限の均一な環境光から来ている；
ii) \(x\)の周りのすべてのサーフェイスは純粋に吸収している(すなわち、光を反射していない);
iii) \(x\)のサーフェイスは拡散している。
これにより、式(1)は次のように変換されます。

\begin{eqnarray}
L_r (x, \omega_{\mathbf o}) &=& L_i \frac{\rho(x)}{\pi} \int_{\mathcal H^2} V(x, \omega_{\mathbf i}) \langle {\mathbf n_{\mathbf x}}, \omega_{\mathbf i} \rangle^{+} d\omega_{\mathbf i} \\
&=& L_i \frac{\rho(x)}{\pi} {\mathcal A}(x) \tag{2}
\end{eqnarray}

ここで，\({\mathcal A}(x)\)は点\(x\)におけるアンビエントオクルージョン 項で，\(\frac{\rho(x)}{\pi}\)はアルベド\(\rho(x)\)を持つディフューズBRDFで，\(V(x, \omega_{\mathbf i})\)は\(x\)における方向\(\omega_{\mathbf i}\)上での可視項で，方向\(\omega_{\mathbf i}\)上でオクルダーが与えられた距離\(r\)よりも近ければ0を返し，そうでない場合は1を返します。以前の研究 [ZIK98, Mit07, BSD08]では、この可視性の項\(V(x, \omega_{\mathbf i})\)をオクルーダーまでの距離に対する減衰関数としてモデル化しており、\({\mathcal A}(x)\)をオブスキュランスと呼んでいることに注意してください。この減衰関数は、近接場相互反射を無視することによって生じる典型的なAOによる過暗化を回避するためのアドホックな解決策を作成するために使用されました; 代わりに、放射計測学的に正しいアンビエントオクルージョン項を維持しながら、この失われた光を追加するための新しい定式化を紹介します(5節)。本稿の残りの部分では、放射計測学的に正しい余弦加重法を用いていますが、付録Aでは、この代替法の下での手法を説明します。

Screen-Space Ambient Occlusion
アンビエントオクルージョン項\({\mathcal A}(x)\)は、シーン内のすべてのジオメトリの影響を受け、一般的にはレイトレーシング[ZIK98]によって計算されますが、インタラクティブなレンダリングに適したポイントベースのアプローチもあります[Bun05, REG+09]。しかし、これはリアルタイムアプリケーションにはまだコストがかかりすぎます。コストのかかる三次元の完全なシーン可視性計算を避けるために、Mittring [Mit07] は、カメラから見えるジオメトリのみがオクルーダーとして機能すると仮定して、すべての計算をスクリーン空間に移動させることを提案しました。これは，GPUのシーンのデプスマップを\(x\)周りの点の球体でサンプリングし，その点がデプスマップ内のジオメトリにオクルードされているかどうかを評価することによって達成されます．それ以来、スクリーン空間サンプリングの考え方にいくつかの改良が加えられ、サンプリング戦略の改良[LS10, SKUT+, HSEE15]やフィルタリングによるノイズの低減[MML12]などが行われてきました。

Horizon-Based Ambient Occlusion
Bavoilら[BSD08]は、光が得られる最大地平角に基づいて非閉塞領域を計算することを提案しています。彼らは積分領域をサーフェイスに対して\(\phi\)の正接によってパラメータ化された方向の集合に変換し、それらのそれぞれについて、式(2)を次のように変換して、非遮蔽立体角の総和を計算しました：

\begin{eqnarray}
{\mathcal A}(x) \approx {\hat {\mathcal A}}(x) = \frac{1}{\pi} \int_0^{\pi} \int_{-\pi/2}^{\pi/2} V(\phi, \theta) | \sin(\theta) | d\theta d\phi \tag{3}
\end{eqnarray}

ここで，\(1/\pi\)項は1にするための正規化項です(すなわち，\({\mathcal A}(x) \in [0, 1]\))。ここでは、実際のアンビエントオクルージョン\({\mathcal A}(x)\)と近似されたスクリーン空間項\({\hat {\mathcal A}}(x)\)を区別していることに注意してください。

Alchemy Ambient Obscurance [MOBH11, ML12]は後にスクリーン空間アプローチのロバスト性を向上させ、使用されるサンプリング手順の効率を向上させました。HBAOは比較的効率的ではありますが、最大地平線を求める際に深度マップから多くのサンプルをピクセルごとに収集する必要があるため、コストがかかります。Timonen [Tim13a]は、画像全体に沿ってラインスイープを実行することでこれを改善し、画像内の多くのピクセルに沿ってサンプリングを償却することで、一定時間内に与えられた方向の最大水平角を見つけることを可能にしています。我々の研究と密接に関連するところでは、同じ著者[Tim13b]は、ラインスキャンとデプスマップのフィルタリングを行うことで、低コストでグランドトゥルースの解と一致するアンビエントオクルージョンの新しい推定器を提案しました。

本研究では、アドホックな減衰関数を必要としない、効率的なアンビエントオクルージョンの定式化を提案することで、これらの研究を改善し、計算時間を短縮し、非常に効率的な解析積分を可能にします。アドホックな減衰関数を回避するための核となるのは、近接場オクルーダーからの間接照明を含む効率的な近似法です。さらに、これらの研究はすべて拡散面を前提としており、その代わりに、我々はアンビエントオクルージョンの概念を非Lambertian面にまで一般化し、スペキュラーオクルージョンのための手法を導入します。

3　Overview

この研究では、主に2つの目的があります。一方では、要求の厳しいリアルタイムアプリケーションにも対応できるような効率的なアンビエントオクルージョン技術を開発することを目指しています。もう一方では、効率的に近似できる大域的な照明効果の量を増やしたいと考えています。最初の目標は、入力データ、パス数、命令数の面で厳しい制限を課しています。これらの制限に縛られながらも、深度バッファとサーフェイス法線のみを入力とし、他のグローバルイルミネーションのソース（具体的にはベークドイラディアンス）を共存させ、強化することができる、スクリーン空間で動作する技術を開発しました。2つ目の目標を達成するために、従来のアンビエントオクルージョンの仮定をいくつか緩和しています。特に、白色（またはモノクロ）ドーム照明の仮定を維持する一方で、純粋にランベルト面の仮定を緩和し、近接場オクルーダーの拡散的な相互反射を含めます。

これまでの制限を取り除いて、式(2)を次のように変換することができます。

\begin{eqnarray}
L_r(x, \omega_{\mathbf o}) = (1 – F(\omega_{\mathbf o}))L_i \frac{\rho(x)}{\pi} {\mathcal G}({\mathcal A}(x)) + F(\omega_{\mathbf o}) {\mathcal L}(x, \omega_{\mathbf o}) {\mathcal S}(x) \tag{4}
\end{eqnarray}

ここで，\(F\)はフレネルリフレクタンス項で，\({\mathcal A}(x)\)は我々のアンビエントオクルージョン項であり（4節)，それはグランドトゥルースの結果に合致し，グランドトゥルースアンビエントオクルージョン(GTAO) と呼びます。\({\mathcal G}(x)\)はアンビエントオクルージョン項に基づく関数で，ディフューズ近接場間接照明を導入します（5節)，そして\({\mathcal S}(x)\)はスペキュラーオクルージョン項で(6節)，BRDF\({\mathcal L}\)で事前畳み込みされたもので乗算されています。以下では，これらの項それぞれについての定式を記述します。

4　GTAO:Ground-Truth Ambient Occlusion

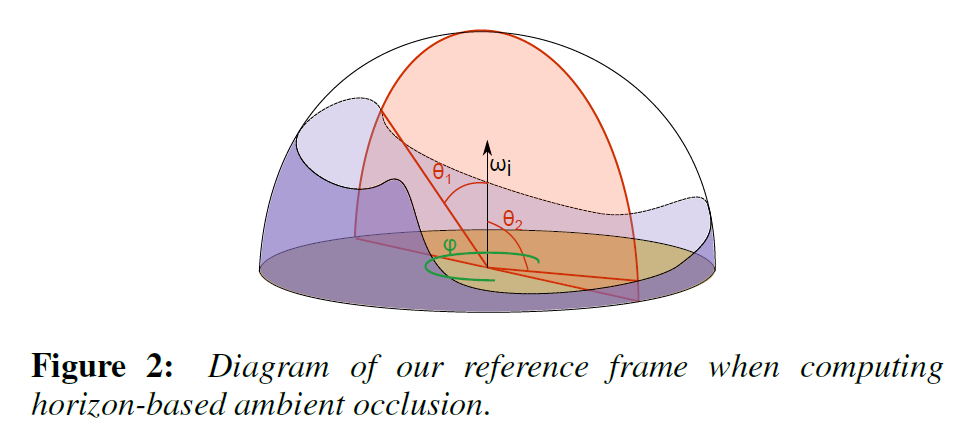
我々のアンビエントオクルージョンの定式化は、Bavoilら[BSD08]の水平線ベースのアプローチを踏襲していますが、品質を犠牲にすることなく効率的な計算を可能にする一連の重要な違いを提示しています。まず最初に、水平線が計算される参照フレーム、つまり積分領域を再構築します。Timonen [Tim13a]に倣い、視野ベクトル\(\omega_{\mathbf o}\)を基準にして水平角を計算します（図2参照）。これは、水平角が\(x\)の周りの全球で探索され、球面積分軸が \(\omega_{\mathbf o}\)に設定されていることを意味します。実際には、これにより定式化を単純化することができ、後述するように必要な超越関数の数を減らすことができます。

※図は[Jimenez 2016]より引用。

第二の主な違いは、Bavoilの研究とは対照的に、我々の可視性の項\(V(\phi, \theta)\)は、オクルーダー距離の関数（アンビエントオブスキュランス）としての連続的な減衰の代わりに、単なるバイナリ関数であるということです。このようにAOを定式化することで、式(3)の内側の積分を、単に2つの最大地平角\(\theta_1(\phi)\)と\(\theta_2(\phi)\)の間の円弧の積分として計算することができます。\(\omega_{\mathbf o}\)の周りの積分を定式化し、2値可視化項を使用すると、式(3)は次のように変換されます：

\begin{eqnarray}
{\mathcal{\hat A}}(x) = \frac{1}{\pi} \int_0^{\pi} \underbrace{\int_{\theta_1(\phi)}^{\theta_2(\phi)} \cos(\theta – \gamma)^{+} | \sin(\theta)| d\theta}_{\hat a} d\phi \tag{5}
\end{eqnarray}

ここで，\(\gamma\)は法線\({\mathbf n}_{\mathbf x}\)と視線ベクトル\(\omega_{\mathbf o}\)の間の角で，\(\cos(\theta)^{+} = \max(\cos(\theta), 0)\)です。この定式化は、実際には非常に重要で、内側の積分\({\hat a}\)を解析的に計算することができます。これは、ランダムな\(\phi\)を用いたモンテカルロ積分を用いて、一番外側の積分だけを数値的に計算する必要があることを意味しています。以下では、水平角と内側の積分\({\hat a}\)の計算方法を詳しく説明します。

最大水平角の計算
式(5)の解法のコアは、回転角\(\phi\)でパラメータ化された画像平面\({\hat {\mathbf t}}(\phi)\)の方向に対する最大水平角\(\theta_1(\phi)\)と\(\theta_2(\phi)\)を求めることです。これを行うために、スクリーンスペースの方向\({\hat {\mathbf t}}(\phi)\)、\({\hat {\mathbf t}}(\phi)\)におけるピクセル\({\hat x}\)（点\(x\)の投影画素）の画素内の\(n \times n\)近傍を探索して各角度を求め、視野ベクトル\(\omega_o\)に対する最大地平角を次のように求めます：

\begin{eqnarray}
\theta_1 (\phi) = \arccos \left( \max_{s < n/2} \langle \omega_s, \omega_o \rangle^{+} \right) \tag{6} \end{eqnarray} ここで，\(\omega_s = \frac{s - x}{|| s - x ||}\)で，\(s\)は画像平面\({\hat s} = {\hat x} + {\hat {\mathbf t}}(\phi) \cdot s\)上のピクセルのワールド空間上の射影です。角\(\theta_2\)は\({\hat s} = {\hat x} - {\hat {\mathbf t}}(\phi) \cdot s\)で類似的に計算されます。これは、\({\hat {\mathcal A}}(x)\) をビューに依存しないようにするために必要であり、また、GPU キャッシュを無駄に浪費してしまうようなニア平面に近いオブジェクトの大きすぎる収集半径を避けるために、ピクセル単位の最大半径にクランプされています。 我々が関心を持っているのは放射計測学的な立体角だけなので、以前の研究のように他の量(例えば最大距離)ではなく、最大角度だけを追跡する必要があります。これにより、AMD GCNハードウェア[AMD12]（我々のターゲットプラットフォーム）では、1/4速の命令（rsqrt）だけで探索ループを計算することができます。この定式化を使用すると、シェーダは完全にメモリに縛られるようになります。

内側部分の積分の解法
Timonen [Tim13a]は、実行時にアクセスされるルックアップテーブル中の事前計算した結果により、この積分（減衰関数を含む）を解きました。しかし、我々の定式化の重要な特性は、計算された水平角\(\theta_1\)と\(\theta_2\)が与えられると、式(5)の内側部分の積分\({\hat a}\)を解析的に次のように解くことができるということです。

\begin{eqnarray}
{\hat a} &=& \frac{1}{4} (- \cos(2\theta_1 – \gamma) + \cos(\gamma) + 2 \theta_1 \sin(\gamma)) \\
&+& \frac{1}{4} (- \cos(2\theta_2 – \gamma) + \cos(\gamma) + 2 \theta_2 \sin(\gamma)). \tag{7}
\end{eqnarray}

この定式化は、法線\({\mathbf n}_{\mathbf x}\)が \({\hat {\mathbf t}}(\phi)\) と \(\omega_{\mathbf o}\) で定義された平面 \(P\) 内にあることを必要とすることに注意することが重要ですが、これは一般的には保持されません。Timonen [Tim13a]に倣って、我々は、正規化された投影法線\( \frac{\bar {\mathbf n}_{\mathbf x}}{|| {\bar {\mathbf n}_{\mathbf x}} ||} \in P\)と\(\omega_{\mathbf o}\)との間の角度として角度\(\gamma\)を\(\gamma = \arccos( \langle \frac{\bar {\mathbf n}_{\mathbf x}}{|| {\bar {\mathbf n}_{\mathbf x}} ||}, \omega_{\mathbf o} \rangle)\)として計算します。このとき，\({\bar {\mathbf n}_{\mathbf x}}\) のノルムを乗算することで内積の変化を補正し、式(5)の状態のままにします：

\begin{eqnarray}
{\hat {\mathcal A}}(x) = \frac{1}{\pi} \int_0^{\pi} || {\bar {\mathbf n}_{\mathbf x}} || {\hat a}(\phi) d\phi \tag{8}
\end{eqnarray}

我々の解析解は、特に高速なacosとsqrt命令を使用することで、非常に高速であることがわかりました[Dro14]。超越的な関数に関しては、最適化の後、2つの cos と 1つの sin に加えて、積分領域を設定するための 3 つの追加の acos 関数を加えたコードが得られました。これによりシェーダのメモリが制限されるため、必要とされる ALU 演算は性能の面でほとんど違いがありません。

4.1　Implementation Details

我々の技法はメモリに縛られているので、メモリへのアクセス数がターゲットプラットフォームの最終的な性能を決定します。60 フレーム/秒で動作するゲームにこの技法を組み込むことを目標としているため、計算に要する時間は約0.5ミリ秒しかなく、最適化の実装が必須となります。一方で、半解像度でアンビエントオクルージョンを計算し、後にフル解像度にアップサンプリングしています。さらに、性能を損なうことなく可能な限り多くのサンプルを計算するために、オクルージョン積分を空間と時間の両方に分散させています。さらに、指数関数的なアキュムレーションバッファを交互に使用することで、時間的なコヒーレンシーを積極的に利用しています。これにより、1ピクセルあたり4×46=96の有効なサンプリング方向が得られます。図3は、最終的な再構成における空間的・時間的ギャザリングの効果を示しています。

※図は[Jimenez 2016]より引用。

アンビエントオブスキュランス技法とは対照的に、我々の定式化では減衰関数を考慮していないため、計算されたオクルージョンが突然不連続になる可能性があります。アーティファクトを最小化するために、保守的な減衰戦略を採用しています。これは、遠距離オクルージョンは一般的に遠距離オクルージョンが間接照明と一緒に組み込まれているため、遠距離オクルージョンの場合はゼロに減衰させるという考え方です。私たちの減衰関数は、与えられた十分に大きな距離から最大探索半径まで、1から0までの線形ブレンドです。

最後に、深度バッファから厚さを推測することはできないので、薄い形状は現実的ではないほどキャストが多くなりすぎる傾向があります。これは、例えばデプスピーリングで解決できますが、我々のケースでは非現実的です。その代わりに、オブジェクトの厚さがスクリーン空間のサイズに近いという仮定に基づいた保守的なヒューリスティックを導入します。このヒューリスティックは地平線探索(式(6))の修正を導入し、探索の各反復\(s \in [1, n/2]\)に対して地平線\(\theta\)を次のように更新します:

\begin{eqnarray}
\theta = \begin{cases}
\max(\theta_s, \theta) & {\rm if} \quad \cos(\theta_s) \geq \cos(\theta_{s-1}) \\
{\rm{blend}}(\theta_{s-1}, \theta_s) & {\rm if} \quad \cos(\theta_s) \lt \cos(\theta_{s-1})\
\end{cases} \tag{9}
\end{eqnarray}

ここで，\(\rm blend\)は指数的な移動平均に基づくブレンド操作で，\(\theta_o = 0\)です。また、このヒューリスティックは、我々のアプリケーションではよくある単純なコーナー（壁など）のオクルージョン結果を偏らせないという特性を持っています。図4は、このヒューリスティックの効果を示しています。

※図は[Jimenez 2016]より引用。

5　Approximated Occlusion-Based Indirect Illumination

アンビエントオクルージョンの大前提の1つは、遮光点\(x\)に到達する唯一の光は、均一な照明環境から直接来るということです。これは、複数の表面反射によって入射した光が完全に失われることを意味します。このエネルギー損失は、エッジやコーナーの過暗化につながります。これらのエリアは、アンビエントオクルージョンの影響が最も大きいエリアですが、近接場相互反射がより支配的なエリアでもあります。アンビエントオクルージョンに関するこれまでの研究（[MML12, Tim13b]など）では、この光の一部を取り戻すために、アドホックな減衰関数を使用しています。しかし、これらは物理的な意味を持たないその場しのぎの解決策です。

この問題を解決するために、我々は、効率的でコストのかかる完全なグローバルイルミネーションの解法の計算を回避しつつ、アルベドが一定の領域にある点の近接場間接照明が周囲のオクルージョン値と強い関係を示すという重要な観測を行いました。これは、変化するアルベドに対しては一般的には当てはまりませんが、我々は、近距離間接照明を\(x\)に反射する近くのオクルーダーを最も気にしており、これは、類似のアルベドの仮定が起こる可能性が高くなります。さらに、アンビエントオクルージョン近傍でのアルベドがほぼ一定であるという仮定は、実行時のパフォーマンス要件の制限を維持するために、各オクルーダーの表面でアルベドをサンプリングしたくなかったという事実によって強いられています。

この重要な観測に基づいて、\(x\)の周りのすべての点\(s\)でのアルベド\(\rho(s)\)が\(\rho(s) = \rho(x)\)であると仮定して、我々は、\(x\)でのアルベドとアンビエントオクルージョンと\(x\)での反射グローバル照明との間のマッピングを設計したいと考えています。この関数\({\mathcal G}({\mathcal A}(x), \rho(x))\)を構築するために、様々なタイプのオクルージョン条件を示すシーンのセットで、異なるアルベド(\(\rho = [0.1, 0.2, 0.3, 0.4, 0.5, 0.7, 0.9]\))で7つのシミュレーションを計算します（図5を参照）。

※図は[Jimenez 2016]より引用。

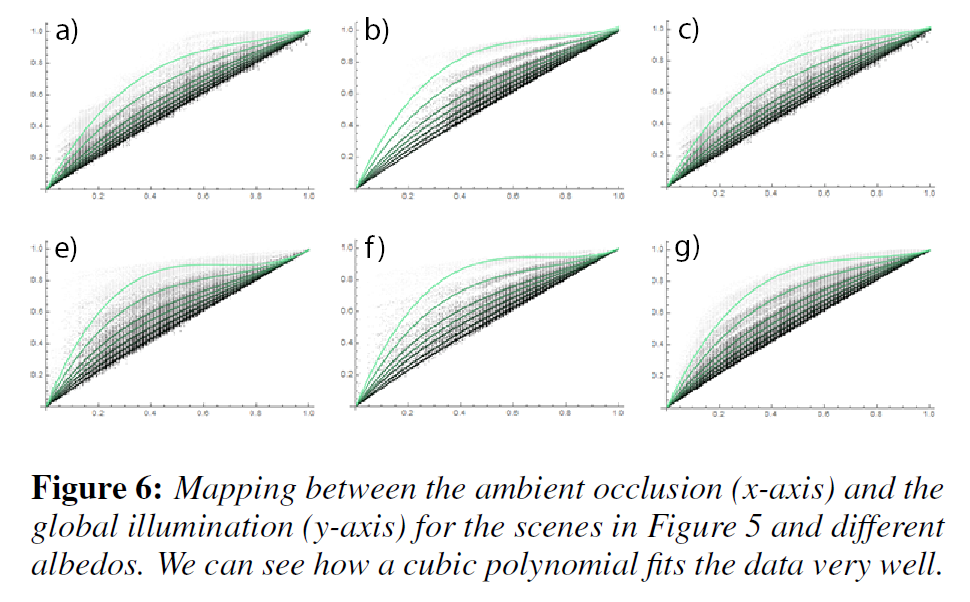
我々は、アンビエントオクルージョンとマルチバウンス間接照明（我々の場合、最大3つのバウンス）の両方を計算します。図6は、各アルベドについて、また、図5の各シーンについて、\({\mathcal A}(x)\)と\({\mathcal G}(x)\)の間のマッピングを示しています。

※図は[Jimenez 2016]より引用。

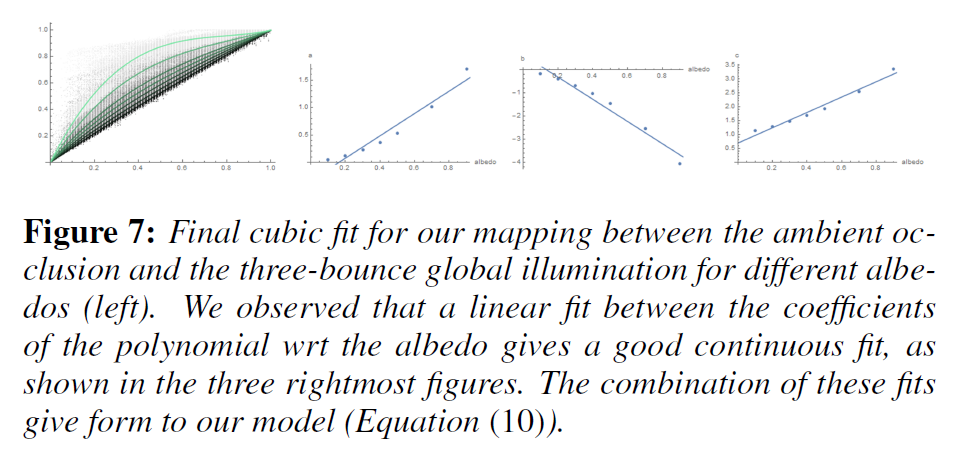
すべての点の組み合わせを取ることにより、各アルベドについて三次多項式を使用してこのマッピングを適合させ(図7(左))、各シーンのアルベドについての多項式係数のセットを生成します。そして、これらの係数が入力アルベドの関数として線形フィットによってよく近似されていることを観察しました（図7）。

※図は，[Jimenez 2016]より引用。

この最後の観察により、アルベド\(\rho\)と周囲のオクルージョン\({\mathcal A}\)との間の二次元マッピングを構築することができます。

\begin{eqnarray}
{\mathcal G}({\mathcal A}, \rho) &=& a (\rho){\mathcal A}^3 – b(\rho){\mathcal A}^2 + c(\rho){\mathcal A} \\
a(\rho) &=& 2.0404 \rho – 0.3324, \\
b(\rho) &=& 4.7951 \rho – 0.6417, \\
c(\rho) &=& 2.7552 \rho + 0.6903. \tag{10}
\end{eqnarray}

このフィッティングベースの近似は、いくつかの要件を満たしています：一方では、グローバルな照明による欠落したエネルギーを再統合するために、任意のアンビエントオクルージョンフレームワークにもシームレスに組み込みすることができます。一方では、すでに計算された情報に基づいているため、高額な光輸送シミュレーションを必要とせず、視覚的にも説得力のある結果を得ることができるため、非常に効率的です。このことから、我々がターゲットとしているリアルタイムアプリケーションに非常に適しています。

6　GTSO: Specular Occlusion

ここでは、Lambertianをベースとしたアンビエントオクルージョンのある対極にあるグロッシーなスペキュラーオクルージョンの解決策を紹介します。本論文では、このように、任意のBRDFをサポートしながら、近接場オクルージョンがプローブベースのライティングを変調するような照明モデルを開発したいと考えています。さらに、プローブ照明が一定の場合には、AOと同様の結果が得られるモデルを開発したいと考えています。

4節と同様に、次のように式(1)を表現するためにすべての光が無限遠の照明環境（ライトプローブ）からの光であると仮定します：

\begin{eqnarray}
L_r (x, \omega_o) = \int_{\mathcal H^2} V(x, \omega_{\mathbf i}) L_i (x, \omega_{\mathbf i}) f_r (x, \omega_{\mathbf i}, \omega_{\mathbf o}) \langle {\mathbf n_{\mathbf x}}, \omega_{\mathbf i} \rangle^{+} d\omega_{\mathbf i} \tag{11}
\end{eqnarray}

この積分を数値積分で計算するのはリアルタイムアプリケーションにはコストがかかりすぎるため、現在の最先端は、Cook-Torrance[CT82]マイクロファセットBRDFを使用する場合、一定の完全可視性(\(\forall \omega_{\mathbf i} | V(x, \omega_{\mathbf i}) = 1\))を仮定した定式化を採用し、積分近似[Laz13, Kar13]を使用することです。

\begin{eqnarray}
L_r (x, \omega_{\mathbf o}) &\approx & {\mathcal L}(x) \cdot {\mathcal F}(x, \omega_{\mathbf o}), \\
{\mathcal L}(x) & = & \frac{1}{C_L} \int_{\mathcal H^2} \overbrace{V(x, \omega_{\mathbf i})}^{=1} L_i (x, \omega_{\mathbf i}) D(x, \omega_{\mathbf h}) \langle {\mathbf n_{\mathbf x}}, \omega_{\mathbf i} \rangle^{+} d\omega_{\mathbf i} \\
{\mathcal F}(x, \omega_{\mathbf o}) & = & \int_{\mathcal H^2} f_r (x, \omega_{\mathbf i}, \omega_{\mathbf o}) \langle {\mathbf n_{\mathbf x}}, \omega_{\mathbf i} \rangle^{+} d\omega_{\mathbf i} \tag{12}
\end{eqnarray}

ここで，\(C_L = \int_{\mathcal H^2}D(x, \omega_{\mathbf h}) \langle {\mathbf n_{\mathbf x}}, \omega_{\mathbf i} \rangle^{+} d\omega_{\mathbf i} \)は最初の積分内で必要とされる常に[0, 1]の範囲内であることを保証する正規化項で，このとき\(L_i(x, \omega_{\mathbf i}) = 1\)であり，\(D(x, \omega_{\mathbf h})\)はサーフェイスの法線分布関数[TS67]で，\(\omega_{\mathbf h}\)はハーフベクトルです。直感的には、2番目の積分は、均一な白色照明環境下での画素における完全なマイクロファセットBRDFであり、事前に計算されたルックアップテーブルに格納することができ、１番目の積分は、実際の照明環境\(L_i(x, \omega_{\mathbf i})\)とCook-Torrance BRDFの分布関数に近似する円対称ローブとの畳み込みです。照明環境を照度キューブマップとして表現する場合、この第1の積分は、異なるサーフェイスラフネスのローブでキューブマップを事前に畳み込むことによって計算されます。ほとんどの近似ではオクルージョンを無視したり、ヒューリスティックで近似したりしますが、これは光沢のあるマテリアルをレンダリングするのに非常に効率的です。

スペキュラーが遮蔽されたライティングを計算するために、我々は分割積分近似に似たアプローチを選択し、可視性の項を定数として最初の積分の形に分離します。本質的には、アンビエントオクルージョンの考えで、\(x\)に到達する照明の量を変調するオクルージョン項を計算することです。これにより、式(12)を3つの積分の積に変換することができます：

\begin{eqnarray}
L_r(x, \omega_{\mathbf o}) \approx {\mathcal S}(x, \omega_{\mathbf o}) \cdot {\mathcal L}(x) \cdot {\mathcal F}(x, \omega_{\mathbf o}) \tag{13}
\end{eqnarray}

ただし，モデリング可視項\(\mathcal S\)は次のように我々のスペキュラーオクルージョン 項として計算されます：

\begin{eqnarray}
{\mathcal S}(x, \omega_{\mathbf o}) = \frac{1}{C_V} \int_{\mathcal H^2} V(x, \omega_{\mathbf i}) f_r (x, \omega_{\mathbf i}, \omega_{\mathbf o}) \langle {\mathbf n_{\mathbf x}}, \omega_{\mathbf i} \rangle^{+} d\omega_{\mathbf i} \tag{14}
\end{eqnarray}

正規化項\(C_V = \int_{\mathcal H^2} f_r(x, \omega_{\mathbf i}, \omega_{\mathbf o}) \langle {\mathbf n_{\mathbf x}}, \omega_{\mathbf i} \rangle^{+} d\omega_{\mathbf i}\)はスペキュラーオクルージョン\(\mathcal S\)を[0, 1]の範囲を保証します。見てわかるように、我々のスペキュラーオクルージョンの定義は、BRDFによって重み付けされており、したがって、方向依存性があります。以下のサブセクションでは、スペキュラーオクルージョン\(\mathcal S\)の計算について詳細に説明します。

興味深いことに、正規化係数\(C_V\)は後者の積分\(\mathcal F\)と同じであるため、式(13)では相殺され、式(13)は次のように残ります：

\begin{eqnarray}
L_r(x, \omega_{\mathbf o}) & \approx & \int_{\mathcal H^2} V(x, \omega_{\mathbf i}) f_r (x, \omega_{\mathbf i}, \omega_{\mathbf o}) \langle {\mathbf n_{\mathbf x}}, \omega_{\mathbf i} \rangle^{+} d\omega_{\mathbf i} \tag{15} \\
&\cdot & \frac{1}{C_L} \int_{\mathcal H^2} L_i (x, \omega_{\mathbf i}) D(x, \omega_h) \langle {\mathbf n_{\mathbf x}}, \omega_{\mathbf i} \rangle^{+} d\omega_{\mathbf i} \tag{16}
\end{eqnarray}

この最終形は、一定のプローブ照明の場合、グランドトゥルースと正確に一致するという性質を持っています。さらに、元の分割積分近似(式(12))と比較すると、主な違いは、可視性の項がBRDF積分に移動され、もはや一定ではないと仮定されていることがわかります。

6.1　Computing Specular Occlusion

スペキュラーオクルージョン\(\mathcal S\)を効率的に計算するための鍵となるアイデアは、可視性とBRDFローブの両方の近似をモデル化し、これらの2つの交点をスペキュラーオクルージョンとして計算することです。これを念頭に置くと、問題は、可視性とBRDFの両方をいかにコンパクトに表現するか、そして、その両方の交点をいかに計算するか、ということに絞られます。

視認性については、ベント法線[Lan02]とアンビエントクルージョン項から計算された円錐形に近似できると仮定しています。これらの2つは、その場で計算することもできますし（4節参照）、事前に計算しておくこともできます（例えば、テクスチャや頂点データとして保存されます）。この表現を選んだのは、4節で計算した高品質のスクリーン空間アンビエントオクルージョンのデータを再利用できるからです。ベント法線\(\mathbf b\)は円錐の方向として機能します。コーンの振幅\(\alpha_v\)を計算するには、アンビエントオクルージョンに依存します。ベント法線の周囲で視界が均一であると仮定すると、\(\alpha_v\)は、すべての方向\(\phi\)の最大水平角\(\theta_1(\phi) = \theta_2(\phi) = \alpha_v\)となります（式(5)参照）。これらの仮定により、アンビエントオクルージョン\({\hat {\mathcal A}}(x)\)は解析的に次のように表すことができます：

\begin{eqnarray}
{\hat {\mathcal A}}(x) = 1 – \cos(\alpha_v (x))^2 \tag{17}
\end{eqnarray}

これは，\({\hat {\mathcal A}}(x)\)の関数として円錐角\(\alpha_v\)を得るために次のように変換することができます：

\begin{eqnarray}
\cos(\alpha_v(x)) = \sqrt{1 – {\hat {\mathcal A}}(x)} \tag{18}
\end{eqnarray}

可視性と同様に、スペキュラーローブを反射方向\(\omega_r\)を中心とした円錐としてモデル化することができます。これは、BRDFのローブが\(\omega_r\)上で回転対称であるように制約することを含むいくつかの仮定を課します（これはマイクロファセットBRDFでは真ではありませんが、実際のBRDFを単一の定数値として近似しているのと同じになります）。また一方で、これにより、以下のように可視性とスペキュラーコーン\(\Omega_i\)とスペキュラー\(\Omega_s\)(図8を参照）の両方の立体角が交差する立体角の間の比としてスペキュラオクルージョンを計算することができます。

\begin{eqnarray}
{\mathcal S}(x, \omega_{\mathbf o}) = \frac{\Omega_i(x, \omega_{\mathbf o})}{\Omega_s(x, \omega_{\mathbf o})} \tag{19}
\end{eqnarray}

この比は解析的に計算することができ、潜在するスペキュラーリフレクタンスの粗い近似であるにもかかわらず、良い結果が得られます。図8（左）は、コーンを用いて可視性とBRDFの両方を近似する場合の例を示しています（詳細は付録Bを参照）。

※図は[Jimenez 2016]より引用。

しかし、我々の目標であるリアルタイムアプリケーションでは、これらの計算はまだ高価であり、結局、ベント法線と反射ベクトル\(\beta = \arccos(\langle {\mathbf b}, \omega_{\mathbf r} \rangle)\)の間の角度、および両方のコーン\(\alpha_v\)と\(\alpha_s\)の振幅によってパラメータ化された、事前に計算された3次元ルックアップテーブルにベイクしてしまうかもしれません。このことを念頭に置いて、我々はより正確な、事前計算ベースの近似を選択し、可視コーン\(\Delta_V\)と実際のBRDF \(F\)の積としてスペキュラーオクルージョン\(\mathcal S\)を計算します（図8、右）。

\begin{eqnarray}
{\mathcal S}(x, \omega_{\mathbf o}) \approx \frac{1}{C_V} \int_{\mathcal H^2} \Delta_v (\alpha_v(x), \beta({\mathbf b}(x), \omega_i)) f_r(x, \omega_{\mathbf i}, \omega_{\mathbf o}) \langle {\mathbf n_{\mathbf x}}, \omega_{\mathbf i} \rangle^{+} d\omega_{\mathbf i} \tag{20}
\end{eqnarray}

\(\Delta_V(\alpha_v, \beta)\)は\(\beta \leq \alpha_v\)の場合に1，そうではない場合に0を返却するバイナリ関数です。ラフネス値\(r\)によってパラメータ化されたGGX NDF[WMLT07]を用いた等方性マイクロファセットベースのBRDFを想定し、法線\(\mathbf n_{\mathbf x}\)に対して角度\(\theta_o = \arccos( \langle {\mathbf n_{\mathbf x}}, \omega_{\mathbf r} \rangle)\)として反射方向\(\omega_{\mathbf r}\)をモデル化します。これらの仮定を用いて、わかりやすくするために空間依存性を省略して、\(\mathcal S\)を4次元関数として表現することができます：

\begin{eqnarray}
{\mathcal S}(\alpha_v, \beta, \gamma, \theta_o) \approx \frac{1}{C_V} \int_{\mathcal H^2} \Delta_V(\alpha_v, \beta) f_r (\omega_i, \theta_o, r) \langle {\mathbf n_{\mathbf x}}, \omega_{\mathbf i} \rangle^{+} d\omega_{\mathbf i} \tag{21}
\end{eqnarray}

この関数は、四次元のテーブルとしてコンパクトにベイクすることができます。また、法線\(\mathbf n_{\mathbf x}\)をベント法線\(\mathbf b\)と仮定することで、少しの誤差を導入する代償として、テーブルの次元を3次元に減らすことができます。この関数が比較的滑らかであることを考えると、実行時に効率的にアクセスできる4次元\(32^4\)（3次元近似では\(32^3\)）BC4 8ビットルックアップテーブルにエンコードすることができます。

7　Results

ここでは、我々の手法を用いて得られた結果を示し、グランドトゥルースとの比較を行います。これらは、明示的なレイトレースされたアンビエントオクルージョン、我々のグローバル照明近似のためのマルチプルバウンスパストレース、およびスペキュラーオクルージョンのためのBRDFレイトレースサンプリングを使用して行われています。

我々は、スタンドアロンのアプリケーションとフル機能の商用ゲームエンジンの両方で我々の技法を実装しました。図9は、モンテカルロ法によるグランドトゥルースと比較した結果です。ホワイトプローブを仮定した環境オクルージョンでは、我々の技術はグランドトゥルースと忠実に一致し、HD解像度と60fpsのゲームで実用的です。図10は、物理ベースのシェーディングと複雑なジオメトリを用いたGTAOのゲーム内での例を示しています。我々の技術は、我々のAO定式化と時空間サンプル積分の両方を利用して、PS4の1080pでスクリーン空間のアンビエントオクルージョンをわずか0.5ミリ秒で計算しています。

※図は[Jimenez 2016]より引用。

※図は，[Jimenez 2016]より引用。

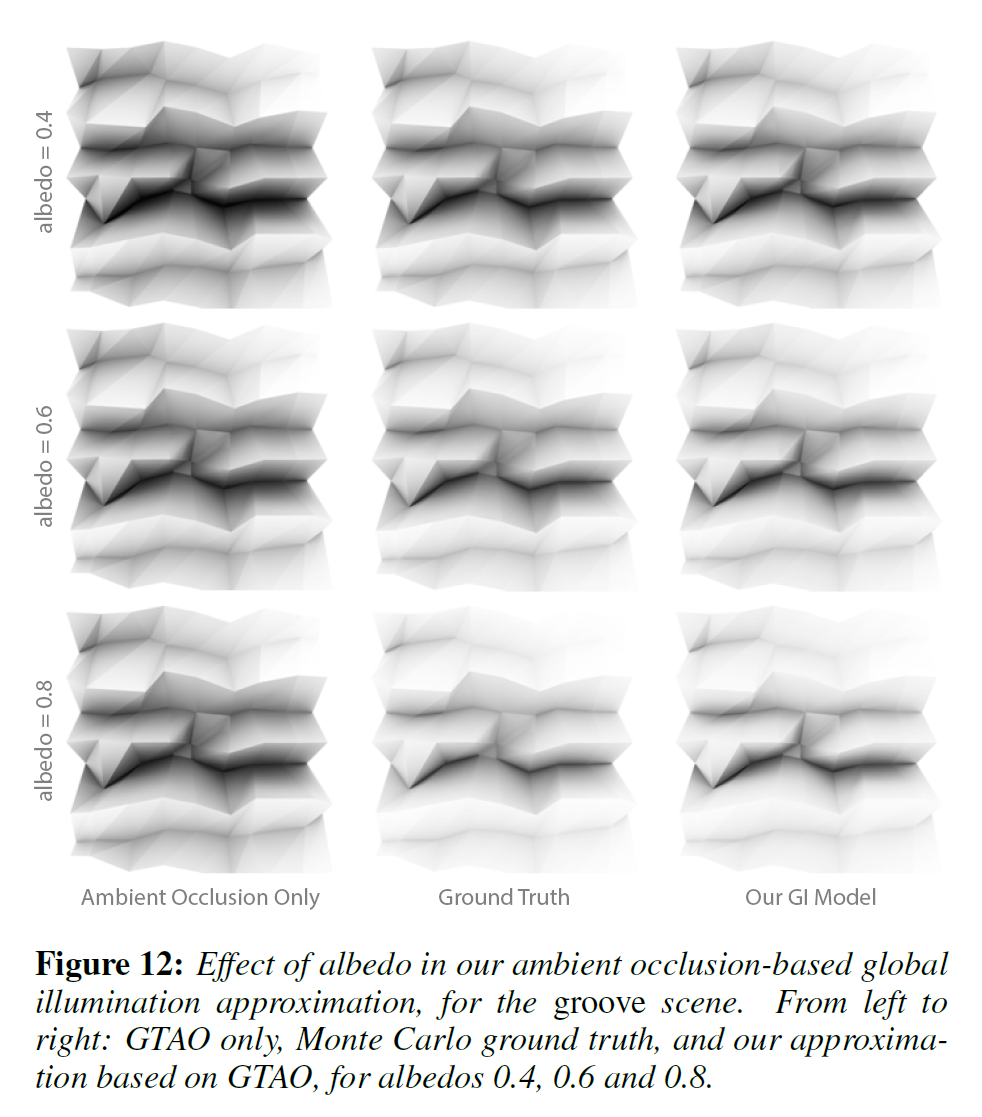
同様に、我々は、我々の近似値を、パスをトレースしたグランドトゥルースに対して、近接場のグローバルな照明を比較しています。図11は、アンビエントオクルージョンのみ（GTAO）でレンダリングされたLauren モデルを示しており、その後、グレーとカラーアルベドの両方でグローバルイルミネーションを含めていますが、図12はグレーアルベドの値を変えて同じ比較を示しています。

※図は，[Jimenez 2016]より引用。

※図は[Jimenez 2016]より引用。

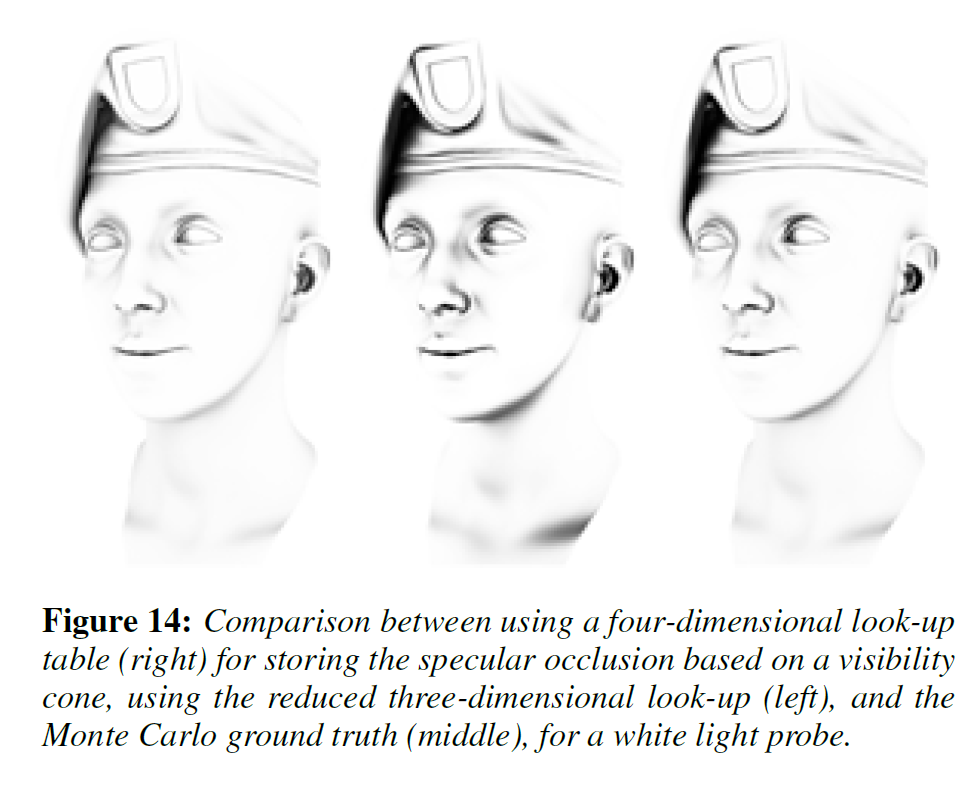
図13は、我々のスペキュラオクルージョン技法とモンテカルロのグランドトゥルースを比較したものです。特に斜線の角度では若干の違いがありますが、我々の技法は、一定でない照明の場合でもオクルージョンを考慮しながら、モデルのスペキュラ外観のほとんどを一致させることができます。最後に、図14は、スペキュラーオクルージョンを計算するための3次元および4次元ルックアップテーブルの使用をグランドトゥルースと比較したものです。

※図は，[Jimenez 2016]より引用。

※図は，[Jimenez 2016]より引用。

8　Conclusions

本研究では、スクリーン空間リアルタイムアンビエントオクルージョンへの貢献をいくつか発表してきた。まず第一に、モンテカルロ法のグランドトゥルースと非常に限られた予算の中で一致するアンビエントオクルージョンの効率的な定式化であるGTAOを発表しました。この定式化は、空間的コヒーレンスと時間的コヒーレンスの両方を積極的に利用した効率的な実装と相まって、1ピクセルあたり100個近くのサンプルを効果的に積分しながら、1フレームあたり1個の計算を行うことができます。GTAOは、シェーディングポイントでの安部院とオクルージョンに基づいて、近接場の拡散反射をシミュレートするシンプルで効果的な手法を用いています。この技術は、これらの相互反射が、局所的なアルベドとアンビエントオクルージョンの関数として、データからモデル化できるという観測に基づいています。これにより、アンビエントオクルージョンに起因する典型的な過暗化を回避することができます。

最後に、アンビエントオクルージョン演算子を一般化してスペキュラーを扱うGround-Truth Specular Occlusionを用いたスペキュラーオクルージョンの近似法を紹介し、一定・非一定のプローブベースの照明から鏡面反射を効率的に計算するための事前計算ルックアップテーブルを用いた効率的な手法を紹介しました。

Acknowledgements

和訳省略

A　Uniformly-weighted GTAO

放射計測学的には正しくありませんが、いくつかの研究 [BSD08] では、式 (2) とは少し異なる定式化を用いており、余弦加重ではなく、前短縮項を削除し、その結果、閉塞を半球内で一様に加重しています。このシナリオでは、GTAOのための我々の定式化も有効であり、式(5)を修正すると次のようになります。

\begin{eqnarray}
{\hat {\mathcal A}}(x) = \frac{1}{2 \pi} \int_0^{\pi} \underbrace{\int_{\theta_1(\phi)}^{\theta_2(\phi)} | \sin (\theta) | d\theta}_{\hat a} d\phi \tag{22}
\end{eqnarray}

余弦項を削除すると、正規化係数を\(1/\pi\)から\(1/2\pi\)に変更するだけでなく、完全に内側部分の積分\(\hat a\)を変更します。幸いなことに、この形式では、この積分は次のような解析解を持っています。

\begin{eqnarray}
{\hat a} = 2 – \cos(\theta_1) – \cos(\theta_2) \tag{23}
\end{eqnarray}

なお、ここでは法線に対する余弦項がないので、余弦加重GTAOに必要な射影（式(8)）は不要です。

このGTAOの定式化は、放射計測学的に補正された余弦加重GTAOに対して3次多項式フィットが行われているため、式（(0)に示された近接場の大域照明近似をサポートしていません。しかしながら、式(22)を用いて計算されたオクルージョンは、6節の可視コーンの開口\(\alpha_v\)を次のように決定するために使用することができます。

\begin{eqnarray}
\cos (\alpha_v(x)) = 1 – {\hat {\mathcal A}}(x) \tag{24}
\end{eqnarray}

B　Cone-to-Cone GTSO

式(19)に基づいてスペキュラーオクルージョンのGTSOを計算するためには、方向と開口部で定義された可視光線とスペキュラーコーン、およびそれらの交点の立体角\(\Omega_i\)を計算する必要があります。可視性コーンについては、6節(式(18))で説明しました。スペキュラーコーンの場合、その方向は反射ベクトル\(\omega_r\)によって定義されます。一方、その開口\(\alpha_s\)は、ラフネス\(r\)（Phong BRDFの場合は鏡面指数\(p\)）によって定義されます。このための厳密な解がないので、我々は、Walterら[WMLT07]によるPhong重要度サンプリングルーチンを使用して開口部をPhong指数\(p\)と関連付けるUludag [Ulu14]によるものと同様のアプローチを選択します

\begin{eqnarray}
\alpha_s = \arccos \left( u^{ \frac{1}{p+2} } \right) \tag{25}
\end{eqnarray}

ここで，\(u\)は定数値です。Uldagとは対照的に、コーンをローブにフィットさせることによって(u=0.244)，\(u\)を求めません。しかし、結果として得られるGTSOとモンテカルログランドトゥルースの参照との差を最小化し、\(u=0.01\)を得ます。次に、より高速な評価のためにラフネスをPhongのスペキュラー指数\(p\)を\(r=(2/(p+2))^{0.5}\)を用いて\(r\)にマッピングすることで、最終的な開口コーンが得られます。

\begin{eqnarray}
\cos(\alpha_s) = 0.01^{\frac{1}{p+2}} = 0.01^{0.5r^2} = e^{-2.30259 r^2} = 2^{-3.32193r^2} \tag{26}
\end{eqnarray}

両方の円錐を得られたら、あとはこれらの円錐から交点の立体角\(\Omega_i\)を計算するだけです。この交点は、円錐の開口部とそれぞれの方向の間の角度、ベント法線\(\mathbf b\)と反射方向\(\omega_{\mathbf r}\)の関数として、[OS07, Maz12]の解析的解を持っています。