わしゃがな！Pocolです。

今回は，SIGGRAPH 2018: Advances in Real-Time Renderingで発表された，Danny Channによる”Material Advances in Call of Duty: WWⅡ”のコースノートを読んでみようと思います。
いつもながら，誤字・誤訳等があるかと思いますので，ご指摘いただける場合は正しい翻訳例と共に指摘いただけるとありがたいです。
あと先に言っておくと，「マジックアワー」は撮影用語のようです（Wikipedia参照)。

1　INTRODUCTION

本稿では、『Call of Duty: WWⅡ』のライトサーフェスシェーダに施されたいくつかの改善点について説明します。グロスを分布の平均法線長に直接マッピングすることで、分散のような中間的な表現をバイパスして、法線マップとグロスマップをミップマップする簡単な方法を詳述しています（2章）。有理関数が解析的にも効率的にも表現できない多くの関数を近似するのに有用なツールであることを示します(3章)。法線マップを持つすべてのサーフェスに対してキャビティマップを自動生成する方法を説明し、これらのテクスチャで表現されたキャビティのオクルージョンと間接照明をどのように扱うかを示します(4章)。最後に、ディフューズBRDFを拡張して、多散乱を伴うLambertian・マイクロファセットをモデル化する方法を述べます(第5節)。また，エネルギー保存について環境分離積分の事前計算が簡単に再利用できる方法についても示します（5.3節)

これらの変更により、「マジックアワー」中にレンダリングされたシーンでは、従来よりも豊なアンビエントルックを実現することができました（図1）。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

1.1　New Gloss Parameterization

ダイブする前に、「Call of Duty: WWⅡ」のグロスのパラメータ化方法の変更を指摘しておきます。以前のCall of Duty: Advanced Warfareでは、GGX [Wal+07]でグロス[Cha15]のパラメータ化を使用していました：

\begin{eqnarray}
\alpha = \sqrt{ \frac{2}{2 + 2^{16g}} } \tag{1}
\end{eqnarray}

これがグロスの新しいパラメータ化です：

\begin{eqnarray}
\alpha = \sqrt{ \frac{2}{1 + 2^{18g}} } \tag{2}
\end{eqnarray}

16 から 18 への変更により、より鋭いスペキュラーハイライトが可能になったことに注目してください。重要なことは、グロスが 0 のときに\(\alpha\)が 1 になるようにしたことで、GGX で利用できるラフネスのフルレンジが得られたことです。言い換えれば、グロス値は以前よりも広い範囲の粗さと滑らかさの両方を表現できるようになりました。

2　SPECULAR ALIASING: MIPMAPPING NORMAL AND GLOSS

法線マップとグロスマップは、異なるスケールで幾何学的な情報を表現していると考えることができます。グロスマップはマイクロファセットの正規分布を格納し、法線マップはマクロスケールの法線を格納します（図2）。法線は、遠くから見るとマイクロファセットの方向になります。このため、ミップマップを生成する際に、法線マップの情報をグロスマップに押し込むことは理にかなっています。

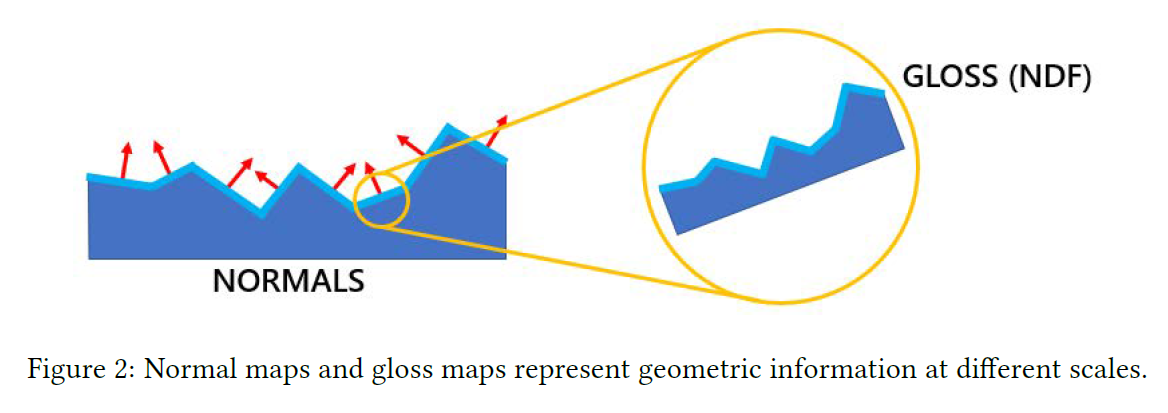
※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

法線マップとグロスマップを別々にミップマップすると、法線マップはミップするときに平坦な面に向かう傾向がありますが、グロスマップは平均化されます。非常にでこぼこしていて、非常に光沢のある表面を想像してみてください。法線のばらつきをグロスマップに押し込むことで、この問題を回避することができます (図 3)。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

スペキュラーエイリアシングに対抗するために多くの技術が提案されています（LEAN [OB10]、CLEAN [Bak11]、Normal Variance [Tok04]、概要については[Hill]を参照）。これらの技術は通常、より多くの情報チャネルを必要としますが、余分なチャネルを追加しない単純化されたバリエーションが存在します。例えば、[Tok04] を使用して分散を推定し、これを使用して既存のグロスチャンネルを調整することができます。

これらの異なるバリエーションと同様に、我々は余分なチャンネルを追加しないよりシンプルなアプローチを取りましたが、以前のアプローチとは異なり、GGX法線分布関数(NDF)に特化しています。さらに，我々の手法は，[Kar18]と同様に，ベースグロスが法線方向の重み付けに影響するように，法線とベースグロスを一緒にフィルタリングします．これは、ベースグロスが法線から派生した分布で事後に畳み込みされる他の手法とは異なります。

まず、半球内の任意の法線の集合を平均化すると（つまり、法線を合計し、その数で割る）、もはや単位長ではない可能性があるベクトルになることに気づきます。我々はこれを[Tok04]に倣って「平均法線」または「短縮法線」(式(3)および図4の\({\mathbf n}_s\))と呼びます。

\begin{eqnarray}
{\mathbf n}_s = \frac{1}{N} \sum_{i=0}^{N-1} {\mathbf n}_i \tag{3}
\end{eqnarray}

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

GGX NDFをランダムにサンプリングし、特定のグロス値[0, 255]についてこの分布に従うランダムなマイクロファセット法線を生成し、これらの分布に対する平均法線を計算すると（2.1.3節に記載されたこの技法のマクロサーフェス面積モデルで，リスト6に対応する疑似コード）、グロスを「短縮法線」の長さに関連付ける表が得られます（リスト8）。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

※表は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

2.1　Randomly Sampling the NDF

なぜNDFをランダムにサンプリングするのでしょうか？そのためにはどのような確率密度関数（PDF）を使うのでしょうか？\(D(\omega)\)が何であるか，我々のNDFを表現し，どのようにして法線マップに関係するかを理解することが鍵となります。

2.1.1　NDF relates to microsurface area

マイクロサーフェイス\(M\)とそのサーフェイスに沿った点\(p_m\)が、対応する法線方向\(\omega_m\)を持つとすると、[Hei14]の式(2)を用いて、空間方程式として\(D(\omega)\)を定義することができます：

\begin{eqnarray}
D(\omega) = \int_M \delta_{\omega}(\omega_m(p_m)) dp_m \tag{4}
\end{eqnarray}

ここで，\(\delta_{\omega}\)はDiracのデルタ関数とします。
このことから、\(D(\omega)\) は \(\omega\) 方向を指すマイクロサーフェイスの面積を表していることがわかります。したがって、\(D(\omega)\) は、法線マップ中の法線、または NDF からランダムに選ばれた法線のいずれかにマイクロサーフェイス面積が関連していると考えることができます。
短縮法線の長さを数学的に計算する方法を考えることができます。平均化のために法線を蓄積する際に、総マイクロサーフェイス面積に対するその法線のマイクロサーフェイス面積の比率に応じて、各法線に重みを割り当てることができます。
[Hei14]を用いて，式(5)は：

\begin{eqnarray}
{\rm microsurface \, area} = \int_M d p_m = \int_{\Omega} D(\omega) d\omega \tag{5}
\end{eqnarray}

となります。
法線ごとの重みを計算することができます：

\begin{eqnarray}
s_{\omega’} = \frac{D(\omega’)}{\int_{\Omega} D(\omega) d\omega} \tag{6}
\end{eqnarray}

我々の法線分布（NDF）の短縮法線長は、この重みの積分にサンプリングされた方向のz成分をかけたものを用いて計算することができます。標本がこれらの次元では対称で、x-成分とy-成分は相殺されますので、短縮法線長を計算するために必要なのはz-成分だけとなります。

\begin{eqnarray}
|| {\mathbf n}_{s, micro} || &=& \int_{\Omega} s_{\omega’} {\omega’}_z d {\omega’} \tag{7} \\
&=& \int_{\Omega} \frac{D(\omega’)}{\int_{\Omega} D(\omega) d\omega} {\omega’}_z d \omega \tag{8} \\
&=& \frac{\int_{\Omega} D(\omega’) {\omega’}_z d \omega’}{ \int{\Omega} D(\omega) d\omega } \tag{9}
\end{eqnarray}

ここでは z-up を使用しているので, サンプリングされた方向の z 成分はその極角の余弦に相当します：

\begin{eqnarray}
{\omega’}_z = \cos\theta’ \tag{10}
\end{eqnarray}

そして，与えられたマイクロサーフェイスの射影面積ははマイクロサーフェイス上で1となります：

\begin{eqnarray}
\int_{\Omega} D(\omega) \cos \theta d\omega = 1 \tag{11}
\end{eqnarray}

我々の短縮法線長は

\begin{eqnarray}
|| {\mathbf n}_{s, micro} || = \frac{1}{\int_{\Omega} D(\omega) d\omega } \tag{12}
\end{eqnarray}

となります。
短縮法線長と総マイクロサーフェイス面積の両方が、我々のNDFに直接関係していることがわかります。興味深いことに、NDFを総マイクロサーフェイス面積に関連付けることは、短縮法線長に関連付ける代わりの方法を提供します。我々はこれを短縮法線を計算するためのマイクロサーフェイス面積モデルと呼んでいます。

2.1.2　Normal map as microsurface

法線マップをマイクロサーフェイスとして仮定した場合、法線マップの各テクセルは何を表しているのでしょうか？各テクセルは、面積を持つ法線方向に配向した無限小のマイクロファセットであると考えることができます：

\begin{eqnarray}
dA_h = \frac{d_A}{\cos \theta} \tag{13}
\end{eqnarray}

ここで、\(d_A\) は、マクロサーフェスに関連付けられたテクセル領域です（図5）。

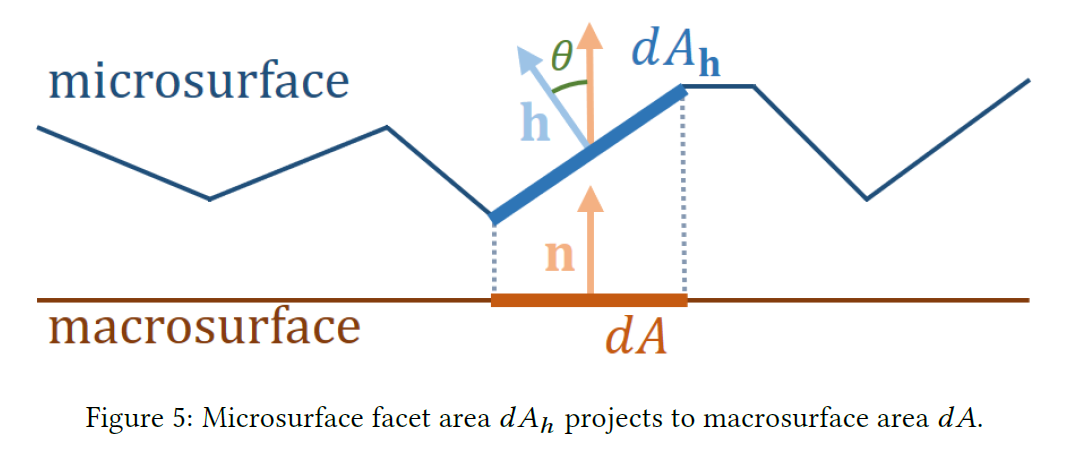
※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

これは、式(12)の短縮法線長の計算に関連するマイクロサーフェイス面積に基づいて法線マップの法線を平均化する方法を提供します（アルゴリズム1）。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

2.1.3　Normal maps as macrosurface

また、法線マップを、各テクセルが等しく重み付けされた法線摂動を表すマクロサーフェイスと考えることもできます。このような場合は、マクロサーフェスで投影された面積に基づいたPDFを使用することになります：

\begin{eqnarray}
p_{\omega} = D(\omega) \cos \theta \tag{14}
\end{eqnarray}

そして重点サンプルは、このPDFを使用します。マイクロファセット方程式の重点サンプリングで使用される標準的なPDFですので、便利に使用できます。このマクロサーフェイス投影面積PDFを使用することで、マクロサーフェイスベースの重み付け関数を使用したルックアップテーブルを生成することができます：

\begin{eqnarray}
t_{\omega’} = \frac{D(\omega’) \cos \theta’}{\int_{\Omega} D(\omega) \cos \theta d\omega} \tag{15}
\end{eqnarray}

ここで、再び、サンプリングされた方向のz成分をかけたこの重みの積分を取ることで、短縮法線長を計算します：

\begin{eqnarray}
|| {\mathbf n}_{s, macro} || &=& \int_{\Omega} t_{\omega’} {\omega’}_z d \omega \tag{16} \\\
&=& \int_{\Omega} \frac{D(\omega’) \cos \theta’}{ \int_{\Omega} D(\omega) \cos \theta d \omega} {\omega’}_z d {\omega’} \tag{17} \\
&=& \int_{\Omega} D(\omega’) \cos \theta’ {\omega’}_z d{\omega’} \tag{18}
\end{eqnarray}

これを短縮法線長を計算するためのマクロサーフェス面積モデルと呼んでいます。この場合、我々はマクロサーフェス面積を扱っているので、マイクロサーフェス面積で重み付けせずに法線を平均化します（アルゴリズム2）。そして、これを式(18)で生成されたテーブルに関連付けることにします。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

重要なことは、我々がマクロサーフェイス面積を使用して生成したテーブルは、マイクロサーフェイス面積のために生成したテーブルとは異なることに注意することです（違いの詳細については図6を参照）。

2.1.4　Converting from macrosurface averaging to microsurface averaging

マクロサーフェスモデルとマイクロサーフェスモデルの変換は、積分内の重みに\(\cos \theta\)またはその逆数を適用する問題であることを示すことができます。
マクロサーフェイス面積の短縮法線長（式(17)）のリファクタリングされた形式から開始します：

\begin{eqnarray}
|| {\mathbf n}_{s, macro} || = \frac{\int_{\Omega} D(\omega’) \cos \theta’ {\omega’}_z d \omega’}{\int_{\Omega} D(\omega) \cos \theta d \omega} \tag{19}
\end{eqnarray}

式(13)(\(\frac{1}{\cos \theta}\))の面積変換を分子と分母の積分に適用して、これをマイクロサーフェイス面積を用いて短縮法線長に変換することができます：

\begin{eqnarray}
|| {\mathbf n}_{s, macro} || &=& \frac{ \int_{\Omega} D(\omega’) \cos \theta’ {\omega’}_z \frac{1}{\cos \theta’} d\omega’ }{\int{\Omega} D(\omega) \cos \theta \frac{1}{\cos \theta} d\omega} \tag{20} \\
&=& \frac{\int_{\Omega} D(\omega’) {\omega’}_z d \omega’}{\int_{\Omega} D(\omega) d\omega} \tag{21} \\
&=& \frac{1}{\int_{\Omega} D(\omega) d \omega} \tag{22}
\end{eqnarray}

マイクロサーフェイス面積方程式をマクロサーフェイス面積方程式に変換することは、逆面積変換を適用するという問題になります。

2.1.5　Differences between microsurface and macrosurface models

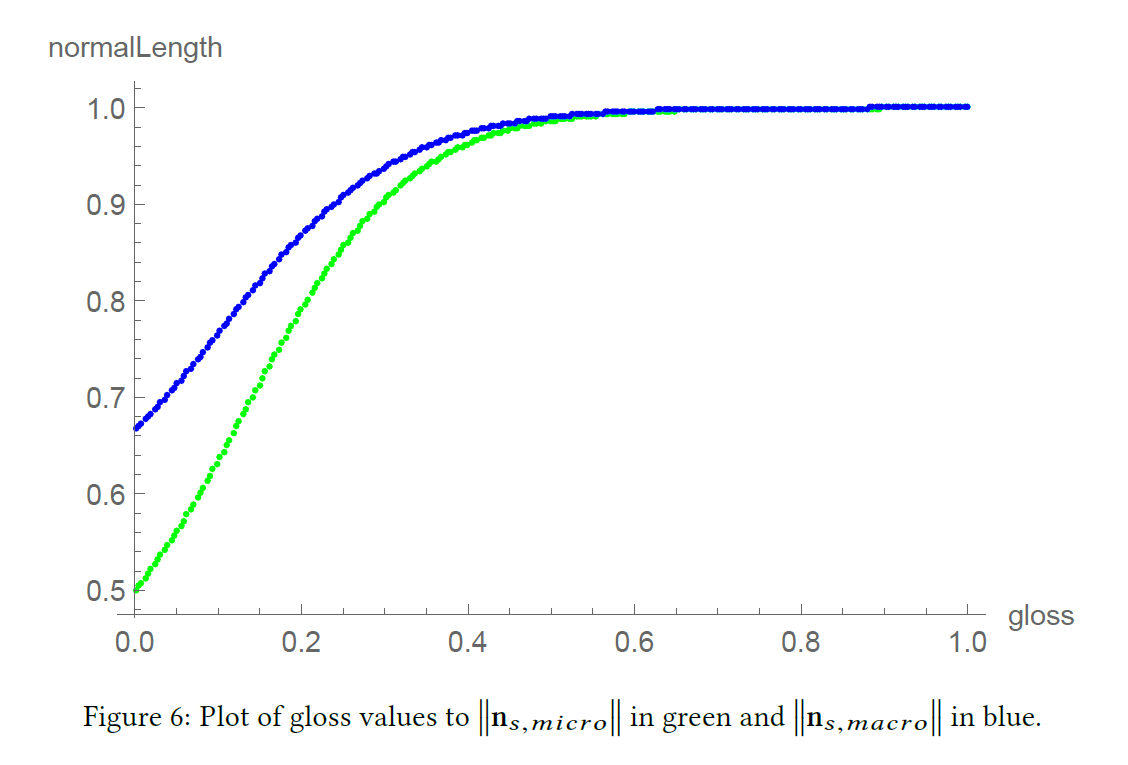
※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

図6は、マイクロサーフェイスとマクロサーフェイルモデル間の法線長の短縮化の違いを示す図です。これらの違いは、法線マップをマイクロサーフェイスモデルとマクロサーフェイスモデルを介してNDFにどのように関連付けるかについての更なる調査の動機付けとなりました。

理論的には、\(D(\omega)\)はマイクロサーフェイス面積に直接関係しているので、マイクロサーフェイス面積モデルを使用する必要があります。しかし、レンダリング中に NDF（グロス）を正しくフィルタリングしようとすると、法線に関連するファセットのマイクロサーフェイス面積を考慮する必要があります（式(13)）。言い換えれば、ピクセルシェーダでNDFテキストを平均化してフィルタリングする際に、法線の方向によるマイクロサーフェイス面積の変化を考慮する必要があるということです。

我々のNDFがマイクロサーフェイス面積に直接関係しているという事実にもかかわらず、マクロサーフェイス面積モデルを使用することを支持する根拠は、ハードウェアフィルタリングがマクロサーフェイス領域で行われるということです。言い換えれば，GPU バイリニアフィルタリングを使用する場合，マクロサーフェス上のピクセルフットプリントを平均化していることになります。

ハードウェアフィルタリングに限定していると仮定すると、2つの解決策が残れされていますが、どちらも理想的ではありません。それは、マイクロサーフェイス面積モデルを使用して不正確な面積測定値を使用してフィルタリングするか、あるいは、マクロサーフェイス面積モデルを使用して、不正確ですが，わずかに修正された分布を適切にフィルタリングするかです。

法線マップはジオメトリ的に平坦で、相関のないファセットを表現していますが、マイクロファセット方程式はジオメトリ項を介して様々な相関度を持っています。つまり、他のマイクロファセットによるマイクロファセットのシャドウイングとマスキングがあります。法線マップの描画と遠く離れた地点におけるNDFで表現される法線マップ，そしてそれらのモデルが目標達成により近いことを理解するためにさらなる研究が必要です。

Call of Duty: WWⅡでは、マクロサーフェスエリアモデルを使用しており、本稿で計算した値は、グロスと短縮法線長に関連するテーブルの値を含め、すべてマクロサーフェス面積の正規化を使用しています。このテーブルを生成するために、式(14) の PDF を用いて GGX を重点サンプリングしました。

2.1.6　Closed-form solution to shortened normal length

Call of Duty: WWⅡの開発中は重点サンプリングを使用して生成されたテーブルを使用しましたが、マイクロサーフェイス(式(12))とマクロサーフェイス面積(式(18))の両方の方法を使用して、短縮された法線長に対する閉形解を導出することもできます：

\begin{eqnarray}
|| {\mathbf n}_{s, micro} || &=& \frac{1}{\int_{\Omega} D_{GGX} (\omega) d\omega} \tag{23} \\
&=& \frac{a}{a + (1-a^2) \tanh^{-1}(a)} \tag{24} \\
|| {\mathbf n}_{s, macro} || &=& \int_{\Omega} D_{GGX} (\omega) \cos \theta \omega_z d \omega \tag{25} \\
&=& \frac{a – (1 – a^2) \tanh^{-1}(a)}{a^3} \tag{26} \\
{\rm where} \, a &=& \sqrt{1 – \alpha^2} \tag{27}
\end{eqnarray}

これらの閉形式解(リスト7のCの実装)は、より速く、より正確なので、我々の重点サンプリング手法(リスト6)に取って代わります。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

2.2　Mipmapping Process

グロスと短縮法線長のテーブルを用いて、各ピクセルがベクトルの方向を通る法線とベクトルの長さを通るグロスの両方を表す短縮法線マップを構築することができます。短縮法線マップの興味深い特性は、マップのフィルタリングが意味のあるものであるということです。例えば、短縮法線の平均は、短縮法線に関連付けられた個々の（マクロサーフェイス面積モデル）NDFを平均化することに相当します。また、我々は単に単位法線をフィルタリングしているのではないので、フィルタリングされた法線の方向は正規分布に従って重み付けされていることにも注目してください。ある方向を指しているグロスのある法線と別の方向を指している粗い法線の間で平均化すると、グロスのある法線に近い法線が得られます。法線の分布がその方向に有利なので、その通りになります（図7では、ミップマップ法線はより正しい所を指しています）。

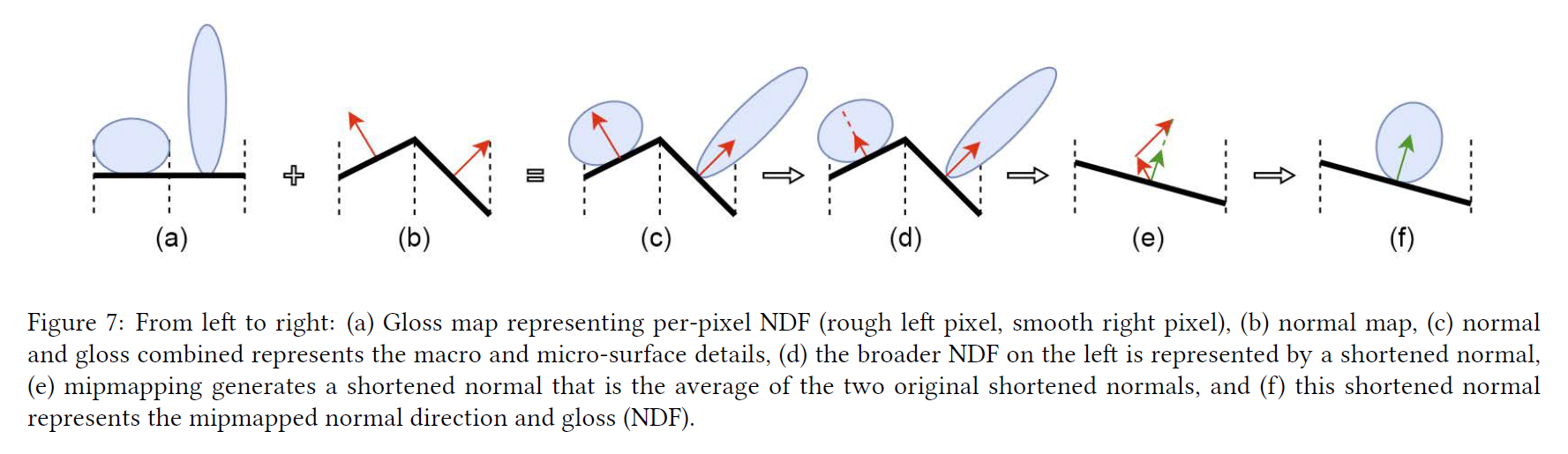
※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

これらの短縮された法線マップをエンコードして、6桁の精度に基づいて10桁の長さまで計算できるようにすれば（リスト8の表の最後のいくつかの法線の長さを参照）、これらの短縮法線を直接GPUに渡して、ハードウェア（バイリニアなど）のフィルタリングを利用できます。その後、ピクセルシェーダで、フィットカーブ(3.1節)を使って短縮法線長からグロスを再構築したり、GGXではそのまま\(\alpha\)または\(\alpha^2\)に変換したりすることができます。残念ながら、BC6Hによる半精度浮動小数点では十分ではなく、非圧縮の16-32ビットフォーマットはメモリ消費量が大きすぎます。

その代わりに、短縮法線のミップマップを生成した後、短縮法線長からグロスを計算し、再正規化します。法線はBC5Sとして、グロスはメタルネスとマテリアルサーフェイスのオクルージョン（4章）も保持している複合テクスチャ内の1つのチャンネルとして別々に保存することにしました。法線とグロスを独立してランタイムフィルタリングすることは、短縮法線をフィルタリングすることとは全く同じではありませんが、近似的なものとなります。アルゴリズム3は、法線マップとグロスマップのミップマッピングで実行されるステップの概要を示しています。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

図8は、\(\frac{255}{255}\)のオーサリングされたグロスマップと、我々のテクニックから生成されたミップマップを示しています。低いミップは，より高い法線変化を符号化しており暗くなり，グロス値が低いことを表しています。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

図9は、法線変化をグロスに押し込んだ結果（左）と、同じサーフェスをクローズアップレンダリングしてバイリニアダウンサンプリングした結果（右）との比較を示しています。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

2.3　Representation

法線マップを考えるとき、具体的には何を表しているのでしょうか？法線マップのピクセルは、カットされたサーフェイスのファセットを表しているのでしょうか、それとも連続した滑らかな表面からのサンプルなのでしょうか（図10）。実際、グロスについても同じ質問をすることができます: グロスはピクセルのフットプリント全体にわたって一貫した光沢を表しているのか、それともピクセルの中心でグロスサンプルを表しているのでしょうか?

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

これらの質問に対する答えは、最も高いソースの解像度であるMIP 0でのオーサリングされた法線と光沢の扱い方を変えます。このプロジェクトでは、法線をファセットとして扱いました。これは主にオーサリングの決定でした。アーティストがオーサリングしたMIP 0のテクスチャを変更したくなかったので、法線をファセットサーフェスを表すものと考えています。

法線が滑らかな曲面を表すという議論は簡単にできます。その場合、ピクセルフットプリント全体のNDFを考慮に入れるようにMIP 0のグロスを修正します。簡単な近似法は、ピクセルフットプリント内でランダムに短縮法線を生成し、法線の方向を補間し、それらを平均化することです。さらに進むと、ピクセル領域のファセットネス/スムースネスを決定するためにフィルタカーネルを使用することができます。

重要なのは、滑らかな表面のアイデアは、いくつかの更なる修正がないと、倍率の下でバラバラになってしまうことです。拡大表示の場合、レンダリングされたピクセルフットプリントはソースの法線とグロスマップの完全な範囲をカバーしていない可能性があるため、基本的な法線分布はそれほど広くはありません。

このような近似手法の問題点は、完全なコンポジットNDFを表現できないことです – これは、グロスのために1つの次元しか使用しない我々のシェーディングモデル（図7を参照）によって制約された最も近い一致を持つ複雑なNDFを表現します。将来的な方向性としては、尖度（ヘイズ）制御、異方性サポート、またはNDFをより完全にモデル化することが考えられます（例：[Yan+14; Jak+14]）。

2.4　Detail Normal Gloss

詳細な法線マップを使用していると問題にぶつかります。詳細法線マップが遠ざかっていき、解像度が低くなると、その法線の変化は詳細グロスチャンネルで表現されます。では、この詳細グロスをベースグロスと組み合わせるにはどうすればよいのでしょうか？

グロスの結合ステップを定義する必要があります。これは、詳細NDFからランダムに法線を選択し、ランダムな詳細法線をベースNDFからランダムに選択された法線の空間に回転させることを想像してみましょう。 これを何度も行い、新しい分布の短縮法線を計算します。

2つのNDF、AとBが与えられると、それぞれのNDFから個別に無作為にサンプリングして、短縮法線\({\mathbf n}_a\)と\({\mathbf n}_b\)を計算することができます：

\begin{eqnarray}
{\mathbf n}_a = \frac{1}{N} \sum_{i=1}^N {\mathbf n}_{a, i} \tag{28}
\end{eqnarray}

\begin{eqnarray}
{\mathbf n}_b = \frac{1}{M} \sum_{j=1}^M {\mathbf n}_{b, j} \tag{29}
\end{eqnarray}

我々のグロス結合ステップは、一方の分布からランダムにサンプリングし、他方の分布からランダムにサンプリングして定義された空間に回転させることに相当します。

\begin{eqnarray}
{\mathbf n}_s = \frac{1}{M} \sum_{j=1}^M \left( \frac{1}{N} \sum_{i=1}^N {\mathbf n}_{a, i|b, j} \right) \tag{30}
\end{eqnarray}

ここで，\({\mathbf n}_{a, i|b, j}\)は\({\mathbf n}_{b, j}\)の空間へと\({\mathbf n}_{a, i}\)を回転したものです。
内側の総和から短縮法線長は

\begin{eqnarray}
|| \frac{1}{N} \sum_{i=1}^N {\mathbf n}_{a, i|b, j} || = || \frac{1}{N} \sum_{i=1}^N {\mathbf n}_{a, i} || = || {\mathbf n}_a || \tag{31}
\end{eqnarray}

となります。
外側の総和は、長さ \(|| {\mathbf n}_a ||\)のベクトルの足し合わせと等価です：

\begin{eqnarray}
{\mathbf n}_s &=& \frac{1}{M} \sum_{j=1}^M ( || {\mathbf n}_a || {\mathbf n}_{b, j} ) \tag{32} \\
&=& || {\mathbf n}_a || \frac{1}{M} \sum_{j=1}^M {\mathbf n}_{b, j} \tag{33} \\
& || {\mathbf n}_s || & = || {\mathbf n}_a || || {\mathbf n}_b || \tag{34}
\end{eqnarray}

次に、グロスを組み合わせるために、AとBの短縮法線長を掛け合わせ、グロスに戻して変換します。これは、詳細法線の平均化に起因する法線方向の変動を無視しています。すなわち、結合しているグロス値が同じ法線に沿っていると仮定します。

\(32 \times 32\)ルックアップテーブル（LUT）を生成し、有理関数フィット（図11）を実行すると、以下の式が得られます（リスト2のシェーダコード）。2 つの次元/引数が対称/逆数であるため、有理関数フィットの自由度を減らすことができます。

\begin{eqnarray}
P(a, b) &=& -0.535580 + 1.002204(a + b) – 0.223910(a^2 + b^2) + 13.323150ab \tag{35} \\
Q(a, b) &=& 1.0 + 8.259559(a + b) + 9.896132(a^2 + b^2) – 22.015902 ab \tag{36} \\
g &=& {\rm clamp} \left( \frac{P(a, b)}{Q(a, b)}, \, 0, \, 1 \right) \tag{37}
\end{eqnarray}

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

我々の法線マップは、上で構築したLUTの前提であるReoriented Normal Maps (RNM) [BH12]を用いてブレンドされていません。その代わりに、ベース法線オフセットに詳細法線オフセット（XとY）を追加し、Zを再計算することで法線がブレンドされます – このメソッドをBlendXY（アルゴリズム4）と呼びます。これにもかかわらず、RNMベースのLUTを使用しているのは、どちらの方法も同様にグロスを結合しているからです; 両方の方法で生成されたテーブルを比較してみたところ、非常に近い結果が得られました。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

短縮法線長を乗算するこのアプローチを検証するために、ブルートフォースアプローチを使用してLUTを生成しました。このアプローチでは、両方のNDFからランダムにサンプリングし、RNMまたはBlendXYを使用して、ベース法線と詳細法線を結合します。新しいNDFから多数の法線を平均化し、グロスに変換すると、RNMの場合は同じ結果になり、BlendXYの場合は非常に似たような結果になります。

3　RATIONAL FUNCTION FITTING

有理関数を用いたフィット関数は[Sch94]で紹介されています。

\begin{eqnarray}
F_{\rm Schlick}({\mathbf v}, {\mathbf h}) = F_0 + (1 – F_0)(1 – {\mathbf v} \cdot {\mathbf h})^5 \tag{38}
\end{eqnarray}

物理ベースのレンダリングで広く使われているSchlick Fresnel（式(38)）を導入した論文です。私の考えでは、有理関数近似の使用とカーネル条件の考え方がより重要なポイントでした。

有理関数とは、多項式の代数的な分数のことです。簡単な例を挙げてみましょう。

\begin{eqnarray}
f(x) = \frac{c_0 + c_1 x + c_2 x^2 + c_3 x^3}{1 + c_4x + c_5x^2} \tag{39}
\end{eqnarray}

カーネル条件は、フィットを実行する際の重要な考え方で、フィットしようとしている関数の顕著な特性は何か？この関数を特別なものにしているのは何か？そして、これらのターゲットにヒットするように近似を調整します。論文では、これらを「カーネル条件」と呼んでいますが、我々は「制約」という用語を使います。

我々が使用する有理関数は、不要な自由度を削除するために、分母多項式の定数項として1.0を持っていることに注意してください。これは，\(x = 0\), \(f(0) = c_0\) のときの制約を簡単に固定する方法を提供してくれます。

3.1　Example 1D Rational Function Fit

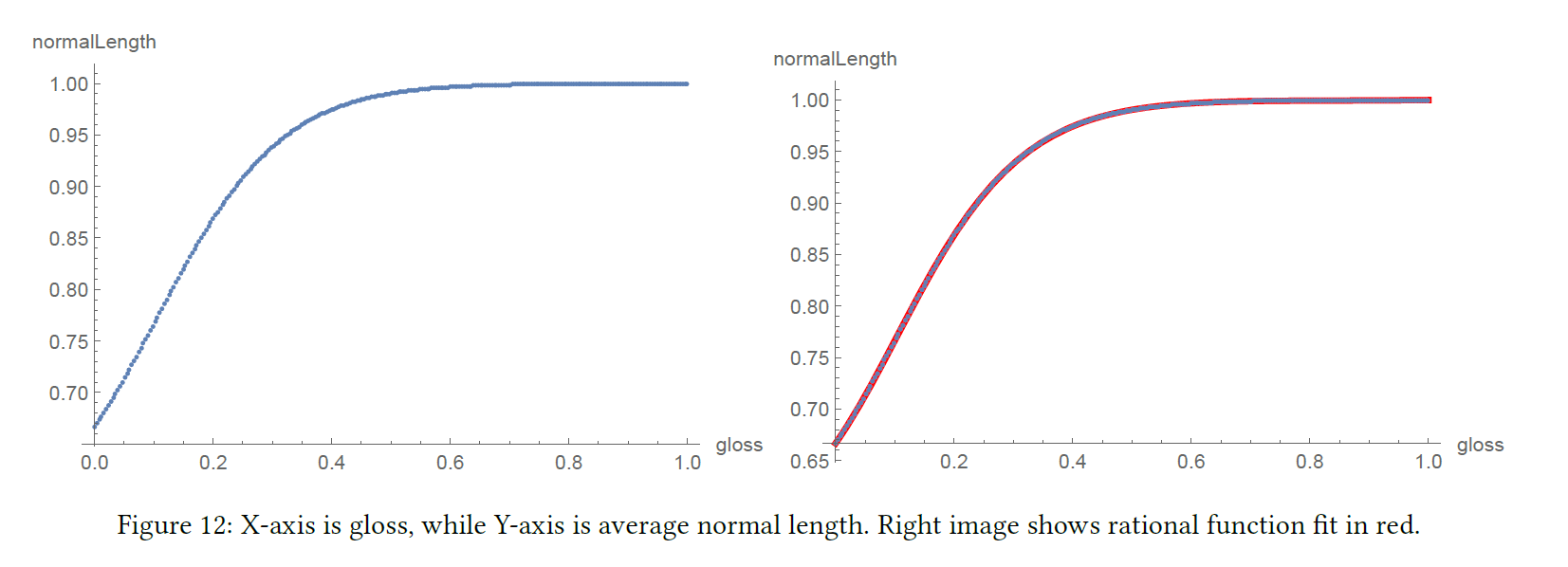
2章では、スペキュラーエイリアシングに対抗するために、通常のミップマッピングとグロスミップマッピングのための我々の手法について説明しました。このプロセスの一部として、グロスを短縮法線長に関連付けるテーブルを生成します (リスト8)。このテーブルを直接使用して、アルゴリズム 3 で GlossToNormalLength と NormalLengthToGloss を評価します。

また、閉形解（式(26)）を使用して GlossToNormalLength を評価することもできます。別の方法として、この手法の有効性のデモンストレーションとして、純粋に表の有理関数フィット (リスト8) を実行します。最初に、制約なしでフィットし、その後、制約で再フィットします。図12は、有理関数フィットとともに、平均法線長に対するグロスのグラフを示しています。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

Mathematica のFindFitと式(39)の有理関数形式を表で使うと，この有理関数近似が得られます．

\begin{eqnarray}
f(x) = \frac{0.66693 + 0.0609009x + 7.32398x^2 + 0.600464x^3}{1 – 1.13467x + 8.78264x^2} \tag{40}
\end{eqnarray}

これは制約のない単純な例ですが、カーブに制約を加えてフィットさせたい場合はどうでしょうか？\(f(0) = 0.66667\)なので、\(c_0 = 0.66667\)であることがわかります。これは、事実上、曲線の開始点を固定していることになります。これは自由度を1つ取り除きます。曲線のこの端では多少の誤差を受け入れることができるので、これを必ずしもこの関数の真の制約とは考えませんが、これは実証として行っています。

もう一つの制約である \(f(1) = 0.999958\) も知っています．前の制約とは異なり、この制約は重要です。なぜなら、曲線のこの端での小さな誤差は、この曲線で生成された短縮法線の光沢を評価する際に大きな誤差につながる可能性があるからです。これにより、曲線の右端を固定しています。

いくつかの並べ替えで、- これは任意の選択であり、他の係数のいずれかを削除することができます。- 残りの係数の関数として\(c_3\)を指定することで、\(c_3\)を削除することができます。

\begin{eqnarray}
c_3 = (0.999958 – 0.66667) – c_1 – c_2 + 0.999958c_4 + 0.999958 c_5 \tag{41}
\end{eqnarray}

Mathematica で再びFindFitを使うと，最終的な有理関数近似が得られます（図12の右図）：

\begin{eqnarray}
f(x) = \frac{0.6667 + 0.0942205x + 7.41935x^2 + 0.56711x^3}{1 – 1.0881x + 8.83582 x^2} \tag{42}
\end{eqnarray}

4　MATERIAL SURFACE OCCLUSION

私たちのアーティストによくある不満は、影になると物が平らに見えるということです。

幾何学的オクルージョンについては、SSAO（GTAOとその変種）、MDAO（中距離AO、コーントレース＋オクルージョンボリュームテクスチャ）、そして自己可視性をエンコードするための頂点単位のベント法線の形で解決策を持っていますが、適切なマテリアルサーフェイスオクルージョンがありません。法線マップで定義されたキャビティやバンプは、間接光をオクルードしなければなりませんし、可能であれば直接光もオクルードしなければなりません。

マテリアルサーフェイスオクルージョンをどのように生成するのか？まずオーサリングされた法線マップから、緩和を用いて高さマップを生成します(4.2節)。次に、その高さマップからGTAOを用いてオクルージョンマップを生成します(4.3節)。これらの作業はすべてオフラインのマテリアル変換ステップで行うので、GTAO シェーダコードを C++ としてコンパイルできるように C++ ラッパーを作成しました。

4.1　Generating a Height Map from a Normal Map

法線マップからオクルージョンマップに移行するために、まず法線マップに対応する中間の高さマップを生成します(図13)。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

まずはきちんとした法線マップから始めることが大切です。最も効果的なマップは、フォトグラメトリーを使って撮影されたものです。法線マップツールを使って描かれたり修正されたりした法線マップは、多くの場合、「不可能な」法線マップ、つまり、実際のサーフェイスに対応していない法線マップになります。このような場合、法線マップと一致する高さのマップは作成できません。テッセレーションやディスプレイスメントシステムのように、生成された高さマップを変位に、法線マップをライティングに使用すると、非現実的なライティングを得ることになります。

法線マップからの高さマップの問題に対する一つの解決策は、従来の手段を用いた線形システムを解くことです[Cou04]が、これは時間がかかり、テクスチャサイズに応じてスケールが悪くなります。Dmitriev と Makarov [DM11]によるもう一つの解決策は、高低差の積分がゼロであると仮定しており、彼らの手法は各ピクセルを個別に処理します。

4.2　Relaxation

代わりに、我々は緩和処理を繰り返し実行します。ここでは、各ピクセルをランダムに選択し、隣のピクセルの高さと隣のピクセルからの高さ差分で高さを計算します。1つのピクセルの調整を何度も繰り返した後、各ピクセルの高さは解に向かって収束していきます。

このブルートフォースアプローチは非常に遅くなりますので、私たちの手法は、ミップチェーンを介して高さを洗練させ、より低い分解能のミップを解いて、それらの解を次の高さのミップの最初の推定値として使用します (アルゴリズム 5)。議論の途中で [Kol15] を見つけましたが、これも非常に似ており、この手法の良い説明となります。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

4.3　Generating an Occlusion Map from a Height Map

法線からハイトマップを作成した後、CLLにHLSL機能を提供するラッパーファイルhlsl2cpp.hを用いてGTAO.hlsl [Jim+16]を呼び出すことで、ハイトマップからオクルージョンマップを作成することができます。GTAOは通常、透視投影を用いて生成された深度バッファ上で動作しますが、GTAOの作者は、正投影深度上で使用できるように修正を加えました。

シェーダにオクルージョン値を設定すると、1.0は「オクルージョンなし」を意味するので、実際には可視性になりますが、この項を使って間接的な拡散照明を調整することができます。また、このオクルージョン項は可視性の余弦加重積分なので、直接照明の減衰に使用するために等面積の円錐角に変換することができます。しかし、その前に、アンビエントオクルージョンの調整について説明します。

4.4　Adjustment of Ambient Occlusion Value

アンビエントオクルージョンの標準的な定式化の問題点は、オクルージョンされた方向は黒く、つまりオクルージョンされた方向からの光が入らないと仮定されていることです。

一般的には、点pにおける周囲のオクルージョンを次のように定義します。

\begin{eqnarray}
A_p = \frac{1}{\pi} \int_{\Omega} V_{p, \omega} \cos \theta d \omega \tag{43}
\end{eqnarray}

ここで、\(V_{p, \omega}\)は、ある有限距離\(d\)について\(\omega\)方向における\(p\)からの可視関数です。このとき、点が影の中にあり、間接光の影響を受けるだけであると仮定すると、ランベルシアン面の出射輝度は通常、次の方法で計算されます。

\begin{eqnarray}
L_p = \frac{\rho}{\pi} E_p A_p \tag{44}
\end{eqnarray}

ここで、\(\rho\)はサーフェイスのアルベド、\(E_p\)は放射照度です。\(A_p\)は半球上の可視性の余弦加重積分なので、遮蔽された方向は最終的な輝度には全く寄与しません。

これは現実世界で実際に起こっていることの近似性に乏しく、ライティング環境についてより良い仮定を用いて、アンビエントオクルージョンを再構築することができます。

式を簡単にするために、放射輝度が1のホワイトファーナスの環境を想定ます。ただし，遮蔽される方向の輝度は黒で，0とします。 アンビエントオクルージョンは次のように定式化できることがわかります。

\begin{eqnarray}
{A’}_{p} = 0 (1 – A_p) + 1 (A_p) \tag{45}
\end{eqnarray}

今、オクルージョン方向に関する以下の仮定に応じて、周囲のオクルージョンを再構築することができるようになりました。
遮蔽された方向は白色の拡散アルベドを持ち、同様に遮蔽されるものは：

\begin{eqnarray}
{A’}_{p} = A_p (1 – A_p) + 1 (A_p) \tag{46}
\end{eqnarray}

となります。
遮蔽された方向は同じ拡散アルベドを持っていますが、遮蔽されていないものは：

\begin{eqnarray}
{A’}_p = \rho (1 – A_p) + 1(A_p) \tag{47}
\end{eqnarray}

となります。
遮蔽された方向は、同じ拡散色を持ち、同様に遮蔽は：

\begin{eqnarray}
{A’}_p = \rho A_p (1 – A_p) + 1(A_p) \tag{48}
\end{eqnarray}

となります。
さらに、[SL96]の反射率モデルを用いて、遮蔽された方向の輝度が、シェーディングされた画素の出射輝度と等しいと仮定することができます。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

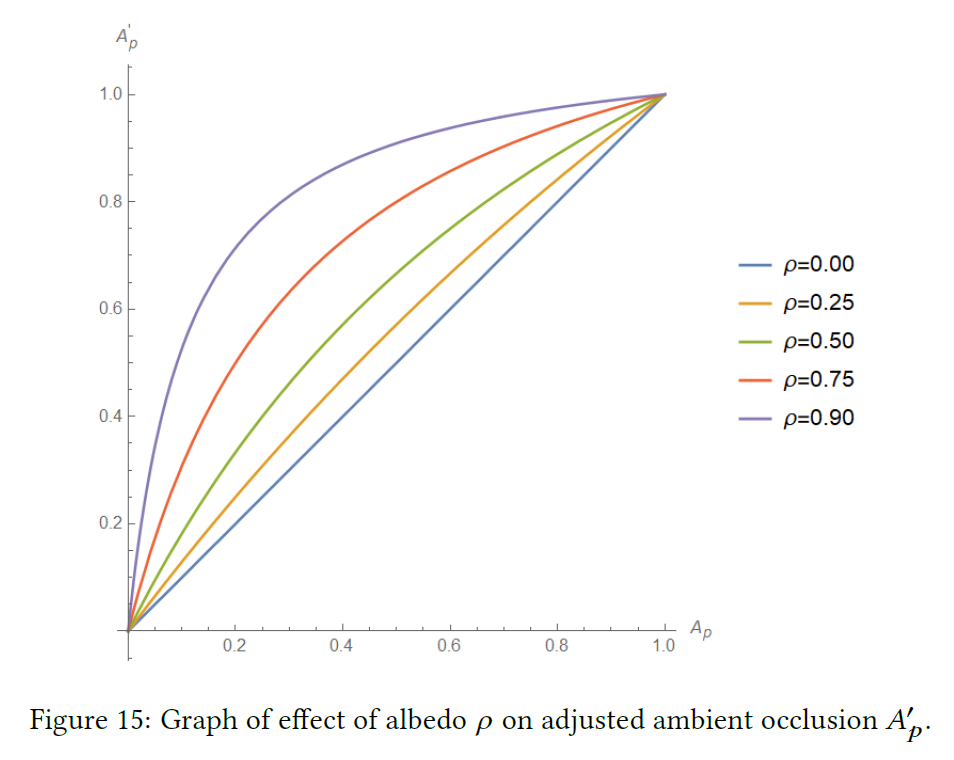
図15は、式(48)の相互反射モデルを仮定した場合で、調整されたアンビエントオクルージョン\({A’}_p\)が、シェーディングされる点の拡散アルベドによってどのように影響されるかを示しています。アルベド\(\rho\)がゼロの場合、遮蔽された方向は黒のままなので、アンビエントオクルージョンは変化しないことに注意してください。アルベド値\(\rho\)が増加すると、調整されたアンビエントオクルージョン\({A’}_p\)はあまり顕著ではなくなる傾向があります。

\begin{eqnarray}
{A’}_p = \frac{A_p}{1 – \rho + \rho A_p} \tag{49}
\end{eqnarray}

今の課題は、どのようにして拡散テクスチャをオーサリングするかということです。以前は、マテリアル サーフェスのオクルージョンがなかったため、アーティストは拡散テクスチャにオクルージョンをベイクする必要がありました。マテリアル サーフェス オクルージョンが自動生成されるようになったので、これらのテクスチャは厳密に拡散アルベドでなければなりません。これは、ビジュアライズとオーサリングの方法を変更したものとなります。

4.5　Converting Visibility Value to Equivalent Cone Angle

視認性の項から等面積の円錐角に変換するのはかなり簡単です。[Jim+16]には積分を使った定式化がありますが、これをジオメトリ的に推論することもできます。

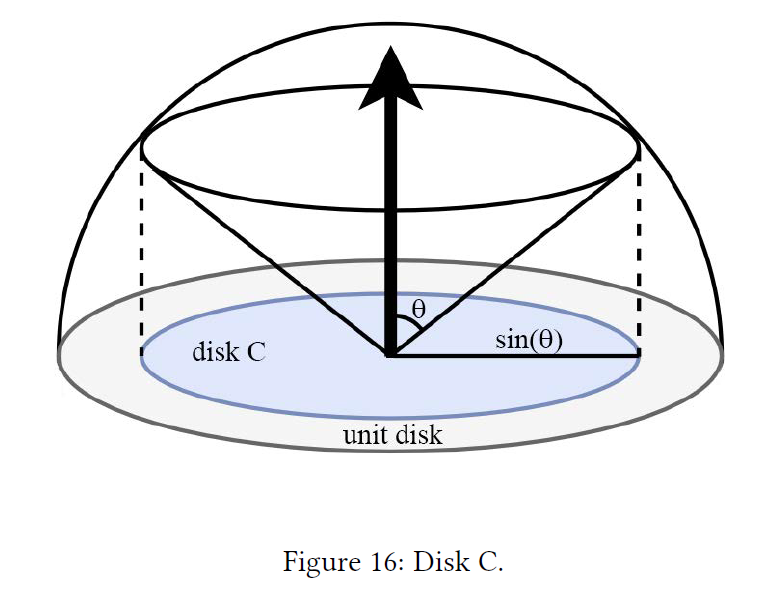
Nusseltアナログ[Wik]を使用して、「余弦加重可視性」（式(50)）として単位円にディスクCの面積を関連付けることができ、ディスクCは半球に射影さ円錐に等面積であると表すことができます(図16).

\begin{eqnarray}
\frac{\text{cos-weighted visibility}}{\text{hemisphere visibility}} &=& \frac{\text{area of disk} \, C}{\text{ area of unit disk}} \tag{50} \\
\frac{V}{1} &=& \frac{\pi r^2}{\pi} \tag{51} \\
V &=& r^2 \tag{52}
\end{eqnarray}

\(r\)はディスクCの半径で，射影された円錐そして円錐角に関係づけることができます：

\begin{eqnarray}
r &=& \sin \theta \tag{53} \\
V &=& \sin^2 \theta \tag{54} \\
V &=& 1 – \cos^2 \theta \tag{55} \\
\cos \theta &=& \sqrt{1 – V} \tag{56}
\end{eqnarray}

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

図17は、右端の画像の直射光のシャドウイングに対するマテリアルサーフェイスオクルージョンを用いた場合の効果を示す図です。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

4.6　Cone-Based Direct Light Occlusion

これで、アンビエントの可視性を円錐角に関連付ける方法ができたので、これをシャドウの直接ライティングに適用することができます。

\begin{eqnarray}
vis_1 = \left\{
\begin{array}{l}
1 \quad {\rm if} \, \cos\theta \lt {\mathbf n} \cdot {\mathbf l} \\
0 \quad {\rm otherwise}
\end{array} \tag{57}
\right.
\end{eqnarray}

この法線指向の円錐は、レンダリングされる点の実際の方向の可視性は粗雑な近似であるため、式(57)を使用したセルフシャドウは貧弱に見えます（図18、右上）。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

代わりに、円錐端から 90 度までのスケールされた\({\mathbf n} \cdot {\mathbf l}\)係数に沿って、ライティングにアドホックなフォールオフを適用します（シェーダコードについては リスト4 を参照）。

\begin{eqnarray}
vis_1 = {\rm clamp} \left( \frac{{\mathbf n} \cdot {\mathbf l}}{\cos \theta}, \, 0, \, 1\right)^2 \tag{58}
\end{eqnarray}

このフォールオフはアドホックなので、将来的には、これを\(V\)の関数として再定義し、正確な\(\cos \theta\)を計算する際に平方根を防ぐことができます。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

[BM16]は似たようなことをしていて、彼らが「マイクロシャドウ」と呼んでいるものを、必ずしも一貫して作成されているとは限らないAOマップに結び付けられた、彼ら自身のアドホックなファールオフを使って適用しています。我々はGTAOを使ってAOマップを生成しているので、我々のファールオフは等面積の円錐角に基づいています。

GPUベースのTessellation and Displacement (T&D)は、シャドウマップのレンダリングを偏らせてz-fightingを避けるため、コーンベースのオクルージョンのようなものを使用することで、これらのサーフェスの直接照明に役立つはずです。

また、理論的にはSSAO技法（GTAOを使用しています）ではT&Dのジオメトリ的なオクルージョンを拾ってしまうので、GPUのT&Dでは間接照明へのオクルージョンマップの適用を省くことになります。実際には、GTAOとマテリアルサーフェイスオクルージョンで生成されたオクルージョン値の最小値を利用しています。GTAOとマテリアルサーフェイスオクルージョンが異なるスケールでオクルージョンを表現することが多いため、これは理想的ではありません。将来的には、これらの値を組み合わせる他の方法を模索するかもしれません。

4.7　Cone-Based Indirect Light Specular Occlusion

可視性円錐が与えれたら、間接的なスペキュラー寄与を減衰させることもできます。円錐が正確な可視性を表している場合、この円錐に対してスペキュラーBRDFを積分して、スペキュラーライトがどれくらい目に届くかを判断する必要があります。

スペキュラーBRDFを可視性円錐について積分すると、この\(32 \times 32 \times 8\)の環境ルックアップ・テーブルが得られます（図19）。このテーブルは、『Call of Duty: Advanced Warfare』で使用した[Kar13]の2Dルックアップ・テーブルを第3の次元である円錐角度に拡張したものです。[Jim+16]は同様の拡張を行い、さらに精度を上げるためにベント法線を使用しています。GGX NDFを重点サンプリングしてLUTを生成するという以前と同じ手法を使用していますが、円錐外に落ちるサンプルを拒否するようにしています。

表の左端のスライスは、完全に覆われていない円錐（全半球）を表しており、以前に使用した2Dルックアップテーブルと同等です。右端のスライスは、完全に閉ざされた円錐（\(\theta = 0\)）を表しています；完全に黒であることに注意してください。

残念ながら、法線が中心の円錐は、実際の方向依存性のあるオクルージョンの近似値としては良くありません。低光沢面では、ほとんどの角度でBRDFローブと円錐の間に有意なオーバーラップがあるので、それは十分に動作しますが、グロスが増加すると、オーバーラップの確率と範囲が減少します。この問題は実際にみることができ、さらに光沢のある表面が不自然に遮蔽されてしまうのと同じになります（図20）。

このため、グロスが増すにつれて完全に覆われていない円錐に向けてルックアップをバイアスするために、円錐角度のアドホックな調整を使用しています。また、サーフェイスの視野角も考慮します。この調整は目で調整しました。

\begin{eqnarray}
\cos \theta’ = \cos \theta (1 – gloss^2)(1 – (1 – ({\mathbf n} \cdot {\mathbf v})^4)) \tag{59}
\end{eqnarray}

残念なことに、この調整だけを使用しても、常に極端な斜視角度で武器の表面を見るため、光沢のあるプレイヤー（ビューモデル）の武器が過大に表示される結果となってしまいました。このため、式(59)を適用する前に、次の式を使用して\(gloss\)にバイアスをかけました。

\begin{eqnarray}
gloss’ = {\rm clamp}(1.5 \, gloss, \, 0, \, 1) \tag{60}
\end{eqnarray}

光沢のあるプレーヤ武器の問題を修正する一方で、この結果、図20の右の画像は、スペキュラーオクルージョンの欠如を示しています。これはゲーム内に同梱されているものですが、将来的には、式(60)を必要とする素材にのみ選択的に適用する可能性があります。シェーダーコードについてはリスト3を参照してください。このアドホックな調整は、与えられたグロスでコーンオクルージョンが実際の方向依存性オクルージョンの良い近似値となる確率について推論することで改善されるかもしれません。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

4.8　Future Directions

我々のコーンベースの直接光減衰の振る舞いは、我々の多重散乱拡散BRDFで起こる暗黙のマイクロファセットシャドウイングと一致しています。理想的には、コーンベースのオクルージョンによるマイクロシャドウイングを含むゲーム内のでこぼこしたサーフェイスのエリアスポットメーター測定が、法線マップの詳細さが低解像度のグロスマップに押し込まれた後、遠方の同じでこぼこした表面と一致することです（2章）。これは、マイクロマスクされた領域がレンダリングされないように、ある程度の視差マッピングが必要になるかもしれません。

また、コーンベースのスペキュラーオクルージョンをリファレンスレンダリングと比較して検証することで、近似の精度を向上させることができます。

5　MULTISCATTERING DIFFUSE BRDF

5.1　Rough Surfaces

Call of Duty: Advanced Warfareでは、スポットメーターを使ってラフサーフェイスの明るさをさまざまな角度から測定したところ、予想とは相反する挙動に気付きました[Char15]。

通常、サーフェイスが最も明るくなるのは、光がサーフェイスが浅い角度からちょっとずれたときで、光の方を向いているときです。この場合はスペキュラー反射が最も強くなります。しかし、これはラフサーフェイスの明るさの測定値とは一致しません。図21の一番右の画像は、この照明の設定を表しており、ラフサーフェイスはここで最も暗く見えます。

これをどのように説明するのでしょうか？図22は、デコボコしたサーフェイスがシャドウイングと再帰反射効果の両方を引き起こすことを示しており、図21のデコボコした壁を目視で確認すると、これらの効果があることが確認されているようです。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

5.2　Smooth Surfaces

[WNO98]では，粗面と平滑面の拡散応答についていくつかの観測がなされています。彼らはラフサーフェイスでの照明の平坦化に気づいていますが, これは前述の再帰反射効果とシャドウイング効果の副産物です。また、平滑面では照明の平坦化とは逆の「丸み」が見られることも明らかにしています。

この丸め込みをエネルギー保存を用いて説明することができます：反射した鏡面光は拡散照明には利用できないため、鏡面反射率が最も高い放牧角の滑らかな表面では、拡散反射率に利用できる光が最も少なくなります。

5.3　Energy Conservation

照明の丸みを出すために、鏡面反射のエネルギーが拡散反射では利用できないランベルシアン拡散を用いたBRDFにエネルギー保存を適用してみました。図23はこのエネルギー保存の効果を示しており、光沢のあるマテリアルの方が光のファールオフが滑らかになっています。最終的な多散乱拡散BRDFは、\(F_0 = 0.04\)と仮定してエネルギー保存が組み込まれており、Lambertと同様の特性を持ちます。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

我々は、間接的なスペキュラー寄与[Kar13]の計算中にどれだけのエネルギーが眼に向かって反射されているかを決定するために、EnvBrdfLutからサンプリングをします。スペキュラー反射で失われた直接光エネルギーを計算するために、EnvBrdfLutから2回目のサンプリングを行うことができます。今回は\({\mathbf n} \cdot {\mathbf v}\)ではなく\({\mathbf n} \cdot {\mathbf l}\)を使用しています。これは、BRDFが逆数であるため、通常、眼に向かって反射した光の割合を計算するために使用するEnvBrdfLutを、光源から反射した散乱光の割合を計算するために使用することができるからです。

結局、次に説明する多重散乱拡散BRDFを使うことになったので、この明示的なエネルギー保存は適用しませんでした。エネルギー保存のシェーダのコードはリスト5を参照してください。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

5.4　Multiple-Scattering Microfacet Model

新しいディフューズライティングモデルから得られるものは何でしょうか？上述の特性に加えて、拡散面の法線分布をスペキュラー面の法線分布と同じにしたいと考えています。このようにして、サーフェイスのグロシネスはスペキュラと拡散の両方の応答に影響を与えます。

Heitz and Dupuy [HD15]は、マイクロファセット自体をランベルシアン拡散反射体として用いて、大まかな拡散応答をモデル化することを選択しました。この方法で拡散反射率をモデル化することには議論があります：スケールによっては、拡散距離は受け取るマイクロファセットが1つの光子に対してマイクロファセットは再放出しないことを意味します。これにも関わらず，マイクロファセットの扱いに一貫性があるため、我々はこのモデルを基礎として使用しています。

多重散乱マイクロファセットモデル[Hei+16]を用いて、GGX正規分布関数に従ったマイクロファセットを用いて多散乱拡散をシミュレーションしました。多重散乱をシミュレートしているため、乱反射したエネルギーは隣接するマイクロファセットに再吸収され、再び乱反射することが可能です。

我々のシミュレーションと[Hei+16]のシミュレーションとの間には、いくつかの違いがあります。私たちの多重散乱シミュレーションは常に100%の光を跳ね返すので、 [Hei+16]のような後からの跳ね返りの彩度がありません。これは後に適用するフィットの次元性を減らすためにモデルを単純化したものです。また、各バウンスに拡散フレネル成分を追加し、鏡面反射率へのエネルギー損失をシミュレートすることでモデルを修正しました。

この拡散フレネル成分については、[Shi+97]に注目します。これは、完全に研磨された表面とその下にある「マット成分」をモデル化したもので，個々のマイクロファセットレベルで光を反射させるときに、まさに我々がモデル化しようとしていることです。

重要なのは、[Shi+97]の式(4)に誤りがあることを発見し、正しいバージョンは次の通りになります。

\begin{eqnarray}
k = \frac{21}{20 \pi} (1 – F_0) \tag{61}
\end{eqnarray}

我々のマイクロファセット拡散フレネル応答は、次のようになります。

\begin{eqnarray}
F_d = \frac{21}{20 \pi} (1 – F_0)(1 – (1 – {\mathbf n} \cdot {\mathbf l})^5) (1 – (1 – {\mathbf n} \cdot {\mathbf v})^5) \tag{62}
\end{eqnarray}

シミュレーションをしてみると、私たちが求めている特性が自然とこの新しいモデルに落とし込まれていることに気がつきました：

• グレージング角の再帰反射率からのラフサーフェイスに対するディフューズライティングの平坦化（図24）
• スペキュラー反射によるエネルギー欠損から光沢面に対してディフューズライティングを丸める（図25）

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

また、他の2つの拡散モデルも評価しました。Oren-Nayar [ON94; Fuj12]とDisney [Bur12]です．Oren-Nayarはラフサーフェイスでは良好な再帰反射効果が得られましたが、滑らかな面ではランベルシアンになってしまい、我々が望むような丸みを帯びた照明を得ることができませんでした。ディズニーの拡散モデル(以下ディズニーディフューズ)はこれらの特徴を持っていますが, アルベドが1を超えるため非現実的です。しかし、ディズニーディフューズは、効率性、物理的な妥当性、そして美的な懸念の間で良い妥協点となっています。そして、私たちのアーティストはコントラストが強化されたため砂がシャドウでより魅力的に見えたので、砂のシェーダーにモデルを使用しています。

5.5　Generating the BRDF Tables

多重散乱マイクロファセットモデルを用いて光子の跳ね返りをシミュレーションするには非常に多くのプロセッサを必要とするため、SN-DBSを用いて半球全体のBRDF応答に対応する大規模なテーブルを生成しました。BRDF Explorerにロードできるように、MERL [Mat+03]パラメータ化を用いてファイルを生成しました。

図26は、完全な多散乱拡散BRDFとランベルシアン拡散との比較を示しています。ラフサーフェイスではライティングの「平坦化」が見られますが、滑らかなサーフェイスでは逆の現象が起きています。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

図27、28、29では、フルBRDFテーブルのステップ性に注目してください。これは、MERLのパラメータ化により、反射方向に向かってより多くのサンプルが割り当てられているためです。対照的に、我々のBRDFスライス・パラメータ化は等角です。BRDF Explorerを拡張して、BRDFスライスを表す90 x 90ピクセルのポータブル・フロート・マップ（PFM）ファイルを読み込めるようにしました。

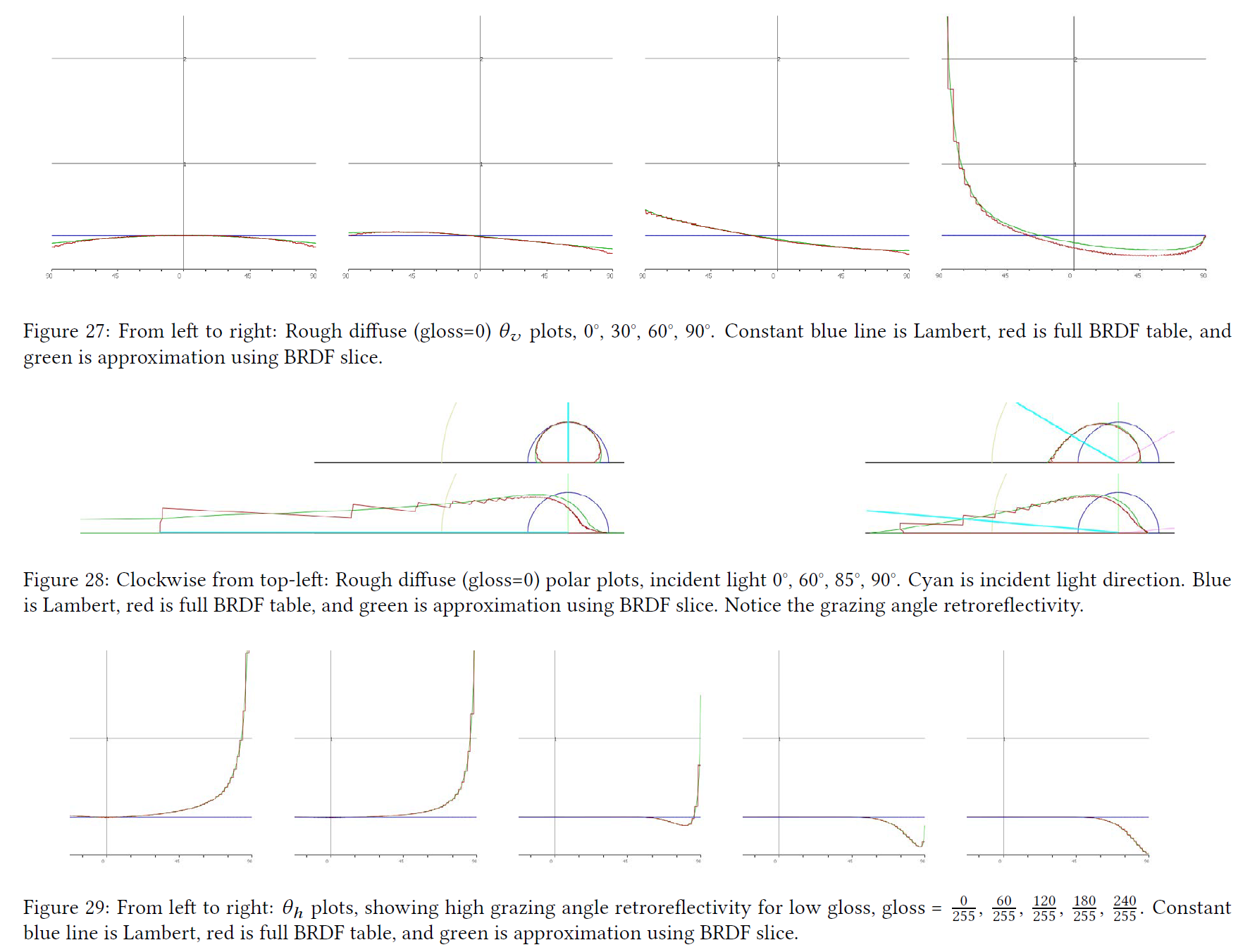
※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

5.6　BRDF Slice

私たちの最初のステップは、問題の次元を下げることでした。BRDFスライスを使用することは、[Bur12]で簡単に触れられています。\(theta_h\)、すなわち\(\arccos({\mathbf n} \cdot {\mathbf h})\)と\(theta_d\)、すなわち\(\arccos({\mathbf l} \cdot {\mathbf h})\)の2次元スライスとしてBRDFをパラメタライズすると、BRDFに良い近似が得られることがわかりました。BRDFの挙動のほとんどは、\(phi_d = 90\)でのこのスライスから来ています。BRDFエクスプローラでBRDFスライスを見ると、BRDFの他のスライス-他の\(\theta_d\)を表すもの-がスライスの縮小版にすぎないことに気づくでしょう。

図30の左のスライスは、我々の拡散多散乱BRDF近似のBRDFスライスを示しています。このスライス表現は、視覚的な解釈に適しています。ラフサーフェイスに対する我々の拡散BRDFの重要な特徴は、再帰反射がかすかに見えることです。図30の右のスライスは、GGXスペキュラを含む非布BRDFを表しています。このスライスでは、左端がスペキュラピークを、上端がフレネルピークを表しています。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

他の論文では、この方法で他のBRDFをパラメータ化することを検討しています。特に[Pac+12]はパラメータ化を行い、有理関数を用いてスライスを近似しました。これは、我々が最初に採用した戦略です – この場合は多散乱拡散BRDFに適用しました。

5.7　2D Rational Function Fit of the BRDF Slice

レンダリングで遭遇する多くの関数を近似する際に有理関数が有効であることを考えると、最初の実験では、BRDFスライスにフィットするために有理関数を使用しました。我々は、NLopt [Joh]とDifferential Evolution（概要については[PI15]を参照）ルーチンの両方を使用してC++コードを使用して、これらのフィットを実行しました。これは、我々は2次元有理関数にフィッティングしたときに、gloss = 0 についてほぼ完全に一致することを導出しました（式63、および図31）。残念なことに、一度グロスに別の次元を追加すると、つまり関数\(f({\mathbf n} \cdot {\mathbf h}, {\mathbf l} \cdot {\mathbf h}, gloss)\)を作成しようとすると、低誤差を維持するために係数の数が劇的に増えてしまいました。

\begin{eqnarray}
f(x, y) &=& \frac{0.568 – 0.692x – 0.938y + 1.326x^2 + 0.301y^2 + 1.96xy – 0.98x^3 + 1.533y^3}{1.0 + 1.731x – 0.997y – 0.998x^2 -0.843y^2 + 9.905xy – 0.971x^3 + 0.948y^3} \tag{63} \\
{\rm where} \, x &=& {\mathbf n} \cdot {\mathbf h} \, {\rm and} \, y= {\mathbf l} \cdot {\mathbf h}
\end{eqnarray}

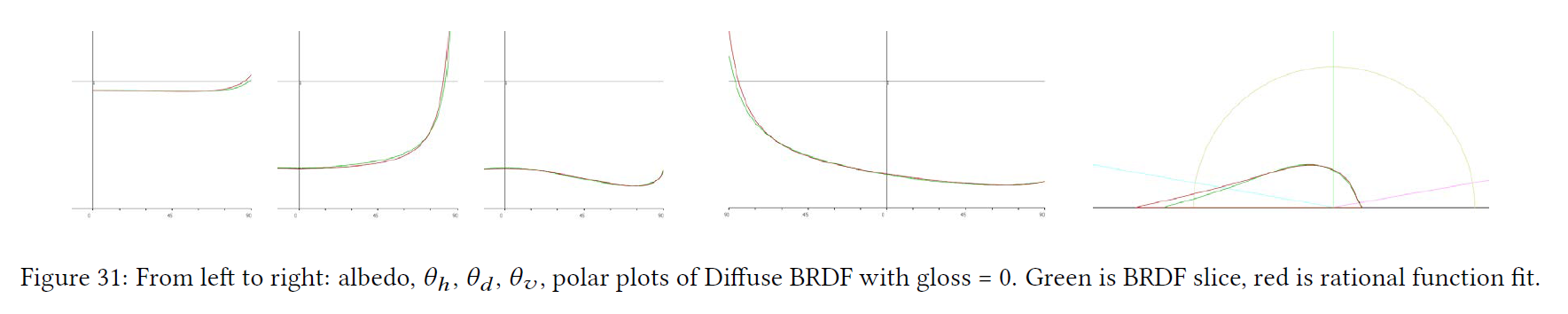
※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

5.8　Hand-Fitting the BRDF

いくつかの実験を行った結果、BRDFをハンドフィッティングすることで、目立たないところでより大きな誤差を許容し、関数の重要な特性を維持したまま、良好な結果が得られることがわかりました。

\begin{eqnarray}
f_0 &=& {\mathbf l} \cdot {\mathbf h} + (1 – {\mathbf l} \cdot {\mathbf h})^5 \tag{64} \\
f_1 &=& (1 – 0.75(1 – {\mathbf n} \cdot {\mathbf l})^5) (1 – 0.75(1 – {\mathbf n} \cdot {\mathbf v})^5) \tag{65} \\
t &=& {\rm clamp}(2.2 g – 0.5, 0, 1 ) \tag{66} \\
f_d &=& f_0 + (f_1 – f_0)t \tag{67} \\
f_b &=& (34.5g^2 – 59g + 24.5) ({\mathbf l} \cdot {\mathbf h}) \cdot 2^{-\max(73.2g – 21.2, 8.9)\sqrt{{\mathbf n} \cdot {\mathbf h}}} \tag{68} \\
f_r &=& \frac{\rho}{\pi}(f_d + f_b) \tag{69}
\end{eqnarray}

ここで、\(g\)はグロス、\(f_0\)は \(gloss=0\)のときのラフファンデーション、\(f_1\)は平滑な拡散BRDF、\(f_b\)はグレージング角での追加の再帰反射バンプ、\(\rho\)は拡散アルベド、\(f_r\)は最終的な多散乱拡散BRDF近似値です。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

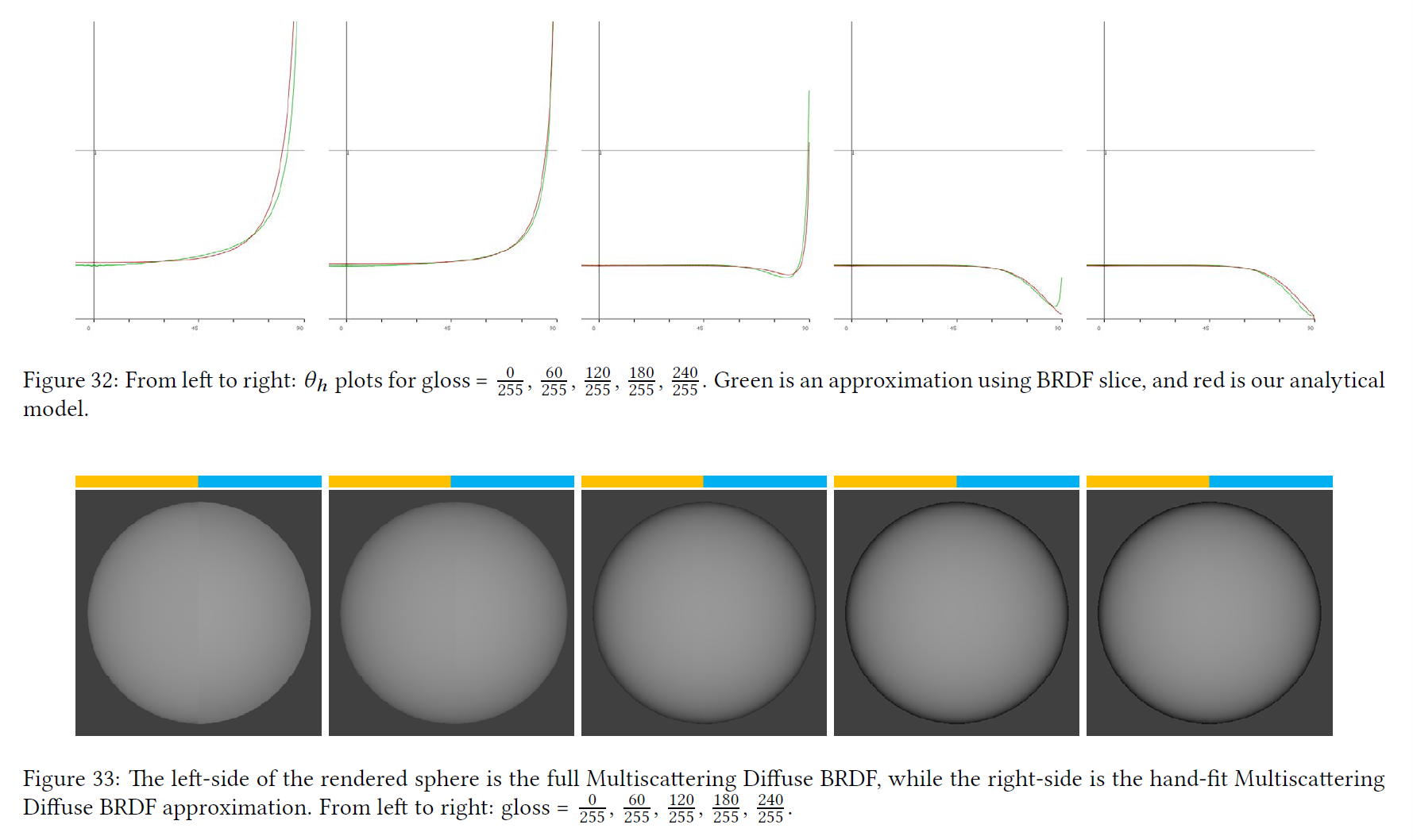
図33は、完全な多散乱拡散BRDFと我々のハンドフィット近似との比較を示し、図34は、Lambertian Diffuseと我々のハンドフィット多散乱拡散BRDF近似との比較を示しています。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

図35は、皮膚上でのランバートと多重散乱の違いを示す図です。基礎となるグロス値が低いため、マルチスキャッタリングディフューズでは顔全体にライティングの一般的な平坦化が見られます。肌はこのマルチスキャッタリングディフューズモデルには好ましくない候補のように見えますが、このモデルがまだ実験段階にあったときに最初にこのモデルの使用を依頼したキャラクター・アーティストには魅力的です。Lambertを使用した時の顔のシルエットが不自然に暗くなっていたのを修正しているようです。今後、写真に対してこの効果を検証していきたいと思います。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

5.9　Future Directions

私たちの近似値には、改善される可能性のある分野がいくつかあります。

多重散乱のシミュレーションを行う際には、拡散反射率に対して100%のアルベドを仮定しています。もし我々の近似にもっと自由度を加えるならば、[Hei+16]モデルがラフサーフェイスで達成した彩度をモデル化することができます。

また、4%のスペキュラー入射反射率(\(F_0\))を想定しており、これは誘電体の範囲の中央に位置する値です。これもまた、元のモデルをより忠実に追いかけるために考慮すべきもう一つの自由度であるかもしれません。

我々はグロスを使用して補間変数\(t\)をパラメータ化しましたが、見たように、誤差はグロスの範囲で均等に分散されていませんでした（図32、\(gloss =\frac{180}{255}\)）。代わりに\(\alpha\)を使用して\(t\)を計算することができます。

私たちは、ハンドチューニングされた近似に対する完全な有理関数解の実際の性能解析を行ったことはありません。有理関数は多数の乗算と乗算加算と1つの除算で構成されているため、適度な数の4分の1レートの命令と比較しても優位性がある可能性があります。

6　LIGHTING STUDIES

図 36 は、ゲーム内でレンダリングされたライティング研究の結果を示しており、スターキャラクターを題材に、有名な写真のライティングを模倣しています。

※図は，Danny Chan, “Material Advances in Call of Duty: WWⅡ”, SIGGRAPH 2018 Courses: Advances in Real-Time Rendering より引用。

7　CONCLUSION

図36の画像は、ライティング研究の元となったオリジナルの写真と比較すると、前回のプロジェクトでは不可能だったフォトリアリズムのレベルを示しています。

このような画質向上に貢献するいくつかの技術が紹介されています。法線とグロスをミップマッピングする方法（2章）では、表面の凹凸が遠方で適切なラフネスに変化することを確実にしました。マテリアルサーフェイスのオクルージョン（4章）のテクニックは、従来のレンダリングでは問題となっていた、ライティングがスカイライトからの光に支配されている「マジックアワー」でのレンダリングを目標にしたものです。これにより、すべてのライティング条件において、影のディテールがより豊かになりました。多重散乱拡散BRDF（5章）は、実世界の照明の観察と測定を基にしたもので、重要なこととして、グロスの範囲を通してより良いマテリアルの差別化を実現しました。

8 ACKNOWLEDGMENTS

和訳省略。