前回までのおさらい

• 超雑訳 Robust Monte Carlo Methods For Light Transport Simulation (1)
• 超雑訳 Robust Monte Carlo Methods For Light Transport Simulation (2)

前回はChapter 1を訳しました。
今回はChapter 2を読んでいくことにします。肝となるモンテカルロ積分となるので，長めになります。

---

Chapter 2

モンテカルロ積分

この章では、モンテカルロ積分について紹介します。主な目的は、確率論の基本的な概念を復習し、使用する表記法と用語を定義し、コンピュータグラフィックスで最も有用であることが証明されている分散削減技術をまとめることです。
　モンテカルロ法に関する良い参考文献には、Kalos & Whitlock [1986]、Hammersley & Handscomb [1964]、Rubinstein [1981]があり、Sobol’ [1994]は、確率や統計学のバックグラウンドがあまりない人のための良い出発点です。Spanier & Gelbard [1969]は中性子輸送問題へのモンテカルロ法の応用のための古典的な参考文献であり、Lewis & Miller [1984]はこの分野の背景情報の良い情報源です。準モンテカルロ法については、Niederreiter [1992]、Beck & Chen [1987]、Kuipers & Niederreiter [1974]を参照してください。

2.1 歴史概略

モンテカルロ法は、第2次世界大戦後の初期にロスアラモス国立研究所で生まれました。米国初の電子計算機（ENIAC）が完成したばかりで、ロスアラモスの科学者たちは、熱核兵器（水爆）の設計に使用する方法を検討していました。1946年末にStanislaw Ulamが中性子の飛行経路をシミュレートするためのランダムサンプリングの使用を提案し，John von Neumannが1947年初頭に詳細な提案を展開しました。これにより、プロジェクトの計算には欠かせない小規模なシミュレーションが可能になりました。MetropolisとUlam [1949]は1949年に彼らのアイデアを記述した論文を発表しましたが、これが1959年に多くの研究に火をつけました[Meyer 1956]。モンテカルロ法の名前は、そのカジノで有名なモナコの都市に由来しています(別のモンテカルロのパイオニアであるNick Metropolisによる提案として)。
　独立した例では、数値問題を解くためにランダムサンプリングがかなり以前に使用されていました [Kalos & Whitlock 1986]。例えば、1777年にBuffon伯爵は、等距離の平行線でマークされた板の上に針を何度も落とした実験を行いました。\(L\)を針の長さとし，\(d > L\)を線間の距離とすると，針が線と交差する確率が次であることを示しました。

\begin{eqnarray}
p = \frac{2L}{\pi d}
\end{eqnarray}

多くの年後、Laplaceは、これが\(\pi\)の値を推定するための粗雑な手段として利用できることを指摘しました。
　同様に、Kelvin卿は、気体の運動論のいくつかの側面を研究するために、私たちが現在モンテカルロ法と呼んでいるものを使用しました。彼の乱数発生器は、ガラス瓶から紙の切れ端を描くことから成り立っていました。バイアスの可能性は重要な懸念事項であり、彼は静電気によって紙が十分に混ざらないのではないかと心配しました。もう一人の初期のモンテカルロ実験者はStudent（W.S.Gossetの別名）で、彼はこの有名な\(t\)-分布の形を推測するための補助としてランダムサンプリングを使用していました。
　モンテカルロ法の起源に関する優れた参考文献としては、Stanislaw Ulam [Ulam 1987]を記念して出版されたLos Alamos Scienceの特集号があります。Kalos & Whitlock [1986]やHammersley & Handscomb [1964]の本にも、上記の戦前のランダムサンプリング実験に関する情報を含む簡単な歴史が書かれています。

2.2 数値積分のための求積法

このセクションでは、標準的な数値積分技術が高次元領域、特に積分が滑らかでない場合にはあまりうまく機能しない理由を説明します。
　次の形式の積分を考えてみましょう。

\begin{eqnarray}
I = \int_{\Omega} f(x) d\mu(x) \tag{2.1}
\end{eqnarray}

ここで，\(\Omega\)は積分領域，\(f : \Omega \rightarrow \mathbb{R}\)は実数値関数で，\(\mu\)は\(\Omega\)上の測度関数です。今、領域を\(s\)次元の単位超立方体とします。

\begin{eqnarray}
\Omega = [0, 1]^s
\end{eqnarray}

そして，測度関数を

\begin{eqnarray}
d\mu(x) = dx^2 \cdots dx^s
\end{eqnarray}

とします。ただし，\(x^j\)は点\(x = (x^1, \cdots , x^s) \in [0, 1]^s\)の\(j\)番目の成分とします。
　この種の積分は、多くの場合、単純にこの形式の和である求積法を使って近似されます。

\begin{eqnarray}
\hat{I} = \sum_{i=1}^{N} w_i f(x_i) \tag{2.2}
\end{eqnarray}

ここで、重み\(w_i\)とサンプル位置\(x_i\)はあらかじめ決定されています。一次元直交則の一般的な例としては、ニュートン-コーツ則（すなわち、中点法、台形法、シンプソン法など）、ガウス-ルジャンドル法などがあります（詳細は、Davis & Rabinowitz [1984]を参照してください）。これらの法則の\(n\)点形式は、通常、積分が十分に多くの連続導関数を持つことを条件に、いくつかの整数\(r \geq 1\)に対して\(O(n^{-r})\)の収束率を得ることができます。例えば、\(f\)が少なくとも4つの連続導関数を持つ場合、シンプソン法を用いた誤差は\(O(n^{-4})\)となります [Davis & Rabinowits 1984]。
　これらの求積法は通常一次元の積分に対しては非常によく機能しますが、高次元に拡張すると問題が発生します。例えば、一般的なアプローチは、次の形式のテンソル積の法則を使用することです。

\begin{eqnarray}
\hat{I} = \sum_{i_1=1}^{n} \sum_{i_2=1}^{n} \cdots \sum_{i_s=1}^{n} w_{i_1} w_{i_2} \cdots w_{i_s} f(x_{i_1}, x_{i_2}, \cdots , x_{i_s})
\end{eqnarray}

ここで\(s\)は次元であり，\(w_i\) と \(x_i\) は，与えられた 1 次元ルールの重みとサンプル位置です。この手法は，ベースとなる1次元規則と同じ収束率を持ちます（これを\(O(n^{-r})\)とします）が，より多くの標本点（すなわち，\(N=n^s\)）を使用します。したがって、総サンプル数に換算すると、収束率は\(O(N^{-r/s})\)しかありません。これは，テンソル積の法則の効率が次元によって急速に低下することを意味しており，これはよく次元の呪いと呼ばれる事実です [Niederreiter 1992, p.2]。
　\(r\)の値を大きくした一次元ルールを使うことで収束率を上げることができますが、これには2つの問題があります。第一に、サンプルの総数\(N=n^s\)は高次元では非現実的になる可能性があります。これは\(r\)とともに\(n\)が線形に増加するためです(具体的には\(n \leq r/2\))。例えば、2点ガウス求積では、少なくとも\(2^s\)のサンプルが必要ですが、シンプソン法では、少なくとも\(3^s\)のサンプルが必要です。第二に、収束率を速くするには、積分器の平滑性を高める必要があります。例えば、関数\(f\)が不連続性を持つ場合、任意の1次元の求積則の収束率はせいぜい\(O(n^{-1})\)であり(不連続性の位置が事前に知られていないと仮定して)、対応するテンソル積の法則は\(O(N^{-1/s})\)以下の収束率で収束することになります。
　もちろん、すべての多次元積分則がテンソル積の形をとるわけではありません。しかし、Bakhvalovの定理 [Davis & Rabinowitsz 1984, p.354]と呼ばれる、任意の決定論的な求積法の収束率を制限する重要な結果があります。本質的には，任意の\(s\)次元の求積法が与えられると，連続的で有界の導関数\(r\)を持つ関数\(f\)が存在し，その誤差は\(N^{-r/s}\)に比例することを述べています．具体的には、\(C_{M}^{r}\)を次のような関数\(f : [0, 1]^s \rightarrow \mathbb{R} \)の集合を表すとします。

\begin{eqnarray}
| \frac{{\partial}^s f }{ {\partial}(x^2)^{a_1} \cdots {\partial}(x^s)^{a_s} } | \leq M
\end{eqnarray}

\(\sum a_i = r\)を持つ，\(a_1, \cdots , a_s\)すべてについて，ベクトル\(x\)の\(j\)番目の座標を\(x^j\)で示すことを思い出してください。ここで、任意の\(N\)点の求積法を考えてみましょう。

\begin{eqnarray}
\hat{I} (f) = \sum_{i=1}^N w_i f(x_i)
\end{eqnarray}

ここで、各\(x_i\)は\([0, 1]^s\)の点であり、いくつかの積分を近似したいとします。

\begin{eqnarray}
I(f) = \int_{[0, 1]^s} f(x^1, \cdots , x^s) dx^1 \cdots dx^s
\end{eqnarray}

このときBakhvalovの定理によれば、関数\(f \in C_{M}^{r}\)が存在し，その誤差は

\begin{eqnarray}
\left| \hat{I}(f) – I(f) \right| \gt k \cdot N^{-r/s}
\end{eqnarray}

となります。ここで定数\(k \gt 0\)は\(M\)と\(r\)にのみ依存します。このように\(f\)が有界で連続的な一次微分を持っていても、\(O(N^{-1/s})\) よりも優れた誤差境界を持つ求積法はありません。

2.3 少しだけ確率論

モンテカルロ積分を説明する前に、確率や統計学の概念をいくつかおさらいします。確率についてはPitman [1993]を、測度論についてはHalmos [1950]を参照してください。確率論の簡単な紹介は，上で引用したモンテカルロの文献にもあります。

2.3.1 累積分布と密度関数

実数確率変数\(X\)の累積分布関数は次のように定義されることを思い出してください。

\begin{eqnarray}
P(x) = P_r \{X \leq x \}
\end{eqnarray}

であり、対応する確率密度関数は

\begin{eqnarray}
p(x) = \frac{dP}{dx}(x)
\end{eqnarray}

です(密度関数またはpdfとしても知られています)。これは重要な関係を導きます

\begin{eqnarray}
P_r \{ \alpha \leq X \leq \beta \} = \int_{\alpha}^{\beta} p(x) dx = P(\beta) – P(\alpha) \tag{2.3}
\end{eqnarray}

多次元乱数ベクトル(\(X^1, \cdots , X^s\))に対応する概念は、同時累積分布関数で

\begin{eqnarray}
P(x^1, \cdots, x^s) = P_r \{ X^i \leq x^i \quad {\rm{for \, all}} \quad i=1, \cdots, s \}
\end{eqnarray}

であり，同時密度関数は

\begin{eqnarray}
p(x^1, \cdots, x^s) = \frac{{\partial}^s P}{\partial x^1 \cdots \partial x^s} (x^1, \cdots, x^s)
\end{eqnarray}

です。このため，任意のルベーグ可測集合 \(D \in \mathbb{R}^s\)について次の関係性を持ちます。

\begin{eqnarray}
P_r \{ x \in D \} = \int_D p(x^1, \cdots, x^s) dx^1 \cdots dx^s \tag{2.4}
\end{eqnarray}

より一般的には、任意の領域\(\Omega\)の値を持つ確率変数\(X\)に対して、その確率測度（分布の確率分布としても知られている）は、任意の可測集合\(D \subset \Omega\)について次のような測度関数\(P\)となります。

\begin{eqnarray}
P(D) = P_r \{ X \in D \}
\end{eqnarray}

特に、確率測度は、\(P(\Omega) = 1\)を満たさなければなりません。対応する密度関数\(p\)は、ラドン・ニコディム微分として定義されます。

\begin{eqnarray}
p(x) = \frac{dP}{d \mu} (x)
\end{eqnarray}

これは次を満たす単純な関数\(p\)となります。

\begin{eqnarray}
P(D) = \int_{D} p(x) d\mu(x) \tag{2.5}
\end{eqnarray}

このように，与えられた領域\(D\)上で\(p(x)\)を積分することで，確率\(X \in D\)を求めることができます。これを(2.3)式と(2.4)式と比較してみると，これは(2.5)式のより一般的な関係の単に特別な場合となります。
　密度関数\(p\)は、それを定義するのに使用される測度\(\mu\)に依存することに注意してください。我々は、特定の測度\(\mu\)に関する密度を表すために、\(p = P_{\mu}\)という表記法を使用しますが、これは解析でよく使用される\(u_x = \partial u / \partial x\)という表記法に対応します。この記法は、同一領域\(\Omega\)上に定義されたいくつかの関連する測度関数（例えば、第3章で説明する立体角や射影された立体角測度など）がある場合に有用となります。測度空間とラドン・ニコディム微分についての詳しい情報は Halmos [1950] を参照してください。

2.3.2 期待値と分散

確率変数\(Y = f(X)\)の期待される値または期待値は、次のように定義されます。

\begin{eqnarray}
E[Y] = \int_{\Omega} f(x) p(x) d\mu(x) \tag{2.6}
\end{eqnarray}

一方，その分散は
\begin{eqnarray}
V[Y] = E[(Y- E[Y])^2 ] \tag{2.7}
\end{eqnarray}

我々は常に、すべての確率変数の期待値と分散が存在すると仮定します（すなわち、対応する積分は有限とします）。
　これらの定義から、任意の定数\(a\)に対して、次のようになることが容易にわかります。

\begin{eqnarray}
E[aY] &=& a E[Y] \\
V[aY] &=& a^2 V[Y]
\end{eqnarray}

　　以下のような恒等式も有用です：

\begin{eqnarray}
E \left[ \sum_{i=1}^N Y_i \right] = \sum_{i=1}^N E[Y_i]
\end{eqnarray}

これは任意の確率変数\(Y_1, \cdots , Y_N\)に対して保たれます。 一方、次の恒等式は、変数\(Y_i\)が独立している場合にのみ保たれます：

\begin{eqnarray}
V \left[ \sum_{i=1}^N Y_i \right] = \sum_{i=1}^{N} V[Y_i]
\end{eqnarray}

これらの規則から、分散のより単純な式を導出できることに注目してください：

\begin{eqnarray}
V[Y] = E[(Y- E[Y])^2] = E[Y^2] – E[Y]^2
\end{eqnarray}

　もう一つの有用な量は、確率変数の標準偏差で、これは単に分散の平方根となります。

\begin{eqnarray}
\sigma [Y] = \sqrt{V[Y]}
\end{eqnarray}

　これはRMS誤差とも呼ばれています。

2.3.3 条件付き密度と周辺密度

\(X \in \Omega_1\)と\(Y \in \Omega_2\)を確率変数のペアとすると、次のようになります。

\begin{eqnarray}
(X, Y) \in \Omega
\end{eqnarray}

ここで，\(\Omega = \Omega_i \times \Omega_2\)です。\(P\)を\((X, Y)\)の同時確率測度とすると，\(P(D)\)は，任意の可測集合\(D \subset \Omega\)について\((X, Y) \in D\)の確率を表します。このとき、対応する同時密度関数\(p(x, y)\)は次を満たします。

\begin{eqnarray}
P(D) = \int_D p(x, y) d{\mu}_1(x) d{\mu}_2(y)
\end{eqnarray}

ここで，\(\mu_1\)と\(\mu_2\)はそれぞれ\(\Omega_1\)上と\(\Omega_2\)上の測度を表します。以下では、測度関数の表記をやめて、

\begin{eqnarray}
P(D) = \int_D p(x, y) dx dy
\end{eqnarray}

と単純に書くことにします。
　\(X\)の周辺密度関数は今次のように定義されます。

\begin{eqnarray}
p(x) = \int_{\Omega_2} p(x, y) dy \tag{2.8}
\end{eqnarray}

一方，条件付き密度関数\(p(y | x)\)は次のように定義されます。

\begin{eqnarray}
p(y | x) = p(x, y) / p(x) \tag{2.9}
\end{eqnarray}

周辺密度\(p(y)\)と条件付き密度\(p(x | y)\)は同様にして定義され，有用な恒等式を導きます。

\begin{eqnarray}
p(x, y) = p(y | x) p(x) = p(x | y) p(y)
\end{eqnarray}

　もう一つの重要な概念は、確率変数\(G = g(X, Y)\)の条件付き期待値であり、次のように定義されます。

\begin{eqnarray}
E[G | x] = \int_{\Omega_2} g(x, y) p(y | x) dy = \frac{ \int g(x, y) p(x, y) dy }{ \int p(x, y) dy } \tag{2.10}
\end{eqnarray}

　また、条件付き期待値には\(E_Y[G]\)という表記法を使用しますが、これは\(Y\)が積分されている密度関数の確率変数であるという事実を強調するものです。
　条件付き期待値と分散の観点から見た\(G\)の分散には、非常に有用な式があります。

\begin{eqnarray}
V[G] = E_X V_Y G + V_X E_Y G \tag{2.11}
\end{eqnarray}

言い換えれば、\(V[G]\)は条件付き分散の平均値に条件付き平均の分散を加えたものとなります。この恒等式を証明するために、次のことを思い出してください。

\begin{eqnarray}
V[F] = E[F^2] – E[F^2]
\end{eqnarray}

そして，次を見てみてください。

\begin{eqnarray}
E_X V_Y G + V_X E_Y G &=& E_X \{ E_Y[G^2] – [E_Y G]^2 \} + E_X [E_Y G]^2 – [E_X E_Y G]^2 \\
&=& E_X E_Y [G^2] – [E_X E_Y G]^2 \\
&=& V[G]
\end{eqnarray}

以下では、この恒等式を使用して、層化サンプリングや期待値の使用など、幾つかの分散削減技術を分析します。

2.4 モンテカルロ積分の基礎

モンテカルロ積分の考え方は、ランダムサンプリングを用いて次の積分を評価することです。

\begin{eqnarray}
I = \int_{\Omega} f(x) d\mu(x)
\end{eqnarray}

基本的な形式では、これは、便利な密度関数\(p\)に従って\(N\)個の点\(X_1, \cdots , X_N\)を独立してサンプリングし、その推定値を次によって計算することによって行われます。

\begin{eqnarray}
F_N = \frac{1}{N} \sum_{i=1}^{N} \frac{f(X_i)}{p(X_i)} \tag{2.12}
\end{eqnarray}

ここでは、結果が確率変数であること、そしてその特性がサンプルポイントの数に依存することを強調するために、\(\hat{I}\)ではなく\(F_N\)という表記を用いています。このタイプの推定量は、調査サンプリングの文献（連続領域ではなく離散領域の場合）で最初に使用され、Horvitz-Thompson推定量として知られていることに注意してください[Horvitz & Thompson 1952]。
　例えば、領域が\(\Omega\)であり、サンプル\(X_i\)が独立して一様にランダムに選ばれているとします。この場合、推定器 (2.12) は次のようになります。

\begin{eqnarray}
F_N = \frac{1}{N} \sum_{i=1}^N f(X_i)
\end{eqnarray}

これは、サンプルの位置がランダムであることを除いて、求積法と同じ形式を持ちます。
　推定量\(F_N\)が平均的に正しい結果を与えることを示すのは簡単です。具体的には\(f(x)/p(x)\)が\(f(x) \neq 0\)のときに有限であることを条件とし，

\begin{eqnarray}
E[F_N] &=& E \left[ \frac{1}{N} \sum_{i=1}^N \frac{f(X_i)}{p(X_i)} \right] \\
&=& \frac{1}{N} \sum_{i=1}^{N} \int_{\Omega} \frac{f(x)}{p(x)} p(x) d\mu (x) \\
&=& \int_{\Omega} f(x) d\mu(x) \\
&=& I
\end{eqnarray}

となります。

モンテカルロ積分の利点
モンテカルロ積分には、以下のような大きな利点があります。第一に、積分の滑らかさに関係なく、どの次元でも\(O(N^{-1/2})\)の速度で収束します。このため、不連続関数の多次元積分を計算する必要がある場合が多いグラフィックスの分野で特に有用です。収束率については後述の2.4.1節で説明します。
　第二に、モンテカルロ積分は簡単です。必要な操作は、サンプリングと点の評価という2つの基本操作だけです。これにより、オブジェクト指向のブラックボックスインターフェースの使用が推奨され、モンテカルロソフトウェアの設計に大きな柔軟性をもたらします。例えば、コンピュータグラフィックスの文脈では、モーションブラー、被写界深度、関与媒質、プロシージャルサーフェスなどの効果を簡単に取り込むことができます。
　第三に、モンテカルロは一般的です。ここでも、これはランダムサンプリングに基づいているという事実に由来しています。サンプリングは、\([0, 1]^s\)と自然な対応関係を持たない領域でも使用することができ、したがって、数値的な求積にはあまり適していません。グラフィックスの例として，光輸送問題がすべての輸送経路の空間上の積分として自然に表現できることを観測します（第8章）．この領域は技術的には無限次元空間ですが（これは数値求積法では困難です），モンテカルロ法では簡単に扱うことができます。
　最後に、モンテカルロ法は、特異点を持つ被積分関数に対しては、求積法よりも適しています。特異点を除去するための解析的変換がない場合でも，重点サンプリング（2.5.2節参照）を適用して，効果的にこのような被積分関数を扱うことができます（後述の棄却サンプリングとメトロポリス法の説明を参照してください）。
　このセクションの残りの部分では、モンテカルロ積分の収束率について説明し、確率変数のサンプリング技術の簡単なおさらいをします。その後、より一般的な種類のモンテカルロ推定量の性質について説明をします。

2.4.1 収束率

モンテカルロ積分の収束率を決定するために、まず\(F_N\)の分散を計算します。表記を簡単にするために\(Y_i = f(X_i)/p(X_i)\)とし，次のようになります。

\begin{eqnarray}
F_N = \frac{1}{N} \sum_{i=1}^N Y_i
\end{eqnarray}

また，\(Y = Y_1\)とします。このとき，次を得ます。

\begin{eqnarray}
V[Y] = E[Y^2] – E[Y]^2 = \int_{\Omega} \frac{ f^2(x) }{ p(x) } d\mu (x) – I^2
\end{eqnarray}

この量が有限であると仮定すると、\(V[F_N]\)の分散が\(N\)に対して線形に減少することを確認するのは簡単です：

\begin{eqnarray}
V[F_N] = V \left[ \frac{1}{N} \sum_{i=1}^N Y_i \right] = \frac{1}{N^2} V \left[ \sum_{i=1}^N Y_i \right] = \frac{1}{N^2} \sum_{i=1}^N V[Y_i] = \frac{1}{N} V[Y] \tag{2.13}
\end{eqnarray}

ここでは、\(V[aY] = a^2 V[Y]\)を使用し、\(Y_i\)が独立したサンプルであるという事実を使用しています。したがって、標準偏差は

\begin{eqnarray}
\sigma [F_N] = \frac{1}{\sqrt{N}} \sigma Y
\end{eqnarray}

で，これはすぐにRMS誤差が\(O(N^{-1/2})\)の変化量で収束することを示しています。
　また、Chebychevの不等式を用いて、絶対誤差の確率的な境界を得ることも可能です：

\begin{eqnarray}
P_r \left\lbrace | F – E[F] | \geq \left( \frac{V[F]}{\delta} \right)^{1/2} \right\rbrace \leq \delta
\end{eqnarray}

この不等式は、\(V[F] \lt \infty\)のような任意の確率変数\(F\)に対して保たれます。この不等式を分散 (2.13) に適用すると、次のようになります。

\begin{eqnarray}
P_r \left\lbrace |F_N – I| \geq N^{-1/2} \left( \frac{V[Y]}{\delta} \right)^{1/2} \right\rbrace \leq \delta
\end{eqnarray}

したがって、任意の固定閾値\(\delta\)に対して、絶対誤差は変化量\(O(N^{-1/2}\)で減少します。
　絶対誤差のよりタイトな境界は、\(F_N\)が\(N \rightarrow \infty\)としての極限で正規分布に収束するという中心極限定理を用いて求めることができます。具体的には、この定理は次の式を示しています。

\begin{eqnarray}
\lim_{N \rightarrow \infty} P_r \left\lbrace \frac{1}{N} \sum_{i=1}^N Y_i – E[Y] \leq t \frac{\sigma[Y]}{\sqrt{N}} \right\rbrace = \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{t} e^{-x^2/2} dx
\end{eqnarray}

ここで、右の式は（累積）正規分布です。この式は、次のように再整理することができます。

\begin{eqnarray}
P_r \lbrace |F_N – I| \geq t \sigma [F_N] \rbrace = \sqrt{2 / \pi} \int_{t}^{\infty} e^{-x^2/2} dx
\end{eqnarray}

右側の積分は，\(t\)の経過とともに非常に急速に減少します。例えば，\(t = 3\)のとき，右辺は約\(0.0003\)です。このように、\(N\)が中心限界定理が適用されるのに十分な大きさであれば、\(F_N\)がその平均値から3つの標準偏差以上異なることは、\(0.3\%\)程度の変化しかありません。
　最後に、モンテカルロ積分は、期待値\(E[Y]\)が存在する限り、分散\(V[Y]\)が無限大であっても収束することに注意してください（収束は遅くなりますが）。これは，次のような方程式が存在するという大数の強法則によって保証されています。

\begin{eqnarray}
P_r \left\lbrace \lim_{N \rightarrow \infty} \frac{1}{N} \sum_{i=1}^{N} Y_i = E[Y] \right\rbrace = 1
\end{eqnarray}

2.4.2 確率変数のサンプリング

確率変数のサンプリングには様々な手法がありますが、ここでは簡単におさらいします。さらなる詳細は、序章で述べられている参考文献を参照してください。
　一つの方法としては、変換法や逆関数法があります。一次元では，密度関数\(p\)から標本化したいとします．\(p\)を対応する累積分布関数とすると、逆関数法は、\(U\)を\([0, 1]\)上の一様乱数である\(X = P^{-1}(U)\)とします。この手法は，周辺分布と条件付き分布を計算して，それぞれの次元を別々に反転させるか，より一般的には，適切なヤコビアン行列式（\(J_g\)が\(g\)のヤコビアンを表すような\(| \det(J_g(x))|^{-1} = p(x)\)）を持つ変換\(x = g(u)\)を導出することによって，簡単にいくつかの次元に拡張することができます．
　変換技法の主な利点は、パラメータ空間\([0, 1]^s\)を層別化し、これらのサンプルを\(\Omega\)にマッピングすることで、サンプルを簡単に層別化できることです（2.6.1節参照）。もう一つの利点は、この手法はサンプルあたりのコストが固定されており、簡単に見積もることができるということです。主な欠点は, 密度\(p(x)\)を解析的に積分しなければならないことですが, これは必ずしも可能ではありません. また，累積分布が解析的な逆行列を持つことが望ましいです，これはなぜかというと数値的な逆行列の方が一般的に遅いためです。
　二つ目のサンプリング技法は、von Neumann[Ulam 1987]による棄却法です。このアイデアは、ある定数\(M\)について次のようないくつかの便利な密度\(q\)からサンプリングすることです。

\begin{eqnarray}
p(x) \leq M q(x)
\end{eqnarray}

一般的には、\(q\)からのサンプルは、変換法によって生成されます。以下の手続きを適用します：

function REJECTION-SAMPLEING()
　　for \(i\)=1 to \(\infty\)
　　　　Sample \(X_i\) according to \(q\).
　　　　Sample \(U_i\) uniformly on \([0, 1]\).
　　　　if \(U_i \leq p(X_i) / (M q(X_i)\)
　　　　　　then return \(X_i\)

この手順で密度関数が\(p\)であるサンプル\(X\)を生成することは容易に検証できます。
　棄却サンプリングの主な利点は、解析的に積分できない密度関数であっても、任意の密度関数で使用できることです。しかし、我々はまだ\(p\)に対して上限となるある関数\(Mq\)を積分可能にする必要があります。さらに、許容される前に取らなければならないサンプルの平均数が\(M\)であるため、この上限は適度にタイトでなければなりません。このように、棄却サンプリングがナイーブに適用された場合、効率は非常に低くなる可能性があります。もう一つの欠点は、層化を適用することが難しいことです：最も近い近似は、ランダムベクトル\((X, U)\)の領域を層化することですが、結果として得られる層化は、変換法ほどではありません。
　第3の一般的なサンプリング手法はメトロポリス法（マルコフ連鎖モンテカルロ法としても知られている）であり、これは第11章で説明します。この手法は高次元空間上の任意の密度をサンプリングするのに便利で、密度関数を正規化する必要がないという利点があります。メトロポリス法の主な欠点は、生成されるサンプルが独立していないことです。したがって，与えられた密度\(p\)から長い連続したサンプルを生成する必要がある場合に最も有用です。
　最後に、特定の分布からサンプリングするための様々な手法があります（Rubinstein [1981]を参照）。例えば、\(X\)が\(k\)個の独立した一様確率変数\(U_1, \cdots, U_k\)の最大値である場合、\(X\)は密度関数\(p(x) = kx^{k-1}\)(ただし，\(0 \leq x \leq 1\)とします）を持ちます。このような “トリック “は，正規分布[Rubinstein 1981]のような統計学における多くの標準分布をサンプリングするために使用できます。

2.4.3 推定器とその性質

ここまでは、ランダムサンプルを使って積分を推定する方法を1つだけ説明してきました。しかし、実際には非常に多様な手法があり、それらはモンテカルロ推定器の概念に包含されています。推定器の様々な性質と、なぜそれが望ましいのかをレビューします。
　モンテカルロ推定器の目的は、関心のある量\(Q\)（推定値とも呼ばれる）の値を近似することです。通常、我々は\(Q\)を与えられた積分の値として定義しますが、より一般的な状況も可能です（例えば、Qは2つの積分の比である可能性があります）。そして、推定器は次の形式の関数として定義されます。

\begin{eqnarray}
F_N = F_N(X_1, \cdots, X_N) \tag{2.14}
\end{eqnarray}

ここで、\(X_i\)は確率変数です。\(F_N\)の特定の数値を推定値と呼びます。\(X_i\)は必ずしも独立ではなく，異なる分布を持つ可能性があることに注意してください。
　コンピュータグラフィックスの標準用語には，統計学との違いがあることに注意してください。統計学では，各\(X_i\)の値を観測値，ベクトル\((X_1, \cdots , X_N)\)を標本，\(N\)を標本サイズと呼びます．一方，コンピュータグラフィックスでは，通常，個々の\(X_i\)の値を標本と呼び，\(N\)を標本数と呼びます．ここでは，通常，グラフィックスの規則を使用します。
　ここで、モンテカルロ推定量の有用な特性をいくつか定義します。量\(F_N – Q\)を誤差 と呼び、その期待値をバイアス と呼びます：

\begin{eqnarray}
\beta [F_N] = E [F_N – Q] \tag{2.15}
\end{eqnarray}

推定器は、すべての標本サイズ\(N\)に対して\(\beta[F_N]=0\)、言い換えれば以下の場合、不偏 と呼ばれます。

\begin{eqnarray}
E[F_N] = Q \quad {\rm for \, all} \quad N \geq 1 \tag{2.16}
\end{eqnarray}

例として，確率変数

\begin{eqnarray}
F_N = \frac{1}{N} \sum_{i=1}^N \frac{f(X_i)}{p(X_i)}
\end{eqnarray}

は(2.4節でみたように）積分\(I = \int_{\Omega} f(x) d\mu(x)\)の不偏推定器となります。
　誤差\(F_N – Q\)が1の確率でゼロになる場合、言い換えれば以下のようになる場合、推定器は一貫性があると呼ばれます。

\begin{eqnarray}
P_r \left\lbrace \lim_{N \rightarrow \infty} F_N = Q \right\rbrace = 1 \tag{2.17}
\end{eqnarray}

推定器が一貫しているためには、\(N\)が増加するにつれてバイアスと分散の両方がゼロになることが十分条件となります：

\begin{eqnarray}
\lim_{N \rightarrow \infty} \beta[F_N] = \lim_{N \rightarrow \infty} V[F_N] = 0
\end{eqnarray}

特に、\(N\)が無限大になるにつれて分散がゼロに減少する限り、不偏推定器は一貫しています。
　不偏推定器を好む主な理由は、誤差の推定が容易であるからです。一般的に、我々の目標は、以下で定義される平均二乗誤差（MSE）を最小化することです。

\begin{eqnarray}
MSE[F] = E[(F – Q)^2] \tag{2.18}
\end{eqnarray}

(ここでは添え字\(N\)を落としています)。一般的に、平均二乗誤差は次のように書き換えることができます。

\begin{eqnarray}
MSE[F] &=& E[(F – Q)^2] \\
&=& E[(F – E[F])^2] + 2E[F – E[F]] (E[F] – Q) + (E[F] – Q)^2 \\
&=& V[F] + \beta[F]^2
\end{eqnarray}

このように、誤差を推定するためには、起こりうるなバイアスの上限を持たなければなりません。一般的に、これは推定値\(Q\)に関する追加の知識を必要とし、適切な境界を見つけるのは大抵困難となります。
　一方、不偏推定器の場合は、平均二乗誤差が分散と同じになるように\(E[F] = Q\)があります：

\begin{eqnarray}
MSE[F] = V[F] = E[(F – E[F])^2]
\end{eqnarray}

これにより、いくつかの独立したサンプルを取るだけで、誤差推定値を得ることがはるかに簡単になります。\(Y_1, \cdots , Y_N\)を不偏推定器\(Y\)の独立標本とし、以下のようにします。

\begin{eqnarray}
F_N = \frac{1}{N} \sum_{i=1}^N Y_i
\end{eqnarray}

(これも偏りのない推定器です)前と同様にして、その量

\begin{eqnarray}
\hat{V}[F_N] = \frac{1}{N – 1} \left\lbrace \left( \frac{1}{N} \sum_{i=1}^N {Y_i}^2 \right) – \left( \frac{1}{N} \sum_{i=1}^N Y_i \right)^2 \right\rbrace
\end{eqnarray}

は変数\(V[F_N]\)の不偏推定量です（Kalos & Whitlock [1986]参照）。このように、不偏推定器では誤差推定値が容易に得られます。
　多くの独立した標本を取ることで、以下のように、不偏推定器の誤差を必要に応じて小さくできることに注意してください。

\begin{eqnarray}
V[F_N] = V[F_1] / N
\end{eqnarray}

しかし、これはまた、実行時間を\(N\)の因子だけ増加させることになる。理想的には、分散と実行時間の両方が小さい推定量を見つけたいところです。このトレードオフは、モンテカルロ推定器の効率性 によって要約されます：

\begin{eqnarray}
\epsilon [F] = \frac{1}{V[F] T[F]} \tag{2.19}
\end{eqnarray}

ここで，\(T[F]\)は\(F\)を評価するために必要とされる時間です。このように、推定器が効率的であればあるほど、与えられた固定の実行時間で得られる分散は小さくなります。

2.5 分散低減Ⅰ：解析的積分

効率的な推定器の設計は、モンテカルロ研究の基本的な目標です。様々な手法が開発されてきましたが、これらは単に分散低減法 と呼ばれることが多いです。以下のセクションでは、コンピュータグラフィックスで最も有用であることが証明されている分散低減法について説明します。これらの手法は、4つの主要な考え方に基づいて、いくつかのカテゴリーに分類することができます：

• 被積分関数に似た関数を解析的に積分する。
• 積分領域をまたいでサンプル点を一様に配置する。
• サンプリング中に収集した情報に基づいてサンプル密度を適応的に制御する
• 値が相関している2つ以上の推定器からのサンプルを結合する。

まず、解析的積分に基づいた手法の議論から始めます。この考え方を利用する方法は実際にはいくつかあり、期待値の利用、重点サンプリング、制御変量法などを含みます。これらは、コンピュータグラフィックスの問題で最も強力で有用な方法のものです。
　多くの分散低減法は、モンテカルロ法が発明されるずっと前に、調査サンプリングの文献で最初に提案されたことに注意してください。たとえば、層化サンプリング、重点サンプリング、および制御変量法などの技術は、すべて調査サンプリングで最初に使用されました [Cochran 1963]。

2.5.1 期待値の利用

おそらく分散を減らす最も明白な方法は、領域の1つ以上の変数に関して解析的に積分することによって、標本空間の次元を減らすことです。この考え方は，一般的に，期待値の利用 または次元の削減 と呼ばれます。具体的には，この方法は，次の形式の推定器を置き換えることから成ります。

\begin{eqnarray}
F = f(X, Y) / p(X, Y) \tag{2.20}
\end{eqnarray}

別の形式では

\begin{eqnarray}
F’ = f'(X) / p(X) \tag{2.21}
\end{eqnarray}

であり，ここで\(f'(x)\)と\(p(x)\)は次のように定義されます

\begin{eqnarray}
f'(x) &=& \int f(x, y) dy \\
p(x) &=& \int p(x, y) dy
\end{eqnarray}

したがって，この手法を適用するためには，\(y\)に関して\(f\)と\(p\)の両方を積分することができなければならなりません。また、周辺密度\(p(x)\)からサンプルすることができなければなりませんが、これは、前と同様に単に\((X, Y)\)を生成し、\(Y\)の値を無視することによって行うことができます。
　この手法の名前は、推定量\(F’\)が単に\(F\)の条件付き期待値であるという事実に由来します：

\begin{eqnarray}
F’ &=& E_Y \left[ \frac{f(X, Y)}{p(X, Y)} \right] \\
&=& \int \frac{f(X, y)}{p(X, y)} p(y | X) dy \\
&=& \int \frac{f(X, y)}{p(X, y)} \frac{p(X, y)}{\int p(X, y’) dy’} dy
&=& f(X) / p(X)
\end{eqnarray}

そのため、分散低減の分析が容易になります。式(2.11)からの次の恒等式を思い出してください

\begin{eqnarray}
V[F] = E_X V_Y F + V_X E_Y F
\end{eqnarray}

そして，\(F’=E_YF\)を用いて，次をすぐさま得ます。

\begin{eqnarray}
V[F] – V[F’] = E_X V_Y F
\end{eqnarray}

この量は常に非負であり，（期待するように）\(Y\)のランダム・サンプリングによって引き起こされた\(F\)の分散の成分を表します。
　解析的に積分された量を評価してサンプルするのが高価すぎない限り、期待値の利用は好ましい分散低減技術です。しかし，期待値がより大きな計算の1つの部分だけに使用される場合，分散が実際に増加することがあることに留意してください。Spanier & Gelbard [1969]は、中性子輸送問題の文脈で、吸収推定量衝突推定量（粒子の経路に沿った各衝突での吸収の期待値を記録する）の分散を比較することによって、このことを例示しています。これらの推定量のそれぞれが、他の推定量よりも分散が小さくなる条件があることを示しています。

2.5.2 重点サンプリング

重点サンプリング とは、被積分関数\(f\)に似た密度関数\(p\)を選択する原理のことです。比例定数が次のようになる\(p(x) = cf(x)\)とするのが最良の選択であることはよく知られている事実です(\(p\)を積分して1になるのを確認してください)。

\begin{eqnarray}
c = \frac{1}{\int_{\Omega} f(y) d\mu(y)} \tag{2.22}
\end{eqnarray}

これにより、以下からサンプル点\(X\)のすべてについて分散がゼロの推定器が得られます。

\begin{eqnarray}
F = \frac{f(X)}{p(X)} = \frac{1}{c}
\end{eqnarray}

　残念ながら、この手法は実用的ではありません。なぜなら、正規化定数\(c\)を計算するために目的の積分の値をすでに知っている必要があるからです。それでもなお、形状が\(f\)に似ている密度関数\(p\)を選択することで、分散を減らすことができます。典型的には，\(p \propto g\)とし，解析的に積分できる関数\(g\)を得るために，\(f\)のいくつかの因子を捨てるか，近似することによって，分散を減らすことができます。また，そのものからサンプルを生成する便利な方法があるような\(p\)を選ぶことも重要です。低次元の積分問題では，\(f\)の離散近似（例えば，分割定数や線形関数）を構築するのが有用な戦略です。これは、離散の初期化段階で行うことも、アルゴリズムの進行に合わせて適応的に行うこともできます。このような近似の積分は非常に安価に計算され維持され、サンプリングは木構造化または部分和によって効率的に行うことができます。
　要約すると、重点サンプリングはモンテカルロ積分の最も有用で強力な手法の一つです。特に、特異点などの理由で、領域の比較的小さな部分で大きな値を持つ積分に役立ちます。

2.5.3 変数変量法

変数変量法では、解析的に積分可能で、積分に近い関数\(g\)を見つけて、それを減算するという考え方です。実質的には、積分は次のように書き換えられます。

\begin{eqnarray}
I = \int_{\Omega} g(x) d\mu(x) + \int_{\Omega} f(x) – g(x) d\mu(x)
\end{eqnarray}

そして，このとき次の形式の推定器でサンプリングされます。

\begin{eqnarray}
F = \int_{\Omega} g(x) d\mu(x) + \frac{1}{N} \sum_{i=1}^N \frac{f(X_i) – g(X_i)}{p(X_i)}
\end{eqnarray}

ここでは、最初の積分の値が正確に知られています(いつものように\(p\)は\(X_i\)が選ばれる密度関数です)。
　この推定器は、以下のような場合には必ず基本推定器(2.12)よりも分散が小さくなります。

\begin{eqnarray}
V \left[ \frac{f(X_i) – g(X_i)}{p(X_i)} \right] \leq V \left[ \frac{f(X_i)}{p(X_i)} \right]
\end{eqnarray}

特に、\(g\)が\(p\)に比例する場合、2つの推定量は定数だけ異なり、その分散は同じであることに注目してください。このことは、\(g\)がすでに重点サンプリングに使用されている場合（比例の定数まで）、それを変数変量法としても使用することは有用ではないことを示唆しています。別の観点から、\(f\)に近似した関数\(g\)が与えられた場合、それを変数変量法として使用するか、重点サンプリングの密度関数として使用するかを決定しなければなりません。特定の\(f\)と\(g\)に依存して、これらの選択のいずれかが最良であることを示すことが可能です。一般的に，\(f – g\)がほぼ一定であれば，重点サンプリングには\(g\)が使用されるべきです [Kalos & Whitlock 1986]。
　重点サンプリングと同様に、変数変量法は、\(f\)のいくつかの因子を近似するか、または離散近似を構築することによって得ることができます。\(g\)からサンプルを生成する必要がないので、そのような関数を構築するのがやや容易になります。しかし、\(g\)が制御変量として有用であるためには、\(g\)の重要な因子をすべて考慮に入れなければならないことに注意してください。\(f_2\)の大きさを推定しなければ，\(f_1\)は変数変量法としては実質的に役に立たないことがわかります。一方、\(f_1\)は、重点サンプリングには問題なく使用できます。
　変数変量法は、これまでのところグラフィックスへの応用はほとんどありませんでした（例えば、Lafortune & Willems [1995a]を参照してください）。この手法の問題点の1つは，厳密に正の積分であっても負の標本値を得る可能性があることです．これは、真の値がゼロに近い積分（例えば、画像の暗部のピクセル）に対して、大きな相対誤差をもたらす可能性があります。一方で、この方法は適用が簡単で、わずかなコストでわずかな分散の減少をもたらす可能性があります。

2.6 分散低減Ⅱ：一様サンプルの配置

分散を減らすためのもう一つの重要な戦略は、サンプルが領域にわたって多少なりとも一様に分布していることを保証することです。これを行うためのいくつかの手法、すなわち、層化サンプリング、ラテン超方格法、直交配列サンプリング、および準モンテカルロ法 を検討します。
　これらの技術では、通常、ドメインは\(s\)次元の単位立方体\([0, 1]^s\)であると仮定されています。他のドメインは、\(T:[0, 1]^s \rightarrow \Omega\)の形式の適切な変換を定義することによって扱うことができます。異なるマッピング\(T\)を選択することによって、変換されたサンプルに異なる密度関数を与えることができることに注意してください。これにより、重点サンプリングを以下に説明する手法に適用することが容易になります。

2.6.1 層化サンプリング

層化サンプリングの考え方は、領域\(\Omega\)を、次のような複数の非重複領域\(\Omega_1, \cdots, \Omega_n\)に細分化することです。

\begin{eqnarray}
\bigcup_{i=1}^n \Omega_i = \Omega
\end{eqnarray}

各領域\(\Omega_i\)を層と呼びます。そして、ある与えられた密度関数\(p_i\)に従って、各\(\Omega_i\)内で一定数のサンプル\(n_i\)が採取されます。
　簡単のために、\(\Omega = [0, 1]^s\)と\(p_i\)が単に\(\Omega_i\)上の定数関数であると仮定すると、次のような形の推定値が得られます。

\begin{eqnarray}
F’ &=& \sum_{i=1}^n v_i F_i \tag{2.23} \\
{\rm where} \quad F_i &=& \frac{1}{n_i} \sum_{j=1}^{n_i} f(X_{i, j}) \tag{2.24}
\end{eqnarray}　

ここで，\(v_i = \mu(\Omega_i)\)は領域\(\Omega_i\)の体積であり，各\(X_{i, j}\)は\(p_i\)から独立したサンプルとします。この推定器の分散は

\begin{eqnarray}
V[F’] = \sum_{i=1}^n {v_i}^2 {\sigma_i}^2 / n_i \tag{2.25}
\end{eqnarray}

ただし，\({\sigma_i}^2 = V[f(X_{i, j})]\)は\(\Omega_i\)内の\(f\)の分散を示します。
　これを層化されていないサンプリングと比較するために、\(n_i = v_i N\)と仮定します。ここで\(N\)は採取されたサンプルの総数であるとします。すると、式(2.25)は次のように単純化されます。

\begin{eqnarray}
V[F’] = \frac{1}{N} \sum_{i=1}^n v_i {\sigma_i}^2
\end{eqnarray}

一方、対応する非層化推定器の分散は次のようになります。

\begin{eqnarray}
V[F] = \frac{1}{N} \left[ \sum_{i=1}^n v_i {\sigma_i}^2 + \sum_{i=1}^n v_i (\mu_i – I)^2 \right] \tag{2.26}
\end{eqnarray}

ここで，\(\mu_i\)は領域\(\Omega_i\)における\(f\)の平均値であり，\(I\)は領域全体についての\(f\)の平均値です。右側の和は常に非負であるため、層別サンプリングは分散を増加させることができません。
　しかし、(2.26)から、層が異なる平均を持っている場合にのみ分散が減少することがわかります。理想的には，\(x_i \in \Omega_i\)が \(x_1 \leq x_2 \leq \cdots \leq x_N\)を意味するような層を見つけることによって被積分関数の範囲を層別化して，達成されるでしょう。
　もう一つの視点は、収束率を分析することです。有界一次微分を持つ関数の場合、層化サンプリングの分散は\(O(N^{-1-2/s})\)の速度で収束しますが、関数が部分的に連続しているだけの場合、分散は\(O(N^{-1-1/s})\)になります[Mitchell 1996]。(標準偏差の収束率は，これらの指数を2で割ることによって得られます)．このように、層化サンプリングは、低次元領域では収束率を顕著に増加させることができますが、高次元領域ではほとんど効果がありません。
　まとめると、層化サンプリングは有用で安価な分散削減手法です。これは主に、被積分関数がが適度によく振る舞う低次元の積分問題に有効です。次元が高い場合や、被積分関数が特異点や急激な振動を持つ場合（例えば、微細なテクスチャなど）は、層化サンプリングはあまり役に立ちません。これは特にグラフィックスの問題に当てはまり、各積分のために取られるサンプル数が比較的少ない場合に当てはまります。

2.6.2 ラテン超方格法

合計\(N\)個のサンプルが採取されるとします。ラテン超方格法の考え方は、領域\([0, 1]^s\)を各次元に沿って\(N\)個の部分区間に細分化し、各部分区間に 1 つのサンプルが存在することを保証することです。これは\(\{1, \cdots , N\}\)の\(s\)個の順列\(\pi_1, \cdots, \pi_s\)を選択し、サンプルの位置を次のようにすることで行うことができます。

\begin{eqnarray}
X_i^j = \frac{\pi_j (i) – U_{i, j}}{N} \tag{2.27}
\end{eqnarray}

ここで，\(X_i^j\)はサンプル\(X_i\)の\(j\)番目の座標で，\(U_{i, j}\)は独立で\([0, 1]\)上の一様に分布しています。2次元では、サンプルパターンは、ラテン方格にある1つのシンボルの出現に対応しています（すなわち、同じ行または列に2回のシンボルが出現しないような\(N\)個のシンボルの\(N \times N\)の配列）。
　ラテン超方格法は、モンテカルロ積分手法としてMcKayら[1979]によって最初に提案されました。これは、少なくとも1920年代から統計的実験の計画に使用されてたラテン方格法と密接に関連している（例えば、農業研究[Fisher 1925, Fisher 1926]）。Yates [1953] と Patterson [1954] は，これらの手法を任意の次元に拡張し，（調査サンプリングと実験計画の背景で）その分散低減特性を分析しました。コンピュータ・グラフィックスでは、N-rooks サンプリングの名のもとに Shirley [1990a] によってラテン方格サンプリングが導入されました [Shirley 1990a, Shirley 1991]。
　モンテカルロ積分のためのラテン超方格法の最初の満足のいく分散分析は、Stein [1987]によって与えられました。まず，関数\(g(x)\)が次のような形式を持つ場合には，加法であると定義します。

\begin{eqnarray}
g(x) = \sum_{j=1}^s g_j (x^j) \tag{2.28}
\end{eqnarray}

ただし，\(x^j\)は\(x \in [0, 1]^s\)の成分の\(j\)番目であることを示します。次に、\(f_{\rm add}\)を\(f\)に対する最良の加算近似、つまり平均二乗誤差を最小化する(2.28)形式の関数を表すとします。

\begin{eqnarray}
\int_{\Omega} (f_{\rm add}(x) – f(x))^2 d\mu(x)
\end{eqnarray}

ここで、\(f\)を2つの成分の和として書くことができます。

\begin{eqnarray}
f(x) = f_{\rm add}(x) + f_{\rm res}(x)
\end{eqnarray}

ただし，\(f_{\rm res}\)はすべての加法関数について直交であるとします。すなわち、任意の加法関数\(g\)について

\begin{eqnarray}
\int_{\Omega} f_{\rm res}(x) g(x) d\mu(x) = 0
\end{eqnarray}

となります。
　その後、Stein [1987]は、ラテン超方格法の分散が次のようになることを示すことができました。

\begin{eqnarray}
V[F’] = \frac{1}{N} \int_{\Omega} {f_{\rm res}}^2 (x) d\mu(x) + o(1/N) \tag{2.29}
\end{eqnarray}

ここで，\(o(1/N)\)は\(1/N\)よりも速く減少する関数を示しています。この式は、\(N\)個の独立したサンプルを用いて分散と比較する必要があり、次のようになります。

\begin{eqnarray}
V[F] = \frac{1}{N} \left( \int_{\Omega} {f_{\rm res}}^2 (x) d\mu(x) + \int_{\Omega} (f_{\rm add}(x) – I)^2 d\mu(x) \right)
\end{eqnarray}

2番目の場合の分散は常に大きくなります（十分に大きい\(N\)の場合）。このように、ラテン超方格法は、被積分関数の加算成分の収束率を向上させます。さらに、独立標本を使用するよりも著しく悪くなることはありません [Owen 1997a]：

\begin{eqnarray}
V[F’] \leq \frac{N}{N – 1} V[F] \quad {\rm for} \, N \geq 2
\end{eqnarray}

ラテン超方格法は実装が簡単で、ほぼ加法的な関数に対して非常によく機能します。しかし、サンプルが2次元で十分に層化されていないため、画像のサンプリングにはあまりうまく機能しません。特殊な場合（垂直または水平のエッジを持つピクセルなど）を除いて、独立したサンプルで得られるのと同じ\(O(1/N)\)分散を持ちます。これは，分散が平滑関数には\(O(N^{-2})\)で，そして部分的連続関数では\(O(N^{-3/2})\)である層化サンプリングよりも劣ります．

2.6.3 直交配列サンプリング

直交配列サンプリング [Owen 1991, Tang 1993]は、これらの欠陥のいくつかに対処する、ラテン超方格法の重要な一般化です。これは、サンプルの1次元射影をすべて層別化するのではなく、ある\(t \geq 2\)に対して\(t\)次元射影をすべて層別化します。これにより、\(t\)またはそれ以下の変数に依存する\(f\)の成分の収束率が向上します。
　強さ\(t\)の直交配列 は、サイズ\(b\)のアルファベットから引き出されたシンボルの\(N \times s\)配列で、すべての\(N \times t\)部分行列が\(b^t\)可能性がある行のそれぞれのコピーの数と同じ数を含むようにします。(部分行列は必ずしも連続しているわけではなく、列の任意の部分集合を含むことができます) \(\lambda\) を各行の出現回数（\(\lambda\) は配列のインデックスとして知られています）とすると，\(N = \lambda b^t\)を表すことは明らかです。次の表は，パラメータが\(OA (N, s, b, t) = (9, 4, 3, 2)\)である直交配列の例を示しています：

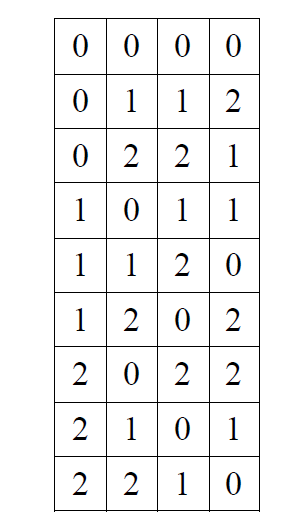
※表は，Eric Veach, “Robust Monte Carlo Methods For Light Transport Simulation”, p.54, Stanford University, 1997 より引用。

強度\(t = 2\) [Bose 1938, Bose & Bush 1952, Addeleman & Kempthorne 1961]、強度\(t = 3\) [Bose & Bush 1952, Bush 1952]、任意の強度\(t \geq 3\)[Bush 1952]の直交配列を構築するための様々な方法が知られています。これらの方法の実装は公開されています[Owen 1995a]。
　\(A\)を強さ\(t\)の\(N \times s\)の直交配列とすると，配列中のシンボルは\( \{0, 1, \cdots , b-1 \}\)です。 直交配列サンプリングの最初のステップは，各列のアルファベットに順列を適用して配列をランダム化することです．つまり

\begin{eqnarray}
\hat{A}_{i, j} = \pi_j ( A_{i, j} ) \quad {\rm for} \, {\rm all} \, i, j
\end{eqnarray}

ここで、\(\pi_1, \cdots, \pi_s\)は、シンボル\(\{0, \cdots , b-1\}\)のランダムな順列です。\({\hat A}\)が元の配列\(A\)と同じ名前のパラメータ\((N, s, b, t)\)を持つ直交配列であることを確認するのは簡単です。このステップでは、可能性のある\(b^s\)行のそれぞれが等確率で\({\hat A}\)において発生することが保証されます。
　ここで、領域を\([0, 1]^s\)とし、各軸を等しい大きさのb間隔に分割して得られる\(b^s\)部分立方体の族を考えてみましょう。\({\hat A}\)の各行は、この部分立方体の族へのインデックスとして解釈することができます。直交配列サンプリングの考え方は、\({\hat A}\)の行で指定された\(N\)個の部分立方体のそれぞれに 1 つのサンプルを取るというもので、具体的には、サンプル\(X_i\)の\(j\)番目の座標は次のようになります。

\begin{eqnarray}
X_i^j = ( {\hat A}_{i, j} + U_{i, j} ) / b
\end{eqnarray}

ただし，\(U_{i, j}\)は\([0, 1]\)上の独立した一様サンプルです。上記のランダム化ステップのため、各\(X_i\)が\([0, 1]^s\)に一様に分布していることを示すのは簡単であり、\(F_N = (1/N) \sum_{i=1}^N f(X_i)\)は通常の積分\(I\)の不偏な推定量となります。
　この手法の利点を見るには，任意の\(t\)座標軸を基準とした標本分布を考えてみてください（すなわち，これらの軸によって広がる部分空間に標本を投影してください）。この部分空間は、各軸を\(b\)間隔に分割することで，\(b^t\)の部分立方体に分割することができます。直交配列サンプリングの主な特性は、これらのサブキューブのそれぞれが同じ数のサンプルを含むことです。これを見るには、投影されたサンプルの座標が直交配列の特定の\(N \times t\)部分行列によって指定されていることを観察してください。直交配列の定義により，起こりうる\(b^t\)行のそれぞれは，この部分行列の中で\(\lambda\)倍になり，各サブキューブには正確に\(\lambda\)サンプルが存在することになります．
　直交配列サンプリングは、明らかにラテン超方格法を一般化したものです。サンプルの1次元射影を層別化するのではなく，\(t\)次元射影を同時に層別化します．(そのような射影はすべて\(\begin{pmatrix} s \\ t \end{pmatrix}\)あります)。

2.6.3.1 分散分解の解析

直交配列サンプリングの分散低減特性は、分散（anova）分解の連続性解析を用いて分析することができます [Owen 1994, Owen 1992]。我々の記述は [Owen 1992] に従い、[Efron & Stein 1981] に基づいています。
　\(S = \{ 1, \cdots, s \}\) をすべての座標指数の集合とし、\(U \subseteq S\)をこれらの指数の任意の部分集合とする（可能な部分集合は全部で\(2^s\)存在します）。ここでは\(j \in U\)の座標変数\(x^j\)の集合を参照するために\(x^U\)という記法を用いることにします。与えられた関数\(f\)の分散分析分解は、総和として書くことができます。

\begin{eqnarray}
f(x) = \sum_{U \subseteq S} f_U (x^U) \tag{2.30}
\end{eqnarray}

ここで，各関数\(f_U\)は\(U\)によってインデックス付けされた変数にのみ依存します。
\(U = \emptyset\)がどの変数にも依存しないときの関数であるとき、総平均と呼ばれています：

\begin{eqnarray}
I = f_{\emptyset} = \int_{[0, 1]^s} f(x) dx
\end{eqnarray}

\(U\)の他の\(2^s – 1\)の部分集合は、変動要因 と呼ばれています。1つの変数だけに依存する\(f\)の成分は主効果 と呼ばれ、以下のように定義されます。

\begin{eqnarray}
f_j(x^j) = \int ( f(x) – I ) \displaystyle \prod_{i \neq j} dx^i
\end{eqnarray}

これらの関数はすべて定数関数\(f_{\emptyset}\)と直交していることに注目してください。同様に、二要因交互作用 は以下のように定義されています。

\begin{eqnarray}
f_{j, k} (x^{j, k}) = \int ( f(x) – I – f_j (x^j) – f_k (x^k)) \displaystyle \prod_{i \neq j, k} dx^i
\end{eqnarray}

これらの関数は，2つの特定の変数に依存する\(f\)の成分を表します。これらの関数は\(f_{\emptyset}\)と直交し、すべての\(f_j\)と直交します。
　一般に，\(f_U\)は次のように定義されます。

\begin{eqnarray}
　f_U(x^U) = \int \left( f(x) – \sum_{v \subset U} f_v(x^V) \right) dx^{S-U} \tag{2.31}
\end{eqnarray}

ここで、総和は\(U (V \neq U)\)のすべての適切な部分集合の上にあります。結果として得られる関数の集合は直交しています。すなわち、\(U \neq V\)の場合はいつでも次を満たします。

\begin{eqnarray}
\int f_U (x^U) f_V(x^V) dx = 0
\end{eqnarray}

これは、次のような便利な性質を暗示しています。

\begin{eqnarray}
\int f^x(x) dx = \sum_{U \subseteq S} \int {f_U}^2 (x^U) dx
\end{eqnarray}

そのため，\(f\)の分散は次のように書くことが可能です。

\begin{eqnarray}
\int (f(x) – I)^2 dx = \sum{|U| \gt 0} \int {f_U}^2 (x^U) dx
\end{eqnarray}

この解析の特定のケースとして、\(f\)に対する最適な加法近似は、次のようになります。

\begin{eqnarray}
f_{add}(x) = I + \sum_{j=1}^s f_j (x^j)
\end{eqnarray}

ここで、残差\(f_{res} = f – f_{add}\)はすべての加法関数に直交します。このようにして、ラテン超方格法の分散は、次のように書き換えることができます。

\begin{eqnarray}
{\sigma_{\rm LH}}^2 = \frac{1}{N} \sum_{|U| \gt 1} \int {f_U}^2(x^U) dx + o(1/N)
\end{eqnarray}

すなわち、分散の単一変数成分は、\(1/N\)よりも速い速度で収束します。
　直交配列サンプリングはこの結果を一般化します；分散[Owen 1992, Owen 1994]が次であることを示すことが可能です。

\begin{eqnarray}
{\sigma_{\rm OA}}^2 = \frac{1}{N} \sum_{|U| \gt t} \int {f_U}^2(x^U) dx + o(1/N)
\end{eqnarray}

すなわち、\(t\)座標以下に依存する被積分関数の全成分について、収束率が向上します。
　\(t=2\)の場合は特にグラフィックスの場合に興味深いです。例えば、この手法を分散レイトレーシングに適用すると、すべての2次元の投影が（ピクセル、レンズ開口部、光源などの上で）十分に層化されていることが保証されます。これは、2つの変数のすべての組み合わせが層状化されることを除いて、Cookら[1984]によって提案されたサンプリング技術と同様の結果を達成します（例えば、ピクセルの\(x\)座標と開口部の\(x\)座標のような組み合わせを含む）。

2.6.3.2 直交配列に基づくラテン超方格法

\(t\)次元の差がよく層化されているので、\(w\)次元の差も\(w \lt t\)に対して層化されていることに注意してください。例えば，任意の1次元射影量において，幅\(1/b\)の各区間に正確に\(\lambda b^{t-1}\)標本が存在します．これは、幅\(1/(\lambda b^t)\)の各区間に1つの標本を配置するラテン超方格法よりも劣ります。
　直交配列サンプリングには、ラテン超方格法と同じ1次元層化特性をもたらす簡単な修正があります。(この結果は、論理的には、直交配列に基づくラテン超方格法と呼ばれます [Tang 1993])。この考え方は、各シンボル\(m\)の\(\lambda b^{t-1}\)の同一のコピーをシンボルのランダムな順列にマッピングすることで、各列内の\(\lambda b^t\)シンボルを単一のシーケンス \(\{0, 1, \cdots, \lambda^t – 1\}\)にリマップすることです。

\begin{eqnarray}
\lambda b^{t-1}m, \cdots, \lambda b^{t-1}(m+1) – 1
\end{eqnarray}

この処理を各列ごとに個別に繰り返します。\(\hat{A}’\)を変更した配列とすると、サンプルの位置は以下のように定義されます。

\begin{eqnarray}
X_{i}^j = \frac{\hat{A}’_{i, j} + U{i, j} }{ \lambda b^t }
\end{eqnarray}

これは，各\(t\)次元の射影についてだけでなく，各 1 次元射影についてもサンプルが最大に層化されることを保証します。これは，分散のさらなる減少につながることを示すことができます [Tang 1993]．
　この手法は、マルチジッタサンプリング [Chiu et al.1994]に類似しており、\(s=2\)と\(t=2\)の特殊な場合に対応します。

2.6.4 準モンテカルロ法

準モンテカルロ法は、ランダム性を完全に排除することで、これらのアイデアをさらに一歩進めます。そのアイデアは、サンプルの位置を決定論的に選択することによって、可能な限り均一にサンプルを分布させることです。

2.6.4.1 ディスクレパンシー

\(P = \lbrace x_1, \cdots, x_N \rbrace \)を\([0, 1]^2\)の点の集合とします。一般的に，準モンテカルロ法の目的は，ある量的尺度に関してサンプルの分布の不規則性 を最小化することです。そのような尺度の1つが\(P\)のスターディスクレパンシーです。\({\mathcal B}^{\ast}\)を原点に1つのコーナーを持つすべての軸平行ボックスの集合とします：

\begin{eqnarray}
{\mathcal B}^{\ast} = \lbrace B = [0, u_1] \times \cdots \times [0, u_s] \, | \, 0 \lt u_i \lt 1 \, {\rm for}\, {\rm all} \, i \rbrace
\end{eqnarray}

理想的には、各ボックス\(B\)が\(P\)の点のうち正確に\(\lambda(B)N\)個の点を含むようにしたいと思います。ここで\(\lambda(B) u_1 \cdots u_s\)は\(B\)の体積です。スターディスクレパンシーは、\(P\)がこの理想的な状態からどれだけ逸脱しているかを単に測定するものです：

\begin{eqnarray}
{D^{\ast}}_N(P) = \sup_{B \in {\mathcal B}^{\ast}} \left| \frac{ \# \lbrace P \cap B \rbrace}{N} – \lambda(B) \right| \tag{2.32}
\end{eqnarray}

ここで, \(\# \lbrace P \cap B \rbrace\)はボックス\(B\)内の\(P\)の点の数を示します。
　ディスクレパンシーは、他の形状の集合（例えば、任意の軸平行バウンディングボックスや凸領域[Niederreiter 1992]）に関しても定義することができます。2次元画像サンプリングでは、任意の半平面と\([0, 1]^2\)を交差させて得られる形状の族を考慮することで、辺に関するディスクレパンシーを測定することが特に有用です[Mitchell 1992]。画像サンプリングに対するディスクレパンシーの関連性は、最初にShirley [1991]によって指摘されました。
　スターディスクレパンシーの重要性は、積分誤差の境界と密接に関係していることです。具体的には、Koksma-Hlawka の不等式は次のように述べています。

\begin{eqnarray}
\left| \frac{1}{N} \sum_{i=1}^{N} f(x_i) – \int_{[0, 1]^s} f(x) dx \right| \leq V_{\rm HK}(f) D^{\ast}_N(P)
\end{eqnarray}

ここで \(V_{\rm HK}(f)\)はHardy と Krause [Niederreiter 1992] の意味での\(f\)の変化 です。 したがって, 変化\(V_{\rm HK}(f)\)が有限であれば, 最大積分誤差はディスクレパンシーに正比例します。離散度の低い点集合や配列を見つけることで、積分誤差が小さいことを保証することができます。
　次元 \(s \geq 2\) の場合、\(f\) が不連続であるときはいつでも変化\(V_{\rm HK}(f)\)は無限大であることに注意することが重要です。これは、不連続性が一般的なコンピュータグラフィックスでは、これらの境界値の有用性を著しく制限しています。また、\(V_{\rm HK}(f)\)は一般的に元の積分よりも評価が難しいので、これらのワーストケース境界は実際に誤差を推定したり、境界化したりするのには役に立たないことにも注意してください。

2.6.4.2　低ディスクレパンシー点群と列

低ディスクレパンシー数列　とは、点 \(x_1, x_2, \cdots\)の無限列であり、スターディスクレパンシーが任意の接頭辞\(P= \lbrace x_1, \cdots , x_N \rbrace\)について

\begin{eqnarray}
D^{\ast}_N(P) = O \left( \frac{(\log N)^s}{N} \right)
\end{eqnarray}

です(\(P\)は実際には多集合であること、つまり要素の多重度が重要であることに注意してください)。この結果は、多くの既知の構造によって達成されており、これが最良であると広く信じられています[Niederreiter 1992]。しかし，任意の次元\(s\)に対する現在の最良の下界は

\begin{eqnarray}
D^{\ast}_N(P) \geq C(s) \cdot \frac{(\log N)^{s/2}}{N}
\end{eqnarray}

です。すなわち，これらの境界線の間には大きなギャップがあります。
　\(P\)が無限列の接頭辞であるという要件を捨てれば、矛盾は少し改善されます。ディスクレパンシーの低い点集合は，次に対して多集合\(P = \lbrace x_1, \cdots , x_N \rbrace\) になるように定義されます。

\begin{eqnarray}
D^{\ast}_N(P) = O \left( \frac{(\log N)^{s-1}}{N} \right)
\end{eqnarray}

(より正確には、単一の点集合\(P\)に適用した場合、その境界は意味をなさないので、これは低ディスクレパンシー点群の構造の定義となります。)
　これらの境界とKoksma-Hlawkaの不等式を組み合わせると、準モンテカルロ積分の誤差は、ばらつきの少ない点集合を用いた場合には最大で\(O((\log N)^{s -1} / N)\)、ばらつきの少ない数列の接頭辞を用いた場合には\(O((\log N)^s / N)\)となります。
　\(N\) と \(s\) の典型的な値では、\((\log N)^s\) は、\(N\) よりもはるかに大きいので、\(N\) が非常に大きくない限り、これらの限界は疑わしい値であることに注意してください。特に、関数 \((\log N)^s / N\)は、\(N \lt e^s\)に対して単調に増加することに注目してください（すなわち、標本サイズが大きくなるほど、誤差限界は悪くなります）。実際には、少なくとも\((\log N)^s \lt N\)までは、これらの誤差限界が意味を持つことを期待すべきではありません。なぜなら，そうでなければ誤差限界は \(N=2\) の場合よりも悪化するからです。Nがどれだけ大きくなければならないかを知るために、\(s=6\)の場合を考えてみましょう。すべての\(N < 10^9\)について、\((\log N)^s/N \gt (\log 2)^s/2\)であることを確認するのは簡単で、したがって、\(N\)がこれよりもかなり大きくなるまでは、意味のある誤差限界を期待すべきではありません。 　しかし、これらの誤差限界は、実際には過度に悲観的です。\(N\)がかなり小さい場合でも、積分が適度によく振舞われていれば、ディスクレパンシーの低い数列は、標準モンテカルロよりも良い結果を与えることがよくあります。

2.6.4.3　Halton列とHammersley点

ここでは、低ディスクレパンシー点集合と列のためのいくつかのよく知られた構造について説明します。一次元では，radical inverse 列 \(x_i = \phi_b(i)\) は，最初に\(i\)の基数-\(b\) 展開を書くことで得られます：

\begin{eqnarray}
i = \sum_{k \leq 0} d_{i, k} b^k
\end{eqnarray}

そして、小数点以下の桁数を反映させて：

\begin{eqnarray}
\phi_b(i) = \sum_{k \leq 0} d_{i, k} b^{-1-k}
\end{eqnarray}

\(b=2\)のときの特別な場合はvan der Corput 列と呼ばれます。

\begin{eqnarray}
\frac{1}{2}, \frac{1}{4}, \frac{3}{4}, \frac{1}{8}, \frac{5}{8}, \frac{3}{8}, \cdots .
\end{eqnarray}

radical-inverse列のディスクレパンシーは任意の基数\(b\)(ただし、暗黙の定数は\(b\)に応じて増加します)において\(O((\log N) / N\)です。
　複数の次元で低ディスクレパンシー列を得るために、各次元で異なるradical inverse数列を使用します：

\begin{eqnarray}
x_i = (\phi_{b_1}(i), \phi_{b_2}(i), \cdots, \phi_{b_s}(i))
\end{eqnarray}

ここで，基数\(b_i\)はすべて互いに素です。この構成の典型的な例はHalton 数列で、\(b_i\)は最初の\(s\)個が素数になるように選ばれます：

\begin{eqnarray}
x_i (\phi_2(i), \phi_3(i), \phi_5(i), \cdots, \phi_{p_s}(i)).
\end{eqnarray}

Halton列は\(O(\log N)^s/N)\)のディスクレパンシーを持ちます。
　サンプル点の数\(N\)があらかじめわかっている場合は、1次元目で等間隔の点\(i/N\)を使うことで、このディスクレパンシーを僅かに改善することができます。この結果はHammersley 点集合として知られています：

\begin{eqnarray}
x_i = (i/N, \phi_2(i), \phi_3(i), \cdots, \phi_{p_{s-1}}(i))
\end{eqnarray}

ここで，\(p_i\)は前に示した\(i\)番目の素数を示します。Hammersley点集合のディスクレパンシーは\(O((\log N)^{s-1}/N)\)です。

2.6.4.4 (t, m, s)-ネットと(t, s)-列

ディスクレパンシーは、点集合の分布の不規則性を示す有用な尺度ですが、どの列が数値積分に最適であるかを常に正確に予測するものではありません。最近では、\((t, m, s)\)-ネットや\((t, s)\)-列が注目されていますが、これらは少し異なる方法で分布の不規則性を定義しています。\(E\)を基数\(b\)の基本区間とすると、これは単に軸平行ボックスの形をしています。

\begin{eqnarray}
E = \prod_{j=1}^s \left[ \frac{t_j}{b^{k_j}}, \frac{t_j + 1}{b^{k_j}} \right)
\end{eqnarray}
)
ここで，指数\(k_j \geq 0\)は整数で，\(0 \leq t_j \leq b^{k_j} – 1\)です。つまり、ボックスの各次元は\(b\)の非正の累乗でなければならず、ボックスは各次元でそのサイズの整数倍にアライメントしなければなりません。基本区間の体積は明らかに

\begin{eqnarray}
\lambda (E) = b^{-\sum_{j=1}^{s} k_j}
\end{eqnarray}

となります。
基数\(b\)における\((0, m, s)\)-ネットは、\(N=b^m\)の大きさの点集合\(P\)で、体積\(1/b^{-m}\)のすべての基本区間が\(P\)の1点を正確に含むようなものと定義されます。これは，\((0, m, s)\)-ネットがそのような区間に関して可能な限り均等に分布していることを意味します。例えば，\(P\)が基数5の\((0, 4, 2)\)-ネットであるとします。この\(P\)は、単位正方形\([0, 1]^2\)の中に\(N=625\)個の点を含み、大きさ\(1 \times 1/625\)のすべての基本区間が\(P\)の点を含むことになります。同様に、サイズ\(1/5 \times 1/125\)，\(1/25 \times 1/25\)，\(1/125 \times 1/5\)そして，\(1/625 \times 1\)のすべての区間には、\(P\)の点がちょうど1つ含まれることになります。
　より一般的な\((t,m,s)\)-ネットの概念は、この定義を多少緩和することで得られます。サイズ\(b^{-m}\)のすべての箱に正確に1つの点を含むことを要求するのではなく、サイズ\(b^{t-m}\)のすべての箱に正確に\(b^t\)個の点を含むことを要求します。明らかに、\(t\)の値は小さい方が良いです。\(t \lt 0\)を許す理由は、より多くの\(b\)と\(s\)の値に対して、このような列の構築を容易にするためです(特に、\(m \leq 2\)の\((0, m, s)\)-ネットは、\(s \geq b + 1\)のときにしか存在しません[Niederreiter 1992])。
　\((t, s)\)-列は、すべての\(m \geq 0\)、\(k \geq 0\)に対して、部分列

\begin{eqnarray}
x_{kb^m+1}, \cdots, x_{kb^{m+1}}
\end{eqnarray}

が基数\(b\)における\((t, m, s)\)-ネットとなるような無限列\(x_1, x_2, \cdots\)と定義します。特に、サイズ\(N=b^m\)のすべてのプレフィックス\(x_1, \cdots, x_N\)は、\((t,m,s)\)-ネットとなります。Sobol’，Faure，Niederreiter，Tezukaの各氏により、様々な\(b\)と\(s\)の値に対するこのような列の明示的な構築が提案されています(Niederreiter[1992]とTezuka[1995]を参照)。
　すべての\((t, s)\)-列は低ディスクレパンシーであり、すべての\((t, m, s)\)-ネットは低ディスクレパンシー点集合です(ただし、\(t\)を固定し、\(m\)を増加させることが条件)。このように、これらの構築は、Halton 列やHammersley 点群と同じように、最悪のケースでの積分境界を持っています。しかし，\((t, s)\)-列や\((t, m, s)\)-ネットは、実際にはもっとうまくいくことが多いことに注意してください。なぜなら、ディスクレパンシーは重要な定数因子で小さくなるからです[Niederreiter 1992]。
　\((t, m, s)\)-ネットの等分布特性を直交配列サンプリングと比較するのは興味深いことです。簡単にするために、\(t＝0\)とし、\(A\)を強度\(m\)の直交配列とします。このとき、\((t, m, s)\)-ネットの専門用語では、直交配列サンプリングは、体積\(1/b^m\)の各基本区間\(E\)に1つのサンプルが存在することを保証します。ここで、\(E\)は\(m\)個の辺が長さ\(1/b\)で、他のすべての辺が長さ1です。Tang[1993]のラテン超方格法の拡張により、さらに、各基本区間\(E\)には、1つの辺が長さ\(1/b^m\)で、他のすべての辺が長さ1であるサンプルが1つ存在することが保証されます。このように、1次元と\(m\)次元の投影は、最大の層化となります。比較のために，\((0, m, s)\)-ネットは，これらの性質の両方を達成しているだけでなく，体積\(1/b^m\)の他の種類の基本区間に1つのサンプルがあることを保証しているので，次元\(2, 3, \cdots, t-1\)の投影も可能な限り層化されています。

2.6.4.5 ランダムに順序を入れ替えた(t, m, s)-ネットと(t, s)-列

準モンテカルロ法の重大な欠点は、サンプルの位置が決定論的であることです。コンピュータ・グラフィックスでは、これは重大なエイリアシング・アーチファクトにつながります[Mitchell 1992]。また、モンテカルロ法のように、独立した複数のサンプルを単純に取ることができないため、誤差の推定値を算出することも困難です。
　これらの問題は、ランダムに並べ替えられた\((t, m, s)\)-ネットや\((t, s)\)列[Owen 1995b]（スクランブルドネットやスクランブルド列とも呼ばれる）を用いることで解決できます。このアイデアは簡単に実現できますが、その分析はより複雑です。
　スクランブルネットにはいくつかの利点があります。最も重要なことは、サンプルポイントが領域\([0, 1]^2\)上に一様に分布しているため、得られる推定値が不偏であることです。これにより、複数の独立したランダムなサンプル（例えば、同じオリジナルの\((t, m, s)\)-ネットの異なる桁のパーミュテーションを使用）を取ることで、不偏のエラー推定値を得ることができます(分散推定のさらなる議論についてはOwen[1997a]を参照してください）。コンピュータグラフィックスの文脈において、スクランブルされたネットは、準モンテカルロ積分で一般的に見られる系統的なエイリアシングアーチファクトを除去する方法でもあります。
　第二に、滑らかな関数の場合、スクランブル・ネットは

\begin{eqnarray}
V[{\hat I}] = O \left( \frac{(\log N)^{s-1}}{N^3} \right)
\end{eqnarray}

の分散をもたらし、その結果、確率的に\(O((\log N)^{(s-1)/2}N^{-3/2})\)の予測誤差をもたらすことを示すことができます[Owen 1997b]。これは、モンテカルロ法の\(O(N^{-1/2})\)や準モンテカルロ法の\(O((\log N)^{s-1}N^{-1})\)よりも改善されています。いずれの場合も、これらの境界は（十分な滑らかさを持つ）最悪ケースの関数\(f\)に適用されますが、準モンテカルロ法では決定論的な点集合を使用しているのに対し、他の境界はサンプリングアルゴリズムによるランダムな選択の平均であることに注意してください。
　スクランブル・ネットは、関数fが滑らかでない場合でも、通常のモンテカルロよりも分散を改善することが可能です[Owen 1997b]。上述の分散分解の分析に関しては、変数\(|U|\)数が少ない成分\(f_U\)に対して、スクランブルネットは最大の改善をもたらします。これらの関数\(f_U\)は、\(f\)自体が滑らかでなくても（\(S-U\)における変数について積分するため）滑らかになることがあり、これらの成分の収束が早くなります。

2.6.4.6 考察

準モンテカルロ法の収束率は、積分値に滑らかさが要求されることや、一般的に使用されるサンプルサイズが比較的小さいことから、コンピュータグラフィックスではほとんど意味を持ちません。その他の問題としては、変動幅\(V_{HK}(f)\)の推定が難しいこと、\((\log N)^{s-1}\)が実際にはNよりもはるかに大きいのが一般的であることなどが挙げられます。準モンテカルロ法ではランダム性がないため、エイリアシングが発生し、誤差の推定ができないという明確なデメリットがあります。
　モンテカルロ法と準モンテカルロ法のハイブリッドは、上述のスクランブル\((t, m, s)\)-ネットのように有望です。このような方法は、不連続な被積分関数に対して標準的なモンテカルロ法よりも優れているわけではありませんが、少なくとも悪いものではありません。
　Keller[1996, 1997]は，準モンテカルロ法をラジオシティ問題（すべての表面が拡散している光輸送問題の特殊なケース）に適用しました。彼は粒子追跡アルゴリズム（Pattanaik & Mudur [1993]に類似）を使用していますが、散乱の方向がHalton 列によって決定されています。彼は、簡単なテストシーンにおいて、標準的なモンテカルロ法よりもわずかに良い収束率を報告しています。主な恩恵は、各ランダムウォークの最初の4次元（光源の初期点の選択と発光方向を制御する）のサンプリングによるものと思われます。

2.7 分散低減Ⅲ：適応的サンプル配置

分散低減法の3つ目のファミリーは，サンプル密度を適応的に制御するというアイデアに基づいており，最も有用な場所（例えば，被積分関数が大きい場合や急激に変化する場合）に多くのサンプルを配置することができます。そのための2つの異なるアプローチについて説明します。1つは適応的サンプリングで，特別な注意を払わないとバイアスが生じる可能性があります。もう1つのアプローチは、ロシアンルーレットと分割と呼ばれる2つの密接に関連した技術で構成されています。これらの技術はバイアスを導入せず、光輸送問題に特に有効です。

2.7.1 適応的サンプリング

適応的サンプリング（シーケンシャルサンプリングとも呼ばれる）の考え方は、被積分関数の変化が最も大きいところでより多くのサンプルを取ることです。これは、これまでに採取されたサンプルを検証し、その情報をもとに今後のサンプルの配置を制御することで行われます。一般的には、特定の領域におけるサンプルの分散を計算し、分散が所定の閾値を超えた場合に、より多くのサンプルを採取することで洗練されます。このような画像サンプリングの手法は、グラフィックスでは数多く提案されています（例えば、Leeら[1985]、Purgathofer[1986]、Kajiya[1986]、[Mitchell 1987]、Painter & Sloan[1989]など）。
　重点サンプリングと同様、適応的サンプリングの目的は、最も効果的な場所にサンプルを集中させることです。しかし，2つの重要な違いがあります．まず，重点サンプリングは，被積分関数が大きい領域により多くのサンプルを配置しようとしますが，適応的サンプリングは，分散値が大きい領域により多くのサンプルを配置しようとします。(もちろん、適応型サンプリングでは、他の基準も自由に使うことができます。)2つ目の重要な違いは、適応型サンプリングでは、事前に得られた情報を使用するのではなく、サンプル密度を「その場で」変更することです。
　適応的サンプリングの主な欠点は、バイアスが生じることであり、それが画像のアーティファクトにつながる可能性があります。これは，まず代表的な領域\(R \subset \Omega\)から\(n\)個の小さなサンプルを抽出し，その情報をもとに領域の残りの部分\(\Omega – R\)のサンプルサイズ\(N\)を決定するというものです。この手法は，バイアスをなくすことができますが，第2段階のサンプリングで発生した異常なサンプルに対応できないため，適応型サンプリングの利点の一部を失うことになります。
　適応的サンプリングのもう一つの問題は、高次元の問題にはあまり効果がないことです。サンプルの問題は，層化サンプリングの場合と同様に発生します：洗練化するために可能な次元が多すぎるのです。例えば、洗練されるべき領域を各軸に沿って2つに分割すると、サンプリングすべき新しい領域が\(2^s\)になります。もし、サンプリングエラーのほとんどが、これらの軸の1つまたは2つに沿った変動によるものであれば、洗練化は非常に非効率的なものとなります。

2.7.2　ロシアンルーレットと分割

ロシアンルーレット と分割 は、粒子輸送問題でよく使われる2つの密接に関連したテクニックです。その目的は、被積分関数が小さいところではサンプル密度を下げ、被積分関数が大きいところではサンプル密度を上げることです。しかし、適応的サンプリングとは異なり、これらの技術はバイアスを導入しません。これらの手法のコンピュータ・グラフィックスへの応用については，Arvo & Kirk [1990]が述べています。

ロシアンルーレット
ロシアンルーレットは通常、多くの項の合計である推定器に適用されます：

\begin{eqnarray}
F = F_1 + \cdots + F_N
\end{eqnarray}

例えば、\(F\)は特定のビューレイに沿ってサーフェイスから反射された放射輝度を表し、各\(F_i\)は特定の光源の寄与を表しているかもしれません。
このタイプの推定器の問題点は、一般的にほとんどの貢献度が非常に小さく、しかもすべての\(F_i\)が評価するために等しく高価であることです。ロシアン・ルーレットの基本的な考え方は、これらの\(F_i\)を次のような形式の新しい推定器に置き換えることによって、小さな寄与に関連する評価のほとんどを無作為にスキップすることです。

\begin{eqnarray}
F_i’ = \begin{cases}
\frac{1}{q_i} F_i & {\rm with} \, {\rm probability} \quad q_i \\
0 & {\rm otherwise}
\end{cases}
\end{eqnarray}

評価確率\(q_i\)は、各\(F_i\)ごとに、その寄与のある便宜的な推定に基づいて選択されます。推定値\(F_i’\)は、\(F_i\)が次のような場合、不偏であることに注意してください。

\begin{eqnarray}
E[F_i’] &=& q_i \cdot \frac{1}{q_i} E[F_i] + (1 – q_i) \cdot 0 \\
&=& E[F_i]
\end{eqnarray}

　この手法は明らかに分散を増加させるもので、先に述べた期待値法の逆バージョンです。しかし、ロシアンルーレットは、\(F\)を評価するのに必要な平均時間を短縮することで、効率を上げることができます。
　例えば、各\(F_i\)が、あるサーフェイスからの反射光に対する特定の光源の寄与を表しているとします。ロシアンルーレットを使った視認性テストの回数を減らすために，まず，光源が完全に視認できると仮定して，各\(F_i\)の暫定的な寄与度\(t_i\)を計算します。次に、固定の閾値\(\delta\)が典型的に選択され、確率\(q_i\)は次のように設定されます。

\begin{eqnarray}
q_i = {\rm min}(1, t_i / \delta)
\end{eqnarray}

したがって、\(\delta\)よりも大きい寄与は常に評価され、小さい寄与はバイアスがかからないようにランダムにスキップされます。
　ロシアンルーレットは、粒子輸送計算で発生するランダムウォークを終了させるためにも使われます。(これはKahnによって導入されたこの方法の本来の目的でした。[Hammersley & Handscomb 1964, p.99]を参照)。前述の例と同様に、推定寄与が比較的小さいウォークをランダムに終了させることです。つまり、現在のウォーク\({\mathrm x_0} {\mathrm x_1} \cdots {\mathrm x}_k\)が与えられた場合、それを拡張する確率は、パスをさらに拡張することで得られるであろう推定寄与に比例するように選択されます。つまり、\(k’ \gt k\)が存在する\({\mathrm x_0} \cdots {\mathrm x}_{k’}\)という形式のパスの寄与になります。これは、領域の効果のない領域に入ったウォークを終了させる効果があります。コンピュータグラフィックスの分野では、レイトレーシングやモンテカルロ法による光輸送計算などに用いられています。

分割
ロシアンルーレットは分割と密接な関係があります。分割とは、推定量\(F_i\)を次のような形式のもので置き換える手法です。

\begin{eqnarray}
F_i’ = \frac{1}{k} \sum_{j=1}^{k} F_{i, j}
\end{eqnarray}

ここで，\(F_{i,j}\)は\(F_i\)からの独立したサンプルです。ロシアンルーレットのように，分割係数\(k\)はサンプル\(F_i\)の推定寄与に基づいて選択されます。(推定寄与が大きいほど、一般的に\(k\)の値も大きくなります。)この変換が不偏であることは簡単に検証できます、つまり

\begin{eqnarray}
E[F_i’] = E[F_i]
\end{eqnarray}

　粒子輸送計算では、1つの粒子が\(k\)個の新しい粒子に分割され、それぞれが独立した経路をたどるという効果があります。各粒子には、元の粒子の重量の\(1/k\)の割合である重量が割り当てられます。一般的にこの手法は、粒子が領域の高寄与領域に入ったときに適用されます。例えば、原子炉のシールドからの漏れを測定しようとしている場合、分割は、すでにシールドをほとんど突き抜けた中性子に適用される可能性があります。
これらの手法の基本的な考え方は同じで、ランダムウォークの現在の状態\({\mathrm x_0} {\mathrm x_1} \cdots {\mathrm x}_k\)が与えられれば、\({\mathrm x}_{k+1}\)のサンプル数を決定する際に、この状態の任意の関数を自由に使用することができます。経路\({\mathrm x_0} \cdots {\mathrm x}_{k+1}\)の寄与が低いと予測される場合は、ほとんどの場合、サンプルを全く採取しませんが、寄与が高い場合は、いくつかの独立したサンプルを採取することにします。これをすべての頂点に適用すると、結果として経路の木構造になります。
　一般的に、ロシアンルーレットや分割は、各サンプルがランダムなステップの連続によって決定されるあらゆるプロセスに適用できます。このシーケンスの任意のプレフィックスを使って，最終的なサンプルの重要性を推定することができます．これを用いて，現在の状態を破棄するか（重要度が低い場合），複製するか（重要度が高い場合）を決定します。このアイデアは、表面的には適応的サンプリングに似ていますが、バイアスを導入することはありません。
　ロシアンルーレットは、無限に続くランダムウォークを偏りなく終了させることができるため、輸送計算には欠かせない手法です。分割もまた、適切に適用されれば有用です[Arvo & Kirk 1990]。これらのテクニックを組み合わせることで、領域内の最も有効性の高い領域にサンプリングの努力を向けることができ、非常に効果的です。

2.8　分散低減Ⅳ：相関推定器

最後にご紹介する分散低減法は、値が相関している2つ以上の推定量を見つけるという考え方に基づいています。これまでのところ、これらの手法はグラフィックではあまり使われていないので、ここでは簡単に説明します。

2.8.1　対称変量

対称変量の考え方は、値が負に相関している2つの推定量\(F_1\)と\(F_2\)を見つけて、それらを足すことです。例えば，目的の積分が\(\int_0^1 f(x) dx\)で，推定量を考えると

\begin{eqnarray}
F = (f(U) + f(1 – U)) /2
\end{eqnarray}

ここで、\(U\)は\([0, 1]\)に一様に分布しています。関数\(f\)が単調増加（または単調減少）であれば、\(f(U)\)と\(f(1-U)\)は負の相関を持つので、\(F\)は2つのサンプルが独立である場合よりも低い分散を持つことになります[Rubinstein 1981, p.135]。さらに，推定量\(F\)は，被積分関数が一次関数であるときは常に正確です(すなわち\(f(x) = ax + b\))。
　この考えは、次の形式のサンプル点のペアを考慮することで、領域\([0, 1]^s\)に簡単に適用できます。

\begin{eqnarray}
X_1 = (U_1, \cdots, U_s) \quad {\rm and} \quad X_2 = (1-U_1, \cdots, 1 – U_s)
\end{eqnarray}

繰り返しになりますが、この方法は線形な被積分関数に対して正確です。2つ以上のサンプルが必要な場合は、領域をいくつかの矩形の領域\(\Omega_i\)に分割し、各領域で上記の形式のサンプルのペアを取ることができます。
　このタイプの対称変量は、\(f\)が各小領域\(\Omega_i\)でほぼ線形になるような滑らかな被積分関数に対して最も有効です。一方、多くのグラフィックス問題では、分散は主に被積分関数の不連続性や特異性に起因しています。これらの寄与は、被積分関数の滑らかな領域で改善された分散を圧倒する傾向があるため、対称変量の有用性は限られています。

2.8.2　回帰法

回帰法は、いくつかの相関性のある推定量を利用する、より高度な方法です。目的の量\(I\)に対する複数の不偏の推定量\(F_1, \cdots , F_n\)が与えられ、\(F_i\)が何らかの形で相関しているとします（例えば、反比例変数の例のように、同じ乱数を異なる形に変換して使用しているため）。このアイデアは、各推定値からいくつかのサンプルを取り、標準的な線形回帰法を適用して、すべての相関関係を考慮に入れた\(I\)の最適な推定値を決定するというものです。
　具体的には、各推定量から\(N\)個のサンプルを取ることで動作します（ここで、\(F_i\)からの\(j\)番目のサンプルを\(F_{i,j}\)とします）。そして，標本平均を計算します。

\begin{eqnarray}
{\hat I}_i = \frac{1}{N} \sum_{j=1}^N F_{i,j} \quad {\rm for} \, i=1, \cdots , n
\end{eqnarray}

サンプリング分散共分散行列\({\hat {\mathrm V}}\)は、\(n \times n\)の正方配列で、その要素は以下のとおりです。

\begin{eqnarray}
{\hat V}_{i, j} = \frac{1}{N – 1} \sum_{k=1}^N (F_{i,k} – {\hat I}_i) (F_{j,k} – {\hat I}_j)
\end{eqnarray}

このとき最終的な推定\(F\)は次のように与えられます。

\begin{eqnarray}
F = ({\mathrm X}^{\ast} {\hat {\mathrm V}}^{-1} {\mathrm X})^{-1} {\mathrm X}^{\ast} {\hat {\mathrm V}}^{-1} {\hat {\mathrm I}} \tag{2.33}
\end{eqnarray}

ここで\({\mathrm X}^{\ast}\)は\({\mathrm X}\)の転置を示し，\({\mathrm X} = { 1 \cdots 1}^{\ast}\)は長さ\(n\)の列ベクトルで, \({\hat {\mathrm I}} = [{\hat I}_1 \cdot {\hat I}_n]^{\ast}\)は標本平均の列ベクトルです。式(2.33)は、目的とする平均\(I\)の標準的な最小分散不偏線形推定量ですが、真の分散共分散行列\({\mathrm V}\)を近似値\({hat {\mathrm V}}\)で置き換えている点が異なります。詳細はHammersley & Handscomb [1964]に記載されています。
　この手法では，標本平均\({\hat I}_i\)と分散共分散行列のエントリ\({\hat V}_{i,j}\)（\({\hat I}_i\)の重み付けに使用される）の両方の推定に同じランダムサンプルが使用されるため，多少のバイアスが生じることに注意してください。このバイアスは，この2つの目的のために異なるランダムサンプルを使用することで回避することができます（もちろん，これはコストの増加につながります）。
　回帰法の主な問題点は、適切な相関推定量のセットを見つけることです。被積分関数に不連続性や特異性がある場合、\(f(U)\)や\(f(1-U)\)のような単純な変換では、有意な相関関係は得られません。もう一つの問題は、この方法では、共分散行列をそれなりの精度で推定するためには、かなりの数のサンプルを取らなければならないことです。