D. Brandon Lloyd氏の博士論文である,Logarithmic Perspective Shadow Mapsを適当に訳していくことにします。
前回はChapter.1をざっくり訳しました。今回はChapter. 2を訳していきます。
日本語としては多々見苦しい点があるかと思いますが,そこはご容赦ください。
CHAPTER 2
Handling shadow map artifacts
シャドウマップに関連する研究の多くは,シャドウマップのアーティファクトを解決しようとする傾向があります。深度に基づくシャドウマップはもともとは1978年にWilliamsによって提案されました(Williams, 1978)。それ最初はオフラインレンダリングについて人気がありました。Segalら(1992)は,後にシャドウマップがテクスチャマッピングの拡張を用いて標準的なグラフィックスハードウェア上で実装可能であること示しました。この採用が対話的なアプリケーションへと先導していきました。対話的なアプリケーションにおいて視覚的なリアリズムに対する増加する要求はシャドウマップのアーティファクトを解決するための近年における活動の突風に拍車をかけています。
このチャプターでは,シャドウマップアーティファクトの分類を示します。その際に,アーティファクトを処理するよう設計されている様々な既存アルゴリズムを示します。
2.1 A classification of shadow map artifacts
シャドウマップはサーフェイス上のライトの可視性を計算するために時間と空間の両方において離散的なサンプルを使用します。サンプリング手法としては,サンプリングアーティファクトを起こしやすいです。図2.1はそれらのアーティファクトが任意の1次元の信号を表現するために離散サンプルを使用した時に発生しうるいくつかについて図示しています。エイリアシングはサンプル周波数があまりにも低く高周波の詳細をとらえることが出来ないときに,高周波が周波数が低いアーティファクトとして目立つ際に初期サンプリングによって導入されます。その他の誤差はサンプルされた信号を再サンプリング化する際に発生する可能性があります。概念上は,再サンプリング化は追加的な離散サンプルが描画されるサンプルからの区分的な連続信号を再構築します。両方のフィルタは再構築のために使用され,周波数の再サンプリング化は出力に影響する可能性があります。
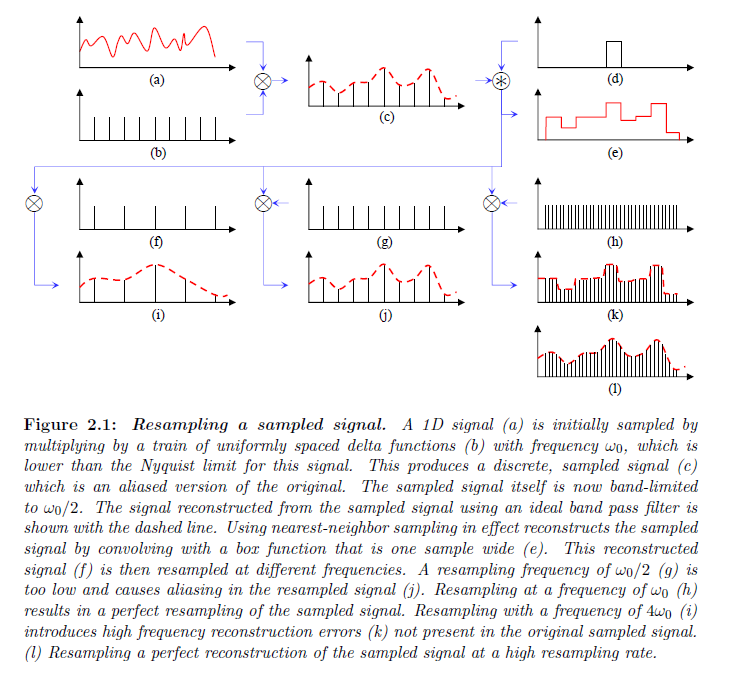
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.25 より引用。
ハードエッジシャドウに関して,ライトの可視性は0または1であるバイナリ値の区分的な連続信号として考えることが出来ます。シャドウマップは,各サーフェイスにおいて直接的に”可視性の信号”をエンコードしません。代わりに,シャドウマップ深度圧縮からの結果としてのバイナリサンプルは可視性の信号を再構築するために使われます。図2.1における1次元信号の例と同様に,シャドウマップのレンダリングは,初期サンプルと考えることができ,画像レンダリング中に生成されたシャドウマップクエリは再サンプリングと考えることができます。
最終的には,シャドウマップの誤差は連続的な値を表現するために離散的な値を使用することから生じます。以下は誤差となる様々なものの一覧です:
- 初期サンプリングエイリアシング:シャドウマップを描画するときに,幾何形状的な特徴が有限解像度のシャドウマップによって捕捉されるよりも高い空間的周波数を持つ場合にエイリアシング誤差が発生する可能性があります。例えば,数平方マイルを覆うシャドウマップ中の松の木の針状葉などです。エイリアシングはシャドウにおける不自然な模様や特徴の欠損を招きます。ハードエッジシャドウを与えるシルエットエッジは完全な再構築を可能するには決して十分にサンプルされない無限大の高周波を含みます。
- 再サンプリング化誤差:画像を描画するときに,異なる周波数においてシャドウマップの様々な部分が再サンプリングされます。例えば,観測者に近いシーンの部分においてはシーンの遠く離れた部分よりも高い周波数にて再サンプルされます。再サンプリング周波数が初期のサンプリング周波数と合致しないときに,2つの種類の誤差が引き起こる可能性があります:
- ●エイリアシング:再サンプリング周波数が初期サンプリング周波数よりも低いときにシャドウマップ上で高周波はエイリアスを特徴づけます。
- ●再構築誤差:再サンプリング化の間,シャドウマップ上で最も近いサンプルは各クエリされた位置における可視性を評価するために使用されます。もし,サンプリング周波数が初期サンプリング周波数より高い場合に,連続したクエリ数はシャドウの境界においてよく知っている階段状のエッジアーティファクトの結果として同一のシャドウマップサンプリングに使われます(図1.6参照)。これらのアーティファクトは一般的にエイリアシングとして呼ばれていますが,厳密に言えば再構築誤差として正確には記述されます(Glassner, 1995, pg. 344)。真のエリアシングは高周波エネルギーがアンダーサンプリングのために低周波として表現されるときに発生します。これらのアーティファクトは再サンプリングがシャドウマップをオーバーサンプルする領域において発生します(図2.1参照)。実際には近傍再サンプリングはボックス関数でシャドウマップを畳み込み,シャドウマップ上でもともと表現されない高周波エッジを導入します。完全な再構築は,低周波信号でより良い滑らかさを生成します。これは依然として正確な結果を与えるものではありませんが,滑らかな信号は半影に似ているので,多くの場合ギザギザな再構築誤差よりも好まれます。信号の平滑化は実際には再構築誤差の代わりに初期サンプリング誤差となります。シャドウマップ上でサンプルされた信号は初期サンプリング周波数が再サンプリング周波数に一致する場合に,近傍再構築であっても忠実に再サンプリング化することができます。
- 評価誤差:シャドウマップは離散的に表現されるので,サンプル点間の可視性は近傍のサンプルから評価されなければなりません。この評価が不正確なときに,誤差が発生する可能性があります。評価誤差は自己シャドウイングのアーティファクトとしてあらわれます。
- 深度量子化誤差:シャドウマップはある限られた精度で深度を格納します。シャドウマップクエリがサンプルと正確に一致している場合であっても,深度量子化は自己シャドウイングのアーティファクトを招く恐れがあります。
- 時間的誤差:前述のアーティファクトのいずれかが画像上に存在する場合に,フレーム間で一貫性がないときに時間的誤差を招く可能があります。例えば,エイリアシングは影のちらつきを引き起こす可能性があります。シーン上でライトまたはオブジェクトがゆっくり動くときに,再構築誤差によるギザギザなシャドウエッジは”クロール”するように現れます。素早く動く際は,この効果はより目立ちにくくなります。
これらの誤差は図2.2と2.3で示されます。シャドウマップにおける研究の多くの目的は元々のアルゴリズムが提案されてから,これらの誤差を解決するためのものです。初期サンプリング,再サンプリング,そして評価誤差を処理するために提案された手法についてこれから説明します。
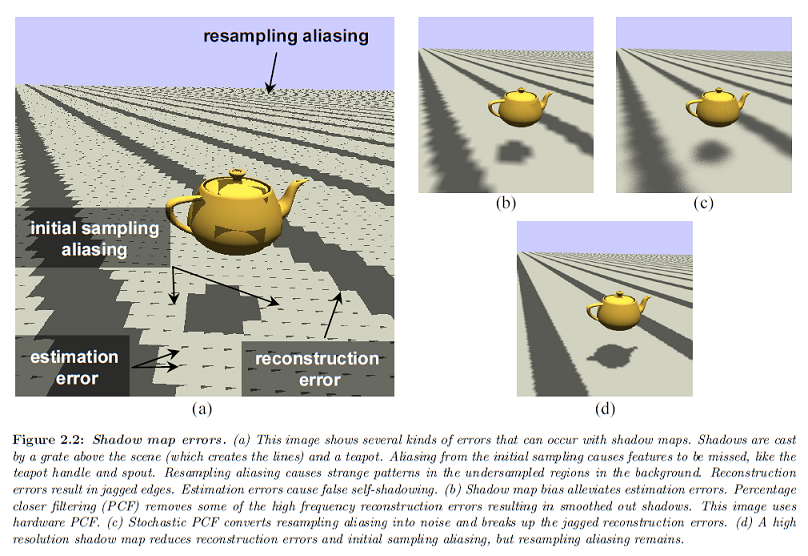
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.28 より引用。
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.29 より引用。
2.2 Handling initial sampling errors
初期サンプリングのエイリアシングは,すべてのサンプリング技法について問題となります。ある初期サンプリングエイリアシングのアーティファクトは幾何形状の単純化と高周波成分を削除する詳細度制御の使用を通じて幾何形状を”事前フィルタリング”することによって緩和される可能性があります。例えば,いくつか穴がある平面の影を遠くに投げかける場合に,穴のいくつかはサンプルされ可能性があり,いずれかはサンプルされる可能性があり,時間的誤差を招きます。もし穴が十分に小さい場合には,遠くからは見えないので,アーティファクトを避けるためにオブジェクトはソリッド平面に簡略化されるかもしれません。けれども,一般的には正確に高周波幾何情報を捕捉する唯一の方法は,シャドウマップの分解能を増加させることです。
初期サンプリングのエイリアシングを取り扱うための他のアプローチは,確率的サンプリングを使用することです(Cook, 1986)。低周波のエイリアシングを拡散させる確率的サンプリングは高周波ノイズへと形成させます。人間にとっては,ノイズはあまり好ましくありません。Akenine-Möllerら(2007)は時間内に確率的に三角形をラスタライズ化するためのハードウェアアーキテクチャを提案しました。これは,モーションブラーがかかったシャドウを描画することによってテンポラルエイリアシングを減らすために使用することができます。
2.3 Handling resampling errors
標準的なテクスチャマッピングは,フィルタリング技法によって再サンプリング誤差を処理します。再サンプリングエイリアシングは,例えばミップマップ(Williams, 1983)や範囲総和テーブル(Crow, 1984)のような技法を用いてテクスチャマップを事前フィルタリングすることによって効率的に処理することができます。再構築誤差は典型的にはサンプル値間のバイリニアや高次の補間で処理します。ですが,これらの手法はシャドウマップで直接的に使用することはできません。シャドウマップは各サーフェイスに対して可視性が同一ではないので,直接的には可視性を記録しません。代わりに,各サーフェイス上でそれぞれに可視性のシグナルを計算するために深度比較が使用されます。深度比較は非線形であるので,標準的な手法は正確に動作しません。例えば,高周波シャドウを含む観測者から離れた画像上の領域を考えます。シーンの範囲上で単一ピクセル内に落ちるシャドウとされる領域と非シャドウとされる領域が変わるかもしれません。ピクセルの範囲上の適切なフィルタリング化によるライトの可視性は0と1の間のどこかになります。サーフェイス上の可視性のシグナルが格納されていた場合に,ミップマップはこの結果を与えます。代替えとして深度を格納します。このときミップマップ化された深度値は返り値が0または1のみである深度比較を実行します。深度値と比較を行う深度のバイリニア補間をする場合も同様です。
再サンプリング誤差はシーンのより良い再構築手法とより良い初期サンプリングを用いて処理できる可能性があります。一般的には,これらの技法は直交であり,大抵組み合わされて使われます。
2.3.1 Improved reconstruction methods
近傍比率フィルタリング(PCF)(Reevesら,1987)は最初にシャドウマップクエリの近傍のサンプルの可視性を計算し,その結果をフィルタします。PCFは近傍を再サンプリングするための適切なサイズ選択することによって再サンプリングエイリアシングと再構築誤差の両方を扱うことが可能です。再サンプリングエイリアシングを処理するために,理想的には近傍はシーンへと投影する生成されたクエリのピクセルと一致すべきです。エイリアスがある領域については,近傍は多数のシャドウマップサンプルで覆われます。一方で,再構築誤差が発生する領域については,近傍は単一のシャドウマップテクセルよりも小さくなります。そのような小さな近傍でのフィルタリングは改善が見られません。したがって,近傍のサイズは1テクセルよりも大きいある最小限にクランプされるべきです。大きな近傍を使用することはギザギザなシャドウエッジをぼかします。この効果はソフトシャドウの半影に似ており,視覚的に満足がいく可能性があります。ですが,遮蔽物からの距離が変化しないので正しい半影ではありません。PCFにおいてより多くのサンプルが使うと,エッジはより滑らかになります。現在のGPU上でのPCFのハードウェア実装は確率的サンプリングの代わりにバイリニア補間を使用しています。これはシャドウがある領域からシャドウがない領域への滑らかな変化を生み出しますが,シャドウエッジに沿ってあるブロック性が存在します。図2.2は,フラグメントプログラムを用いて適用したネイティブハードウェアのPCFと確率的なPCFの両方を示しています。
シルエットシャドウマップ(Senら,2003)はシャドウキャスターのシルエットエッジの位置についての追加の情報を持つシャドウマップを増大させることによってハードエッジを再構築します。描画されるシルエットエッジはテクセル内に落ちるエッジに沿った単一点の座標として各テクセルにおいてシャドウマップへと格納されます。シャドウマップクエリの近傍における点の座標はシルエットエッジを再構築するために使われます。深度情報は再構築されたエッジのサイドがシャドウとされるかシャドウとされないかどうかを位置するクエリを決めるために使用されます。テクセルごとに一点だけが格納されるので,複数のエッジが同じテクセル内に落としこまれるときに誤差が発生します。
分散シャドウマップ(Donnelly & Lauritzen, 2006)はテクセル内の深度分布の近似を保存します。これらの値は標準的なテクニックでフィルタすることができます。分散シャドウマップは,平面のレシーバーに平行な平面の遮蔽物に対してPCFを行った正確な結果を計算します。その他の設定について,フィルタされた遮蔽されていない領域の割合に基づき上限を与えますが,実際には大体うまく動作します。しかしながら,深度中の分散は高いときに,分散シャドウマップは光がシャドウへと漏れる奇妙なアーティファクトを引き起こす可能があります。
畳み込みシャドウマップ(Annenら,2007)は深度値の代わりに可視関数の近似を保存します。深度比較によって生成される可視関数はHeavisideの階段関数として表現することができます。この関数は,フーリエ基底関数で展開されます。表現の利点はシャドウマップが事前フィルタすることができるので,非線形深度比較が”線形化”することができるということです。畳み込みシャドウマップは多数の基本画像を生成するために通常のシャドウマップによって構築されます。事前フィルタ化は事前フィルタした基本画像によって単純に可視関数を適用することが出来ます。このアルゴリズムの欠点の1つは,ハードエッジを得るために多数の基本画像が必要とされる可能性があることです。
Scherzerら(2007)は,テンポラルスムージングとシャドウエッジをより正確な再構築の両方を与えるために前フレームからのシャドウイングの情報を再利用しました。ヒストリーバッファは各ピクセルに対して最後のフレームにおけるフラグメントの視空間深度と同じように前のフレームの結果に対するシャドウマップクエリの重みづけ平均を画像上に保存しています。ヒストリーバッファは,各フレーム後にバッファの以前の値と現在のフレームに対してシャドウマップから計算されたクエリ結果の重みづけ結合によって更新されます。更新されたヒストリーバッファはシャドウマップを描画するのに使われます。クエリ結果の重みは各ピクセルごとに独立して計算されます。各フラグメントは,前のフレームの視空間へと逆変換され,その深度はヒストリーバッファ上に保存されたものと比較されます。深度がユーザーが指定した許容内である場合には,前のヒストリーは重み0がアサインされ,現在のフレームに対するクエリ結果は重み1がアサインされます。これは非遮蔽を扱う性質上必要があるのためです。一方で,重みは現在のクエリ結果の確実性を用いて計算されます。この確実性はシャドウマップの上のテクセルに一致する中心からのクエリ位置の距離に基づいています。中心から離れたクエリ位置は正確性が低くく,ヒストリーバッファ上で低い影響度を持つので,これらのクエリの結果として低い確実性がアサインされます。各フレームについてシャドウマップのジッタリングすることは,時間に関して,ヒストリーバッファが正確なシャドウエッジに収束することになり高い確実性の結果を示します。しかしながら,アルゴリズムはオブジェクトの移動や光源の移動によりシャドウが移動するため収束しない可能性があり,過度な平滑化やひどいシャドウを招きます。
2.3.2 Improved sampling methods
サンプルの数を増加させることなく再構築誤差を処理する他の方法は,シャドウマップの描画においてより良いサンプル分布を使用することです。シャドウマップクエリの分布に合うより密な初期サンプリングは,再構築誤差がより低いです。より良いサンプリングはシーンの一部に関係がある,シャドウマップのワーピング,パーティショニング,そしてイレギュラーサンプリングシャドウマップをフィルタリングすることによって得ることができます。これからこれらのアプローチを説明します。
2.3.2.1 Shadow map fitting algorithm
シャドウマップのフィッティングは向きと,その空間と深度解像度を最大化するためにシャドウマップを描画するのに使われるライトの錐台の空間的な範囲の選択から構成されます。Brabecら(2002)は深度の範囲とシャドウマップの空間的な範囲がシーンの可視可能な部分に制限することができるということに気づきました。深度解像度を最大限利用するために,ライト錐台のニア平面とファー平面を可視オブジェクトを密接に囲うように設定しました。ライトとニア平面間の遮蔽物の深度は0にクランプされます。従って,遮蔽は可視領域に対して利用可能な深度解像度を最大化すると同時に,シャドウマップ上で表現されます。シーンの可視部分上の境界を得るために,射影テクスチャリングを用いて視錐台内に存在する領域を記すためにライト位置の視点からのシーンを描画します。その結果はリードバックされ,可視領域に対して最もタイトでフィッティングしているバウンディングボックスを計算するために使用されます。GPUからのリードバックはコストが高い傾向があります。より安価ではあるものの,可視領域上のタイトな境界を得るための正確性が劣る方法は視錐台とシーンのバウンディングボックスと,ライトの空間的境界の制限を持つスポットライトのようなライトに関しての交差を計算することです。
MartinとTan(2004)が気づいたように,可視領域の最もタイトなバウンディングクワッドはあるフレームから次のフレームへでいつも連続的に変化するとは限りません。シャドウマップの解像度がエイリアシングと再構築誤差を除去するのに十分高い場合,バウンディングクワッドの向き上の不連続シフトはシャドウ上で気が付く変化を生み出さないかもしれません。しかし,シャドウマップ解像度上の制限のために,変化が連続ではないときに”ポップ”として目に見える誤差に大抵なります。MartinとTanはシャドウマップがカメラの視線方向とシャドウマップの軸の一つに整列させることによって視錐台に対して配向することを提案しました。この提案は,ライトとカメラが移動するような再構築誤差アーティファクトについての適応に一貫性があります。このアプローチが抱える問題の1つはカメラがゆっくりと移動するときに,静的ライトを持つ静的オブジェクトからの影上のギザギザのエッジはまだ “クロール”が見えることです。シャドウは固定されたままでなければなりません。この問題は、ワールドの軸の一つとシャドウマップの向きを整列させ、シャドウマップのテクセルのワールド空間幅に対応する単位でフレームからフレームへとシャドウマップの範囲をシフトすることによって回避することができます。しかしながら,ギザギザなエッジはオブジェクトが移動するとき,またはライトが動くときにまだクロールします。移動するカメラを持つ静的なシーンについて,複数のフレームにわたって再利用できるかもしれないので,必要不可欠なものよりも大きいシャドウマップを描画することは望ましいかもしれません。
2.3.2.2 Warping algorithms
Brabecら(2002)は,無指向性光源に対して非線形ワーピングを使用しましたが,シャドウマップ誤差を修正する目的のためではありませんでした。再構築誤差を減らすためのシャドウマップワーピングの利用は最初に,透視シャドウマップ(PSMs)(Stamminger & Drettakis, 2002)で導入されました。PSMはカメラの透視変換後の空間で描画されます。透視変換後の空間では,観測者に近いオブジェクトは大きくなり,遠いオブジェクトは小さくなるので視錐台はキューブへと歪められます。この空間でのシャドウマップは観測者近くのサンプル密度は増加します。正確なワーピングはシャドウマップの射影行列が設定される方法に依存します。そして,元々の論文ではこれは明示的に示されていません。著者のウェブページに視錐台キューブの中心を中心とした透視投影を用いたPSMについての”レシピ”が載せられています。異なる画像平面の角度を持つ射影を用いて異なるワーピングが生成されます(Appendix A参照)。透視変換後の空間で動作するカメラは透視変換によりある有限の点が無限平面へと位置付け,逆もまた同様であるという事実により複雑です。これが意味するのは,方向光源が点光源になる可能性があります。逆についても同様で,線に沿った深度の順番が逆転し,無限遠での平面周囲のカメラの後ろの遮蔽物が包み隠されます。後者の問題を回避するために,PSMsは透視変換後の空間においてすべてのオブジェクトが前に位置し,シーンの可視部分を遮蔽するのに十分なだけ後ろに戻った視点位置である仮想カメラの中で描画されます。Kozlov(2004)は仮想カメラのシフトを避けるようにするために無限遠での平面周囲を包み込むことが可能であるシャドウマップの射影行列についての公式を提案しました。
ライト空間透視シャドウマップ(LiSPSMs)(Wimmerら, 2004)は透視変換後の空間の難しさを避けるPSMsの一般化です。LiSPSMsはライトの方向に垂直で,視線方向に沿った方向の透視投影を用いてシャドウマップを歪めます。点光源に対して,最初にライトの位置が無限遠に移動し,方向光源になるようなライトの射影行列が適用されます。このときに,透視ワーピングが適用されます。ワーピングの強さは透視
投影のニア平面の距離\(n’\)によって制御されます。俯瞰のディレクショナルライトについては,PSMを使用する際と同等の視錐台のニア平面の距離に等しくなるような\(n’\)を設定します。\(n’ = {\infty}\)を設定することは,標準のシャドウマップを生成します。LiPSMsは眼の視線方向に調整されたシャドウマップの面積に沿った最大エイリアシング誤差を最小化するパラメータが使用されます。
台形シャドウマップ(TSMs)(Martin & Tan, 2004)はワーピングパラメータについて異なる定式を使用するということ除いてLiSPSMsに極めて似ています。TSMsはシャドウマップのユーザーが指定した比率(例えば0.8)にユーザーが指定した視野錐台の比率(例えば0.5)を写像するヒューリスティックを使用してワーピングパラメータを計算します。この方法では,より多くのシャドウマップのサンプルが観測者に近い領域にあてることが可能です。
これらの手法のすべてにおいて欠点の1つは,すべてのライト位置に対してワーピングが効果的ではないということです。方向光源に対して,ワーピングはいパン的に視線方向に対して垂直なライト位置について最も効果的です。ライト方向と視線方向の間の角度\({\gamma}\)が0に近づくと,PSMは標準のシャドウマップに戻します。LiSPSMsもまた\({\gamma}\)の関数としてワーピングを離れて傾斜することによって過剰な誤差を避けるために標準のシャドウマップに戻します。
ChongとGortler(2004)は画像中のピクセルとシャドウマップ上のテクセルの間が一対一に一致するのを確証するためにシーン内の単一平面のみに一般的な射影変換を使用しました。彼は突出した平面サーフェイスのいくつかを覆うために少ない数のシャドウマップを使用しました。
ChongとGortler(2006)もまたシーンを描画するために最適な透視投影を計算するフレームワークを提案しました。彼は以前の手法の透視ワーピングがライトの視線方向に直交な画像平面で標準的なシャドウマップを描画するのに等しいということに気づきました。その手法は,シャドウ境界に近いピクセルについて誤差尺度を計算することに従った画像平面の方向を最適化します。これらのピクセルはGPUからの読み戻しとCPU上でそれを解析することでシャドウを持つシーンの低解像度な画像を描画することによって見つけることが出来ます(ワーピングと画像平面の方向に詳細についてはAppendix Aを参照してください)。
2.3.2.3 Partitioning algorithms
パーティショニングアルゴリズムはシャドウマップのサンプル分布を制御するために複数のシャドウマップを使用します。いくつかのアルゴリズムは,z分割と呼ばれる,z軸(視線方向)に沿って視錐台をサブ錐台へと分割し,それぞれに対して分割したシャドウマップを描画するアプローチを使用しています。複数のサンライトバッファ(Tadamuraら,1999)は太陽からの半影を持つシャドウのオフラインレンダリングに対してこのアプローチを使用しました。彼らは,カメラ視点からの距離に幾何学的に増加する間隔で視錐台を分割しました。カスケードシャドウマップ(Engel, 2007)は類似した技法ですが,リアルタイムアプリケーションで使用することを意図しています。平行分割シャドウマップ(PSSMs)(Zhangら,2006a)は幾何学的なものと均一なものの間隔を用いて生成された分割位置の平均を用いて視錐台を分割します。
Kozlov(2004)はPSMsを改善する手法としてカメラの透視投影後の空間でキューブマップを使用しました。分割されたシャドウマップは,透視投影後の視錐台の単位キューブのバックフェースにフィットします。ワールド空間上では,これは透視投影で歪められたシャドウマップが側面に一致し,標準的なシャドウマップが端面に一致することに相当します。我々はこれを面分割と呼びます。単一シャドウマップのワーピングに関してこのアプローチの利点はワーピングがすべてのライト位置に対して使用することが可能であるということです。
z分割と面分割は単に視錐台に基づいており,シーン上のサーフェイスの位置や向きは考慮していません。適応的分割スキームは解像度が必要とされる場所でシャドウマップを改善し,それゆえ高品質なシャドウを生成する傾向があるためこれらの要因を考慮することが可能です。
適応的シャドウマップ(ASMs)(Fernandoら, 2001)は固定解像度のタイルの四分木としてシャドウマップを表現しました。四分木はシャドウエッジの近い所が漸進的に改善します。各イタレーションで,アルゴリズムはシーンを描画し,アルファチャンネル上に投影された領域のシャドウマップのテクセルをエンコードするために特殊なミップマップテクスチャを用いてカラーチャンネルへとポリゴンIDをエンコードします。結果画像はリードバックされ,シャドウマップが改善されるべきかどうかを決定するためのコスト測定尺度を用いて解析されます。
解像度適合シャドウマップ(RMSMs)(Lefohnら, 2007)もまたシャドウマップのタイルを格納するために四分木を使用します。しかしながらASMsと違って,四分木はシャドウエッジにおいて反復的に改善されません。代替として,各ピクセルにおいて十分な解像度を持つ四分木全体が各フレームごとに生成されます。カメラ視点からのビューは最初にページと呼ばれる十分な解像度のタイルを求めて各ピクセルに対してエンコードするフラグメントプログラムを用いて描画されます。同一平面上の隣接するピクセルに対するページのリクエストも同様です。RMSMsはCPUへ読み戻しする前に重複したページのリクエストを効率的に削除するためにこの時間一貫性を活用します。空間的に隣接するページはこのときにスーパーページへとビニングすることによって一緒にグループ化されます。アルゴリズムはスーパーページを描画し,四分木へと関係するページをコピー出力します。RMSMsは適応的シャドウマップに勝るいくつかの利点を持っています。RMSMsはGPU上でシーン解析を行います。GPU上では,リードバックのサイズを非常に減らせます。ASMsは低解像度画像を描画することによってこのコストを減らしますが,いくつかのシャドウエッジの欠落を引き起こす可能性があります。またRMSMアルゴリズムは動的なシーンについてより適切です。ASMの品質は四分木が各フレームごとに無効になり,品質が収束する前に多数のフレームが必要とされるので,ライトが移動するときに極めて低下する可能性があります。シャドウエッジにおいて改良をしないことによって,RMSMsは増加メモリ要求のコストで高品質なシャドウの高速な生成をトレードオフします。
クエリ仮想シャドウマップ(QVSMs)(Giegl & Wimmer, 2007b)は四分木の改良に基づく他の適応的分割スキームです。QVSMsは最初に四分木のルートにおいて単一のシャドウマップタイルを用いてシャドウを描画します。シャドウマップは4つのサブタイルへとリファインされ,各サブタイルごとにシャドウが更新されます。ピクセルの数の変化を数えるためにオクル―ジョンクエリが使用されます。サブタイルは変更されたピクセルの数がユーザーが指定した閾値を下回るまでさらにリファインされます。また,QVSMsはより良い品質を達成するためにワーピング(LiSPSM)を使用します。高いコストであるシーンの描画の繰り返しを避けるために,QVSMsはシャドウマップクエリの位置を計算するために視空間深度バッファを使用したディファードシェーディングの変形を使用します。このアプローチは大きな柔軟性を提供できる一方で,またタイルをキャッシュすることができず,複数のフレームで再利用できないということも意味しています。
調和仮想シャドウマップ(FVSMs)(Giegl & Wimmer, 2007a)は四分木がより粗粒されることを除く,RMSMsに似た非反復の四分木分割を使用します。RMSMsは32×32のタイルサイズを使用します。FVSMsは最大割り当て可能なテクスチャサイズ(4096×4096)までのタイルを使用します。シーンの解析はGPUから読み戻した画像上でエンコードされた情報を用いてCPU上で実行されます。CPU上で解析を行う利点は,四分木をリファインところを決めるためにより洗練されたアルゴリズムを使用可能であることです。エンコードされた画像はリードバックのコストを最小化するために低解像度(256×256)で描画されますが,重要な情報が欠落する可能があり,誤差を招きます。QVSMsのように,FVSMsはシャドウに対してディファードシェーディングを使用します。
タイルドシャドウマップ(Arvo, 2004)は単一で,固定解像度のシャドウマップを帰納的な誤差測定によって導かれる異なるサイズへと分割する適応的スキームです。これは、単純なデータ構造をもたらしますが,一部のタイルが過度に圧縮されたりまたは一方あるいは両方の方向に沿って細長くなる場合があります。Chong(2003)は誤差尺度を最小化するために最適化されたワーピングと組み合わせた欲張り分割スキームを使用して2次元シーン上に1次元のシャドウマップを描画するアルゴリズムを提案しました。不運にも,このアプローチは3次元に一般化するには難しいです。Forsyth(2006)は欲張りアルゴリズムを使用して複数のライトの錐台に類似のサンプリング密度を必要とするオブジェクトをクラスタ化する分割技法を提案しています。しかしながら,この手法は光源からの距離のみに基づいています。従って,サーフェイス方向によりエイリアシングを処理することができません。
2.3.2.4 Irregular sampling
イレギュラーZバッファアルゴリズム(Johnsonら,2004; Aila & Laine, 2004b)についてのサンプル位置は明確に指定することできます。シャドウマップのサンプル位置のようにシャドウマップクエリの位置を選択することによって,再構築誤差を完全に排除することが可能です。このアプローチの主要な欠点は、それが効率的に実装される(Jhonsonら, 2005)ためにグラフィックス・ハードウェアに根本的変化を必要とする不規則なデータ構造を使用するということです。
2.3.3 Object-space hybrids
シャドウボリュームのような純粋なオブジェクト空間のシャドウアルゴリズムは,再サンプリングの問題を持ちません。一部のハイブリッドアルゴリズムはエイリアシングを減らすためにオブジェクト空間の技法とシャドウマップを組み合わせます。McCoolら(McCool, 2000)はシャドウマップ中でエッジを探索し,シャドウボリュームを構築するためにこれらを使用しました。シャドウマップの画像ベースの表現は暗黙的に遮蔽物の融合を行います。これはそのほかのシャドウボリューム内で生成された冗長なシャドウボリュームを排除し,フィルレートの消費を減らします。ChanとDurand(Chan & Durand, 2004)はシャドウエッジに近い領域のシャドウボリュームの描画を制限するためにシャドウマップを使用しました。これらの両方の手法はアーティファクトフリーなエッジを生成しますが,シャドウマップの解像度が不十分である場合に小さな特徴が欠ける可能があります。Govindarajuら(2003)は最悪なアーティファクトを持つ画像上の領域やシャドウマップの至る所でシャドウポリゴンを使用しました。
2.4 Handling estimation errors (self-shadowing artifacts)
標準的なシャドウマップはサンプルされたシーン上で遮蔽されているフェースを表すものを格納します。遮蔽表現のある距離内では,シャドウマップクエリはサンプリングと深度値の量子化によって離散化が引き起こされるため確実に計算することができません(図2.4参照)。これは間違った自己シャドウイングを招きます。Williams(1978)は自己シャドウイングのアーティファクトを回避するようにするために実物の遮蔽物のサーフェイスから十分に離れた遮蔽表現を押す効果になる深度値に固定バイアスを加算しました。あまりにも小さすぎるバイアスを選択すると問題を訂正することができず,一方であまりにも大きすぎるバイアスを選択するとシャドウの位置の目立つシフトを引き起こし,シルエットエッジ周囲に光が”漏れる”ということを引き起こす可能性があります。単一の固定バイアスは一般的なシーンには適しておらず,必要なバイアスの量は多角形の深度勾配に比例します。代わりに,バイアスは深度傾斜を考慮してされるべきです。
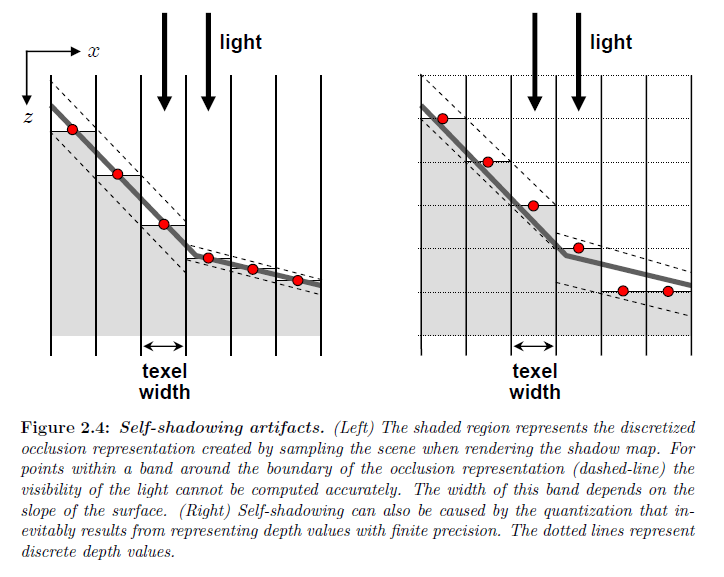
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.39 より引用。
Woo(1992)はシーン中のサーフェイスから離れた遮蔽表現を保つために最初と次の深度レイヤーの中間点を保存しました。遮蔽表現がサーフェイスに近づくシルエットエッジ付近は誤差を起こす可能性があります。WangとMolnar(1994)はシャドウマップ上にセカンドサーフェイスの深度を保存しました。このテクニックは閉じたオブジェクトのセカンドサーフェイスが裏に面しているという観測に基づいています。たとえ,セカンドサーフェイス上のクエリに対して結果が間違っていたとしても,ライティング方程式はどっちみちシャドウであるとしてサーフェイスを陰影づけます。この手法もまたシルエットエッジ付近で問題があります。2層シャドウマップ(Weiskopf & Ertl, 2003)はこれらのアプローチを一般化し,最初と次のフロントに面した深度レイヤーの関数に基づいてバイアスを計算します。
勾配シャドウマップ(Schüler, 2006)は深度比較を実行する前に隣接するクエリ位置に対する深度値をバイリニア補間します。これはより適切な遮蔽表現を生み出します。補間は深度の不連続性を横切って遮蔽サーフェイスを生成しますが,引き起こされた誤差は離散化によって生じたものよりも悪くありません。毛羽だった深度テストは誤差が発生した時に自己シャドウイングアーティファクトが目立ちづらくなる遮蔽表現の境界付近の範囲上で0から1への転移します。アルゴリズムはバイアスを計算するために勾配を使用します。Grant(1992)は深度値の代わりに遮蔽物のサーフェイス平面方程式を格納することによって,より適切な遮蔽表現を計算しました。このアプローチは複数のプリミティブによって覆われたテクセルに対して問題があります。なぜかというと,ピクセルごとに保存される平面方程式が1個のみであるからです。HourcadeとNicolas(1985)は深度値の代わりにポリゴンIDを格納しました。ポリゴンIDは深度比較として同じ不正確さを対象としません。各テクセルごとに1つのIDが保存されるので,1つ以上のポリゴンによってテクセルが覆われるときに誤差はまだ起こる可能性があります。オブジェクト全体に対して単一のIDを使用することは自己シャドウイングの問題がポリゴンからのオブジェクト境界へと移動させますが,この時に正しい自己シャドウイングを得るために異なるIDを持つ凸片へと分解することに注意しなければいけません。
Brabecら(2002)は,利用可能な深度範囲をシーンの可視部分に密にフィッティングすることによって深度値の量子化によって引き起こされる自己シャドウイングを解決しました。また彼らは範囲内で均一な分布を得るために深度値を再マップしました。これが必要になるのはなぜかというと,点光源に関してシャドウマップを描画するために使われる透視投影が分配する深度値が \(1/z\) に比例するためです。これが深度値のほとんどがニア平面に近くにまとまって割り当てられ,その他の場所で大きな量子化誤差が発生します。深度値の再マッピング化は最大量子化誤差が最小化され,深度範囲全体上で量子化誤差が均一に分配されることを確実にします。
2.5 Summary
シャドウマップの誤差を解決するために多く手法が提案されていますが,リアルタイムアプリケーションに対して複雑で,動的なシーン上で高品質なハードエッジシャドウを現在提供する技法は1つもありません。
効果的なシャドウマップアルゴリズムは、おそらくこの章で示された技術のいくつかの組み合わせが必要になります。幸運にも,これらのテクニックの多くはコストがかかりません。例えば,バイアスはサンプル間の空間がより小さくなる傾向があるのでワーピングやパーティショニングのようなサンプルの再分布技法を用いたときに自己シャドウイングアーティファクトがより小さくするのを可能にするのを処理するために使われます。けれども,これ他のテクニックを持つフィルタリングを組み合わせることはより複雑である可能性があります。ワーピング技法では,サイズやフィルタカーネルの形状でさえシャドウマップ上で変化させる必要があります。分割スキームについては,パーティションの境界付近で正確にフィルタされた結果を得るのと同じように,わずかにパーティションが重なるためケアを行う必要があります。
対数透視シャドウマップは,リアルタイム·アプリケーションのための高いシャドウマップの品質への一歩です。適切なハードウェアサポートと,それらは既存のワーピングアルゴリズムの同様の良好な性能特性を有しますが,より高い品質を提供します。